Stochastische Analysis

Die stochastische Analysis ist ein Teilgebiet der Mathematik, genauer der Wahrscheinlichkeitstheorie. Sie beschäftigt sich mit der Verallgemeinerung von Begriffsbildungen, Aussagen und Modellen der Analysis auf stochastische Prozesse, also auf Funktionen, deren Werte zufällig sind. Im Zentrum der stochastischen Analysis stehen die Formulierung und die Untersuchung von stochastischen Integralen und, darauf aufbauend, von stochastischen Differentialgleichungen.

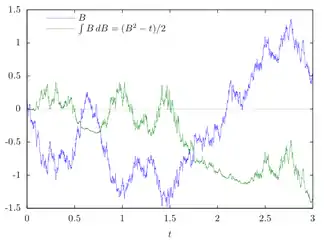
Ein Pfad des Wiener-Prozesses (blau) und eines damit berechneten stochastischen Integrals (grün)

Historisch geht das Fachgebiet auf Arbeiten des japanischen Mathematikers Kiyoshi Itō ab 1944 zurück. Der wesentliche Impuls dafür war die mathematische Beschreibung des physikalischen Phänomens der brownschen Bewegung durch Albert Einstein und Norbert Wiener. Dieses Modell, der Wiener-Prozess, bildet mit seinen zahlreichen bemerkenswerten Eigenschaften und Verallgemeinerungen einen Startpunkt der stochastischen Analysis. Anwendungen des Fachgebiets finden sich unter anderem in der Biologie, in der Physik und in den Ingenieurwissenschaften, vor allem aber in der Finanzmathematik. Einen ersten Höhepunkt bildete hier das 1973 veröffentlichte bahnbrechende Black-Scholes-Modell zur Bewertung von Optionen auf eine Aktie, deren Kursentwicklung durch eine stochastische Differentialgleichung beschrieben wird.

Einführung

Besonders elementar und klar treten die Begrifflichkeiten der stochastischen Analysis bei ihrem Hauptanwendungsgebiet, der Finanzmathematik, zu Tage. Dazu werden im Folgenden die Vorgänge beim Handel mit einem Finanzinstrument beschrieben, das der Einfachheit halber Aktie genannt wird und einige idealisierte Annahmen erfüllt. Insbesondere soll es möglich sein, das Finanzinstrument jederzeit in beliebigen Mengen zu kaufen und zu verkaufen.[1]

Vom Kursgewinn beim Aktienhandel zum stochastischen Integral

Der Gewinn (oder Verlust) beim Besitz von Aktienanteilen innerhalb eines bestimmten Zeitraums hängt auf offensichtliche Weise davon ab, wie viele Anteile man von der Aktie besitzt und wie sich ihr Preis, der Börsenkurs, in diesem Zeitraum ändert. Besitzt man beispielsweise $H_{1}=4{,}27$ Anteile einer Aktie mit Anfangskurs $S_{0}=106{,}12\,\mathrm {\euro}$ und steigt der Kurs, etwa innerhalb eines Tages, auf $S_{1}=107{,}58\,\mathrm {\euro}$ , so beträgt der Kursgewinn gerundet

H_{1}\cdot (S_{1}-S_{0})=4{,}27\cdot (107{,}58\,\mathrm {\euro} -106{,}12\,\mathrm {\euro} )=6{,}23\,\mathrm {\euro}

.

Nach diesem Tag könnten weitere Anteile der Aktie gekauft oder verkauft werden, sodass man nun $H_{2}$ Anteile besitzt, also zum Beispiel $H_{2}=5{,}27$ , wenn man noch eine ganze Aktie hinzukauft. Fällt daraufhin der Aktienkurs bis zum folgenden Tag auf $S_{2}=105{,}96\,\mathrm {\euro}$ , lässt sich der Gesamtgewinn innerhalb der zwei Tage durch

H_{1}\cdot (S_{1}-S_{0})+H_{2}\cdot (S_{2}-S_{1})=-2{,}30\,\mathrm {\euro}

bestimmen. Es ist somit im betrachteten Zeitraum ein negativer Gewinn, also ein Verlust eingetreten. Allgemein ist der Gesamtgewinn $G_{n}$ nach $n$ Zeitabschnitten die Summe der Teilgewinne jedes einzelnen Abschnitts:

G_{n}=\sum _{k=1}^{n}H_{k}\cdot \Delta S_{k}=H_{1}\cdot (S_{1}-S_{0})+H_{2}\cdot (S_{2}-S_{1})+\ldots +H_{n}\cdot (S_{n}-S_{n-1})

.

Dabei bezeichnet $\Delta S_{k}=S_{k}-S_{k-1}$ die Kursänderung im $k$ -ten Zeitabschnitt und $H_{k}$ gibt an, wie viele Anteile der Aktie der Aktionär in diesem Zeitraum besitzt.[2]

Die Analysis kommt bei diesen elementaren Überlegungen ins Spiel, wenn nicht mehr nur eine Folge diskreter Handelszeitpunkte, sondern alle Zeitpunkte $t$ aus einem Zeitintervall $[0,T]$ betrachtet werden. Eine Aktie hat zu jedem Zeitpunkt $t$ einen Kurs $S_{t}$ , der sich im Allgemeinen „ständig ändert“. Auch die gehaltenen Anteile $H_{t}$ können in idealisierter Weise als ein sich kontinuierlich ändernder Prozess, der sogenannte Portfolioprozess, angesehen werden. Der Gesamtgewinn $G_{T}$ während des Zeitintervalls $[0,T]$ kann dann allerdings nicht mehr durch die oben dargestellte einfache Summierung endlich vieler Teilgewinne bestimmt werden. Er ergibt sich stattdessen durch Integration des Portfolioprozesses gewichtet mit den Änderungen des Aktienkurses, als Formel

G_{T}=\int _{0}^{T}H_{t}\,\mathrm {d} S_{t}

geschrieben.[3] Eine Grundaufgabe der stochastischen Analysis ist es, solche stochastischen Integrale für möglichst allgemeine Integranden $H_{t}$ und Integratoren $S_{t}$ mathematisch zu definieren und ihre Eigenschaften zu untersuchen.

Von einem Modell für den Aktienkurs zu stochastischen Differentialgleichungen

Die Überlegungen, die zu obiger Darstellung des Gewinns als ein stochastisches Integral führen, sind so allgemein, dass sie sinngemäß für beliebige zeitlich veränderliche Größen durchgeführt werden können. Im konkreten Beispiel des Aktienhandels stellt sich daher die Frage, wie ein mathematisches Modell für die zeitliche Entwicklung des Kurses $S_{t}$ aussehen könnte. Reale Kursverläufe scheinen sich „zufällig“ auf und ab zu bewegen. Aus Sicht der Mathematik ist es also naheliegend, jedes $S_{t}$ als eine Zufallsvariable zu modellieren, also als eine Funktion, die jedem Ergebnis $\omega$ eines (abstrakten) Zufallsexperiments den Wert $S_{t}(\omega )$ zuordnet. Der Aktienkurs hängt dann sowohl vom Zeitpunkt $t$ als auch von dem Zufallsergebnis $\omega$ ab: Er ist ein stochastischer Prozess.[4]

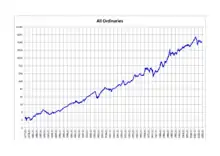
Der australische Aktienindex All Ordinaries zeigt über den Zeitraum von 1875 bis 2013 ein ausgeprägtes exponentielles Wachstum. In logarithmischer Darstellung folgt er also ungefähr einer Gerade.

In der Realität erscheinen Aktienkurse zwar zufällig, sind aber nicht völlig regellos. Über längere Zeiträume „ungestörte“ Kursverläufe weisen häufig als Grundtendenz ein exponentielles Wachstum auf, steigen also beispielsweise von Jahr zu Jahr um einige Prozent. Das zeigt sich normalerweise noch deutlicher bei Aktienindizes, bei denen über eine Anzahl von Einzelkursen gemittelt wird, wie etwa – in besonders ausgeprägter Weise – in der nebenstehenden Grafik des australischen Aktienindex All Ordinaries. Ein völlig ungestörtes exponentielles Wachstum von $S_{t}$ würde bedeuten, dass die Änderung $\Delta S_{t}=S_{t+\Delta t}-S_{t}$ in einem kurzen Zeitraum $\Delta t$ proportional zu $S_{t}$ und zu $\Delta t$ ist:

\Delta S_{t}=\mu \cdot S_{t}\cdot \Delta t

mit einer Wachstumsrate $\mu$ . Bei einem Sparguthaben entspräche dies dem exponentiellen Wachstum durch Zinseszins. Bei Aktien wird dieses Wachstumsgesetz hingegen in der Realität offenbar durch eine komplizierte Zufallsbewegung überlagert. Die Statistik und die Wahrscheinlichkeitstheorie legen es nahe, bei zufälligen Störungen, die sich aus vielen kleinen Einzeländerungen zusammensetzen, von einer Normalverteilung als einfachstem Modell auszugehen. Außerdem zeigt sich, dass die Varianz der Störungen proportional zum betrachteten Zeitraum $\Delta t$ ist. Der Wiener-Prozess $W_{t}$ besitzt alle diese gewünschten Eigenschaften, eignet sich also als ein Modell für die zeitliche Entwicklung der Zufallskomponente des Aktienkurses. Insgesamt führen diese Überlegungen zu folgender Modellgleichung für die Änderung $\Delta S_{t}$ in einem Zeitintervall $\Delta t$ :

\Delta S_{t}=\mu \cdot S_{t}\cdot \Delta t+\sigma \cdot S_{t}\cdot \Delta W_{t}

.

Dabei bezeichnen $\Delta W_{t}=W_{t+\Delta t}-W_{t}$ die Änderung des Wiener-Prozesses im betrachteten Zeitraum und $\sigma$ eine Proportionalitätskonstante, die modelliert, wie stark sich die Zufallskomponente auf die Kursänderung auswirkt, die sogenannte Volatilität.[5]

Ein möglicher Pfad einer Lösung der stochastischen Differentialgleichung zur Aktienkursmodellierung

Das weitere Vorgehen der klassischen Analysis wäre nun, das Zeitintervall $\Delta t$ gegen null konvergieren zu lassen und so eine gewöhnliche Differentialgleichung für die gesuchte Funktion zu gewinnen. Das ist hier auf diese Weise nicht möglich, denn wie sich herausstellt sind weder die Pfade des Wiener-Prozesses noch die des gesuchten Aktienkursprozesses differenzierbar, lassen sich also nicht durch klassische Differentialrechnung untersuchen. Stattdessen erhält man eine stochastische Differentialgleichung, die meist in der Form

\mathrm {d} S_{t}=\mu \cdot S_{t}\cdot \mathrm {d} t+\sigma \cdot S_{t}\cdot \mathrm {d} W_{t}

geschrieben wird. Die dabei verwendeten Differentiale sind ein reiner Notationsbestandteil und es ist Aufgabe der stochastischen Analysis, solchen Gleichungen erst einen mathematischen Sinn zu geben. Das gelingt durch die Beobachtung, dass wegen des Fundamentalsatzes der Analysis Beziehungen zwischen einer differenzierbaren Funktion und ihrer Ableitung auch mithilfe ihres Integrals geschrieben werden können. Entsprechend ist eine stochastische Differentialgleichung nur eine intuitive Schreibweise einer Integralgleichung mit einem stochastischen Integral.[6] Die stochastische Analysis beschäftigt sich unter anderem mit den Fragen, unter welchen Voraussetzungen stochastische Differentialgleichungen eindeutig lösbar sind und welche analytischen und wahrscheinlichkeitstheoretischen Eigenschaften die Lösungen haben. Für einige einfache Typen stochastischer Differentialgleichungen gibt es Methoden, um die Lösungen explizit zu berechnen. So hat zum Beispiel die oben hergeleitete Gleichung für den Aktienkurs als Lösung die sogenannte geometrische brownsche Bewegung. Wie es aber auch schon bei gewöhnlichen Differentialgleichungen der Fall ist, können bei vielen stochastischen Differentialgleichungen die Lösungen nur numerisch berechnet werden.

Geschichte

Die Anfänge: Mathematische Modelle für die brownsche Bewegung

Als brownsche Bewegung wird das physikalische Phänomen bezeichnet, dass kleine Partikel, die in einer Flüssigkeit oder in einem Gas schweben, sich auf eine unregelmäßig und zufällig erscheinende Art „zitternd“ bewegen. Sie ist nach dem Botaniker Robert Brown benannt, der sie 1827 zuerst bei der mikroskopischen Untersuchung von Pollenkörnern in einem Wassertropfen beobachtete und beschrieb. In der Folgezeit zeigten Experimente, dass die physikalische Ursache der brownschen Bewegung in der Wärmebewegung der Flüssigkeitsmoleküle liegt. Diese stoßen ständig gegen die viel größeren Partikel und versetzen sie dadurch selbst in eine unregelmäßige Bewegung.[7]

Eine zu ihrer Zeit wissenschaftlich nur wenig beachtete frühe Anwendung der brownschen Bewegung in der Finanzmathematik untersuchte der französische Mathematiker Louis Bachelier, der im Jahr 1900 mit der Hilfe von Zufallsbewegungen versuchte, die Aktienkurse an der Pariser Börse zu modellieren und damit Preisformeln für Optionsscheine herzuleiten. Er nahm damit zahlreiche Ideen aus dem erst 73 Jahre später vorgestellten berühmten Black-Scholes-Modell vorweg.[7]

Albert Einstein, 1905

Die brownsche Bewegung gelangte wieder in das Licht der wissenschaftlichen Öffentlichkeit, als Albert Einstein 1905, also in seinem annus mirabilis, ein mathematisches Modell für das physikalische Phänomen vorstellte. Er nahm darin an, dass die brownsche Bewegung, in moderner Sprechweise, ein stochastischer Prozess mit stetigen Pfaden und unabhängigen normalverteilten Zuwächsen ist, also grundlegende und aus physikalischer Sicht sinnvolle Bedingungen erfüllt. Andere, physikalisch ebenso notwendige Bedingungen setzte er jedoch nicht voraus, vor allem nicht, dass ein Teilchen in einem festen Zeitraum nur eine endliche Wegstrecke zurücklegen kann, die sogenannte Rektifizierbarkeit der Pfade. Da 1905 die maßtheoretische Fundierung der Wahrscheinlichkeitstheorie durch Émile Borel und Henri Lebesgue gerade erst begonnen hatte, konnte Einstein allerdings nicht beweisen, dass sein Modell als ein mathematisches Objekt tatsächlich existiert.[8]

Eine mathematische Konstruktion von Einsteins Modell gelang erst 1923 dem US-amerikanischen Mathematiker Norbert Wiener. Er verwendete dazu einen 1913 von Percy John Daniell entwickelten Zugang zur Maßtheorie sowie die Theorie der Fourierreihen. Bei der Untersuchung der Eigenschaften dieses, ihm zu Ehren auch Wiener-Prozess genannten, Modells zeigte sich, dass dessen Pfade nicht rektifizierbar sind. So stellte sich im Nachhinein heraus, dass Einstein genau die „richtigen“ Eigenschaften in seinem Modell ausgewählt hatte; mit der zusätzlichen Annahme der Rektifizierbarkeit hätte es mathematisch gar nicht existiert.[9]

Im Jahr 1931 fand der sowjetische Mathematiker Andrei Nikolajewitsch Kolmogorow eine Möglichkeit, stochastische Prozesse mithilfe der Analysis zu untersuchen. Er betrachtete Verallgemeinerungen des Wiener-Prozesses, die sogenannten Markow-Prozesse, und entwickelte eine Theorie zu ihrer Beschreibung. Er zeigte, dass sich diese Prozesse in einen nichtzufälligen Drift-Term und in einen rein stochastischen Anteil zerlegen lassen. Damit stellte Kolmogorow einen Zusammenhang zwischen ihren Wahrscheinlichkeitsverteilungen und bestimmten partiellen Differentialgleichungen, den Kolmogorow-Gleichungen, dar. Er verwendete dabei Methoden der klassischen Analysis; eine Verallgemeinerung von Integral- und Differentialrechnung hin zu einer „stochastischen Analysis“ fand sich bei ihm noch nicht.[9]

Der Ansatz von Itō und die weitere Entwicklung

Kiyoshi Itō, 1970

Am Beginn der stochastischen Analysis steht eine Arbeit des japanischen Mathematikers Kiyoshi Itō (1915–2008) aus dem Jahr 1944 mit dem schlichten Titel Stochastic Integral. Itō, der damit als der Begründer des Fachgebiets gilt, konstruierte darin eine allgemeine stochastische Differentialgleichung zur Untersuchung von Markow-Prozessen. Den dabei auftretenden stochastischen Differentialen gab er einen Sinn durch die Konstruktion eines neuen Integralbegriffs für stochastische Prozesse, des Itō-Integrals. In seinen folgenden Arbeiten stellte er zudem eine Verbindung zu Kolmogorows Ergebnissen her, indem er bewies, dass die Lösungen seiner stochastischen Differentialgleichung die Kolmogorow-Gleichungen erfüllen. Dazu veröffentlichte er 1951 eines der grundlegendsten Ergebnisse der stochastischen Analysis, die Itō-Formel. Diese verallgemeinert die Kettenregel, die Produktregel, die Substitutionsregel und die partielle Integration der klassischen Analysis auf stochastische Differentiale bzw. Integrale von sogenannten Itō-Prozessen.[10]

Itōs Arbeiten stellten damit den Startpunkt einer raschen Entwicklung des Fachgebiets dar, die auch heute noch anhält. Wie sich allerdings im Jahr 2000 herausstellte, hatte der deutsch-französische Mathematiker Wolfgang Döblin bereits 1940 zahlreiche von Itōs Ideen vorweggenommen. Weil Döblin, der für Frankreich im Zweiten Weltkrieg kämpfte, seine Arbeit in einem versiegelten Umschlag an die Pariser Académie des sciences schickte, seine Notizen verbrannte und anschließend Suizid beging, um der Gefangennahme durch die deutsche Wehrmacht zu entgehen, wusste jedoch 60 Jahre lang niemand von Döblins Resultaten.[11]

Paul-André Meyer, 1969

In der Folgezeit von Itōs Arbeiten lag der Schwerpunkt der mathematischen Forschung auf Verallgemeinerungen seiner Ergebnisse. Joseph L. Doob erweiterte 1953 in seinem einflussreichen Buch über stochastische Prozesse Itōs Integral vom Wiener-Prozess auf Prozesse mit unkorrelierten Zuwächsen. Doob beschäftigte sich zudem mit der Fragestellung, wie sein Zerlegungssatz für diskrete Prozesse auf den zeitkontinuierlichen Fall verallgemeinert werden kann. Dieses Problem wurde 1962 von Paul-André Meyer gelöst. Meyer zeigte, dass eine solche Zerlegung, die Doob-Meyer-Zerlegung, nur unter einer Zusatzbedingung, die er „Klasse (D)“ nannte, möglich ist.[12] Im Jahr 1970 verallgemeinerten Catherine Doléans-Dade und Meyer das Itō-Integral auf sogenannte Semimartingale als Integratoren, also auf stochastische Prozesse, die sich aus einem lokalen Martingal und einem Prozess mit lokal endlicher Variation zusammensetzen. Semimartingale sind in gewisser Weise die allgemeinste Klasse von stochastischen Prozessen, für die sich ein sinnvoller Integralbegriff definieren lässt.[13][14]

Aus Sicht der Anwendungen der stochastischen Analysis ist das historisch bedeutsamste Ergebnis das nach Vorarbeiten des Wirtschaftswissenschaftlers Paul A. Samuelson und des Mathematikers Henry McKean von Fischer Black, Myron S. Scholes und Robert C. Merton 1973 veröffentlichte Black-Scholes-Modell zur Bewertung von Finanzoptionen. Darin ist der Kurs der zugrunde liegenden Aktie durch die im Einführungsabschnitt dieses Artikels hergeleitete stochastische Differentialgleichung gegeben. Die Itō-Formel, angewendet auf den Preis einer Option als Funktion von Zeit und Aktienkurs, führt dann zusammen mit einer ökonomischen Argumentation mittels eines Hedgegeschäfts auf eine bestimmte partielle Differentialgleichung, die Black-Scholes-Gleichung. Diese lässt sich explizit lösen und ergibt somit Formeln für den Wert von Kauf- und Verkaufsoptionen auf die Aktie. Scholes und Merton erhielten 1997 für ihre Leistungen den Alfred-Nobel-Gedächtnispreis für Wirtschaftswissenschaften („Wirtschaftsnobelpreis“); Black war bereits zwei Jahre zuvor verstorben.[15]

Weitere Entwicklungen der stochastischen Analysis sind beispielsweise die stochastische Differentialgeometrie, die sich mit stochastischen Prozessen auf Mannigfaltigkeiten beschäftigt, und der Malliavin-Kalkül (nach Paul Malliavin), eine Verallgemeinerung der Variationsrechnung auf Funktionale stochastischer Prozesse.[16] Ein anderes aktuelles Forschungsthema sind Theorie und Anwendungen stochastischer partieller Differentialgleichungen.[17]

Grundlegende Begriffe, Aussagen und Methoden

Der Wiener-Prozess und seine analytischen Eigenschaften

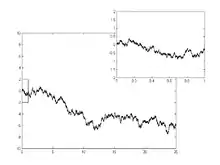
Ein Beispielpfad des Wiener-Prozesses mit einer Ausschnittvergrößerung; er ist auf allen Zeitskalen so „gezackt“, dass er an keiner Stelle differenzierbar ist.

Der Wiener-Prozess steht nicht nur historisch als Modell für die brownsche Bewegung am Anfang der stochastischen Analysis; wegen seiner zahlreichen mathematisch interessanten Eigenschaften ist er als „Grundtyp“ eines Zufallsprozesses ein zentrales Untersuchungsobjekt des Fachgebiets. Der Wiener-Prozess $(W_{t})_{t\geq 0}$ lässt sich definieren als stochastischer Prozess mit unabhängigen, stationären und normalverteilten Zuwächsen, der fast sicher stetige Pfade hat und auf $W_{0}=0$ normiert ist.[18] Aus der Definition ergeben sich zahlreiche wichtige Eigenschaften, die sich in natürlicher Weise auf allgemeinere Klassen stochastischer Prozesse verallgemeinern lassen. So ist der Wiener-Prozess ein typischer Vertreter der Gauß-Prozesse, der Markow-Prozesse und der Lévy-Prozesse.

Der Wiener-Prozess ist zudem ein sogenanntes Martingal. Der Zuwachs $W_{t+\Delta t}-W_{t}$ hat also, gegeben den aktuellen Wert $W_{t}$ , den bedingten Erwartungswert null. Vereinfacht und anschaulich ausgedrückt: Er verhält sich wie der Gewinn eines Spielers, der an einem fairen Glücksspiel teilnimmt, also an einem Spiel, bei dem sich Gewinne und Verluste im Mittel ausgleichen. Der Martingalbegriff ist ein zentrales Konzept der modernen Wahrscheinlichkeitstheorie, denn einerseits führen stochastische Modelle häufig auf ein Martingal oder können in ein solches transformiert werden, andererseits lassen sich für diese Prozessklasse zahlreiche Sätze beweisen, wie beispielsweise die Doobsche Maximalungleichung, das Optional Sampling Theorem oder die Martingalkonvergenzsätze.[19]

Die Pfade des Wiener-Prozesses sind fast sicher an keiner Stelle $t$ differenzierbar, sind also anschaulich auf allen Zeitskalen so stark „gezackt“, dass nirgends eine Tangente angelegt werden kann. Damit entziehen sie sich der Differentialrechnung im klassischen Sinne. Sie sind allerdings nach Definition stetig, sodass sie problemlos als Integrand eines klassischen Integrals auftreten können. Die Pfade des Wiener-Prozesses sind außerdem von unendlicher Variation, die Gesamtsummen ihrer Änderungen auf einem endlichen Zeitintervall sind also unbeschränkt. Das hat zur Folge, dass ein Integral mit dem Wiener-Prozess als Integrator nicht pfadweise als ein klassisches Stieltjesintegral aufgefasst werden kann; hierzu ist daher ein neuer „stochastischer“ Integralbegriff nötig.[20]

Stochastische Integrale

Im Einführungsabschnitt dieses Artikels wurde dargestellt, wie ein stochastisches Integral als ein Grenzwert von Summen aufgefasst werden kann, bei denen eine Zeitschrittweite gegen null konvergiert. Diese Überlegung lässt sich mathematisch präzisieren und führt auf diese Weise zu einer möglichen Definition eines Integrals mit dem Wiener-Prozess als Integrator, dem Itō-Integral.[21] In modernen Lehrbüchern wird jedoch meist eine etwas abstraktere Konstruktion verwendet, die mehr dem üblichen Vorgehen bei der Definition des Lebesgue-Integrals ähnelt: Zunächst wird ein Integral für elementare Prozesse, also für stückweise konstante Prozesse, als Integranden definiert. Dieser Integralbegriff wird dann mithilfe von Dichtheitsargumenten schrittweise auf allgemeinere Integranden fortgesetzt.[22] In dieser allgemeinen Form sind dann stochastische Integrale

\int _{0}^{T}H_{t}\,\mathrm {d} X_{t}

für Semimartingale $(X_{t})$ als Integratoren und adaptierte stochastische Prozesse $(H_{t})$ mit càglàd-Pfaden möglich. Beide Prozesse können also auch Sprungstellen besitzen.[23]

Analog zum Begriff der Integralfunktion in der klassischen Analysis betrachtet man auch in der stochastischen Analysis das Integral als Funktion der oberen Integrationsgrenze und erhält so wieder einen stochastischen Prozess

G_{t}=\int _{0}^{t}H_{s}\,\mathrm {d} X_{s}

oder in Differentialschreibweise

\mathrm {d} G_{t}=H_{t}\,\mathrm {d} X_{t}

.

Es lässt sich zeigen, dass $(G_{t})$ ebenfalls ein Semimartingal ist.[24] Wenn der Integrator $(X_{t})$ sogar ein Martingal ist, also zum Beispiel der Wiener-Prozess, und der Integrand gewissen Beschränktheitsbedingungen genügt, dann ist $(G_{t})$ ebenfalls ein Martingal. Das stochastische Integral lässt sich in diesem Fall also als eine zeitkontinuierliche Martingaltransformation auffassen.[25]

Die Itō-Formel

Für das Itō-Integral und seine Verallgemeinerungen gelten einige der üblichen Rechenregeln der Analysis nur in modifizierter Form. Das liegt anschaulich daran, dass wegen der unendlichen Variation des Wiener-Prozesses $(W_{t})$ bei kleinen Zeitänderungen $\Delta t$ nicht nur die zugehörigen Änderungen $\Delta W_{t}$ berücksichtigt werden müssen, sondern auch deren Quadrate $(\Delta W_{t})^{2}$ , die selbst in der Größenordnung von $\Delta t$ liegen. Die sich dadurch ergebenden „neuen“ Rechenregeln werden in der Itō-Formel zusammengefasst. Bereits in ihrer einfachsten Form wird deutlich, wie die Kettenregel für den Wiener-Prozess abgeändert werden muss: Ist $h$ eine zweimal stetig differenzierbare Funktion, dann gilt für den Prozess $X_{t}=h(W_{t})$ in Differentialschreibweise

\mathrm {d} X_{t}=h'(W_{t})\,\mathrm {d} W_{t}+{\frac {1}{2}}h''(W_{t})\,\mathrm {d} t

.

Im Vergleich zur klassischen Kettenregel erhält man also einen zusätzlichen Term, der die zweite Ableitung von $h$ enthält.[26] Die Itō-Formel lässt sich auf vektorwertige Semimartingale verallgemeinern.[27]

Die Zusatzterme dieses Itō-Kalküls machen konkrete Rechnungen mitunter aufwändig und unübersichtlich. Deshalb bietet sich für manche Anwendungsaufgaben ein anderer stochastischer Integralbegriff an, das Stratonowitsch-Integral (nach Ruslan Stratonowitsch). Sein Hauptvorteil gegenüber dem Itō-Integral ist es, dass die Rechenregeln im Wesentlichen denen der klassischen Analysis entsprechen. Insbesondere in physikalischen Problemstellungen ist daher eine Formulierung mit dem Stratonowitsch-Integral häufig natürlicher. Es besitzt jedoch einige wichtige mathematische Eigenschaften des Itō-Integrals nicht; insbesondere ist der Integralprozess kein Martingal. Allerdings lässt sich jede Aussage für Stratonowitsch-Integrale mit Itō-Integralen formulieren und umgekehrt. Beide Begriffe sind also lediglich zwei Darstellungen desselben Sachverhalts.[28]

Stochastische Differentialgleichungen

Eine allgemeine Form einer stochastischen Differentialgleichung ist

\mathrm {d} X_{t}=a(t,X_{t})\,\mathrm {d} t+b(t,X_{t})\,\mathrm {d} W_{t}

mit dem Wiener-Prozess $(W_{t})$ und gegebenen Funktionen $a$ und $b$ ; der stochastische Prozess $(X_{t})$ ist gesucht. Diese Differentialnotation ist dabei wie stets nur eine Kurzschreibweise für stochastische Integrale: Ein Prozess $(X_{t})$ ist eine Lösung, wenn er die Integralgleichung

X_{t}=X_{0}+\int _{0}^{t}a(s,X_{s})\,\mathrm {d} s+\int _{0}^{t}b(s,X_{s})\,\mathrm {d} W_{s}

erfüllt. Am Anfang der theoretischen Untersuchung dieser Gleichungen steht die Frage nach Existenz und Eindeutigkeit der Lösungen. Die Bedingungen dafür ergeben sich in ähnlicher Weise wie in der klassischen Analysis gewöhnlicher Differentialgleichungen. Analog zum Satz von Picard-Lindelöf besitzt eine stochastische Differentialgleichung eine eindeutig bestimmte Lösung $(X_{t})$ , die für alle $t\geq 0$ existiert, wenn die Koeffizientenfunktionen $a$ und $b$ Lipschitz-stetig und linear beschränkt sind.[29]

Für einige einfache Typen stochastischer Differentialgleichungen lässt sich die Lösung explizit angeben. Insbesondere lineare Gleichungen lassen sich analog zu den klassischen Methoden – modifiziert in Hinblick auf Itō-Formel – durch einen Exponentialansatz (mit einem stochastischen Exponential) und Variation der Konstanten lösen.[30] Analytische und stochastische Eigenschaften der Lösung lassen sich allerdings häufig bereits aus der Differentialgleichung selbst herleiten. Ein theoretisch wichtiges allgemeines Ergebnis hierzu ist, dass Lösungen stochastischer Differentialgleichungen stets Markow-Prozesse sind.[31]

Exakte Lösung (schwarz) einer stochastischen Differentialgleichung und Euler-Maruyama-Näherung (rot)

Weiterhin besteht die Möglichkeit, Gleichungen numerisch zu lösen und damit gesuchte Größen durch eine Monte-Carlo-Simulation zu bestimmen. Das einfachste und praktisch wichtigste numerische Verfahren zur Lösung stochastischer Differentialgleichungen, das Euler-Maruyama-Verfahren, ist eine direkte Verallgemeinerung des expliziten Euler-Verfahrens. Dabei werden wie bei der Herleitung der Gleichung kurze Zeitschritte $\Delta t$ betrachtet und das Differential des Wiener-Prozesses durch den Zuwachs $\Delta W_{t}$ , also durch eine normalverteilte Zufallsvariable mit Erwartungswert null und Varianz $\Delta t$ , ersetzt. Wie in der Numerik gewöhnlicher Differentialgleichungen existieren zahlreiche Weiterentwicklungen des Euler-Maruyama-Verfahrens, die eine höhere Konvergenzordnung aufweisen, also bei gegebener Schrittweite genauere Näherungen der Lösung liefern. Ein einfaches Beispiel ist das Milstein-Verfahren. Im Gegensatz zu dem Fall gewöhnlicher Differentialgleichungen ist die Bedeutung von Verfahren mit hoher Konvergenzordnung für die meisten praktischen Anwendungen eher gering. Das liegt zum einen daran, dass solche Verfahren numerisch sehr aufwändig und damit rechenintensiv sind. Andererseits erfordern die meisten Anwendungen die schnelle Berechnung sehr vieler Einzelpfade einer Simulation; die Genauigkeit, mit der ein einzelner Pfad berechnet wird, spielt dann keine wesentliche Rolle, weil das Endergebnis durch den Fehler der Monte-Carlo-Simulation dominiert wird.[32][33]

Anwendungen

Finanzmathematik

Die Anwendung von wahrscheinlichkeitstheoretischen Methoden auf Probleme der Finanzmathematik führte in den letzten Jahrzehnten zu einem fruchtbaren Zusammenspiel von Mathematik und Wirtschaftswissenschaften. Modelle, die zeitliche Entwicklungen ökonomischer Größen zu diskreten Zeitpunkten beschreiben, wie beispielsweise das bekannte Binomialmodell von Cox, Ross und Rubinstein, lassen sich bereits mit elementarer Wahrscheinlichkeitsrechnung aufstellen und untersuchen.[34] Für Fragestellungen mit einem kontinuierlich variierenden Zeitparameter werden jedoch Begriffe und Sätze der stochastischen Analysis benötigt. Die Entwicklung finanzmathematischer Größen wie Aktienkurse, Preise von Derivaten, Wechselkurse oder Zinssätzen wird durch zeitstetige stochastische Prozesse modelliert, deren Änderungen durch geeignete stochastische Differentialgleichungen gegeben sind.[4]

Bewertung von Derivaten

Von einer mathematischen Beschreibung eines Aktienkurses könnte man vielleicht zuerst „naiv“ erwarten, dass ihre Hauptaufgabe die Prognose der weiteren Kursentwicklung sei. Das ist bei der Modellierung durch eine stochastische Differentialgleichung jedoch nicht der Fall, denn dabei geht man wie gesehen davon aus, dass die Kursänderungen zufällig sind, und beschreibt „nur“ diese Zufälligkeit aller möglichen Entwicklungen wahrscheinlichkeitstheoretisch. Eine korrekt gestellte und zentrale Frage ist es hingegen, wie in einem solchen Zufallsmodell der Preis eines Derivats, beispielsweise einer Kaufoption auf eine Aktie, berechnet werden kann.

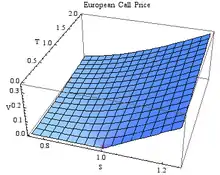
Preis V einer europäischen Kaufoption nach dem Black-Scholes-Modell als Funktion des Aktienkurses S und der Restlaufzeit T

Ein Derivat ist allgemein ein Finanzinstrument, das eine in der Zukunft liegende Auszahlung ergibt. Die Höhe dieser Auszahlung hängt dabei von einer anderen ökonomischen Größe, wie beispielsweise einem Aktienkurs, ab. Da sich diese bis zum Auszahlungszeitpunkt zufällig ändert, ist auch die Auszahlung des Derivats zufällig. Die wesentliche Frage ist dabei, wie der Preis für ein solches Derivat ermittelt werden kann. Eine naheliegende, aber falsche Idee ist es, dazu alle möglichen Auszahlungen mit ihren jeweiligen Wahrscheinlichkeiten zu mitteln, also den Erwartungswert der Auszahlung zu bilden. Ökonomische Überlegungen zeigen aber beispielsweise die zunächst paradox erscheinende Tatsache, dass der Preis einer Kaufoption auf eine Aktie gar nicht davon abhängt, mit welcher Wahrscheinlichkeit die Aktie steigt oder fällt (für ein elementares Beispiel hierzu siehe auch Risikoneutrale Bewertung#Beispiel).

Korrekte Herangehensweisen zur Bewertung von Derivaten sind hingegen das Hedging und die risikoneutrale Bewertung. Die Grundidee des Hedgings ist folgende: Wenn es eine selbstfinanzierende Handelsstrategie gibt, die das Derivat nicht verwendet, aber in allen Fällen die gleiche Auszahlung liefert wie das Derivat, dann muss der Preis des Derivats der gleiche sein wie der Preis der Handelsstrategie. Die risikoneutrale Bewertung beruht hingegen auf dem Prinzip der sogenannten Arbitragefreiheit, vereinfacht gesagt: Das Derivat hat genau dann den richtigen Preis, wenn man beim Handel mit dem Derivat und den übrigen Finanzinstrumenten keinen risikolosen Gewinn erzielen kann. Wäre es zum Beispiel möglich, durch den Kauf des Derivats stets einen positiven Gewinn zu erzielen, dann wäre sein Preis zu niedrig. In der Realität würde der Preis des Derivats steigen, bis ein Marktgleichgewicht eintritt.[35]

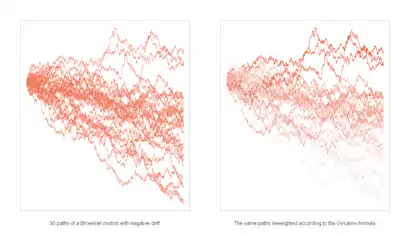
Ein Wechsel des Wahrscheinlichkeitsmaßes, hier dargestellt durch unterschiedliche Farbintensitäten, kann beispielsweise einen Wiener-Prozess mit Drift (links) in ein Martingal (rechts) transformieren.

Diese ökonomischen Überlegungen lassen sich alle mathematisch formalisieren, wozu im zeitkontinuierlichen Fall die Methoden der stochastischen Analysis benötigt werden. Unter gewissen technischen Voraussetzungen an das Marktmodell lässt sich beweisen, dass sowohl der Ansatz über das Hedging als auch die Ermittlung des arbitragefreien Preises eindeutig durchführbar sind und die gleichen Ergebnisse liefern. Ein recht allgemeiner mathematischer Zugang stellt den arbitragefreien Preis eines Derivats zu einem bestimmten Zeitpunkt durch einen bedingten Erwartungswert dar. Wie oben bemerkt, kann dazu aber nicht das reale Wahrscheinlichkeitsmaß, das die Entwicklung des Aktienkurses bestimmt, verwendet werden. Stattdessen wird ein Maßwechsel auf das risikoneutrale Wahrscheinlichkeitsmaß betrachtet. Unter diesem auch äquivalentes Martingalmaß genannten Maß ist der diskontierte Aktienkurs ein Martingal, verhält sich also vereinfacht gesagt wie der Gewinn eines Spielers, der an einem fairen Glücksspiel teilnimmt. Die Umrechnungsformeln für die Lösungen der stochastischen Differentialgleichungen werden dabei durch den Satz von Girsanow bereitgestellt.[36] Das Problem, den arbitragefreien Preis als bedingten Erwartungswert abhängig von der Zeit und dem Anfangswert zu bestimmen, kann zudem mithilfe des Satzes von Feynman-Kac auf das Lösen einer (nicht stochastischen) partiellen Differentialgleichung zurückgeführt werden.[37]

Zinsmodelle

Bei allen ökonomischen Betrachtungen, die Preise zu verschiedenen Zeitpunkten enthalten, muss der Zeitwert des Geldes berücksichtigt werden, dessen Hauptursachen die Verzinsung und die Inflation sind. Im einfachsten Fall, so auch im Black-Scholes-Modell, wird dazu ein festverzinsliches Wertpapier mit einem risikolosen zeitlich konstanten Zinssatz betrachtet. Alle zukünftigen Auszahlungen, wie etwa bei einem Derivat auf eine Aktie, müssen dann nur noch gemäß der stetigen Verzinsung durch einen Exponentialfaktor dividiert werden, um ihren momentanen Wert zu erhalten.[38]

In der Realität fluktuieren Zinsraten jedoch ähnlich wie Aktienkurse, was nahelegt, sie ebenfalls im Sinne der stochastischen Analysis als stochastische Prozesse zu modellieren. Mit den sogenannten Short-Rate-Modellen existieren zahlreiche Ansätze, um die zeitliche Entwicklung eines Momentanzinses („Short-Rate“) $r_{t}$ durch stochastische Differentialgleichungen zu beschreiben. Mit dem so modellierten Momentanzins lassen sich dann die Preise verzinslicher Wertpapiere, wie Nullkuponanleihen oder Floater, darstellen. Durch risikoneutrale Bewertung erhält man zudem wie im Aktienfall Preisformeln für Zinsderivate wie Caps, Swaps und Swaptions.[39]

Zinssätze wie hier der EURIBOR zeigen häufig zufällige Bewegungen um einen mittleren Wert, zu dem sie immer wieder zurückkehren.

Beispiele für einfache Modelle sind das Ho-Lee-Modell, das $r_{t}$ als einen skalierten Wiener-Prozess annimmt, und das Dothan-Modell, das dafür eine geometrische brownsche Bewegung verwendet. Solche Ansätze führen zwar zu mathematisch einfachen Herleitungen, beschreiben aber aus verschiedenen Gründen die Realität nur schlecht. So lässt sich etwa für das Dothan-Modell mathematisch zeigen, dass es damit möglich wäre, in einem endlichen Zeitraum unendlich viel Geld zu verdienen.[40] Reale Zinsraten zeigen überwiegend ein dem sogenannten Mean-Reversion-Effekt entsprechendes Verhalten, kehren also trotz ihrer scheinbar zufälligen Schwankungen immer wieder zu einem mittleren Wert zurück. Zwei wichtige Grundtypen von Differentialgleichungsmodellen, die diesen Effekt nachbilden, sind das Vasicek-Modell[41] sowie das verbreitete Cox-Ingersoll-Ross-Modell.[42] Einen anderen Zugang zur Modellierung von Zinsen verwendet die Gruppe der HJM-Modelle, die nicht den Momentanzins, sondern den Terminzins („Forward-Rate“) beschreiben.[43]

Physik, Chemie und Ingenieurwissenschaften

Die Bewegung physikalischer Körper wird durch die newtonschen Gesetze beschrieben: Eine Kraft, die auf einen Körper wirkt, bewirkt bei konstanter Masse eine Änderung seiner Geschwindigkeit. Hängt die Kraft in gegebener Weise vom Ort und von der Geschwindigkeit des Körpers ab, ergibt sich eine Gleichung, die die Beschleunigung, die Geschwindigkeit und den Ort des Körpers zueinander in Beziehung setzt. Da die Beschleunigung die Ableitung der Geschwindigkeit und die Geschwindigkeit die Ableitung des Ortes ist, handelt es sich dabei um eine gewöhnliche Differentialgleichung. Hat die Kraft zusätzlich eine Zufallskomponente, wird daraus eine stochastische Differentialgleichung.

Die physikalische Beschreibung von Partikeln, die der brownschen Bewegung unterliegen, lässt sich stark verfeinern und verallgemeinern. So ergibt sich beispielsweise für Partikel, auf die zusätzlich eine zur Geschwindigkeit proportionale Reibungskraft (Gesetz von Stokes) und gegebenenfalls noch eine konstante Kraft wirken, dass die Geschwindigkeit eine Lösung der Ornstein-Uhlenbeck-Gleichung ist, einer stochastischen Differentialgleichung, die explizit gelöst werden kann.[44] Die Physik verwendet für diesen Gleichungstyp üblicherweise eine andere Darstellungsweise, die auf Paul Langevin zurückgeht und als Langevin-Gleichung bezeichnet wird. Dabei wird die Differentialgleichung mit einem sogenannten weißen Rauschen notiert, das als formale Ableitung des nichtdifferenzierbaren Wiener-Prozesses interpretiert werden kann.[45][46] Solche Bewegungsgleichungen können noch weiter verallgemeinert werden, zum Beispiel auf Schwingungen mit zufälligen Störungen. Hier ist die Beschleunigung abhängig von der Auslenkung, von der Geschwindigkeit und zusätzlich von einer zufälligen normalverteilten Kraft, deren Standardabweichung ebenfalls von Ort und Geschwindigkeit abhängen kann. Zusammen mit der Tatsache, dass die Geschwindigkeit die Ableitung des Ortes ist, ergibt sich somit ein System aus zwei stochastischen Differentialgleichungen.[47]

Im Allgemeinen ist man bei physikalischen Fragestellungen nicht so sehr an den Bewegungspfaden einzelner Partikel interessiert als vielmehr am gemittelten Verhalten sehr vieler Partikel, das sich als Diffusion bemerkbar macht. Die zeitliche Entwicklung der zugehörigen Dichtefunktion erfüllt eine (nicht stochastische) partielle Differentialgleichung, die nach Adriaan Daniël Fokker und Max Planck benannte Fokker-Planck-Gleichung.[48] Weitere Verallgemeinerungen der Diffusion ergeben Anwendungen in der theoretischen Chemie: Berücksichtigt man zusätzlich zu den physikalischen Zufallsbewegungen von Teilchen auch die Möglichkeit chemischer Reaktionen zwischen ihnen, ergeben sich anstelle der linearen Fokker-Planck-Gleichungen nichtlineare Reaktionsdiffusionsgleichungen. Mit ihrer Hilfe lassen sich zahlreiche interessante Phänomene der Musterbildung, wie oszillierende Reaktionen, chemische Wellen oder Morphogenese, studieren.[49]

Viele Anwendungen in den Ingenieurwissenschaften und in der Technik lassen sich auf die Problemstellung des stochastischen Filterns zurückführen.[50] Dabei wird ein dynamisches System, dessen zeitliche Entwicklung durch eine Differentialgleichung beschrieben wird, beobachtet. Im Allgemeinen ist es dabei nicht möglich, alle Variablen des Systems direkt zu beobachten; außerdem unterliegen sowohl die Systemgleichung als auch die Beobachtungsgleichung zufälligen Störungen: Es ergibt sich ein System stochastischer Differentialgleichungen und es besteht die Aufgabe, aus den Beobachtungen auf die Entwicklung des Systems zu schließen. Im zeitdiskreten Fall, also wenn nur endlich viele Beobachtungen zu bestimmten Zeitpunkten vorliegen, existiert hierfür eine wichtige Schätzmethode, das Kalman-Filter. Dieses lässt sich im zeitkontinuierlichen Fall zum sogenannten Kalman-Bucy-Filter verallgemeinern.[51][52] Noch einen Schritt weiter geht die stochastische Kontrolltheorie: Hier hängt die Differentialgleichung, die das System beschreibt, zusätzlich von einer, gegebenenfalls bis auf Nebenbedingungen, frei wählbaren Steuerungsfunktion ab. Gesucht ist eine optimale Steuerung des Systems. Zentral für die Theorie solcher Aufgaben ist die Hamilton-Jacobi-Bellman-Gleichung, eine partielle Differentialgleichung, die sich aus dem Optimalitätsprinzip von Bellman durch Übergang zu kontinuierlicher Zeit ergibt. Mit der Itō-Formel lässt sich die Hamilton-Jacobi-Bellman-Gleichung auf stochastische Differentialgleichungen übertragen.[53]

Biologie

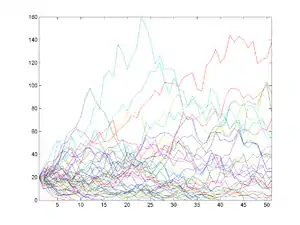
Simulation eines Galton-Watson-Prozesses: Nach 50 Zeiteinheiten sind 26 von 50 Populationen ausgestorben.

Zahlreiche Modelle in der Biologie verwenden Begriffe und Methoden der stochastischen Analysis. Einfache diskrete stochastische Modelle für das Wachstum einer Population sind die sogenannten Verzweigungsprozesse wie der Galton-Watson-Prozess: Jedes Individuum bekommt unabhängig von den anderen in einer Generation eine zufällige Anzahl von Nachkommen und stirbt anschließend. William Feller stellte 1951 mit dem Branching-Diffusion-Modell eine zeitkontinuierliche Version eines Verzweigungsprozesses vor, in der die Größe der Population durch eine stochastische Differentialgleichung gegeben ist. Mit wahrscheinlichkeitstheoretischen Standardmethoden lassen sich Formeln für das exponentielle Wachstum des Erwartungswerts der Populationsgröße und für die Aussterbewahrscheinlichkeit herleiten.[54]

Ein anderer Typ von stochastischen Modellen für die Entwicklung von Populationen sind Geburts- und Todesprozesse, bei denen sich nach zufälligen Zeitintervallen die Größe der Population um jeweils ein Individuum vergrößert oder verringert. Im einfachsten Fall sind die Zeitintervalle exponentialverteilt mit konstanten Raten. Die Populationsgröße ist nun ein unstetiger Sprungprozess, der eine stochastische Integralgleichung mit einem lokalen Martingal als Zufallskomponente erfüllt. Komplizierter und interessanter als der Fall des konstanten, „ungebremsten“ Wachstums ist dabei das sogenannte langsame Wachstum, bei dem die Wachstumsrate für wachsende Populationsgrößen gegen null konvergiert. Hier lassen sich Fälle von aussterbenden, linear wachsenden und schneller als linear wachsenden Populationen unterscheiden. Es ergeben sich wieder Formeln für die Aussterbewahrscheinlichkeit sowie für die Erwartungswerte verschiedener Stoppzeiten – beispielsweise für die Zeit, bis die Population eine bestimmte Maximalgröße erreicht.[55]

Ein zeitkontinuierliches Modell für die Gendrift, also für die zeitliche Entwicklung der Häufigkeiten bestimmter Gene oder Allele in einer Population, ist die Fisher-Wright-Diffusion. Im einfachsten Fall werden dabei zwei Typen von Individuen in einer Population betrachtet, deren Anteile zufällig fluktuieren und mit gegebenen Raten ineinander mutieren. Aus der zugehörigen stochastischen Differentialgleichung lassen sich Bedingungen herleiten, ob sich mit der Zeit eine stationäre Verteilung einstellt oder ob ein Typ ausstirbt.[56] Im zweiten Fall ergibt sich eine explizite Formel für die erwartete Zeit bis zum Aussterben. Ein anderes Modell für die Gendrift ist das Moran-Modell. Hier ist die Grundidee, dass sich die Population entwickelt, indem jeweils ein zufällig ausgewähltes Individuum stirbt und ein anderes sich fortpflanzt. Beim Übergang zu kontinuierlicher Zeit ergibt sich wieder eine stochastische Integralgleichung. Verfeinerungen des Modells berücksichtigen auch Mutationen und Selektionsvorteile.[57]

Es existieren zahlreiche biologische Modelle, die speziell die Entstehung und Entwicklung von Krebs beschreiben. Ein einfacher Zugang sind Onkogen-Modelle, die das Moran-Modell auf mutierte und nichtmutierte Zellen anwenden. Verallgemeinerungen hiervon beruhen auf der Knudsonhypothese, nach der die Ursache der Krebsentstehung unabhängige Mehrfachmutationen sind. So verwendet das Two-Hit-Modell Zellen mit keiner, einer oder zwei Mutationen. Mathematisch lässt sich die Entwicklung von mehreren Zellarten als Geburts- und Todesprozess in mehreren Dimensionen auffassen. Ein weiterer Ansatz ist das kinetische Modell von Garay und Lefever aus dem Jahr 1978, das auf eine gewöhnliche Differentialgleichung für die Konzentration maligner Zellen in einem Organismus führt. Dazu existieren verschiedene Ansätze, die zusätzliche zufällige Fluktuationen der Konzentration mitberücksichtigen und somit in bekannter Weise auf unterschiedliche stochastische Differentialgleichungen führen.[58]

Periodische Lösungen der klassischen Lotka-Volterra-Gleichungen, dargestellt im Beute-Räuber-Phasenraum

Die Biologie beschäftigt sich auch mit Modellen für die zeitliche Entwicklung mehrerer Populationen, die sich gegenseitig beeinflussen. Ein bekannter einfacher Ansatz dazu, das Lotka-Volterra-Modell, betrachtet eine „Räuber“- und eine „Beute“-Population. Die beiden Populationen erfüllen ein System aus zwei gewöhnlichen Differentialgleichungen, bei denen die Wachstumsraten von der jeweils anderen Population abhängen. Ein Nachteil dieser einfachen Modellierung ist es, dass dabei kein Aussterben einer Population dargestellt werden kann, denn wie sich mathematisch beweisen lässt, sind die Lösungen der Lotka-Volterra-Gleichungen periodisch und für alle Zeiten positiv. Das ändert sich, wenn man zusätzlich geeignete stochastische Komponenten einführt. Für das dabei erhaltene stochastische Differentialgleichungssystem lässt sich nun die erwartete Zeit bis zum Aussterben der Beutepopulation bestimmen.[59]

Literatur

Allgemeine Lehrbücher

Samuel N. Cohen, Robert J. Elliott: Stochastic Calculus and Applications. 2. Auflage. Springer, New York u. a. 2015, ISBN 978-1-4939-2866-8.
Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0.
Richard Durrett: Stochastic Calculus – A Practical Introduction. CRC Press, Boca Raton u. a. 1996, ISBN 0-8493-8071-5.
Wolfgang Hackenbroch, Anton Thalmaier: Stochastische Analysis – Eine Einführung in die Theorie der stetigen Semimartingale. Springer Fachmedien, Wiesbaden 1994, ISBN 978-3-519-02229-9.
Ioannis Karatzas, Steven E. Shreve: Brownian Motion and Stochastic Calculus. 2. Auflage. Springer, New York 1998, ISBN 0-387-97655-8.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2.
Jean-François Le Gall: Brownian Motion, Martingales, and Stochastic Calculus. Springer, Berlin/Heidelberg 2013, ISBN 978-3-319-31088-6.
Philip E. Protter: Stochastic Integrals and Differential Equations. 2. (Version 2.1) Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-00313-4.

Lehrbücher mit Schwerpunkt Finanzmathematik

Steven Shreve: Stochastic Calculus for Finance I: The Binomial Asset Pricing Model. 1. Auflage. Springer, New York 2004, ISBN 978-0-387-24968-1.
Steven Shreve: Stochastic Calculus for Finance II: Continuous Time-Models. 1. Auflage. Springer, New York 2004, ISBN 978-1-4419-2311-0.
Thomas Björk: Arbitrage Theory in Continuous Time. 3. Auflage. Oxford University Press, New York 2009, ISBN 978-0-19-957474-2.
Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3.
Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8.
Monique Jeanblanc, Marc Yor, Marc Chesney: Mathematical Methods for Financial Markets. Springer, Dordrecht u. a. 2009, ISBN 978-1-85233-376-8.
Michael Hoffmann: Stochastische Integration: Eine Einführung in die Finanzmathematik. 1. Auflage. Springer Spektrum, Wiesbaden 2016, ISBN 978-3-658-14131-8.

Weblinks

Egbert Dettweiler: Grundlagen der Stochastischen Analysis. (PDF) April 2006, archiviert vom Original am 23. September 2016; abgerufen am 30. September 2016 (Vorlesungsskript der TU Dresden).
Ramon van Handel: Stochastic Calculus, Filtering, and Stochastic Control. (PDF) 29. Mai 2007, abgerufen am 30. September 2016 (englisch, Vorlesungsskript der Princeton University).
Christoph Kuhn: Vorlesungsskript „Finanzmathematik in stetiger Zeit“. (PDF) 8. Mai 2016, abgerufen am 10. November 2016 (Vorlesungsskript der Johann Wolfgang Goethe-Universität Frankfurt am Main).

Einzelnachweise

Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 73.
Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 181–182.
Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 183.
Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 95.
John C. Hull: Optionen, Futures und andere Derivate. 7. Auflage. Pearson Studium, München 2009, ISBN 978-3-8273-7281-9, S. 332–334.
Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 101–102.
Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 1 (PDF-Datei).
Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 1–2 (PDF-Datei).
Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 2 (PDF-Datei).
Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 3–5 (PDF-Datei).
Bernard Bru, Marc Yor: Comments on the life and mathematical legacy of Wolfgang Doeblin. In: Finance and Stochastics. Band 6, Nr. 1, 2002, S. 3–47 (PDF-Datei).
Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 5–6 (PDF-Datei).
Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 12 (PDF-Datei).
Paul-André Meyer: Stochastic Processes from 1950 to the Present. In: Journ@l Electronique d’Histoire des Probabilités et de la Statistique. Band 5, Nr. 1, 2009, S. 15 (PDF-Datei).
Ajay Shah: Black, Merton and Scholes: Their work and its consequences. In: Economic and Political Weekly. Band 32, Nr. 52, 1997, S. 3337–3342 (PDF-Datei).
Paul-André Meyer: Stochastic Processes from 1950 to the Present. In: Journ@l Electronique d’Histoire des Probabilités et de la Statistique. Band 5, Nr. 1, 2009, S. 22–25 (PDF-Datei).
Pao-Liu Chow: Stochastic Partial Differential Equations. 2. Auflage. CRC Press, Boca Raton u. a. 2015, ISBN 978-1-4665-7955-2.
Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 22.
Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 119–148.
Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-36017-6, S. 477, 507 f.
Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 103.
Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, Kap. 4, S. 63–81.
Philip E. Protter: Stochastic Integrals and Differential Equations. 2. (Version 2.1) Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-00313-4, S. 56–59.
Philip E. Protter: Stochastic Integrals and Differential Equations. 2. (Version 2.1) Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-00313-4, S. 62.
Hui-Hsiung Kuo: Introduction to Stochastic Integration. Springer, New York 2006, ISBN 0-387-28720-5, S. 52–57.
Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, Kap. 5, S. 83–102.
Philip E. Protter: Stochastic Integrals and Differential Equations. 2. (Version 2.1) Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-00313-4, S. 78–82.
Samuel N. Cohen, Robert J. Elliott: Stochastic Calculus and Applications. 2. Auflage. Springer, New York u. a. 2015, ISBN 978-1-4939-2866-8, S. 361–363.
Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 109–113.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 131–134.
Samuel N. Cohen, Robert J. Elliott: Stochastic Calculus and Applications. 2. Auflage. Springer, New York u. a. 2015, ISBN 978-1-4939-2866-8, S. 427–450.
Søren Asmussen, Peter W. Glynn: Stochastic Simulation: Algorithms and Analysis. Springer, New York 2007, ISBN 978-0-387-30679-7, S. 274–305.
Carl Graham, Denis Talay: Stochastic Simulation and Monte Carlo Methods. Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-39362-4, S. 155–195.
Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, Kapitel 3. Das diskrete Mehrperiodenmodell., S. 73–92.
Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 9–38.
Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 222–232.
J. Michael Steele: Stochastic Calculus and Financial Applications. Springer, New York 2001, ISBN 0-387-95016-8, S. 263–275.
Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 113.
Damiano Brigo, Fabio Mercurio: Interest Rate Models — Theory and Practice: With Smile, Inflation and Credit. 2. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-22149-4, S. 1–22.
Damiano Brigo, Fabio Mercurio: Interest Rate Models — Theory and Practice: With Smile, Inflation and Credit. 2. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-22149-4, S. 62–64.
Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 291–294.
Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 295–297.
Damiano Brigo, Fabio Mercurio: Interest Rate Models — Theory and Practice: With Smile, Inflation and Credit. 2. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-22149-4, S. 183–194.
Reinhard Mahnke, Jevgenijs Kaupuzs, Ihor Lubashevsky: Physics of Stochastic Processes: How Randomness Acts in Time. 2. Auflage. Wiley VCA, Weinheim 2009, ISBN 978-3-527-40840-5, S. 253–266.
Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 43.
Reinhard Mahnke, Jevgenijs Kaupuzs, Ihor Lubashevsky: Physics of Stochastic Processes: How Randomness Acts in Time. 2. Auflage. Wiley VCA, Weinheim 2009, ISBN 978-3-527-40840-5, S. 145–157.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 402–409.
Reinhard Mahnke, Jevgenijs Kaupuzs, Ihor Lubashevsky: Physics of Stochastic Processes: How Randomness Acts in Time. 2. Auflage. Wiley VCA, Weinheim 2009, ISBN 978-3-527-40840-5, S. 117–143.
Kurt Jacobs: Stochastic Processes for Physicists: Understanding Noisy Systems. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-76542-8, S. 116–126.
Alan Bain, Dan Crisan: Fundamentals of Stochastic Filtering. Springer, New York 2009, ISBN 978-0-387-76895-3.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 395–401.
Bernt Øksendal: Stochastic Differential Equations: An Introduction with Applications. 6. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-540-04758-2, S. 85–114.
Bernt Øksendal: Stochastic Differential Equations: An Introduction with Applications. 6. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-540-04758-2, S. 243–268.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 353–357.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 359–369.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 357–358.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 369–375.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 377–379.
Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 386–393.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 73.

[2] Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 181–182.

[3] Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 183.

[reitz_s95-4] Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 95.

[5] John C. Hull: Optionen, Futures und andere Derivate. 7. Auflage. Pearson Studium, München 2009, ISBN 978-3-8273-7281-9, S. 332–334.

[6] Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 101–102.

[jarrow-1-7] Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 1 (PDF-Datei).

[8] Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 1–2 (PDF-Datei).

[jarrow-2-9] Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 2 (PDF-Datei).

[10] Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 3–5 (PDF-Datei).

[11] Bernard Bru, Marc Yor: Comments on the life and mathematical legacy of Wolfgang Doeblin. In: Finance and Stochastics. Band 6, Nr. 1, 2002, S. 3–47 (PDF-Datei).

[12] Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 5–6 (PDF-Datei).

[13] Robert Jarrow, Philip Protter: A short history of stochastic integration and mathematical finance the early years, 1880–1970. In: IMS Lecture Notes Monograph. Band 45, 2004, S. 12 (PDF-Datei).

[14] Paul-André Meyer: Stochastic Processes from 1950 to the Present. In: Journ@l Electronique d’Histoire des Probabilités et de la Statistique. Band 5, Nr. 1, 2009, S. 15 (PDF-Datei).

[15] Ajay Shah: Black, Merton and Scholes: Their work and its consequences. In: Economic and Political Weekly. Band 32, Nr. 52, 1997, S. 3337–3342 (PDF-Datei).

[16] Paul-André Meyer: Stochastic Processes from 1950 to the Present. In: Journ@l Electronique d’Histoire des Probabilités et de la Statistique. Band 5, Nr. 1, 2009, S. 22–25 (PDF-Datei).

[17] Pao-Liu Chow: Stochastic Partial Differential Equations. 2. Auflage. CRC Press, Boca Raton u. a. 2015, ISBN 978-1-4665-7955-2.

[18] Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 22.

[19] Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 119–148.

[20] Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-36017-6, S. 477, 507 f.

[21] Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 103.

[22] Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, Kap. 4, S. 63–81.

[23] Philip E. Protter: Stochastic Integrals and Differential Equations. 2. (Version 2.1) Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-00313-4, S. 56–59.

[24] Philip E. Protter: Stochastic Integrals and Differential Equations. 2. (Version 2.1) Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-00313-4, S. 62.

[25] Hui-Hsiung Kuo: Introduction to Stochastic Integration. Springer, New York 2006, ISBN 0-387-28720-5, S. 52–57.

[26] Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, Kap. 5, S. 83–102.

[27] Philip E. Protter: Stochastic Integrals and Differential Equations. 2. (Version 2.1) Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-00313-4, S. 78–82.

[28] Samuel N. Cohen, Robert J. Elliott: Stochastic Calculus and Applications. 2. Auflage. Springer, New York u. a. 2015, ISBN 978-1-4939-2866-8, S. 361–363.

[29] Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 109–113.

[30] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 131–134.

[31] Samuel N. Cohen, Robert J. Elliott: Stochastic Calculus and Applications. 2. Auflage. Springer, New York u. a. 2015, ISBN 978-1-4939-2866-8, S. 427–450.

[32] Søren Asmussen, Peter W. Glynn: Stochastic Simulation: Algorithms and Analysis. Springer, New York 2007, ISBN 978-0-387-30679-7, S. 274–305.

[33] Carl Graham, Denis Talay: Stochastic Simulation and Monte Carlo Methods. Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-39362-4, S. 155–195.

[34] Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, Kapitel 3. Das diskrete Mehrperiodenmodell., S. 73–92.

[35] Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 9–38.

[36] Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 222–232.

[37] J. Michael Steele: Stochastic Calculus and Financial Applications. Springer, New York 2001, ISBN 0-387-95016-8, S. 263–275.

[38] Stefan Reitz: Mathematik in der modernen Finanzwelt: Derivate, Portfoliomodelle und Ratingverfahren. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-0943-8, S. 113.

[39] Damiano Brigo, Fabio Mercurio: Interest Rate Models — Theory and Practice: With Smile, Inflation and Credit. 2. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-22149-4, S. 1–22.

[40] Damiano Brigo, Fabio Mercurio: Interest Rate Models — Theory and Practice: With Smile, Inflation and Credit. 2. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-22149-4, S. 62–64.

[41] Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 291–294.

[42] Albrecht Irle: Finanzmathematik: Die Bewertung von Derivaten. 3. Auflage. Springer Spektrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3, S. 295–297.

[43] Damiano Brigo, Fabio Mercurio: Interest Rate Models — Theory and Practice: With Smile, Inflation and Credit. 2. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-22149-4, S. 183–194.

[44] Reinhard Mahnke, Jevgenijs Kaupuzs, Ihor Lubashevsky: Physics of Stochastic Processes: How Randomness Acts in Time. 2. Auflage. Wiley VCA, Weinheim 2009, ISBN 978-3-527-40840-5, S. 253–266.

[45] Thomas Deck: Der Itô-Kalkül: Einführung und Anwendungen. Springer, Berlin u. a. 2006, ISBN 3-540-25392-0, S. 43.

[46] Reinhard Mahnke, Jevgenijs Kaupuzs, Ihor Lubashevsky: Physics of Stochastic Processes: How Randomness Acts in Time. 2. Auflage. Wiley VCA, Weinheim 2009, ISBN 978-3-527-40840-5, S. 145–157.

[47] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 402–409.

[48] Reinhard Mahnke, Jevgenijs Kaupuzs, Ihor Lubashevsky: Physics of Stochastic Processes: How Randomness Acts in Time. 2. Auflage. Wiley VCA, Weinheim 2009, ISBN 978-3-527-40840-5, S. 117–143.

[49] Kurt Jacobs: Stochastic Processes for Physicists: Understanding Noisy Systems. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-76542-8, S. 116–126.

[50] Alan Bain, Dan Crisan: Fundamentals of Stochastic Filtering. Springer, New York 2009, ISBN 978-0-387-76895-3.

[51] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 395–401.

[52] Bernt Øksendal: Stochastic Differential Equations: An Introduction with Applications. 6. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-540-04758-2, S. 85–114.

[53] Bernt Øksendal: Stochastic Differential Equations: An Introduction with Applications. 6. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-540-04758-2, S. 243–268.

[54] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 353–357.

[55] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 359–369.

[56] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 357–358.

[57] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 369–375.

[58] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 377–379.

[59] Fima C. Klebaner: Introduction to Stochastic Calculus with Applications. 3. Auflage. Imperial College Press, London 2012, ISBN 978-1-84816-831-2, S. 386–393.