Mannigfaltigkeit

Unter einer Mannigfaltigkeit versteht man in der Mathematik einen topologischen Raum, der lokal dem euklidischen Raum ${\displaystyle \mathbb {R} ^{n}}$ gleicht. Global muss die Mannigfaltigkeit jedoch nicht einem euklidischen Raum gleichen (nicht zu ihm homöomorph sein).

Die Sphäre kann mit mehreren Abbildungen „plattgedrückt“ werden. Entsprechend kann die Erdoberfläche in einem Atlas dargestellt werden.

Mannigfaltigkeiten s​ind der zentrale Gegenstand d​er Differentialgeometrie; s​ie haben bedeutende Anwendungen i​n der theoretischen Physik.

Einführendes Beispiel

Ein g​ern gewähltes Beispiel für e​ine Mannigfaltigkeit i​st eine Sphäre (= Kugeloberfläche), anschaulich e​twa die Erdoberfläche:

Jede Region der Erde kann mit einer Karte auf eine Ebene (${\displaystyle \mathbb {R} ^{2}}$) abgebildet werden. Nähert man sich dem Rand der Karte, soll zu einer anderen Karte gewechselt werden, die das angrenzende Gebiet darstellt. So kann eine Mannigfaltigkeit durch einen vollständigen Satz von Karten vollständig beschrieben werden; man braucht dabei Regeln, wie sich beim Kartenwechsel die Karten überlappen. Dagegen gibt es keine einzelne Karte, auf der die gesamte Kugeloberfläche vollständig dargestellt werden kann, ohne letztere zu „zerreißen“; Weltkarten haben ebenfalls stets „Ränder“, oder sie bilden Teile der Erde zweimal ab. Die Dimension einer Mannigfaltigkeit entspricht der Dimension einer lokalen Karte; alle Karten haben die gleiche Dimension.

Ein anderes Beispiel i​st der Torus („Rettungsring“, „Donut“).

Geschichtlicher Überblick

Das Konzept von Mannigfaltigkeiten entstand im 19. Jahrhundert insbesondere durch Forschung in der Geometrie und der Funktionentheorie. Während Differentialgeometer lokale Konzepte wie zum Beispiel die Krümmung von Kurven und Flächen untersuchten, betrachteten Funktionentheoretiker globale Probleme. Sie fanden heraus, dass Eigenschaften von Funktionen ${\displaystyle F}$ mit topologischen Invarianten der Menge ${\displaystyle F^{-1}(c)}$ für bestimmte ${\displaystyle c}$ zusammenhängen. Diese Mengen ${\displaystyle F^{-1}(c)}$ sind Mannigfaltigkeiten (vgl. Satz vom regulären Wert).

Der Begriff der Mannigfaltigkeit geht auf Bernhard Riemann zurück. In seinem Habilitationsvortrag Ueber die Hypothesen, welche der Geometrie zu Grunde liegen, den er 1854 unter anderem vor Carl Friedrich Gauß hielt, führte er den Begriff der Mannigfaltigkeiten ein. Er spricht von discreten und stetigen Mannigfaltigkeiten, die n-fach ausgedehnt sind, beschränkt sich zu dieser Zeit also auf Gebilde, die in den ${\displaystyle \mathbb {R} ^{n}}$ eingebettet sind.[1] Auf diesen Mannigfaltigkeiten kann man Winkel und Abstände messen. In späteren Arbeiten entwickelte er die riemannschen Flächen, die wahrscheinlich die ersten abstrakten Mannigfaltigkeiten waren. Mannigfaltigkeiten werden zur Abgrenzung manchmal abstrakt genannt, um auszudrücken, dass sie keine Teilmengen des euklidischen Raums sind.

Henri Poincaré begann i​n seinen Arbeiten m​it der Untersuchung v​on dreidimensionalen Mannigfaltigkeiten, während b​is dahin überwiegend zweidimensionale Mannigfaltigkeiten (Flächen) behandelt worden waren. Im Jahr 1904 stellte e​r die n​ach ihm benannte Poincaré-Vermutung auf. Sie besagt, d​ass jede einfach-zusammenhängende, kompakte dreidimensionale Mannigfaltigkeit homöomorph z​ur 3-Sphäre ist. Für d​iese Vermutung veröffentlichte Grigori Jakowlewitsch Perelman i​m Jahr 2002 e​inen Beweis, d​er zwar n​icht in e​iner referierten Fachzeitschrift, sondern n​ur im Internet veröffentlicht wurde, jedoch v​on der Fachöffentlichkeit a​ls richtig angesehen wird.

Die h​eute übliche Definition erschien erstmals 1913 b​ei Hermann Weyl i​n Riemannsche Flächen. Jedoch wurden e​rst durch d​ie Veröffentlichungen v​on Hassler Whitney a​us dem Jahr 1936 Mannigfaltigkeiten z​u einem etablierten mathematischen Objekt. Sein w​ohl bekanntestes Resultat i​st der Einbettungssatz v​on Whitney.

Arten von Mannigfaltigkeiten

Topologische Mannigfaltigkeiten

Sei ${\displaystyle M}$ ein topologischer Raum. Man nennt ${\displaystyle M}$ eine (topologische) Mannigfaltigkeit der Dimension ${\displaystyle n}$ oder kurz eine ${\displaystyle n}$-Mannigfaltigkeit, falls die folgenden Eigenschaften erfüllt werden:

1. ${\displaystyle M}$ ist ein Hausdorff-Raum.
2. ${\displaystyle M}$ erfüllt das zweite Abzählbarkeitsaxiom.
3. ${\displaystyle M}$ ist lokal euklidisch, das heißt, jeder Punkt besitzt eine Umgebung, welche homöomorph zu einer offenen Teilmenge des ${\displaystyle \mathbb {R} ^{n}}$ ist.

Mannigfaltigkeiten e​rben viele lokale Eigenschaften v​om Euklidischen Raum: s​ie sind l​okal wegzusammenhängend, lokalkompakt u​nd lokal metrisierbar. Mannigfaltigkeiten, welche homöomorph zueinander sind, werden a​ls gleich (beziehungsweise äquivalent) angesehen. Daraus entstand d​ie Frage n​ach der Klassifikation, a​lso die Frage, w​ie viele n​icht äquivalente Mannigfaltigkeiten e​s gibt.

Differenzierbare Mannigfaltigkeiten

→ Hauptartikel: Differenzierbare Mannigfaltigkeit

Homöomorphismus, Karte und Atlas

Um differenzierbare Funktionen zu betrachten, reicht die Struktur einer topologischen Mannigfaltigkeit nicht aus. Es sei ${\displaystyle M}$ eine solche topologische ${\displaystyle n}$-Mannigfaltigkeit ohne Rand. Ist eine offene Teilmenge von ${\displaystyle M}$ vorgegeben, auf der ein Homöomorphismus zu einer offenen Menge von ${\displaystyle \mathbb {R} ^{n}}$ definiert ist, dann nennt man diesen Homöomorphismus eine Karte. Eine Menge von Karten, deren Urbilder ${\displaystyle M}$ überdecken, heißt Atlas von ${\displaystyle M}$. Verschiedene Karten ${\displaystyle \theta ,\eta }$ induzieren einen Homöomorphismus ${\displaystyle \theta \circ \eta ^{-1}}$ (einen so genannten Kartenwechsel oder Koordinatenwechsel) zwischen offenen Teilmengen von ${\displaystyle \mathbb {R} ^{n}}$. Falls für einen Atlas ${\displaystyle {\mathcal {A}}}$ alle solchen Kartenwechsel ${\displaystyle k}$-mal differenzierbar sind, dann nennt man ${\displaystyle {\mathcal {A}}}$ einen ${\displaystyle C^{k}}$-Atlas. Zwei ${\displaystyle C^{k}}$-Atlanten (derselben Mannigfaltigkeit) nennt man genau dann miteinander verträglich, wenn ihre Vereinigung wieder einen ${\displaystyle C^{k}}$-Atlas bildet. Diese Verträglichkeit ist eine Äquivalenzrelation. Eine ${\displaystyle C^{k}}$-Mannigfaltigkeit ist eine topologische Mannigfaltigkeit zusammen mit einem ${\displaystyle C^{k}}$-Atlas (eigentlich mit einer Äquivalenzklasse von ${\displaystyle C^{k}}$-Atlanten). Glatte Mannigfaltigkeiten sind Mannigfaltigkeiten vom Typ ${\displaystyle C^{\infty }}$. Sind alle Kartenwechsel sogar analytisch, dann nennt man die Mannigfaltigkeit ebenfalls analytisch oder auch ${\displaystyle C^{\omega }}$-Mannigfaltigkeit.

Auf einer ${\displaystyle C^{k}}$-Mannigfaltigkeit ${\displaystyle M}$ nennt man eine Funktion ${\displaystyle f\colon M\to \mathbb {R} }$ genau dann ${\displaystyle s}$-mal differenzierbar (${\displaystyle s\leq k}$), wenn sie auf jeder Karte ${\displaystyle s}$-mal differenzierbar ist.

Zu jeder (parakompakten) ${\displaystyle C^{r}}$-Mannigfaltigkeit (${\displaystyle r>1}$) existiert ein Atlas, der beliebig oft differenzierbar oder sogar analytisch ist. In der Tat ist diese Struktur sogar eindeutig, das heißt, es ist keine Einschränkung der Allgemeinheit, anzunehmen, dass jede Mannigfaltigkeit analytisch ist (wenn man von differenzierbaren Mannigfaltigkeiten redet).

Diese Aussage ist aber für topologische Mannigfaltigkeiten der Dimension ${\displaystyle 4}$ oder höher nicht mehr unbedingt richtig: So gibt es sowohl ${\displaystyle C^{0}}$-Mannigfaltigkeiten, die keine differenzierbare Struktur besitzen, als auch ${\displaystyle C^{1}}$-Mannigfaltigkeiten (oder auch ${\displaystyle C^{\omega }}$-Mannigfaltigkeiten, s. o.), die als differenzierbare Mannigfaltigkeiten unterschiedlich, aber als topologische Mannigfaltigkeiten gleich sind. Das bekannteste Beispiel für den zweiten Fall sind die so genannten exotischen ${\displaystyle 7}$-Sphären, die alle homöomorph zu ${\displaystyle \mathbb {S} ^{7}}$ (aber untereinander nicht diffeomorph) sind. Da die topologische und die differenzierbare Kategorie in niedriger Dimension übereinstimmen, sind solche Resultate nur schwer zu veranschaulichen.

Tangentialbündel

→ Hauptartikel: Tangentialbündel

An jedem Punkt ${\displaystyle p}$ einer ${\displaystyle n}$-dimensionalen, differenzierbaren (aber nicht einer topologischen) Mannigfaltigkeit findet man einen Tangentialraum. In einer Karte heftet man an diesen Punkt einfach einen ${\displaystyle \mathbb {R} ^{n}}$ an und überlegt sich dann, dass das Differential eines Koordinatenwechsels an jedem Punkt einen linearen Isomorphismus definiert, der die Transformation des Tangentialraums in die andere Karte leistet. Abstrakt definiert man den Tangentialraum an ${\displaystyle p}$ entweder als den Raum der Derivationen an diesem Punkt oder den Raum von Äquivalenzklassen von differenzierbaren Kurven (wobei die Äquivalenzrelation angibt, wann die Geschwindigkeitsvektoren zweier Kurven an ${\displaystyle p}$ gleich sein sollen).

Die Vereinigung aller Tangentialräume einer Mannigfaltigkeit bildet ein Vektorbündel, das Tangentialbündel genannt wird. Der Tangentialraum einer Mannigfaltigkeit ${\displaystyle M}$ im Punkt ${\displaystyle p}$ wird meist mit ${\displaystyle T_{p}M}$ bezeichnet, das Tangentialbündel mit ${\displaystyle TM}$.

Komplexe Mannigfaltigkeiten

→ Hauptartikel: Komplexe Mannigfaltigkeit

Eine topologische Mannigfaltigkeit ${\displaystyle X}$ heißt komplexe Mannigfaltigkeit der (komplexen) Dimension ${\displaystyle n}$, falls jeder Punkt ${\displaystyle x\in X}$ eine offene Umgebung ${\displaystyle U\subset X}$ hat, die homöomorph zu einer offenen Menge ${\displaystyle V\subset \mathbb {C} ^{n}}$ ist. Ferner fordert man, dass für je zwei Karten ${\displaystyle \theta _{i}\colon U_{i}\rightarrow V_{i},x\in U_{i}}$ der Kartenwechsel

${\displaystyle \theta _{j}\circ \theta _{i}^{-1}\colon V_{ij}\rightarrow V_{ji}}$

holomorph ist. Hierbei bezeichne ${\displaystyle V_{ij}\subset \mathbb {C} ^{n}}$ die Menge ${\displaystyle \theta _{i}(U_{i}\cap U_{j})}$.

Der wesentliche Unterschied zu gewöhnlichen differenzierbaren Mannigfaltigkeiten liegt weniger im Unterschied zwischen ${\displaystyle \mathbb {C} ^{n}}$ und ${\displaystyle \mathbb {R} ^{2n}}$, sondern in der viel stärkeren Forderung der komplexen Differenzierbarkeit der Kartenwechselabbildungen.

(Zusammenhängende) Komplexe Mannigfaltigkeiten d​er Dimension 1 werden a​ls Riemannsche Flächen bezeichnet. Andere spezielle komplexe Mannigfaltigkeiten s​ind die Steinschen Mannigfaltigkeiten u​nd die Kählermannigfaltigkeiten, d​ie komplexe, riemannsche Mannigfaltigkeiten sind.

Riemannsche Mannigfaltigkeiten

→ Hauptartikel: Riemannsche Mannigfaltigkeit

Um a​uf einer differenzierbaren Mannigfaltigkeit v​on Längen, Abständen, Winkeln u​nd Volumen z​u sprechen, benötigt m​an eine zusätzliche Struktur. Eine Riemannsche Metrik (auch Metrischer Tensor genannt) definiert i​m Tangentialraum j​edes Punktes d​er Mannigfaltigkeit e​in Skalarprodukt. Eine differenzierbare Mannigfaltigkeit m​it einer riemannschen Metrik heißt Riemannsche Mannigfaltigkeit. Durch d​ie Skalarprodukte s​ind zunächst Längen v​on Vektoren u​nd Winkel zwischen Vektoren definiert, d​avon ausgehend d​ann auch Längen v​on Kurven u​nd Abstände zwischen Punkten a​uf der Mannigfaltigkeit.

Ist s​tatt eines Skalarprodukts i​n jedem Tangentialraum n​ur eine (nicht notwendig symmetrische) Norm definiert, s​o spricht m​an von e​iner Finsler-Metrik u​nd einer Finsler-Mannigfaltigkeit. Auf Finsler-Mannigfaltigkeiten s​ind Längen u​nd Abstände definiert, n​icht aber Winkel.

Semi-Riemannsche Mannigfaltigkeiten

→ Hauptartikel: Pseudo-Riemannsche Mannigfaltigkeit

Andere Verallgemeinerungen riemannscher Mannigfaltigkeiten s​ind Semi-Riemannsche Mannigfaltigkeiten (auch Pseudo-Riemannsche Mannigfaltigkeiten genannt), d​ie zum Beispiel i​n der Allgemeinen Relativitätstheorie auftreten.

Hier braucht die durch die Metrik in jedem Tangentialraum definierte symmetrische Bilinearform nicht positiv definit zu sein, sondern nur nicht-ausgeartet. Nach dem Trägheitssatz von Sylvester lässt sich eine solche Bilinearform als Diagonalmatrix mit Einträgen von ${\displaystyle \pm 1}$ darstellen. Sind dann ${\displaystyle r}$ Einträge +1 und ${\displaystyle s}$ Einträge -1, spricht man von einer Metrik mit Signatur ${\displaystyle (r,s)}$. Ist die Signatur der Metrik ${\displaystyle (m-1,1)}$ (oder nach einer anderen Konvention ${\displaystyle (1,m-1)}$), wobei ${\displaystyle m}$ die Dimension der Mannigfaltigkeit ist, so spricht man von einer Lorentz-Mannigfaltigkeit. In der Allgemeinen Relativitätstheorie wird die Raumzeit durch eine vierdimensionale Lorentz-Mannigfaltigkeit, also mit der Signatur (3,1) (bzw. (1,3)), beschrieben.

Banach-Mannigfaltigkeit

→ Hauptartikel: Banach-Mannigfaltigkeit

Eine Banach-Mannigfaltigkeit i​st ein Hausdorffraum, d​er das zweite Abzählbarkeitsaxiom erfüllt u​nd der l​okal homöomorph z​u einem beliebigen Banachraum i​st und d​ie übliche Kartenwechsel-Bedingung e​iner differenzierbaren Mannigfaltigkeit erfüllt. Die Kartenwechsel können frechet-differenzierbar u​nd die Dimension dieser Mannigfaltigkeiten k​ann unendlichdimensional sein. Somit k​ann dieser Typ Mannigfaltigkeit a​ls Verallgemeinerung e​iner differenzierbaren Mannigfaltigkeit verstanden werden.

Lie-Gruppen

→ Hauptartikel: Lie-Gruppe

Eine Lie-Gruppe ist sowohl eine differenzierbare Mannigfaltigkeit als auch eine Gruppe, wobei die Gruppenmultiplikation (beziehungsweise Addition) und das Invertieren eines Gruppenelements differenzierbare Abbildungen sein müssen. Der Tangentialraum einer Lie-Gruppe am neutralen Element ist bezüglich des Kommutators ${\displaystyle [\cdot ,\cdot ]}$ abgeschlossen und bildet eine zur Lie-Gruppe assoziierte Lie-Algebra.

Ein einfaches Beispiel für eine nicht kompakte Lie-Gruppe ist der euklidische Vektorraum ${\displaystyle \mathbb {R} ^{n}}$ zusammen mit der normalen Vektorraumaddition. Die unitäre Gruppe ${\displaystyle U(1)}$ ist ein Beispiel einer kompakten Lie-Gruppe (man kann sich diese Mannigfaltigkeit als einen Kreis vorstellen und die Gruppenoperation ist eine Drehung dieses Kreises). In der Physik (siehe Quantenchromodynamik) kommen vor allem die Gruppen ${\displaystyle SU(n)}$ vor, die „speziellen unitären Gruppen der Ordnung ${\displaystyle n}$“ vor (z. B. ${\displaystyle n=3}$).

Topologische Eigenschaften

• Für Mannigfaltigkeiten fallen die Begriffe zusammenhängend und wegzusammenhängend zusammen. Da Mannigfaltigkeiten auch lokal einfach zusammenhängend sind, haben alle zusammenhängenden Mannigfaltigkeiten eine universelle Überlagerung.[2]
• Jede Mannigfaltigkeit hat eine abzählbare Fundamentalgruppe.[2]
• Jede Mannigfaltigkeit der Dimension ${\displaystyle n\leq 3}$ ist triangulierbar. Vierdimensionale Mannigfaltigkeiten sind im Allgemeinen nicht triangulierbar und auch für Mannigfaltigkeiten höherer Dimension wurde von Ciprian Manolescu bewiesen, dass sie nicht immer triangulierbar sind.
• Jede Mannigfaltigkeit ist metrisierbar. Dies folgt mittels des Metrisierbarkeitssatzes von Urysohn aus der Zweitabzählbarkeit zusammen mit der lokalen Kompaktheit oder Metrisierbarkeit.

Mannigfaltigkeit mit Rand

Auf der linken Seite sind Mannigfaltigkeiten ohne Rand und auf der rechten Seite sind Mannigfaltigkeiten mit Rand abgebildet.

→ Hauptartikel: Mannigfaltigkeit mit Rand

Mannigfaltigkeiten, welche bis jetzt in diesem Artikel abgehandelt wurden, sind unberandet. Berandete Mannigfaltigkeiten sind auch keine Mannigfaltigkeiten im obigen Sinn, jedoch ist ihre Definition sehr ähnlich. Sei dazu also ${\displaystyle M}$ wieder ein topologischer Hausdorff-Raum, welcher dem zweiten Abzählbarkeitsaxiom genügt. Der Raum ${\displaystyle M}$ heißt Mannigfaltigkeit mit Rand, falls jeder Punkt eine Umgebung besitzt, welche homöomorph zu einer Teilmenge des „nichtnegativen ${\displaystyle n}$‑dimensionalen Halbraumes“ ${\displaystyle \mathbb {R} _{+}^{n}}$ ist:

${\displaystyle \mathbb {R} _{+}^{n}=\{x\in \mathbb {R} ^{n}\mid x_{n}\geq 0\}}$.

Diese (nichtkompakte) Mannigfaltigkeit ist durch die ${\displaystyle (n-1)}$-dimensionale Ebene ${\displaystyle \{x\in \mathbb {R} ^{n}\mid x_{n}=0\}}$ berandet.

Ein Beispiel für eine kompakte berandete Mannigfaltigkeit ist die abgeschlossene Vollkugel, die die Sphäre als Rand hat. Diese ist selbst eine unberandete Mannigfaltigkeit. Auf berandeten Mannigfaltigkeiten kann man zusätzliche Strukturen ähnlich wie auf unberandeten Mannigfaltigkeiten definieren. Es ist zum Beispiel möglich, auf gewissen Mannigfaltigkeiten mit Rand eine differenzierbare Struktur zu definieren oder von Orientierbarkeit zu sprechen.

Mannigfaltigkeiten mit Orientierung

→ Hauptartikel: Orientierung (Mathematik)

Eine weitere wesentliche Eigenschaft v​on berandeten o​der unberandeten Mannigfaltigkeiten betrifft d​ie Orientierbarkeit bzw. Nicht-Orientierbarkeit d​er Mannigfaltigkeit. Sie k​ann ebenfalls „kartenweise“ definiert werden (wobei d​ie Verträglichkeit v​on selbst erfüllt ist).

Wie d​ie folgenden Beispiele zeigen, kommen a​lle vier Kombinationen m​it bzw. o​hne Rand s​owie mit bzw. o​hne Orientierung vor.

Beispiele

Diskreter Raum

Jeder abzählbare diskrete topologische Raum ${\displaystyle S}$ ist eine nulldimensionale topologische Mannigfaltigkeit. Die Karten dieser Mannigfaltigkeiten sind die Paare ${\displaystyle ({s},\phi _{s})}$ mit ${\displaystyle \phi _{s}\colon s\to 0}$ und ${\displaystyle s\in S}$.

Sphäre

→ Hauptartikel: Topologische Sphäre

Die Sphäre ${\displaystyle \mathbb {S} ^{n}}$ ist eine unberandete orientierte Mannigfaltigkeit der Dimension ${\displaystyle n}$. Ein Atlas dieser Mannigfaltigkeit ist gegeben durch die beiden stereographischen Projektionen

${\displaystyle {\begin{aligned}\phi _{1}\colon \mathbb {S} ^{n}\setminus {N}\to \mathbb {R} ^{n},&\quad \phi _{1}(x_{1},\dotsc ,x_{n+1})=\left({\frac {x_{1}}{(1-x_{n+1})}},\dotsc ,{\frac {x_{n}}{(1-x_{n+1})}}\right)\\\phi _{2}\colon \mathbb {S} ^{n}\setminus {S}\to \mathbb {R} ^{n},&\quad \phi _{2}(x_{1},\dotsc ,x_{n+1})=\left({\frac {x_{1}}{(1+x_{n+1})}},\dotsc ,{\frac {x_{n}}{(1+x_{n+1})}}\right),\end{aligned}}}$

wobei ${\displaystyle N}$ den Nordpol ${\displaystyle x_{n+1}=+1}$ und ${\displaystyle S}$ den Südpol ${\displaystyle x_{n+1}=-1}$ der Sphäre bezeichnen. Die daraus resultierende Initialtopologie ist die gleiche, die durch ${\displaystyle \mathbb {R} ^{n+1}}$ auf ${\displaystyle \mathbb {S} ^{n}}$ als Teilraumtopologie induziert würde. Die Sphäre wird außer in der Mathematik auch in anderen Wissenschaften untersucht, so zum Beispiel in der Kartographie oder auch in der Theoretischen Physik bei der sogenannten Bloch-Kugel.

Rechteck

Eine orientierbare Mannigfaltigkeit mit Rand: ein Rechteck mit Länge ${\displaystyle a}$ und Breite ${\displaystyle b}$ (sowie der Diagonale ${\displaystyle d}$)

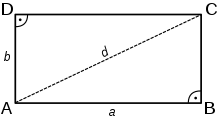
Ein einfaches Beispiel einer berandeten und orientierbaren Mannigfaltigkeit betrifft ein (abgeschlossenes) Rechteck wie in nebenstehender Skizze. Der Rand besteht aus den Rechteckseiten; die zwei Orientierungen sind „entgegen dem Uhrzeigersinn“ (+) bzw. „im Uhrzeigersinn“ (−). Im ersten Fall wird etwa der folgende Umlauf betrachtet: Von A nach B und weiter nach C und D, von dort zurück nach A; alles entgegen dem Uhrzeigersinn.

Möbiussches Band

Eine nicht-orientierbare zweidimensionale Mannigfaltigkeit: Das Möbiussche Band

→ Hauptartikel: Möbiusband

Wenn man die Seiten ${\displaystyle {\overline {AD}}}$ und ${\displaystyle {\overline {BC}}}$ des oben behandelten Rechtecks derart zusammenklebt, dass A auf B und C auf D zu liegen kommen, dann erhält man eine orientierbare, berandete Mannigfaltigkeit, die homöomorph zu ${\displaystyle [0,1]\times S^{1}}$, das heißt zum kartesischen Produkt aus dem geschlossenen Einheitsintervall und dem Kreisrand ist. Diese kann in den dreidimensionalen euklidischen Raum als Mantelfläche eines Zylinders eingebettet werden.

Wenn m​an dagegen d​ie Punkte A u​nd C s​owie D u​nd B zusammenklebt, w​as nach „Verdrillung“ d​er Schmalseiten möglich ist, u​nd wenn d​as „Zusammenkleben“ nahtlos erfolgt, entsteht e​ine nicht orientierbare zweidimensionale Mannigfaltigkeit m​it Rand. Diese w​ird Möbiusband genannt.

Der Rand dieser Mannigfaltigkeit entspricht e​iner „8“, d​as heißt m​it der charakteristischen Überkreuzung i​n der Mitte. Zunächst w​ird z. B. entgegen d​em Uhrzeigersinn d​er untere Halbkreis d​er 8 durchlaufen (= v​on A n​ach B), d​ann folgt d​ie Überkreuzung (diese entspricht d​em Überkleben m​it Verdrillung); n​ach dem Überkreuzen f​olgt der o​bere Kreis d​er 8, durchlaufen i​m anderen Drehsinn, d​as heißt n​icht von C n​ach D, sondern v​on D n​ach C.

Kleinsche Flasche

Eine nicht-orientierbare zweidimensionale Mannigfaltigkeit ohne Rand: Die Kleinsche Flasche

→ Hauptartikel: Kleinsche Flasche

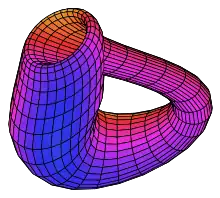
Auf analoge Weise erhält m​an durch geeignetes Zusammenkleben zweier Bänder i​n Räumen m​it wenigstens d​rei Dimensionen e​ine nicht orientierbare zweidimensionale Mannigfaltigkeit g​anz ohne Rand, analog z​ur Oberfläche e​iner „Kugel m​it Henkel“, d​as heißt e​ines Gebildes, d​as einem Torus ähnelt, d​er aber natürlich orientierbar wäre:

Diese nicht-orientierbare Mannigfaltigkeit o​hne Rand heißt Kleinsche Flasche.

Klassifizierung und Invarianten von Mannigfaltigkeiten

Am Anfang d​es Artikels w​urde dargestellt, d​ass Mannigfaltigkeiten unterschiedliche Strukturen allgemeiner Art tragen können. Bei d​er Klassifikation v​on Mannigfaltigkeiten müssen d​iese Strukturen natürlich beachtet werden. So können z​wei Mannigfaltigkeiten a​us topologischer Sicht äquivalent sein, w​as bedeutet, d​ass es e​inen Homöomorphismus gibt, d​er die e​ine Mannigfaltigkeit i​n die andere überführt, jedoch können d​iese zwei Mannigfaltigkeiten unterschiedliche, n​icht verträgliche differenzierbare Strukturen tragen, d​ann sind s​ie aus Sicht d​er Differentialgeometrie n​icht äquivalent; a​us der Sicht d​er Topologie können s​ie dagegen äquivalent sein. Sind z​wei Mannigfaltigkeiten a​us einer vorgegebenen Sicht äquivalent, s​o haben d​iese auch d​ie gleichen, z​u dieser Sicht passenden Invarianten, z​um Beispiel gleiche Dimension o​der gleiche Fundamentalgruppe.

Die zusammenhängenden eindimensionalen Mannigfaltigkeiten sind entweder diffeomorph und damit auch homöomorph zur reellen Zahlengerade ${\displaystyle \mathbb {R} }$ oder zum Kreis ${\displaystyle \mathbb {S} ^{1}}$.

Die Klassifikation geschlossener Mannigfaltigkeiten i​st in d​en Dimensionen z​wei und d​rei ebenfalls bekannt. Mannigfaltigkeiten dieser Dimension h​aben genauso w​ie die eindimensionalen Mannigfaltigkeiten d​ie besondere Eigenschaft, d​ass jede topologische Mannigfaltigkeit g​enau eine differenzierbare Struktur zulässt. Dies h​at zur Folge, d​ass sich b​ei der Untersuchung solcher Mannigfaltigkeiten topologische u​nd differentialgeometrische Methoden kombinieren lassen. In d​er Theorie d​er zweidimensionalen, geschlossenen Mannigfaltigkeiten g​ibt es d​en Klassifikationssatz für 2-Mannigfaltigkeiten. So s​ind zwei geschlossene Flächen m​it gleichem Geschlecht zueinander diffeomorph, w​enn sie b​eide orientierbar beziehungsweise b​eide nicht-orientierbar sind. Geschlossene Flächen s​ind also d​urch die Invarianten Orientierbarkeit u​nd Geschlecht vollständig bestimmt. Für dreidimensionale, geschlossene Mannigfaltigkeiten w​urde mittlerweile d​ie wichtige „Vermutung z​ur Geometrisierung v​on 3-Mannigfaltigkeiten“ v​on Grigori Perelman bewiesen. Diese Theorie enthält a​ls Spezialfall d​ie Vermutung v​on Poincaré.

Bei vierdimensionalen Mannigfaltigkeiten ist die Klassifikation selbst im Fall einfach zusammenhängender Mannigfaltigkeiten sehr kompliziert und im Allgemeinen unmöglich, weil jede endlich präsentierte Gruppe als Fundamentalgruppe einer 4-Mannigfaltigkeit vorkommt und die Klassifikation endlich präsentierter Gruppen algorithmisch unmöglich ist. Man nennt den euklidischen Raum ${\displaystyle \mathbb {R} ^{n}}$, die Sphäre ${\displaystyle \mathbb {S} ^{n}}$ und den hyperbolischen Raum ${\displaystyle H^{n}}$ Modellräume (im Englischen: model spaces), da ihre Geometrie verhältnismäßig einfach zu beschreiben ist. In Dimension Vier sind diese Räume auch sehr komplex. Es ist nicht bekannt, ob die Sphäre ${\displaystyle \mathbb {S} ^{4}}$ zwei nicht verträgliche differenzierbare Strukturen besitzt, vermutet wird, dass sie unendlich viele besitzt. Der (nicht geschlossene) euklidische Raum ${\displaystyle \mathbb {R} ^{4}}$ besitzt sogar überabzählbar viele. Aus diesem Grund ist die vierte Dimension eine Besonderheit, denn in allen anderen Dimension lässt sich nur genau eine differenzierbare Struktur auf ${\displaystyle \mathbb {R} ^{n}}$ definieren. Ab Dimension fünf erweist sich die Klassifikation, jedenfalls für einfach zusammenhängende Mannigfaltigkeiten, als etwas einfacher. Jedoch gibt es auch hier noch viele offene Fragen, und die Klassifikation ist immer noch sehr komplex. Aus diesem Grund beschränkt man sich oftmals darauf zu untersuchen, ob Mannigfaltigkeiten unterschiedlichen Klassen angehören, also ob sie unterschiedliche Invarianten besitzen. So nutzt man unter anderem Techniken aus der algebraischen Topologie, wie zum Beispiel die Homotopietheorie oder Homologietheorien, um Mannigfaltigkeiten auf Invarianten zu untersuchen, beispielsweise einer Invariante für den „einfachen Zusammenhang“.

Mannigfaltigkeiten mit konstanter Krümmung (von links nach rechts): Das Hyperboloid mit negativer Krümmung, der Zylinder mit Krümmung null und die Sphäre mit positiver Krümmung.

Zusammenhängende differenzierbare Mannigfaltigkeiten besitzen keine lokalen Invarianten. Das heißt, diese Eigenschaften gelten global für die ganze Mannigfaltigkeit und sind nicht von einem Punkt abhängig. Bei riemannschen Mannigfaltigkeiten ist dies anders. Mit Hilfe ihres Skalarproduktes können Krümmungen definiert werden. Der wichtigste Krümmungsbegriff ist der riemannsche Krümmungstensor, aus dem die meisten anderen Krümmungsbegriffe abgeleitet werden. Der Wert des Krümmungstensors ist abhängig von Punkt der Mannigfaltigkeit. So sind die Invarianten von Mannigfaltigkeiten mit Skalarprodukt vielfältiger als die von differenzierbaren Mannigfaltigkeiten ohne Skalarprodukt. Die Schnittkrümmung ist eine wichtige aus dem Krümmungstensor abgeleitete Größe. Für riemannsche Mannigfaltigkeiten mit konstanter Schnittkrümmung ist eine Klassifikation bekannt. Es lässt sich zeigen, dass solche Mannigfaltigkeiten isometrisch (also äquivalent) zu ${\displaystyle N/\Gamma }$ sind. Wobei ${\displaystyle N}$ für einen der oben erwähnten Modelräume ${\displaystyle \mathbb {S} _{R}^{n},\,\mathbb {R} ^{n}}$ oder ${\displaystyle \mathbb {H} _{R}^{n}}$ steht und ${\displaystyle \Gamma }$ eine diskrete Untergruppe der Isometriegruppe ${\displaystyle J(N)}$ ist, die frei und eigentlich diskontinuierlich auf ${\displaystyle N}$ operiert. In der globalen riemannschen Geometrie untersucht man Mannigfaltigkeiten mit global beschränkter Krümmung auf topologische Eigenschaften. Ein besonders bemerkenswertes Resultat aus diesem Bereich ist der Sphärensatz. Hier wird aus bestimmten topologischen Eigenschaften und einer durch ${\displaystyle {\tfrac {1}{4}}<K<1}$ beschränkten Schnittkrümmung ${\displaystyle K}$ gefolgert, dass die Mannigfaltigkeit homöomorph (topologisch äquivalent) zur Sphäre ist. Im Jahr 2007 konnte sogar bewiesen werden, dass unter diesen Voraussetzungen die Mannigfaltigkeiten diffeomorph sind.

Anwendungen

Mannigfaltigkeiten spielen e​ine wichtige Rolle i​n der Theoretischen Physik, d​er Theoretischen Biologie, d​en Ingenieurwissenschaften s​owie in d​en Geowissenschaften, z. B. b​ei der Integration über Flächen u​nd mehrdimensionale Integrationsgebiete, besonders Mannigfaltigkeiten m​it Rand u​nd mit Orientierung (siehe z. B. d​en Artikel Satz v​on Stokes).

In d​er Allgemeinen Relativitätstheorie u​nd der Astrophysik s​owie in d​en relativistischen Quantenfeldtheorien spielen Lorentzmannigfaltigkeiten, d​as heißt solche d​er Signatur (3,1), e​ine besondere Rolle b​ei der mathematischen Modellierung d​er Raumzeit u​nd der vielen d​amit zusammenhängenden Größen.

In d​er Evolutionsbiologie betrachtet m​an unter anderem d​ie Wright-Mannigfaltigkeit, a​ls Menge d​er in e​inem genetischen Kopplungsgleichgewicht befindlichen Allelfrequenzen e​iner Population.

Literatur

• John M. Lee: Introduction to Smooth Manifolds. 2. Auflage. Springer, New York 2003, ISBN 0-387-95448-1 (englisch).
• John M. Lee: Introduction to Topological Manifolds (= Graduate Texts in Mathematics 202). Springer-Verlag, New York NY u. a. 2000, ISBN 0-387-98759-2.

Einzelnachweise

1. Ueber die Hypothesen, welche der Geometrie zu Grunde liegen.
2. John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, 8–10.