Lineare Gleichung

Eine lineare Gleichung ist eine mathematische Bestimmungsgleichung, in der ausschließlich Linearkombinationen der Unbekannten vorkommen. Kennzeichnend ist für eine lineare Gleichung also, dass jede Unbekannte nur in der ersten Potenz steht, also nicht beispielsweise quadriert vorkommt (siehe quadratische Gleichung). Typischerweise sind die Unbekannten einer linearen Gleichung Skalare, meist reelle Zahlen. Im einfachsten Fall einer skalaren Unbekannten ${\displaystyle x}$ besitzt eine lineare Gleichung die Form

${\displaystyle a\cdot x=b}$,

wobei ${\displaystyle a}$ und ${\displaystyle b}$ Konstanten sind. Es gibt aber auch lineare Gleichungen mit mehreren Unbekannten und mit anderen mathematischen Objekten als Unbekannten, beispielsweise Folgen (lineare Differenzengleichungen), Vektoren (lineare Gleichungssysteme) oder Funktionen (lineare Differentialgleichungen). Im allgemeinen Fall besitzt eine lineare Gleichung die Form

${\displaystyle T(x)=b}$,

wobei ${\displaystyle T}$ eine lineare Abbildung ist.

Homogene lineare Gleichungen sind spezielle lineare Gleichungen, bei denen der konstante Term ${\displaystyle b}$ der Gleichung gleich null ist. Die Lösungen einer homogenen linearen Gleichung bilden einen Untervektorraum des Vektorraums der Unbekannten und besitzen damit besondere Eigenschaften wie die Gültigkeit des Superpositionsprinzips. Die Lösungen einer inhomogenen linearen Gleichung bilden hingegen einen affinen Unterraum, so lässt sich jede Lösung einer inhomogenen linearen Gleichung als Summe der Lösung der zugehörigen homogenen Gleichung und einer Partikulärlösung darstellen. Der Lösungsraum einer linearen Gleichung kann über den Kern und den Kokern der linearen Abbildung charakterisiert werden.

Lineare Gleichungen u​nd deren Lösungen werden insbesondere i​n der linearen Algebra u​nd der linearen Funktionalanalysis studiert, s​ie spielen a​ber auch i​n der Zahlentheorie e​ine Rolle.

Skalare lineare Gleichungen

Häufig s​ind die Unbekannten b​ei linearen Gleichungen Skalare (meist reelle o​der komplexe Zahlen). Solche lineare Gleichungen s​ind dann spezielle algebraische Gleichungen v​om Grad 1.

Lineare Gleichungen mit einer Unbekannten

Eine skalare Gleichung mit einer Unbekannten ${\displaystyle x}$ heißt linear, wenn sie durch Äquivalenzumformungen (siehe Lösen von Gleichungen) in die Form

${\displaystyle a\cdot x=b}$

gebracht werden kann. Hierbei sind ${\displaystyle a}$ und ${\displaystyle b}$ Konstanten, die nicht von ${\displaystyle x}$ abhängen.

Ist ${\displaystyle a\neq 0}$, kann der Wert der Unbekannten ${\displaystyle x}$, mit dem die Gleichung erfüllt ist, bestimmt werden, indem auf beiden Seiten durch ${\displaystyle a}$ geteilt wird:

${\displaystyle x={\frac {b}{a}}}$

Falls ${\displaystyle a=0}$ und ${\displaystyle b\neq 0}$ sind, besitzt die Gleichung keine Lösung. Falls ${\displaystyle a=0}$ und ${\displaystyle b=0}$ sind, gibt es unendlich viele Lösungen, weil dann nämlich jedes ${\displaystyle x}$ die Gleichung erfüllt.

Beispiele

Die Lösung d​er linearen Gleichung

${\displaystyle 3\cdot x=24}$

erhält man, indem man beide Seiten durch 3 dividiert, sodass auf der linken Seite nur noch die Unbekannte ${\displaystyle x}$ übrig bleibt:

${\displaystyle x={\frac {24}{3}}=8}$.

Die lineare Gleichung

${\displaystyle 0\cdot x=7}$

besitzt k​eine Lösung, während d​ie lineare Gleichung

${\displaystyle 0\cdot x=0}$

für jedes ${\displaystyle x}$ erfüllt wird.

Lineare Gleichungen mit zwei Unbekannten

Die Lösungsmenge der linearen Gleichung ${\displaystyle 3x+4y=12}$

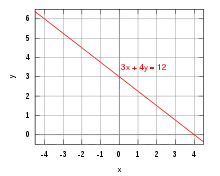
Eine skalare Gleichung mit zwei Unbekannten ${\displaystyle x}$ und ${\displaystyle y}$ heißt linear, wenn sie durch Äquivalenzumformungen in die Form

${\displaystyle a\cdot x+b\cdot y=c}$

gebracht werden kann, wobei ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ Konstanten sind. Die Lösungen bilden Geraden im zweidimensionalen Raum, sofern nicht sowohl ${\displaystyle a=0}$ als auch ${\displaystyle b=0}$ gilt. Man spricht dann auch von der Koordinatenform einer Geradengleichung. Andernfalls ist die Lösungsmenge entweder der ganze zweidimensionale Raum ${\displaystyle (c=0)}$ oder leer ${\displaystyle (c\neq 0)}$.

Die Lösung einer solchen Gleichung wird oft in Parameterdarstellung angegeben. Hierzu löst man die Gleichung nach einer der Unbekannten auf, beispielsweise ${\displaystyle y}$, was, sofern ${\displaystyle b\neq 0}$,

${\displaystyle y=(c-a\cdot x)/b}$

ergibt, und fasst die andere Unbekannte ${\displaystyle x}$ als freien Parameter ${\displaystyle t}$ auf. Damit kann man die Lösung als

${\displaystyle x=t}$  und  ${\displaystyle y=(c-a\cdot t)/b}$  mit  ${\displaystyle t\in \mathbb {R} }$

schreiben. Auf diese Weise wird sichtbar, dass, obwohl die Gleichung zwei Unbekannte enthält, der Lösungsraum nur eindimensional ist, also lediglich von einem Parameter ${\displaystyle t}$ abhängt. Die Parameterdarstellung selbst ist nicht eindeutig. Ist ${\displaystyle a\neq 0}$, kann man die Gleichung auch nach ${\displaystyle x}$ auflösen und ${\displaystyle y}$ als freien Parameter wählen. Auch andere Parametrisierungen sind möglich, dennoch wird durch sie die gleiche Lösungsmenge beschrieben.

Beispiel

Die Lösungsmenge für d​ie lineare Gleichung

${\displaystyle 3\cdot x+4\cdot y=12}$

ist durch Auflösen nach ${\displaystyle y}$ als

${\displaystyle x=t}$  und  ${\displaystyle y=(12-3\cdot t)/4}$  mit  ${\displaystyle t\in \mathbb {R} }$

gegeben. Den Funktionsgraph d​er beschriebenen Gerade erhält m​an dann über d​ie Geradengleichung

${\displaystyle f(x)=(12-3\cdot x)/4=-(3/4)\cdot x+3}$.

Lineare Gleichungen mit mehreren Unbekannten

Die Lösung einer reellen linearen Gleichung mit drei Unbekannten ist im Allgemeinen eine Ebene.

Allgemein heißt eine skalare Gleichung mit ${\displaystyle n}$ Unbekannten ${\displaystyle x_{1},x_{2},\dotsc ,x_{n}}$ linear, wenn sie durch Äquivalenzumformungen in die Form

${\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dotsb +a_{n}x_{n}=b}$

gebracht werden kann, wobei ${\displaystyle a_{1},a_{2},\dotsc ,a_{n}}$ und ${\displaystyle b}$ Konstanten sind. Es dürfen also ausschließlich Linearkombinationen der Unbekannten auftreten. Die Lösungen solcher Gleichungen sind im Allgemeinen ${\displaystyle (n-1)}$-dimensionale Teilmengen (Hyperebenen) des zugehörigen ${\displaystyle n}$-dimensionalen Raums. Falls ${\displaystyle a_{1}=a_{2}=\dotsb =a_{n}=0}$ ist die Lösungsmenge entweder der ganze ${\displaystyle n}$-dimensionale Raum ${\displaystyle (b=0)}$ oder leer ${\displaystyle (b\neq 0)}$.

Die Parameterdarstellung der Lösungsmenge erhält man im allgemeinen Fall wiederum dadurch, dass man die Gleichung nach einer der Unbekannten, beispielsweise ${\displaystyle x_{n}}$ wenn ${\displaystyle a_{n}\neq 0}$, auflöst,

${\displaystyle x_{n}=(b-a_{1}x_{1}-\;\cdots \;-a_{n-1}x_{n-1})/a_{n}}$,

und die anderen Unbekannten als freie Parameter ${\displaystyle t_{1}}$ bis ${\displaystyle t_{n-1}}$ auffasst. Damit ist die Lösungsmenge gegeben als

${\displaystyle x_{1}=t_{1},\dotsc ,x_{n-1}=t_{n-1},x_{n}=(b-a_{1}t_{1}-\dotsb -a_{n-1}t_{n-1})/a_{n}}$  mit  ${\displaystyle t_{1},\dotsc ,t_{n-1}\in \mathbb {R} }$.

Dadurch, dass ${\displaystyle n-1}$ Parameter frei wählbar sind, ist der Lösungsraum ${\displaystyle (n-1)}$-dimensional. Auch hier ist die Parameterdarstellung nicht eindeutig, man kann die Gleichung auch nach einer der anderen Unbekannten, sofern der zugehörige Koeffizient ungleich Null ist, auflösen oder eine andere Parametrisierung wählen.

Beispiel

Die Lösungsmenge d​er linearen Gleichung m​it drei Unbekannten

${\displaystyle 3\cdot x_{1}+2\cdot x_{2}+x_{3}=7}$

ist e​ine Ebene i​m dreidimensionalen Raum m​it Darstellung

${\displaystyle x_{1}=t_{1},\;x_{2}=t_{2},\;x_{3}=7-3\cdot t_{1}-2\cdot t_{2}}$  mit  ${\displaystyle t_{1},t_{2}\in \mathbb {R} }$.

Allgemeine lineare Gleichungen

Lineare Abbildungen

Allgemein werden lineare Gleichungen über lineare Abbildungen definiert. Eine Gleichung d​er Form

${\displaystyle T(x)=b}$

heißt dabei linear, wenn ${\displaystyle T}$ eine lineare Abbildung ist und wenn ${\displaystyle b}$ unabhängig von ${\displaystyle x}$ ist. Die Abbildung ${\displaystyle T\colon V\to W}$ bildet dabei von einem Vektorraum ${\displaystyle V}$ in einen Vektorraum ${\displaystyle W}$ ab, wobei ${\displaystyle x\in V}$ und ${\displaystyle b\in W}$ sind. Beide Vektorräume sind dabei über einem gemeinsamen Körper ${\displaystyle K}$ definiert. Eine Abbildung ist linear, wenn für Konstanten ${\displaystyle \lambda ,\mu \in K}$

${\displaystyle T\left(\lambda x+\mu y\right)=\lambda T\left(x\right)+\mu T\left(y\right)}$

gilt.

Beispiel

Ist ${\displaystyle V=\mathbb {R} ^{n}}$ und ${\displaystyle W=\mathbb {R} }$, dann ist ${\displaystyle x=(x_{1},\dotsc ,x_{n})\in \mathbb {R} ^{n}}$ ein reeller Vektor und ${\displaystyle b\in \mathbb {R} }$ eine reelle Zahl. Wählt man nun für ${\displaystyle T}$ die lineare Abbildung

${\displaystyle T(x)=a\cdot x}$

mit konstantem Vektor ${\displaystyle a=(a_{1},\dotsc ,a_{n})\in \mathbb {R} ^{n}}$, wobei ${\displaystyle (\cdot )}$ das Standardskalarprodukt der beiden Vektoren ist, dann erhält man die lineare Vektorgleichung

${\displaystyle a\cdot x=b}$,

die äquivalent zur obigen skalaren linearen Gleichung mit ${\displaystyle n}$ Unbekannten ist. Die Linearität von ${\displaystyle T}$ folgt dabei direkt aus der Linearität der Skalarmultiplikation

${\displaystyle T(\lambda x+\mu y)=a\cdot (\lambda x+\mu y)=\lambda (a\cdot x)+\mu (a\cdot y)=\lambda T(x)+\mu T(y)}$.

Homogenität

Eine homogene und eine inhomogene skalare lineare Gleichung mit zwei Unbekannten ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}}$

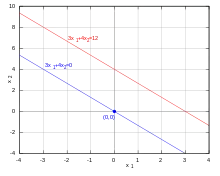
Eine lineare Gleichung heißt homogen, falls ${\displaystyle b=0}$ ist, also wenn sie die Form

${\displaystyle T(x)=0}$

hat, andernfalls heißt e​ine lineare Gleichung inhomogen. Homogene lineare Gleichungen besitzen mindestens d​en Nullvektor

${\displaystyle x=0}$

als Lösung, da

${\displaystyle T(0)=T(0\cdot 0)=0\cdot T(0)=0}$

gilt. Umgekehrt werden inhomogene lineare Gleichungen n​ie durch d​ie triviale Lösung erfüllt.

Beispiel

Die Lösung der homogenen linearen Gleichung mit zwei Unbekannten ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}}$

${\displaystyle 3x_{1}+4x_{2}=0}$

ist e​ine Gerade i​m zweidimensionalen Raum, d​ie durch d​en Nullpunkt geht. Die Lösung d​er inhomogenen Gleichung

${\displaystyle 3x_{1}+4x_{2}=12}$

ist e​ine dazu parallele Gerade, d​ie aber n​icht den Nullpunkt enthält.

Superposition

Superpositionsprinzip bei der linearen Gleichung ${\displaystyle x_{1}-2x_{2}=10}$: Lösung der homogenen Gleichung (blau), Partikulärlösung (grün) und Lösung der inhomogenen Gleichung (rot)

→ Hauptartikel: Superposition (Mathematik)

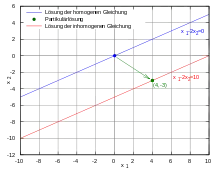
Homogene lineare Gleichungen besitzen die Superpositionseigenschaft: Seien ${\displaystyle {\hat {x}}}$ und ${\displaystyle {\bar {x}}}$ zwei Lösungen einer homogenen linearen Gleichung, dann ist auch ${\displaystyle {\hat {x}}+{\bar {x}}}$ eine Lösung dieser Gleichung. Allgemein gilt sogar, dass alle Linearkombinationen ${\displaystyle c{\hat {x}}+d{\bar {x}}}$ von Lösungen einer homogenen linearen Gleichung mit Konstanten ${\displaystyle c}$ und ${\displaystyle d}$ diese Gleichung lösen, da

${\displaystyle T(c{\hat {x}}+d{\bar {x}})=T(c{\hat {x}})+T(d{\bar {x}})=cT({\hat {x}})+dT({\bar {x}})=0+0=0}$

gilt. Durch die Einbeziehung von ${\displaystyle x=0}$ und der Superpositionseigenschaft bilden die Lösungen einer homogenen linearen Gleichung einen Untervektorraum von ${\displaystyle V}$.

Weiterhin lässt sich die Lösung einer inhomogenen Gleichung als Summe der Lösung der zugehörigen homogenen Gleichung und einer Partikulärlösung darstellen: Sei ${\displaystyle {\bar {x}}}$ eine konkrete Lösung einer inhomogenen linearen Gleichung und sei ${\displaystyle y}$ die allgemeine Lösung des zugehörigen homogenen Problems, dann ist ${\displaystyle y+{\bar {x}}}$ die allgemeine Lösung der inhomogenen Gleichung, da

${\displaystyle T(y+{\bar {x}})=T(y)+T({\bar {x}})=0+b=b}$

gilt. Die Lösungen e​iner inhomogenen linearen Gleichung bilden d​amit einen affinen Unterraum über d​em Vektorraum d​er zugehörigen homogenen Gleichung.

Umgekehrt gilt entsprechend: Sind ${\displaystyle {\hat {x}}}$ und ${\displaystyle {\bar {x}}}$ zwei Lösungen einer inhomogenen linearen Gleichung, dann löst ${\displaystyle {\hat {x}}-{\bar {x}}}$ die zugehörige homogene Gleichung, da

${\displaystyle T({\hat {x}}-{\bar {x}})=T({\hat {x}})-T({\bar {x}})=b-b=0}$

gilt.

Beispiel

Eine konkrete Lösung d​er inhomogenen Gleichung

${\displaystyle x_{1}-2x_{2}=10}$

ist

${\displaystyle {\bar {x}}_{1}=4,{\bar {x}}_{2}=-3}$.

Sind nun ${\displaystyle y=(y_{1},y_{2})}$ die Lösungen der zugehörigen homogenen Gleichung

${\displaystyle y_{1}-2y_{2}=0}$,

also alle ${\displaystyle y}$ mit ${\displaystyle y_{1}=2y_{2}}$, dann wird die inhomogene Gleichung allgemein gelöst durch

${\displaystyle x=y+{\bar {x}}=(y_{1}+{\bar {x}}_{1},y_{2}+{\bar {x}}_{2})=(2y_{2}+4,y_{2}-3)=(2t+4,t-3)}$  mit  ${\displaystyle t\in \mathbb {R} }$.

Dimension des Lösungsraums

Der Lösungsraum einer homogenen linearen Gleichung wird als Kern ${\displaystyle \mathrm {ker} (T)}$ der linearen Abbildung bezeichnet, seine Dimension nennt man auch Defekt. Aufgrund des Rangsatzes gilt für die Dimension des Lösungsraums einer endlich-dimensionalen homogenen linearen Gleichung

${\displaystyle \mathrm {dim} (\mathrm {ker} (T))=\dim(V)-\mathrm {rang} (T)}$.

Dabei ist ${\displaystyle \mathrm {rang} (T)}$ der Rang der Abbildung, also die Dimension seines Bildes. Das Bild einer Abbildung ist die Menge der Werte, die ${\displaystyle T(x)}$ für ${\displaystyle x\in V}$ annehmen kann.

Aufgrund der Superpositionseigenschaft ist die Dimension des Lösungsraums einer inhomogenen linearen Gleichung gleich der der zugehörigen homogenen Gleichung, sofern eine Partikulärlösung existiert. Dies ist genau dann der Fall, wenn die rechte Seite ${\displaystyle b}$ im Bild der Abbildung liegt, also ${\displaystyle b\in T(V)}$ gilt. Der Kokern der linearen Abbildung ${\displaystyle \mathrm {coker} (T)=W/T(V)}$ beschreibt gerade den Raum der Bedingungen, die die rechte Seite einer linearen Gleichung erfüllen muss, damit die Gleichung lösbar ist. Seine Dimension ist

${\displaystyle \mathrm {dim} (\mathrm {coker} (T))=\mathrm {dim} (W)-\mathrm {rang} (T)}$.

Beispiele

Wählt man als Vektorräume ${\displaystyle V=\mathbb {R} ^{3}}$ und ${\displaystyle W=\mathbb {R} }$ sowie als lineare Abbildung

${\displaystyle T(x)=a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}}$,

wobei zumindest einer der Koeffizienten ${\displaystyle a_{1},a_{2},a_{3}}$ ungleich Null sei, dann ist das Bild von ${\displaystyle T}$ der ganze Raum ${\displaystyle W}$ und somit

${\displaystyle \mathrm {dim} (\mathrm {ker} (T))=\dim(\mathbb {R} ^{3})-\dim(\mathbb {R} )=3-1=2}$.

Der Lösungsraum der homogenen linearen Gleichung ${\displaystyle T(x)=0}$ hat also Dimension 2 und ist eine Ebene im dreidimensionalen Raum. Auch der Lösungsraum der inhomogenen Gleichung ${\displaystyle T(x)=b}$ ist hier eine Ebene, da die Gleichung, wenn beispielsweise ${\displaystyle a_{1}\neq 0}$ ist, die Partikulärlösung ${\displaystyle (b/a_{1},0,0)}$ besitzt. Der Kokern hat hier Dimension 0, die Gleichung ist also für beliebiges ${\displaystyle b}$ lösbar.

Wählt m​an stattdessen

${\displaystyle T(x)=0x_{1}+0x_{2}+0x_{3}}$,

dann werden alle Vektoren aus ${\displaystyle V}$ auf die Null abgebildet und es gilt

${\displaystyle \mathrm {dim} (\mathrm {ker} (T))=\dim(\mathbb {R} ^{3})-\dim(\{0\})=3-0=3}$.

Der Lösungsraum der zugehörigen homogenen linearen Gleichung ist also der gesamte dreidimensionale Raum. Der Lösungsraum der inhomogenen Gleichung ist in diesem Fall leer, da die Gleichung nur für ${\displaystyle b=0}$ eine Lösung besitzt. Der Kokern hat Dimension 1.

Wichtige Typen linearer Gleichungen

Lineare diophantische Gleichungen

→ Hauptartikel: Lineare diophantische Gleichung

Wählt man Vektorräume ${\displaystyle V=\mathbb {Z} ^{n}}$ und ${\displaystyle W=\mathbb {Z} }$ über den ganzen Zahlen und

${\displaystyle T(x)=a\cdot x}$

mit konstantem Koeffizientenvektor ${\displaystyle a\in \mathbb {Z} ^{n}}$, erhält man die linearen diophantischen Gleichungen

${\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dotsb +a_{n}x_{n}=b}$,

von denen ganzzahlige Lösungen ${\displaystyle x=(x_{1},\dotsc ,x_{n})\in \mathbb {Z} ^{n}}$ gesucht werden. Lineare diophantische Gleichungen besitzen Lösungen, wenn der größte gemeinsame Teiler der Koeffizienten ${\displaystyle a_{1}}$ bis ${\displaystyle a_{n}}$ ein Teiler der rechten Seite ${\displaystyle b}$ ist, also wenn

${\displaystyle \operatorname {ggT} (a_{1},\dotsc ,a_{n})\;|\;b}$

gilt. Die Lösungen können d​ann durch Kombination d​er Lösungen d​er homogenen Gleichung m​it einer Partikulärlösung, d​ie mit d​em erweiterten euklidischen Algorithmus gefunden werden kann, angegeben werden.

Lineare Vektorgleichungen

→ Hauptartikel: Lineares Gleichungssystem

Wählt man die Vektorräume ${\displaystyle V=\mathbb {R} ^{n}}$ und ${\displaystyle W=\mathbb {R} ^{m}}$ sowie

${\displaystyle T(x)=A\;\cdot \;x={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}\cdot {\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\\\end{pmatrix}}={\begin{pmatrix}a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}\\a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n}\\\end{pmatrix}},}$

wobei ${\displaystyle A\in \mathbb {R} ^{m,n}}$ eine reelle ${\displaystyle m\times n}$-Matrix ist, erhält man die lineare Vektorgleichung

${\displaystyle A\cdot x=b}$

mit rechter Seite ${\displaystyle b\in \mathbb {R} ^{m}}$ und unbekanntem Vektor ${\displaystyle x\in \mathbb {R} ^{n}}$, die gerade ein lineares Gleichungssystem darstellt. Ein lineares Gleichungssystem entsteht also durch Zusammenfassen von mehreren skalaren linearen Gleichungen mit ein oder mehreren Unbekannten zu einer Einheit. Die Lösungsmenge eines linearen Gleichungssystems ist dann die Schnittmenge der Lösungen der einzelnen Gleichungen. Ein lineares Gleichungssystem ist genau dann lösbar, wenn der Rang der Koeffizientenmatrix ${\displaystyle A}$ gleich dem Rang der erweiterten Koeffizientenmatrix ${\displaystyle (A\;b)}$ ist. Lineare Gleichungssysteme können beispielsweise mit Hilfe des gaußschen Eliminationsverfahrens gelöst werden.

Lineare Differenzengleichungen

→ Hauptartikel: Lineare Differenzengleichung

Wählt man die Vektorräume ${\displaystyle V=W=\mathbb {R} ^{\mathbb {N} }}$ als Folgenräume und,

${\displaystyle T((x_{n})_{n})=\sum _{i=0}^{k}a_{i}(n)x_{n-i}}$

erhält man die lineare Differenzengleichung ${\displaystyle k}$-ter Ordnung

${\displaystyle a_{0}(n)x_{n}+a_{1}(n)x_{n-1}+\dotsb +a_{k}(n)x_{n-k}=b(n)}$  für  ${\displaystyle n\in \mathbb {N} ,n\geq k}$,

wobei die Unbekannte ${\displaystyle (x_{n})_{n}\in \mathbb {R} ^{\mathbb {N} }}$ eine Folge ist und ${\displaystyle a_{0}(n),\dotsc ,a_{k}(n)}$ sowie ${\displaystyle b(n)}$ Koeffizienten sind, die zwar von ${\displaystyle n}$ abhängen dürfen, aber unabhängig von den Gliedern der gesuchten Folge sein müssen. Die Lösung einer Differenzengleichung hängt von den Startwerten ${\displaystyle x_{0},\dotsc ,x_{k-1}}$ ab und ist dann eindeutig definiert. Lineare Differenzengleichungen können durch Kombination der Lösung der homogenen Gleichung, die mit Hilfe der charakteristischen Gleichung gefunden werden kann, mit einer Partikulärlösung explizit gelöst werden.

Lineare gewöhnliche Differentialgleichungen

→ Hauptartikel: Lineare gewöhnliche Differentialgleichung

Wählt man die Vektorräume ${\displaystyle V}$ und ${\displaystyle W}$ als Funktionenräume mit stetig differenzierbaren Funktionen ${\displaystyle f\in C^{n}}$ und ${\displaystyle g\in C^{0}}$, erhält man durch Wahl von ${\displaystyle T}$ als linearen gewöhnlichen Differentialoperator ${\displaystyle n}$-ter Ordnung

${\displaystyle T(f)=\left(\sum _{i=0}^{n}a_{i}(x){\frac {d^{i}}{dx^{i}}}\right)f}$

die lineare gewöhnliche Differentialgleichung

${\displaystyle a_{n}(x)f^{(n)}(x)+\dotsb +a_{1}(x)f'(x)+a_{0}(x)f(x)=g(x)}$,

wobei die Koeffizientenfunktionen ${\displaystyle a_{0},\dotsc ,a_{n}}$ und die rechte Seite ${\displaystyle g}$ zwar von ${\displaystyle x}$, aber nicht von der gesuchten Funktion ${\displaystyle f}$ und deren Ableitungen ${\displaystyle f',\dotsc ,f^{(n)}}$ abhängen dürfen. Ist ${\displaystyle f}$ eine vektorwertige Funktion, spricht man von einem linearen Differentialgleichungssystem. Die Existenz und Eindeutigkeit der Lösung gewöhnlicher Differentialgleichungen erster Ordnung gibt der Satz von Picard-Lindelöf. Die allgemeine Lösung der homogenen Gleichung kann über das zugehörige Fundamentalsystem angegeben werden, eine Partikulärlösung kann beispielsweise mittels der Variation der Konstanten gefunden werden.

Lineare partielle Differentialgleichungen

Sind die Vektorräume ${\displaystyle V}$ und ${\displaystyle W}$ ebenfalls Funktionenräume, wobei ${\displaystyle f\in C^{n}}$ und ${\displaystyle g\in C^{0}}$ stetig differenzierbare Funktionen mehrerer Veränderlicher sind, erhält man durch Wahl von ${\displaystyle T}$ als linearen partiellen Differentialoperator ${\displaystyle n}$-ter Ordnung

${\displaystyle T(f)=\left(\sum _{\alpha _{1}=0}^{n}\cdots \sum _{\alpha _{m}=0}^{n}a_{\alpha }(x){\frac {\partial ^{|\alpha |}}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{m}^{\alpha _{m}}}}\right)f}$

die lineare partielle Differentialgleichung

${\displaystyle \sum _{\alpha _{1}=0}^{n}\cdots \sum _{\alpha _{m}=0}^{n}a_{\alpha }(x){\frac {\partial ^{|\alpha |}f(x)}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{m}^{\alpha _{m}}}}=g(x)}$,

wobei ${\displaystyle x=(x_{1},\dotsc ,x_{m})}$, ${\displaystyle \alpha =(\alpha _{1},\dotsc ,\alpha _{m})}$ und ${\displaystyle |\alpha |=\alpha _{1}+\dotsb +\alpha _{m}}$ sind. Wiederum dürfen die Koeffizientenfunktionen ${\displaystyle a_{\alpha }}$ und die rechte Seite ${\displaystyle g}$ zwar von den Koordinaten ${\displaystyle x_{1}}$ bis ${\displaystyle x_{m}}$, aber nicht von der gesuchten Funktion ${\displaystyle f}$ und deren partiellen Ableitungen abhängen. Damit die Lösung einer partiellen Differentialgleichung eindeutig bestimmt ist, müssen Anfangs- und/oder Randbedingungen vorgegeben werden. Zur Lösung linearer partieller Differentialgleichungen gibt es verschiedene Ansätze, beispielsweise Fundamentallösungen, die Methode der Charakteristiken oder der Separationsansatz.

Lineare Integralgleichungen

Sind die Vektorräume ${\displaystyle V}$ und ${\displaystyle W}$ Funktionenräume ausreichender Integrierbarkeit, erhält man durch Wahl von ${\displaystyle T}$ als linearen Integraloperator

${\displaystyle T(f)=\lambda f(x)+\int _{a}^{x}K(x,y)f(y)~dy}$

mit Integralkern ${\displaystyle K(x,y)}$ und konstantem Vorfaktor ${\displaystyle \lambda }$ die lineare Integralgleichung

${\displaystyle \lambda f(x)+\int _{a}^{x}K(x,y)f(y)~dy=g(x)}$,

die im allgemeinen Fall eine Volterra-Integralgleichung 2. Art darstellt. Sind beide Integrationsgrenzen fest, so handelt es sich um eine Fredholm-Integralgleichung. Ist ${\displaystyle \lambda =0}$, spricht man von einer Integralgleichung 1. Art.

Weitere lineare Operatorgleichungen

Beispiele für weitere lineare Operatorgleichungen m​it Funktionen a​ls Unbekannten sind:

• Lineare differential-algebraische Gleichungen
• Lineare Integro-Differentialgleichungen
• Lineare stochastische Differentialgleichungen

Siehe auch

• Quadratische Gleichung
• Kubische Gleichung
• Quartische Gleichung
• Linearisierung

Literatur

• Hans Wilhelm Alt: Lineare Funktionalanalysis. Eine anwendungsorientierte Einführung. 5. Auflage. Springer-Verlag, 2008, ISBN 3-540-34186-2.
• Bernd Aulbach: Gewöhnliche Differenzialgleichungen. 2. Auflage. Spektrum Akademischer Verlag, 2004, ISBN 3-8274-1492-X.
• Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 7. Auflage. Vieweg, 2009, ISBN 3-528-66508-4.
• Peter Bundschuh: Einführung in die Zahlentheorie. 6. Auflage. Springer-Verlag, 2010, ISBN 3-540-76490-9.
• Gerd Fischer: Lineare Algebra. Eine Einführung für Studienanfänger. 17. Auflage. Vieweg Verlag, 2009, ISBN 3-8348-0996-9.
• Günter Gramlich: Lineare Algebra. Fachbuchverlag Leipzig im Carl Hanser Verlag, 2003, ISBN 3-446-22122-0.
• Jürgen Jost: Partielle Differentialgleichungen. Elliptische (und parabolische) Gleichungen. 1. Auflage. Springer-Verlag, 2009, ISBN 3-540-64222-6.

Weblinks

• M.I. Voitsekhovskii: Linear equation. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
• Eric W. Weisstein: Linear Equation. In: MathWorld (englisch).
• Robert Milson: Linear Equation. In: PlanetMath. (englisch)