Zinseszins

Zinseszins ist im Finanzwesen ein Zins, der auf fällige, dem Kapital hinzugefügte (kapitalisierte) Zinsen erhoben wird, die damit zum geltenden Zinssatz zusammen mit dem Kapital erneut verzinst werden.

Allgemeines

Die Verzinsung von Kapital (in Form des Darlehens (Kredits) oder als Geldanlage) ist der Preis für die befristete Überlassung der knappen Ressource Kapital. Wird fälliger Kreditzins bezahlt oder fälliger Habenzins vom Anleger verbraucht (umgekehrt beim Negativzins), stellt sich die Frage des Zinseszinses nicht, weil dann künftig lediglich das reine Kapital zu verzinsen ist. Erst wenn die fälligen Kredit- oder Habenzinsen durch Kapitalisierung zum Bestandteil des Kapitals werden, tritt der Effekt des Zinseszinses ein. Denn durch Kapitalisierung erhöht sich das Kapital um den nicht bezahlten oder nicht verbrauchten Zins, sodass dieser ebenfalls weiter verzinst wird. Bekanntestes Beispiel ist die Kapitalisierung des gutgeschriebenen und nicht verbrauchten Sparzinses auf Sparbüchern.[1]

Geschichte

Religiöse oder weltliche Vorschriften befassten sich in der Vergangenheit häufig mit Zinsverboten oder dem Verbot von Zinseszinsen. Begründet wird das Verbot von Zinseszinsen damit, dass der Schuldner durch die Zinslast nicht erdrückt werden soll. Der Zinseszins ist so alt wie der Zins, von dem er abhängt. Um 2400 v. Chr. dürfte bei den Sumerern der älteste Zinsbegriff (maš; deutsch „Kalb, Ziegenjunges“) entstanden sein, ein Begriff, der auf den Naturallohn hindeutet.[2] Auch der Zinseszins (mašmaš) hat hier seinen Ursprung. Als Entlastung für das zinseszinsbedingte Anwachsen der Schulden ermöglichten die Sumerer unter ihrem König En-metena um 2402 v. Chr. einen Schuldenerlass. Im Codex Hammurapi von 1755/1754 v. Chr. durfte Zinseszins berechnet werden, soweit fälliger und nicht bezahlter Zins vom Kapitalstock getrennt blieb und der Gläubiger ihn für den Schuldner verzinste. Das Vorgehen sollte vor ungebührlicher Zahlungsmoral des Schuldners schützen.[3]

Das römische Recht sah Zinseszins (usurae usurarum) vor und war bei Cicero noch statthaft.[4] Als Regelfall kannte es das mutuum, ein zinsloses Darlehen meist aus Gefälligkeit an Verwandte oder Freunde, bei dem Zinsen nur über ein eigenes Rechtsgeschäft, die Stipulation, erhoben werden durften. Mit dem spätantiken Kaiser Iustinian kam im 6. Jahrhundert n. Chr. ein Verbot für die Fälle, in denen rückständige Zinsen die Höhe des Kapitalstocks überschritten und ihn gar verdoppelten (ultra alterum tantum).[5] Eine dahingehend lautende Vorschrift ist im österreichischen § 1335 ABGB noch heute enthalten. Die Digesten halten fest, was bereits der spätklassische Jurist Ulpian ausführte, nämlich die umfassende Unzulässigkeit von Zinseszins.[6] Justinian wiederholte die Forderung: nullo modo usurae usurarum a debitoribus exigantur.[7] Bereits Diokletian hatte verlangt, dass bei der Kreditablösung keine Nachteile erwachsen dürften und er ließ Zinseszinsen nicht zu (Anatozismus (griechisch ανατοκισμός anatokismós „Nehmen von Zinseszins“, aus aná „auf“ und tókos „Zins“)).

Der indische Mathematiker Aryabhata legte im 5. Jahrhundert erste mathematische Zinseszinsberechnungen vor.[8]

Dort, wo ein Zinsverbot galt, erübrigte sich das Thema des Zinseszinses. Das jüdische Bundesbuch verbot zwischen 1000 und 800 vor Christus den Zins bei Krediten an Arme (Ex 22,24 ). Das Deuteronominum verlangt: „Du sollst von Deinen Volksgenossen keinen Zins nehmen, weder Zins für Geld, noch Zins für Speise, noch Zins für irgendetwas, was man leihen kann“ (Dtn 23,20 ). Unter „Volksgenossen“ verstand der Tanach nur die Juden. Mit Aufkommen des Christentums stieß die Zinszahlung auf heftige Kritik der Kirche, denn in Not geratene bedürftige Personen sollten zinslose Darlehen bekommen (Lev 25,36-37 ). Als eigentlicher Ausgangspunkt des Zinsverbots gilt das Gebot des 5. Buch Mose „Du soll von deinem Bruder nicht Zins nehmen, weder für Geld noch für Speise noch für alles wofür man Zinsen nehmen kann“ (Dtn 23,20-21 ). Das kanonische Recht erklärte Zinseinnahmen für Raub.[9] Der Islam übernahm das christliche Zinsverbot und forderte nach 622 n. Chr. dazu auf, nicht Zins (arabisch ribā; „Zuwachs, Vermehrung“) zu nehmen, indem die Gläubiger in mehrfachen Beträgen wiedernehmen, was sie ausgeliehen haben (Koran, Sure 3:130).[10] Gleich mehrere Suren befassen sich mit dem Zinsverbot. In Sure 2:275 erklärt Allah den Kaufvertrag (bay‘) für zulässig (halāl) und den Zins für verboten (harām).

Im Mittelalter war die Erhebung von Zinseszins „Schaden“ gleichgestellt. Der italienische Rechenmeister Leonardo Fibonacci legte 1228 weitere Zinseszinsberechnungen auf der Grundlage des Julianischen Kalenders vor.[11] In Österreich gestattete das Fridericianum im Jahre 1244 den Juden in Artikel 23 den Zinseszins.[12] In Frankfurt am Main verpflichtete sich 1368 ein Schuldner gegenüber seinem jüdischen Gläubiger, sich von nicht bezahlten Zinsen Zinseszinsen berechnen zu lassen. Der Mainzer Erzbischof Dietrich Schenk von Erbach verbot 1457 den Juden seiner Diözese den Zinseszins, musste dies jedoch im selben Jahr wieder revidieren.[13] Kaiser Friedrich III. erklärte im Jahre 1470, Handel und Gewerbe könnten ohne Zinseszins nicht bestehen; es sei das kleinere Übel, wenn man den Juden das Nehmen von Zinseszins erlaube, als wenn man es den Christen zulasse.[14] Das kirchliche Zinsverbot und die weltlichen Höchstzinsen beschränkten sich ab dem 16. Jahrhundert auf den Zinseszins.[15]

In Schleswig-Holstein erließ Herzog Friedrich III. am 23. März 1654 eine „Constitution von den Zinseszinsen der Capitalien der Minderjährigen“, die die Berechnung von Zinseszinsen unter Geldstrafe stellte. Jakob I Bernoulli forderte 1689 eine tägliche Berechnung der Zinseszinsen.[16] Eine Triersche Verordnung vom 31. Oktober 1768 bestimmte: „Wer Zinsen von Zinsen nimmt, wird gleich demjenigen bestraft, welcher sich mehr als 6 % bezahlen lässt“.[17] Der Moralphilosoph Richard Price entwickelte im Jahre 1772 die Parabel vom Josephspfennig als Ratschlag an seine Regierung zur Sanierung des englischen Staatshaushalts, der durch den Zinseszinseffekt ein Haushaltsdefizit aufwies. Price rechnete vor, wenn Josef von Nazaret bei der Geburt seines Sohnes Jesus Christus einen Penny zu 5 % Zins angelegt hätte, so wäre dies bei Kapitalisierung zum Gewicht von 150 Millionen Erden angewachsen.[18] Er beschrieb, dass „Geld, das Zinseszinsen trägt, wächst anfangs langsam; da aber die Rate des Wachstums sich fortwährend beschleunigt, wird sie nach einiger Zeit so rasch, dass sie jeder Einbildung spottet“.[19]

Das preußische Landrecht (PrALR) von 1794 stellte fest: „Zinsen von Zinsen dürfen nicht gefordert werden“ (I 11, § 818 APL), es sei denn, es liegt eine gerichtliche Zustimmung vor (I 11, § 820 APL). Der französische Code civil wich vom absoluten Zinseszinsverbot ab. War der Zinsrückstand höher als ein Jahresbetrag, so konnte er durch Gerichtsurteil zinstragend werden (Art. 1154 Code civil). Daran knüpfte das 1812 in Kraft getretene österreichische ABGB an, indem es vorsah: „Zinsen von Zinsen dürfen nie genommen werden; doch können zweijährige oder noch ältere Zinsenrückstände mittelst Uebereinkommens als ein neues Capital verschrieben werden“ (§ 998 ABGB). Das Oberhandelsgericht (OHG) Lübeck entschied 1855, dass Zinseszinsen beim Kontokorrent zulässig sind.[20] Das sächsische BGB vom März 1865 verbot Zinsen von rückständigen Zinsen, selbst wenn letztere rechtskräftig anerkannt sind (§ 679 Sachsen-BGB). Die Juristen unterschieden in jener Zeit zwischen Zinsen, die als solche verzinst werden (anatocismus separatus) und den nach eingetretener Fälligkeit kapitalisierten Zinsen (anatocismus conjunctus). Kein Anatozismus lag mithin vor, wenn die Zinsen bezahlt oder verbraucht sind.

Karl Marx fasste in seinem 1867 erschienenen Hauptwerk Das Kapital den Akkumulationsprozess des Kapitals in der Wirtschaft als Akkumulation von Zinseszins auf und sah den Zinseszins als Teil des Mehrwerts, der in Kapital zurückverwandelt wird.[21] Albert Einstein soll im Jahr 1921 bemerkt haben, dass die „größte Erfindung des menschlichen Denkens der Zinseszins“ sei.[22]

Rechtsfragen

Das BGB ist vom Grundsatz der Vertragsfreiheit geprägt, was Spielraum für Zinsfreiheit einräumt. Zinsvereinbarungen sind generell erlaubt, nur bestimmte, den Zinsschuldner benachteiligende Vereinbarungen sind untersagt. So ist die vorherige Verabredung von Zinseszins (Anatozismus) gemäß § 248 Abs. 1 BGB verboten. Entgegenstehende Vereinbarungen sind nichtig, § 134 BGB. Ausnahmen gibt es für Kreditinstitute nach § 248 Abs. 2 BGB und beim Kontokorrent unter Kaufleuten (§ 355 Abs. 1 HGB). Das Zinseszinsverbot dient den übrigen Marktteilnehmern zum Schuldnerschutz.[23] Nach § 289 BGB sind in Erweiterung des § 248 BGB Verzugszinsen zinsfrei.[24] In § 497 Abs. 2 BGB ist das Recht des Kreditgebers, Zinseszinsen bei Verbraucherdarlehensverträgen zu verlangen, zwar nicht ausgeschlossen, jedoch auf die Höhe des gesetzlichen Zinssatzes (§ 246 BGB) eingeschränkt.

Wirtschaftliche Bedeutung

Der Zins ist Risikomaß und Risikoprämie bei der Einstufung des Kreditrisikos durch den Kreditgeber oder Anleger. Auf der anderen Seite geht der Zinsschuldner durch seine Zinszahlungspflicht und der Gefahr eines Zinseszinses ein mehr oder weniger großes Finanzrisiko ein, das ihn unter bestimmten Voraussetzungen in die Insolvenz treiben kann. Der Zinseszins belastet daher Schuldner zusätzlich, begünstigt die Gläubiger und trägt zu einem exponentiellen Wachstum von deren Schulden bzw. Vermögen bei. Dieses Wachstum fällt umso höher aus, je höher das zu verzinsende Kapital und/oder das Zinsniveau und je länger die Laufzeit sind. Solange ein Schuldner Schuldentragfähigkeit und Kapitaldienstfähigkeit besitzt, kann er den Kapitaldienst (Zins und Tilgung) aufbringen, so dass sich für ihn das Problem des Zinseszinses nicht stellt. Sind diese Voraussetzungen nicht mehr gegeben und rückständige Zinsen werden mit verzinst, gerät er in eine Schuldenfalle. Sie besteht vor allem darin, dass die exponentiell wachsenden Schulden immer weniger durch Vermögen gedeckt werden und die Einnahmen zur Deckung der Zinslast (Zinsdeckungsgrad) tendenziell nicht mehr ausreichen.

Das Problem der Zinseszinsen wird bei der Staatsverschuldung oft falsch dargestellt. Zinseszinsen können nur bei Staaten auftreten, die ihre Zinsen auf Staatsschulden (etwa Staatsanleihen) nicht mehr bezahlen oder für deren Bezahlung eine Neuverschuldung erforderlich ist. Zur ersteren Kategorie gehört Argentinien, das bereits die Zahlung des Kapitaldienstes für seine erste, 1825 emittierte Staatsanleihe im Jahre 1829 für die nächsten 28 Jahre bis 1857 einstellte.[25] Diesem Moratorium folgte ein weiteres im April 1987. Kommt es nicht zu einem Zinsverzicht der Gläubiger, führen die unbezahlten Zinsen zu einer Erhöhung der Staatsschulden. Staaten mit Verschuldungskrisen verhielten sich seither meist nach der zweiten Variante und zahlten ihre Zinsen, indem sie diese durch eine Neuverschuldung im Staatshaushalt refinanzierten. Dazu gehörten insbesondere die USA, die PIIGS-Staaten, hochverschuldete Entwicklungsländer und auch Deutschland (bis 2013). Seit 2014 erwirtschaftet Deutschland Haushaltsüberschüsse, so dass sich das Zinseszinsproblem nicht mehr stellt.

Bei einem Zahlungsverbot oder Moratorium geht der Zinsanspruch des Gläubigers nicht verloren, sondern dieser erhöht die Gesamtforderung des Gläubigers und löst bei Kapitalisierung Zinseszinsen aus. Der Zinseszins-Effekt entsteht bei Staaten, wenn mindestens die Zinsen zur Neuverschuldung oder deren Erhöhung beitragen. Werden rückständige Zinsen etwa bei einer Umschuldung oder Konsolidierung berücksichtigt, entstehen ebenfalls Zinseszinsen. Diese Voraussetzungen gelten auch für Zinseszinsen anderer Wirtschaftssubjekte wie Unternehmen und Privathaushalten, wenn diese ihren Schuldendienst durch weitere Kredite finanzieren müssen.

Liegt bei Staaten, Unternehmen oder Privathaushalten die Zinseszinsproblematik vor, so ist diese Finanzsituation ein deutliches Indiz für ein wirtschaftliches Problem eines Schuldners. Volkswirtschaftliche Kennzahlen wie Wirtschaftswachstum (gemessen am Bruttoinlandsprodukt), Unternehmensgewinne und Einkommen müssen nachhaltig und progressiv steigen, um die Zahlung der Zinslast zu gewährleisten.

International

Dem Schuldnerschutz dienen international gesetzliche Höchstzinsen, Zinswucher, Zinseszinsverbote und absolute Zinsverbote. In der Schweiz ist der Anatozismus in Art. 314 Abs. 3 OR verankert, auch hier gibt es Ausnahmen für das Kontokorrent und für Kreditinstitute. In Österreich erlaubt § 1335 ABGB den Zinseszins solange, bis die Zinsschuld auf den Betrag der Hauptschuld angewachsen ist. Erst vom Tag der Streitanhängigkeit an können Zinseszinsen verlangt werden. In Frankreich regelt nunmehr Art. 1343-2 CC, dass von aufgelaufenen Zinsen ein Jahr lang Zinseszins berechnet werden darf. Luxemburg hingegen verbietet in Art. 1154 Code civil den Zinseszins innerhalb von einem Jahr.[26]

Zinseszinsrechnung

Mit der Berechnung des Zinseszinses in Abhängigkeit vom Zinssatz sowie der Höhe und Dauer einer Kapitalanlage beschäftigt sich die Zinseszinsrechnung, ein Teilgebiet der Finanzmathematik. Die Zinseszinsrechnung beantwortet die Frage, auf welches Endkapital $K_{n}$ ein anfängliches Kapital $K_{0}$ nach insgesamt $n$ Zeiträumen angewachsen ist, wenn in jedem dieser Zeiträume mit dem festen Zinssatz von $p$ % verzinst wird.

Die Zinseszinsformel mit dem Zinsfuß p lautet:

K_{n}=K_{0}\left(1+{\frac {p}{100}}\right)^{n}

oder alternativ mit dem Zinsfaktor q:

K_{n}=K_{0}\cdot q^{n}

mit $K_{n}$ = Endkapital; $K_{0}$ = Anfangskapital; $p$ = Zinsfuß bzw. $q$ = Zinsfaktor und $n$ = Anzahl der geltenden Zeiträume/Jahre.

Die Formel leitet sich aus folgendem Zusammenhang her: Ein Sparer tätigt eine einmalige Kapitalanlage auf einem Konto eines Kreditinstituts in Höhe eines anfänglichen Kapitals. Dieses Kapital wird während einer bestimmten Anlagedauer mit Zinseszins verzinst. Die Anlagedauer bestehe aus mehreren gleich langen Zeiträumen, die mit Hilfe der Natürlichen Zahlen (als Index $i$ ) fortlaufend durchgezählt werden. Damit kann man die Anlagedauer als Summe aller $n$ Zeiträume formulieren:

{{\text{Anlagedauer}}={\text{Zeitraum}}_{1}+{\text{Zeitraum}}_{2}+\dots +{\text{Zeitraum}}_{i}+\dots +{\text{Zeitraum}}_{(n-1)}+{\text{Zeitraum}}_{n}}

Zu Beginn des ersten Zeitraums ( $i=1$ ) liegt auf dem Konto des Sparers das anfängliche Kapital $K_{0}$ :

{\text{Anfangskapital zu Beginn von Zeitraum}}_{1}\colon K_{0}

Wichtig sind die beiden verwendeten Indexwerte. Der erste Zeitraum erhält den Indexwert $i=1$ , während das Anfangskapital mit $i=0$ nummeriert wird. Die unterschiedliche Nummerierung kommt dadurch zustande, dass das ursprüngliche Anfangskapital $K_{0}$ während des ersten Zeitraumes sich nicht verändert. Die Zinsen werden erst nach Ablauf des ersten Zeitraumes also zu Beginn des zweiten Zeitraums gutgeschrieben.

Der Sparer hat sich entschieden, für die Anlagedauer nicht auf sein Kapital zuzugreifen. Dafür „belohnt“ ihn das Kreditinstitut bzw. letztlich der Kreditnehmer mit einer Gutschrift von Zinsen. Übliche Praxis ist nun, dass wiederholt jeweils am Ende von jedem der $n$ Zeiträume innerhalb der Anlagedauer Zinsen gutgeschrieben werden.

Es wird also z. B. für den ersten Zeitraum der Zinswert $Z_{1}$ vergütet:

{\text{Zinswert für den Zeitraum}}_{1}\colon Z_{1}

Die konkrete Höhe des Zinswertes $Z_{1}$ im ersten Zeitraum bestimmt sich wie folgt: Das Kreditinstitut drückt die „Belohnung“ des Sparers für die Überlassung des Kapitals in prozentualer Form als Zinssatz aus, also z. B. „sechs Prozent“ $\left(6\,\%={\tfrac {6}{100}}\right)$ . Die Zahl vor dem Prozentzeichen wird Zinsfuß $p$ genannt. Der am Ende des ersten Zeitraums gutgeschriebene Zinswert $Z_{1}$ verhält sich zum anfänglichen Kapitalwert $K_{0}$ genau so, wie sich der Zinsfuß $p$ zum Wert 100 verhält. Dieser Zusammenhang stellt eine Verhältnisgleichung (Proportion) dar.

{\frac {{\text{Zinswert für Zeitraum}}_{1}}{{\text{Kapitalwert zu Beginn von Zeitraum}}_{1}}}={\frac {{\text{Zinsfuß für Zeitraum}}_{1}}{100}}\qquad \Leftrightarrow \qquad {\frac {Z_{1}}{K_{0}}}={\frac {p}{100}}

.

Diese Verhältnisgleichung lässt sich umformen zu:

Z_{1}=K_{0}\cdot {\frac {p}{100}}

.

Dieser Zusammenhang zwischen Zinswert und Kapitalwert im ersten Zeitraum lässt sich so verallgemeinern, dass er für jedes $Z_{i}$ und Kapitalwert $K_{(i-1)}$ in jedem $i$ -ten Zeitraum gilt:

Z_{i}=K_{i-1}\cdot {\frac {p}{100}}

.

Bis hierhin wurde die „Verzinsung für einen Zeitraum“ betrachtet.

Zur Betrachtung des Zinseszinses muss erneut berücksichtigt werden, dass der Sparer für das „zur Verfügung stellen“ des anfänglichen Kapitals $K_{0}$ nach Maßgabe der obigen Zinswert-Formel „belohnt“ wird. Seinem Konto wird am Ende des ersten Zeitraums also folgender Zinswert $Z_{1}$ gutgeschrieben:

Z_{1}=K_{0}\cdot {\frac {p}{100}}

.

Somit wächst das anfängliche Kapital $K_{0}$ bis zum Ende des ersten Zeitraums genau um diesen Zinswert $Z_{1}$ . Ihre Summe ergibt den neuen Kontostand. Diese Summe nennt man auch das (vorläufige) Endkapital $K_{1}$ , das folgerichtig mit dem Indexwert $i=1$ versehen wird:

K_{1}=K_{0}+Z_{1}=K_{0}+K_{0}\cdot {\frac {p}{100}}=K_{0}\left(1+{\frac {p}{100}}\right)

.

Dieses (vorläufige) Endkapital $K_{1}$ ist nun zugleich das Anfangskapital für den zweiten Zeitraum ( $i=2$ ). Es „erwirtschaftet“ darin den Zinswert $Z_{2}$ , der erneut hinzuaddiert wird:

{K_{2}=K_{1}+Z_{2}=K_{1}+K_{1}\cdot {\frac {p}{100}}=K_{1}\left(1+{\frac {p}{100}}\right)=K_{0}\left(1+{\frac {p}{100}}\right)\left(1+{\frac {p}{100}}\right)=K_{0}\left(1+{\frac {p}{100}}\right)^{2}}

.

Für positive Zinsfüße $p>0$ gilt stets

1+{\frac {p}{100}}>1

Dieser Term wird daher Aufzinsfaktor genannt.

Damit wirkt bereits während des zweiten Zeitraums der Zinseszins-Effekt: Das Anfangskapital $K_{0}$ im ersten Zeitraum wächst mit dem Aufzinsungsfaktor $1+{\frac {p}{100}}$ auf das (vorläufige) Endkapital $K_{1}$ . Auf die gleiche Weise steigt das Kapital $K_{1}$ im zweiten Zeitraum mit demselben Aufzinsungsfaktor auf das (vorläufige) Endkapital $K_{2}$ . Über beide Zeiträume hinweg betrachtet ist das anfängliche Kapital $K_{0}$ jedoch überproportional, nämlich mit dem Quadrat des Aufzinsungsfaktors, auf das (vorläufige) Endkapital $K_{2}$ angewachsen.

Verallgemeinert bedeutet dies, dass sich am Ende der Anlagedauer, also nach insgesamt $n$ Zinszeiträumen, schließlich das Endkapital $K_{n}$ durch $n$ -maliges Multiplizieren des Anfangskapitals $K_{0}$ mit dem Aufzinsungsfaktor

K_{n}=K_{0}\left(1+{\frac {p}{100}}\right)^{n}

ergibt.

Beispiel

Das Anfangskapital beträgt 1000 €, die Verzinsung 5 %, betrachtet werden 50 Jahre.

Ohne Zinseszins

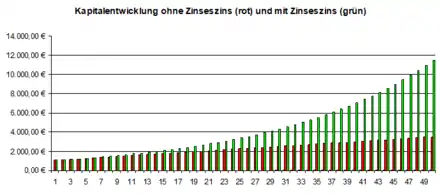
Vergleich der Kapitalentwicklung mit und ohne Zinseszins bei einer Verzinsung von 5 % in Abhängigkeit von der Laufzeit in Jahren

Die jährlich anfallenden 5 % Zinsen werden nicht dem Anfangskapital zugeschlagen und damit wieder angelegt, sondern entnommen und getrennt gesammelt. Nach 50 Jahren erhöht sich so die Summe aus Anfangskapital und getrennt gesammelten Einzeljahreszinsen auf 3500 €:

K_{50}=1000{,}00\,\mathrm {\euro} +\left(1000{,}00\,\mathrm {\euro} \cdot {\frac {5}{100}}\right)\cdot 50=3500{,}00\,\mathrm {\euro}

.

Mit Zinseszins

Werden die jährlichen Zinsen immer dem jeweils neu anzulegenden Betrag zugeschlagen (kapitalisiert), wird aus den anfänglichen 1000 € bei ansonsten unveränderten Parametern in derselben Zeit eine Summe von 11.467 €:

K_{50}=1000{,}00\,\mathrm {\euro} \cdot \left(1+{\frac {5}{100}}\right)^{50}=11467{,}40\,\mathrm {\euro}

.

Auswirkungen

Wird allerdings über den gleichen Zeitraum eine Inflation von beispielsweise 3 % mit eingerechnet, so reduziert sich der Zinseszinseffekt durch die Geldentwertung erheblich, da nach 50 Jahren das Geld nur noch einen Wert relativ zum Ursprungswert von 0,228 hat: dieser Wert ergibt sich aus

{\frac {1}{(100\,\%+3\,\%)^{50}}}={\frac {1}{1{,}03^{50}}}

.

Die 11.467 € haben dann nur noch eine Kaufkraft von 2.616 € bezogen auf den Zeitpunkt des Anfangskapitals. Berechnet man hingegen die Geldentwertung auf die Summe aus Anfangskapital und die getrennt gesammelten Einzeljahreszinsen ohne Zinseszins von zusammen 3500 €, so hat man nach 50 Jahren nur noch eine Kaufkraft von 798 € und somit deutlich weniger als das eingesetzte Kapital. Um den Wert eines Guthabens im Falle einer Inflation zu bewahren, ist folgendes zu beachten: da die Inflation eine exponentielle Geldentwertung hervorruft, muss eine Verzinsung ebenfalls exponentiell über den Zinseszins erfolgen, da ansonsten – ohne Mitverzinsung der Zinsen – auch bei einem Zinssatz, der deutlich über der Inflationsrate liegt, der reale Wert eines Guthabens auf lange Sicht verfällt.

Der bei Staatsverschuldung wirkende Zinseszinseffekt kann bei ausreichendem Wirtschaftswachstum kompensiert werden. Wenn ein Staat beispielsweise seine Schulden mit 5 % verzinsen muss und eine Inflationsrate von 3 % vorliegt, so müsste das reale Wirtschaftswachstum jährlich etwa 2 % betragen, damit die reale Schuldenquote nicht zunimmt, wenn die Zinsen durch Neuverschuldung bezahlt werden (bei gleichbleibenden Altschulden). In diesem Fall würden die Inflation und das reale Wirtschaftswachstum den Zinseszinseffekt dauerhaft kompensieren, da Inflation und Wirtschaftswachstum dem gleichen exponentiellen Wachstum wie der Zinseszinseffekt unterliegen. Die nominale Wachstumsrate der Staatseinnahmen entspricht dann dem Zinssatz der Staatsschulden. Reicht das Wirtschaftswachstum nicht aus, um den Zinseszinseffekt vollständig zu kompensieren, so muss langfristig entweder der Zinssatz sinken, die Inflation steigen oder jährlich der Teil der Zinslast aufgebracht werden, der nicht durch Inflation und Wirtschaftswachstum kompensiert wird. Bei einem realen Wirtschaftswachstum von 0 % müsste jährlich mindestens die Differenz von Zinssatz und Inflation – in diesem Beispiel also 2 % – aufgebracht werden, damit es auch auf Dauer nicht zu einer Überschuldung kommt.

Konsequenzen

Exponentielles Wachstum

Werden Zinsen kapitalisiert, hat dies eine zukünftige Mitverzinsung auch der kapitalisierten Zinsen zur Folge. Dadurch ergibt sich ein exponentieller Anstieg des Gesamtkapitals. Die Zinseszinsformel ist also eine Sonderform der Formeln des exponentiellen Wachstums:

K(t)=K_{0}\left(1+{\frac {p}{100}}\right)^{t}=K_{0}\cdot q^{t}=K_{0}\cdot e^{rt}

In dieser Darstellung ist die Zeit $t$ eine reelle Zahl ohne Zeiteinheit und gibt die Anzahl der Zinsperioden an. Dabei wird der Bruch ${\tfrac {p}{100}}$ als Wachstumsrate und die Zahl $q=1+{\tfrac {p}{100}}$ als Wachstumsfaktor bezeichnet. Die Zahl $r=\ln(q)$ im Exponenten kann ebenfalls als Rate bezeichnet werden, da sie bei kleinen Zinssätzen unterhalb von 10 % annähernd gleich der Wachstumsrate ist:

r=\ln(1+{\frac {p}{100}})\approx {\frac {p}{100}}\quad {\text{falls}}\quad |p|<10

Bei Rechnungen mit physikalischen Zeiten und explizit aufgeführter Zinsperiode (z. B. $T=1\ {\text{Jahr}}$ ) kann die Periodendauer $T$ in die Wachstumskonstante $\lambda =r/T$ umgerechnet werden:

K(t)=K_{0}\left(1+{\frac {p}{100}}\right)^{t/T}=K_{0}\cdot q^{t/T}=K_{0}\cdot e^{rt/T}=K_{0}\cdot e^{\lambda t}

Ein Beispiel für die extremen Beträge, die durch die Annahme von über lange Zeit gleichbleibenden Wachstumsraten aufgrund von Zinseszinseffekten rechnerisch erhalten werden, ist der im Jahr Null angelegte Josephspfennig.

Aus den Zinseszins-Formeln kann man die 72er-Regel als Näherungsformel ableiten, wann sich ein Investment (Anlage eines Betrages zu einem Zinssatz) verdoppelt hat.

Vermögenskonzentration

Vermögenskonzentration im Zeitverlauf

Bei zufälligen Schwankungen der individuellen Renditen wird durch den Zinseszins eine Vermögenskonzentration verursacht. Joseph E. Fargione, Clarence Lehman und Stephen Polasky zeigten im Jahr 2011, dass der Zufall allein in Kombination mit dem Zinseszinseffekt zu einer unbegrenzten Konzentration des Vermögens führen kann.[27]

Bei einer Population mit $n$ unabhängigen Kapitalvermögen und einem gleichmäßig verteilten Anfangsvermögen $W_{0}=nK_{0}$ ergibt sich das $i$ -te Kapitalvermögen nach $t$ Zinsperioden aus der Zinseszinsformel zu

K_{i}(t)=K_{0}\left(1+{\frac {p_{i,1}}{100}}\right)\left(1+{\frac {p_{i,2}}{100}}\right)\dots \left(1+{\frac {p_{i,t}}{100}}\right)=K_{0}q_{i,1}q_{i,2}\dots q_{i,t}=K_{0}e^{r_{i,1}}e^{r_{i,2}}\dots e^{r_{i,t}}

.

Somit ist für $i=1,2,\dots ,n$ und für $t=1,2,3,\dots$

K_{i}(t)=K_{0}e^{r_{i,1}+r_{i,2}+\dots +r_{i,t}}=K_{0}e^{x_{i}(t)}\quad {\text{mit}}\quad x_{i}(t)=\sum _{k=1}^{t}r_{i,k}

.

Nimmt man an, dass die Raten $r_{i,k}$ aus einer Normalverteilung mit Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ gezogen werden, dann sind die Exponenten $x_{i}(t)$ als Summe der $t$ Zufallszahlen $r_{i,1}+r_{i,2}+\dots +r_{i,t}$ normalverteilt mit Erwartungswert $\mu t$ und Varianz $\sigma ^{2}t$ ; dieses folgt aus der Invarianz der Normalverteilung gegenüber der Faltung. Man betrachtet nun zuerst den Fall $t=1$ , also die Situation nach genau einer Zinsperiode: Zu dieser Zeit sind die Exponenten $x_{i}$ normalverteilt mit Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ , daher sind die Potenzen $e^{x_{i}}$ logarithmisch normalverteilt mit den Parametern $\mu$ und $\sigma$ . Das Gesamtvermögen lässt sich einfach durch die Summe der individuellen Kapitalvermögen berechnen:

W_{Total}=\sum _{i=1}^{n}K_{i}=K_{0}\sum _{i=1}^{n}e^{x_{i}}=nK_{0}\left({\frac {1}{n}}\sum _{i=1}^{n}e^{x_{i}}\right)=W_{0}\left({\frac {1}{n}}\sum _{i=1}^{n}e^{x_{i}}\right)

Aufgrund der Gesetze der großen Zahlen stabilisiert sich für wachsendes $n$ der arithmetische Mittelwert der Potenzen $e^{x_{i}}$ um den Erwartungswert einer logarithmischen Normalverteilung mit den Parametern $\mu$ und $\sigma$ . Wenn die Anzahl der individuellen Kapitalvermögen groß genug ist, kann somit der Mittelwert durch den Erwartungswert ersetzt werden und das Gesamtvermögen durch ein Integral dargestellt werden:

W_{Total}=W_{0}\int _{0}^{\infty }{\frac {1}{\sigma y{\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {\ln(y)-\mu }{\sigma }}\right)^{2}}y\,\mathrm {d} y=W_{0}\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x

Um das Teilvermögen an der Spitze der Population zu ermitteln, muss die untere Integrationsgrenze von $-\infty$ auf den Wert $\mu +h\sigma$ mit einer noch näher zu bestimmenden Konstante $h$ angehoben werden:

W_{Top}=W_{0}\int _{\mu +h\sigma }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x=W_{Total}-W_{0}\int _{-\infty }^{\mu +h\sigma }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x

Der auf diese Weise ausgewählte Bruchteil der Population berechnet sich dann zu

\int _{\mu +h\sigma }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}\mathrm {d} x=1-\int _{-\infty }^{\mu +h\sigma }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}\mathrm {d} x=1-\int _{-\infty }^{h}{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}z^{2}}\mathrm {d} z=1-\Phi (h)

.

Dabei bezeichnet $\Phi$ das gaußsche Fehlerintegral bzw. die Verteilungsfunktion der Standardnormalverteilung und $\Phi ^{-1}$ die zugehörige inverse Verteilungsfunktion. Bestimmt man nun die Konstante $h$ durch $h=\Phi ^{-1}(1-{\tfrac {a}{100}})$ , dann ist der so ausgewählte Bruchteil der Population gleich $a\,\%$ . Der so bestimmte Wert für $h$ ist das $(1-{\tfrac {a}{100}})$ -Quantil und wird kürzer als $a\,\%$ -Fraktil bezeichnet. Beispielsweise ergibt sich das $1\,\%$ -Fraktil für das obere Prozent der Population zu $h=\Phi ^{-1}(0{,}99)\approx 2{,}326$ . Näherungswerte für die $a\,\%$ -Fraktile können einer Tabelle der Standardnormalverteilung entnommen werden. Der Vermögensanteil der oberen $a\,\%$ der Population wird berechnet, indem das Teilvermögen durch das Gesamtvermögen geteilt wird:

{\frac {W_{Top~a\%}}{W_{Total}}}={\frac {W_{0}\int _{\mu +h\sigma }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}{W_{0}\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}}=1-{\frac {\int _{-\infty }^{\mu +h\sigma }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}{\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}}\quad {\text{mit}}\quad h=\Phi ^{-1}\left(1-{\frac {a}{100}}\right)

Wegen

e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}=e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}+x}=e^{-{\frac {1}{2}}\left(\left({\frac {x-\mu }{\sigma }}\right)^{2}-2\left(x-\mu \right)+\sigma ^{2}\right)+\mu +{\frac {1}{2}}\sigma ^{2}}=e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}-\sigma \right)^{2}+\mu +{\frac {1}{2}}\sigma ^{2}}=e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}-\sigma \right)^{2}}e^{\mu +{\frac {1}{2}}\sigma ^{2}}

ist

\int _{-\infty }^{\xi }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x=\left(\int _{-\infty }^{\xi }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}-\sigma \right)^{2}}\mathrm {d} x\right)e^{\mu +{\frac {1}{2}}\sigma ^{2}}=\Phi \left({\frac {\xi -\mu }{\sigma }}-\sigma \right)e^{\mu +{\frac {1}{2}}\sigma ^{2}}

,

deshalb gilt

\int _{-\infty }^{\mu +h\sigma }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x=\Phi \left({\frac {\mu +h\sigma -\mu }{\sigma }}-\sigma \right)e^{\mu +{\frac {1}{2}}\sigma ^{2}}=\Phi \left(h-\sigma \right)e^{\mu +{\frac {1}{2}}\sigma ^{2}}

und

\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x=\lim _{\xi \to \infty }\Phi \left({\frac {\xi -\mu }{\sigma }}-\sigma \right)e^{\mu +{\frac {1}{2}}\sigma ^{2}}=1\cdot e^{\mu +{\frac {1}{2}}\sigma ^{2}}=e^{\mu +{\frac {1}{2}}\sigma ^{2}}

.

Somit ergibt sich:

W_{Total}=W_{0}\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x=W_{0}e^{\mu +{\frac {1}{2}}\sigma ^{2}}

{\frac {W_{Top~a\%}}{W_{Total}}}=1-{\frac {\int _{-\infty }^{\mu +h\sigma }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}{\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}}=1-{\frac {\Phi \left(h-\sigma \right)e^{\mu +{\frac {1}{2}}\sigma ^{2}}}{e^{\mu +{\frac {1}{2}}\sigma ^{2}}}}=1-\Phi \left(h-\sigma \right)=\Phi \left(\sigma -h\right)

Der Zinseszinseffekt bewirkt eine Änderung des Gesamtvermögens um den Faktor $e^{\mu +{\frac {1}{2}}\sigma ^{2}}$ und einen Anstieg des Vermögensanteils an der Spitze der Population, der konkret durch eine Verschiebung im Argument von $\Phi$ um die Streubreite $\sigma$ verursacht wird. Ohne diese Verschiebung wäre der Vermögensanteil aufgrund der gleichmäßigen Vermögensverteilung nur $a\,\%$ . Weil das Fehlerintegral $\Phi$ streng monoton wachsend ist, führt die Verschiebung um $\sigma >0$ zu einer Vergrößerung des Anteils, und es gilt:

{\frac {W_{Top~a\%}}{W_{Total}}}=\Phi (\sigma -h)>\Phi (-h)=1-\Phi (h)=1-(1-{\frac {a}{100}})=a\,\%

Zur Konzentration kommt es, weil durch das unbeschränkte Anwachsen der Streuung die Verschiebung mit der Zeit immer größer wird: Die Varianz von $x_{i}(t)$ ist $\sigma ^{2}t$ , also ist die Streuung und damit die Verschiebung gleich $\sigma {\sqrt {t}}$ . Man erhält nun das Gesamtvermögen und den Vermögensanteil nach $t$ Zinsperioden, indem die Rechnung mit $\mu t$ und $\sigma {\sqrt {t}}$ anstelle von $\mu$ und $\sigma$ wiederholt wird. Es ergibt sich:

W_{Total}(t)=W_{0}\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi t}}}}e^{-{\frac {1}{2t}}\left({\frac {x-\mu t}{\sigma }}\right)^{2}}e^{x}\mathrm {d} x=W_{0}e^{\left(\mu +{\frac {1}{2}}\sigma ^{2}\right)t}

{\frac {W_{Top~a\%}(t)}{W_{Total}(t)}}={\frac {W_{0}\int _{\mu t+h\sigma {\sqrt {t}}}^{\infty }{\frac {1}{\sigma {\sqrt {2\pi t}}}}e^{-{\frac {1}{2t}}\left({\frac {x-\mu t}{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}{W_{0}\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi t}}}}e^{-{\frac {1}{2t}}\left({\frac {x-\mu t}{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}}=\Phi \left(\sigma {\sqrt {t}}-h\right)

Das Fehlerintegral $\Phi$ kann aufgrund des Zusammenhangs $\Phi (x)={\tfrac {1}{2}}\left(1+\operatorname {erf} \left({\tfrac {x}{\sqrt {2}}}\right)\right)$ durch die Fehlerfunktion $\operatorname {erf}$ ersetzt werden. Dadurch lässt sich der Vermögensanteil der oberen $a\,\%$ der Population zur Zeit $t$ wie in der Quelle darstellen:[28]

{\frac {W_{Top~a\%}(t)}{W_{Total}(t)}}={\frac {\int _{\mu t+h\sigma {\sqrt {t}}}^{\infty }{\frac {1}{\sigma {\sqrt {2\pi t}}}}e^{-{\frac {1}{2t}}\left({\frac {x-\mu t}{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}{\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi t}}}}e^{-{\frac {1}{2t}}\left({\frac {x-\mu t}{\sigma }}\right)^{2}}e^{x}\mathrm {d} x}}={\frac {1}{2}}\left(1+\operatorname {erf} \left({\frac {\sigma {\sqrt {t}}-h}{\sqrt {2}}}\right)\right)\quad {\text{mit}}\quad h=\Phi ^{-1}\left(1-{\frac {a}{100}}\right)

Für jeden noch so kleinen Wert für $a$ geht der Vermögensanteil der oberen $a\,\%$ der Population mit der Zeit gegen die Zahl 1. Das bedeutet, dass ein beliebig kleiner Bruchteil der Population nach einiger Zeit nahezu 100 % des gesamten Vermögens besitzt. Der Konzentrationsprozess hängt dabei nur von der Streubreite $\sigma$ ab und ist unabhängig von der mittleren Rate $\mu$ , so dass dieser Mechanismus den Wohlstand in wachsenden, stagnierenden oder schrumpfenden Volkswirtschaften konzentriert. Aufgrund des zentralen Grenzwertsatzes gilt dieses Ergebnis selbst dann, wenn die Raten $r_{i,k}$ selber nicht normalverteilt sind.

Wird beispielsweise für jeden Menschen jedes Jahr eine Münze geworfen und sein Vermögen danach entweder um 20 % verringert oder um 30 % vergrößert, so sind die entsprechenden Raten $r_{i,k}\in \{\ln(0{,}8),\ln(1{,}3)\}$ nicht normalverteilt, sondern zweipunktverteilt mit $\mu ={\tfrac {1}{2}}(\ln 0{,}8+\ln 1{,}3)$ und $\sigma ={\tfrac {1}{2}}(\ln 1{,}3-\ln 0{,}8)$ . Aufgrund des zentralen Grenzwertsatzes nähert sich jedoch die Verteilung der Exponenten $x_{i}(t)=r_{i,1}+r_{i,2}+\dots +r_{i,t}$ mit zunehmender Zeit $t$ immer besser an eine Normalverteilung mit Erwartungswert $\mu t$ und Varianz $\sigma ^{2}t$ an. Deshalb kommt es auch in diesem Beispiel zu einer Vermögenskonzentration an der Spitze der Population. Verzichtet man hingegen auf die Zinseszinsen und verwendet nur einfache Verzinsung, so verschwindet in diesem Fall der Konzentrationseffekt (vgl. dazu die dritte Simulation der Vermögenskonzentration nach Fargione, Lehman und Polasky).[29]

Siehe auch

Rentenrechnung
Sparkassenformel
Zinsrechnung (in diesem Artikel finden sich auch weitere Formeln zur Zinseszinsrechnung)

Weblinks

Wiktionary: Zins – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: ${\color {BlueViolet}{\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$ Mathematik für die Schule – Zinsrechnung

Einzelnachweise

Gerhard Müller, Josef Löffelholz: Bank-Lexikon: Handwörterbuch für das Bank- u. Sparkassenwesen. 1978, Sp. 1735 f. (eingeschränkte Vorschau in der Google-Buchsuche).
Oliver Brand: Das internationale Zinsrecht Englands. 2002, S. 11 f (eingeschränkte Vorschau in der Google-Buchsuche).
Louis Delaporte: La Mésopotamie. 1923, S. 142.
August Friedrich von Pauly: Paulys Real-Encyclopädie der classischen Altertumswissenschaft. Bände 1–2, 1894, S. 2069.
Ulpian: Digesten. 12, 6, 26, 1.
Heinrich Honsell: Römisches Recht. 2015, S. 95.
Codex Iustinianus 4, 32, 28 pr. a. A.
Léon Rodet: Leçons de Calcul d‘Aryabhata. In: Journal Asiatique. 1879, S. 402 ff.
Karl Friedrich Ferdinand Kniep: Die Mora des Schuldners nach Römischem und heutigem Recht. Band 2, 1872, S. 228. (Volltext in der Google-Buchsuche).
Steffen Jörg: Das Zinsverbot in der islamischen Wirtschaftsordnung. 2015, S. 54 (eingeschränkte Vorschau in der Google-Buchsuche).
Leonardo Fibonacci: Liber abaci. 1288, S. 399 ff.
Böhlaus Nachf.: Mittheilungen des Instituts für Oesterreichische Geschichtsforschung. Band 26, 1905, S. 147
Otto Stobbe: Die Juden in Deutschland während des Mittelalters in politischer, socialer und rechtlicher Beziehung. 1866, S. 111 f. (Volltext in der Google-Buchsuche).
Eugen Nübling: Die Judengemeinden des Mittelalters: insbesondere die Judengemeinde der Reichsstadt Ulm. 1896, S. 98.
John T. Noonan: The scholastic Analysis of Usury. 1957, S. 154.
Jakob Bernoulli: Opera I. 1689, S. 427 ff.
Julius Albert Gruchot: Beiträge zur Erläuterung des preußischen Rechts, des Handels- und Wechselrechts. Band 13, 1869, S. 235 (eingeschränkte Vorschau in der Google-Buchsuche).
Richard Price: An Appeal to the Public on the Subject of National Debt. 1772, S. 9.
Richard Price: An Appeal to the Public on the Subject of National Debt. 1772, S. 8.
OHG Lübeck, Urteil vom 26. November 1855
Karl Marx, Friedrich Engels: Werke. Band 25, 1961, S. 411.
Hubert Beyerle: Der Zins ist nicht zu fassen. In: Die Zeit, Nr. 44/2005.
Otto Palandt, Christian Grüneberg: BGB-Kommentar. 24. Auflage, 2014, § 248 Rn. 1.
Otto Palandt, Christian Grüneberg: BGB-Kommentar. 24. Auflage, 2014, § 289 Rn. 1.
Melchior Palyi, Paul Quittner: Handwörterbuch des Bankwesens. 1933, S. 496 (eingeschränkte Vorschau in der Google-Buchsuche).
Udo Reifner, Michael Schröder (Hrsg.): Usury Laws. 2012, S. 117 (eingeschränkte Vorschau in der Google-Buchsuche).
Joseph E. Fargione u. a.: Entrepreneurs, Chance, and the Deterministic Concentration of Wealth. 21. Juli 2011; doi:10.1371/journal.pone.0020728
Joseph E. Fargione u. a.: Entrepreneurs, Chance, and the Deterministic Concentration of Wealth. Results; doi:10.1371/journal.pone.0020728#s3
Simulationen der Vermögenskonzentration nach Fargione, Lehman und Polasky (Memento vom 14. September 2020 im Internet Archive)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Gerhard Müller, Josef Löffelholz: Bank-Lexikon: Handwörterbuch für das Bank- u. Sparkassenwesen. 1978, Sp. 1735 f. (eingeschränkte Vorschau in der Google-Buchsuche).

[2] Oliver Brand: Das internationale Zinsrecht Englands. 2002, S. 11 f (eingeschränkte Vorschau in der Google-Buchsuche).

[3] Louis Delaporte: La Mésopotamie. 1923, S. 142.

[4] August Friedrich von Pauly: Paulys Real-Encyclopädie der classischen Altertumswissenschaft. Bände 1–2, 1894, S. 2069.

[5] Ulpian: Digesten. 12, 6, 26, 1.

[6] Heinrich Honsell: Römisches Recht. 2015, S. 95.

[7] Codex Iustinianus 4, 32, 28 pr. a. A.

[8] Léon Rodet: Leçons de Calcul d‘Aryabhata. In: Journal Asiatique. 1879, S. 402 ff.

[9] Karl Friedrich Ferdinand Kniep: Die Mora des Schuldners nach Römischem und heutigem Recht. Band 2, 1872, S. 228. (Volltext in der Google-Buchsuche).

[10] Steffen Jörg: Das Zinsverbot in der islamischen Wirtschaftsordnung. 2015, S. 54 (eingeschränkte Vorschau in der Google-Buchsuche).

[11] Leonardo Fibonacci: Liber abaci. 1288, S. 399 ff.

[12] Böhlaus Nachf.: Mittheilungen des Instituts für Oesterreichische Geschichtsforschung. Band 26, 1905, S. 147

[13] Otto Stobbe: Die Juden in Deutschland während des Mittelalters in politischer, socialer und rechtlicher Beziehung. 1866, S. 111 f. (Volltext in der Google-Buchsuche).

[14] Eugen Nübling: Die Judengemeinden des Mittelalters: insbesondere die Judengemeinde der Reichsstadt Ulm. 1896, S. 98.

[15] John T. Noonan: The scholastic Analysis of Usury. 1957, S. 154.

[16] Jakob Bernoulli: Opera I. 1689, S. 427 ff.

[17] Julius Albert Gruchot: Beiträge zur Erläuterung des preußischen Rechts, des Handels- und Wechselrechts. Band 13, 1869, S. 235 (eingeschränkte Vorschau in der Google-Buchsuche).

[18] Richard Price: An Appeal to the Public on the Subject of National Debt. 1772, S. 9.

[19] Richard Price: An Appeal to the Public on the Subject of National Debt. 1772, S. 8.

[20] OHG Lübeck, Urteil vom 26. November 1855

[21] Karl Marx, Friedrich Engels: Werke. Band 25, 1961, S. 411.

[22] Hubert Beyerle: Der Zins ist nicht zu fassen. In: Die Zeit, Nr. 44/2005.

[23] Otto Palandt, Christian Grüneberg: BGB-Kommentar. 24. Auflage, 2014, § 248 Rn. 1.

[24] Otto Palandt, Christian Grüneberg: BGB-Kommentar. 24. Auflage, 2014, § 289 Rn. 1.

[25] Melchior Palyi, Paul Quittner: Handwörterbuch des Bankwesens. 1933, S. 496 (eingeschränkte Vorschau in der Google-Buchsuche).

[26] Udo Reifner, Michael Schröder (Hrsg.): Usury Laws. 2012, S. 117 (eingeschränkte Vorschau in der Google-Buchsuche).

[27] Joseph E. Fargione u. a.: Entrepreneurs, Chance, and the Deterministic Concentration of Wealth. 21. Juli 2011; doi:10.1371/journal.pone.0020728

[28] Joseph E. Fargione u. a.: Entrepreneurs, Chance, and the Deterministic Concentration of Wealth. Results; doi:10.1371/journal.pone.0020728#s3

[29] Simulationen der Vermögenskonzentration nach Fargione, Lehman und Polasky (Memento vom 14. September 2020 im Internet Archive)