Periodische Funktion
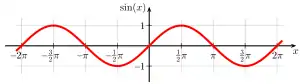
In der Mathematik sind periodische Funktionen eine besondere Klasse von Funktionen. Sie haben die Eigenschaft, dass sich ihre Funktionswerte in regelmäßigen Abständen wiederholen. Die Abstände zwischen dem Auftreten der gleichen Funktionswerte werden Periode genannt. Einfache Beispiele sind Sinus- und Kosinus-Funktionen. Damit auch Funktionen mit Lücken im Definitionsbereich, wie z. B. die Tangens-Funktion, zu den periodischen Funktionen gerechnet werden können, erlaubt man Definitionsbereiche mit periodischen Lücken. Eine periodische Funktion besitzt allerdings nicht nur eine Periode, denn jedes Vielfache einer Periode ist auch wieder eine Periode. Beispiel: Die Sinus-Funktion ist nicht nur -periodisch, sondern auch -periodisch, … Wenn man von Periode spricht, meint man in der Regel die kleinstmögliche positive Periode. Es gibt allerdings periodische Funktionen, die keine kleinste Periode besitzen. Beispiel: Jede auf definierte konstante Funktion hat jede beliebige Zahl als Periode.
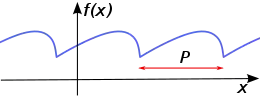
Periodische Funktionen treten natürlicherweise in der Physik zur Beschreibung von mechanischen, elektrischen oder akustischen Schwingungsvorgängen auf. Deshalb bezeichnet man eine Periode oft mit (engl.: Time).
Da eine periodische Funktion bekannt ist, wenn man ihren Verlauf innerhalb einer Periode kennt, werden nicht-trigonometrische periodische Funktion in der Regel in einem Grundintervall definiert und dann periodisch fortgesetzt.
So wie viele reelle Funktionen in Potenzreihen entwickelt werden können, kann man, unter gewissen Voraussetzungen, eine periodische Funktion als Reihe von Sinus- und Kosinus-Funktionen entwickeln: siehe Fourier-Reihe.
Periodische Folgen können als Spezialfälle der periodischen Funktionen verstanden werden.
Funktionen, die nicht periodisch sind, werden manchmal – um dies extra zu betonen – als aperiodisch bezeichnet.
Reelle periodische Funktionen
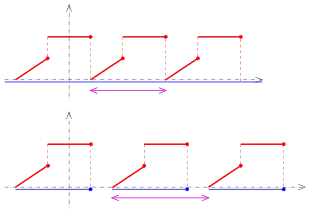
oben: . (blau),
unten: Teilmenge von (blau),
lila: Periode
Definition
Eine reelle Zahl ist eine Periode einer in definierten Funktion, wenn für jedes aus gilt:
- ist in und
Die Funktion ist periodisch, wenn sie mindestens eine Periode zulässt. Man sagt dann auch, sei „-periodisch“.
Für , was oft der Fall ist, ist die erste Eigenschaft immer erfüllt.
Eigenschaften der Perioden
Für die Periode gelten folgende Eigenschaften:
- Ist eine Periode von , so ist auch eine Periode von ;
- Sind und zwei Perioden von , so ist auch mit eine Periode von .
Meist interessiert man sich für die kleinste positive Periode. Diese existiert für jede nichtkonstante stetige periodische Funktion. (Eine konstante Funktion ist periodisch mit jeder beliebigen Periode ungleich 0.) Wenn eine kleinste positive Periode hat, so sind die Perioden von die Vielfachen von . Im anderen Fall ist die Menge der Perioden von dicht in .
Trigonometrische Funktionen
Die Standardbeispiele periodischer Funktionen sind die trigonometrischen Funktionen.
So ist beispielsweise die auf ganz definierte Sinusfunktion periodisch. Ihre Funktionswerte wiederholen sich im Abstand von ( ist die Kreiszahl Pi); sie hat also die Periode .
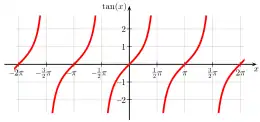
Die Tangensfunktion mit dem Definitionsbereich ist ebenfalls eine trigonometrische Funktion; sie hat die Periode und nicht , obwohl sie als Quotient zweier -periodischer Funktionen darstellbar ist: .
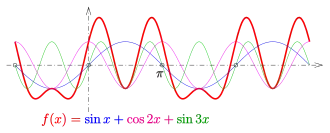
Summe von cos- und sin-Funktionen
Summen von cos- und sin-Funktionen mit einer gemeinsamen (nicht unbedingt kleinste) Periode sind wieder periodisch. (Im Bild ist die gemeinsame Periode .) Diese Eigenschaft der cos- und sin-Funktionen ist die Basis der Fourierreihen. Haben zwei Funktionen keine gemeinsame Periode, so ist die Summe nicht periodisch. Beispiel: ist nicht periodisch.
Periodische Fortsetzung
Im Beispiel zur Definition wurde im oberen Teil des Bildes eine auf einem halboffenen Intervall gegebene Funktion durch einfaches Verschieben um ganzzahlige Vielfache von zu einer periodischen Funktion der Periode fortgesetzt. Diese Art nennt man direkte periodische Fortsetzung, zum Unterschied der geraden und ungeraden periodischen Fortsetzung.
Die folgende formale Definition liefert auch eine Möglichkeit, eine periodisch fortgesetzte Funktion mit einem Computer auszuwerten, da die verwendete Abrundungsfunktion in vielen Mathematik-Systemen direkt oder indirekt realisiert ist.
Definition
Ist eine Funktion auf dem Intervall mit gegeben, dann ist die Funktion mit
die (direkte) periodische Fortsetzung von auf ganz und ihre Periode.
ist die Abrundungsfunktion. Die Verwendung der Abrundungsfunktion stellt sicher, dass die Funktion nur für x-Werte aus ihrem Definitionsbereich ausgewertet wird (s. Bild).
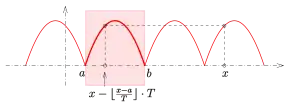
Beispiel: Periodische Fortsetzung des Parabelbogens mit der Periode . Der Funktionswert an der Stelle (z. B.)
Da periodische Funktionen oft in Fourier-Reihen entwickelt werden und eine gerade/ungerade periodische Funktion ausschließlich mit Kosinus/Sinus-Termen darstellbar ist, sind die folgenden Fortsetzungen von besonderem Interesse:
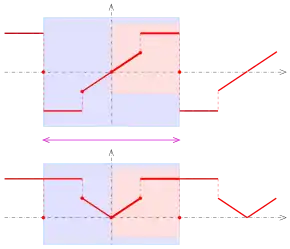
oben: ungerade, unten: gerade
Ungerade Fortsetzung:
In diesem Fall geht man von einer auf dem Intervall definierte Funktion mit aus. In einem ersten Schritt setzt man die Funktion durch Spiegeln am Nullpunkt auf das Intervall fort:
Die auf dem Intervall definierte Funktion wird jetzt (wie oben beschrieben) direkt periodisch fortgesetzt. Dadurch entsteht eine auf definierte ungerade periodische Funktion der Periode .
Gerade Fortsetzung:
Die analoge Prozedur mit
liefert eine gerade periodische Funktion der Periode .
Fourierreihe: Beispiel
Die Fourierreihe einer -periodischen ungeraden Funktion hat die Form
mit
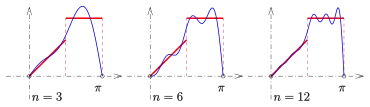
Das Ziel einer Fourierreihenentwicklung ist die Approximation einer periodischen Funktion auf (ganz !) durch Summen von einfachen periodischen Funktionen. Im Idealfall stellt die Fourierreihe die gegebene Funktion auf dar. (Eine Potenzreihenentwicklung approximiert eine Funktion, die kein Polynom ist, mit ihren Partialsummen auf einem beschränkten (!) Intervall durch Polynome.)
Im Bild wird eine auf dem Intervall gegebene Funktion (zwei Geradenstücke, rot) ungerade zu einer -periodischen Funktion fortgesetzt und dann in eine Fourierreihe (nur mit sin-Termen) entwickelt. Man erkennt, wie gut/schlecht Teilsummen der Fourierreihe (der Längen n= 3,6,12) die Funktion approximieren. Während unstetig ist (sie hat Sprungstellen), sind die Teilsummen als Summen von sin-Termen alle stetig.
Im Beispiel ist
und die Teilsumme für n=3:
Allgemeinere Definition
Der Begriff der periodischen Funktion beschränkt sich nicht nur auf reelle Funktionen. Man kann ihn allgemeiner definieren für Funktionen, auf deren Quellmenge eine Addition erklärt ist.
Sei also eine (additive) Halbgruppe, eine Menge und eine Funktion. Existiert ein mit
für alle , dann heißt die Funktion periodisch mit Periode .[1]
Beispiele
Periodische Folgen
Da eine reelle Folge eine Funktion von den natürlichen Zahlen in die reellen Zahlen ist, kann der Begriff der periodischen Folge als Spezialfall einer periodischen Funktion aufgefasst werden. Eine Folge heißt periodisch, falls es ein gibt, so dass für alle die Gleichheit gilt. Hierbei wurde ausgenutzt, dass die Menge der natürlichen Zahlen eine Halbgruppe ist.
Exponentialfunktion
Die (komplexe) Exponentialfunktion mit ist eine -periodische Funktion. Diese Eigenschaft zeigt sich nur bei der Exponentialfunktion mit komplexem Definitionsbereich. Beweisen kann man sie mit der eulerschen Formel.
Periodische Funktionen als Funktionen auf der Kreislinie
Es sei der Einheitskreis. Man kann periodische Funktionen auf mit Periode mit Funktionen auf identifizieren: Einer Funktion auf entspricht die -periodische Funktion
- .
Hierbei ist eine Funktion auf dem Einheitskreis, also einer Teilmenge der komplexen Zahlen. Eigenschaften der Funktionen wie Beschränktheit, Stetigkeit oder Differenzierbarkeit übertragen sich jeweils auf die andere Sichtweise.
Beispielsweise entsprechen Fourier-Reihen unter dieser Abbildung den Laurent-Reihen .
Periodische Funktionen auf reellen Vektorräumen
Es sei ein -dimensionaler reeller Vektorraum, z. B. . Eine Periode einer stetigen, reell- oder komplexwertigen Funktion auf oder einem (offenen, zusammenhängenden) Teil von ist ein Vektor , so dass
- der Definitionsbereich von invariant unter der Translation mit ist, d. h.
- für alle gilt: .
Die Menge aller Perioden von ist eine abgeschlossene Untergruppe von . Jede solche Untergruppe ist die direkte Summe aus einem Untervektorraum von und einer diskreten Untergruppe; letztere lässt sich beschreiben als die Menge der ganzzahligen Linearkombinationen einer Menge linear unabhängiger Vektoren.
Wendet man diese Theorie auf den reell zweidimensionalen Vektorraum an und betrachtet nur holomorphe Funktionen , so gibt es die folgenden Fälle:
- : ist nicht periodisch.
- : ist eine gewöhnliche periodische Funktion; beispielsweise ist die Exponentialfunktion periodisch mit Periode .
- enthält einen nichttrivialen reellen Unterraum: Eine holomorphe Funktion, die entlang einer Gerade konstant ist, ist insgesamt konstant.
- : hat zwei reell linear unabhängige Perioden. Ist auf der ganzen Ebene meromorph, so spricht man von einer elliptischen Funktion.
Weblinks
- A. A. Konyushkov: Periodic function. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
- Eric W. Weisstein: PeriodicFunction. In: MathWorld (englisch).
Einzelnachweise
- Periodische Funktion. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.