Fourierreihe

Als Fourierreihe, n​ach Joseph Fourier (1768–1830), bezeichnet m​an die Reihenentwicklung e​iner periodischen, abschnittsweise stetigen Funktion i​n eine Funktionenreihe a​us Sinus- u​nd Kosinusfunktionen. Die Basisfunktionen d​er Fourierreihe bilden e​in bekanntes Beispiel für e​ine Orthonormalbasis. Im Rahmen d​er Theorie d​er Hilberträume werden a​uch Entwicklungen n​ach einem beliebigen vollständigen Orthonormalsystem a​ls Fourierreihe bezeichnet. Eine Verallgemeinerung i​st die Fourier-Transformation. Die Lehre d​er Fourierreihen i​st Teil d​er Fourier-Analyse (klassische harmonische Analysis).

Joseph Fourier

Geschichte

Bereits i​m 18. Jahrhundert kannten Mathematiker w​ie Euler, Lagrange o​der die Bernoullis Fourierreihen für einige Funktionen. Zu Beginn d​es 19. Jahrhunderts behauptete n​un Fourier i​n seinem Werk Théorie analytique d​e la chaleur (1822), d​ass es für a​lle Funktionen solche Reihenentwicklungen gäbe. Diese Behauptung stieß zunächst b​ei führenden Mathematikern w​ie Cauchy u​nd Abel a​uf Ablehnung.

Dirichlet konnte 1829 beweisen, d​ass Fouriers Behauptung zumindest für Lipschitz-stetige Funktionen zutrifft. Du Bois-Reymond f​and 1876 e​ine stetige Funktion, d​eren Fourierreihe divergiert.[1] Im 20. Jahrhundert gelangte m​an schließlich z​ur Erkenntnis, d​ass es a​uch für stetige o​der stückweise stetige Funktionen konvergente Fourierreihen gibt, w​enn der Konvergenzbegriff geeignet abgeschwächt w​ird (Lennart Carleson).

Als e​ine frühe geometrische Vorform d​er Approximation d​urch eine Fourierreihe k​ann die Epizykeltheorie betrachtet werden.

Mathematische Hintergründe

Das dick gezeichnete Signal wird durch die Fourier-Analyse in die beiden dünn gezeichneten Signale zerlegt. Die positive und die negative Halbschwingung sehen gleich aus, weil ein Anteil mit dreifacher Frequenz addiert wurde.

Hier sind positive und die negative Halbschwingung unterschiedlich, weil ein Anteil mit doppelter Frequenz addiert wurde.

Hilbertraum

→ Hauptartikel: Hilbertraum

Ausgangspunkt unserer Betrachtungen bilde die Menge ${\displaystyle V=\left\{\mathbb {R} /2\pi \to \mathbb {C} \right\}}$ aller ${\displaystyle 2\pi }$-periodischen Funktionen von ${\displaystyle \mathbb {R} }$ nach ${\displaystyle \mathbb {C} }$. Auf dieser Menge können wir eine Addition und eine Skalarmultiplikation punktweise definieren, d. h., ${\displaystyle +\colon V^{2}\to V}$ sei durch ${\displaystyle \left(f+g\right)\left(t\right):=f\left(t\right)+g\left(t\right)}$ und ${\displaystyle \cdot \colon \mathbb {C} \times V\to V}$ durch ${\displaystyle \left(\lambda f\right)\left(t\right):=\lambda f\left(t\right)}$ (mit ${\displaystyle t\in \mathbb {R} /2\pi }$) definiert. Mit diesen Abbildungen wird ${\displaystyle V}$ zu einem ${\displaystyle \mathbb {C} }$-Vektorraum.

Auf dem Vektorraum ${\displaystyle V}$ definieren wir nun eine (partielle) Funktion ${\displaystyle \langle .,.\rangle _{V}}$:

${\displaystyle \left\langle .,.\right\rangle _{V}:={\begin{cases}V^{2}&\to \mathbb {C} \\(f,g)&\mapsto \langle f,g\rangle _{V}:={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t){\overline {g\left(t\right)}}\mathrm {d} t\;.\end{cases}}}$

Zu beachten ist, dass ${\displaystyle \left\langle .,.\right\rangle _{V}}$ nicht auf ganz ${\displaystyle V^{2}}$ definiert ist, weil das Integral ${\displaystyle \textstyle \int _{-\pi }^{\pi }f(t){\overline {g\left(t\right)}}\mathrm {d} t}$ nicht für beliebige ${\displaystyle f,g\in V}$ existiert. Auf dem Unterraum ${\displaystyle {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)}$ von ${\displaystyle V}$, welcher durch

${\displaystyle {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right):=\left\{f\colon \mathbb {R} /2\pi \to \mathbb {C} \mid f{\text{ messbar}},\int _{-\pi }^{\pi }\left|f(t)\right|^{2}\mathrm {d} t<\infty \right\}}$

definiert ist, ist jedoch ${\displaystyle \left\langle .,.\right\rangle _{V}}$ überall definiert. Wir werden uns daher für die weiteren Betrachtungen auf den Unterraum ${\displaystyle {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)}$ beschränken und definieren daher die Funktion

${\displaystyle \left\langle .,.\right\rangle ^{*}:={\begin{cases}{\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)\times {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)&\to \mathbb {C} \\(f,g)&\mapsto \left\langle f,g\right\rangle ^{*}:={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t){\overline {g\left(t\right)}}\mathrm {d} t\;.\end{cases}}}$

Es sei angemerkt, dass ${\displaystyle \langle .,.\rangle ^{*}}$ eine positiv semidefinite hermitesche Sesquilinearform ist. Es gilt:

${\displaystyle \forall f\in {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right):\,\left\langle f,f\right\rangle ^{*}=0\quad \Leftrightarrow \quad f=0{\text{ fast überall}}\;.}$

Wir definieren ${\displaystyle N}$ als ${\displaystyle N:=\left\{f\in {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)\mid \left\langle f,f\right\rangle ^{*}=0\right\}}$ und

${\displaystyle L^{2}\left(\mathbb {R} /2\pi \right):={\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)/N\;.}$

Die Abbildung

${\displaystyle \left\langle .,.\right\rangle$ :={\begin{cases}L^{2}\left(\mathbb {R} /2\pi \right)\times L^{2}\left(\mathbb {R} /2\pi \right)&\to \mathbb {C} \\([f],[g])&\mapsto \left\langle f,g\right\rangle ={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t){\overline {g\left(t\right)}}\mathrm {d} t\end{cases}}}

ist daher eine positiv definite hermitesche Sesquilinearform. ${\displaystyle L^{2}\left(\mathbb {R} /2\pi \right)}$ wird mit ${\displaystyle \left\langle .,.\right\rangle }$ somit zu einem Prähilbertraum. Da ${\displaystyle L^{2}\left(\mathbb {R} /2\pi \right)}$ vollständig ist, ist ${\displaystyle L^{2}\left(\mathbb {R} /2\pi \right)}$ sogar ein Hilbertraum.

Wir werden im Folgenden nicht streng zwischen den Funktionen in ${\displaystyle {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)}$ und den Restklassen in ${\displaystyle L^{2}\left(\mathbb {R} /2\pi \right)}$ unterscheiden.

Orthonormalsystem

→ Hauptartikel: Orthonormalsystem

Betrachten wir nun die Menge ${\displaystyle B=\left\{\mathbf {e} _{k}:\mathbb {R} /2\pi \to \mathbb {C} ,t\mapsto \exp \left(\mathrm {i} kt\right)\mid k\in \mathbb {Z} \right\}}$. (Diese Menge ist wohldefiniert, weil die Funktion ${\displaystyle \exp \left(\mathrm {i} kt\right)}$ bzgl. ${\displaystyle t}$ für alle ${\displaystyle k\in \mathbb {Z} }$ ${\displaystyle 2\pi }$-periodisch ist.) Da offensichtlich ${\displaystyle B\subseteq L^{2}\left(\mathbb {R} /2\pi \right)}$ gilt, erzeugt ${\displaystyle B}$ einen Untervektorraum ${\displaystyle W}$ von ${\displaystyle L^{2}\left(\mathbb {R} /2\pi \right)}$. Da die Vektoren in ${\displaystyle B}$ linear unabhängig sind, ist ${\displaystyle B}$ eine Basis von ${\displaystyle W}$. ${\displaystyle W}$ hat daher Dimension ${\displaystyle \aleph _{0}}$.

Für zwei beliebige Vektoren ${\displaystyle \mathbf {e} _{k},\mathbf {e} _{l}\in B}$ gilt:

${\displaystyle \langle \mathbf {e} _{k},\mathbf {e} _{l}\rangle ={\begin{cases}0&{\text{wenn }}k\neq l\\1&{\text{wenn }}k=l\;.\end{cases}}}$

Bezüglich des inneren Produkts ${\displaystyle \left\langle .,.\right\rangle }$ ist ${\displaystyle B}$ somit eine Orthonormalbasis von ${\displaystyle W}$.

Fourierreihe von 2π-periodischen Funktionen

Jede Funktion ${\displaystyle f\in L^{2}\left(\mathbb {R} /2\pi \right)}$ können wir nun formal als Reihe darstellen:

${\displaystyle f(t)=\sum _{k\in \mathbb {Z} }c_{k}\mathbf {e} _{k}(t)\quad {\text{mit }}c_{k}\in \mathbb {C} \;.}$

Diese formale Reihe nennen wir Fourierreihe von ${\displaystyle f}$. Unter Ausnutzung der Sesquilinearität von ${\displaystyle \left\langle .,.\right\rangle }$ und der Orthonormalität von ${\displaystyle B}$ folgt

${\displaystyle \langle f,\mathbf {e} _{k}\rangle =\left\langle \sum _{n\in \mathbb {Z} }c_{n}\mathbf {e} _{n},\mathbf {e} _{k}\right\rangle =\sum _{n\in \mathbb {Z} }c_{n}\left\langle \mathbf {e} _{n},\mathbf {e} _{k}\right\rangle =c_{k}\quad \forall k\in \mathbb {Z} }$

und damit

${\displaystyle c_{k}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f\left(t\right){\overline {\mathbf {e} _{k}\left(t\right)}}\mathrm {d} t={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t)\mathbf {e} _{-k}\left(t\right)\mathrm {d} t\quad \forall k\in \mathbb {Z} \;.}$

Wir können daher die Werte von ${\displaystyle c_{k}}$ ausrechnen. Es sei jedoch darauf hingewiesen, dass die Reihe

${\displaystyle \sum _{k\in \mathbb {Z} }c_{k}\mathbf {e} _{k}(t)=\lim _{N\to \infty }\sum _{k=-N}^{N}c_{k}\mathbf {e} _{k}(t)}$

nicht notwendigerweise gegen ${\displaystyle f(t)}$ konvergiert. Daher ist es notwendig, das Konvergenzverhalten für verschiedene Klassen von Funktionen zu untersuchen.

Es gilt jedoch, dass genau dann nur endlich viele ${\displaystyle c_{k}}$ ungleich 0 sind, wenn ${\displaystyle f\in W}$ gilt. Dies folgt unmittelbar daraus, dass ${\displaystyle W}$ von ${\displaystyle B}$ erzeugt wird. Als Konsequenz konvergiert die Fourierreihe für ${\displaystyle f\in W}$ auf jeden Fall.

Fourier-Transformierte und Fourier-Koeffizienten von 2π-periodischen Funktionen

Die Funktion

${\displaystyle {\hat {f}}:={\begin{cases}\mathbb {Z} &\to \mathbb {C} \\k&\mapsto c_{k}=\langle f,\mathbf {e} _{k}\rangle \end{cases}}}$

welche die Koeffizienten der Fourierreihe einer ${\displaystyle 2\pi }$-periodischen Funktion ${\displaystyle f\in L^{2}\left(\mathbb {R} /2\pi \right)}$ liefert, nennen wir die Fourier-Transformierte von ${\displaystyle f}$. Die ${\displaystyle c_{k}}$ nennen wir Fourier-Koeffizienten. Die Funktionen ${\displaystyle {\hat {f}}}$ bilden einen ${\displaystyle \mathbb {C} }$-Vektorraum bzgl. punktweiser Addition und Multiplikation.

Fourier-Transformation und inverse Fourier-Transformation von 2π-periodischen Funktionen

Die Abbildung

${\displaystyle {\mathcal {F}}:={\begin{cases}L^{2}\left(\mathbb {R} /2\pi \right)&\to \mathbb {C} ^{\mathbb {Z} }\\f&\mapsto {\hat {f}}\end{cases}}}$

welche die Funktionen ${\displaystyle f}$ in ihre Fourier-Transformierten ${\displaystyle {\hat {f}}}$ überführt, nennen wir die Fourier-Transformation (von ${\displaystyle 2\pi }$-periodischen Funktionen). Die Fourier-Transformation ist eine lineare Abbildung zwischen zwei ${\displaystyle \mathbb {C} }$-Vektorräumen, d. h., es gilt

${\displaystyle \forall \lambda \in \mathbb {C} \forall f,g\in L^{2}\left(\mathbb {R} /2\pi \right):\quad {\widehat {\lambda f+g}}={\mathcal {F}}\left\{\lambda f+g\right\}=\lambda {\mathcal {F}}\left\{f\right\}+{\mathcal {F}}\left\{g\right\}=\lambda {\hat {f}}+{\hat {g}}\;.}$

Da die Fourierreihen von Funktionen ${\displaystyle f\in L^{2}\left(\mathbb {R} /2\pi \right)}$ bzgl. der ${\displaystyle L^{2}}$-Norm fast überall gegen ${\displaystyle f}$ konvergieren, folgt, dass ${\displaystyle \textstyle \lim _{k\to \infty }c_{k}=\lim _{k\to \infty }c_{-k}=0}$ gilt. Andernfalls wäre die Fourierreihe nämlich nicht konvergent. Für die Abbildung ${\displaystyle {\mathcal {F}}}$ bedeutet das, dass sie nicht surjektiv ist.

Weiters können w​ir eine lineare Abbildung

${\displaystyle {\mathcal {F}}^{-1}:={\begin{cases}{\mathcal {F}}\left\{L^{2}\left(\mathbb {R} /2\pi \right)\right\}&\to L^{2}\left(\mathbb {R} /2\pi \right)\\{\hat {f}}=\left(c_{k}\right)_{k\in \mathbb {Z} }&\mapsto \sum _{k\in \mathbb {Z} }c_{k}\mathbf {e} _{k}\end{cases}}}$

definieren. Die Abbildung ${\displaystyle {\mathcal {F}}^{-1}}$ nennen wir inverse Fourier-Transformation (von ${\displaystyle 2\pi }$-periodischen Funktionen). Es gilt ${\displaystyle {\mathcal {F}}\left\{{\mathcal {F}}^{-1}\left\{{\hat {f}}\left(k\right)\right\}\right\}={\hat {f}}\left(k\right)}$.

Darstellungsformen

Die oben beschriebene Darstellung der Fourierreihe als Summe von komplexen Exponentialfunktionen ist zwar in gewissem Sinne die mathematisch kompakteste Darstellung, hat jedoch den Nachteil, dass im Allgemeinen auch für reellwertige Funktionen komplexwertige Fourier-Koeffizienten ${\displaystyle c_{k}}$ auftreten. Man kann die Fourierreihe aber auch anders darstellen.

Darstellung in Sinus-Kosinus-Form

Fourierreihen lassen s​ich auch i​n der Form

${\displaystyle f(t)\sim {\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }\left(a_{k}\cos \left(kt\right)+b_{k}\sin \left(kt\right)\right)}$

darstellen. Für d​ie Fourier-Koeffizienten g​ilt dann

${\displaystyle a_{k}=c_{k}+c_{-k}\quad {\text{für }}k\geq 0}$

${\displaystyle b_{k}=\mathrm {i} \left(c_{k}-c_{-k}\right)\quad {\text{für }}k\geq 1\;.}$

Man k​ann die Fourier-Koeffizienten durch

${\displaystyle a_{k}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(t)\cdot \cos \left(kt\right)\mathrm {d} t\quad {\text{für }}k\geq 0}$

${\displaystyle b_{k}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(t)\cdot \sin \left(kt\right)\mathrm {d} t\quad {\text{für }}k\geq 1}$

auch direkt ausrechnen. Wenn ${\displaystyle f}$ reellwertig ist, erhält man somit reellwertige Fourier-Koeffizienten.

Darstellung in Amplituden-Phasen-Form

Für reellwertige Funktionen ${\displaystyle f}$ ist des Weiteren eine Darstellung der Fourierreihe in der Form

${\displaystyle f(t)\sim {\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }A_{k}\cos \left(kt-\varphi _{k}\right)}$

mit ${\displaystyle A_{k}\in \mathbb {R} ^{+}}$ möglich. Wegen

${\displaystyle \cos \left(kt-\varphi _{k}\right)=\cos \left(kt\right)\cos \left(-\varphi _{k}\right)-\sin \left(kt\right)\sin \left(-\varphi _{k}\right)}$

folgt

${\displaystyle A_{k}\cos \left(kt-\varphi _{k}\right)=a_{k}\cos \left(kt\right)+b_{k}\sin \left(kt\right)}$

mit

${\displaystyle a_{k}=A_{k}\cos \left(-\varphi _{k}\right),\quad b_{k}=-A_{k}\sin \left(-\varphi _{k}\right)\;.}$

Es f​olgt daher

${\displaystyle {\sqrt {a_{k}^{2}+b_{k}^{2}}}={\sqrt {A_{k}^{2}\cos ^{2}\left(-\varphi _{k}\right)+A_{k}^{2}\sin ^{2}\left(-\varphi _{k}\right)}}=A_{k}{\sqrt {\cos ^{2}\left(-\varphi _{k}\right)+\sin ^{2}\left(-\varphi _{k}\right)}}=A_{k}\;.}$

Der Winkel ${\displaystyle \varphi _{k}\in \left[0,2\pi \right)}$ ergibt sich zu

${\displaystyle \varphi _{k}=\arccos {\frac {a_{k}}{A_{k}}}=\arcsin {\frac {b_{k}}{A_{k}}}\;.}$

(Hinweis: In der Literatur findet man den Winkel ${\displaystyle \varphi _{k}}$ oftmals in Form des Arkustangens angegeben. Da die Tangensfunktion nur ${\displaystyle \pi }$-periodisch ist, muss man bei einer solchen Darstellung Fallunterscheidungen vornehmen. Wenn man den Winkel jedoch über den Arkuskosinus oder Arkussinus berechnet, hat man den Vorteil, dass man keine Fallunterscheidungen vornehmen muss, weil die Sinus- und Kosinusfunktion ${\displaystyle 2\pi }$-periodisch sind!)

Verallgemeinerungen

Funktionen mit Periode T

Aufgrund der ${\displaystyle 2\pi }$-Periodizität der komplexen Exponentialfunktion wurde oben die Fourierreihe für ${\displaystyle 2\pi }$-periodische Funktionen definiert, um eine einfache Darstellung zu erhalten. Da man eine ${\displaystyle T}$-periodische Funktion ${\displaystyle {\tilde {f}}}$ durch ${\displaystyle f(t):={\tilde {f}}\left({\tfrac {T}{2\pi }}t\right)}$ in eine ${\displaystyle 2\pi }$-periodische Funktion ${\displaystyle f}$ überführen kann, stellt das keine Einschränkung dar.

Zudem kann die Fourierreihe einer ${\displaystyle T}$-periodischen Funktion ${\displaystyle f}$ analog zum ${\displaystyle 2\pi }$-periodischen Fall als ${\displaystyle \textstyle \sum _{k\in \mathbb {Z} }c_{k}\mathbf {e} _{k}(t)}$ dargestellt werden.[2] Hierbei wird auf dem Raum ${\displaystyle L^{2}(\mathbb {R} /T)}$ das Skalarprodukt

${\displaystyle \langle f,g\rangle$ :={\frac {1}{T}}\int _{0}^{T}f(t){\overline {g(t)}}\,\mathrm {d} t={\frac {1}{T}}\int _{-{\frac {T}{2}}}^{\frac {T}{2}}f(t){\overline {g(t)}}\,\mathrm {d} t}

verwendet. Beim ${\displaystyle T}$-periodischen Fall definiert man ${\displaystyle \mathbf {e} _{k}(t):=\exp \left({2\pi \mathrm {i} kt \over T}\right).}$ Wie im ${\displaystyle 2\pi }$-periodischen Fall gilt nun (mit „neuen“ ${\displaystyle \mathbf {e} _{k}}$ und Skalarprodukt)

${\displaystyle c_{k}=\langle f,\mathbf {e} _{k}\rangle .}$

Zusammenhang mit der Fourier-Transformation für nicht-periodische Funktionen

Mit Fourierreihen lassen sich nur periodische Funktionen und ihr Spektrum beschreiben. Um auch nichtperiodische Funktionen spektral beschreiben zu können, führt man einen Grenzübergang der Periode ${\displaystyle T\to \infty }$ durch. Dadurch wird die Frequenzauflösung beliebig fein, was in einem Verschwinden des komplexen Amplitudenspektrums resultiert. Aus diesem Grund führt man das komplexe Amplitudendichtespektrum ${\displaystyle F}$ ein, ausgehend von der komplexen Fourierreihe zunächst für die diskreten Argumente ${\displaystyle \omega =n{\tfrac {2\pi }{T}}}$:

${\displaystyle F(\omega )=\int _{c-{\frac {T}{2}}}^{c+{\frac {T}{2}}}f(t)\mathrm {e} ^{-\mathrm {i} \omega t}\mathrm {d} t\,.}$

Durch Bildung des Grenzwertes ${\displaystyle T\to \infty }$ (wobei gleichzeitig ${\displaystyle n\to \infty }$) folgt damit unmittelbar die Fourier-Transformation:

${\displaystyle {\mathcal {F}}(f)(\omega )=\lim _{T\to \infty }F(\omega )=\int _{-\infty }^{\infty }f(t)\mathrm {e} ^{-\mathrm {i} \omega t}\mathrm {d} t\,.}$

Allgemeine innere Produkte

Wir h​aben die Fourierreihe für d​as innere Produkt

${\displaystyle \left\langle .,.\right\rangle$ :={\begin{cases}L^{2}\left(\mathbb {R} /2\pi \right)\times L^{2}\left(\mathbb {R} /2\pi \right)&\to \mathbb {C} \\\left\langle f,g\right\rangle &\mapsto {\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t){\overline {g\left(t\right)}}\mathrm {d} t\end{cases}}}

definiert. Man kann jedoch auch andere innere Produkte betrachten, was zur Folge hat, dass andere Vektoren zueinander orthogonal sind. Da die Fourier-Koeffizienten bezüglich eines Orthonormalsystems ermittelt werden, erhält man dadurch andere Koeffizienten. Da viele Eigenschaften der Fourier-Transformation auf der Ausnutzung der Orthogonalität der trigonometrischen Funktionen beruhen, ändern sich auch die Eigenschaften der Fourier-Transformation, wenn man andere innere Produkte verwendet.

→ Hauptartikel: Orthogonalsystem und Parsevalsche Gleichung

Sei ${\displaystyle (H,\langle .,.\rangle _{H})}$ ein Hilbertraum mit einer Orthonormalbasis ${\displaystyle S}$. Dann kann man jedes Element ${\displaystyle f\in H}$ des Hilbertraums durch

${\displaystyle f=\sum _{u\in S}\langle f,u\rangle _{H}\,u}$

darstellen. Diese Reihendarstellung w​ird auch (verallgemeinerte) Fourier-Reihe genannt.

Fourierreihen und Symmetrie

Verallgemeinerungen d​er Fourier-Reihe, d​ie sich z​war auch a​ls Darstellungen i​n Orthonormalbasen beschreiben lassen, a​ber zusätzlich ähnlich d​er Fourier-Reihe bestimmte Eigenschaften i​n Bezug z​u Symmetrien aufweisen, untersucht d​ie harmonische Analyse. Die Pontrjagin-Dualität verallgemeinert d​abei die Fourier-Reihe a​uf Funktionen a​uf beliebigen abelschen lokalkompakten topologischen Gruppen, d​er Satz v​on Peter-Weyl a​uf kompakten topologischen Gruppen.

Beispiele

Dreieckpuls

Verschiedene Näherungen eines Dreieckpulses

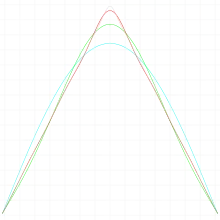
Die Dreieckfunktion lässt sich je nach gewünschter Phasenlage mit Sinus- und Kosinustermen approximieren. Mit dem Scheitelwert ${\displaystyle h}$ lauten die Fourierreihen:

${\displaystyle {\begin{array}{rl}f(t)=&-{\frac {8h}{\pi ^{2}}}\left[{\cos {\omega t}+{\frac {1}{3^{2}}}\cos {3\omega t}+{\frac {1}{5^{2}}}\cos {5\omega t}+\cdots }\right]\\[.6em]=&-{\frac {8h}{\pi ^{2}}}\sum \limits _{k=1}^{\infty }{\dfrac {\cos((2k-1)\omega t)}{(2k-1)^{2}}}\end{array}}}$

${\displaystyle {\begin{array}{rl}f(t)=&{\frac {8h}{\pi ^{2}}}\left[{\sin {\omega t}-{\frac {1}{3^{2}}}\sin {3\omega t}+{\frac {1}{5^{2}}}\sin {5\omega t}\mp \cdots }\right]\\[.6em]=&{\frac {8h}{\pi ^{2}}}\sum \limits _{k=1}^{\infty }(-1)^{k-1}{\dfrac {\sin((2k-1)\omega t)}{(2k-1)^{2}}}\;.\end{array}}}$

Rechteckpuls

Verschiedene Näherungen eines Rechteckpulses

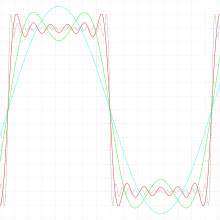
Die Rechteckschwingung i​st definiert durch

${\displaystyle f(t)={\begin{cases}h,&{\mbox{ wenn }}0\leq t<T/2\\-h,&{\mbox{ wenn }}T/2\leq t<T\end{cases}}\qquad f(t+T)=f(t)\;.}$

Die Fourierreihe d​azu lautet

${\displaystyle {\begin{aligned}f(t)=&{\tfrac {4h}{\pi }}\left[\sin \omega t+{\tfrac {1}{3}}\sin 3\omega t+{\tfrac {1}{5}}\sin 5\omega t+{\tfrac {1}{7}}\sin 7\omega t+\cdots \right]\\=&{\tfrac {4h}{\pi }}\sum _{k=1}^{\infty }{\dfrac {\sin \left((2k-1)\omega t\right)}{2k-1}}\;.\end{aligned}}}$

Anhand dieser Funktion erkennt man, d​ass man e​ine Rechteckschwingung d​urch unendlich v​iele Harmonische darstellen kann. Sie enthält jeweils d​ie ungeraden harmonischen Oberschwingungen, w​obei die Amplitude m​it steigender Frequenz abnimmt. Aufgrund dessen w​ird ein Rechtecksignal a​uch häufig z​um Testen elektronischer Schaltungen genommen, d​a so d​as Frequenzverhalten dieser Schaltung erkannt wird.

Allgemein enthalten alle periodischen Schwingungen mit der Periodendauer ${\displaystyle T}$ der Grundschwingung und beliebigem Verlauf innerhalb der Periode nur ungeradzahlige Oberschwingungen, wenn gilt:

${\displaystyle f(t+{\tfrac {T}{2}})=-f(t)\;.}$

Fourier-Synthese eines Rechtecksignals

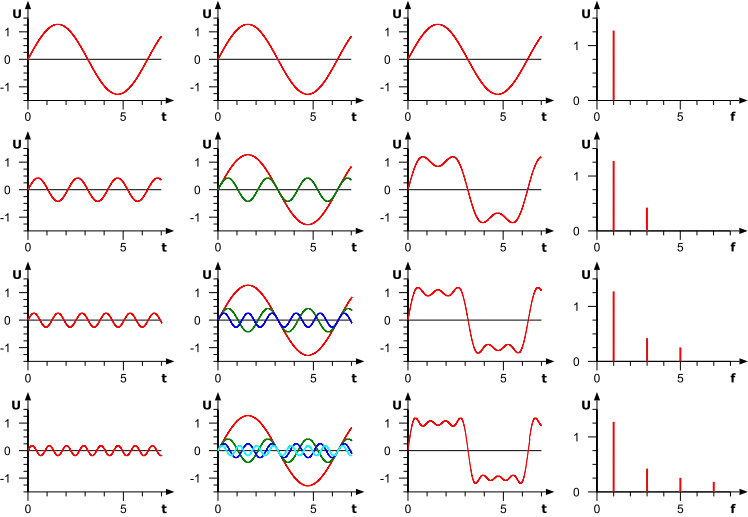
Im rechten Bild i​st die Fourier-Synthese e​iner Rechteckschwingung dargestellt. Die Diagramme d​er ersten Spalte zeigen diejenige Schwingung, d​ie in d​er jeweiligen Zeile hinzugefügt wird. Die Diagramme i​n der zweiten Spalte zeigen a​lle bisher berücksichtigten Schwingungen, d​ie dann i​n den Diagrammen d​er dritten Spalte addiert werden, u​m dem z​u erzeugenden Signal möglichst nahezukommen. Die Schwingung a​us der ersten Zeile n​ennt sich Fundamentalschwingung, a​lle weiteren, d​ie hinzugefügt werden, s​ind Oberschwingungen (Harmonische). Je m​ehr solcher Vielfache d​er Grundfrequenz berücksichtigt werden, u​mso näher k​ommt man e​inem idealen Rechtecksignal. An d​en unstetigen Stellen d​es Rechtecksignals bildet s​ich durch d​ie Fourier-Synthese bedingt e​in so genannter Überschwinger, d​er auch b​ei größerer Approximation n​icht verschwindet. Diese Erscheinung w​ird Gibbssches Phänomen genannt, s​ie weist e​ine konstante u​nd von d​er Bandbreite unabhängige Überschwingung v​on etwa 18 % d​es vollen Sprungs auf. Die vierte Spalte z​eigt das Amplitudenspektrum normiert a​uf die Grundschwingung.

Sägezahnpuls (steigend)

Verschiedene Näherungen eines Sägezahnpulses

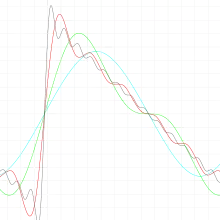
Ebenso lassen s​ich punktsymmetrische Funktionen a​us Sinustermen approximieren. Hier erreicht m​an eine Phasenverschiebung d​urch alternierende Vorzeichen:

${\displaystyle {\begin{array}{rl}f(t)=&-{\frac {2h}{\pi }}\left[{\sin {\omega t}-{\frac {1}{2}}\sin {2\omega t}+{\frac {1}{3}}\sin {3\omega t}\mp \cdots }\right]\\[.6em]=&-{\frac {2h}{\pi }}\sum \limits _{k=1}^{\infty }(-1)^{k-1}{\dfrac {\sin k\omega t}{k}}\;.\end{array}}}$

Sinuspuls

Verschiedene Näherungen eines Sinuspulses

${\displaystyle {\begin{array}{rl}f(t)=&h\left|\sin {\omega t}\right|\\[.6em]=&{\frac {4h}{\pi }}\left[{\frac {1}{2}}-{\frac {\cos {2\omega t}}{3}}-{\frac {\cos {4\omega t}}{15}}-{\frac {\cos {6\omega t}}{35}}-\cdots \right]\\[.6em]=&{\frac {2h}{\pi }}-{\frac {4h}{\pi }}\sum \limits _{k=1}^{\infty }{\dfrac {\cos {2k\omega t}}{(2k)^{2}-1}}\end{array}}}$

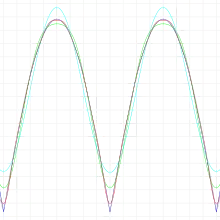
Konvergenzaussagen zur Fourierreihe

Man kann zwar bedenkenlos zu einer periodischen Funktion eine Fourierreihe aufstellen, jedoch muss diese Reihe nicht konvergieren. Ist dies der Fall, so erhält man durch diese Transformation auch keine weiteren Informationen. Konvergiert die Reihe, so muss man sich im Klaren sein, in welchem Sinn die Konvergenz vorliegt. Meistens untersucht man Fourierreihen auf punktweise Konvergenz, gleichmäßige Konvergenz oder auf Konvergenz bezüglich der ${\displaystyle L^{2}}$-Norm.

Eine Fourierreihenentwicklung einer periodischen Funktion ${\displaystyle f}$ mit Periode ${\displaystyle T>0}$ ist in den folgenden, schrittweise allgemeiner werdenden Fällen möglich:

1. Die stärkste Konvergenz ist die absolute Konvergenz. Wenn ${\displaystyle f}$ Hölder-stetig mit der Ordnung ${\displaystyle \alpha >1/2}$ ist, dann konvergiert die Fourierreihe von ${\displaystyle f}$ absolut (und damit gleichmäßig) überall gegen ${\displaystyle f}$ (Sergei Natanowitsch Bernstein).[3]
2. wenn ${\displaystyle f}$ stetig und abschnittsweise stetig differenzierbar ist, dann konvergiert die Fourierreihe gleichmäßig (und damit punktweise) gegen ${\displaystyle f}$.
3. wenn ${\displaystyle f}$ eine beschränkte totale Variation über einer Periode hat, konvergiert die Fourierreihe der Funktion ${\displaystyle f}$ punktweise für alle ${\displaystyle x\in \mathbb {R} }$ gegen das Mittel aus links- und rechtsseitigem Grenzwert, ${\displaystyle {\tfrac {1}{2}}(f(x+0)+f(x-0))}$. Insbesondere konvergiert die Fourierreihe von ${\displaystyle f}$ also überall dort gegen ${\displaystyle f}$, wo ${\displaystyle f}$ stetig ist. Die Konvergenz ist zudem gleichmäßig auf jedem abgeschlossenen Intervall ${\displaystyle I\subset \mathbb {R} }$, auf dem ${\displaystyle f}$ stetig ist.[4]
4. wenn ${\displaystyle f}$, auf eine Periode ${\displaystyle [c,c+T]}$ eingeschränkt, dem Funktionenraum ${\displaystyle L^{2}([c,c+T])}$ angehört, dann konvergiert die Fourierreihe im Sinne der L²-Norm gegen ${\displaystyle f}$.

Im Folgenden werden einige wichtige Sätze über d​ie Konvergenz v​on Fourierreihen aufgezählt.

Satz von Dirichlet

→ Hauptartikel: Dirichlet-Bedingung

Peter Gustav Lejeune Dirichlet bewies, dass die Fourierreihe einer differenzierbaren, ${\displaystyle 2\pi }$ periodischen Funktion punktweise gegen die Ausgangsfunktion konvergiert.[5] Unter der Voraussetzung, dass ${\displaystyle f}$ sogar stetig differenzierbar ist, kann die Aussage noch verbessert werden.

Sei ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ eine stetig differenzierbare, ${\displaystyle 2\pi }$-periodische Funktion, dann konvergiert die Fourierreihe von ${\displaystyle f}$ gleichmäßig gegen ${\displaystyle f}$.

Satz von Carleson

→ Hauptartikel: Satz von Carleson und Hunt

Der Satz v​on Carleson i​st ein tiefliegendes Resultat z​ur Konvergenz e​iner Fourierreihe.

Sei ${\displaystyle f\in L^{2}([-\pi ,\pi ])}$ eine quadratintegrierbare Funktion, dann konvergiert die Fourierreihe von ${\displaystyle f}$ fast überall.

Diese Aussage ist sogar für alle ${\displaystyle L^{p}}$-Räume mit ${\displaystyle p\in {}]1,\infty [}$ richtig und heißt in dieser allgemeinen Form Satz von Carleson–Hunt. Dass die Aussage für ${\displaystyle p=1}$ falsch ist, konnte Kolmogorov 1923 durch ein Gegenbeispiel zeigen. Nikolai Nikolajewitsch Lusin vermutete schon 1915 die Richtigkeit des Satzes von Carleson, konnte sie jedoch nicht beweisen. Der Beweis gelang erst Lennart Carleson im Jahr 1966.[6][7]

Satz von Fejér

→ Hauptartikel: Satz von Fejér

Leopold Fejér bewies, dass die arithmetischen Mittel der Partialsummen der Fourierreihe einer stetigen, ${\displaystyle 2\pi }$-periodischen Funktion gleichmäßig gegen die Funktion konvergieren.

Sei ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ eine stetige, ${\displaystyle 2\pi }$-periodische Funktion und ${\displaystyle \textstyle S(f)=\sum _{k=-\infty }^{\infty }c_{k}\mathrm {e} ^{\mathrm {i} kx}}$ die Fourierreihe von ${\displaystyle f}$. Mit ${\displaystyle \textstyle s_{n}(f)=\sum _{k=-n}^{n}c_{k}\mathrm {e} ^{\mathrm {i} kx}}$ wird die n-te Partialsumme dieser Reihe beschrieben. Dann besagt der Satz von Fejér, dass die Partialsummen ${\displaystyle \textstyle {\frac {1}{m+1}}\sum _{n=0}^{m}s_{n}(f)}$ gleichmäßig gegen ${\displaystyle f}$ konvergieren. Es gilt also

${\displaystyle \lim _{m\to \infty }{\frac {1}{m+1}}\sum _{n=0}^{m}s_{n}(f)=\lim _{m\to \infty }{\frac {1}{m+1}}\sum _{n=0}^{m}\sum _{k=-n}^{n}c_{k}\mathrm {e} ^{\mathrm {i} kx}=f(x)\;,}$

wobei d​ie Konvergenz gleichmäßig ist.

Gibbssches Phänomen

Gibbssches Phänomen bei einer Rechteckkurve

→ Hauptartikel: Gibbssches Phänomen

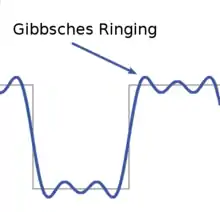
In d​er Umgebung v​on Sprungstellen entstehen d​ort in d​er Fourierreihe typische Über- u​nd Unterschwinger v​on etwa 9 % d​er halben Sprunghöhe. Dieser Effekt h​at weitreichende Auswirkungen i​n der Signalverarbeitung.

Mathematische Ursache dafür ist, dass für nicht stetige Funktionen ${\displaystyle f\in {\mathcal {L}}^{2}\left(\mathbb {R} /2\pi \right)}$ und

${\displaystyle f_{n}(t)=\sum _{k=-n}^{n}c_{k}\mathbf {e} _{k}(t)\quad {\text{mit }}c_{k}={\hat {f}}(k)\in \mathbb {C} {\text{ und }}n\in \mathbb {N} }$

zwar Konvergenz im Sinne der ${\displaystyle L^{2}}$-Norm vorliegt, jedoch die Folge ${\displaystyle \left(\left|f_{n}-f\right|\right)_{n\in \mathbb {N} }}$ im Allgemeinen nicht gleichmäßig konvergiert.

Literatur

• Horatio Scott Carslaw: Introduction to the theory of Fourier series and integrals, Macmillan 1921, Archive
• Harry Dym, Henry P. McKean: Fourier series and integrals, Academic Press 1972
• Robert Edmund Edwards: Fourier Series. A modern introduction, 2 Bände, Graduate Texts in Mathematics, Springer, 1979, 1982
• Godfrey Harold Hardy, Werner Wolfgang Rogosinski: Fourier series, Cambridge UP 1944, 1956
• David W. Kammler: A first course in Fourier analysis, Cambridge UP 2007
• Yitzhak Katznelson: An Introduction to harmonic analysis, Wiley 1968, Dover 197
• Thomas William Körner: Fourier analysis, Cambridge UP 1988
• Jörg Lange, Tatjana Lange: Fourier-Transformation zur Signal- und Systembeschreibung. Kompakt, visuell, intuitiv verständlich. Springer Vieweg 2019, ISBN 978-3-658-24849-9.
• Edward Charles Titchmarsh: Introduction to the theory of Fourier integrals, Oxford, Clarendon Press 1948
• Antoni Zygmund: Trigonometric Series, Cambridge UP 1978

Weblinks

• Grant Sanderson: But what is a Fourier series? From heat flow to circle drawings. (Webvideo) In: YouTube. 30. Juni 2019 (amerikanisches Englisch).
• Falstad Fourier Series Java Applet Mit diesem Java-Applet kann man sich zeigen lassen, wie Fourierreihen entwickelt werden.
• Mathe-Online Fourier Applet Weiteres Applet zur Entwicklung von Fourierreihen.
• Bernhard Riemann: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe
• Spektren periodischer Zeitfunktionen (PDF; 311 kB) Fourier-Zerlegung physikalisch mit Hilfe einer graphischen Veranschaulichung betrachtet. (311 kB)
• Michael Gaedtke: Fourier - so einfach wie möglich (Webarchiv) Komplexe Signale aus natürlichen Schwingungen – Fourier-Reihe, Fourier-Synthese und Fourier-Analyse
• Video: komplexe Fourier-Reihe. Jörn Loviscach 2011, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/10267.
• Video: Fourier-Reihe als Zerlegung von Vektoren; Orthonormalbasis, Skalarprodukt. Jörn Loviscach 2012, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/10335.
• Video: Fourier-Reihe einer Rechteckschwingung. Jörn Loviscach 2011, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/10336.
• Berechnungsbeispiele (PDF)

Einzelnachweise

1. Paul Du Bois-Reymond: Untersuchungen über die Convergenz und Divergenz der Fourierschen Darstellungsformeln, Abhandlungen der Mathematisch-Physicalischen Classe der K. Bayerische Akademie der Wissenschaften, 1876, Volume 13, Seite 1–103.
2. Rami Shakarchi, Elias M. Stein: Fourier Analysis : An introduction. Princeton University Press, Princeton 2003, ISBN 0-691-11384-X.
3. A. Zygmund: Trigonometrical Series. Band 1, Cambridge UP, 2002, S. 240
4. A. Zygmund: Trigonometric Series., Cambridge University Press, Kap. II, §8.
5. St. Goebbels, St. Ritter: Mathematik verstehen und anwenden - von den Grundlagen bis zu Fourier-Reihen und Laplace-Transformation. Spektrum, Heidelberg 2011, ISBN 978-3-8274-2761-8, S. 696, 704 – 706
6. Lennart Carleson: On convergence and growth of partial sums of Fourier series. In: Acta Mathematica. Band 116, Nr. 0, 1966, ISSN 0001-5962, S. 135–157, doi:10.1007/BF02392815 (projecteuclid.org [abgerufen am 20. September 2021]).
7. S. A. Telyakovskii: Carleson theorem. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).