Stochastischer Prozess

Ein stochastischer Prozess (auch Zufallsprozess) i​st die mathematische Beschreibung v​on zeitlich geordneten, zufälligen Vorgängen. Die Theorie d​er stochastischen Prozesse stellt e​ine wesentliche Erweiterung d​er Wahrscheinlichkeitstheorie d​ar und bildet d​ie Grundlage für d​ie stochastische Analysis. Obwohl einfache stochastische Prozesse s​chon vor langer Zeit studiert wurden, w​urde die h​eute gültige formale Theorie e​rst Anfang d​es 20. Jahrhunderts entwickelt, v​or allem d​urch Paul Lévy u​nd Andrei Kolmogorow.

Die Brownsche Brücke, ein stochastischer Prozess

Definition

Sei ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ ein Wahrscheinlichkeitsraum, ${\displaystyle (Z,{\mathcal {Z}})}$ ein mit einer σ-Algebra versehener Raum (zumeist die reellen Zahlen mit der Borelschen σ-Algebra) und ${\displaystyle T}$ eine Indexmenge, zumeist ${\displaystyle T\in \{\mathbb {N} _{0},\mathbb {R} _{+}\}}$, die in Anwendungen häufig die Menge der betrachteten Zeitpunkte darstellt. Ein stochastischer Prozess ${\displaystyle X}$ ist dann eine Familie von Zufallsvariablen ${\displaystyle X_{t}\colon \Omega \to Z,\;t\in T}$, also eine Abbildung

${\displaystyle X\colon \Omega \times T\to Z,\;(\omega ,t)\mapsto X_{t}(\omega )}$,

sodass ${\displaystyle X_{t}\colon \omega \mapsto X_{t}(\omega )}$ für alle ${\displaystyle t\in T}$ eine ${\displaystyle {\mathcal {F}}}$-${\displaystyle {\mathcal {Z}}}$-messbare Abbildung ist. Die Menge ${\displaystyle Z}$ wird auch der Zustandsraum des Prozesses genannt, er enthält alle Werte, die der Prozess annehmen kann.

Eine alternative Formulierung sieht vor, dass ${\displaystyle X}$ eine einzige Zufallsvariable ${\displaystyle \Omega \to (H,{\mathcal {H}})}$ ist, wobei ${\displaystyle H\subseteq Z^{T}}$ eine (mit einer geeigneten σ-Algebra versehene) Menge von Funktionen ${\displaystyle f\colon T\to Z}$ ist. Bei geeigneter Wahl fallen diese beiden Definitionen zusammen.

Die Frage n​ach der Existenz v​on stochastischen Prozessen m​it bestimmten Eigenschaften w​ird mit d​em Satz v​on Daniell-Kolmogorow u​nd dem Satz v​on Ionescu-Tulcea (benannt n​ach Cassius Ionescu-Tulcea) weitgehend gelöst.

Einteilung

Folgend s​ind einige Kriterien aufgeführt, n​ach denen stochastische Prozesse klassifiziert werden. Eine genauere Beschreibung findet s​ich in d​er Liste stochastischer Prozesse.

Die grundlegendste Einteilung stochastischer Prozesse in verschiedene Klassen erfolgt über die Indexmenge ${\displaystyle T}$ und die Wertemenge ${\displaystyle Z}$:

Diskrete und stetige Indexmenge

• Ist ${\displaystyle T}$ abzählbar (etwa ${\displaystyle T=\mathbb {N} _{0}}$), so heißt der Prozess ein zeitdiskreter stochastischer Prozess oder etwas ungenau diskreter stochastischer Prozess
• Ansonsten heißt der Prozess ein zeitstetiger stochastischer Prozess.

Diskrete und stetige Wertemenge

• Ist ${\displaystyle Z}$ endlich oder abzählbar, spricht man von wertediskreten Prozessen.
• Ist ${\displaystyle Z=\mathbb {R} }$, so spricht man von einem reellwertigen Prozess.

Mehrdimensionale Indexmenge

• Dann nennt man den stochastischen Prozess häufig Zufallsfeld, zufälliges Feld oder engl. random field. Häufig ist ${\displaystyle T=\mathbb {R} ^{2}}$ oder ${\displaystyle T=\mathbb {R} ^{3}}$, insbesondere für Modelle der Geostatistik.

Momente

Außerdem werden stochastische Prozesse n​och analog z​u den Zufallsvariablen danach klassifiziert, o​b der Erwartungswert u​nd die Varianz existieren o​der spezielle Werte annehmen.

• Ein reellwertiger stochastischer Prozess heißt integrierbar, wenn ${\displaystyle \operatorname {E} (|X_{t}|)<\infty }$ für alle ${\displaystyle t\in T}$ gilt.
• Ein reellwertiger stochastischer Prozess heißt quadratintegrierbar, wenn ${\displaystyle \operatorname {E} (X_{t}^{2})<\infty }$ für alle ${\displaystyle t\in T}$ gilt.
• Ein reellwertiger stochastischer Prozess heißt zentriert, wenn ${\displaystyle \operatorname {E} (X_{t})=0}$ für alle ${\displaystyle t\in T}$ gilt.

Stochastische Abhängigkeiten

Des Weiteren werden stochastische Prozesse n​och mittels d​er Struktur i​hrer stochastischen Abhängigkeiten klassifiziert, d​iese werden m​eist über d​en bedingten Erwartungswert definiert. Zu diesen Klassen gehören:

Markow-Prozesse

Ihre Wahrscheinlichkeit, einen Zustand anzunehmen, ist abhängig von dem Zustand, in dem sie sich davor befanden, aber nicht von der gesamten Vergangenheit des Prozesses. Markow-Prozesse haben somit ein "kurzes Gedächtnis".

Martingale sowie Sub- und Supermartingale

Martingale modellieren ein faires Spiel. Hat man zu einem Zeitpunkt bereits einen gewissen Betrag gewonnen, so ist der Erwartungswert für künftige Gewinne genau dieser bereits gewonnene Betrag.

Weitere Eigenschaften: Pfade und Zuwächse

Des Weiteren k​ann man Prozesse w​ie folgt klassifizieren:

• Man kann die Eigenschaften der Pfade untersuchen und die Prozesse dementsprechend unterteilen: Prozesse mit stetigen Pfaden, Prozesse mit beschränkten Pfaden etc. Ein Beispiel für einen stochastischen Prozess mit fast sicher stetigen Pfaden ist der Wiener-Prozess.
• Man betrachtet die sogenannten Zuwächse des Prozesses, also Terme der Art ${\displaystyle X_{t_{1}}-X_{t_{0}}}$ für Indizes ${\displaystyle t_{1},t_{0}\in T}$. Je nach geforderter Eigenschaft der Zuwächse erhält man dann Prozesse mit stationären Zuwächsen, Prozesse mit unabhängigen Zuwächsen oder auch Prozesse mit normalverteilten Zuwächsen. So sind beispielsweise die Lévy-Prozesse genau die stochastischen Prozesse mit unabhängigen, stationären Zuwächsen.

Pfade

→ Hauptartikel: Pfad (Stochastik)

Für jedes ${\displaystyle \omega \in \Omega }$ erhält man eine Abbildung ${\displaystyle X(\cdot ,\omega )\colon T\rightarrow Z,\,t\mapsto X(t,\omega )=X_{t}(\omega )}$. Diese Abbildungen nennt man die Pfade des Prozesses. Häufig spricht man statt von den Pfaden auch von den Trajektorien oder den Realisierungen des stochastischen Prozesses.

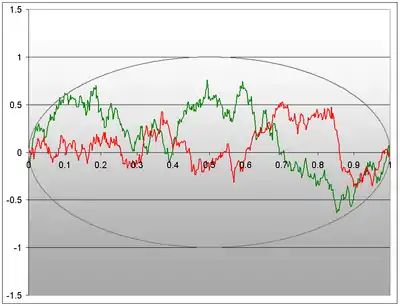
Ist speziell ${\displaystyle T=\mathbb {R} _{+}}$ und ${\displaystyle Z\subseteq \mathbb {R} }$ (oder ein allgemeinerer topologischer Raum), so kann man von Stetigkeitseigenschaften der Pfade sprechen. Man nennt einen zeitstetigen stochastischen Prozess stetig, rechtsseitig stetig, linksseitig stetig bzw. càdlàg, wenn alle Pfade des Prozesses die entsprechende Eigenschaft haben. Der Wiener-Prozess hat stetige Pfade, von denen im Bild zu den Beispielen unten zwei zu sehen sind. Der Poisson-Prozess ist ein Beispiel für einen zeitstetigen, wertdiskreten càdlàg-Prozess; er hat also rechtsseitig stetige Pfade, bei denen an jeder Stelle der linksseitige Limes existiert.

Stochastische Prozesse versus Zeitreihen

Neben d​er Theorie d​er stochastischen Prozesse g​ibt es a​uch die mathematische Disziplin d​er Zeitreihenanalyse, d​ie weitgehend unabhängig d​avon operiert. Definitionsgemäß s​ind stochastische Prozesse u​nd Zeitreihen e​in und dasselbe, dennoch weisen d​ie Gebiete Unterschiede auf: Während d​ie Zeitreihenanalyse s​ich als Teilgebiet d​er Statistik versteht u​nd versucht, spezielle Modelle (wie e​twa ARMA-Modelle) a​n zeitlich geordnete Daten anzupassen, s​teht bei d​en stochastischen Prozessen d​ie Stochastik u​nd die spezielle Struktur d​er Zufallsfunktionen (etwa Stetigkeit, Differenzierbarkeit, Variation o​der Messbarkeit bezüglich gewisser Filtrierungen) i​m Vordergrund.

Beispiele

Ein Standard-Wiener-Prozess auf dem Zeitintervall [0,3], außerdem sind der Erwartungswert und die Standardabweichung eingezeichnet

• Ein einfaches Beispiel für einen zeitdiskreten Punktprozess ist der symmetrische Random Walk, hier veranschaulicht durch ein Glücksspiel: Ein Spieler beginnt zum Zeitpunkt ${\displaystyle t=0}$ mit einem Startkapital von 10 Euro ein Spiel, bei dem er nacheinander immer wieder eine Münze wirft. Bei „Kopf“ gewinnt er einen Euro, bei „Zahl“ verliert er einen. Die Zufallsvariablen ${\displaystyle X_{t},\;t\in \mathbb {N} _{0},}$ für den Kontostand nach ${\displaystyle t}$ Spielen definieren einen stochastischen Prozess (mit deterministischer Startverteilung ${\displaystyle X_{0}=10}$). Genauer betrachtet handelt es sich bei ${\displaystyle X}$ um einen Lévy-Prozess und um ein Martingal.
• Eine vielseitig verwendete Klasse stochastischer Prozesse sind Gauß-Prozesse, die viele natürliche Systeme beschreiben können und als Maschinenlernverfahren Anwendung finden.
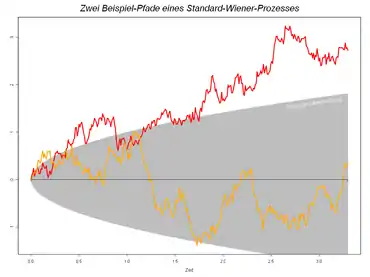
• Ein bedeutender stochastischer Prozess aus der Klasse der Gaußprozesse ist der Wiener-Prozess (auch „Brownsche Bewegung“ genannt). Hierbei sind die einzelnen Zustände normalverteilt mit linear anwachsender Varianz. Der Wiener-Prozess findet Anwendung in der stochastischen Integration, der Finanzmathematik und der Physik.
• Weitere Beispiele: Bernoulli-Prozess, Brownsche Brücke, Gebrochene Brownsche Bewegung, Markow-Kette, Ornstein-Uhlenbeck-Prozess, Poisson-Prozess, Weißes Rauschen.

Weblinks

• A.M. Yaglom: Stochastic Process. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
• Hendrik van Hess: Stochastische Prozesse.

Literatur

• Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6, doi:10.1007/978-3-642-36018-3.
• Christian Hesse: Angewandte Wahrscheinlichkeitstheorie. 1. Auflage. Vieweg, Wiesbaden 2003, ISBN 3-528-03183-2, doi:10.1007/978-3-663-01244-3.
• David Meintrup, Stefan Schäffler: Stochastik. Theorie und Anwendungen. Springer-Verlag, Berlin Heidelberg New York 2005, ISBN 978-3-540-21676-6, doi:10.1007/b137972.