Geschwindigkeit

Die Geschwindigkeit ist neben dem Ort und der Beschleunigung einer der grundlegenden Begriffe der Kinematik, eines Teilgebiets der Mechanik. Die Geschwindigkeit beschreibt, wie schnell und in welcher Richtung ein Körper oder ein Phänomen (beispielsweise ein Wellenberg) im Lauf der Zeit seinen Ort verändert. Eine Geschwindigkeit wird durch ihren Betrag und die Bewegungsrichtung angegeben; es handelt sich also um eine vektorielle Größe. Als Formelzeichen ist ${\vec {v}}$ üblich nach dem lateinischen bzw. englischen Wort für Geschwindigkeit (lateinisch velocitas, englisch velocity).

Physikalische Größe

Name

Geschwindigkeit

Formelzeichen

v

Größen- und Einheitensystem	Einheit	Dimension
SI	m·s⁻¹	L·T⁻¹
cgs	cm · s⁻¹	L·T⁻¹
Planck	c	c

Oft wird mit dem Wort Geschwindigkeit nur ihr Betrag gemeint (Formelzeichen $v$ ), der anschaulich gesprochen das momentane „Tempo“ der Bewegung wiedergibt, wie es beispielsweise im Auto vom Tachometer angezeigt wird. $v$ gibt an, welche Wegstrecke ein Körper innerhalb einer bestimmten Zeitspanne zurücklegt, wenn die Geschwindigkeit entsprechend lange konstant bleibt. Die international verwendete Einheit ist Meter pro Sekunde (m/s), gebräuchlich sind auch Kilometer pro Stunde (km/h) und – vor allem in der See- und Luftfahrt – Knoten (kn).

Die höchstmögliche Geschwindigkeit, mit der sich die Wirkung einer bestimmten Ursache räumlich ausbreiten kann, ist die Lichtgeschwindigkeit $c$ . Diese Obergrenze gilt also auch für jedwede Informationsübertragung. Körper, die eine Masse besitzen, können sich nur mit geringeren Geschwindigkeiten als $c$ bewegen.

Eine Geschwindigkeitsangabe ist immer relativ zu einem Bezugssystem zu verstehen. Ruht ein Körper in einem Bezugssystem, so hat er in einem anderen Bezugssystem, welches sich gegenüber dem ersten mit der Geschwindigkeit ${\vec {v}}$ bewegt, die entgegengesetzt gleich große Geschwindigkeit $-{\vec {v}}$ .

Begriffsgeschichte und Etymologie

Die genaue Fassung der alltäglichen Begriffe von Geschwindigkeit und Bewegung galt seit der Antike und das ganze Mittelalter hindurch als problematisch (siehe z. B. „Achilles und die Schildkröte“ und das „Pfeil-Paradoxon“). Die Klärung im physikalischen Sinn stammt von Galileo Galilei und markiert den wissenschaftlichen Durchbruch zur neuzeitlichen Physik am Anfang des 17. Jahrhunderts.[1] Bis dahin war nur die Durchschnittsgeschwindigkeit längs einer gegebenen endlichen Strecke genau definiert worden, und eine Geschwindigkeitszunahme, wie beispielsweise beim freien Fall, stellte man sich als Folge kleiner Sprünge des Geschwindigkeitsbetrags vor. Bei Galilei hingegen überstreicht eine stetig variierende Geschwindigkeit ein Kontinuum aller Zwischenwerte, die er nicht als Durchschnittsgeschwindigkeit eines gegebenen Stückchens der Strecke, sondern als Momentangeschwindigkeit am jeweiligen Punkt der Bahn begriff. Die genaue Fassung dieses Geschwindigkeitsbegriffs mithilfe des Grenzübergangs zu unendlich kleinen Strecken wurde erst Ende des 17. Jahrhunderts von Isaac Newton gegeben. Dabei wurden die beiden Aspekte Betrag und Richtung der Geschwindigkeit zunächst nur getrennt behandelt, bis sie im 19. Jahrhundert zu einer einzigen mathematischen Größe, dem Geschwindigkeitsvektor, zusammengeführt wurden.

Das Wort Geschwindigkeit geht auf mittelhochdeutsch geswinde zurück ('schnell, vorschnell, ungestüm, kühn'), mittelniederdeutsch geswint, geswine ('stark', Bedeutungsverstärkung durch das Präfix ge-), mittelhochdeutsch swinde, swint ('gewaltig, stark, heftig, gewandt, schnell, böse, gefährlich') zurück. Althochdeutsches Vorkommen wird durch Namen wie Amalswind, Swindbert, Swinda erwiesen.[2]

Definition

Bahnkurve (blau), Ortsvektoren (

{\vec {r}}_{\mathrm {A} }

,

{\vec {r}}_{\mathrm {B} }

), Sehne (

\Delta {\vec {r}}

) und Wegstrecke (Strecke von

A

nach

B

entlang der Bahnkurve)

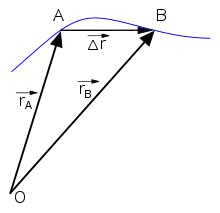
Der Begriff der Geschwindigkeit (Symbol ${\vec {v}}$ ) an einem bestimmten Punkt ( $A$ ) der Bahnkurve ergibt sich näherungsweise aus der Ortsänderung $\Delta {\vec {r}}$ im Zeitraum $\Delta t$ :

{\vec {v}}_{\mathrm {AB} }\approx {\frac {\Delta {\vec {r}}}{\Delta t}}

Dabei ist $\Delta {\vec {r}}={\vec {r}}_{\mathrm {B} }-{\vec {r}}_{\mathrm {A} }$ die Sehne des Streckenabschnitts zwischen den Punkten $A$ und $B$ , an denen sich der Körper zu Beginn bzw. am Ende des Zeitraums $\Delta t$ befindet. Der Vektor ${\vec {v}}_{\mathrm {AB} }$ hat die Richtung der Sehne $\Delta {\vec {r}}$ .

Aus dieser Geschwindigkeit ergibt sich die Momentangeschwindigkeit am Punkt $A$ , wenn man ihm den Punkt $B$ so nahe kommen lässt, dass der Quotient ${\tfrac {\Delta {\vec {r}}}{\Delta t}}$ einem bestimmten Wert, dem Grenzwert, zustrebt. Gleichzeitig strebt das Zeitintervall gegen Null, was als $\lim _{\Delta t\rightarrow 0}$ geschrieben wird. Dieser Vorgang, der Grenzübergang genannt wird, findet in der Differentialrechnung eine mathematisch exakte Grundlage. Die Momentangeschwindigkeit am Punkt $A$ ist damit (in drei gleichwertigen Schreibweisen):

{\vec {v}}=\lim _{\Delta t\rightarrow 0}{\frac {\Delta {\vec {r}}}{\Delta t}}={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}={\dot {\vec {r}}}

Wegstrecken bei einer Bewegung mit gekrümmter Bahnkurve

Sonderfall der geradlinigen Bewegung

Da die Sehne $\Delta {\vec {r}}$ beim Grenzübergang die Richtung der Tangente an die Bahnkurve annimmt, ist dies auch die Richtung der Momentangeschwindigkeit.

Der Betrag der Momentangeschwindigkeit (das „Tempo“ oder die Bahngeschwindigkeit) ist durch den Betrag des Geschwindigkeitsvektors

v=\left|{\vec {v}}\right|=\left|\lim _{\Delta t\rightarrow 0}{\frac {\Delta {\vec {r}}}{\Delta t}}\right|=\left|{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}\right|=\left|{\dot {\vec {r}}}\right|

gegeben, wobei $\left|{\vec {r}}\right|=r$ der Betrag des Ortsvektors ${\vec {r}}$ ist. Die Bahngeschwindigkeit ist nicht dasselbe wie $\left|{\dot {r}}\right|$ , wie man beispielsweise an der Kreisbewegung mit $r={\text{konst.}},\ v\neq 0,\ {\dot {r}}=0$ sehen kann.

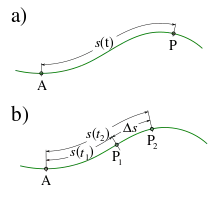
Den Betrag der Momentangeschwindigkeit kann man auch als Skalar erhalten, wenn man statt der dreidimensionalen Bahnkurve nur die Wegstrecke (Symbol $s$ ) entlang der Bahnkurve berücksichtigt (s. Abb.). Man bildet den Grenzwert, den der Quotient aus zurückgelegter Wegstrecke $\Delta s$ und benötigter Zeit $\Delta t$ annimmt:

v=\lim _{\Delta t\rightarrow 0}{\frac {\Delta s}{\Delta t}}={\frac {\mathrm {d} s}{\mathrm {d} t}}={\dot {s}}

Durchschnittsgeschwindigkeit

Wenn man zur Berechnung der Geschwindigkeit die gesamte zurückgelegte Strecke durch die gesamte verstrichene Zeit teilt, so erhält man als Ergebnis die Durchschnittsgeschwindigkeit. Die Information über die zeitliche Veränderung geht dabei verloren. Wenn beispielsweise ein Auto eine Strecke von 100 km in einer Stunde zurücklegt, so hatte es eine Durchschnittsgeschwindigkeit von 100 km/h. Dabei kann es tatsächlich mit konstanter Geschwindigkeit 100 km/h gefahren sein oder eine Viertelstunde mit einer Geschwindigkeit von 200 km/h und eine Dreiviertelstunde mit einer Geschwindigkeit von 66,7 km/h.

Man beachte, dass die Durchschnittsgeschwindigkeit stets den zeitlichen Mittelwert der Geschwindigkeit darstellt. Fährt ein Auto zunächst für eine halbe Stunde eine konstante Geschwindigkeit von 50 km/h und anschließend eine halbe Stunde mit einer konstanten Geschwindigkeit von 100 km/h, so beträgt die Durchschnittsgeschwindigkeit 75 km/h. Fährt das Auto aber zunächst eine Strecke von 25 km mit einer konstanten Geschwindigkeit von 50 km/h und danach eine Strecke von 25 km mit einer konstanten Geschwindigkeit von 100 km/h, so wird für den zweiten Bewegungsabschnitt nur die Hälfte der Zeit benötigt (eine Viertelstunde). Folglich beträgt in diesem Fall die Durchschnittsgeschwindigkeit 66,7 km/h, obwohl dies vielleicht der Intuition widerspricht.

Ein weiteres Beispiel für Körper mit veränderlicher Geschwindigkeit sind Himmelskörper, deren Geschwindigkeiten auf Ellipsenbahnen um einen Zentralkörper variieren. Beim Merkur beträgt die Durchschnittsgeschwindigkeit 47,36 km/s, schwankt allerdings wegen der merklichen Exzentrizität zwischen 39 und 59 km/s.

Anfangsgeschwindigkeit

Wenn die Geschwindigkeit eines Körpers oder Massenpunkts zu Beginn eines bestimmten Bewegungsabschnittes interessiert, wird sie auch als Anfangsgeschwindigkeit (Formelzeichen meist $v_{0}$ ) bezeichnet.

Die Anfangsgeschwindigkeit ist eine der Anfangsbedingungen beim Lösen der Bewegungsgleichungen in der klassischen Mechanik, zum Beispiel für numerische Simulationen in der Himmelsmechanik. Sie ist ein wichtiger Parameter z. B. für die Flugbahn beim senkrechten und schrägen Wurf sowie für die Reichweite von Schusswaffen oder Raketen.

Beispiele:

Beim Wurf wird sie auch als Abwurfgeschwindigkeit bezeichnet.
In der Außenballistik wird sie mit der Mündungsgeschwindigkeit identifiziert, mit der ein Projektil den Lauf der Waffe verlässt.
Anfangsgeschwindigkeit der ballistischen Flugbahn einer Rakete ist die Brennschlussgeschwindigkeit.
Die Einschussgeschwindigkeit eines Raumflugkörpers in eine Umlaufbahn oder Übergangsbahn bestimmt deren Gestalt.
Die Eintrittsgeschwindigkeit in die Erdatmosphäre eindringender Objekte (wie Meteoroide) ist wesentlich für ihr weiteres Schicksal.

Endgeschwindigkeit

Die vertikal nach unten gerichtete Gewichtskraft

{\vec {G}}={\vec {F}}_{\mathrm {G} }={\vec {F}}_{\mathrm {g} }

ist gleich der vertikal nach oben gerichteten aerodynamischen Widerstandskraft

{\vec {F}}_{\mathrm {d} }

. Die Kräfte heben sich auf, so dass der Körper keine weitere Beschleunigung erfährt. Die Endgeschwindigkeit ist erreicht.

Die Endgeschwindigkeit (auch: Grenzgeschwindigkeit) ist die Geschwindigkeit, die ein Objekt am Ende seiner Beschleunigung erreicht hat.

Ein Objekt erreicht seine Endgeschwindigkeit, wenn die bremsenden Kräften durch Zu- oder Abnahme der Geschwindigkeit so stark geworden sind, dass sich ein Kräftegleichgewicht aller beteiligten Kräfte ausbildet. Die Beschleunigung bei Erreichen der Endgeschwindigkeit ist daher null.

Der Begriff wird auch in der Technik verwendet. Im Automobilsektor spricht man zum Beispiel von Endgeschwindigkeit oder Maximalgeschwindigkeit, wenn sich das Fahrzeug begrenzt durch Motorleistung und äußere Umstände nicht weiter beschleunigen lässt.

Einfache Sonderfälle

Geradlinig gleichförmige Bewegung

Von geradlinig gleichförmiger Bewegung spricht man, wenn die Geschwindigkeit $v$ an jedem Punkt der geradlinig verlaufenden Bahn die gleiche ist, was gleichbedeutend mit der Beschleunigung $a=0$ ist:

v={\frac {s}{t}}

Hierbei ist $s$ der in der Zeitspanne $t$ zurückgelegte Weg.

Gleichmäßig beschleunigte Bewegung

Bei einer geradlinigen gleichmäßig beschleunigten Bewegung hat die Beschleunigung $a$ in jedem Punkt geradlinig verlaufenden Bahn den gleichen Betrag und die gleiche Richtung:

v=a\cdot t+v_{0}

Hierbei steht ${v}_{0}$ für die Anfangsgeschwindigkeit.

Kreisbewegung

Die Geschwindigkeit einer Kreisbewegung bezeichnet man als Umfangsgeschwindigkeit oder allgemein als Bahngeschwindigkeit:

{\vec {v}}={\vec {\omega }}\times {\vec {r}}

Hierbei steht $\omega$ für die Winkelgeschwindigkeit und $r$ für den Radius der Kreisbewegung.

Bei einer gleichförmigen Kreisbewegung ist die Umfangsgeschwindigkeit konstant und kann als Quotient aus der auf der Kreisbahn zurückgelegten Streckenlänge und der dafür benötigten Zeit $T$ ausgedrückt werden:

v={\frac {2\cdot \pi \cdot r}{T}}

Beziehungen zu anderen physikalischen Größen

Aus dem zeitlichen Verlauf der Geschwindigkeit kann man auf die zurückgelegte Strecke schließen, indem man über die Zeit integriert:

\Delta s=\int _{t_{1}}^{t_{2}}v(t)\,\mathrm {d} t

Im einfachsten Fall, nämlich bei konstanter Geschwindigkeit, wird daraus $\Delta s=v\cdot \Delta t$ .

Die erste Ableitung der Geschwindigkeit nach der Zeit ist die Beschleunigung: ${\vec {a}}(t)={\dot {\vec {v}}}(t)={\ddot {\vec {s}}}(t)$ .

Die zweite Ableitung der Geschwindigkeit nach der Zeit ergibt den Ruck einer Bewegung: ${\vec {j}}(t)={\ddot {\vec {v}}}(t)={\dot {\vec {a}}}(t)$ .

Der Impuls – also anschaulich gesprochen der „Schwung“ – eines Körpers der Masse $m$ berechnet sich nach ${\vec {p}}=m\cdot {\vec {v}}$ , während die kinetische Energie durch $E_{\mathrm {kin} }={\tfrac {1}{2}}mv^{2}={\tfrac {p^{2}}{2m}}$ gegeben ist. Streng genommen gelten die letzten beiden Gleichungen nur näherungsweise für den sogenannten nichtrelativistischen Fall, also für Geschwindigkeiten, die viel kleiner als die Lichtgeschwindigkeit sind.

Messung

Am einfachsten kann die Geschwindigkeit bestimmt werden, indem man misst,

welche Zeit für eine bestimmte Wegstrecke benötigt wird oder
welche Strecke in einem gegebenen Zeitintervall zurückgelegt wird.

In beiden Fällen wird eigentlich nur eine Durchschnittsgeschwindigkeit gemessen. Wenn das Weg- bzw. Zeitintervall aber kurz genug gewählt wird oder die Bewegung annähernd gleichförmig ist, kann man mit beiden Methoden befriedigende Genauigkeiten erreichen. Ein Beispiel für die Methode 1 wäre die Messung der Lichtgeschwindigkeit nach Hippolyte Fizeau. Methode 2 wird unter anderem angewendet, wenn Geschwindigkeitswerte aus GPS-Daten berechnet werden.

Die Geschwindigkeit eines Fahrzeugs lässt sich leicht mit einem Tachometer bestimmen. Dieses misst eigentlich die Drehzahl des Rades, welche direkt proportional zur Geschwindigkeit ist.

Es kann aber praktisch jeder andere geschwindigkeitsabhängige Effekt auch für eine Messmethode verwendet werden, so z. B. der Doppler-Effekt im Doppler-Radar, der Impuls im ballistischen Pendel oder der Staudruck in der Prandtlsonde.

Einheiten

Die SI-Einheit der Geschwindigkeit ist Meter pro Sekunde (m/s). Eine weitere gebräuchliche Einheit der Geschwindigkeit ist Kilometer pro Stunde (km/h).

In der Alltagssprache wird auch die Bezeichnung „Stundenkilometer“ verwendet. Da in der Physik eine derartige Zusammensetzung zweier Einheiten (hier: „Stunde“ und „Kilometer“) als eine Multiplikation dieser Einheiten verstanden wird, wird der Ausdruck „Stundenkilometer“ in den Naturwissenschaften normalerweise nicht verwendet.

Als nicht metrische Einheit wird vor allem in den USA und einigen anderen englischsprachigen Ländern Meilen pro Stunde (mph) benutzt. In der See- und Luftfahrt ist außerdem die Einheit Knoten (kn) gebräuchlich. Ein Knoten ist eine Seemeile (sm) pro Stunde. Vertikalgeschwindigkeiten in der motorisierten Luftfahrt werden oft in Fuß pro Minute (LFM von engl. linear feet per minute oder nur fpm von engl. feet per minute) angegeben.

Fast nur in der Luftfahrt wird die Mach-Zahl verwendet, die keine absolute Größe angibt, sondern das Verhältnis der Geschwindigkeit zur lokalen Schallgeschwindigkeit angibt. Die Schallgeschwindigkeit ist stark temperaturabhängig aber nicht luftdruckabhängig. Der Grund für die Nutzung dieser Zahl ist, dass aerodynamische Effekte von ihr abhängen.

Umrechnung gebräuchlicher Geschwindigkeitseinheiten:

	Meter pro Sekunde	Kilometer pro Stunde	Knoten (= Seemeilen pro Stunde)	Meilen pro Stunde	Lichtgeschwindigkeit
1 m/s	00 1	00 3,6	00 1,944	00 2,237	0 3,336 · 10⁻⁹
1 km/h	00 0,2778	00 1	00 0,5400	00 0,6215	0 9,266 · 10⁻¹⁰
1 kn	00 0,5144	00 1,852	00 1	00 1,151	0 1,716 · 10⁻⁹
1 mph	00 0,4469	00 1,609	00 0,8688	00 1	0 1,491· 10⁻⁹
1  $c$	00 299792458	00 1,079 · 10⁹	00 5,827 · 10⁸	00 6,707 · 10⁸	00 1

Anmerkung: Die fett gedruckten Umrechnungsfaktoren sind exakt, alle anderen auf vier geltende Ziffern gerundet.

Geschwindigkeiten und Bezugssystem

Vorbeifliegendes Flugzeug mit Geschwindigkeit (rot), Radialgeschwindigkeit (grün) und Tangentialgeschwindigkeit (blau)

Je nach verwendetem Bezugssystem bzw. Koordinatensystem haben sich verschiedene Bezeichnungen eingebürgert:

Im homogenen Schwerefeld wird oft ein kartesisches Koordinatensystem verwendet. Geschwindigkeiten, die parallel zur Fallbeschleunigung ${\vec {g}}$ gerichtet sind, werden meist als Vertikalgeschwindigkeiten, solche, die orthogonal zu dieser Richtung sind, als Horizontalgeschwindigkeiten bezeichnet.

Bei Polarkoordinaten ist die Radialgeschwindigkeit ${\vec {v}}_{\mathrm {r} }$ die Komponente des Geschwindigkeitsvektors in Richtung des Ortsvektors, also längs der Verbindungslinie zwischen dem bewegten Objekt und dem Koordinatenursprung. Die Komponente senkrecht dazu heißt Umfangsgeschwindigkeit ${\vec {v}}_{\perp }$ . Somit ergibt sich: ${\vec {v}}={\vec {v}}_{\perp }+{\vec {v}}_{\mathrm {r} }$ . Das Vektorprodukt aus der Winkelgeschwindigkeit und dem Ortsvektor ergibt die Umfangsgeschwindigkeit: ${\vec {v}}_{\perp }={\vec {\omega }}\times {\vec {r}}$ .

Bei Bewegungen auf einer Kreisbahn um den Koordinatenursprung, aber auch nur in diesem Fall, ist die Radialgeschwindigkeit null und die Umfangsgeschwindigkeit gleich der Tangentialgeschwindigkeit, also der Bahngeschwindigkeit längs der Tangente an die Bahnkurve.

Aus der Änderung des Abstands zum Koordinatenursprung (Radius) folgt die Radialgeschwindigkeit: ${\vec {v}}_{\mathrm {r} }={\dot {r}}\,{\frac {\vec {r}}{|{\vec {r}}|}}$ .

Setzt man voraus, dass es ein allgemein gültiges Bezugssystem gibt, so nennt man die Geschwindigkeiten, die in diesem System gemessen werden, Absolutgeschwindigkeiten. Geschwindigkeiten, die sich auf einen Punkt beziehen, der sich selbst in diesem System bewegt, heißen Relativgeschwindigkeiten. Beispiel: Eine Straßenbahn fährt mit einer Geschwindigkeit von 50 km/h. Darin bewegt sich ein Fahrgast mit einer Relativgeschwindigkeit (gegenüber der Straßenbahn) von 5 km/h. Seine Absolutgeschwindigkeit (vom ruhenden Beobachter auf der Straße aus gesehen) beträgt also 55 km/h oder 45 km/h, je nachdem, ob er sich in Fahrtrichtung oder gegen die Fahrtrichtung bewegt.

Das Relativitätsprinzip besagt jedoch, dass es keinen physikalischen Grund gibt, warum man ein bestimmtes Bezugssystem herausgreifen und gegenüber anderen Systemen bevorzugen sollte. Sämtliche physikalischen Gesetze, die in einem Inertialsystem gelten, gelten auch in jedem anderen. Welche Bewegungen man als „absolut“ ansieht, ist also vollkommen willkürlich. Deswegen wird der Begriff der Absolutgeschwindigkeit spätestens seit der speziellen Relativitätstheorie vermieden. Stattdessen sind alle Geschwindigkeiten Relativgeschwindigkeiten. Aus diesem Relativitätsprinzip folgt, zusammen mit der Invarianz der Lichtgeschwindigkeit, dass Geschwindigkeiten nicht – wie im obigen Beispiel stillschweigend angenommen – einfach addiert werden dürfen. Stattdessen gilt das relativistische Additionstheorem für Geschwindigkeiten. Dies macht sich jedoch erst bei sehr hohen Geschwindigkeiten bemerkbar.

Geschwindigkeit zahlreicher Teilchen

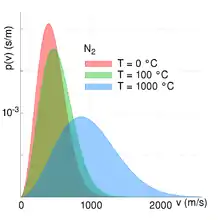
Temperaturabhängigkeit der Geschwindigkeitsverteilung für Stickstoff

Betrachtet man ein System aus vielen Teilchen, so ist es meist nicht mehr sinnvoll oder überhaupt möglich, für jedes einzelne Teilchen eine bestimmte Geschwindigkeit anzugeben. Stattdessen arbeitet man mit der Geschwindigkeitsverteilung, die angibt, wie häufig ein bestimmter Bereich von Geschwindigkeiten in dem Teilchenensemble auftritt. In einem idealen Gas gilt beispielsweise die Maxwell-Boltzmann-Verteilung (siehe nebenstehende Abbildung): Die meisten Teilchen haben eine Geschwindigkeit in der Nähe der wahrscheinlichsten Geschwindigkeit, die durch das Maximum der Maxwell-Boltzmann-Verteilung angezeigt wird. Sehr kleine und sehr große Geschwindigkeiten kommen auch vor, werden aber nur von ganz wenigen Teilchen angenommen. Die Lage des Maximums ist temperaturabhängig. Je heißer das Gas ist, desto höher ist die wahrscheinlichste Geschwindigkeit. Mehr Teilchen erreichen dann hohe Geschwindigkeiten. Dies zeigt, dass die Temperatur ein Maß für die mittlere kinetische Energie der Teilchen ist. Doch sind auch bei niedrigen Temperaturen sehr hohe Geschwindigkeiten nicht vollständig ausgeschlossen. Mit der Geschwindigkeitsverteilung lassen sich viele physikalische Transportphänomene erklären, wie z. B. die Diffusion in Gasen.

Strömungsgeschwindigkeit eines Fluids

Die mittlere Strömungsgeschwindigkeit eines Gases oder einer Flüssigkeit $v_{\mathrm {A} }$ ergibt sich aus der Volumenstromstärke $Q={\tfrac {\mathrm {d} V}{\mathrm {d} t}}$ durch den Strömungsquerschnitt $A$ :

v_{\mathrm {A} }={\frac {Q}{A}}

Allerdings können sich die lokalen Strömungsgeschwindigkeiten sehr stark voneinander unterscheiden. Beispielsweise ist die Geschwindigkeit in der Mitte eines idealen Rohres am größten und fällt durch die Reibung zur Wandung hin bis auf Null ab. Man muss daher die Strömung eines Mediums als Vektorfeld auffassen. Wenn die Geschwindigkeitsvektoren zeitlich konstant sind, spricht man von einer stationären Strömung. Verhalten sich die Geschwindigkeiten im Gegensatz dazu chaotisch, so handelt es sich um eine turbulente Strömung. Bei der Charakterisierung des Strömungsverhaltens hilft die Reynoldszahl, die die Strömungsgeschwindigkeit in Relation zu der Abmessungen des angeströmten Körpers und zur Viskosität des Fluids setzt.

Mathematisch wird das Verhalten der Geschwindigkeiten durch die Navier-Stokes-Gleichungen modelliert, die als Differenzialgleichungen die Geschwindigkeitsvektoren mit inneren und äußeren Kräften in Beziehung setzen. Damit haben sie für die Bewegung eines Fluids eine ähnliche Bedeutung wie die Grundgleichung der Mechanik für Massenpunkte und starre Körper.

Geschwindigkeit von Wellen

Der rote Punkt bewegt sich mit Phasengeschwindigkeit und die grünen Punkte mit Gruppengeschwindigkeit

Die komplexe Bewegung von Wellen macht es nötig, verschiedene Geschwindigkeitsbegriffe zu verwenden. (Insbesondere kann mit dem Wort Ausbreitungsgeschwindigkeit verschiedenes gemeint sein.)

Die Auslenkungsgeschwindigkeit mechanischer Wellen wird als Schnelle bezeichnet. Das bekannteste Beispiel ist die Schwingungsgeschwindigkeit der Luftteilchen in einer Schallwelle.
Die Geschwindigkeit, mit der sich ein Punkt bestimmter Phase vorwärts bewegt, heißt Phasengeschwindigkeit. Es gilt: $v_{\mathrm {p} }={\frac {\lambda }{T}}={\frac {\omega }{k}}$ . Hierbei sind $\lambda$ die Wellenlänge, $T$ die Periodendauer, $\omega$ die Kreisfrequenz und $k$ die Kreiswellenzahl. Die Geschwindigkeit, mit der sich die Wellenkämme im Meer fortbewegen, ist ein typisches Beispiel für eine Phasengeschwindigkeit.
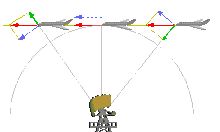
Die Geschwindigkeit, mit der sich ein ganzes Wellenpaket bewegt, wird Gruppengeschwindigkeit genannt: $v_{\mathrm {g} }={\frac {\partial \mathbf {\omega } }{\partial \mathbf {k} }}$ .

Phasen- und Gruppengeschwindigkeit stimmen nur in seltenen Fällen überein (z. B. Ausbreitung von Licht im Vakuum). In der Regel unterscheiden sie sich. Ein anschauliches extremes Beispiel ist die Fortbewegung von Schlangen: Fasst man die Schlange als eine Welle auf, so ist die Geschwindigkeit ihres Vorankommens eine Gruppengeschwindigkeit. Die Phasengeschwindigkeit ist beim Schlängeln jedoch Null, denn die Stellen, an denen sich der Körper der Schlange nach rechts oder links krümmt, sind durch den Untergrund vorgegeben und bewegen sich nicht über den Boden.

In aller Regel ist die Phasengeschwindigkeit einer physikalischen Welle von der Frequenz bzw. der Kreiswellenzahl abhängig. Diesen Effekt bezeichnet man als Dispersion. Er ist unter anderem dafür verantwortlich, dass Licht verschiedener Wellenlänge von einem Prisma unterschiedlich stark gebrochen wird.

Relativitätstheorie

Aus den Gesetzen der klassischen Physik folgt für Geschwindigkeiten unter anderem:

Die Messwerte für Längen und Zeiten sind unabhängig vom Bewegungszustand (und damit der Geschwindigkeit) des Beobachters. Insbesondere stimmen alle Beobachter darin überein, ob zwei Ereignisse gleichzeitig stattfinden oder nicht.
Bei einem Wechsel des Bezugssystems gilt die Galilei-Transformation. Dies bedeutet, dass Geschwindigkeiten von Bewegungen, die sich überlagern, vektoriell addiert werden dürfen.
Es gibt keine theoretische Obergrenze für die Geschwindigkeit von Bewegungen.
Zwar wird es von den Gesetzen der klassischen Physik nicht verlangt, aber es wurde vor Einstein allgemein angenommen, dass es für alle Geschwindigkeiten ein universelles Bezugssystem, den „Äther“, gebe. Wenn dem so wäre, müsste die Ausbreitungsgeschwindigkeit von elektromagnetischen Wellen vom Bewegungszustand des Empfängers abhängen.

Letztere Abhängigkeit ließ sich mit dem Michelson-Morley-Experiment nicht nachweisen. Einstein postulierte, dass das Relativitätsprinzip, das bereits aus der klassischen Mechanik bekannt war, auch auf alle anderen Phänomene der Physik, insbesondere die Ausbreitung des Lichts, angewendet werden müsse und dass die Lichtgeschwindigkeit unabhängig vom Bewegungszustand des Senders sei. Daraus folgerte er, dass die oben genannten Aussagen der klassischen Mechanik modifiziert werden müssen.[3] Im Detail heißt dies:

Die Messwerte für Längen und Zeiten sind abhängig vom Bewegungszustand (und damit der Geschwindigkeit) des Beobachters (siehe Zeitdilatation und Längenkontraktion). Auch die Gleichzeitigkeit ist relativ.
Bei einem Wechsel des Bezugssystems gilt die Lorentz-Transformation. Dies bedeutet, dass Geschwindigkeiten von Bewegungen, die sich überlagern, nicht einfach vektoriell addiert werden dürfen.
Bewegungen von Körpern können nur mit Geschwindigkeiten erfolgen, die geringer als die Lichtgeschwindigkeit sind. Auch Informationen können nicht schneller als das Licht übertragen werden.
Es gibt keinen „Äther“.

Die Effekte, die sich aus der speziellen Relativitätstheorie ergeben, machen sich jedoch erst bei sehr hohen Geschwindigkeiten bemerkbar. Der Lorentz-Faktor, der für Zeitdilatation und Längenkontraktion maßgeblich ist, ergibt erst für Geschwindigkeiten von $v>4{,}2\cdot 10^{7}\,\mathrm {\tfrac {m}{s}}$ eine Abweichung von mehr als einem Prozent. Folglich stellt die klassische Mechanik selbst für die schnellsten bisher gebauten Raumfahrzeuge eine äußerst präzise Näherung dar.

Siehe auch

Liste von Größenordnungen der Geschwindigkeit

Weblinks

Commons: Geschwindigkeit – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Geschwindigkeit – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Formelsammlung Klassische Mechanik – Lern- und Lehrmaterialien

Beispiele zur Messung der Geschwindigkeit in Alltagssituationen (LEIFI)

Anmerkungen und Einzelnachweise

Ueli Niederer: Galileo Galilei und die Entwicklung der Physik. In: Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich. Band 127, Nr. 3, 1982, S. 205–229 (online [PDF; abgerufen am 6. März 2016]).
Wolfgang Pfeifer, Etymologisches Wörterbuch des Deutschen, dtv, 5. Auflage 2000, S. 438.
Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 1905, S. 891–921 (als Faksimile; PDF; 2,0 MB).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Niederer_2002-1] Ueli Niederer: Galileo Galilei und die Entwicklung der Physik. In: Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich. Band 127, Nr. 3, 1982, S. 205–229 (online [PDF; abgerufen am 6. März 2016]).

[2] Wolfgang Pfeifer, Etymologisches Wörterbuch des Deutschen, dtv, 5. Auflage 2000, S. 438.

[Ea-3] Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 1905, S. 891–921 (als Faksimile; PDF; 2,0 MB).