Beschleunigung

Beschleunigung ist in der Physik die Änderung des Bewegungszustands eines Körpers. Als physikalische Größe ist die Beschleunigung die momentane zeitliche Änderungsrate der Geschwindigkeit. Sie ist eine vektorielle, also gerichtete Größe. Die Beschleunigung ist, neben dem Ort und der Geschwindigkeit, eine zentrale Größe in der Kinematik, einem Teilgebiet der Mechanik.

Physikalische Größe

Name

Beschleunigung

Formelzeichen

${\vec {a}}$

Größen- und Einheitensystem	Einheit	Dimension
SI	m/s²	L·T⁻²
cgs	Gal = cm/s²	L·T⁻²

In der Umgangssprache bezeichnet Beschleunigung oft nur eine Steigerung des „Tempos“, also des Betrags der Geschwindigkeit. Im physikalischen Sinn ist aber jede Änderung einer Bewegung eine Beschleunigung, z. B. auch eine Abnahme des Geschwindigkeitsbetrages – wie ein Bremsvorgang – oder eine reine Richtungsänderung bei gleichbleibendem Geschwindigkeitsbetrag – wie bei einer Kurvenfahrt mit einem Auto. Darüber hinaus gibt es in Physik und Technischer Mechanik Begriffe wie Zentripetalbeschleunigung oder Gravitationsbeschleunigung o. ä., mit denen diejenige Beschleunigung bezeichnet wird, die sich in der Bewegung des Körpers zeigen würde, wenn ausschließlich die im Begriff genannte Kraft einwirkte. Ob und wie der Körper tatsächlich beschleunigt wird, hängt aber allein von der Vektorsumme aller auf ihn wirkenden Kräfte ab.

Die SI-Einheit der Beschleunigung ist m/s². Bei einer Beschleunigung von 1 m/s² verändert sich die Geschwindigkeit pro Sekunde um 1 m/s. In den Geowissenschaften ist daneben auch die Einheit Gal für 0,01 m/s² gebräuchlich.

Beschleunigungen kommen bei allen realen Bewegungsvorgängen, z. B. von Fahrzeugen, Flugzeugen oder Aufzügen, vor. Durch die mit ihnen auftretende Trägheitskraft wirken sie sich mehr oder weniger deutlich auf beförderte Menschen und Sachen aus.

Für Kreisbewegungen ist analog die Winkelbeschleunigung als Änderung der Winkelgeschwindigkeit, also die zweite zeitliche Ableitung eines Winkels, definiert.

Definition

Allgemeine Definition

Geometrische Konstruktion der Differenz der Geschwindigkeitsvektoren

Die Beschleunigung ${\vec {a}}$ ist die Geschwindigkeitsänderung pro Zeitintervall. Am Einfachsten lässt sie sich bei konstanter Beschleunigung berechnen. Wenn die Geschwindigkeiten $v(t_{1})$ zum Zeitpunkt $t_{1}$ sowie $v(t_{2})$ zum Zeitpunkt $t_{2}$ bekannt sind, berechnet sich die Beschleunigung innerhalb der Zeitspanne $\Delta t=t_{2}-t_{1}$ aus der Differenz der Geschwindigkeiten $\Delta v=v(t_{2})-v(t_{1})$ gemäß

a={\frac {\Delta v}{\Delta t}}.

Bei einer konstanten Beschleunigung, die nicht in Richtung des Geschwindigkeitsvektors ${\vec {v}}$ erfolgt, muss die Differenz der Geschwindigkeiten $\Delta {\vec {v}}={\vec {v}}(t_{2})-{\vec {v}}(t_{1})$ vektoriell bestimmt werden, wie in der Abbildung veranschaulicht. Wenn sich die Beschleunigung während der betrachteten Zeitspanne ändert, erhält man mit obiger Rechnung die mittlere Beschleunigung, auch Durchschnittsbeschleunigung genannt.

Um die Beschleunigung für einen bestimmten Zeitpunkt statt für ein Zeitintervall zu berechnen, muss man vom Differenzenquotienten zum Differentialquotienten übergehen. Die Beschleunigung ist dann die erste zeitliche Ableitung der Geschwindigkeit nach der Zeit:

{\vec {a}}(t)={\frac {\mathrm {d} {\vec {v}}(t)}{\mathrm {d} t}}={\dot {\vec {v}}}(t)

Da die Geschwindigkeit die Ableitung des Ortes nach der Zeit ist, kann man die Beschleunigung auch als zweite Ableitung des Ortsvektors ${\vec {r}}$ darstellen:

{\vec {a}}(t)={\frac {\mathrm {d} ^{2}{\vec {r}}(t)}{\mathrm {d} t^{2}}}={\ddot {\vec {r}}}(t)

Beispiele zur Berechnung über die Geschwindigkeit

Ein Auto bewegt sich zum Zeitpunkt $t_{1}=0\,\mathrm {s}$ mit einer Geschwindigkeit von $v_{1}=10\,\mathrm {\tfrac {m}{s}}$ über die Straße (das sind 36 km/h). Zehn Sekunden später, zum Zeitpunkt $t_{2}=10\,\mathrm {s}$ , beträgt die Geschwindigkeit $v_{2}=30\,\mathrm {\tfrac {m}{s}}$ (das sind 108 km/h). Die durchschnittliche Beschleunigung des Autos in diesem Zeitintervall war dann

a={\frac {v_{2}-v_{1}}{t_{2}-t_{1}}}=2\,\mathrm {\frac {m}{s^{2}}}

.

Die Geschwindigkeit hat also pro Sekunde durchschnittlich um 2 m/s (also um 7,2 km/h) zugenommen.

Ein PKW, der vor der roten Ampel innerhalb von $\Delta t=3\,\mathrm {s}$ von „Tempo 50“ ( $v_{1}=50\,\mathrm {\tfrac {km}{h}} \approx 14\,\mathrm {\tfrac {m}{s}}$ ) auf Null abgebremst wird, erfährt die Beschleunigung

a={\frac {0-v_{1}}{\Delta t}}\approx -5\,\mathrm {\frac {m}{s^{2}}}

.

Gekrümmte Wege

Tangenteneinheitsvektor und Normaleneinheitsvektor bei einer Raumkurve

Die Beschleunigung eines Körpers, der sich entlang eines Weges (einer Raumkurve) bewegt, lässt sich mit den Frenetschen Formeln berechnen. Dies ermöglicht eine additive Zerlegung der Beschleunigung in eine Beschleunigung in Bewegungsrichtung (Tangentialbeschleunigung) und eine Beschleunigung senkrecht zur Bewegungsrichtung (Normalbeschleunigung oder Radialbeschleunigung).

Der Vektor der Geschwindigkeit ${\vec {v}}$ kann als Produkt aus seinem Betrag $v$ und dem Tangenteneinheitsvektor ${\hat {t}}$ dargestellt werden:

{\vec {v}}=v\,{\hat {t}}

Der Tangenteneinheitsvektor ist ein Vektor der Länge $1$ , der an jedem Punkt des Weges die Richtung der Bewegung anzeigt. Die Ableitung dieses Ausdrucks nach der Zeit ist die Beschleunigung:

{\vec {a}}={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}=\left({\frac {\mathrm {d} v}{\mathrm {d} t}}\right){\hat {t}}+v\left({\frac {\mathrm {d} {\hat {t}}}{\mathrm {d} t}}\right)

Die zeitliche Ableitung des Tangenteneinheitsvektors kann über die Bogenlänge $s$ berechnet werden:

{\frac {\mathrm {d} {\hat {t}}}{\mathrm {d} t}}=\underbrace {\frac {\mathrm {d} {\hat {t}}}{\mathrm {d} s}} _{{\hat {n}}/\rho }\underbrace {\frac {\mathrm {d} s}{\mathrm {d} t}} _{v}={\frac {v}{\rho }}{\hat {n}}

Dabei führt man den Krümmungsradius $\rho$ und den Normaleneinheitsvektor ${\hat {n}}$ ein. Der Krümmungsradius ist ein Maß für die Stärke der Krümmung und der Normaleneinheitsvektor zeigt senkrecht zur Bahnkurve in Richtung des Krümmungsmittelpunkts. Man definiert die Tangentialbeschleunigung $a_{t}$ und Radialbeschleunigung $a_{n}$ so:

a_{t}={\dot {v}}

a_{n}={\frac {v^{2}}{\rho }}

Die Beschleunigung lässt sich damit in zwei Komponenten zerlegen:

{\vec {a}}=a_{t}{\hat {t}}+a_{n}{\hat {n}}

Ist die Tangentialbeschleunigung Null, so ändert der Körper nur seine Bewegungsrichtung. Der Betrag der Geschwindigkeit bleibt dabei erhalten. Um den Betrag der Geschwindigkeit zu ändern, muss also eine Kraft wirken, die eine Komponente in Richtung des Tangentialvektors besitzt.

Zentrifugalbeschleunigung

Ein Sonderfall obenstehender Überlegung ist eine Kreisbewegung mit konstantem Geschwindigkeitsbetrag. In diesem Fall ist die Beschleunigung nach innen auf den Kreismittelpunkt hin gerichtet, also immer senkrecht zur momentanen Bewegungsrichtung auf der Kreisbahn. Dieser Sonderfall einer reinen Radialbeschleunigung heißt Zentripetalbeschleunigung. Durch sie wird nicht der Betrag der Geschwindigkeit verändert, sondern nur deren Richtung, was eben gerade eine Kreisbahn ergibt. Bezüglich eines mitrotierenden (und daher beschleunigten) Bezugssystems wird ein Objekt vom Mittelpunkt weg nach außen beschleunigt, dann wird die Bezeichnung Zentrifugalbeschleunigung verwendet.

Eine Zentrifuge nutzt diesen Effekt, um Dinge einer konstanten Beschleunigung auszusetzen. Der Krümmungsradius entspricht dabei, da es sich um eine Kreisbewegung handelt, dem Abstand $r$ des Zentrifugiergutes zur Drehachse. Die Beschleunigung, der das Zentrifugiergut der Bahngeschwindigkeit $v$ ausgesetzt ist, lässt sich dann auch durch die Winkelgeschwindigkeit $\omega$ ausdrücken:

a_{n}={\frac {v^{2}}{r}}=r\,\omega ^{2}

Negative und positive Beschleunigung

Bei einem Körper, der sich entlang einer Linie bewegt, wird der Tangenteneinheitsvektor üblicherweise in Bewegungsrichtung gewählt. Ist die Tangentialbeschleunigung negativ, so verringert sich die Geschwindigkeit des Körpers. Bei Fahrzeugen spricht man von einer Verzögerung oder Bremsung des Fahrzeugs. Wird in diesem Zusammenhang der Begriff Beschleunigung gebraucht, so ist meist eine positive Tangentialbeschleunigung gemeint, die die Geschwindigkeit des Fahrzeugs erhöht.

Ruck

Die zeitliche Ableitung der Beschleunigung (also die dritte Ableitung des Ortsvektors nach der Zeit) wird Ruck ${\vec {\jmath }}$ genannt:

{\vec {\jmath }}(t)={\dot {\vec {a}}}(t)={\frac {\mathrm {d} ^{3}{\vec {r}}(t)}{\mathrm {d} t^{3}}}

Maßeinheiten

Die Maßeinheit für die Angabe einer Beschleunigung ist standardmäßig die Einheit Meter pro Quadratsekunde (m/s²), also (m/s)/s. Allgemein können Belastungen technischer Geräte oder die Angabe von Belastungsgrenzen als g-Kraft, also als „Kraft pro Masse“, erfolgen. Diese wird als Vielfaches der normalen Erdbeschleunigung (Normfallbeschleunigung) g = 9,80665 m/s² angegeben. In den Geowissenschaften ist daneben auch die Einheit Gal = 0,01 m/s² gebräuchlich.

Beschleunigung von Kraftfahrzeugen

Bei Kraftfahrzeugen wird die erreichbare positive Beschleunigung als ein wesentlicher Parameter zur Klassifizierung der Leistung verwendet. Angegeben wird meist ein Mittelwert in der Form „In … Sekunden von 0 auf 100 km/h“ (auch 60, 160 oder 200 km/h).

Beispiel: Wenn ein Fahrzeug eine Beschleunigung von 0 auf 100 km/h in 2,5 Sekunden erreicht, entspricht dies einem mittleren Beschleunigungswert von

$a={\frac {\Delta v}{\Delta t}}={\frac {27{,}8\,\mathrm {\frac {m}{s}} }{2{,}5\,\mathrm {s} }}=11\,\mathrm {\frac {m}{s^{2}}}$ .

Zusammenhang zwischen Beschleunigung und Kraft

Isaac Newton beschrieb als Erster, dass zum Auftreten einer Beschleunigung eine Kraft notwendig ist. Sein Gesetz beschreibt die Proportionalität von Kraft und Beschleunigung für Körper in einem Inertialsystem. Ein Inertialsystem ist ein Bezugssystem, bei dem sich kräftefreie Körper geradlinig gleichförmig bewegen. Die Beschleunigung ist dann das Verhältnis von Kraft $F$ zu Masse $m\colon$

{\vec {a}}={\frac {\vec {F}}{m}}

Soll die Beschleunigung in einem beschleunigten Bezugssystem berechnet werden, so sind zusätzlich Trägheitskräfte zu berücksichtigen.

Beschleunigung und Potential

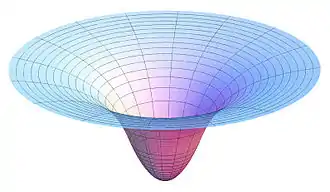
Zweidimensionaler Querschnitt durch ein Gravitationspotential einer homogenen Kugel. Die Wendepunkte befinden sich an der Oberfläche der Kugel.

Beschleunigungsfeld und Potential

Ist eine Kraft auf ein Teilchen proportional zu seiner Masse, dies ist zum Beispiel bei der Gravitation der Fall, so lässt sie sich auch durch ein Beschleunigungsfeld beschreiben. Dieses Vektorfeld ordnet jedem Ort ${\vec {r}}$ im Raum eine Beschleunigung ${\vec {a}}({\vec {r}})$ zu. Es lässt sich häufig als Gradient eines Potentials $\Phi ({\vec {r}})$ schreiben. Anschaulich lässt sich das Potential als Schüssel wie im Bild rechts auffassen. Der negative Gradient liefert einen Vektor, der in Richtung des steilsten Abfalls (maximale negative Steigung) zeigt. Seine Richtung gibt also an, in welche Richtung eine Kugel losrollen würde, die in die Schüssel gelegt wird. Mit einem Potential oder Beschleunigungsfeld lässt sich dann für jede Anfangsbedingung, also Anfangsgeschwindigkeit und -position, die Bewegung eines Teilchens (Trajektorie) berechnen.

Auch wenn die Kraft auf ein Teilchen nicht proportional zu seiner Masse ist, lässt sich häufig ein Kraftfeld und ein Potential aufstellen, beispielsweise ein Coulombpotential für ein elektrisch geladenes Teilchen. In diesem Fall ist die Beschleunigung jedoch von der Masse $m$ und von der Ladung $q$ des Teilchens abhängig:

{\vec {a}}={\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}\,{\vec {r}}=-{\frac {q}{m}}\nabla \Phi ({\vec {r}})

Konstante Beschleunigung

Trajektorie (Anfangsposition

{\vec {r}}_{0}

und Anfangsgeschwindigkeit

{\vec {v}}_{0}

) in einem homogenen Beschleunigungsfeld

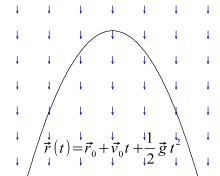
Bei einer gleichmäßigen Beschleunigung ist das Beschleunigungsfeld zeitlich konstant und homogen, also die Beschleunigung in allen Punkten des Raums in Betrag und Richtung identisch, beispielsweise gleich dem Vektor ${\vec {g}}$ :

{\vec {a}}({\vec {r}})={\vec {g}}

für alle

{\vec {r}}

Mit einem solchen Ansatz lässt sich lokal (nicht global) das Gravitationsfeld der Erde beschreiben. Ein Teilchen in einem solchen Gravitationspotential bewegt sich auf einer parabelförmigen Bahn, bei einem Gravitationsfeld auch Wurfparabel genannt. Auch bei einem freien Fall (ohne Luftwiderstand) werden alle Körper gleich beschleunigt. Auf der Erde beträgt die Beschleunigung in Richtung Erdmittelpunkt ungefähr 9,81 Meter pro Quadratsekunde. Das Gravitationspotential der Erde ist jedoch nicht ganz kugelsymmetrisch, da die Erdgestalt von einer Kugel abweicht (Erdabplattung) und der innere Aufbau der Erde nicht völlig homogen ist (Schwereanomalie). Die Erdbeschleunigung kann daher regional leicht unterschiedlich sein. Unabhängig vom Potential muss bei Messungen gegebenenfalls auch die Beschleunigung durch die Erdrotation berücksichtigt werden. Ein Beschleunigungsmesser zur Bestimmung der Schwerebeschleunigung wird Gravimeter genannt.

Messung

Es gibt prinzipiell zwei Möglichkeiten, Beschleunigungen zu messen oder anzugeben. Die Beschleunigung eines Objekts kann kinematisch bezüglich eines Weges (Raumkurve) betrachtet werden. Dazu wird die Momentangeschwindigkeit bestimmt, ihre Änderungsrate ist die Beschleunigung. Die andere Möglichkeit ist, einen Beschleunigungssensor zu verwenden. Dieser bestimmt mit Hilfe einer Testmasse die Trägheitskraft, aus der dann mit Hilfe der newtonschen Grundgleichung der Mechanik auf die Beschleunigung geschlossen wird.

Rechenbeispiel zur Messung über die Trägheit

In einem Aufzug befindet sich eine Federwaage, an der eine Masse von einem Kilogramm hängt ( $m=1\,\mathrm {kg}$ ). Wenn der Aufzug im Vergleich zur Erde ruht, so zeigt die Waage eine Gewichtskraft von 9,8 Newton an. Der Betrag der Schwerebeschleunigung beträgt demnach

a={\frac {F}{m}}=9{,}8\,\mathrm {\frac {m}{s^{2}}} .

Zeigt die Federwaage einen Moment später zum Beispiel eine Kraft von 14,7 Newton an, so ist die Beschleunigung des Aufzugs 4,9 m/s² im Vergleich zur Erde nach oben.

Anwendung von Beschleunigungsmessungen

Wenn die Anfangsgeschwindigkeit und -position bekannt sind, ermöglicht die kontinuierliche Messung der Beschleunigung in allen drei Dimensionen eine Positionsbestimmung zu jedem Zeitpunkt. Die Position lässt sich daraus einfach durch zweifache Integration über die Zeit bestimmen. Für den Fall, dass beispielsweise das GPS-Gerät eines Flugzeugs ausfällt, ermöglicht diese Methode eine relativ genaue Ortsbestimmung über einen mittellangen Zeitraum. Ein Navigationssystem, das die Position durch Messung der Beschleunigung bestimmt, heißt Trägheitsnavigationssystem.

Beschleunigung in der speziellen Relativitätstheorie

Ebenso wie in der klassischen Mechanik können Beschleunigungen auch in der speziellen Relativitätstheorie (SRT) als Ableitung der Geschwindigkeit nach der Zeit dargestellt werden. Da der Zeitbegriff aufgrund der Lorentz-Transformation und Zeitdilatation in der SRT jedoch komplexer ausfällt, führt dies auch zu komplexeren Formulierungen der Beschleunigung und ihres Zusammenhangs mit der Kraft. Insbesondere ergibt sich, dass kein massebehafteter Körper auf Lichtgeschwindigkeit beschleunigt werden kann.

Äquivalenzprinzip und allgemeine Relativitätstheorie

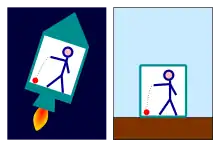
Nach dem Äquivalenzprinzip der allgemeinen Relativitätstheorie lässt sich nicht unterscheiden, ob sich ein Beobachter auf der Erde befindet oder in einer Rakete, die im Weltraum mit Erdbeschleunigung g beschleunigt.

Das Äquivalenzprinzip besagt, dass in einem frei fallenden Bezugssystem keine Gravitationsfelder existieren. Es geht auf die Überlegungen von Galileo Galilei und Isaac Newton zurück, die erkannt haben, dass alle Körper unabhängig von ihrer Masse von der Gravitation gleich beschleunigt werden. Ein Beobachter in einem Labor kann nicht feststellen, ob sich sein Labor in der Schwerelosigkeit oder im freien Fall befindet. Er kann innerhalb seines Labors auch nicht feststellen, ob sein Labor gleichförmig beschleunigt bewegt wird oder ob es sich in einem äußeren homogenen Gravitationsfeld befindet.

Mit der allgemeinen Relativitätstheorie lässt sich ein Gravitationsfeld durch die Metrik der Raumzeit, also die Maßvorschrift in einem vierdimensionalen Raum aus Orts- und Zeitkoordinaten ausdrücken. Ein Inertialsystem hat eine flache Metrik. Nichtbeschleunigte Beobachter bewegen sich immer auf dem kürzesten Weg (einer Geodäte) durch die Raumzeit. In einem flachen Raum, also einem Inertialsystem, ist dies eine gerade Weltlinie. Gravitation bewirkt eine Raumkrümmung. Das bedeutet, dass die Metrik des Raumes nicht mehr flach ist. Dies führt dazu, dass die Bewegung, die in der vierdimensionalen Raumzeit einer Geodäte folgt, im dreidimensionalen Anschauungsraum vom außenstehenden Beobachter meist als beschleunigte Bewegung längs einer gekrümmten Kurve wahrgenommen wird.

Beispiele

Größenordnung typischer Beschleunigungen aus dem Alltag:[1]

Der ICE erreicht eine Beschleunigung von etwa 0,5 m/s², ein moderner S-Bahn-Triebwagen sogar 1,0 m/s².
Während der ersten Schritte eines Sprints beschleunigt ein Sportler seinen Körper mit etwa 4 m/s².
Die Erdbeschleunigung durch die Erdanziehung ist 9,81 m/s².
Die Kugel beim Kugelstoßen wird in der Abstoßphase mit etwa 10 m/s² beschleunigt.
Bei einer Waschmaschine wirken im Schleudergang mehr als 300 g (≈ 3.000 m/s²) an der Trommelwand.
Ein Tennisball kann Beschleunigungen bis zu 10.000 m/s² erfahren.
Bei Nesselzellen wird der Stachel mit bis zu 5.410.000 g (≈ 53 Millionen m/s²) beschleunigt.

Top Fuel Funny Cars beschleunigen mit ca. 8000 PS und 5 g auf über 500 km/h

Bei Dragsterrennstrecken wird u. a. die Zeit für die ersten 60 Fuß (ca. 18 m) gemessen. Während sehr schnelle Straßenfahrzeuge wie der Tesla Model S P90D hierfür ca. 2,4 Sekunden benötigen, passiert ein Top Fuel Dragster die Marke typischerweise in weniger als 0,85 Sekunden. Die Ziellinie bei 1000 Fuß, gut 300 Metern, wird in unter 3,7 Sekunden mit über 530 km/h passiert.

Einen neuen Weltrekord für Elektrofahrzeuge in der Formula Student erzielte im Juni 2016 ein von Studenten der ETH Zürich und der Hochschule Luzern gebauter Elektro-Rennwagen, der in 1,513 Sekunden und innerhalb von weniger als 30 Metern von Null auf 100 km/h beschleunigte.[2]

Weblinks

Wiktionary: Beschleunigung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Literatur von und über Beschleunigung im Katalog der Deutschen Nationalbibliothek
Untersuchungen zur Beschleunigung an der Atwoodschen Fallmaschine (PDF-Datei; 325 kB)
Umrechnen zwischen den verschiedenen Einheiten der Beschleunigung
Beschleunigung bei LEIFIphysik

Einzelnachweise

Beschleunigung. In: lernhelfer.de: Schülerlexikon Physik. 2010, abgerufen am 16. Januar 2018.
In 1,513 Sekunden von Null auf Hundert. Bei: ethz.ch. 22. Juni 2016, abgerufen am 28. Juli 2016.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Beschleunigung. In: lernhelfer.de: Schülerlexikon Physik. 2010, abgerufen am 16. Januar 2018.

[2] In 1,513 Sekunden von Null auf Hundert. Bei: ethz.ch. 22. Juni 2016, abgerufen am 28. Juli 2016.