Logarithmische Darstellung

Die logarithmische Darstellung verwendet eine Achsenbeschriftung, bei der in einer linearen Teilung nicht der Zahlenwert einer darzustellenden Größe aufgetragen wird, sondern der Logarithmus ihres Zahlenwerts. In einem Diagramm wird diese Darstellung auf eine oder beide Achsen angewendet.

Obere Skale linear in

\lg x

geteilt
Untere Skale logarithmisch in

x

geteilt

Verteilung der Beitragszahlen der aktivsten Autoren in der deutschsprachigen Wikipedia

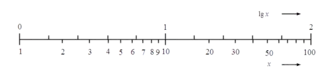
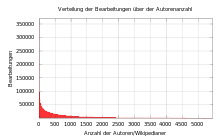
Eine solche Darstellung ist vor allem dann hilfreich, wenn der Wertebereich der dargestellten Daten viele Größenordnungen umfasst. Durch die logarithmische Darstellung werden Zusammenhänge im Bereich der kleinen Werte besser überschaubar. Verschiedene mathematische Zusammenhänge können durch logarithmische Darstellung besser verdeutlicht bzw. erst erkennbar gemacht werden.

Grundsätzlich gilt, dass in Richtung der logarithmischen Achse gleiche Abstände gleiche Faktoren wiedergeben; entspricht also ein Abstand dem Faktor 10, dann entspricht der doppelte Abstand im Diagramm dem Faktor 10².

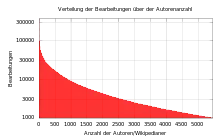
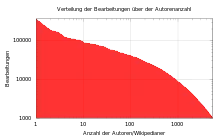
Dieselbe Verteilung in einfach logarithmischer Darstellung

Dieselbe Verteilung in doppelt logarithmischer Darstellung

Übliche Darstellungsmöglichkeiten

Bode-Diagramm eines Tiefpasses:
oben Phasen-Frequenzgang einfach logarithmisch,
unten Amplituden-Frequenzgang doppelt logarithmisch

Wachstum der Bevölkerung Englands auf einer logarithmischen Skala (1,67 Decade).

Wenn numerische Zusammenhänge im Vordergrund stehen, wird mit dem dekadischen Logarithmus gearbeitet; bei eher prinzipieller Betrachtung wird der natürliche Logarithmus verwendet.

Das abgebildete Bode-Diagramm zeigt als Anwendung in der Elektrotechnik die Übertragungsfunktion eines Tiefpasses über einen Frequenzbereich von mehr als vier Zehnerpotenzen.

Vor allem vor der Einführung von Computergrafiken war Logarithmenpapier ein wichtiges Hilfsmittel zur Darstellung. Für die Zeichnung von Diagrammen in logarithmischer Darstellung gibt es einfachlogarithmisches Papier oder doppeltlogarithmisches Papier. Die Möglichkeiten grafischer Darstellungen am Computer haben die Verwendung logarithmischer Skalen vereinfacht und den Gebrauch von solchem Papier stark reduziert.

Mathematische Modellierung

Mit dem Übergang auf neue Variable

X=\log(x)

und

Y=\log(y)

ergeben sich für einige Funktionen Vereinfachungen in der Darstellung, und bestimmte Zusammenhänge werden veranschaulicht. Umgekehrt lässt sich aus einem geradlinigen Verlauf in einer Folge von Messpunkten bei geeignet geteilten Achsen auf die zugrunde liegende Funktion schließen.

Ein Potenzgesetz wird in doppelt logarithmischer Darstellung zur Geraden

y=a\,x^{b}\,\Rightarrow \;Y=\log(a)+bX

Der Sonderfall einer nach rechts unter einem Winkel von 45° fallenden Geraden (bei gleichen Maßstäben auf beiden Achsen) weist auf $b=-1$ , also auf umgekehrte Proportionalität.

Ein exponentieller Verlauf lässt sich in einfach logarithmischer Darstellung als Gerade darstellen

y=a\,\mathrm {e} ^{bx}\,\Rightarrow \;Y=\log(a)+bx\cdot \log(\mathrm {e} )

Eine Funktion von der Form einer Normalverteilung (gaußsche Glockenkurve) wird in einfach logarithmischer Darstellung zu einer Parabel

y=a\,\mathrm {e} ^{bx^{2}}\,\Rightarrow \;Y=\log(a)+bx^{2}\cdot \log(\mathrm {e} )

Eine Funktion von der Form einer logarithmischen Normalverteilung wird in einfach logarithmischer Darstellung zu einer Normalverteilung und in doppelt logarithmischer Darstellung zu einer Parabel

y=a\,\mathrm {e} ^{b(\log(x))^{2}}\,\Rightarrow \;y=a\,\mathrm {e} ^{bX^{2}}

y=a\,\mathrm {e} ^{b(\log(x))^{2}}\,\Rightarrow \;Y=\log(a)+bX^{2}\cdot \log(\mathrm {e} )

Weitere Anwendungen

Für bestimmte Aufgabenstellungen hat es sich eingebürgert, eine Achse als Logarithmus des Logarithmus zu skalieren (log(log(y))), beispielsweise die vertikale Achse bei der grafischen Darstellung von Öl-Viskositäten nach Ubbelohde-Walther oder im Weibull-Wahrscheinlichkeitspapier.[1] Hier wird die zweifach logarithmierte Achse gelegentlich auch als doppelt-logarithmisch bezeichnet.

Einzelnachweise

Qualitätsmanagement in der Automobilindustrie – 3, „Zuverlässigkeitssicherung bei Automobilherstellern und Lieferanten“, herausgegeben vom VDA 2000, ISSN 0943-9412, Abschnitt 2.4.3

Weblinks

xkcd-Webcomic: Humorvolle Comic-Darstellung von sehr großen und sehr kleinen Längenskalen

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Qualitätsmanagement in der Automobilindustrie – 3, „Zuverlässigkeitssicherung bei Automobilherstellern und Lieferanten“, herausgegeben vom VDA 2000, ISSN 0943-9412, Abschnitt 2.4.3