Quantenmechanik

Die Quantenmechanik ist eine physikalische Theorie, mit der die Eigenschaften und Gesetzmäßigkeiten von Zuständen und Vorgängen der Materie beschrieben werden. Im Gegensatz zu den Theorien der klassischen Physik erlaubt sie die zutreffende Berechnung physikalischer Eigenschaften von Materie im Größenbereich der Atome und darunter. Die Quantenmechanik ist eine der Hauptsäulen der modernen Physik. Sie bildet die Grundlage zur Beschreibung von Phänomenen der Atomphysik, der Festkörperphysik und der Kern- und Elementarteilchenphysik, aber auch verwandter Wissenschaften wie der Quantenchemie.

Die Quantenmechanik sichtbar gemacht: Rastertunnelmikroskopaufnahme von Kobaltatomen auf einer Kupferoberfläche. Das Messverfahren nutzt Effekte, die erst durch die Quantenmechanik erklärt werden können. Auch die Interpretation der beobachteten Strukturen beruht auf Konzepten der Quantenmechanik.

Grundlagen

Die Grundlagen der Quantenmechanik wurden zwischen 1925 und 1932 von Werner Heisenberg, Erwin Schrödinger, Max Born, Pascual Jordan, Wolfgang Pauli, Paul Dirac, John von Neumann und weiteren Physikern erarbeitet, nachdem erst die klassische Physik und dann die älteren Quantentheorien bei der systematischen Beschreibung der Vorgänge in den Atomen versagt hatten. Die Quantenmechanik erhielt ihren Namen sowohl in Anlehnung an die Klassische Mechanik als auch in Abgrenzung von ihr. Wie diese bleibt die Quantenmechanik einerseits auf die Bewegung von massebehafteten Teilchen unter der Wirkung von Kräften beschränkt und behandelt z. B. noch keine Entstehungs- und Vernichtungsprozesse. Andererseits werden einige zentrale Begriffe der klassischen Mechanik, unter anderem „Ort“ und „Bahn“ eines Teilchens, durch grundlegend andere, der Quantenphysik besser angepasste Konzepte ersetzt.

Die Quantenmechanik bezieht sich auf materielle Objekte und modelliert diese als einzelne Teilchen oder als Systeme, die aus einer bestimmten Anzahl von einzelnen Teilchen bestehen. Mit diesen Modellen können Elementarteilchen, Atome, Moleküle oder die makroskopische Materie detailliert beschrieben werden. Zur Berechnung deren möglicher Zustände mit ihren jeweiligen physikalischen Eigenschaften und Reaktionsweisen wird ein der Quantenmechanik eigener mathematischer Formalismus genutzt.

Die Quantenmechanik unterscheidet sich nicht nur in ihrer mathematischen Struktur grundlegend von der klassischen Physik. Sie verwendet Begriffe und Konzepte, die sich der Anschaulichkeit entziehen und auch einigen Prinzipien widersprechen, die in der klassischen Physik als fundamental und selbstverständlich angesehen werden. Durch Anwendung von Korrespondenzregeln und Konzepten der Dekohärenztheorie können viele Gesetzmäßigkeiten der klassischen Physik, insbesondere die gesamte klassische Mechanik, als Grenzfälle der Quantenmechanik beschrieben werden. Allerdings gibt es auch zahlreiche Quanteneffekte ohne klassischen Grenzfall. Zur Deutung der Theorie wurde eine Reihe verschiedener Interpretationen der Quantenmechanik entwickelt, die sich insbesondere in ihrer Konzeption des Messprozesses und in ihren metaphysischen Prämissen unterscheiden.

Auf der Quantenmechanik und ihren Begriffen bauen die weiterführenden Quantenfeldtheorien auf, angefangen mit der Quantenelektrodynamik ab ca. 1930, mit denen auch die Prozesse der Erzeugung und Vernichtung von Teilchen analysiert werden können.

Genauere Informationen zum mathematischen Formalismus finden sich im Artikel Mathematische Struktur der Quantenmechanik.

Geschichte

Werner Heisenberg, Nobelpreis für Physik 1932 „für die Begründung der Quantenmechanik“

Anfang des 20. Jahrhunderts begann die Entwicklung der Quantenphysik zunächst mit den sogenannten alten Quantentheorien.[1] Max Planck stellte 1900 zur Herleitung des nach ihm benannten Strahlungsgesetzes die Hypothese auf, dass ein Oszillator Energie nur in ganzzahligen Vielfachen des Energiequantums $\Delta E=hf$ aufnehmen oder abgeben kann ( $h$ ist das Plancksche Wirkungsquantum, $f$ ist die Frequenz des Oszillators). 1905 erklärte Albert Einstein den photoelektrischen Effekt durch die Lichtquantenhypothese. Demnach besteht Licht aus diskreten Partikeln gleicher Energie $E$ , denen mit der Frequenz $f=E/h$ auch eine Welleneigenschaft zukommt.

Im Zeitraum ab 1913 entwickelte Niels Bohr das nach ihm benannte Atommodell. Dieses basiert auf der Annahme, dass Elektronen im Atom nur Zustände von ganz bestimmten Energien einnehmen können und dass die Elektronen bei der Emission oder Absorption von Licht von einem Energieniveau auf ein anderes „springen“ (siehe Elektronischer Übergang). Bei der Formulierung seiner Theorie nutzte Bohr das Korrespondenzprinzip, dem zufolge sich das quantentheoretisch berechnete optische Spektrum von Atomen im Grenzfall großer Quantenzahlen dem klassisch berechneten Spektrum annähern muss. Mit dem Bohrschen Atommodell und seinen Erweiterungen, dem Schalenmodell und dem Bohr-Sommerfeld-Modell, gelangen einige Erfolge, darunter die Erklärung des Wasserstoffspektrums, der Röntgenlinien und des Stark-Effekts sowie die Erklärung des Aufbaus des Periodensystems der Elemente.

Schnell erwiesen sich diese frühen Atommodelle jedoch als unzureichend. So versagten sie bereits bei der Anwendung auf das Anregungsspektrum von Helium, beim Wert des Bahndrehimpulses des elektronischen Grundzustandes von Wasserstoff und bei der Beschreibung verschiedener spektroskopischer Beobachtungen, wie z. B. des anomalen Zeeman-Effekts oder der Feinstruktur.

Im Jahr 1924 veröffentlichte Louis de Broglie seine Theorie der Materiewellen, wonach jegliche Materie einen Wellencharakter aufweisen kann und umgekehrt Wellen auch einen Teilchencharakter aufweisen können.[2] Diese Arbeit führte die Quantenphänomene auf eine gemeinsame Erklärung zurück, die jedoch wieder heuristischer Natur war und auch keine Berechnung der Spektren von Atomen ermöglichte. Daher wird sie als letzte den alten Quantentheorien zugeordnet, war jedoch richtungsweisend für die Entwicklung der Quantenmechanik.

Die moderne Quantenmechanik fand ihren Beginn im Jahr 1925 mit der Formulierung der Matrizenmechanik durch Werner Heisenberg, Max Born und Pascual Jordan.[3][4][5] Während Heisenberg im ersten dieser Aufsätze noch von „quantentheoretischer Mechanik“ gesprochen hatte, wurde in den beiden späteren Aufsätzen die noch heute gebräuchliche Bezeichnung „Quantenmechanik“ geprägt. Wenige Monate später stellte Erwin Schrödinger über einen völlig anderen Ansatz – ausgehend von De Broglies Theorie der Materiewellen – die Wellenmechanik bzw. die Schrödingergleichung auf.[6] Kurz darauf konnte Schrödinger nachweisen, dass die Wellenmechanik mit der Matrizenmechanik mathematisch äquivalent ist.[7] Schon 1926 brachte J. H. Van Vleck in den USA unter dem Titel Quantum Principles and Line Spectra das erste Lehrbuch zur neuen Quantenmechanik heraus. Das erste deutschsprachige Lehrbuch, Gruppentheorie und Quantenmechanik von dem Mathematiker Hermann Weyl, folgte 1928.

Heisenberg entdeckte die nach ihm benannte Unschärferelation im Jahr 1927; im gleichen Jahr wurde auch die bis heute vorherrschende Kopenhagener Interpretation der Quantenmechanik formuliert. In den Jahren ab etwa 1927 vereinigte Paul Dirac die Quantenmechanik mit der speziellen Relativitätstheorie. Er führte auch erstmals die Verwendung der Operator-Theorie inklusive der Bra-Ket-Notation ein und beschrieb diesen mathematischen Kalkül 1930 in seinem Buch Principles of Quantum Mechanics.[8] Zur gleichen Zeit formulierte John von Neumann eine strenge mathematische Basis für die Quantenmechanik im Rahmen der Theorie linearer Operatoren auf Hilberträumen, die er 1932 in seinem Buch Mathematische Grundlagen der Quantenmechanik beschrieb.[9] Die in dieser Aufbauphase formulierten Ergebnisse haben bis heute Bestand und werden allgemein zur Beschreibung quantenmechanischer Aufgabenstellungen verwendet.

Grundlegende Eigenschaften

Diese Darstellung geht von der Kopenhagener Interpretation der Quantenmechanik aus, die ab 1927 vor allem von Niels Bohr und Werner Heisenberg erarbeitet wurde. Trotz ihrer begrifflichen und logischen Schwierigkeiten hat sie gegenüber anderen Interpretationen bis heute eine vorherrschende Stellung inne. Auf Formeln wird im Folgenden weitgehend verzichtet, Genaueres siehe unter Mathematische Struktur der Quantenmechanik.

Observable und Zustände

Im Rahmen der klassischen Mechanik lässt sich aus dem Ort und der Geschwindigkeit eines (punktförmigen) Teilchens bei Kenntnis der wirkenden Kräfte dessen Bahnkurve vollständig vorausberechnen. Der Zustand des Teilchens lässt sich also eindeutig durch zwei Größen beschreiben, die (immer in idealen Messungen) mit eindeutigem Ergebnis gemessen werden können. Eine gesonderte Behandlung des Zustandes und der Messgrößen (oder „Observablen“) ist damit in der klassischen Mechanik nicht nötig, weil der Zustand die Messwerte festlegt und umgekehrt.

Die Natur zeigt jedoch Quantenphänomene, die sich mit diesen Begriffen nicht beschreiben lassen. Es ist im Allgemeinen nicht mehr vorhersagbar, an welchem Ort und mit welcher Geschwindigkeit ein Teilchen nachgewiesen wird. Wenn beispielsweise ein Streuexperiment mit einem Teilchen unter exakt gleichen Ausgangsbedingungen wiederholt wird, muss man für das Teilchen nach dem Streuvorgang immer denselben Zustand ansetzen (siehe Deterministische Zeitentwicklung), gleichwohl kann es an verschiedenen Orten des Schirms auftreffen. Der Zustand des Teilchens nach dem Streuprozess legt also seine Flugrichtung nicht fest. Allgemein gilt: In der Quantenmechanik gibt es Zustände, die auch dann nicht die Vorhersage eines einzelnen Messergebnisses ermöglichen, wenn der Zustand exakt bekannt ist. Es lässt sich dann jedem der möglichen Messwerte nur noch eine Wahrscheinlichkeit zuordnen. Daher werden in der Quantenmechanik Messgrößen und Zustände getrennt behandelt und es werden für diese Größen andere Konzepte verwendet als in der klassischen Mechanik.

Allen messbaren Eigenschaften eines physikalischen Systems werden in der Quantenmechanik mathematische Objekte zugeordnet, die sogenannten Observablen. Beispiele sind der Ort eines Teilchens, sein Impuls, sein Drehimpuls oder seine Energie. Es gibt zu jeder Observablen einen Satz von speziellen Zuständen, bei denen das Ergebnis einer Messung nicht streuen kann, sondern eindeutig festliegt. Ein solcher Zustand wird „Eigenzustand“ der betreffenden Observablen genannt, und das zugehörige Messergebnis ist einer der „Eigenwerte“ der Observablen.[10] In allen anderen Zuständen, die nicht Eigenzustand zu dieser Observablen sind, sind verschiedene Messergebnisse möglich. Sicher ist aber, dass bei dieser Messung einer der Eigenwerte festgestellt wird und dass das System anschließend im entsprechenden Eigenzustand dieser Observablen ist. Zu der Frage, welcher der Eigenwerte für die zweite Observable zu erwarten ist oder — gleichbedeutend — in welchem Zustand sich das System nach dieser Messung befinden wird, lässt sich nur eine Wahrscheinlichkeitsverteilung angeben, die aus dem Anfangszustand zu ermitteln ist.

Verschiedene Observablen haben im Allgemeinen auch verschiedene Eigenzustände. Dann ist für ein System, das sich als Anfangszustand im Eigenzustand einer Observablen befindet, das Messergebnis einer zweiten Observablen unbestimmt. Der Anfangszustand selbst wird dazu als Überlagerung (Superposition) aller möglichen Eigenzustände der zweiten Observablen interpretiert. Den Anteil eines bestimmten Eigenzustands bezeichnet man als dessen Wahrscheinlichkeitsamplitude. Das Betragsquadrat einer Wahrscheinlichkeitsamplitude gibt die Wahrscheinlichkeit an, bei einer Messung am Anfangszustand den entsprechenden Eigenwert der zweiten Observablen zu erhalten (Bornsche Regel oder Bornsche Wahrscheinlichkeitsinterpretation). Allgemein lässt sich jeder beliebige quantenmechanische Zustand als Überlagerung von verschiedenen Eigenzuständen einer Observablen darstellen. Verschiedene Zustände unterscheiden sich nur dadurch, welche dieser Eigenzustände mit welchem Anteil zu der Überlagerung beitragen.

Bei manchen Observablen, zum Beispiel beim Drehimpuls, sind nur diskrete Eigenwerte erlaubt. Beim Teilchenort hingegen bilden die Eigenwerte ein Kontinuum. Die Wahrscheinlichkeitsamplitude dafür, das Teilchen an einem bestimmten Ort zu finden, wird deshalb in Form einer ortsabhängigen Funktion, der so genannten Wellenfunktion angegeben. Das Betragsquadrat der Wellenfunktion an einem bestimmten Ort gibt die räumliche Dichte der Aufenthaltswahrscheinlichkeit an, das Teilchen dort zu finden.

Nicht alle quantenmechanischen Observablen haben einen klassischen Gegenpart. Ein Beispiel ist der Spin, der nicht auf aus der klassischen Physik bekannte Eigenschaften wie Ladung, Masse, Ort oder Impuls zurückgeführt werden kann.

Mathematische Formulierung

Für die mathematische Behandlung physikalischer Vorgänge soll der Zustand des betrachteten Systems zum betrachteten Zeitpunkt alle Angaben enthalten, die – bei bekannten äußeren Kräften – zur Berechnung seines zukünftigen Verhaltens erforderlich sind. Daher ist der Zustand eines Massenpunktes zu einem bestimmten Zeitpunkt t in der klassischen Physik schon durch die Angabe von Ort ${\vec {r}}=(x,y,z)$ und Impuls ${\vec {p}}=(p_{x},p_{y},p_{z})$ gegeben, zusammen also durch einen Punkt in einem 6-dimensionalen Raum, der Zustandsraum oder Phasenraum genannt wird. Genau in dieser Definition liegt begründet, dass die Quantenphänomene in der klassischen Physik keine Erklärung finden können. Dies zeigt sich beispielsweise in der unten beschriebenen Heisenbergschen Unschärferelation, der zufolge Ort und Impuls eines Quantenobjekts prinzipiell nicht gleichzeitig eindeutig bestimmt sein können.

In der Quantenmechanik wird der Zustand durch einen Vektor im Hilbertraum wiedergegeben, die übliche Notation ist $\vert \psi \rangle ,$ vereinfacht wird auch oft nur $\,\psi$ geschrieben. Dabei ist zu berücksichtigen, dass zwei verschiedene Vektoren genau dann denselben physikalischen Zustand bezeichnen, wenn sie sich nur um einen konstanten Zahlenfaktor unterscheiden. Eine unter vielen Möglichkeiten, $\vert \psi \rangle$ zu repräsentieren, ist die Wellenfunktion $\psi ({\vec {r}})$ (die ganze Funktion, nicht nur ihr Wert an einem Ort ${\vec {r}}$ ), oft ebenfalls einfach als $\,\psi$ geschrieben. Betrachtet man die zeitliche Entwicklung des Zustands, schreibt man $\vert \psi (t)\rangle$ beziehungsweise $\psi ({\vec {r}},t).$ Zwei Wellenfunktionen, die sich nur durch einen konstanten Faktor unterscheiden, geben denselben Zustand wieder.

Eine Observable wird allgemein durch einen linearen Operator ${\hat {O}}$ dargestellt, der mathematisch auf einen Zustandsvektor wirkt und als Ergebnis einen neuen Vektor des Zustandsraums erzeugt: ${\hat {O}}\vert \psi \rangle =\vert \phi \rangle .$ Falls $\vert \psi \rangle$ ein Eigenzustand dieser Observablen ist, gilt die Eigenwertgleichung ${\hat {O}}\vert \psi \rangle =a\cdot \vert \psi \rangle .$ Darin ist der Faktor $\,a$ der Eigenwert, also der für diesen Zustand eindeutig festgelegte Messwert der Observablen ${\hat {O}}.$ Meist wird der Zustandsvektor $\vert \psi \rangle$ dann durch einen unteren Index gekennzeichnet, z. B. $\vert \psi _{a}\rangle$ oder $\vert \psi _{n}\rangle ,$ worin $a$ der Eigenwert selber ist bzw. n (die „Quantenzahl“) seine laufende Nummer in der Liste aller Eigenwerte (sofern eine solche Liste existiert, also nicht für kontinuierliche Eigenwerte).

Deterministische Zeitentwicklung

Die Beschreibung der zeitlichen Entwicklung eines isolierten Systems erfolgt in der Quantenmechanik analog zur klassischen Mechanik durch eine Bewegungsgleichung, die Schrödingergleichung. Durch Lösen dieser Differentialgleichung lässt sich berechnen, wie sich die Wellenfunktion des Systems entwickelt:

\mathrm {i} \hbar {\frac {\partial }{\partial t}}\psi ={\hat {H}}\psi

mit dem Hamilton-Operator ${\hat {H}}$ , der die Gesamtenergie des quantenmechanischen Systems beschreibt. Der Hamilton-Operator setzt sich zusammen aus einem Term für die kinetische Energie der Teilchen des Systems und einem zweiten Term, der im Falle mehrerer Teilchen die Wechselwirkungen zwischen ihnen beschreibt sowie im Fall externer Felder die potentielle Energie, wobei die externen Felder auch zeitabhängig sein können. Wechselwirkungen zwischen verschiedenen Teilchen werden also – anders als in der newtonschen Mechanik – nicht als Kräfte, sondern ähnlich zur Methodik der klassischen hamiltonschen Mechanik als Energieterme beschrieben. Hierbei ist in den typischen Anwendungen auf Atome, Moleküle, Festkörper insbesondere die elektromagnetische Wechselwirkung relevant.

Die Schrödingergleichung ist eine partielle Differentialgleichung erster Ordnung in der Zeitkoordinate, die Zeitentwicklung des quantenmechanischen Zustands eines geschlossenen Systems ist also vollständig deterministisch.

Stationäre Zustände

Wenn der Hamilton-Operator ${\hat {H}}$ eines Systems nicht selbst von der Zeit abhängt, gibt es für dieses System stationäre Zustände, also solche, die sich im Zeitverlauf nicht ändern. Es sind die Eigenzustände zum Hamilton-Operator ${\hat {H}}$ . Nur in ihnen hat das System eine wohldefinierte Energie $\,E$ , eben den jeweiligen Eigenwert:

{\hat {H}}\psi =E\psi \,.

Die Schrödingergleichung reduziert sich in diesem Fall auf

\mathrm {i} \hbar {\frac {\partial }{\partial t}}\psi =E\psi

und hat die Lösung

\psi (t)=\psi (0)\cdot e^{-i{\frac {E}{\hbar }}t}\,.

Die zeitliche Entwicklung drückt sich also einzig in einem zusätzlichen Exponentialfaktor aus, einem Phasenfaktor. Das bedeutet, dass der durch $\psi (t)$ beschriebene Zustand derselbe ist wie $\psi (0)$ – ein stationärer Zustand eben. Nur die quantenmechanische Phase ändert sich, und zwar mit der Kreisfrequenz $\omega ={\tfrac {E}{\hbar }}$ . Auch für andere Observable als die Energie ist in stationären Zuständen die Wahrscheinlichkeit, einen bestimmten Wert zu messen, von der Zeit unabhängig.

Interferenz

Doppelspaltexperiment mit Teilchen

Eine weitere wesentliche Eigenschaft des quantenmechanischen Zustandes ist die Möglichkeit zur Interferenz. Wenn z. B. $\psi _{1}(x)$ und $\psi _{2}(x)$ Lösungen derselben Schrödingergleichung sind, ist es auch ihre Summe $\Psi (x)=\psi _{1}(x)+\psi _{2}(x)$ . In dieser Eigenschaft drückt sich das bei Wellen aller Art geltende Superpositionsprinzip aus. Mathematisch ergibt sie sich hier aus der Linearität der Schrödingergleichung. Die entsprechende räumliche Wahrscheinlichkeitsverteilung für ein Teilchen im Zustand $\vert \Psi \rangle$ ist (bis auf einen konstanten Normierungsfaktor) durch das Betragsquadrat $\vert \Psi (x)\vert ^{2}=\vert [\psi _{1}(x)+\psi _{2}(x)]\vert ^{2}$ gegeben. Im Zustand $\vert \Psi \rangle$ ist die Aufenthaltswahrscheinlichkeit daher nicht die Summe der beiden einzelnen Aufenthaltswahrscheinlichkeiten $\vert \psi _{1}(x)\vert ^{2}$ und $\vert \psi _{2}(x)\vert ^{2}$ , wie man es für klassische Teilchen erwarten würde. Vielmehr ist sie Null an jedem Ort, wo $\psi _{1}(x)=-\psi _{2}(x)$ gilt (destruktive Interferenz), während sie an Orten mit $\psi _{1}(x)=\psi _{2}(x)$ doppelt so groß ist wie die Summe der beiden einzelnen Aufenthaltswahrscheinlichkeiten (konstruktive Interferenz). Diese Eigenschaft weist auch Licht auf, das zum Beispiel hinter einem Doppelspalt ein Interferenzmuster entstehen lässt. Die Quantenmechanik sagt dementsprechend für Teilchen ähnliche Interferenzerscheinungen wie für Licht voraus.

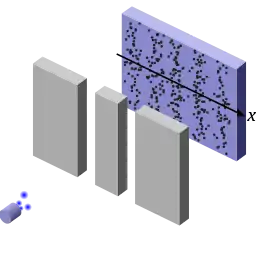
Das Doppelspaltexperiment zeigt sowohl die statistische Natur der Quantenmechanik als auch den Interferenzeffekt und ist damit ein gutes Beispiel für den Welle-Teilchen-Dualismus. Dabei werden mikroskopische „Teilchen“, zum Beispiel Elektronen, in einem breiten Strahl auf ein Hindernis mit zwei eng beieinander liegenden Spalten gesendet und weiter hinten auf einem Leuchtschirm aufgefangen. In der Verteilung der Elektronen auf dem Schirm würde man unter Annahme des klassischen Teilchenmodells zwei klar voneinander abgrenzbare Häufungen erwarten. Das kann man sich so vorstellen, als ob man kleine Kugeln von oben durch zwei Schlitze fallen ließe; diese werden unter jedem Schlitz je einen Haufen bilden. Die mit Elektronen tatsächlich beobachteten Messergebnisse sind anders (siehe Abbildung rechts).[11] Mit der klassischen Teilchenvorstellung stimmen sie nur insoweit überein, als jedes einzelne Elektron auf dem Schirm genau einen einzigen Leuchtpunkt verursacht. Bei der Ausführung des Experiments mit vielen Elektronen (gleich, ob gleichzeitig oder nacheinander auf die Spalte gesendet) wird die Wahrscheinlichkeitsverteilung der Ortsmesswerte sichtbar, die nicht den klassisch erwarteten zwei Häufungen entspricht. Sie weist stattdessen wie beim Licht ausgeprägte Interferenzstreifen auf, in denen sich die destruktive und konstruktive Interferenz abwechseln.

Messprozess

Hinter einem Doppelspalt wird ein Muster aus eindeutig lokalisierten Elektronen gemessen.

Eine Messung an einem physikalischen Objekt bestimmt den augenblicklichen Wert einer physikalischen Größe. Im Formalismus der Quantenmechanik wird die gemessene Größe durch einen Operator beschrieben, und der Messwert ist ein Eigenwert dieses Operators. Im Allgemeinen sind die Zustände des Systems Überlagerungen von Eigenzuständen zu verschiedenen Eigenwerten, trotzdem wird bei einer einzelnen Messung kein verwaschenes Bild mehrerer Werte gemessen, sondern stets ein eindeutiger Wert. Mit der Messung wird auch festgestellt, dass das Objekt zu diesem Zeitpunkt einen zu diesem Eigenwert gehörenden Eigenzustand des Operators einnimmt. Sofern es sich um eine Messung handelt, die das Objekt intakt lässt, muss eine sofortige Wiederholung der Messung nämlich mit Sicherheit dasselbe Ergebnis liefern, denn jede Änderung des Zustands gemäß der Schrödingergleichung würde eine gewisse Zeit brauchen.

Das quantenmechanische Messproblem entsteht daraus, dass der Übergang von dem Zustand vor der Messung zu dem durch die Messung festgestellten Zustand nicht als eine zeitliche Entwicklung gemäß der Schrödingergleichung verstanden werden kann. Dieser Übergang wird als Kollaps der Wellenfunktion oder als Zustandsreduktion bezeichnet. Von den Komponenten, die die Wellenfunktion vor der Messung hat, verschwinden im Kollaps alle diejenigen, die zu anderen Eigenwerten als dem festgestellten Messwert gehören. In den entsprechenden Formulierungen der Quantenmechanik erfolgt dieser Kollaps beim Vorgang des Messens. Doch dies ist nur eine ungenaue und unbefriedigende Umschreibung in der Alltagssprache. Die Vorgänge in der Messapparatur sind ausnahmslos physikalische Vorgänge. Wenn aber die Quantenmechanik die zutreffende grundlegende Theorie aller physikalischen Vorgänge ist, müsste sie alle physikalischen Systeme – inklusive der Messvorrichtung selbst – und deren wechselseitige Wirkung aufeinander beschreiben können. Der Quantenmechanik zufolge überführt der Messvorgang das untersuchte System und die Messvorrichtung in einen Zustand, in dem sie miteinander verschränkt sind. Wenn dann – spätestens durch das Ablesen an der Messvorrichtung – das Messergebnis festgestellt wird, stellt sich wieder das Problem der Zustandsreduktion. Offenbar mangelt es an einer Definition in physikalischen Begriffen, was genau den Unterschied einer „Messung“ zu allen anderen physikalischen Prozessen ausmacht, so dass sie den Kollaps der Wellenfunktion verursachen kann. Insbesondere bleibt offen, wo man die Grenze zwischen dem zu beschreibenden Quantensystem und der klassischen „Messapparatur“ festlegen soll. Dies wird als Demarkationsproblem bezeichnet. Für die konkrete Vorhersage der Wahrscheinlichkeitsverteilung der Messergebnisse am untersuchten System ist es allerdings unerheblich, wo man diese Grenze zieht, also welche Teile der Messapparatur man mit in die quantenmechanische Betrachtung einbezieht. Fest steht nur, dass zwischen dem Beginn der Messung und dem Registrieren des einzelnen eindeutigen Ergebnisses die Zustandsreduktion erfolgen muss.

Die Kopenhagener Interpretation erklärt den Kollaps und die Fragen zur Demarkation nicht weiter: Eine Messung wird schlicht beschrieben als Interaktion eines Quantensystems mit einem Messgerät, das selber als klassisches physikalisches System aufgefasst wird. Die oben gegebene Beschreibung von Observablen und Zuständen ist an dieser Interpretation orientiert. Davon stark unterschieden ist die Interpretation nach der Viele-Welten-Theorie. Sie betrachtet die im Kollaps verschwundenen Komponenten zu anderen Messwerten nicht als verschwunden, sondern nimmt an, dass diese gleichartige Zweige des Universums darstellen, welche untereinander fortan effektiv keine Information mehr austauschen können. Zu diesen und weiteren Sichtweisen siehe Interpretationen der Quantenmechanik.

Ein weiterer wichtiger Unterschied zwischen der quantenmechanischen und der klassischen Messung zeigt sich bei aufeinanderfolgenden Messungen von zwei verschiedenen Größen. Da die (ideale) klassische Messung das gemessene System gar nicht verändert, bleibt hier die Reihenfolge der beiden Messungen ohne Wirkung auf die Ergebnisse. Nach der Quantenmechanik aber wird der anfängliche Zustand durch eine Messung im Allgemeinen verändert, außer es handelt sich schon um einen Eigenzustand der betreffenden Observablen. Bei zwei aufeinanderfolgenden Messungen ist die Reihenfolge daher nur dann unerheblich, wenn sich das System in einem gemeinsamen Eigenzustand beider Observablen befindet. Andernfalls tritt bei mindestens einer der Messungen eine Zustandsreduktion auf, und das betreffende Messergebnis ist nur noch mit Wahrscheinlichkeit vorherzusagen. Für bestimmte Paare von Observablen trifft dies immer zu, denn sie haben überhaupt keinen gemeinsamen Eigenzustand. Solche Observablen werden komplementäre Observablen genannt. Ein Beispiel für ein Paar komplementärer Observablen sind Ort und Impuls. Hat z. B. ein Teilchen einen bestimmten Impuls, so wird eine Messung des Impulses genau diesen Wert ergeben. Eine nachfolgende Ortsmessung ergibt dann einen Wert aus einer unendlich breiten Wahrscheinlichkeitsverteilung, denn bei feststehendem Impuls ist der Ort völlig unbestimmt. Wird aber die Reihenfolge vertauscht, also die Ortsmessung zuerst ausgeführt, ist danach der Impuls unbestimmt, und damit auch das Ergebnis der nachfolgenden Impulsmessung.

Heisenbergsche Unschärferelation

Das Unschärfeprinzip der Quantenmechanik, das in Form der Heisenbergschen Unschärferelation bekannt ist, setzt die kleinstmöglichen theoretisch erreichbaren Unsicherheitsbereiche zweier Messgrößen in Beziehung. Es gilt für jedes Paar von komplementären Observablen, insbesondere für Paare von Observablen, die wie Ort und Impuls oder Drehwinkel und Drehimpuls physikalische Messgrößen beschreiben, die in der klassischen Mechanik als kanonisch konjugiert bezeichnet werden und kontinuierliche Werte annehmen können.

Hat für das betrachtete System eine dieser Größen einen exakt bestimmten Wert (Unsicherheitsbereich Null), dann ist der Wert der anderen völlig unbestimmt (Unsicherheitsbereich unendlich). Dieser Extremfall ist allerdings nur theoretisch von Interesse, denn keine reale Messung kann völlig exakt sein. Tatsächlich ist der Endzustand der Messung der Observablen $A$ daher kein reiner Eigenzustand der Observablen $A$ , sondern eine Überlagerung mehrerer dieser Zustände zu einem gewissen Bereich von Eigenwerten zu $A$ . Bezeichnet man mit $\Delta A$ den Unsicherheitsbereich von $A$ , mathematisch definiert durch die sog. Standardabweichung, dann gilt für den ebenso definierten Unsicherheitsbereich $\Delta B$ der kanonisch konjugierten Observablen $B$ die Ungleichung

\Delta A\cdot \Delta B\geq {\frac {h}{4\pi }}={\frac {\hbar }{2}}

.

Darin ist $h$ das Plancksche Wirkungsquantum und $\hbar \,=\,h/2\pi$ .

Selbst wenn beide Messgeräte beliebig genau messen können, wird die Schärfe der Messung von $B$ durch die der Messung von $A$ beschränkt. Es gibt keinen Zustand, in dem die Messwerte von zwei kanonisch konjugierten Observablen mit kleinerer Unschärfe streuen. Für das Beispiel von Ort und Impuls bedeutet das, dass in der Quantenmechanik die Beschreibung der Bewegung eines Teilchens durch eine Bahnkurve nur mit begrenzter Genauigkeit sinnvoll und insbesondere im Innern eines Atoms unmöglich ist.

Eine ähnliche Unschärferelation gilt zwischen Energie und Zeit. Diese nimmt aber hier eine Sonderrolle ein, da in der Quantenmechanik aus formalen Gründen der Zeit keine Observable zugeordnet ist.

Tunneleffekt

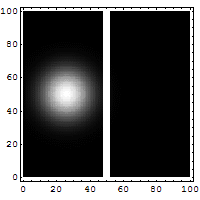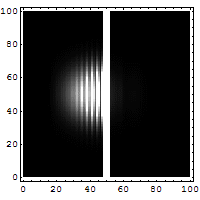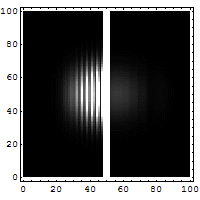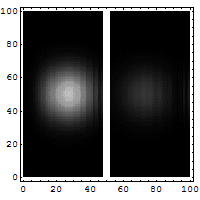
Durchtunneln und Reflexion an einer Potentialbarriere durch ein Elektron-Wellenpaket. Ein Teil des Wellenpaketes geht durch die Barriere hindurch, was nach der klassischen Physik nicht möglich wäre.

Der Tunneleffekt ist einer der bekannteren Quanteneffekte, die im Gegensatz zur klassischen Physik und zur Alltagserfahrung stehen. Er beschreibt das Verhalten eines Teilchens an einer Potentialbarriere. Im Rahmen der klassischen Mechanik kann ein Teilchen eine solche Barriere nur überwinden, wenn seine Energie höher als der höchste Punkt der Barriere ist, andernfalls prallt es ab. Nach der Quantenmechanik kann das Teilchen hingegen mit einer gewissen Wahrscheinlichkeit die Barriere auch im klassisch verbotenen Fall überwinden. Andererseits wird das Teilchen auch dann mit einer gewissen Wahrscheinlichkeit an der Barriere reflektiert, wenn seine Energie höher als die Barriere ist. Die Wahrscheinlichkeiten für das Tunneln beziehungsweise für die Reflexion können bei bekannter Form der Potentialbarriere präzise berechnet werden.

Der Tunneleffekt hat eine große Bedeutung in verschiedenen Bereichen der Physik wie zum Beispiel bei der Beschreibung des Alpha-Zerfalls, der Kernfusion, der Funktionsweise der Feldemissions- und Rastertunnelmikroskopie oder bei der Erklärung des Zustandekommens der chemischen Bindung.

Verschränkung, EPR-Experiment

Wenn zwei Quantensysteme miteinander in Wechselwirkung treten, müssen sie als ein Gesamtsystem betrachtet werden. Selbst wenn vor der Wechselwirkung der quantenmechanische Zustand dieses Gesamtsystems einfach aus den beiden wohldefinierten Anfangszuständen der beiden Teilsysteme zusammengesetzt ist, entwickelt er sich durch die Wechselwirkung zu einer Superposition von Zuständen, die jeweils aus solchen Paaren von Zuständen der Teilsysteme gebildet sind. Es sind mit verschiedener Wahrscheinlichkeit verschiedene Paarungen möglich (z. B. beim Stoß der elastische oder der inelastische Stoß, oder Ablenkung um verschiedene Winkel etc.). In jedem dieser Paare sind die Endzustände der Teilsysteme so aufeinander abgestimmt, dass die Erhaltungssätze (Energie, Impuls, Drehimpuls, Ladung etc.) erfüllt sind. Der Zustand des Gesamtsystems liegt eindeutig fest und ist eine Superposition aller möglichen Paarungen. Er kann nicht – wie der Anfangszustand vor der Wechselwirkung – einfach aus je einem bestimmten Zustand beider Teilsysteme gebildet werden. Dann ist mit einer Messung, die nur an einem Teilsystem ausgeführt wird und dieses in einem bestimmten seiner möglichen Endzustände findet, auch eindeutig festgestellt, dass das andere Teilsystem sich im dazu passenden Endzustand befindet. Es besteht nun eine Korrelation zwischen den physikalischen Eigenschaften der Teilsysteme. Daher bezeichnet man den Zustand des Gesamtsystems als verschränkt. Die Verschränkung bleibt auch dann erhalten, wenn der Zeitpunkt der Wechselwirkung schon weit in der Vergangenheit liegt und die zwei Teilsysteme sich inzwischen weit voneinander entfernt haben. Es ist zum Beispiel möglich, ein Paar von Elektronen so zu präparieren, dass sie sich räumlich entfernen und für keins der Elektronen einzeln die Richtung des Spins vorhersagbar ist, während es feststeht, dass das eine Elektron den Spin „down“ aufweist, wenn das andere Elektron mit dem Spin „up“ beobachtet wurde, und umgekehrt. Diese Korrelationen sind auch beobachtbar, wenn erst nach der Wechselwirkung entschieden wird, welche beliebige Richtung im Raum als Up- bzw. Down-Achse definiert wird.

Folge der Verschränkung ist, dass die Durchführung einer Messung an einem Ort die Messergebnisse an einem (im Prinzip beliebig weit entfernten) anderen Ort beeinflusst, und das ohne jede Zeitverzögerung, also mit Überlichtgeschwindigkeit. Dieses Phänomen war einer der Gründe, weshalb Albert Einstein die Quantenmechanik ablehnte. Er betrachtete die Separierbarkeit oder „Lokalität“ physikalischer Systeme (d. h. die Existenz wohlbestimmter lokaler physikalischer Eigenschaften) als ein fundamentales Prinzip der Physik und versuchte nachzuweisen, dass die Quantenmechanik unvollständig ist. Dazu entwickelte er 1935 gemeinsam mit Boris Podolsky und Nathan Rosen ein Gedankenexperiment, das als Einstein-Podolsky-Rosen-Paradoxon (EPR-Paradoxon) bekannt wurde. Sie zeigten damit, dass aus dem Prinzip der Lokalität das Vorhandensein zusätzlicher Eigenschaften der Systeme folgt, die von der Quantenmechanik nicht beschrieben werden (sogenannte verborgene Variablen); somit sei die Theorie unvollständig.[12] Es blieb jedoch unklar, ob das aus der klassischen Physik bekannte Lokalitätsprinzip tatsächlich auch in der Quantenmechanik gilt. Erst im Jahr 1964 gelang es John Stewart Bell, das EPR-Gedankenexperiment um die experimentell überprüfbare Bellsche Ungleichung zu erweitern und damit die Lokalitätsannahme auf die Probe zu stellen.[13] Alle seitdem durchgeführten Experimente haben die von der Quantenmechanik vorhergesagte Verletzung der Bellschen Ungleichung gezeigt und damit Einsteins Lokalitätsannahme widerlegt.[14]

Weiterhin zeigt die genaue theoretische Analyse des EPR-Effektes, dass dieser nicht im Widerspruch zur speziellen Relativitätstheorie steht, da auf diese Weise keine Information übertragen werden kann: Die einzelne Messung ergibt – unabhängig davon, ob das andere Teilchen bereits gemessen wurde – stets ein am Ort und zum Zeitpunkt der Messung unvorhersagbares Ergebnis. Erst, wenn das Ergebnis der anderen Messung – frühestens durch Kommunikation mit Lichtgeschwindigkeit – bekannt wird, kann man die Korrelation feststellen oder ausnutzen.

Identische Teilchen, Pauli-Prinzip

Durch die prinzipielle Unmöglichkeit, den Zustand eines quantenphysikalischen Systems nach klassischen Maßstäben „vollständig“ zu bestimmen, verliert eine Unterscheidung zwischen mehreren Teilchen mit gänzlich identischen intrinsischen Eigenschaften (wie beispielsweise Masse oder Ladung, nicht aber zustandsabhängigen Größen wie Energie oder Impuls) in der Quantenmechanik ihren Sinn. Nach den Vorstellungen der klassischen Mechanik können beliebig genaue Orts- und Impulsmessungen simultan an mehreren Teilchen durchgeführt werden – ob identisch oder nicht –, woraus (zumindest prinzipiell) die zukünftige Bahn jedes Teilchens genau vorhergesagt werden kann. Findet man später ein Teilchen an einem bestimmten Ort, kann man ihm eindeutig seinen Ausgangspunkt zuordnen und mit Sicherheit sagen, an beiden Orten habe es sich um dasselbe Teilchen gehandelt. Eine quantenmechanische Betrachtung lässt eine solche „Durchnummerierung“ von identischen Teilchen nicht zu. Das ist deshalb wichtig, weil z. B. alle Elektronen in diesem Sinne identische Teilchen sind. Es ist also beispielsweise unmöglich die Frage zu beantworten, ob bei zwei aufeinander folgenden Messungen an einzelnen Elektronen „dasselbe“ oder ein „anderes“ Elektron beobachtet wurde. Hier sind die Worte „dasselbe“ und „anderes“ in Anführungszeichen gesetzt, weil sie zwar umgangssprachlich klar erscheinen mögen, für identische Teilchen aber gar keinen Sinn ergeben. Es ist nicht nur unmöglich, die gestellte Frage zu beantworten, sie lässt sich schon gar nicht physikalisch sinnvoll stellen.

Da das Vertauschen zweier identischer Teilchen keine der physikalischen Eigenschaften des Zustands eines Vielteilchensystems ändert, muss der Zustandsvektor gleich bleiben oder kann höchstens sein Vorzeichen wechseln. Identische Teilchen bezeichnet man als Bosonen, wenn bei deren Vertauschung der Zustandsvektor gleich bleibt, als Fermionen, wenn er das Vorzeichen wechselt. Das Spin-Statistik-Theorem besagt, dass alle Teilchen mit ganzzahligem Spin Bosonen sind (z. B. die Photonen) und alle Teilchen mit halbzahligem Spin Fermionen. Dies lässt sich nicht im Rahmen der Quantenmechanik, sondern erst aus der Quantenfeldtheorie ableiten.

Eine wichtige Konsequenz ist die als „Pauli-Prinzip“ bekannte Regel, dass zwei identische Fermionen nicht die gleichen Einteilchenzustände einnehmen können. Es schließt bei den Atomen die Mehrfachbesetzung elektronischer Zustände aus und erzwingt deren „Auffüllung“ bis zur Fermi-Energie. Das ist von großer praktischer Bedeutung, denn es ermöglicht den Atomen, vielgestaltige chemische Verbindungen einzugehen. Das Spin-Statistik-Theorem bewirkt außerdem erhebliche Unterschiede im thermodynamischen Verhalten zwischen Systemen mit vielen identischen Teilchen. Bosonen gehorchen der Bose-Einstein-Statistik, die z. B. die Wärmestrahlung beschreibt, Fermionen der Fermi-Dirac-Statistik, die z. B. die elektronischen Eigenschaften von Leitern und Halbleitern erklärt.

Weiterführende Aspekte

Dekohärenz

a) klassische Streuung
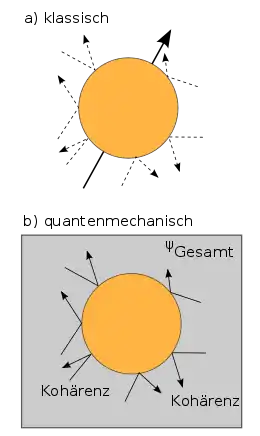
b) Dekohärenz durch Delokalisierung der quantenmechanischen Kohärenz

Die Dekohärenz ist ein modernes Konzept der Quantenmechanik, das bei makroskopischen Systemen die äußerst effiziente Unterdrückung der Folgen der Kohärenz beschreibt. Damit kann im Rahmen der Quantenmechanik erklärt werden, dass makroskopische Systeme keine Superpositionseffekte zeigen, sich also (von Ausnahmen abgesehen) „klassisch“ verhalten. Dekohärenz ist damit heute ein wichtiger Bestandteil des Korrespondenzprinzips der Quantenmechanik.

Zur Veranschaulichung dieses Effektes sei das Beispiel eines makroskopischen Objekts betrachtet, das dem Einfluss einer isotropen Lichtstrahlung – im Folgenden auch als Umgebung bezeichnet – ausgesetzt ist.[15] Im Rahmen der klassischen Physik ist der Einfluss des einfallenden Lichts auf die Bewegung des Objekts vernachlässigbar, da der mit dem Stoß eines Photons verbundene Impulsübertrag sehr gering ist und sich die Stöße aus verschiedenen Richtungen im Mittel kompensieren. Bei quantenmechanischer Betrachtung findet bei jedem Stoß eine Verschränkung des Objekts mit einem Photon statt (siehe oben), sodass das Objekt und das Photon nun als ein erweitertes Gesamtsystem betrachtet werden müssen. Die für Interferenzeffekte entscheidenden festen Phasenbeziehungen des quantenmechanischen Zustands erstrecken sich nun also über zwei Teilsysteme, das Objekt und das Photon, man spricht auch von einer Delokalisierung der Kohärenz.

Bei isolierter Betrachtung des (Teil)zustands des Objekts äußert sich jeder Stoß in einer Verschiebung seiner quantenmechanischen Phasenbeziehungen und damit in einer Verringerung seiner Interferenzfähigkeit. Hierbei handelt es sich um einen reinen Quanteneffekt, der unabhängig von einem mit dem Stoß verbundenen Impuls- oder Energieübertrag ist. Die praktisch unvermeidlichen, zahlreich auftretenden Wechselwirkungen makroskopischer Objekte mit ihrer Umgebung führen so zu einer effektiven Ausmittelung aller quantenmechanischen Interferenzeffekte. Die für die Dekohärenz charakteristische Zeitskala, die Dekohärenzzeit τ_d, ist im Allgemeinen unter Normalbedingungen äußerst kurz (z. B. etwa 10⁻²⁶ s),[16] die Dekohärenz gilt daher als der effizienteste bekannte physikalische Effekt. Bei makroskopischen („klassischen“) Objekten sind daher nur noch solche Zustände anzutreffen, die den Prozess der Dekohärenz schon abgeschlossen haben und ihm nicht weiter unterworfen sind. Die verbleibende inkohärente Überlagerung quantenmechanischer Zustände entspricht demnach genau den Zuständen der makroskopischen bzw. klassischen Physik. Die Dekohärenz liefert so eine quantenmechanische Erklärung für das klassische Verhalten von makroskopischen Systemen.

Relativistische Quantenmechanik

Feynman-Diagramme sind eine Notation für Teilchenreaktionen in der Quantenfeldtheorie.

Die Quantenmechanik wurde zuerst noch ohne Berücksichtigung der speziellen Relativitätstheorie entwickelt. Die Schrödingergleichung ist eine Differentialgleichung erster Ordnung in der Zeit, aber zweiter Ordnung in der Raumkoordinate, sie ist also nicht relativistisch kovariant. In der relativistischen Quantenmechanik muss sie durch eine kovariante Gleichung ersetzt werden. Nach der Klein-Gordon-Gleichung, die eine partielle Differentialgleichung zweiter Ordnung in Raum und Zeit ist, setzte sich vor allem die Dirac-Gleichung durch, welche als Pendant in erster Ordnung in Raum und Zeit verstanden werden kann.

Mit der Dirac-Gleichung konnten wichtige am Elektron beobachtete physikalische Phänomene erstmals erklärt oder sogar vorhergesagt werden. Während der halbzahlige Spin in der nichtrelativistischen Quantenmechanik ad hoc als zusätzliches Konstrukt und entgegen den Regeln der Drehimpulsquantelung eingeführt werden muss, ergibt sich seine Existenz zwanglos aus der mathematischen Struktur der Dirac-Gleichung. Auch folgt aus der Dirac-Gleichung richtig, dass das magnetische Moment des Elektrons im Verhältnis zum Spin, der gyromagnetische Faktor, fast genau doppelt so groß ist wie das für eine kreisende Ladung. Auch die Feinstruktur des Wasserstoffspektrums erweist sich als ein relativistischer Effekt, der mit der Dirac-Gleichung berechnet werden kann. Eine weitere erfolgreiche Anwendung der Dirac-Gleichung ist die Beschreibung der Winkelverteilung bei der Streuung von Photonen an Elektronen, also des Compton-Effekts, durch die Klein-Nishina-Formel. Eine weitere zutreffende Folge der Dirac-Gleichung war die zu ihrer Zeit ungeheuerliche Vorhersage der Existenz eines Antiteilchens zum Elektron, des Positrons.

Trotz dieser Erfolge sind diese Theorien jedoch insofern lückenhaft, als sie die Erzeugung und Vernichtung von Teilchen nicht beschreiben können, einen bei hochrelativistischen Energien allgegenwärtigen Effekt. Als sehr fruchtbar erwies sich hier die Entwicklung der Quantenfeldtheorie. In dieser Theorie werden sowohl materielle Objekte als auch deren Wechselwirkungen durch Felder beschrieben, die gemäß bestimmten Quantisierungsregeln, wie z. B. der zweiten Quantisierung, quantisiert werden. Die Quantenfeldtheorie beschreibt nicht nur die Entstehung und Vernichtung von Elementarteilchen (Paarerzeugung, Annihilation), sondern liefert auch eine tiefere Erklärung für deren Ununterscheidbarkeit, für den Zusammenhang zwischen Spin und Statistik von Quantenobjekten sowie für die Existenz von Antiteilchen.[17]

Interpretation

Die klassischen physikalischen Theorien, zum Beispiel die klassische Mechanik oder die Elektrodynamik, haben eine klare Interpretation, das heißt, den Symbolen der Theorie (Ort, Geschwindigkeit, Kraft beziehungsweise Spannungen und Felder) ist eine intuitive, klare Entsprechung in Experimenten (also eine messbare Größe) zugeordnet. Da die Quantenmechanik in ihrer mathematischen Formulierung auf sehr abstrakten Objekten, wie etwa Wellenfunktionen, basiert, ist eine Interpretation nicht mehr intuitiv möglich. Daher wurden seit dem Zeitpunkt der Entstehung der Theorie eine Reihe verschiedener Interpretationen vorgeschlagen. Sie unterscheiden sich in ihren Aussagen über die Existenz von Quantenobjekten und ihren Eigenschaften.

Die Standpunkte der meisten Interpretationen der Quantenmechanik können grob in zwei Gruppen aufgeteilt werden, die instrumentalistische Position und die realistische Position.[18] Gemäß der instrumentalistischen Position stellt die Quantenmechanik, beziehungsweise ein auf ihrer Basis ausgearbeitetes Modell, keine Abbildung der „Realität“ dar. Vielmehr handele es sich bei dieser Theorie lediglich um einen nützlichen mathematischen Formalismus, der sich als Werkzeug zur Berechnung von Messergebnissen bewährt hat. Diese ursprünglich insbesondere von Bohr im Rahmen der Kopenhagener Interpretation vertretene pragmatische Sicht dominierte bis in die 1960er Jahre die Diskussion um die Interpretation der Quantenmechanik und prägt bis heute viele gängige Lehrbuchdarstellungen.[19]

Neben dieser pragmatischen Variante der Kopenhagener Interpretation existiert heute eine Vielzahl alternativer Interpretationen, die bis auf wenige Ausnahmen das Ziel einer realistischen Deutung der Quantenmechanik verfolgen. In der Wissenschaftstheorie wird eine Interpretation als wissenschaftlich-realistisch bezeichnet, wenn sie davon ausgeht, dass die Objekte und Strukturen der Theorie treue Abbildungen der Realität darstellen und dass sowohl ihre Aussagen über beobachtbare Phänomene als auch ihre Aussagen über nicht beobachtbare Entitäten als (näherungsweise) wahr angenommen werden können.

In vielen Arbeiten zur Quantenphysik wird Realismus gleichgesetzt mit dem Prinzip der Wertdefiniertheit.[20][21] Dieses Prinzip basiert auf der Annahme, dass einem physikalischen Objekt physikalische Eigenschaften zugeordnet werden können, die es mit einem bestimmten Wert eindeutig entweder hat oder nicht hat. Beispielsweise spricht man bei der Beschreibung der Schwingung eines Pendels davon, dass das Pendel (zu einem bestimmten Zeitpunkt und innerhalb einer gegebenen Genauigkeit) eine Auslenkung $x$ hat.

In der Kopenhagener Interpretation wird die Annahme der Wertdefiniertheit aufgegeben. Ein Quantenobjekt hat demnach im Allgemeinen keine solchen Eigenschaften, vielmehr entstehen Eigenschaften erst im Moment und im speziellen Kontext der Durchführung einer Messung. Die Schlussfolgerung, dass die Wertdefiniertheit aufgegeben werden muss, ist allerdings weder aus logischer noch aus empirischer Sicht zwingend. So geht beispielsweise die (im Experiment von der Kopenhagener Interpretation nicht unterscheidbare) De-Broglie-Bohm-Theorie davon aus, dass Quantenobjekte Teilchen sind, die sich entlang wohldefinierter Bahnkurven bewegen, wobei diese Bahnen selbst aber der Beobachtung entzogen sind.

Zusammenhänge mit anderen physikalischen Theorien

Klassischer Grenzfall

Niels Bohr formulierte 1923 das sogenannte Korrespondenzprinzip, wonach die Eigenschaften von Quantensystemen im Grenzwert großer Quantenzahlen mit hoher Genauigkeit den Gesetzen der klassischen Physik entsprechen. Dieser Grenzwert bei großen Systemen wird als „klassischer Grenzfall“ oder „Korrespondenz-Limit“ bezeichnet. Hintergrund dieses Prinzips ist, dass klassische Theorien wie die klassische Mechanik oder die klassische Elektrodynamik an makroskopischen Systemen (Federn, Kondensatoren etc.) entwickelt wurden und diese daher sehr genau beschreiben können. Daraus resultiert die Erwartung, dass die Quantenmechanik im Falle „großer“ Systeme diese klassischen Eigenschaften reproduziert beziehungsweise ihnen nicht widerspricht.

Ein wichtiges Beispiel für diesen Zusammenhang zwischen der klassischen Mechanik und der Quantenmechanik ist das Ehrenfestsche Theorem. Es besagt, dass die Mittelwerte der quantenmechanischen Orts- und Impulsobservablen eines Teilchens in guter Näherung der klassischen Bewegungsgleichung folgen, sofern die Kräfte, die auf das Teilchen wirken, nicht zu stark mit dem Ort variieren.

Das Korrespondenzprinzip ist daher ein wichtiges Hilfsmittel bei der Konstruktion und Verifikation quantenmechanischer Modellsysteme: Zum einen liefern „klassische“ Modelle mikroskopischer Systeme wertvolle heuristische Anhaltspunkte zur quantenmechanischen Beschreibung des Systems. Zum anderen kann die Berechnung des klassischen Grenzfalls zur Plausibilisierung der quantenmechanischen Modellrechnungen herangezogen werden. Sofern sich im klassischen Grenzfall physikalisch unsinnige Resultate ergeben, kann das entsprechende Modell verworfen werden.

Umgekehrt bedeutet diese Korrespondenz aber auch, dass die korrekte quantenmechanische Beschreibung eines Systems, inklusive einiger nicht-klassischer Effekte wie etwa des Tunneleffekts, oft näherungsweise mittels klassischer Begriffe möglich ist; solche Näherungen erlauben oft ein tieferes Verständnis der quantenmechanischen Systeme. Man spricht hier auch von semiklassischer Physik. Beispiele für semiklassische Beschreibungen sind die WKB-Näherung und die Gutzwillersche Spurformel.

Allerdings besitzen die oben beschriebenen Korrespondenzregeln keine universale Gültigkeit, da sie nur unter bestimmten einschränkenden Randbedingungen gelten und die Dekohärenz (siehe oben) nicht berücksichtigen.[22][23][24][25] Weiterhin nähern sich nicht alle Quanteneffekte bei Anwendung der Korrespondenzregeln einem klassischen Grenzfall. Wie bereits das Schrödingers-Katze-Gedankenexperiment veranschaulicht, können „kleine“ Quanteneffekte wie z. B. der Zerfall eines radioaktiven Atoms durch Verstärker prinzipiell beliebig vergrößert werden. Zwar bewirken Dekohärenzeffekte bei makroskopischen Systemen in der Regel eine sehr effiziente Ausmittelung von Interferenzeffekten, jedoch weist auch der Zustand makroskopischer Systeme noch quantenmechanische Korrelationen auf, die z. B. in Form der sogenannten Leggett-Garg-Ungleichungen in experimentell überprüfbarer Form beschrieben werden können.[26] Ein weiteres Beispiel für Quanteneffekte, für die keine Korrespondenzregel gilt, sind die Folgen der Ununterscheidbarkeit gleicher Teilchen, etwa die Verdoppelung der Wahrscheinlichkeit einer Ablenkung um 90° beim Stoß (neben weiteren Interferenzerscheinungen in der Winkelverteilung), ganz gleich, wie gering die Energie der Teilchen ist und wie weit entfernt voneinander sie bleiben, wenn es sich nur um zwei gleiche Bosonen (z. B. α-Teilchen) handelt.

Verhältnis zur allgemeinen Relativitätstheorie

Da die Gravitationskraft im Vergleich zu den anderen Grundkräften der Physik sehr schwach ist, treten allgemein-relativistische Effekte hauptsächlich bei massiven Objekten, wie z. B. Sternen oder schwarzen Löchern auf, während Quanteneffekte überwiegend bei mikroskopischen Systemen beobachtet werden. Daher gibt es nur wenige empirische Daten zu Quanteneffekten, die durch die Gravitation verursacht sind. Zu den wenigen verfügbaren experimentellen Ergebnissen gehören das Pound-Rebka-Experiment und der Nachweis diskreter gebundener Zustände von Neutronen im Gravitationsfeld.[27][28]

Die oben genannten Experimente können im Rahmen der nicht-relativistischen Quantenmechanik beschrieben werden, indem für den Potentialterm der Schrödingergleichung das Gravitationspotential verwendet wird.[27] Die Gravitation wird hier als klassisches (also nicht quantisiertes) Feld betrachtet. Eine Vereinheitlichung der Gravitation mit den übrigen drei Grundkräften der Physik, die in ihrer allgemeinsten Form als Quantenfeldtheorien formuliert sind, lässt sich auf diesem Weg also nicht erreichen. Die Vereinheitlichung der Quantentheorie mit der allgemeinen Relativitätstheorie ist ein aktuelles Forschungsthema; der aktuelle Stand ist im Artikel Quantengravitation beschrieben.

Anwendungen

Quantenphysikalische Effekte spielen bei zahlreichen Anwendungsfällen der modernen Technik eine wesentliche Rolle. Beispiele sind der Laser, das Elektronenmikroskop, die Atomuhr oder in der Medizin die bildgebenden Verfahren auf Basis von Röntgenstrahlung bzw. Kernspinresonanz. Die Untersuchung von Halbleitern führte zur Erfindung der Diode und des Transistors, ohne die es die moderne Elektronik nicht gäbe. Auch bei der Entwicklung von Kernwaffen spielen die Konzepte der Quantenmechanik eine wesentliche Rolle.

Bei der Erfindung beziehungsweise Entwicklung dieser und zahlreicher weiterer Anwendungen kommen die Konzepte und der mathematische Formalismus der Quantenmechanik jedoch nur selten direkt zum Einsatz. In der Regel sind hierfür die anwendungsnäheren Konzepte, Begriffe und Regeln der Festkörperphysik, der Chemie, der Materialwissenschaften oder der Kernphysik von größerer praktischer Bedeutung. Die Relevanz der Quantenmechanik ergibt sich hingegen aus der überragenden Bedeutung, die diese Theorie bei der Formulierung des theoretischen Fundamentes vieler wissenschaftlicher Disziplinen hat.

Im Folgenden sind einige Beispiele für Anwendungen der Quantenmechanik beschrieben:

Atomphysik und Chemie

5f₋₂-Orbital des Wasserstoffatoms

Die chemischen Eigenschaften aller Stoffe sind ein Ergebnis der elektronischen Struktur der Atome und Moleküle, aus denen sie aufgebaut sind. Grundsätzlich lässt sich diese elektronische Struktur durch Lösung der Schrödingergleichung für alle involvierten Atomkerne und Elektronen quantitativ berechnen. Eine exakte analytische Lösung ist jedoch nur für den Spezialfall der wasserstoffähnlichen Systeme – also Systeme mit einem Atomkern und einem Elektron – möglich. Bei komplexeren Systemen – also in praktisch allen realen Anwendungen in der Chemie oder der Biologie – kann die Vielteilchen-Schrödingergleichung daher nur unter Verwendung von numerischen Methoden gelöst werden. Diese Berechnungen sind bereits für einfache Systeme sehr aufwändig. Beispielsweise dauerte die Ab-initio-Berechnung der Struktur und des Infrarot-Spektrums von Propan mit einem marktgängigen PC im Jahr 2010 einige Minuten, die entsprechende Berechnung für ein Steroid bereits mehrere Tage.[29] Daher spielen in der theoretischen Chemie Modellvereinfachungen und numerische Verfahren zur effizienten Lösung der Schrödingergleichung eine große Rolle, und die Entwicklung entsprechender Verfahren hat sich zu einer eigenen umfangreichen Disziplin entwickelt.

Ein in der Chemie besonders häufig verwendetes, stark vereinfachtes Modell ist das Orbitalmodell. Bei diesem Modell wird der Vielteilchenzustand der Elektronen der betrachteten Atome durch eine Summe der Einteilchenzustände der Elektronen gebildet. Das Modell beinhaltet verschiedene Näherungen (unter anderem: Vernachlässigung der Coulomb-Abstoßung der Elektronen untereinander, Entkopplung der Bewegung der Elektronen von der Kernbewegung), erlaubt jedoch eine näherungsweise korrekte Beschreibung der Energieniveaus des Atoms. Der Vorteil dieses Modells liegt neben der vergleichsweise einfachen Berechenbarkeit insbesondere in der anschaulichen Aussagekraft sowohl der Quantenzahlen als auch der grafischen Darstellung der Orbitale.

Das Orbitalmodell erlaubt die Klassifizierung von Elektronenkonfigurationen nach einfachen Aufbauregeln (Hundsche Regeln). Auch die Regeln zur chemischen Stabilität (Oktettregel bzw. Edelgasregel, Magische Zahlen) und die Systematik des Periodensystems der Elemente lassen sich durch dieses quantenmechanische Modell rechtfertigen.

Durch Linearkombination mehrerer Atom-Orbitale lässt sich die Methode auf sogenannte Molekülorbitale erweitern, wobei Rechnungen in diesem Fall wesentlich aufwändiger werden, da Moleküle keine Kugelsymmetrie aufweisen. Die Berechnung der Struktur und der chemischen Eigenschaften komplexer Moleküle auf Basis von Näherungslösungen der Schrödingergleichung ist der Gegenstand der Molekularphysik. Dieses Gebiet legte den Grundstein für die Etablierung der Quantenchemie beziehungsweise der Computerchemie als Teildisziplinen der theoretischen Chemie.

Kernphysik

Einfaches Modell des Alphazerfalls: Im Inneren des Kerns verbinden sich Nukleonen zu Alphateilchen, die den Coulombwall durch Tunneln überwinden können.

Die Kernphysik ist ein weiteres großes Anwendungsgebiet der Quantentheorie. Atomkerne sind aus Nukleonen zusammengesetzte Quantensysteme mit einer sehr komplexen Struktur. Bei ihrer theoretischen Beschreibung kommen – abhängig von der konkreten Fragestellung – eine Reihe konzeptionell sehr unterschiedlicher Kernmodelle zur Anwendung, die in der Regel auf der Quantenmechanik oder der Quantenfeldtheorie basieren.[30][31] Im Folgenden sind einige wichtige Anwendungsfälle der Quantenmechanik in der Kernphysik aufgeführt:

Einteilchenmodelle gehen davon aus, dass sich die Nukleonen innerhalb des Atomkerns frei bewegen können. Der Einfluss der anderen Nukleonen wird durch ein mittleres Kernpotential beschrieben. Beispiele: Schalenmodell, Fermigasmodell.
Clustermodelle beschreiben Kerne als Aggregate von kleinen Nukleonen-Clustern, insbesondere Alphateilchen, die sich durch eine hohe Bindungsenergie auszeichnen. Zu den physikalischen Prozessen, die mit diesem Modell erklärt werden können, zählt der Alphazerfall: Bestimmte instabile Kerne, wie z. B. ${}_{92}^{238}\mathrm {U}$ zerfallen durch Emission von Alphateilchen, wobei die Zerfallswahrscheinlichkeit quantenmechanisch durch den Tunneleffekt beschrieben werden kann.[32]
Die quantenmechanische Streutheorie ist die Grundlage zur Berechnung von Streuquerschnitten, die einen Vergleich von Modellrechnungen und den Ergebnissen von Streuexperimenten ermöglichen. Ein häufig verwendetes Näherungsverfahren ist Fermis goldene Regel, die die Übergangsrate (Übergangswahrscheinlichkeit pro Zeit) eines Anfangszustands in einen anderen Zustand unter dem Einfluss einer Störung beschreibt.

Festkörperphysik

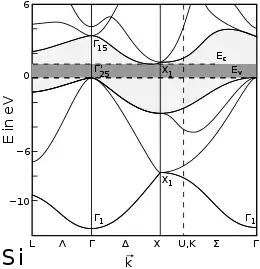
Bandstruktur von Silicium entlang den Symmetrierichtungen

Die Vielzahl prinzipiell möglicher chemischer Zusammensetzungen von kondensierter Materie – also von makroskopischer Materie im festen oder flüssigen Zustand – und die große Anzahl an Atomen, aus welchen kondensierte Materie besteht, spiegelt sich in einer großen Vielfalt von Materialeigenschaften wider (siehe Hauptartikel Materie). Die meisten dieser Eigenschaften lassen sich nicht im Rahmen der klassischen Physik beschreiben, während sich quantenmechanische Modelle kondensierter Materie als überaus erfolgreich erwiesen haben.

Aufgrund der großen Anzahl beteiligter Teilchen ist eine direkte Lösung der Schrödingergleichung für alle mikroskopischen Komponenten eines makroskopischen Stückes Materie unpraktikabel. Stattdessen werden Modelle und Lösungsverfahren angewendet, die an die zugrundeliegende Materiegattung (Metall, Halbleiter, Ionenkristall etc.) und an die zu untersuchenden Eigenschaften angepasst sind. In den gängigen Modellen kondensierter Materie sind Atomkerne und Elektronen die relevanten Grundbausteine kondensierter Materie. Hierbei werden in der Regel Atomkerne und innere Elektronen zu einem Ionenrumpf zusammengefasst, wodurch sich die Anzahl der im Modell zu berücksichtigenden Komponenten und Wechselwirkungen stark reduziert. Von den 4 Grundkräften der Physik wird lediglich die elektromagnetische Wechselwirkung berücksichtigt, die Gravitation und die Kernkräfte sind hingegen für die in der Physik kondensierter Materie betrachteten Effekte und Energieskalen irrelevant.

Trotz dieser Vereinfachungen handelt es sich bei Modellen kondensierter Materie um komplexe quantenmechanische Vielteilchenprobleme, wobei insbesondere die Berücksichtigung der Elektron-Elektron-Wechselwirkung eine Herausforderung darstellt. Für viele Anwendungszwecke, wie z. B. die Berechnung der Ladungsverteilung, des Phononenspektrums oder der strukturellen Eigenschaften, ist die Berechnung des elektronischen Grundzustandes ausreichend. In diesem Fall kann das elektronische Vielteilchenproblem unter Anwendung der Dichtefunktionaltheorie oder anderer Verfahren als ein effektives Einteilchenproblem umformuliert werden, welches heute routinemäßig auch für komplexe Systeme berechnet werden kann.[33]

Häufig sind neben den Grundzustandseigenschaften auch die elementaren Anregungen kondensierter Materie von Interesse. Beispielsweise basieren alle experimentellen Methoden der Festkörperspektroskopie auf dem Prinzip, dass durch einen externen Stimulus (z. B. Licht oder Neutronen) bestimmte Freiheitsgrade einer Probe angeregt bzw. abgeregt werden. Bei den elementaren Anregungen handelt es sich um kollektive quantenmechanische Effekte, denen – ähnlich einem freien Quantenobjekt – eine Energie und eine Wellenlänge bzw. ein Wellenvektor zugeordnet werden kann, weshalb sie auch als Quasiteilchen bezeichnet werden. Beispiele sind das Phonon (Energiequant der Gitterschwingung), oder das Exciton (Elektron-Loch-Paar). Quasiteilchen verschiedener Typen können miteinander wechselwirken und so aneinander streuen oder sich verbinden und neue Quantenobjekte mit Eigenschaften bilden, die sich drastisch von den Eigenschaften freier Elektronen unterscheiden. Ein bekanntes Beispiel sind die Cooper-Paare, die gemäß der BCS-Theorie die Supraleitung von Metallen ermöglichen.

Quanteninformatik

Von Interesse ist auch die Suche nach robusten Methoden zur direkten Manipulation von Quantenzuständen.[34] Es werden seit einigen Jahren Anstrengungen unternommen, einen Quantencomputer zu entwickeln, welcher durch Ausnutzung der verschiedenen Eigenzustände und der Wahrscheinlichkeitsnatur eines quantenmechanischen Systems hochparallel arbeiten würde.[34] Einsatzgebiet eines solchen Quantenrechners wäre beispielsweise das Knacken moderner Verschlüsselungsmethoden. Im Gegenzug hat man mit der Quantenkryptographie ein System zum theoretisch absolut sicheren Schlüsselaustausch gefunden, in der Praxis ist diese Methode häufig etwas abgewandelt und unsicherer, da es hier auch auf die Übertragungsgeschwindigkeit ankommt. Ein Thema ist dabei die Quantenteleportation, die sich mit Möglichkeiten zur Übertragung von Quantenzuständen über beliebige Entfernungen beschäftigt.[35]

Rezeption

Physik

Jahr	Name	Begründung für die Preisvergabe
1932	Werner Heisenberg (verliehen 1933)	für die Begründung der Quantenmechanik, deren Anwendung zur Entdeckung der allo- tropen Formen des Wasserstoffs geführt hat
1933	Erwin Schrödinger und P. A. M. Dirac	für die Entdeckung neuer produktiver Formen der Atomtheorie
1945	Wolfgang Pauli	für die Entdeckung des als Pauli-Prinzip bezeichneten Ausschlussprinzips
1954	Max Born	„für seine grundlegenden Forschungen in der Quantenmechanik, besonders für seine statistische Interpretation der Wellenfunktion“

Zwei Jahre nach den ersten Veröffentlichungen hatte sich die Quantenmechanik in der Kopenhagener Interpretation durchgesetzt. Als wichtiger Meilenstein gilt die fünfte Solvay-Konferenz im Jahr 1927. Rasch erlangte die Theorie den Status einer zentralen Säule im Theoriengebäude der Physik.[36] Im Hinblick auf ihre Leistungsfähigkeit bei konkreten Anwendungen (jedoch nicht im Hinblick auf ihre Interpretation, siehe oben) ist die Quantenmechanik bis heute praktisch unumstritten. Zwar existieren eine Reihe alternativer, empirisch nicht-äquivalenter Theorien, wie die Familie der Dynamischer-Kollaps-Theorien oder die Nichtgleichgewichts-Versionen der De-Broglie-Bohm-Theorie, jedoch haben diese Theorien gegenüber der Quantenmechanik nur eine marginale Bedeutung.[37]

Für die Entwicklung der Quantenmechanik wurden mehrere Nobelpreise der Physik vergeben:

Hinzu kam eine Reihe weiterer Nobelpreise für Weiterentwicklungen und Anwendungen der Quantenmechanik sowie für die Entdeckung von Effekten, die nur im Rahmen der Quantenmechanik erklärt werden können (siehe Liste der Nobelpreisträger für Physik). Auch einige Nobelpreise für Chemie wurden für erfolgreiche Anwendungen der Quantenmechanik vergeben, darunter die Preise an Robert Mulliken (1929, „für seine grundlegenden Arbeiten über die chemischen Bindungen und die Elektronenstruktur der Moleküle mit Hilfe der Orbital-Methode“), an Walter Kohn (1998, „für seine Entwicklung quantenchemischer Methoden“) oder an John Anthony Pople (1998, „für die Entwicklung von Methoden, mit denen die Eigenschaften von Molekülen und deren Zusammenwirken in chemischen Prozessen theoretisch erforscht werden können“).

Populärwissenschaftliche Darstellungen

Bereits kurz nach Begründung der Quantenmechanik veröffentlichten verschiedene Quantenphysiker, z. B. Born, de Broglie, Heisenberg oder Bohr, eine Reihe semi-populärwissenschaftlicher Bücher, die sich insbesondere mit philosophischen Aspekten der Theorie befassten.[38] Der Physiker G. Gamov veranschaulichte in seinem Buch Mr. Tompkins Explores the Atom die Eigenschaften von Quantenobjekten, indem er seinen Protagonisten verschiedene Abenteuer in einer fiktiven Quantenwelt erleben lässt. Auch die 1964 veröffentlichten Feynman-Vorlesungen über Physik, echte Lehrbücher, aber für die damalige Zeit sensationell anregend geschrieben, wurden in hohen Stückzahlen verkauft.[39] Allerdings erreichten Publikationen über die Quantenmechanik bis in die 1970er Jahre bei weitem nicht das Maß an öffentlicher Wahrnehmung, das beispielsweise der Relativitätstheorie und der Kosmologie zuteilwurde. Weiterhin prägten die praktischen Auswirkungen der Kernphysik, insbesondere die Risiken von Kernwaffen und Kernenergie, die öffentliche Diskussion über die moderne Physik.[38]

Auch in Film und Fernsehen wurde die Quantenmechanik gelegentlich in populärwissenschaftlicher Form dargestellt, z. B. in Sendungen des Physikers Harald Lesch.

Einfluss auf populäre Kultur, Geistes- und Sozialwissenschaften sowie Vereinnahmung durch die Esoterik

Mit dem Aufkommen der New-Age-Gegenkultur ab Anfang der 1970er Jahre entstand ein verstärktes Interesse an Literatur mit aus der Wissenschaft entlehnten Ausdrücken, in der Verbindungen zwischen der Quantenmechanik, dem menschlichen Bewusstsein und fernöstlicher Religion hergestellt wurden.[40] Bücher wie F. Capras Tao der Physik oder G. Zukavs Dancing Wu Li Masters wurden Bestseller.[41] Die Quantenmechanik – so eine Kernaussage dieser Bücher – enthalte holistische und mystische Implikationen, die eine Verbindung von Spiritualität, Bewusstsein und Physik zu einem „organischen“ Weltbild nahelegten.[40][42]

Ab den 1980er Jahren erlebte der Markt für quantenmechanisch inspirierte Literatur einen weiteren kräftigen Aufschwung, und das Wort „Quanten“ entwickelte sich zu einem in vielen Komposita verwendeten Modewort.[43] Die veröffentlichten Bücher umfassten ein breites Themenspektrum, welches von allgemeinverständlichen Darstellungen über weitere Bücher zu dem Themenkomplex „Quantenmechanik und Bewusstsein“ bis hin zu Themen wie dem „Quantum Learning“, „Quantum Golf“ oder den „Quantum Carrots“ reichte.[43] Ein bekanntes Beispiel für die Erweiterung quantenmechanischer Konzepte auf Bereiche jenseits ihrer Anwendbarkeit ist der Film What the Bleep do we (k)now!?.

Die Literaturwissenschaftlerin Elizabeth Leane kommt zu einer zwiespältigen Bewertung des Genres. Einerseits misst sie ihm pädagogische Bedeutung bei der allgemeinverständlichen Darstellung von Wissenschaft zu. Andererseits weist sie auf das Problem von Bedeutungsverschiebungen hin, die durch die Verwendung von Metaphern und „fiktionalen Techniken“ erzeugt werden.[44] Am Beispiel von Zukavs Dancing Wu Li Masters, einem der meistverkauften und am häufigsten zitierten Bücher, die Quantenmechanik und Esoterik verquicken,[45] zeigt sie eine rhetorische Umdeutung der Quantenmechanik zur Unterstützung eines anthropozentrischen Weltbildes auf.[46] Der Soziologe S. Restivo weist auf prinzipielle linguistische und konzeptionelle Probleme bei Versuchen hin, Quantenmechanik umgangssprachlich zu beschreiben und mit Mystik zu verbinden.[47] Viele Physiker, etwa J. S. Bell, M. Gell-Mann oder V. Stenger, lehnen Hypothesen, die Verbindungen zwischen Quantenmechanik und Bewusstsein herstellen, als spekulativ ab.[48][49][50] Einen neuen Anlauf hierzu legte im Jahr 2015 der Politikwissenschaftler Alexander Wendt mit dem Buch Quantum Mind and Social Science vor.[51]

Kunst

Quantum Man (2006), J. Voss-Andreae

Quantum Corral (2009), J. Voss-Andreae

Die Quantenmechanik wurde und wird in der Kunst, insbesondere in der Belletristik, aber auch in der bildenden Kunst und punktuell im Theater, wahrgenommen und künstlerisch verarbeitet.

Die Literaturwissenschaftlerin E. Emter weist Rezeptionsspuren der Quantentheorie in Texten von R. Musil (Der Mann ohne Eigenschaften), H. Broch, E. Jünger, G. Benn, Carl Einstein und B. Brecht nach, wobei sich ihre Studie auf den deutschen Sprachraum und die Jahre 1925 bis 1970 beschränkt.[52][53]

In den letzten Jahren erlangten Arbeiten von Bildhauern Aufmerksamkeit, die Quantenobjekte als Skulpturen darstellen.[54] Der Bildhauer J. Voss-Andreae geht davon aus, dass Kunst, die nicht an die Textform gebunden ist, Möglichkeiten zur Darstellung von Realität hat, die der Wissenschaft nicht zur Verfügung stehen.[55] Ein Beispiel ist seine Skulptur Quantum Man (siehe Abbildung rechts), die von Kommentatoren als Symbolisierung des Welle-Teilchen-Dualismus und der Beobachterperspektive interpretiert wird.[55] Weitere bekannte Beispiele für künstlerische Darstellungen von Quantenobjekten sind die Skulpturen Quantum Corral und die Spin Family desselben Künstlers sowie die Quantum Cloud von A. Gormley.[55]

Auch einige Theaterstücke thematisieren die Quantenmechanik, so z. B. Tom Stoppards Bühnenstück Hapgood oder das Stück QED des US-amerikanischen Dramatikers P. Parnell.[56] In seinem Bühnenstück Kopenhagen überträgt der Schriftsteller M. Frayn das Heisenbergsche Unschärfeprinzip in ein Unschärfeprinzip des menschlichen Verhaltens.[57]

Literatur

Standard-Lehrbücher

Claude Cohen-Tannoudji: Quantenmechanik. de Gruyter, 1999, ISBN 3-11-016458-2.
Richard Feynman: Feynman Vorlesungen über Physik. Band 3: Quantenmechanik. Oldenbourg, 2007, ISBN 978-3-486-58109-6.
Torsten Fließbach: Quantenmechanik: Lehrbuch zur Theoretischen Physik III. Spektrum Akademischer Verlag, 2008, ISBN 978-3-8274-2020-6.
Walter Greiner: Theoretische Physik. Band 4: Quantenmechanik – Einführung. Deutsch-Verlag, Frankfurt am Main 2005, ISBN 3-8171-1765-5.
Gernot Münster: Quantentheorie. De Gruyter, 2020, ISBN 978-3-11-047995-9.
Wolfgang Nolting: Grundkurs Theoretische Physik 5/1 (Quantenmechanik – Grundlagen). Springer, 2008, ISBN 978-3-540-68868-6.
Wolfgang Nolting: Grundkurs Theoretische Physik 5/2 (Quantenmechanik – Methoden und Anwendungen). Springer, 2012, ISBN 978-3-642-24420-9.

Allgemeinverständliche Einführungen

Tony Hey, Patrick Walters: Das Quantenuniversum. ISBN 3-8274-0315-4.
Anton Zeilinger: Einsteins Schleier, Die neue Welt der Quantenphysik. Goldmann, 2003, ISBN 3-442-15302-6.
Silvia Arroyo Camejo: Skurrile Quantenwelt. Springer, Berlin 2006, ISBN 3-540-29720-0.
Gert-Ludwig Ingold: Quantentheorie. C.H.Beck, München 2002, ISBN 3-406-47986-3.
Claus Kiefer: Quantentheorie. S. Fischer, Frankfurt am Main 2012, ISBN 978-3-596-19035-5.
Transnational College of Lex: What is Quantum Mechanics? A Physics Adventure. Language Research Foundation, Boston, 1996, ISBN 0-9643504-1-6. (Das Buch mit 566 Seiten ist Teil eines japanischen Projektes, in dem gleichzeitig naturwissenschaftliche und sprachliche Kenntnisse – hier Englisch – vermittelt werden sollen.)
John Gribbin, Friedrich Griese: Auf der Suche nach Schrödingers Katze: Quantenphysik und Wirklichkeit. Piper Taschenbuch, 2010, ISBN 978-3-492-24030-7.

Anwendungen

Atomphysik und theoretische Chemie:

E. G. Lewars: Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Springer, 2010, ISBN 978-90-481-3860-9.
A. Szabo, N. S. Ostlund: Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. Dover Publications, 1996, ISBN 0-486-69186-1.
P. W. Atkins, R. S. Friedman: Molecular Quantum Mechanics. 4. Auflage. Oxford University Press, Oxford 2004, ISBN 0-19-927498-3.
W. Kutzelnigg: Einführung in die Theoretische Chemie. Wiley-VCH, Weinheim 2002, ISBN 3-527-30609-9.
J. Reinhold: Quantentheorie der Moleküle. 3. Auflage. Teubner, 2006, ISBN 3-8351-0037-8.

Kernphysik:

B. Povh, K. Rith, C. Scholz, F. Zetsche, W. Rodejohann: Teilchen und Kerne: Eine Einführung in die physikalischen Konzepte. 9. Auflage. Springer, 2014, ISBN 978-3-642-37821-8.
J. Bleck-Neuhaus: Elementare Teilchen: Moderne Physik von den Atomen bis zum Standard-Modell. 1. Auflage. Springer, 2010, ISBN 978-3-540-85299-5.

Physik kondensierter Materie:

S. G. Louie, M. L. Cohen: Conceptual Foundations of Materials: A Standard Model for Ground- and Excited-State Properties. Elsevier, 2006, ISBN 0-444-50976-3.

Quanteninformatik:

M. A. Nielsen, Isaac L. Chuang: Quantum Computation and Quantum Information. Cambridge University Press, 2000, ISBN 0-521-63503-9.

Interpretationen der Quantenmechanik

David Albert: Quantum Mechanics and Experience. Harvard University Press, Cambridge, MA 1992. Zugleich eine sehr gut und leicht lesbare Einführung mit sehr einfachen Modellen.
Kurt Baumann, Roman U. Sexl: Die Deutungen der Quantentheorie. (= Facetten der Physik. Band 11). 3., überarbeitete Auflage. Vieweg, Braunschweig 1987, ISBN 3-528-28540-0. Kritische Überlegungen, ergänzt mit berühmten Originalabhandlungen (in deutscher Übersetzung) von Max Born, Werner Heisenberg, Albert Einstein, Niels Bohr, Erwin Schrödinger, Wladimir Fock, David Bohm, John Stewart Bell, Bryce DeWitt
John Stewart Bell: Speakable and unspeakable in quantum mechanics. Cambridge University Press, Cambridge 1988. bündelt Bells Originalaufsätze; für Interpretationsfragen wichtig u. a. die Texte zur Bohmschen Interpretation, größtenteils physikalisch voraussetzungsreich
Jeffrey Bub: Interpreting the Quantum World. Cambridge University Press, Cambridge 1997, ISBN 0-521-56082-9.
Jeffrey Bub: The Interpretation of Quantum Mechanics. Reidel, Dordrecht 1974, ISBN 90-277-0465-1.
Nancy Cartwright: Another Philosopher Looks at Quantum Mechanics, or: What Quantum Theory is Not. (PDF; 205 kB)Instrumentalistische Reaktion auf Putnam 2005: Quantenmechanik kann als „lebende und arbeitende Theorie“ uninterpretiert bleiben.
Hong Dingguo: On the Neutral Status of QM in the Dispute of Realism vs. Anti-Realism. In: Robert S. Cohen, Risto Hilpinen, Qiu Renzong (Hrsg.): Realism and Anti-Realism in the Philosophy of Science. Kluwer Academic Publishers, Dordrecht 1996, ISBN 0-7923-3233-4, S. 307–316.
Peter Forrest: Quantum metaphysics. Blackwell, Oxford 1988, ISBN 0-631-16371-9. Diskussion realistischer metaphysischer Interpretationsoptionen
Bas van Fraassen: Quantum Mechanics. An Empiricist View. Oxford University Press, Oxford 1991, ISBN 0-19-823980-7 Ausgearbeitete antirealistische Interpretation aus der Position des konstruktiven Empirismus
R. I. G. Hughes: The structure and interpretation of quantum mechanics. Harvard Univ. Pr., Cambridge, Mass. 1989, ISBN 0-674-84391-6. Zugleich eine vollwertige, aber nur Schulmathematik voraussetzende Einführung in die Theorie
E. Joos u. a.: Decoherence and the Appearance of a Classical World in Quantum Theory. Springer, Berlin 2003, ISBN 3-540-00390-8. Ausführliche Diskussion des klassischen Grenzfalls und dessen Relevanz für die Interpretation der Quantentheorie
Tim Maudlin: Quantum Non-Locality and Relativity. Blackwell, Oxford U. K./ Cambridge MA 1994, ISBN 0-631-18609-3.
Hilary Putnam: A Philosopher Looks at Quantum Mechanics (Again). In: The British Journal for the Philosophy of Science. 56/4 (2005), S. 615–634. Ablehnung „kopenhagener“ Interpretationen als bloßen Zurückweisungen eines wissenschaftlichen Realismus und der statistischen Interpretation (Born), Diskussion der wichtigsten verbleibenden realistischen Optionen: spontaner Kollaps (GRW) und Bohm
Michael Redhead: Incompleteness, nonlocality and realism: a prolegomenon to the philosophy of quantum mechanics. Clarendon Press, Oxford 1987, ISBN 0-19-824937-3. Eines der wichtigsten weiterführenden Werke, inklusive einer knappen Darstellung der Theorie
Hans Reichenbach: Philosophic Foundations Of Quantum Mechanics. University Of California Press, 1944.
Pieter E. Vermaas: A Philosopher’s Understanding of Quantum Mechanics. Possibilities and Impossibilities of a Modal Interpretation. Cambridge University Press, 1999, ISBN 0-521-65108-5. Nach kurzer Einführung in den Formalismus ähnlich von Neumann ausführliche Darstellung und Diskussion verschiedener Varianten modaler Interpretationen, u. a. van Fraassens, Bubs; Verteidigung einer Variante von Dieks-Kochen.
John Archibald Wheeler (Hrsg.): Quantum theory and measurement. Princeton Univ. Press, Princeton, NJ 1983, ISBN 0-691-08315-0. Standard-Handbuch mit den wichtigsten Texten aus der Interpretationsgeschichte, umfangreicher und aktueller als Sexl/Baumann.

Audios

Herbert Pietschmann: Einführung in die Quantenmechanik. nerds_on_air, ORANGE 94.0.

Videos

Robert Griffiths, Alain Aspect, Anton Zeilinger u. a.: Resources. Kursmaterial (Videos, Folien, Handouts) iqc.uwaterloo.ca, abgerufen am 24. Juli 2012.

Weblinks

Wikibooks: Quantenmechanik – Lern- und Lehrmaterialien

Commons: Quantenmechanik – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Quantenmechanik – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Interaktive Experimente zur Quantenmechanik: Quantenzufall, Interferenz von einzelnen Quanten, Verschränkung, Kryptographie etc. (flash-plugin erforderlich) – von der Friedrich-Alexander-Universität Erlangen-Nürnberg
Olga Teider: Einführung in die Quantentheorie mit interaktiven Experimenten (flash-plugin erforderlich) – von der Universität Ulm
Jenann Ismael: Quantum Mechanics. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Peter J. Lewis: Interpretations of Quantum Mechanics. In: J. Fieser, B. Dowden (Hrsg.): Internet Encyclopedia of Philosophy.
Thomas Neusius / Christian Ströbele: Quanten, Mathematik und Philosophie einer physikalischen Idee Kursmaterial, beginnend auf Schulniveau
Georg Bernhardt: Prüfungsfragen zur Quantenmechanik. PDF, deutsch, 336 kB.
Anton Zeilinger: On the Interpretation and Philosophical Foundation of Quantum Mechanics. (PDF; 62 kB) In: U. Ketvel u. a. (Hrsg.): Vastakohtien todellisuus. Festschrift for K. V. Laurikainen. Helsinki University Press, 1996.
Physik-Nobelpreisträger Theodor W. Hänsch über die Quantenmechanik, deren Grundlagen, Entwicklung, Anwendungen, Interpretationen Interview, 22. Juli 2008
Eine Sammlung der philosophisch bedeutsamsten Experimente der Quantenphysik, einfach erklärt (Memento vom 1. Februar 2015 im Internet Archive)
Auf der Suche nach dem Quantenmodell Allgemeinverständliche Übersicht der Interpretationen der Quantenmechanik, Oktober 2021

Einzelnachweise

Vgl. Max Planck: The origin and development of the quantum theory. The Clarendon press, Oxford 1922; Armin Hermann: Von Planck bis Bohr – Die ersten fünfzehn Jahre in der Entwicklung der Quantentheorie. In: Angewandte Chemie. Band 82, Nr. 1, 1970, S. 1–7, ISSN 0044-8249; Cathryn Carson: The Origins of the Quantum Theory (PDF; 376 kB). In: Beam Line. (Stanford Linear Accelerator Center). Band 30, Nr. 2, 2000, S. 6–19.
L. de Broglie: Recherches sur la théorie des Quanta. Doktorarbeit. Engl. Übersetzung (übers. A.F. Kracklauer): In: Ann. de Phys. 10. Serie, Band III, 1925.
W. Heisenberg: Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. In: Zeitschrift für Physik. Band 33, 1925, S. 879–893, doi:10.1007/BF01328377.
M. Born, P. Jordan: Zur Quantenmechanik. In: Zeitschrift für Physik. Band 34, 1925, S. 858–888, doi:10.1007/BF01328531.
M. Born, W. Heisenberg, P. Jordan: Zur Quantenmechanik II. In: Zeitschrift für Physik. Band 35, 1926, S. 557–615, doi:10.1007/BF01379806.
E. Schrödinger: Quantisierung als Eigenwertproblem I. In: Annalen der Physik. Band 79, 1926, S. 361–376, doi:10.1002/andp.19263840404; E. Schrödinger: Quantisierung als Eigenwertproblem II. In: Annalen der Physik. Band 79, 1926, S. 489–527, doi:10.1002/andp.19263840602; E. Schrödinger: Quantisierung als Eigenwertproblem III. In: Annalen der Physik. Band 80, 1926, S. 437–490, doi:10.1002/andp.19263851302; E. Schrödinger: Quantisierung als Eigenwertproblem IV. In: Annalen der Physik. Band 81, 1926, S. 109–139, doi:10.1002/andp.19263861802.
E. Schrödinger: Über das Verhältnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen. In: Annalen der Physik. Band 79, 1926, S. 734–756, doi:10.1002/andp.19263840804.
P. A. M. Dirac: Principles of Quantum Mechanics. 4. Auflage. Oxford University Press, 1958, ISBN 0-19-851208-2.
John von Neumann: Mathematische Grundlagen der Quantenmechanik. 2. Auflage. Springer, Berlin 1996, Engl. (autorisierte) Ausg. (übers. R. T. Beyer): Mathematical Foundations of Quantum Mechanics. Princeton Univ. Press, 1955 (dort S. 28ff.)
Im mathematischen Sinn sind Spektralwerte eines Operators mit kontinuierlichem Spektrum, wie z. B. des Orts- oder des Impulsoperators, wegen fehlender Normierbarkeit keine eigentlichen Eigenwerte. In physikalischen Lehrbüchern gilt jedoch in der Regel die Konvention, dass auch Spektralwerte eines kontinuierlichen Spektrums als Eigenwerte bezeichnet werden. Der vorliegende Artikel schließt sich dieser Konvention an. Siehe z. B. P. Reineker u. a.: Theoretische Physik III: Quantenmechanik 1. Band 3, 2007, S. 124. [https://de.wikipedia.org/w/index.php?title=Wikipedia:Defekte_Weblinks&dwl=http://books.google.de/books?id=uhJbvVSnSLMC&lpg=PA124&hl=de&pg=PA124 Seite nicht mehr abrufbar], Suche in Webarchiven: @1@2Vorlage:Toter Link/books.google.de[http://timetravel.mementoweb.org/list/2010/http://books.google.de/books?id=uhJbvVSnSLMC&lpg=PA124&hl=de&pg=PA124 (google books)]
A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, H. Ezawa: Demonstration of single-electron build-up of an interference pattern. In: American Journal of Physics. Band 57, 1989, S. 117–120, doi:10.1119/1.16104.
A. Einstein, B. Podolsky, N. Rosen: Can quantum-mechanical description of physical reality be considered complete? In: Physical Review. Band 47, 1935, S. 777–780, doi:10.1103/PhysRev.47.777.
J.S. Bell: On the Einstein Podolsky Rosen paradox. In: Physics. 1 #3, 1964, S. 195.
A. Aspect u. a.: Experimental Tests of Realistic Local Theories via Bell’s Theorem. In: Physical Review Letters. Band 47, 1981, S. 460, doi:10.1103/PhysRevLett.47.460; A. Aspect u. a.: Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. In: Physical Review Letters. Band 49, 1982, S. 91, doi:10.1103/PhysRevLett.49.91; A. Aspect u. a.: Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. In: Physical Review Letters. Band 49, 1982, S. 1804, doi:10.1103/PhysRevLett.49.1804; M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe, D. J. Wineland: Experimental violation of Bell’s inequalities with efficient detection. In: Nature. Band 409, 2001, S. 791–794, doi:10.1038/35057215.
M. Schlosshauer: Decoherence and the Classical-to-Quantum Transition. Bei: books.google.de. Springer, 2007, S. 7.
Omnes schätzt die Dekohärenzzeit für ein Pendel mit einer Masse von 10 g auf τ_d = 1,6 · 10⁻²⁶ s. Siehe R. Omnes: Understanding Quantum Mechanics. Princeton University Press, 1999, S. 202 und S. 75.
F. Wilczek: Quantum Field Theory. In: Compendium of Quantum Physics. Springer, 2009, S. 549 ff.
Die Gruppierung in Instrumentalismus versus Realismus ist eine starke Vereinfachung der tatsächlich vorhandenen Vielfalt verschiedener Positionen der Wissenschaftstheorie. Ein ausführlicher Überblick über die wichtigsten erkenntnistheoretischen Positionen in der Physik findet sich zum Beispiel in Bernard d’Espagnat: Reality and the Physicist. Cambridge University Press, 1989.
H. P. Stapp: The Copenhagen Interpretation. In: American Journal of Physics. Band 40, 1972, S. 1098.
In der englischsprachigen Literatur findet sich eine Vielzahl verschiedener Bezeichnungen für die Wertdefiniertheit: „value-definiteness“, „intrinsic property“, „pre-assigned initial values“ (Home und Whitaker), „precise value principle“ (Hughes), „classical principle C“ (Feyerabend), sowie Bells „beables“. Auch das in der Messtechnik verwendete Konzept des „wahren Wertes“ setzt Wertdefiniertheit voraus.
Zur erkenntnistheoretischen Einordnung der Wertdefiniertheit gibt es unterschiedliche Auffassungen. Feyerabend bezeichnete sie als ein „klassisches Prinzip“, und d’Espagnat ordnet sie dem physikalischen Realismus zu. Für den Physiker T. Norsen lässt sich das Prinzip der Wertdefiniertheit hingegen keiner der gängigen realistischen Positionen der Erkenntnistheorie zuordnen, weshalb er die Verwendung des Begriffes „Realismus“ in diesem Zusammenhang ablehnt: T. Norsen: Against ‘realism’. In: Foundations of Physics. Vol. 37, 2007, S. 311. (online)
A. O. Bolivar: Quantum-Classical Correspondence: Dynamical Quantization and the Classical Limit. Springer, 2004, Kap. 5. (google books)
A. J. Makowski: A brief survey of various formulations of the correspondence principle. In: Eur. J. Phys. 2006, 27, S. 1133–1139.
M. Schlosshauer, Decoherence and the Classical-to-Quantum Transition. Springer, 2007, S. 8. (google books)
N.P. Landsmann: Between Classical and Quantum. In: Handbook of the Philosophy of Science: Philosophy of Physics Part A. Elsevier, 2007, S. 417 ff und S. 515 ff. (google books)
A. J. Leggett: Realism and the physical world. In: Rep. Prog. Phys. 2008, 022001.
V. V. Nesvizhevsky, K. V. Protasov: Quantum states of neutrons in the earth’s gravitational field: state of the art, applications, perspectives. In: Trends in quantum gravity research. Nova Science, 2006, S. 65. (google books)
T. Jenke: Realization of a gravity-resonance-spectroscopy technique. In: Nature Physics. 7, 2011, S. 468. (online)
E. G. Lewars: Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Springer, 2010, S. 2. (google books)
„[…] our understanding of the nucleus itself is seemingly quite incomplete. More than 30 nuclear models – based on strikingly different assumptions – are currently employed. Each provides some insight into nuclear structure or dynamics, but none can claim to be more than a partial truth, often in conflict with the partial truths offered by other models.“ In: N. D. Cook: Models of the Atomic Nucleus. Springer, 2006, S. 5.
Eine wichtige Ausnahme ist das Tröpfchenmodell, eine empirische Formel zur Berechnung der Bindungsenergie von Atomkernen.
Klaus Bethge: Kernphysik. Springer, 1996, ISBN 3-540-61236-X.
S. G. Louie, M. L. Cohen: Conceptual Foundations of Materials: A Standard Model for Ground- and Excited-State Properties. Elsevier, 2006. (google books)
Michael A. Nielsen, Isaac L. Chuang: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge 2000, ISBN 0-521-63503-9.
S. Olmschenk, D. N. Matsukevich, P. Maunz, D. Hayes, L.-M. Duan, C. Monroe: Quantum Teleportation between Distant Matter Qubits. In: Science. 323, 486 (2009).
„In an amazingly short period the Copenhagen interpretation gained ascendancy as the correct view of quantum phenomena.“ J. T. Cushing: Quantum Mechanics: Historical Contingency and the Copenhagen Hegemony. Univ. of Chicago Press, 1994, Kap. 7.2. (google books)
„But for GRW to move beyond being regarding as a set of interesting ideas, and to be taken fairly seriously as a genuine alternative to the standard theory, it is also essential that it makes some predictions clearly at variance with regular quantum theory that may then be checked experimentally.“ A. Whitacker: The New Quantum Age: From Bell’s Theorem to Quantum Computation and Teleportation. Oxford University Press, 2011, S. 258. (google books)
E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 28. (google books)
„[…] he developed the Feynman Lectures on Physics, which have sold over a million copies and are still widely read today.“ In: Encyclopedia of Science and Technology Communication. Sage Pubn, 2010, S. 299. (google books)
E. Leane, Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 31 ff. (google books)
E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 32 ff. (google books)
F. Capra: The Tao of Physics. Shambhala Publications, 1975, S. 54, S. 140, Kap. 18.
E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 34. (google books)
E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 86 ff und S. 4. (google books)
E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 95–96. (google books)
E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 104/105. (google books)
Sal Restivo: The Social Relations of Physics, Mysticism and Mathematics. Springer, 1985, Kap. 2. (google books)
J. S. Bell: Speakable and unspeakable in quantum mechanics. 2. Auflage. Cambridge University Press, 2004, S. 170. (google books)
„While many questions about quantum mechanics are still not fully resolved, there is no point in introducing needless mystification where in fact no problem exists. Yet a great deal of recent writing about quantum mechanics has done just that.“ In: Murray Gell-Mann: The Quark and the Jaguar: Adventures in the Simple and the Complex. Owl Books, 2002, Kap. 12 Quantum Mechanics and Flapdoodle.
V. J. Stenger: Quantum Gods: Creation, Chaos, and the Search for Cosmic Consciousness. Prometheus Books, 2009.
Alexander Wendt: Quantum Mind and Social Science – unifying physical and social ontology. Cambridge University Press, Cambridge (England) 2015, ISBN 978-1-107-44292-4.
E. Emter: Literatur und Quantentheorie. Die Rezeption der modernen Physik in Schriften zur Literatur und Philosophie deutschsprachiger Autoren (1925–1970). de Gruyter, 1995, Kap. 3.2 (google books).
A. Schirrmacher, Rezension von E. Emters Buch Literatur und Quantentheorie. Die Rezeption der modernen Physik in Schriften zur Literatur und Philosophie deutschsprachiger Autoren (1925–1970). In: H-SOZ-U-KULT. 1997. Online-Artikel (abgerufen am 4. Januar 2012).
S. Farr: Sculpture show takes steps in right direction. (Memento vom 29. September 2007 im Internet Archive). Abgerufen am 4. Januar 2012.
P. Ball: Worlds Within Worlds: Quantum Objects by Julian Voss-Andreae. In: Nature. 462, 2009, S. 416. Online-Artikel (kostenpflichtig).
D. Vanderbeke: Routledge Companion to Literature amd Science. Taylor & Francis, 2010, S. 198. (google books)
G. Bar-On: Copenhagen. In: The Columbia Encyclopedia of Modern Drama. 2007, S. 288. (google books)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Vgl. Max Planck: The origin and development of the quantum theory. The Clarendon press, Oxford 1922; Armin Hermann: Von Planck bis Bohr – Die ersten fünfzehn Jahre in der Entwicklung der Quantentheorie. In: Angewandte Chemie. Band 82, Nr. 1, 1970, S. 1–7, ISSN 0044-8249; Cathryn Carson: The Origins of the Quantum Theory (PDF; 376 kB). In: Beam Line. (Stanford Linear Accelerator Center). Band 30, Nr. 2, 2000, S. 6–19.

[deBroglie1924-2] L. de Broglie: Recherches sur la théorie des Quanta. Doktorarbeit. Engl. Übersetzung (übers. A.F. Kracklauer): In: Ann. de Phys. 10. Serie, Band III, 1925.

[Heisenberg1925a-3] W. Heisenberg: Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. In: Zeitschrift für Physik. Band 33, 1925, S. 879–893, doi:10.1007/BF01328377.

[Born_Jordan1926-4] M. Born, P. Jordan: Zur Quantenmechanik. In: Zeitschrift für Physik. Band 34, 1925, S. 858–888, doi:10.1007/BF01328531.

[Born_Heisenberg_Jordan_1926-5] M. Born, W. Heisenberg, P. Jordan: Zur Quantenmechanik II. In: Zeitschrift für Physik. Band 35, 1926, S. 557–615, doi:10.1007/BF01379806.

[Schroedinger1926-6] E. Schrödinger: Quantisierung als Eigenwertproblem I. In: Annalen der Physik. Band 79, 1926, S. 361–376, doi:10.1002/andp.19263840404; E. Schrödinger: Quantisierung als Eigenwertproblem II. In: Annalen der Physik. Band 79, 1926, S. 489–527, doi:10.1002/andp.19263840602; E. Schrödinger: Quantisierung als Eigenwertproblem III. In: Annalen der Physik. Band 80, 1926, S. 437–490, doi:10.1002/andp.19263851302; E. Schrödinger: Quantisierung als Eigenwertproblem IV. In: Annalen der Physik. Band 81, 1926, S. 109–139, doi:10.1002/andp.19263861802.

[Schroedinger1926a-7] E. Schrödinger: Über das Verhältnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen. In: Annalen der Physik. Band 79, 1926, S. 734–756, doi:10.1002/andp.19263840804.

[Dirac1930-8] P. A. M. Dirac: Principles of Quantum Mechanics. 4. Auflage. Oxford University Press, 1958, ISBN 0-19-851208-2.

[vonNeumann1955-9] John von Neumann: Mathematische Grundlagen der Quantenmechanik. 2. Auflage. Springer, Berlin 1996, Engl. (autorisierte) Ausg. (übers. R. T. Beyer): Mathematical Foundations of Quantum Mechanics. Princeton Univ. Press, 1955 (dort S. 28ff.)

[Note_Kontinuierliches_Spektrum-10] Im mathematischen Sinn sind Spektralwerte eines Operators mit kontinuierlichem Spektrum, wie z. B. des Orts- oder des Impulsoperators, wegen fehlender Normierbarkeit keine eigentlichen Eigenwerte. In physikalischen Lehrbüchern gilt jedoch in der Regel die Konvention, dass auch Spektralwerte eines kontinuierlichen Spektrums als Eigenwerte bezeichnet werden. Der vorliegende Artikel schließt sich dieser Konvention an. Siehe z. B. P. Reineker u. a.: Theoretische Physik III: Quantenmechanik 1. Band 3, 2007, S. 124. [https://de.wikipedia.org/w/index.php?title=Wikipedia:Defekte_Weblinks&dwl=http://books.google.de/books?id=uhJbvVSnSLMC&lpg=PA124&hl=de&pg=PA124 Seite nicht mehr abrufbar], Suche in Webarchiven: @1@2Vorlage:Toter Link/books.google.de[http://timetravel.mementoweb.org/list/2010/http://books.google.de/books?id=uhJbvVSnSLMC&lpg=PA124&hl=de&pg=PA124 (google books)]

[Tonomura1989-11] A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, H. Ezawa: Demonstration of single-electron build-up of an interference pattern. In: American Journal of Physics. Band 57, 1989, S. 117–120, doi:10.1119/1.16104.

[EPR1935-12] A. Einstein, B. Podolsky, N. Rosen: Can quantum-mechanical description of physical reality be considered complete? In: Physical Review. Band 47, 1935, S. 777–780, doi:10.1103/PhysRev.47.777.

[Bell1964-13] J.S. Bell: On the Einstein Podolsky Rosen paradox. In: Physics. 1 #3, 1964, S. 195.

[Bell-Experimente-14] A. Aspect u. a.: Experimental Tests of Realistic Local Theories via Bell’s Theorem. In: Physical Review Letters. Band 47, 1981, S. 460, doi:10.1103/PhysRevLett.47.460; A. Aspect u. a.: Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. In: Physical Review Letters. Band 49, 1982, S. 91, doi:10.1103/PhysRevLett.49.91; A. Aspect u. a.: Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. In: Physical Review Letters. Band 49, 1982, S. 1804, doi:10.1103/PhysRevLett.49.1804; M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe, D. J. Wineland: Experimental violation of Bell’s inequalities with efficient detection. In: Nature. Band 409, 2001, S. 791–794, doi:10.1038/35057215.

[Schlosshauer2007-15] M. Schlosshauer: Decoherence and the Classical-to-Quantum Transition. Bei: books.google.de. Springer, 2007, S. 7.

[Dekohärenzzeit_Omnes-16] Omnes schätzt die Dekohärenzzeit für ein Pendel mit einer Masse von 10 g auf τ_d = 1,6 · 10⁻²⁶ s. Siehe R. Omnes: Understanding Quantum Mechanics. Princeton University Press, 1999, S. 202 und S. 75.

[Wilczek_2010-17] F. Wilczek: Quantum Field Theory. In: Compendium of Quantum Physics. Springer, 2009, S. 549 ff.

[EspagnatInstrumentalismus-18] Die Gruppierung in Instrumentalismus versus Realismus ist eine starke Vereinfachung der tatsächlich vorhandenen Vielfalt verschiedener Positionen der Wissenschaftstheorie. Ein ausführlicher Überblick über die wichtigsten erkenntnistheoretischen Positionen in der Physik findet sich zum Beispiel in Bernard d’Espagnat: Reality and the Physicist. Cambridge University Press, 1989.

[Stapp_1972-19] H. P. Stapp: The Copenhagen Interpretation. In: American Journal of Physics. Band 40, 1972, S. 1098.

[Value-Definiteness-20] In der englischsprachigen Literatur findet sich eine Vielzahl verschiedener Bezeichnungen für die Wertdefiniertheit: „value-definiteness“, „intrinsic property“, „pre-assigned initial values“ (Home und Whitaker), „precise value principle“ (Hughes), „classical principle C“ (Feyerabend), sowie Bells „beables“. Auch das in der Messtechnik verwendete Konzept des „wahren Wertes“ setzt Wertdefiniertheit voraus.

[AgainstRealism-21] Zur erkenntnistheoretischen Einordnung der Wertdefiniertheit gibt es unterschiedliche Auffassungen. Feyerabend bezeichnete sie als ein „klassisches Prinzip“, und d’Espagnat ordnet sie dem physikalischen Realismus zu. Für den Physiker T. Norsen lässt sich das Prinzip der Wertdefiniertheit hingegen keiner der gängigen realistischen Positionen der Erkenntnistheorie zuordnen, weshalb er die Verwendung des Begriffes „Realismus“ in diesem Zusammenhang ablehnt: T. Norsen: Against ‘realism’. In: Foundations of Physics. Vol. 37, 2007, S. 311. (online)

[Bolivar-22] A. O. Bolivar: Quantum-Classical Correspondence: Dynamical Quantization and the Classical Limit. Springer, 2004, Kap. 5. (google books)

[Kakowski-23] A. J. Makowski: A brief survey of various formulations of the correspondence principle. In: Eur. J. Phys. 2006, 27, S. 1133–1139.

[Schlosshauer2007b-24] M. Schlosshauer, Decoherence and the Classical-to-Quantum Transition. Springer, 2007, S. 8. (google books)

[Landsmann2007-25] N.P. Landsmann: Between Classical and Quantum. In: Handbook of the Philosophy of Science: Philosophy of Physics Part A. Elsevier, 2007, S. 417 ff und S. 515 ff. (google books)

[Leggett2008-26] A. J. Leggett: Realism and the physical world. In: Rep. Prog. Phys. 2008, 022001.

[Nesvizhevsky_2006-27] V. V. Nesvizhevsky, K. V. Protasov: Quantum states of neutrons in the earth’s gravitational field: state of the art, applications, perspectives. In: Trends in quantum gravity research. Nova Science, 2006, S. 65. (google books)

[Jenke_2011-28] T. Jenke: Realization of a gravity-resonance-spectroscopy technique. In: Nature Physics. 7, 2011, S. 468. (online)

[Lewars2010-29] E. G. Lewars: Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Springer, 2010, S. 2. (google books)

[Cook_2006-30] „[…] our understanding of the nucleus itself is seemingly quite incomplete. More than 30 nuclear models – based on strikingly different assumptions – are currently employed. Each provides some insight into nuclear structure or dynamics, but none can claim to be more than a partial truth, often in conflict with the partial truths offered by other models.“ In: N. D. Cook: Models of the Atomic Nucleus. Springer, 2006, S. 5.

[Tröpfchenmodell-31] Eine wichtige Ausnahme ist das Tröpfchenmodell, eine empirische Formel zur Berechnung der Bindungsenergie von Atomkernen.

[32] Klaus Bethge: Kernphysik. Springer, 1996, ISBN 3-540-61236-X.

[Cohen_2006-33] S. G. Louie, M. L. Cohen: Conceptual Foundations of Materials: A Standard Model for Ground- and Excited-State Properties. Elsevier, 2006. (google books)

[NielsenChuang-34] Michael A. Nielsen, Isaac L. Chuang: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge 2000, ISBN 0-521-63503-9.

[Olmschenk_2009-35] S. Olmschenk, D. N. Matsukevich, P. Maunz, D. Hayes, L.-M. Duan, C. Monroe: Quantum Teleportation between Distant Matter Qubits. In: Science. 323, 486 (2009).

[Cushing_1994-36] „In an amazingly short period the Copenhagen interpretation gained ascendancy as the correct view of quantum phenomena.“ J. T. Cushing: Quantum Mechanics: Historical Contingency and the Copenhagen Hegemony. Univ. of Chicago Press, 1994, Kap. 7.2. (google books)

[Whitacker_2012-37] „But for GRW to move beyond being regarding as a set of interesting ideas, and to be taken fairly seriously as a genuine alternative to the standard theory, it is also essential that it makes some predictions clearly at variance with regular quantum theory that may then be checked experimentally.“ A. Whitacker: The New Quantum Age: From Bell’s Theorem to Quantum Computation and Teleportation. Oxford University Press, 2011, S. 258. (google books)

[LeaneSemipopPhil-38] E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 28. (google books)

[EncCommFeynman-39] „[…] he developed the Feynman Lectures on Physics, which have sold over a million copies and are still widely read today.“ In: Encyclopedia of Science and Technology Communication. Sage Pubn, 2010, S. 299. (google books)

[LeaneHistory1970-40] E. Leane, Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 31 ff. (google books)

[LeaneBestseller-41] E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 32 ff. (google books)

[CapraOrganic-42] F. Capra: The Tao of Physics. Shambhala Publications, 1975, S. 54, S. 140, Kap. 18.

[LeaneHistory1980-43] E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 34. (google books)

[LeaneMetaphorGeneral-44] E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 86 ff und S. 4. (google books)

[LeaneZukavReception-45] E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 95–96. (google books)

[LeaneAnthropocentrism-46] E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, S. 104/105. (google books)

[RestivoPitfalls-47] Sal Restivo: The Social Relations of Physics, Mysticism and Mathematics. Springer, 1985, Kap. 2. (google books)

[BellSpeakableConsciousness-48] J. S. Bell: Speakable and unspeakable in quantum mechanics. 2. Auflage. Cambridge University Press, 2004, S. 170. (google books)

[GellMannFlapdoodle-49] „While many questions about quantum mechanics are still not fully resolved, there is no point in introducing needless mystification where in fact no problem exists. Yet a great deal of recent writing about quantum mechanics has done just that.“ In: Murray Gell-Mann: The Quark and the Jaguar: Adventures in the Simple and the Complex. Owl Books, 2002, Kap. 12 Quantum Mechanics and Flapdoodle.

[Stenger_2009-50] V. J. Stenger: Quantum Gods: Creation, Chaos, and the Search for Cosmic Consciousness. Prometheus Books, 2009.

[Wendt2015-51] Alexander Wendt: Quantum Mind and Social Science – unifying physical and social ontology. Cambridge University Press, Cambridge (England) 2015, ISBN 978-1-107-44292-4.

[EmterRezeptionLiteratur-52] E. Emter: Literatur und Quantentheorie. Die Rezeption der modernen Physik in Schriften zur Literatur und Philosophie deutschsprachiger Autoren (1925–1970). de Gruyter, 1995, Kap. 3.2 (google books).

[SchirrmacherRezensionEmter-53] A. Schirrmacher, Rezension von E. Emters Buch Literatur und Quantentheorie. Die Rezeption der modernen Physik in Schriften zur Literatur und Philosophie deutschsprachiger Autoren (1925–1970). In: H-SOZ-U-KULT. 1997. Online-Artikel (abgerufen am 4. Januar 2012).

[FarrOpinionExhibition-54] S. Farr: Sculpture show takes steps in right direction. (Memento vom 29. September 2007 im Internet Archive). Abgerufen am 4. Januar 2012.

[BallOpinion-55] P. Ball: Worlds Within Worlds: Quantum Objects by Julian Voss-Andreae. In: Nature. 462, 2009, S. 416. Online-Artikel (kostenpflichtig).

[Vanderbeke_2010-56] D. Vanderbeke: Routledge Companion to Literature amd Science. Taylor & Francis, 2010, S. 198. (google books)

[Baron2007-57] G. Bar-On: Copenhagen. In: The Columbia Encyclopedia of Modern Drama. 2007, S. 288. (google books)