Schrödingers Katze

Bei Schrödingers Katze handelt es sich um ein Gedankenexperiment aus der Physik, das 1935 von Erwin Schrödinger beschrieben wurde,[1] um einen wesentlichen Schwachpunkt der Kopenhagener Interpretation der Quantenmechanik in Bezug auf die physikalische Realität aufzuzeigen.[2] Es problematisiert die Kopenhagener Deutung der Quantenphysik (die direkte Übertragung quantenmechanischer Begriffe auf die makroskopische Welt) in Form eines Paradoxons. Das Paradoxon besteht erstens darin, dass in dem Gedankenexperiment eine Katze in einen Zustand gebracht wird, in dem sie nach der Kopenhagener Deutung gleichzeitig „lebendig“ und „tot“ ist. Zweitens würde, ebenfalls nach der Kopenhagener Deutung, dieser unbestimmte Zustand so lange bestehen bleiben, bis er von einem Beobachter untersucht wird. Dann erst würde die Katze auf einen der Zustände „lebendig“ oder „tot“ festgelegt. Beides widerspricht der Anschauung und Alltagserfahrung mit makroskopischen Dingen.

Schrödingers Katze: In einer Kiste befinden sich eine Katze, ein radioaktives Präparat, ein Detektor für die beim Zerfall erzeugte Strahlung und eine tödliche Menge Gift, die bei Ansprechen des Detektors freigesetzt wird.

Das Gedankenexperiment beruht darauf, dass immer, wenn ein System gemäß der Kopenhagener Deutung zwei verschiedene Zustände einnehmen kann, auch die kohärente Überlagerung der beiden Zustände einen möglichen Zustand darstellt. Erst wenn eine Beobachtung oder Messung durchgeführt wird, mit der man zwischen den beiden ursprünglichen Zuständen unterscheiden kann, nimmt das System einen von beiden an. In Anlehnung an das Gedankenexperiment mit einem makroskopischen System spricht man auch bei einem quantenmechanischen System von einem Katzenzustand, wenn man die beiden Zustände in einer solchen Überlagerung durch eine Messung unterscheiden kann.

Hintergrund

Die Quantenmechanik beschreibt den Zustand und die Entwicklung eines physikalischen Systems mittels eines Zustandsvektors. Im Allgemeinen ist dieser eine gewichtete Summe der Eigenzustände, in denen eine durch Messung bestimmbare Größe einen jeweils wohldefinierten Messwert hat. Jeden einzelnen dieser Messwerte könnte man bei einer Messung dieser Größe erhalten; d. h., bei einem solchen quantenmechanischen Zustand ist das Ergebnis einer einzelnen Messung nicht eindeutig bestimmt. So ergeben sich in wiederholten Experimenten an Systemen mit demselben Zustandsvektor die Messergebnisse derselben physikalischen Größe zufällig mit verschiedenen Werten, wobei deren Wahrscheinlichkeitsverteilung gemäß der Quantenmechanik aus dem Zustandsvektor zu ermitteln ist. Unmittelbar nach der Messung liegt das System sicher in dem Eigenzustand vor, zu dem das gerade erhaltene Messergebnis gehört. Dieser Vorgang der Zustandsreduktion wird durch ein eigenes Postulat in die Quantenmechanik (in ihrer Kopenhagener Deutung) eingeführt. Er bezeichnet das quantenmechanische Messproblem und ist auch heute noch nicht befriedigend verstanden.

Zum Zeitpunkt von Schrödingers Veröffentlichung waren solche Quanteneffekte nur im mikroskopischen Bereich bekannt, die Anwendbarkeit der Quantenmechanik auf komplexe makroskopische Prozesse, z. B. auf den Messprozess selbst, war jedoch unklar. Schrödingers Gedankenexperiment dient der Illustration der konzeptionellen Schwierigkeiten, die mit der Anwendung des Begriffs des Quantenzustands auf makroskopische Systeme verbunden sind. Heute ist die Quantentheorie makroskopischer Systeme ein umfangreich untersuchtes Teilgebiet der Physik.

Das Gedankenexperiment

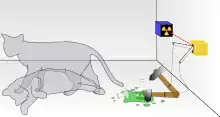
Ohne Wechselwirkung mit der Außenwelt befindet sich Schrödingers Katze, quantenmechanisch beschrieben, in einem überlagerten Zustand. Sie ist sowohl lebendig als auch tot.

In dem Gedankenexperiment befinden sich in einem geschlossenen Kasten eine Katze und ein instabiler Atomkern, der innerhalb einer bestimmten Zeitspanne mit einer gewissen Wahrscheinlichkeit zerfällt. Der Zerfall löst mittels eines Geigerzählers die Freisetzung von Giftgas aus, welches die Katze tötet.

Schrödinger argumentiert nun, dass – wenn die Quantenphysik auch auf makroskopische Systeme anwendbar wäre – nicht nur der Atomkern, sondern auch die Katze in einen Zustand der Überlagerung geraten müsste. Diese Überlagerung würde erst beendet, wenn jemand den Kasten öffnet und den Zustand der Katze überprüft. Dies stellt eine Messung dar, die entweder das Ergebnis „tot“ oder „lebendig“ feststellt. Bis dahin wäre die Katze also lebendig und gleichzeitig tot. Diese Schlussfolgerung erscheint paradox.

Schrödinger selbst formuliert das 1935 in seinem Aufsatz Die gegenwärtige Situation in der Quantenmechanik. § 5. Sind die Variablen wirklich verwaschen?

„Man kann auch ganz burleske Fälle konstruieren. Eine Katze wird in eine Stahlkammer gesperrt, zusammen mit folgender Höllenmaschine (die man gegen den direkten Zugriff der Katze sichern muß): in einem Geigerschen Zählrohr befindet sich eine winzige Menge radioaktiver Substanz, so wenig, daß im Laufe einer Stunde vielleicht eines von den Atomen zerfällt, ebenso wahrscheinlich aber auch keines; geschieht es, so spricht das Zählrohr an und betätigt über ein Relais ein Hämmerchen, das ein Kölbchen mit Blausäure zertrümmert. Hat man dieses ganze System eine Stunde lang sich selbst überlassen, so wird man sich sagen, daß die Katze noch lebt, wenn inzwischen kein Atom zerfallen ist. Der erste Atomzerfall würde sie vergiftet haben. Die Psi-Funktion des ganzen Systems würde das so zum Ausdruck bringen, daß in ihr die lebende und die tote Katze (s.v.v.) zu gleichen Teilen gemischt oder verschmiert sind. Das Typische an solchen Fällen ist, daß eine ursprünglich auf den Atombereich beschränkte Unbestimmtheit sich in grobsinnliche Unbestimmtheit umsetzt, die sich dann durch direkte Beobachtung entscheiden läßt. Das hindert uns, in so naiver Weise ein „verwaschenes Modell“ als Abbild der Wirklichkeit gelten zu lassen. An sich enthielte es nichts Unklares oder Widerspruchsvolles. Es ist ein Unterschied zwischen einer verwackelten oder unscharf eingestellten Photographie und einer Aufnahme von Wolken und Nebelschwaden.“

– Erwin Schrödinger[3]

Realisierbarkeit

Der Dekohärenz-Effekt

Gemäß der Dekohärenztheorie tritt die von Schrödinger beschriebene Situation in der Realität nicht ein, da es bei makroskopischen Systemen immer zu einer Unterdrückung der Kohärenzeigenschaften des quantenmechanischen Zustands kommt. Der gegenseitige Austausch weniger Photonen der Wärmestrahlung zwischen der Umgebung, der Wand des Kastens und der Katze würde bereits aufgrund innerer thermischer Wechselwirkungen in kürzester Zeit zur vollständigen Dekohärenz der makroskopischen Zustände führen.[4] Dadurch findet nach extrem kurzer Zeit ein effektiver Kollaps der Wellenfunktion im Sinne der Kopenhagener Deutung statt. Die Dekohärenztheorie nimmt damit ernst, dass die Vergiftungsapparatur und die Katze makroskopische Objekte sind, die auf irreversible Weise nicht erst auf den „Messprozess“ durch das Öffnen des Kastens reagieren, sondern direkt auf die ersten unmittelbaren Auswirkungen des atomaren Zerfalls.

Reale Experimente mit kohärenten Systemen

Trotz des Einflusses der Dekohärenz kann das Gedankenexperiment mit realen Experimenten überprüft werden. Dabei muss die Wechselwirkung mit der Umgebung vollständig abgeschirmt werden. Eine solche Isolation erreicht man sehr gut bei Photonen als Untersuchungsobjekten, da Photonen selbst nicht von anderen Photonen beeinflusst werden und somit von der Dekohärenz wenig betroffen sind. Bei fester Materie ist eine Isolation sehr viel schwieriger und gelang bisher nur bei sehr kleinen Objekten. Zum Beispiel konnte bei einem Experiment mit Fullerenen nachgewiesen werden, dass ein solches aus 60 Kohlenstoffatomen bestehendes einzelnes Molekül gleichzeitig unterschiedliche Wege durch verschiedene Spalte eines Hindernisses nehmen kann.[5] Die experimentellen Bedingungen, die hier ausreichend vor Dekohärenz schützten, waren ein hohes Vakuum, Dunkelheit und eine sehr kurze Zeitspanne zwischen Erzeugung und Überprüfung der Überlagerung. Bei Quantencomputern versucht man die Dekohärenz von Elektronen zu unterdrücken, indem man mithilfe sehr tiefer Temperaturen und Supraleitung deren Freiheitsgrade einschränkt. Die überlagerten Zustände nutzt man dann zur Durchführung von parallelen Rechenoperationen.

Diese Experimente bestätigen die Annahme, dass die Gesetze der Quantenmechanik auch für makroskopische Systeme gelten.

Interpretationen

Unabhängig von der Dekohärenztheorie werden die Abläufe im hypothetischen perfekt verschlossenen Kasten in den verschiedenen Schulen und Deutungen der Quantenmechanik sehr unterschiedlich interpretiert.

Kopenhagener Deutung

Kopenhagener Deutung:
Beim radioaktiven Zerfall erfolgt eine Verzweigung des Zustands. Nach einem Zufallsprinzip kollabiert jedoch einer der beiden Zweige sofort wieder, nachdem die Kohärenz zwischen den Zuständen z. B. aufgrund einer Messung weit genug abgeklungen ist.

In der Kopenhagener Deutung der Quantenmechanik erfolgt im Moment der Messung ein Kollaps der Wellenfunktion des gemessenen Systems. Beim Öffnen des Raums und Beobachtung seines Inneren (Messung) springt der Atomkern, der sich zuvor im Zustand der Überlagerung befand, in einen der zu diesem Messapparat gehörenden Eigenzustände. Erst bei der Messung (hier durch einen äußeren Beobachter) entscheidet sich also, ob die Katze tot oder lebendig ist. Vor der Messung kann über den Zustand der Katze lediglich eine Wahrscheinlichkeitsaussage getroffen werden. Der Messvorgang selbst wird dabei wie in der klassischen Physik beschrieben.

Spätere Interpreten der Kopenhagener Deutung wie Carl Friedrich von Weizsäcker erkennen an, dass das makroskopische Ansprechen der „Höllenmaschine“ die Entstehung eines irreversiblen „Dokuments“ über den erfolgten Atomzerfall zur Folge hat, mit anderen Worten, eine Messung hat stattgefunden. Die Wellenfunktion kollabiert ohne weiteres menschliches Zutun; die Katze ist entweder lebendig oder tot.

Mit den 50-Prozent-Wahrscheinlichkeiten für die beiden möglichen Eigenzustände beschreibt die Wellenfunktion vor der Messung gewissermaßen nicht wirklich das System, sondern das unvollständige Wissen über das System. Fröhner[6] hat nachgewiesen, dass die quantenmechanischen Wahrscheinlichkeiten widerspruchsfrei als Bayessche Wahrscheinlichkeiten aufgefasst werden können. Diese ändern sich, indem die Messung den Informationsstand des Beobachters verändert. Dazu wird keine Zeit benötigt; was kollabiert („zusammenbricht“), ist nichts Physikalisches, sondern nur der Informationsmangel des Beobachters. Ganz entsprechend haben sich hierzu Heisenberg 1960 in einer brieflichen Diskussion (siehe Zitat bei Fröhner) und Styer[7] geäußert.

Viele-Welten-Interpretation

Viele-Welten-Interpretation:
Hier verzweigt sich beim Zerfall das gesamte Universum. Gemäß der Theorie bleiben beide Zweige als gleichberechtigte Realitäten erhalten und entwickeln sich von nun an unabhängig voneinander weiter.

Die Viele-Welten-Interpretation geht auf den Physiker Hugh Everett zurück. Sie ist keine neue oder zusätzliche Theorie, sondern eine alternative Interpretation der Quantenmechanik. Die Viele-Welten-Interpretation spricht allen möglichen Zuständen (also hier „Katze tot“ und „Katze lebendig“) gleichermaßen physikalische Realität zu. Es gibt dann tatsächlich ein Universum, in dem das Atom zerfallen ist, und eines, in dem das Atom noch nicht zerfallen ist. Im ersten Universum öffnen wir den Kasten und finden die Katze tot, im zweiten Universum ist die Katze lebendig.

Unsere Erinnerungen und das, was wir als Realität wahrnehmen, entsprechen dann nur einer von unzähligen möglichen (und gleichermaßen realisierten) Geschichten des Universums.

Ensembletheorie

Vertreter der Ensembletheorie würden das Gedankenexperiment auf eine Gesamtheit von Systemen beziehen (also mehrere Kästen mit Katzen): Nach einem bestimmten Zeitintervall sind dann die Hälfte aller Katzen tot und die andere Hälfte lebendig. Hier greift das empirische Gesetz der großen Zahlen, d. h. je öfter man dieses Experiment durchführt, desto sicherer ist es, dass die relative Häufigkeit sich der theoretischen Wahrscheinlichkeit annähert.

Bohmsche Mechanik

Bohmsche Mechanik:
Auch diese Theorie berücksichtigt beide Zweige. Jedoch markiert ein deterministischer Mechanismus einen der Zweige als Realität, während alle anderen Zweige als sogenannte Pilotwellen nur die möglichen Quanteninterferenzen auskundschaften.

Die bohmsche Mechanik ist eine alternative Formulierung der Quantenmechanik. Sie fügt der Quantenmechanik eine zusätzliche Bewegungsgleichung hinzu, die den Ort sämtlicher Teilchen zu jeder Zeit festlegt. Die Beschreibung wird dadurch deterministisch. Die Bohmsche Mechanik legt also zu jeder Zeit genau fest, ob die Katze tot oder lebendig ist. Man kann den Anfangszustand des Systems jedoch nicht genau messen, ohne das System zu stören. Daher kann man für das Ergebnis nur Wahrscheinlichkeiten für den Fall einer toten oder einer lebendigen Katze angeben.

Katzenzustand

Allgemeine Überlegung

In einem allgemeineren Sinn wird in der Quantenmechanik eine Überlagerung zweier kohärenter Zustände, die hinreichend unterschiedlich und klassischen Zuständen ähnlich sind, als Katzenzustand bezeichnet. Um einen solchen Zustand zu präparieren, ist es notwendig, das System von der Umgebung abzuschirmen. Typische experimentelle Realisierungen sind Spin-Ausrichtungen oder Teilchenpositionen. Erste mesoskopische Katzenzustände wurden mit Elektronenstrahlen und Strahlteilern erzeugt, bei denen eine Überlagerung der Zustände bestand, dass ein Elektron in dem einen oder dem anderen Teilstrahl ist. Mitte der 1990er Jahre ist es gelungen, einen mesoskopischen Katzenzustand für ein einzelnes Atom bezüglich seiner Position zu erzeugen.[8] Darauf aufbauend wurden größere Systeme aus einzelnen Atomen erzeugt, bei denen zum Beispiel mit sechs Atomen die Überlagerung der beiden Zustände, bei denen alle Atome Spin-Up. oder alle Atome Spin-Down. untersucht wurden.[9] Diese Formulierung wurde von David Bohm vorgeschlagen, der den Spin als Observable 1935 in einem Gedankenexperiment zum Einstein-Podolsky-Rosen-Paradoxon formulierte.[10]

Katzenzustand beim Quantencomputer

Konkreter Spezialfall ist der Katzenzustand als Zustand in einem Register eines Quantencomputers, der aus der Überlagerung der beiden Zustände besteht, bei denen alle Qubits |0⟩ bzw. alle |1⟩ sind. In der Bra-Ket-Notation wird er als proportional zu |00…0⟩ +|11…1⟩ geschrieben.

Katzenzustand in der Quantenoptik

Wignerfunktion eines quantenoptischen Katzenzustandes mit α=2,5. Neben den beiden Hügeln für

|\alpha \rangle

und

|{-\alpha }\rangle

enthält der Katzenzustand eine Interferenzstruktur in der Mitte.

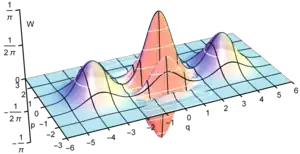
In der Quantenoptik wird ein Katzenzustand als kohärente Überlagerung von zwei bestimmten kohärenten Zuständen mit entgegengesetzten Phasen definiert:

|\mathrm {cat} _{e}\rangle \propto |\alpha \rangle +|{-}\alpha \rangle

,

wobei

|\alpha \rangle =e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over {\sqrt {n!}}}|n\rangle

,

und

|{-}\alpha \rangle =e^{-{|{-}\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{({-}\alpha )^{n} \over {\sqrt {n!}}}|n\rangle

als kohärente Zustände in der Zahlenbasis (Fock-Zustand) definiert sind. Wenn man die beiden Zustände addiert, enthält der Katzenzustand nur gerade Fock-Zustands-Terme:

|\mathrm {cat} _{e}\rangle \propto 2e^{-{|\alpha |^{2} \over 2}}\left({\alpha ^{0} \over {\sqrt {0!}}}|0\rangle +{\alpha ^{2} \over {\sqrt {2!}}}|2\rangle +{\alpha ^{4} \over {\sqrt {4!}}}|4\rangle +\dots \right)

.

Als Ergebnis dieser Eigenschaft wird der obige Zustand oft als gerader Katzenzustand bezeichnet. Alternativ kann man einen ungeraden Katzenzustand mit

|\mathrm {cat} _{o}\rangle \propto |\alpha \rangle -|{-}\alpha \rangle

definieren, der nur ungerade Fock-Zustände enthält

|\mathrm {cat} _{o}\rangle \propto 2e^{-{|\alpha |^{2} \over 2}}\left({\alpha ^{1} \over {\sqrt {1!}}}|1\rangle +{\alpha ^{3} \over {\sqrt {3!}}}|3\rangle +{\alpha ^{5} \over {\sqrt {5!}}}|5\rangle +\dots \right)

.

Siehe auch

Wigners Freund stellt eine Erweiterung dieses Gedankenexperiments dar
Der sogenannte Quantenselbstmord zieht andere Schlüsse aus einem vergleichbaren Experiment

Literatur

Karl von Meyenn (Hrsg.): Eine Entdeckung von ganz außerordentlicher Tragweite: Schrödingers Briefwechsel zur Wellenmechanik und zum Katzenparadoxon. Springer, Berlin/Heidelberg 2011, ISBN 978-3-642-04334-5.
John Gribbin: Auf der Suche nach Schrödingers Katze: Quantenphysik und Wirklichkeit. Aus dem Englischen von Friedrich Griese. Piper, München/Zürich 2004, ISBN 3-492-24030-5.

Weblinks

Wikiquote: Erwin Schrödinger – Zitate

Commons: Schrödingers Katze – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Schrödingers Katze – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Ist Schrödingers Katze tot? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 15. Sep. 2004.
Schrödingers Katze kann aufatmen – und sei es auch nur ein letztes Mal. auf: quanten.de
Wie Erwin Schrödingers Katze zu Weltruhm kam. In: Die Welt, 12. August 2013
Reincarnation can save Schrödinger's cat. In: Nature. Bd. 454, 2. Juli 2008, S. 8–9.
Quantum superposition of distinct macroscopic states. In: Nature. Bd. 406, 6. Juli 2000, S. 43–46. (PDF) doi:10.1038/35017505 – Versuch einer experimentellen Realisierung des Gedankenexperiments mit makroskopischen elektrischen Strömen, die angeblich gleichzeitig in zwei Richtungen fließen.
Zvi Schreiber: The nine lives of Schrödingers Cat. Diplomarbeit. Imperial College 1995, Schrödingers Katze in verschiedenen Interpretationen der Quantenmechanik, Arxiv

Einzelnachweise

Die gegenwärtige Situation in der Quantenmechanik. In: Naturwissenschaften. (Organ der Gesellschaft Deutscher Naturforscher und Ärzte – Berlin, Springer) – Bd. 23, 1935 doi:10.1007/BF01491891 (Teil 1), doi:10.1007/BF01491914 (Teil 2), doi:10.1007/BF01491987 (Teil 3). Die Katze taucht im ersten und im zweiten Teil, S. 812 bzw. S. 827, auf.
Arroyo Camejo, Silvia.: Skurrile Quantenwelt. 1. Auflage. Springer, Berlin 2006, ISBN 978-3-540-29720-8.
Erwin Schrödinger: Naturwissenschaften. 48, 807; 49, 823; 50, 844, November 1935.
H. P. J. Haken, H. H. C. Wolf: The Physics of Atoms and Quanta: Introduction to Experiments and Theory (Advanced Texts in Physics). 6. Auflage. Springer, 2000, S. 406. (google books)
Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand Van Der Zouw, Anton Zeilinger: Wave–particle duality of C₆₀. In: Nature. 401, Nr. 6754, 1999, S. 680–2. bibcode:1999Natur.401..680A. doi:10.1038/44348. PMID 18494170.
F. H. Fröhner: Missing Link between Probability Theory and Quantum Mechanics: the Riesz-Fejér Theorem. Zeitschrift für Naturforschung 53a (1998), S. 637–654
Daniel F. Styer: The Strange World of Quantum Mechanics. Cambridge University Press, 2000, ISBN 0-521-66780-1, S. 115
C. Monroe, D. M. Meekhof, B. E. King, D. J. Wineland: A “Schrödinger cat” superposition state of an atom. In: Science. 272(5265), 1996, S. 1131–1136.
D. Leibfried, E. Knill, S. Seidelin, J. Britton, R. B. Blakestad, J. Chiaverini, D. Hume, W. M. Itano, J. D. Jost, C. Langer, R. Ozeri, R. Reichle, D. J. Wineland: Creation of a six atom 'Schrödinger_cat' state. In: Nature. 1. Dezember 2005, S. 639–642
Amir D. Aczel: Entanglement: the unlikely story of how scientists, mathematicians, and philosophers proved Einstein’s spookiest theory. Penguin, 2001, ISBN 0-452-28457-0.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Die gegenwärtige Situation in der Quantenmechanik. In: Naturwissenschaften. (Organ der Gesellschaft Deutscher Naturforscher und Ärzte – Berlin, Springer) – Bd. 23, 1935 doi:10.1007/BF01491891 (Teil 1), doi:10.1007/BF01491914 (Teil 2), doi:10.1007/BF01491987 (Teil 3). Die Katze taucht im ersten und im zweiten Teil, S. 812 bzw. S. 827, auf.

[2] Arroyo Camejo, Silvia.: Skurrile Quantenwelt. 1. Auflage. Springer, Berlin 2006, ISBN 978-3-540-29720-8.

[3] Erwin Schrödinger: Naturwissenschaften. 48, 807; 49, 823; 50, 844, November 1935.

[Haken2000-4] H. P. J. Haken, H. H. C. Wolf: The Physics of Atoms and Quanta: Introduction to Experiments and Theory (Advanced Texts in Physics). 6. Auflage. Springer, 2000, S. 406. (google books)

[5] Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand Van Der Zouw, Anton Zeilinger: Wave–particle duality of C₆₀. In: Nature. 401, Nr. 6754, 1999, S. 680–2. bibcode:1999Natur.401..680A. doi:10.1038/44348. PMID 18494170.

[6] F. H. Fröhner: Missing Link between Probability Theory and Quantum Mechanics: the Riesz-Fejér Theorem. Zeitschrift für Naturforschung 53a (1998), S. 637–654

[7] Daniel F. Styer: The Strange World of Quantum Mechanics. Cambridge University Press, 2000, ISBN 0-521-66780-1, S. 115

[1atcat-8] C. Monroe, D. M. Meekhof, B. E. King, D. J. Wineland: A “Schrödinger cat” superposition state of an atom. In: Science. 272(5265), 1996, S. 1131–1136.

[fn3-9] D. Leibfried, E. Knill, S. Seidelin, J. Britton, R. B. Blakestad, J. Chiaverini, D. Hume, W. M. Itano, J. D. Jost, C. Langer, R. Ozeri, R. Reichle, D. J. Wineland: Creation of a six atom 'Schrödinger_cat' state. In: Nature. 1. Dezember 2005, S. 639–642

[10] Amir D. Aczel: Entanglement: the unlikely story of how scientists, mathematicians, and philosophers proved Einstein’s spookiest theory. Penguin, 2001, ISBN 0-452-28457-0.