Energie
Energie ist eine fundamentale physikalische Größe, die in allen Teilgebieten der Physik sowie in der Technik, Chemie, Biologie und der Wirtschaft eine zentrale Rolle spielt. Ihre SI-Einheit ist das Joule. Die praktische Bedeutung der Energie liegt oft darin, dass ein physikalisches System in dem Maß Wärme abgeben, Arbeit leisten oder Strahlung aussenden kann, in dem seine Energie sich verringert. In einem gegenüber der Umgebung abgeschlossenen System ändert sich die Gesamtenergie nicht (Energieerhaltungssatz). Die Bedeutung der Energie in der theoretischen Physik liegt unter anderem darin, dass der Energieerhaltungssatz, ursprünglich eine Erfahrungstatsache, schon daraus gefolgert werden kann, dass die grundlegenden physikalischen Naturgesetze zeitlich unveränderlich sind.
| Physikalische Größe | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name | Energie | |||||||||
| Formelzeichen | ||||||||||
| ||||||||||
Energie gibt es in verschiedenen Energieformen, die ineinander umgewandelt werden können. Beispiele von Energieformen sind potentielle, kinetische, elektrische, chemische und Wärmeenergie (thermische Energie). Beispiele für solche Umwandlungen von Energie sind, dass ein Mensch ein Paket hochhebt oder ein Fahrrad beschleunigt, dass eine Batterie geladen wird, ein Lebewesen Stoffwechsel betreibt oder eine Heizung Wärme abgibt.
In vielen Fällen lässt sich mittels einer Formel die Energie eines Systems aus der momentanen Größe der Parameter und Variablen des Systems berechnen. Allein die mathematische Struktur dieser Formel bestimmt nach den hamiltonschen Bewegungsgleichungen, der Schrödingergleichung oder der Dirac-Gleichung die ganze zeitliche Entwicklung des Systems in allen Einzelheiten.
Gemäß der Relativitätstheorie sind Ruheenergie und Masse durch die Äquivalenz von Masse und Energie () verknüpft.
Geschichte des Begriffs
Das Wort Energie geht auf altgriechisch ἐνέργεια, energeia zurück, das in der griechischen Antike eine rein philosophische Bedeutung im Sinne von „lebendiger Wirklichkeit und Wirksamkeit“ hatte[1] (siehe auch „Akt und Potenz“). Als naturwissenschaftlicher Begriff wurde das Wort selbst erst 1807 von dem Physiker Thomas Young in die Mechanik eingeführt. Die neue Größe Energie sollte die Stärke ganz bestimmter Wirkungen angeben, die ein bewegter Körper durch seine Bewegung hervorrufen kann, und die sich nicht allein durch seinen Impuls („Masse mal Geschwindigkeit“) bestimmen lassen. Über den Impuls war seit den Untersuchungen des Stoßes zweier Körper durch Christiaan Huygens, Christopher Wren und John Wallis um das Jahr 1668 herum bekannt, dass er bei elastischen wie bei unelastischen Körpern erhalten bleibt, also das richtige Maß für die verursachten Veränderungen und damit für die unzerstörbare „Größe der Bewegung“ ist. Bei anderen Vorgängen aber verursachen Körper verschiedener Masse, auch wenn sie gleichen Impuls haben, verschieden große Wirkungen. Dazu gehört etwa die Höhe, die ein Körper in Aufwärtsbewegung erreicht, oder die Tiefe des Lochs, das er beim Aufprall in eine weiche Masse schlägt. Hierbei nimmt die Wirkung nicht mit der Geschwindigkeit proportional zu, wie der Impuls, sondern mit dem Quadrat der Geschwindigkeit. Daher bezeichnete Gottfried Wilhelm Leibniz 1686[2] die Größe als das wahre Maß für die Größe der Bewegung und nannte sie vis viva („lebendige Kraft“). Dieser Name folgte dem damaligen Sprachgebrauch, in dem ein Körper nur durch die ihm innewohnenden Kräfte Wirkungen verursachen konnte. Der Name lebendige Kraft hat aber durch „Verwechslung mit dem Newtonschen Kraftbegriff eine unheilvolle Verwirrung der Ideen und eine zahllose Schar von Missverständnissen hervorgerufen“ (so Max Planck 1887 in seiner preisgekrönten Darstellung der Geschichte des Energieerhaltungssatzes.[3]) Leibniz argumentierte wie folgt:
Ein Gewicht von auf die Höhe zu heben erfordert genauso viel Arbeit wie ein Gewicht auf die Höhe zu heben (Hebelgesetz). Nach Galileo Galilei ist im freien Fall , also ist die Endgeschwindigkeit im ersten Fall doppelt so hoch wie im zweiten Fall. Setzt man für die innewohnende (lebendige) Kraft an , mit der man diese Arbeit (latente Form der lebendigen Kraft) messen will, so ist bei Erhaltung der lebendigen Kraft , das heißt und nicht wie die Anhänger von Descartes meinten.[4]
Den korrekten Vorfaktor in der kinetischen Energie leitete schon Daniel Bernoulli 1726 ab.[5] Bei ihm wie bei anderen analytischen Mechanikern des 18. Jahrhunderts wie Leonhard Euler (z. B. Behandlung der elastischen Deformation), Joseph Louis Lagrange (Mécanique Analytique 1788) finden sich auch Vorläufer des Konzepts der potentiellen Energie (der Term Potentialfunktion stammt von George Green 1828 und unabhängig wurde sie von Carl Friedrich Gauß 1840 eingeführt, war aber als Potential schon Lagrange und Laplace bekannt). Das Konzept war schon Leibniz (in seiner Ableitung von ) und Johann I Bernoulli bekannt, der als erster 1735 das Prinzip der Erhaltung der lebendigen Kräfte formulierte (die Vorstellung hatte aber auch Leibniz zum Beispiel im 5. Brief an Samuel Clarke), das insbesondere vom Leibniz-Schüler Christian Wolff verbreitet wurde. Von potentieller Energie sprach man damals als der latenten Form der lebendigen Kraft, die sich zum Beispiel beim inelastischen Stoß auf kleinere Teilchen des Körpers verteile.[6]
Um die genannten Wirkungen der Bewegung des Körpers vorhersagen zu können, definierte Young die Größe Energie als die Fähigkeit des Körpers, gegen eine widerstehende Kraft eine gewisse Strecke zurückzulegen.[7] Er bemerkte auch, dass Arbeit, die in Form von Hubarbeit an einem Körper geleistet wird, sich später quantitativ in dessen Energie wiederfindet, kam aber noch nicht auf den Begriff der Umwandlung verschiedener Energieformen und behielt auch die Formel von Leibniz bei und war im Großen und Ganzen noch ein Anhänger des Cartesianischen Standpunkts der Kräfte.[8]
Im 18. Jahrhundert war man in der Mechanik und Physik an der Energie nicht sonderlich interessiert, wichtige Forscher wie Euler[9] sahen den Streit um die Vis Viva, das wahre Kraftmaß, als Angelegenheit der Philosophen und man befasste sich mit der Lösung der Bewegungsgleichungen vor allem in der Himmelsmechanik. Der Energiebegriff im heutigen Sinn fand seinen Ursprung nicht bei den analytischen Mechanikern des 18. Jahrhunderts, sondern bei den angewandten Mathematikern der französischen Schule,[10] darunter Lazare Carnot, der schrieb, dass die lebendige Kraft sich entweder als oder Kraft mal Weg (als latente lebendige Kraft) manifestieren kann.[11] Eine quantitative Definition der Arbeit („Kraft mal Weg“, bzw. ) wurde auch 1829 gleichzeitig von Coriolis und Poncelet gegeben, offenbar unabhängig voneinander[12] und auch von Young. Coriolis fand dabei auch den richtigen Ausdruck für die Bewegungsenergie, die 1853 von Rankine erstmals kinetische Energie genannt wurde.[3]
Im Zusammenhang mit der Dampfmaschine entwickelte sich die Vorstellung, dass Wärmeenergie bei vielen Prozessen die Ursache für eine bewegende Energie, oder mechanische Arbeit ist. Ausgangspunkt war, dass Wasser durch Hitze in den gasförmigen Zustand überführt wird und die Gasausdehnung genutzt wird, um einen Kolben in einem Zylinder zu bewegen. Durch die Kraftbewegung des Kolbens vermindert sich die gespeicherte Wärmeenergie des Wasserdampfes. Demonstriert wurde der Zusammenhang von mechanischer Energie und Wärme in berühmt gewordenen Experimenten von Benjamin Thompson (Graf Rumford, München 1796, 1798) und Humphry Davy (1799).
Der Physiker Nicolas Carnot erkannte, dass beim Verrichten von mechanischer Arbeit eine Volumenänderung des Dampfs nötig ist. Außerdem fand er heraus, dass die Abkühlung des heißen Wassers in der Dampfmaschine nicht nur durch Wärmeleitung erfolgt. Diese Erkenntnisse veröffentlichte Carnot 1824 in einer viel beachteten Schrift über das Funktionsprinzip der Dampfmaschine. Émile Clapeyron brachte 1834 Carnots Erkenntnisse in eine mathematische Form und entwickelte die noch heute verwendete graphische Darstellung des Carnot-Kreisprozesses.
1841 veröffentlichte der deutsche Arzt Julius Robert Mayer seine Idee, dass Energie weder erschaffen noch vernichtet, sondern nur umgewandelt werden kann. Er schrieb an einen Freund: „Meine Behauptung ist …: Fallkraft, Bewegung, Wärme, Licht, Elektrizität und chemische Differenz der Ponderabilien sind ein und dasselbe Objekt in verschiedenen Erscheinungsformen.[13]“ Die Wärmemenge, die bei einer Dampfmaschine verloren gegangen ist, entspräche genau der mechanischen Arbeit, die die Maschine leistet. Dies ist heute bekannt als „Energieerhaltung“, oder auch „Erster Hauptsatz der Thermodynamik“.
Der Physiker Rudolf Clausius verbesserte im Jahr 1854 die Vorstellungen über die Energieumwandlung. Er zeigte, dass nur ein Teil der Wärmeenergie in mechanische Arbeit umgewandelt werden kann. Ein Körper, bei dem die Temperatur konstant bleibt, kann keine mechanische Arbeit leisten. Clausius entwickelte den zweiten Hauptsatz der Thermodynamik und führte den Begriff der Entropie ein. Nach dem zweiten Hauptsatz ist es unmöglich, dass Wärme eigenständig von einem kälteren auf einen wärmeren Körper übergeht.
Hermann von Helmholtz formulierte im Jahr 1847 das Prinzip „über die Erhaltung der Kraft“ und der Unmöglichkeit eines Perpetuum mobiles (perpetuus, lat. ewig; mobilis, lat.: beweglich) 1. Art. Viele Erfinder wollten damals noch Maschinen herstellen, die mehr Energie erzeugten als hineingesteckt wurde. Helmholtz fand seine Erkenntnisse durch Arbeiten mit elektrischer Energie aus galvanischen Elementen, insbesondere einer Zink/Brom-Zelle. In späteren Jahren verknüpfte er die Entropie und die Wärmeentwicklung einer chemischen Umwandlung zur freien Energie. Sowohl Mayer als auch Helmholtz hatten aber in den 1840er Jahren Schwierigkeiten, ihre Erkenntnisse zu veröffentlichen, da beide zunächst als fachfremde Außenseiter galten und die Physiker in Deutschland in einer Abwehrhaltung gegen die seit Ende des 18. Jahrhunderts einflussreiche Naturphilosophie des Kreises um Schelling waren und man beide verdächtigte, Anhänger dieser spekulativen Physik zu sein.[14]
Josiah Gibbs kam im Jahr 1878 zu ähnlichen Erkenntnissen wie Helmholtz bei elektrochemischen Zellen. Chemische Reaktionen laufen nur ab, wenn die Freie Energie abnimmt. Mittels der freien Energie lässt sich voraussagen, ob eine chemische Stoffumwandlung überhaupt möglich ist oder wie sich das chemische Gleichgewicht einer Reaktion bei einer Temperaturänderung verhält.
Nachdem schon Wilhelm Wien (1900), Max Abraham (1902), und Hendrik Lorentz (1904) Überlegungen zur elektromagnetischen Masse publiziert hatten veröffentlichte Albert Einstein im Rahmen seiner speziellen Relativitätstheorie 1905 die Erkenntnis, dass Masse und Energie äquivalent sind.
Energieformen und Energieumwandlung



Energie kann in einem System auf unterschiedliche Weise enthalten sein. Diese Möglichkeiten werden Energieformen genannt. Beispiele für Energieformen sind die kinetische Energie, die chemische Energie, die elektrische Energie, die Strahlungsenergie oder die potentielle Energie. Verschiedene Energieformen können ineinander umgewandelt werden, wobei die Summe der Energiemengen über die verschiedenen Energieformen vor und nach der Energieumwandlung stets die gleiche ist.
Eine Umwandlung kann nur so erfolgen, dass auch alle anderen Erhaltungsgrößen des Systems vor und nach der Umwandlung den gleichen Wert besitzen. Beispielsweise wird die Umwandlung kinetischer Energie durch die Erhaltung des Impuls und des Drehimpuls des Systems eingeschränkt. Ein Kreisel kann nur dann abgebremst werden und damit Energie verlieren, wenn er gleichzeitig Drehimpuls abgibt. Auch auf molekularer Ebene gibt es solche Einschränkungen. Viele chemische Reaktionen, die energetisch möglich wären, laufen nicht spontan ab, weil sie die Impulserhaltung verletzen würden. Weitere Erhaltungsgrößen sind die Zahl der Baryonen und die Zahl der Leptonen. Sie schränken die Umwandlung von Energie durch Kernreaktionen ein. Die Energie, die in der Masse von Materie steckt, lässt sich nur mit einer gleich großen Menge von Antimaterie vollständig in eine andere Energieform umwandeln. Ohne Antimaterie gelingt die Umwandlung mit Hilfe von Kernspaltung oder Kernfusion nur zu einem kleinen Teil.
Die Thermodynamik gibt mit dem zweiten Hauptsatz der Thermodynamik eine weitere Bedingung für eine Umwandlung vor: Die Entropie eines abgeschlossenen Systems kann nicht abnehmen. Entnahme von Wärme, ohne dass parallel andere Prozesse ablaufen, bedeutet eine Abkühlung. Eine niedrigere Temperatur entspricht jedoch einer verminderten Entropie und steht damit im Widerspruch zum zweiten Hauptsatz. Um dennoch Wärme in eine andere Energieform umzuwandeln, muss im Gegenzug zur Abkühlung ein anderer Teil des Systems erwärmt werden. Die Umwandlung von thermischer Energie in andere Energieformen setzt daher immer eine Temperaturdifferenz voraus. Außerdem kann nicht die gesamte in der Temperaturdifferenz gespeicherte Wärmemenge umgesetzt werden. Wärmekraftmaschinen dienen dazu, Wärme in mechanische Energie umzuwandeln. Das Verhältnis der durch den zweiten Hauptsatz gegebenen maximal möglichen Arbeit zur verbrauchten Wärmemenge wird Carnot-Wirkungsgrad genannt. Er ist umso größer, je größer die Temperaturdifferenz ist, mit der die Wärmekraftmaschine arbeitet.
Andere Umwandlungen sind nicht so stark von den Einschränkungen durch Erhaltungssätze und Thermodynamik betroffen. So lässt sich elektrische Energie mit wenig technischem Aufwand nahezu vollständig in viele andere Energieformen überführen. Elektromotoren wandeln sie beispielsweise in kinetische Energie um.
Die meisten Umwandlungen erfolgen nicht vollständig in eine einzige Energieform, sondern es wird ein Teil der Energie in Wärme gewandelt. In mechanischen Anwendungen wird die Wärme meist durch Reibung erzeugt. Bei elektrischen Anwendungen sind häufig der elektrische Widerstand oder Wirbelströme die Ursache für die Erzeugung von Wärme. Diese Wärme wird in der Regel nicht genutzt und als Verlust bezeichnet. Im Zusammenhang mit elektrischem Strom kann auch die Abstrahlung elektromagnetischer Wellen als unerwünschter Verlust auftreten. Das Verhältnis zwischen erfolgreich umgewandelter Energie und eingesetzter Energie wird Wirkungsgrad genannt.
Bei technischen Anwendungen wird häufig eine Reihe von Energieumwandlungen gekoppelt. In einem Kohlekraftwerk wird zunächst die chemische Energie der Kohle durch Verbrennung in Wärme umgesetzt und auf Wasserdampf übertragen. Turbinen wandeln die Wärme des Dampfs in mechanische Energie um und treiben wiederum Generatoren an, die die mechanische Energie in elektrische Energie umwandeln.
Energie in der klassischen Mechanik
.jpg.webp)
In der klassischen Mechanik ist die Energie eines Systems seine Fähigkeit, Arbeit zu leisten. Die Arbeit wandelt Energie zwischen verschiedenen Energieformen um. Die spezielle Form der newtonschen Gesetze gewährleistet, dass sich dabei die Summe aller Energien nicht ändert. Reibung und die mit ihr einhergehenden Energieverluste sind in dieser Betrachtung nicht berücksichtigt.
Das Noether-Theorem erlaubt eine allgemeinere Definition der Energie, die den Aspekt der Energieerhaltung automatisch berücksichtigt. Alle Naturgesetze der klassischen Mechanik sind invariant in Bezug auf Verschiebungen in der Zeit. Sie zeichnen sich dadurch aus, dass sie zu allen Zeiten unverändert in der gleichen Form gelten. Das Noether-Theorem besagt nun, dass es zu dieser Symmetrie in Bezug auf Verschiebung in der Zeit eine physikalische Größe gibt, deren Wert sich nicht mit der Zeit verändert. Diese Größe ist die Energie.
Aus dem Energieerhaltungssatz und unvermeidlichen Energieverlusten durch Reibung folgt, dass es unmöglich ist, eine mechanische Maschine zu bauen, die von sich aus beliebig lange läuft (Perpetuum Mobile). Außerdem erlaubt die Energieerhaltung zusammen mit der Impulserhaltung Aussagen über das Ergebnis von Stößen zwischen Objekten, ohne dass der genaue Mechanismus beim Stoß bekannt sein muss.
Energie und Bewegung
Die kinetische Energie ist diejenige Energie, die dem Bewegungszustand eines Körpers innewohnt. Sie ist proportional zur Masse und zum Quadrat der Geschwindigkeit relativ zu dem Inertialsystem, in dem man den Körper beschreibt.
- .
Der Betrag der kinetischen Energie ist also von dem Standpunkt abhängig, von dem aus man das System beschreibt. Häufig verwendet man ein Inertialsystem, das in Bezug auf den Erdboden ruht.
Ein ausgedehnter Körper kann neben einer Translationsbewegung auch eine Drehbewegung durchführen. Die kinetische Energie, die in der Drehbewegung steckt, nennt man Rotationsenergie. Diese ist proportional zum Quadrat der Winkelgeschwindigkeit und zum Trägheitsmoment des Körpers.
Energie und Potential
Potentielle Energie, auch Lageenergie genannt, kommt einem Körper durch seine Lage in einem Kraftfeld zu, sofern es sich um eine konservative Kraft handelt. Dies könnte beispielsweise das Erdschwerefeld oder das Kraftfeld einer Feder sein. Die potentielle Energie nimmt in Kraftrichtung ab und entgegen der Kraftrichtung zu, senkrecht zur Kraftrichtung ist sie konstant. Bewegt sich der Körper von einem Punkt, an dem er eine hohe potentielle Energie hat, zu einem Punkt, an dem diese geringer ist, leistet er genau so viel physikalische Arbeit, wie sich seine potentielle Energie vermindert hat. Diese Aussage gilt unabhängig davon, auf welchem Weg der Körper vom einen zum anderen Punkt gelangt ist.
Die potentielle Energie eines Körpers mit der Masse in einem homogenen Gravitationsfeld mit Gravitationsbeschleunigung ist proportional zur Höhe über dem Ursprung des Koordinatensystems:
- .
Beim freien Fall wird diese potentielle Energie in kinetische Energie umgewandelt, indem der Körper beschleunigt wird.
Da der Koordinatenursprung beliebig gewählt werden kann, ist die Lageenergie des Körpers niemals absolut gegeben und auch nicht messbar. Messbar sind nur ihre Änderungen.
Bei periodischen Bewegungen wird regelmäßig potentielle in kinetische Energie und wieder zurück in potentielle Energie verwandelt. Beim Pendel ist beispielsweise an den Umkehrpunkten die potentielle Energie maximal; die kinetische Energie ist hier null. Wenn der Faden gerade senkrecht hängt, erreicht die Masse ihre maximale Geschwindigkeit und damit auch ihre maximale kinetische Energie; die potentielle Energie hat hier ein Minimum. Ein Planet hat bei seinem sonnenfernsten Punkt zwar die höchste potentielle, aber auch die geringste kinetische Energie. Bis zum sonnennächsten Punkt erhöht sich seine Bahngeschwindigkeit gerade so sehr, dass die Zunahme der kinetischen Energie die Abnahme der potentiellen Energie genau kompensiert.
Elastische Energie ist die potentielle Energie der aus ihrer Ruhelage verschobenen Atome oder Moleküle in einem elastisch deformierten Körper, beispielsweise einer mechanischen Feder. Allgemein bezeichnet man die Energie, die bei der elastischen oder plastischen Verformung in dem Körper gespeichert (oder freigesetzt) wird, als Deformationsenergie.
Energie in der Thermodynamik

Thermische Energie ist die Energie, die in der ungeordneten Bewegung der Atome oder Moleküle eines Stoffes gespeichert ist. Sie wird umgangssprachlich auch als „Wärmeenergie“ oder „Wärmeinhalt“ bezeichnet. Die Umwandlung thermischer Energie in andere Energieformen wird durch die Thermodynamik beschrieben. Hier wird zwischen der im System enthaltenen Energie (innere Energie, Enthalpie) und der Wärme, der über die Systemgrenze transportierten thermischen Energie, unterschieden.
Die Summe aus thermischer Energie, Schwingungsenergie im Körper und Bindungsenergie bezeichnet man als Innere Energie. Dabei wird in manchem Quellen auch zwischen der thermischen inneren Energie, der chemischen inneren Energie und der Kernenergie als innerer Energie unterschieden, was aber den Rahmen der Thermodynamik verlässt.[15]
Umwandlung thermischer Energie in mechanische Arbeit
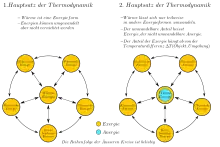
Während alle Energieformen unter gewissen Bedingungen (siehe #Energieformen und Energieumwandlung) vollständig in thermische Energie umgewandelt werden können (erster Hauptsatz der Thermodynamik), gilt das in umgekehrter Richtung nicht. Der zweite Hauptsatz der Thermodynamik beschreibt hier eine ganz wesentliche Einschränkung (Bild 1). Abhängig von der Temperatur, bei der die Wärme zur Verfügung steht, lässt sich nur ein mehr oder weniger großer Anteil über einen Kreisprozess in mechanische Arbeit umwandeln, während der Rest an die Umgebung abgegeben wird. In der technischen Thermodynamik werden die umwandelbaren Anteile einer Energieform auch als Exergie bezeichnet. Die Exergie ist keine Zustandsgröße im eigentlichen Sinne, denn sie hängt nicht nur vom Zustand des Systems ab, sondern auch vom Zustand der Umgebung, der im Einzelfall gegeben ist, im Allgemeinen angenommen werden muss. Dann lässt sich anhand von Exergie-Flussbildern einer Energie-Wandlungskette verfolgen, wo vermeidbare Verluste (Reibung oder andere dissipative Vorgänge) zu verzeichnen sind. In Bild 2 erkennt man, dass bei der Umwandlung von chemischer Energie (100 % Exergie) in Wärme bei einer mittleren Temperatur von 1000 °C der Exergie-Anteil nur noch 80 % beträgt. Wird diese Energie als Wärme in einem Dampfkessel auf Wasserdampf mit 273 °C übertragen, so verbleiben nur noch ca. 50 % und bei der Übertragung in einen mit 20 °C beheizten Raum nur noch etwa 7 %. Dabei wurde stets eine Umgebungstemperatur von 0 °C angenommen.
Berechnung der maximalen Arbeit (Exergie)
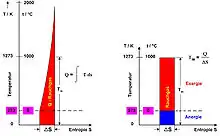
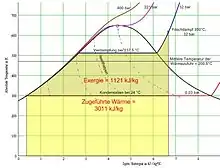
Bei der Berechnung des exergetischen Anteils von thermischer Energie ist zu berücksichtigen, ob die Wärmequelle eine konstante Temperatur besitzt, wie das in einem Siedewasser-Reaktor bei circa 270 °C der Fall ist, oder ob die Wärmeabgabe aus einem sich abkühlenden Medium, Rauchgas, erfolgt. Im ersten Fall kann der exergetische Anteil über den Carnot-Wirkungsgrad aus der oberen Prozess-Temperatur und der Umgebungstemperatur bestimmt werden, andernfalls erhält man die Wärme und die Exergie aus dem Flächenintegral, das aus dem T-S-Diagramm in Bild 3 und aus dem T-s-Diagramm in Bild 4 erkennbar ist. Die Formel lautet:
- .
Die Beziehung kann auch direkt aus den Diagrammen abgelesen werden. Hierbei sind: T die absolute Temperatur in K, S die Entropie in J/K, H die Enthalpie in J, Index 1: Ausgangszustand, Index U: Umgebungszustand.
Die Enthalpie-Differenz ist im Wesentlichen (in diesem Falle) die aus dem Brennstoff der Verbrennungsluft als Wärme zugeführte Energie. Sie erscheint als Fläche unter der Kurve der isobaren Wärmezufuhr. Der exergetische Anteil liegt oberhalb der Umgebungstemperatur, der andere nicht verwertbare Anteil, der „Anergie“ genannt wird, unterhalb dieser Linie. Bei der Abnahme der Exergie in einer Energie-Umwandlungskette spricht man auch von einer Energieentwertung.
Bei der Übertragung der Wärme aus dem Rauchgas auf das Arbeitsmedium, das Wasser, das dabei verdampft und überhitzt wird, entsteht ein weiterer Exergieverlust. Die maximale aus dem Dampfmassenstrom gewinnbare mechanische Leistung darf für einen Prozess mit Heißdampf von beispielsweise 16 bar und 350 °C keinesfalls über den Carnot-Wirkungsgrad mit dieser Temperatur berechnet werden. Das Ergebnis mit einem Wirkungsgrad von 52 % wäre falsch. Es würde dem zweiten Hauptsatz widersprechen, da die mittlere Temperatur der Wärmezufuhr in den Wasser-Dampf-Kreislauf niedriger ist. Erfolgt keine interne Wärmeübertragung (regenerative Speisewasservorwärmung) aus kondensierendem Dampf auf das Speisewasser, wie bei Dampfmaschinen, bei denen im theoretisch günstigsten Fall der Dampf reversibel auf Wasser mit Umgebungszustand gebracht werden kann, so erreicht man bei 15 °C Umgebungstemperatur nur einen maximalen Wirkungsgrad von 34,4 %. Der reversibel geführte Clausius-Rankine-Prozess in Bild 4 mit einem Dampfdruck von 32 bar und Kondensation bei 24 °C erreicht dagegen 37,2 %. Die realen Prozesse erreichen bei diesen Dampfparametern nur weitaus niedrigere Wirkungsgrade.
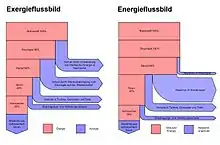
Energie- und Exergie-Flussbild der Stromerzeugung
In Bild 5 ist ein vereinfachtes Energieflussbild der Stromerzeugung durch ein großes Dampfkraftwerk (Frischdampfzustand 260 bar, 545 °C, Speisewasservorwärmung auf 276 °C) mit der Verteilung bis zum Endverbraucher einem entsprechenden Exergieflussbild gegenübergestellt. Man erkennt daraus, dass ein wesentlicher Teil der Energieentwertung nicht im Kondensator oder im nachgeschalteten Kühlturm des Kraftwerkes erfolgt, wo die Abwärme abgeführt wird, sondern bei der Umwandlung der chemischen Energie des Brennstoffes in thermische Energie (Verbrennung) und bei der Wärmeübertragung vom Rauchgas auf den Wasserdampf. Die Zahlenwerte für die Stromverteilung sind Anhaltswerte, sie können im Einzelfall geringfügig abweichen.
Sonnenenergie
Auch die Sonnenenergie, die durch Strahlung auf die Erde gelangt, erfährt auf dem Weg bis zur Erdoberfläche einen Exergieverlust. Während die innere Energie der Sonne bei rund 15 Millionen K noch praktisch aus reiner Exergie besteht, strahlt die Sonne mit einer Oberflächentemperatur von rund 6000 K auf die Erdoberfläche, deren Temperatur mit ca. 300 K anzusetzen ist. Durch Konzentration der Sonnenstrahlen in einem Kollektor käme man also – auch im Hochgebirge, wo die Absorption durch die Erdatmosphäre kaum eine Rolle spielt – über die Temperatur der Sonnenoberfläche nicht hinaus. Es ergäbe sich über den Carnot-Faktor ein Wirkungsgrad von ca. 95 %. Dann würde allerdings keine Energie mehr übertragen. Das thermodynamische Limit liegt darunter bei einer Absorbertemperatur von 2500 K mit einem Wirkungsgrad von ca. 85 %. In der Praxis kommen dissipative Verluste hinzu, angefangen von der Absorption in der Atmosphäre, über die Materialeigenschaften der kristallinen Zellen bis zum ohmschen Widerstand der Fotovoltaikanlagen, sodass bis heute nur Wirkungsgrade von weniger als 20 % erreicht werden können. Der höchste derzeit erreichte Wirkungsgrad ist 18,7 %.
Kraft-Wärme-Kopplung (KWK)
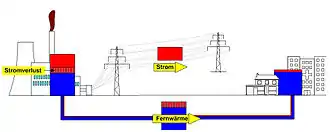
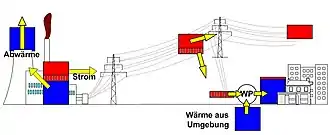
Zum Heizen wird meist Wärme mit nur einem geringen Exergieanteil benötigt. Deshalb ist das Heizen mit elektrischem Strom über eine Widerstandsheizung „Energieverschwendung“. Überall dort, wo mechanische Energie oder Strom aus Wärme erzeugt wird und gleichzeitig Wärmebedarf existiert, ist die Nutzung der Abwärme zum Heizen sinnvoller als die getrennte Bereitstellung von Wärme. In einem Heizkraftwerk wird, wenn es mit Dampf betrieben wird, Dampf aus der Turbine entnommen, dessen Temperatur gerade noch ausreichend hoch ist, um die Kondensationswärme über ein Fernwärmenetz zum Verbraucher zu leiten. Alternativ wird auch in Blockheizkraftwerken (BHKW) die Abwärme von stationären Verbrennungsmotoren genutzt. Auch die Wärmepumpe ist hier zu nennen. Sie wendet Arbeit auf, um Wärme (Energie) aus der Umgebung aufzunehmen und zusammen mit der Antriebsarbeit als Heizwärme bei entsprechend hoher Temperatur abzugeben. Wenn Grundwasser mit 10 °C als Wärmequelle zur Verfügung steht und ein Raum mit 20 °C zu beheizen ist, könnte eine Wärmepumpe mit Carnot-Prozess durch Einsatz von einer Kilowattstunde Antriebsarbeit 29 kWh Wärme liefern (Arbeitszahl =29). Reale Wärmepumpen, die mit wechselweise verdampfenden und kondensierenden Kältemitteln bei unterschiedlichen Drücken betrieben werden, erreichen Arbeitszahlen von ca. 3 bis 5.
Chemische Energie
Als chemische Energie wird die Energieform bezeichnet, die in Form einer chemischen Verbindung in einem Energieträger gespeichert ist und bei chemischen Reaktionen freigesetzt werden kann. Sie beschreibt also die Energie, die mit elektrischen Kräften in Atomen und Molekülen verbunden ist und kann unterteilt werden in einerseits kinetischer Energie der Elektronen in den Atomen und andererseits der elektrischen Energie der Wechselwirkung von Elektronen und Protonen.
Sie wird bei exothermen Reaktionen frei und muss für endotherme Reaktionen hinzugefügt werden.
Energie in der Elektrodynamik
In einem elektrischen Feld kann, sofern kein zeitlich veränderliches Magnetfeld vorliegt, ein elektrisches Potential definiert werden. Ein Ladungsträger besitzt dann eine potentielle elektrische (elektrostatische) Energie, die proportional zum Potential und zu seiner Ladungsmenge ist. Da der Nullpunkt des Potentials frei festgelegt werden kann, ist auch die Energie nicht absolut definiert. Für zwei Punkte im Potentialfeld ist aber die Differenz der Energien unabhängig von der Wahl des Potentialnullpunktes. Potentialdifferenzen entsprechen in der Elektrotechnik Spannungen; als Nullpunkt der Potentialskala wird üblicherweise das Potential der Erde gewählt.
Für Anordnungen zweier elektrischer Leiter ist die elektrostatische Energie proportional zum Quadrat der Differenz der elektrischen Potentiale der beiden Leiter. Das Doppelte der Proportionalitätskonstante nennt man elektrische Kapazität. Kondensatoren sind elektrotechnische Bauelemente, die hohe Kapazität besitzen und daher Energie speichern können.
Gleichwertig mit der Sichtweise, dass die elektrostatische Energie von Ladungen getragen wird, ist die Interpretation, dass sich die Energie auf den leeren Raum zwischen den Ladungen verteilt. Die Energiedichte, also die Energie pro Volumenelement, ist bei dieser Betrachtungsweise proportional zum Quadrat der elektrischen Feldstärke. Befindet sich in dem elektrischen Feld ein Dielektrikum, so ist die Energie außerdem proportional zur Dielektrizitätskonstante.
Bewegt sich eine Ladung im Vakuum zu einem Ort, an dem ein geringeres elektrisches Potential herrscht, erhöht sich die kinetische Energie der Ladung gerade so viel, wie die potentielle Energie geringer wird. Dies geschieht beispielsweise mit Elektronen in einer Elektronenröhre, in einer Röntgenröhre oder in einem Kathodenstrahlröhrenbildschirm. Bewegt sich eine Ladung dagegen entlang eines Potentialgefälles in einem Leiter, gibt sie ihre aufgenommene Energie sofort in Form von Wärme an das Leitermedium ab. Die Leistung ist dabei proportional zum Potentialgefälle und zur Stromstärke.
Elektrische Energie kann transportiert werden, indem sich Ladungsträger ohne nennenswertes Potentialgefälle entlang von Leitern bewegen. Dies ist beispielsweise in Freileitungen oder in Stromkabeln der Fall, mit deren Hilfe elektrische Energie vom Kraftwerk bis zum Verbraucher fließt.
Magnetische Energie ist in magnetischen Feldern wie im supraleitenden magnetischen Energiespeicher enthalten.
In einem idealen elektrischen Schwingkreis gespeicherte Energie wandelt sich fortlaufend zwischen der elektrischen Form und der magnetischen Form. Zu jedem Zeitpunkt ist die Summe der Teilenergien gleich (Energieerhaltung). Hierbei hat der reine magnetische respektive elektrische Anteil der Energie die doppelte Frequenz der elektrischen Schwingung.
Energie in der Relativitätstheorie
Nach der speziellen Relativitätstheorie entspricht der Masse eines ruhenden Objekts eine Ruheenergie von
- .
Die Ruheenergie ist somit bis auf den Faktor (Quadrat der Lichtgeschwindigkeit ) der Masse äquivalent. Die Ruheenergie kann bei bestimmten Vorgängen in andere Energieformen umgewandelt werden und umgekehrt. So haben die Reaktionsprodukte der Kernspaltung und der Kernfusion messbar niedrigere Massen als die Ausgangsstoffe. In der Elementarteilchenphysik wird umgekehrt auch die Erzeugung von Teilchen und damit von Ruheenergie aus anderen Energieformen beobachtet.
In der klassischen Mechanik wird die Ruheenergie nicht mitgerechnet, da sie ohne Belang ist, solange sich Teilchen nicht in andere Teilchen umwandeln.
Die allgemeine Relativitätstheorie verallgemeinert das Konzept der Energie weiter und enthält eine einheitliche Darstellung von Energien und Impulsen als Quellen für Raumkrümmungen über den Energie-Impuls-Tensor. Aus diesem lassen sich durch Kontraktionen die für einen Beobachter messbaren Größen wie Energiedichte gewinnen. Für die Untersuchung der Entwicklung von Raumzeiten ist der Energieinhalt entscheidend. So kann man aus Energiebedingungen den Kollaps der Raumzeit zu einer Singularität vorhersagen.
Energie in der Quantenmechanik
In der Quantenmechanik bestimmt der Hamiltonoperator, welche Energie an einem physikalischen System gemessen werden kann. Gebundene Zustände des Systems können dabei nur diskreten, also nicht beliebigen Energiewerten entsprechen. Deshalb haben die bei Übergängen zwischen diesen Zuständen emittierten Teilchen oder Strahlen Linienspektren.
Die Quantelung der Energie tritt bei elektromagnetischen Wellen auf: Eine Welle der Frequenz kann Energie nur in Paketen abgeben, wobei das plancksche Wirkungsquantum ist.
Technische Nutzung der Energie
Eine Erzeugung von Energie ist aufgrund des Energieerhaltungssatzes nicht möglich. Die Bezeichnung Energieerzeugung wird im Wirtschaftsleben aber dennoch verwendet, um die Umwandlung einer bestimmten Energieform (zum Beispiel elektrischer Strom) aus einer anderen Form (zum Beispiel chemischer Energie in Form von Kohle) auszudrücken. Analog gibt es im strengen physikalischen Sinne auch keinen Energieverbrauch,[16] wirtschaftlich gemeint ist damit aber der Übergang von einer gut nutzbaren Primärenergie (zum Beispiel Erdöl, Gas, Kohle) in eine nicht mehr weiter nutzbare Energieform (zum Beispiel Abwärme in der Umwelt). Von Energieeinsparung ist die Rede, wenn effizientere Prozesse gefunden werden, die weniger Primärenergie für denselben Zweck benötigen, oder anderweitig, zum Beispiel durch Konsumverzicht, der Primärenergieeinsatz reduziert wird.
Die Physik beschreibt den oben salopp eingeführten „Energieverbrauch“ mit dem exakten Begriff der Entropiezunahme. Während in einem abgeschlossenen System die Energie stets erhalten bleibt, nimmt die Entropie mit der Zeit stets zu oder bleibt bestenfalls konstant. Je höher die Entropie, desto schlechter nutzbar ist die Energie. Statt von Entropiezunahme kann man anschaulich auch von Energieentwertung sprechen.
Das Gesetz der Entropiezunahme verhindert insbesondere, Wärmeenergie direkt in Bewegungs- oder elektrische Energie umzuwandeln. Stattdessen sind immer eine Wärmequelle und eine Wärmesenke (= Kühlung) erforderlich. Der maximale Wirkungsgrad kann gemäß Carnot aus der Temperaturdifferenz berechnet werden.
Der Grenzfall einer Energieumwandlung ohne Entropiezunahme wird als reversibler Prozess bezeichnet. Als Beispiel einer nahezu reversiblen Energieumwandlung sei ein Satellit auf einer elliptischen Umlaufbahn um die Erde genannt: Am höchsten Punkt der Bahn hat er hohe potentielle Energie und geringe kinetische Energie, am niedrigsten Punkt der Bahn ist es genau umgekehrt. Die Umwandlung kann hier ohne nennenswerte Verluste tausendfach im Jahr erfolgen. In supraleitenden Resonatoren kann Energie millionen- oder gar milliardenfach pro Sekunde zwischen Strahlungsenergie und elektrischer Energie hin- und hergewandelt werden, ebenfalls mit Verlusten von weniger als einem Promille pro Umwandlung.
Bei vielen Prozessen, die in der Vergangenheit noch mit hohen Verlusten ergo erheblicher Entropiezunahme verbunden waren, ermöglicht der technologische Fortschritt zunehmend geringere Verluste. So verwandelt eine Energiesparlampe oder LED elektrische Energie wesentlich effizienter in Licht als eine Glühlampe. Eine Wärmepumpe erzeugt durch Nutzung von Wärme aus der Umwelt bei einer bestimmten elektrischen Leistung oft vielfach mehr Wärme als ein herkömmliches Elektroheizgerät bei gleicher Leistung. In anderen Bereichen liegt der Stand der Technik aber schon seit geraumer Zeit nah am theoretischen Maximum, so dass hier nur noch kleine Fortschritte möglich sind. So verwandeln gute Elektromotoren über 90 Prozent der eingesetzten elektrischen Energie in nutzbare mechanische Energie und nur einen kleinen Teil in nutzlose Wärme.
Energiesparen bedeutet im physikalischen Sinn, die Energieentwertung und Entropiezunahme bei der Energieumwandlung oder Energienutzung zu minimieren.
Spezifische Energie
Spezifisch heißt in den Naturwissenschaften „auf eine bestimmte Bemessungsgrundlage bezogen“ (Bezogene Größe). Die spezifische Energie wird auf eine gewisse Eigenschaft eines Systems bezogen, die durch eine physikalische Größe beschrieben werden kann.
Nach DIN 5485 ist die spezifische Energie speziell massenbezogen, und die volumetrische Energiedichte die dimensional bezogene Bezeichnung.
- Beispiele
- Energie je Volumen in J/m³ (Dimension ): Enthalpie (Thermodynamik), spezifische Enthalpien wie z. B. die Schmelzenthalpie, Verdampfungsenthalpie, Kristallisationsenthalpie, Brennwert und Heizwert (Energietechnik), spezifische Verdichtungsenergie (Materialkunde), spezifische Energie von Sprengstoff
- Energie je Masse in J/kg (Dimension ): spezifische Arbeit, spezifische latente Wärme (Thermodynamik), Brennwert und Heizwert fester Brennstoffe, spezifische Energie des Energiespeichers (Energietechnik), Elektrische Kapazität und Energiedichte des Plattenkondensators (Elektrotechnik), spezifische Energie des Massenpunkts (Mechanik)
Nicht als spezifisch, sondern als molar bezeichnet die Thermodynamik und Chemie stoffbezogene Energiewerte:
- Energie je Stoffmenge in J/Mol (Dimension ): molare Enthalpie (Thermodynamik)
Energieversorgung und -verbrauch
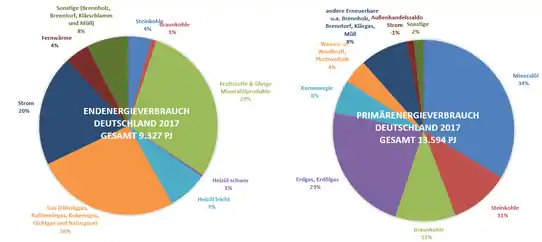
Mit Energieverbrauch wird umgangssprachlich die Nutzung von verschiedenen Energien in für Menschen gut verwendbaren Formen bezeichnet. Energieversorgung bezeichnet die Belieferung von Verbrauchern mit diesen Energieformen, inklusive der dazu notwendigen Energieinfrastruktur.
Die letztendlich an Verbraucher belieferte Energie bezeichnet man dabei als Endenergie. Es kann sich dabei sowohl um Primärenergie wie Erdgas zum Betrieb einer Heizung als auch um sogenannte Sekundärenergie wie Strom oder Fernwärme handeln, die aus Primärenergie durch eine verlustbehaftete Wandlung erzeugt wurde. Der Weg, den die Primärenergie vom ursprünglichen Primärenergieaufkommen über die Wandlung in andere Energieformen bis zur Endenergie und ihrem Verbrauch in unterschiedlichen Sektoren für unterschiedliche Zwecke nimmt, wird für eine Volkswirtschaft in Energiebilanzen beschrieben.
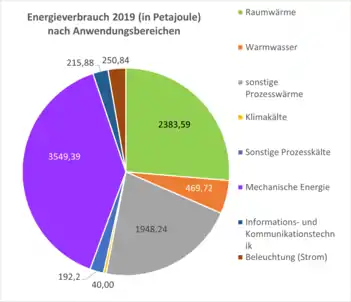
Die wichtigsten Anwendungsbereiche von Endenergie sind Wärme und Verkehr (siehe Grafik für Deutschland). Der wichtigste Energieträger in der deutschen Wärmeerzeugung ist Erdgas.[17] Der wichtigste Energieträger für Verkehr und Transport sind Mineralöle (Kraftstoffe).[18] Nur etwa 20 % des deutschen Endenergiebedarfs wird durch Strom gedeckt.
Einige Energieträger können über Leitungen die Verbraucher erreichen, wie typischerweise Brenngase, elektrische Energie, Prozess- und Heizwärme. Mineralöle, insbesondere Kraftstoffe (Benzine, Dieselkraftstoffe, Kerosin) werden mit Tankwagen über Zwischenlager an Tankstellen oder direkt an den Verbraucher geliefert.[19] Lagerfähig und gut transportfähig sind auch Steinkohle, Heizöl, Kernbrennstoff und Biomasse.
Der Energiebedarf ist weltweit sehr unterschiedlich und in den Industrieländern um ein Vielfaches höher als zum Beispiel in der Dritten Welt (siehe Liste der Staaten mit dem höchsten Energieverbrauch).
In industriell hoch entwickelten Ländern spielt seit dem frühen 20. Jahrhundert die flächendeckende Versorgung der Allgemeinheit mit elektrischer Energie eine große Rolle. Weiterhin sind die Beschaffung, der Transport und die Veredlung von Brennstoffen zu Heizzwecken wichtige Wirtschaftszweige.
Energiequelle
Einheiten
Neben der abgeleiteten SI-Einheit Joule sind je nach Anwendungsgebiet noch andere Energieeinheiten in Gebrauch. Wattsekunde (Ws) und Newtonmeter (Nm) sind mit dem Joule identisch.
Das Elektronenvolt (eV) wird in der Atomphysik, der Kernphysik und der Elementarteilchenphysik zur Angabe von Teilchenenergien und Energieniveaus verwendet. Seltener kommt in der Atomphysik das Rydberg vor. Die cgs-Einheit erg wird häufig in der theoretischen Physik benutzt.
Die Kalorie war in der Kalorimetrie üblich und wird heute noch umgangssprachlich und im Warenverkehr zusätzlich zur gesetzlichen Einheit Joule bei der Angabe des physiologischen Brennwerts von Lebensmitteln verwendet. In Kilowattstunden (kWh) messen Energieversorger die Menge der an die Kunden gelieferten Energie. Die Steinkohleeinheit und die Öleinheit dienen zur Angabe des Energieinhaltes von Primärenergieträgern. Mit dem TNT-Äquivalent misst man die Sprengkraft von Sprengstoffen.
Liste
Die folgenden Umrechnungen in diverse Einheiten gelten exakt (die Zahlenwerte wurden durch Definitionen festgelegt), ausgenommen dort, wo „≈“ steht.
| Nicht-SI-Einheit | Joule |
|---|---|
| Elektronenvolt (eV) | 1,602.176.634 · 10−19 J |
| Hartree-Energie | ≈ 4,359.744.722.21 · 10−18 J |
| Erg | 1 · 10−7 J |
| Foot-pound | 1,355.817.948.331.400.4 J |
| Kalorie (cal) | 4,1868 J |
| Kilopondmeter (kpm) | 9,80665 J |
| Literatmosphäre | 1,013.25 · 102 J |
| BTU | 1,055.055.852.62 · 103 J |
| Metertonne | 9,806.65 · 103 J |
| PS-Stunde | 2,647.795.5 · 106 J |
| kWh | 3,6 · 106 J |
| kgTNT | 4,184 · 106 J |
| kgSKE | 2,930.76 · 107 J |
| Benzinäquivalent | 3,2 · 107 J |
| Öläquivalent | 4,186.8 · 107 J |
| Therm | 1,055.055.852.62 · 108 J |
| Planck-Energie | ≈ 1,956 · 109 J |
| Quad | 1,055.055.852.62 · 1018 J |
| Foe (Bethe) | 1 · 1044 J |
Umrechnungen
In der folgenden Umrechnungstabelle ist jeweils die links angegebene Einheit gleich der Zahl mal der oben angegebenen Einheit:
| Joule (Wattsekunde) | Kilowattstunde | Elektronenvolt | Kilopondmeter | Kalorie | Erg | |
|---|---|---|---|---|---|---|
| 1 kg·m2/s2 | 1 | 2,778 · 10−7 | 6,242 · 1018 | 0,102 | 0,239 | 107 |
| 1 kW·h | 3,6 · 106 | 1 | 2,25 · 1025 | 3,667 · 105 | 8,60 · 105 | 3,6 · 1013 |
| 1 eV | 1,602 · 10−19 | 4,45 · 10−26 | 1 | 1,63 · 10−20 | 3,83 · 10−20 | 1,602 · 10−12 |
| 1 kp·m | 9,80665 | 2,72 · 10−6 | 6,13 · 1019 | 1 | 2,34 | 9,80665 · 107 |
| 1 calIT | 4,1868 | 1,163 · 10−6 | 2,611 · 1019 | 0,427 | 1 | 4,1868 · 107 |
| 1 g·cm2/s2 | 10−7 | 2,778 · 10−14 | 6,242 · 1011 | 1,02 · 10−8 | 2,39 · 10−8 | 1 |
Größenordnungen
Energie ist eine Größe, die auch im Alltag einen um viele Größenordnungen unterschiedlichen Wert annehmen kann. Beispiele sind:
- 1 J = 1 Ws = 1 Nm
- potentielle Energie, die beim Anheben einer Schokoladentafel (ca. 100 g) um 1 Meter in dieser gespeichert wird.
- 3,6·106 J = 3600 kJ = 3600 kWs = 1 kWh
- Abrechnungseinheit für elektrische Energie (ugs. Strom), Gas usw. Ein europäischer Privathaushalt benötigt pro Jahr ca. 2000–4000 kWh an elektrischer Energie.
- 2,9·107 J = 8,141 kWh = 1 kg SKE
- eine Steinkohleeinheit entspricht der Energiemenge, die beim Verbrennen von 1 kg Steinkohle umgewandelt wird. Dies ist ein gängiges Maß bei der Angabe von Primärenergie-Mengen. (1998 betrug der weltweite Primärenergie-Umsatz 14,1 Gt SKE = 390·1018 J)
- 1 eV = 1,602 176 565(35) · 10−19 J
- Die Einheit Elektronvolt wird unter anderem in der Festkörper-, Kern- und Elementarteilchenphysik verwendet. Ein Photon von violettem Licht hat eine Energie von ca. 3 eV, eines von rotem ca. 1,75 eV.
- 1 kg Masse ≙ 8,99 · 1016 J
- (89.875.517.873.681.764 J) gemäß der Beziehung von Einstein: E = mc2.
Formeln
- Spannenergie einer gespannten Feder:
- wobei die Federkonstante und die Auslenkung der Feder aus der Ruhelage ist.
- Potentielle Energie eines Körpers mit Masse in einem homogenen Gravitationsfeld:
- wobei die Masse, die Erdbeschleunigung und die Höhe, in welcher sich der Körper befindet, ist.
- Kinetische Energie eines Körpers mit Masse und der Geschwindigkeit :
- .
- Rotationsenergie eines Körpers:
- wobei das Trägheitsmoment um die betreffende Drehachse und die Winkelgeschwindigkeit ist.
- elektrische Energie in einem Stromkreis:
- wobei die elektrische Spannung, der Strom durch die Leitung und die Zeitdauer ist.
- Magnetische Feldenergie einer stromdurchflossenen idealen Spule:
- wobei die Induktivität und die elektrische Stromstärke ist.
- Relativistische Energie eines freien Teilchens der Masse mit Geschwindigkeit :
- wobei die Lichtgeschwindigkeit ist.
- Energie von Lichtquanten (Photonen):
- wobei das plancksche Wirkungsquantum und die Frequenz ist.
- Energie eines Erdbebens:
- Tonnen TNT,
- wobei die Magnitude auf der Richterskala ist.
- Arbeit (Energieänderung) ist das Integral der Kraft längs des zurückgelegten Wegs :
- Die an einem System im Zeitintervall verrichtete Arbeit kann auch über die Leistung definiert werden:[20]
Literatur
- Jennifer Coopersmith: Energy – the subtle concept. Oxford University Press, 2010, ISBN 0-19-954650-9.
- Max Jammer: Energy. In: Donald M. Borchert (Hrsg.): Encyclopedia of Philosophy. Band 3. Thomson Gale, 2005, S. 225–234.
- Marc Lange: Energy (Addendum). In: Donald M. Borchert (Hrsg.): Encyclopedia of Philosophy. Band 3. Thomson Gale, 2005, S. 234–237.
- Yehuda Elkana: Discovery of the conservation of Energy. Harvard University Press 1974, (Vorwort I. Bernard Cohen).
- István Szabó: Geschichte der mechanischen Prinzipien. Birkhäuser 1979.
- Martin Buchholz: Energie – Wie verschwendet man etwas, das nicht weniger werden kann? Springer, Heidelberg/Berlin, ISBN 978-3662497418.
Weblinks
- Was ist Energie? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 10. Nov. 2002.
Einzelnachweise
- Rudolf Eisler: Wörterbuch der philosophischen Begriffe (1904)
- Leibniz: Brevis demonstratio erroris memorabilis Cartesii. Acta Eruditorum, 1686.
- Max Planck: Das Princip von der Erhaltung der Energie. B.G. Teubner, Leipzig 1887.
- Dargestellt nach Max Jammer, Energy, Encyclopedia of Philosophy.
- Bernoulli: Examen principiorum mechanicae. Comm. Acad. Petropol. 1726, S. 126. Siehe Szabo: Geschichte der mechanischen Prinzipien. Birkhäuser 1979, S. 71.
- Max Jammer: Energy, Encyclopedia of Philosophy. S. 228.
- Thomas Young: A course of lectures on natural philosophy and the mechanical arts. Johnson, 1807, S. 44. „The same idea is somewhat more concisely expressed by the term energy which indicates the tendency of a body to ascend or to penetrate to a certain distance in opposition to a retarding force.“
- Max Jammer: Artikel Energy, Encyclopedia of Philosophy.
- Siehe Szabo: Geschichte der mechanischen Prinzipien. S. 78, zur Nicht-Kenntnisnahme Eulers der Streitschrift von Immanuel Kant von 1749 über die Wahre Schätzung der lebendigen Kräfte.
- Max Jammer: Artikel Energy, Encyclopedia of Philosophy.
- Essai sur les machines en général. 1783, 2. Auflage 1803 als Principes fondamentaux de l´equilibre et du mouvement.
- Alexandre Moatti: Gaspard-Gustave de Coriolis (1792–1843): un mathématicien, théoricien de la mécanique appliquée. Dissertation an der Universität von Paris, 2011 (PDF; 6,4 MB; französisch).
- Hans Joachim Störig: Kleine Weltgeschichte der Wissenschaft. Band 2. Fischer Taschenbuch, Hamburg 1982, ISBN 3-596-26399-9, S. 89–91, 1280.
- Walther Gerlach: Fortschritte der Naturwissenschaft im 19. Jahrhundert. In: Propyläen Weltgeschichte. Band 8 (19. Jahrhundert), 1960.
- Friedhelm Kuypers: Physik für Ingenieure und Naturwissenschaftler: Band 1 – Mechanik und Thermodynamik. John Wiley & Sons, 4. Oktober 2012, ISBN 978-3-527-66957-8, S. 248– (Abgerufen am 13. Juni 2013).
- Siehe auch: Martin Buchholz: Energie - Wie verschwendet man etwas, das nicht weniger werden kann? In: Science Slam Finale 2011. 19. November 2011, abgerufen am 30. April 2020. bzw. Martin Buchholz: Energie - Wie verschwendet man etwas, das nicht weniger werden kann? 1. Auflage. Springer, Berlin Heidelberg 2016, ISBN 978-3-662-49741-8, S. 27 ff.
- Nettowärmeerzeugung in Deutschland nach ausgewählten Energieträgern in den Jahren 2018 und 2019. Abgerufen am 23. November 2021.
- Endenergieverbrauch nach Sektoren und Energieträger. Abgerufen am 23. November 2021.
- Mineralöllogistik. Abgerufen am 23. November 2021.
- Peter Kurzweil: Physik Formelsammlung. 2008, S. 15.

