Allgemeine Relativitätstheorie

Die allgemeine Relativitätstheorie (; kurz ART) beschreibt die Wechselwirkung zwischen Materie (einschließlich Feldern) einerseits sowie Raum und Zeit andererseits. Sie deutet Gravitation als geometrische Eigenschaft der gekrümmten vierdimensionalen Raumzeit. Die Grundlagen der Theorie wurden maßgeblich von Albert Einstein entwickelt, der den Kern der Theorie am 25. November 1915 der Preußischen Akademie der Wissenschaften vortrug. Zur Beschreibung der gekrümmten Raumzeit bediente er sich der Differentialgeometrie.

Die allgemeine Relativitätstheorie erweitert die spezielle Relativitätstheorie und das Newtonsche Gravitationsgesetz und geht in diese über bei hinreichend kleinen Raumzeitgebieten bzw. Massedichten und Geschwindigkeiten. In zahlreichen Tests der allgemeinen Relativitätstheorie wurde sie experimentell bestätigt und gilt in der von Einstein formulierten Form als einzige allgemein anerkannte Gravitationstheorie.

Ungeklärt ist ihre Beziehung zur Quantenphysik, dem zweiten Grundpfeiler der modernen Physik des 20. Jahrhunderts. Daher gibt es noch keine vereinheitlichte Theorie der Quantengravitation.

Einführung

Grundlegend für die allgemeine Relativitätstheorie ist eine Wechselwirkung zwischen allen Typen physikalischer Systeme, die Energie und Impuls tragen können („Materie“), und der Raumzeit mit zwei Eigenschaften:

Energie und Impuls der Materie beeinflussen die Geometrie der Raumzeit, in der sie sich befinden. Dieser Einfluss lässt sich über einen allgemeinen Krümmungsbegriff formulieren, und in der ART werden Raum und Zeit durch den Begriff der Raumzeitkrümmung beschrieben.
Materie, auf die keine Kraft ausgeübt wird, bewegt sich in Raum und Zeit entlang einer Geodäte. In ungekrümmten Räumen (frei von Gravitation) sind solche Geodäten einfache Geraden, wie etwa im 3-dimensionalen Raum der klassischen Mechanik. Während jedoch der Einfluss von Materie auf Bewegung in der klassischen Mechanik mithilfe einer gravitativen Kraft beschrieben wird, verweist die ART ausschließlich auf die nunmehr gekrümmte Geometrie der Raumzeit. Ebenso wie in der speziellen Relativitätstheorie wird dabei die Bewegung eines Gegenstands entlang eines bestimmten Weges im Raum abstrakter als Weg in den vier Dimensionen der Raumzeit interpretiert und als Weltlinie bezeichnet. Erfolgt die Bewegung dabei kräftefrei (abgesehen von der Gravitation), ist die Weltlinie eine zeitartige Geodäte. Allerdings ist eine zeitartige Geodäte der Raumzeit im Allgemeinen keine Gerade im dreidimensionalen Raum, sondern eine Verbindung zwischen zwei Ereignissen mit zeitartigem Abstand, für welche die verstrichene Eigenzeit einen Extremwert annimmt.[1]

Die erste Aussage beschreibt eine Wirkung der Materie auf die Raumzeit, die zweite beschreibt die Auswirkung der Raumzeit auf die Bewegung der Materie. Die Anwesenheit von Materie verändert also die geometrischen Verhältnisse der Raumzeit, aus denen sich auch die Bewegungsgleichungen der Materie ergeben. Die ART betrachtet dabei die räumlichen und zeitlichen Koordinaten als gleichberechtigt und behandelt alle zeitlichen Änderungen als geometrisches Problem.

Geschichte

Verallgemeinerung des Äquivalenzprinzips

Das klassische Äquivalenzprinzip, manchmal auch als schwaches Äquivalenzprinzip bezeichnet, geht auf Überlegungen Galileo Galileis (1636/38) und Experimente auf dem Gebiet der Kinematik zurück. Die ursprüngliche Formulierung des Äquivalenzprinzips von Galilei besagt, dass alle Körper unabhängig von ihren Eigenschaften im Vakuum dasselbe Fallverhalten aufweisen. Das heißt, zwei Körper unter Einfluss der Schwerkraft, die den gleichen Ort zu aufeinander folgenden Zeiten verlassen, verhalten sich in dem Sinne identisch, dass sie dieselbe Bahn durchlaufen, unabhängig von allen anderen Eigenschaften der Körper wie chemischer Zusammensetzung, Größe, Form und Masse. Die Einschränkung auf das Vakuum ergibt sich dadurch, dass sonst Reibungseffekte und Auftriebskräfte eine Rolle spielen, die von den Eigenschaften des Gegenstands abhängig sind. Isaac Newton formulierte in seiner Philosophiae Naturalis Principia Mathematica (1687) das Äquivalenzprinzip als Gleichheit von träger Masse und schwerer Masse. Das heißt, dass im Gravitationsgesetz und im Trägheitsgesetz dieselbe Masse vorkommt.

Albert Einstein hielt das Äquivalenzprinzip, das 1900 durch das Eötvös-Experiment bereits mit einer Genauigkeit von 10⁻⁹ bestätigt war, für eine entscheidende Eigenschaft der Gravitation. Daher erweiterte Einstein das Prinzip auf nichtmechanische Phänomene und machte es zum Ausgangspunkt seiner Gravitationstheorie.

Die Aufstellung der Feldgleichungen

Die Grundlagen der allgemeinen Relativitätstheorie wurden im Wesentlichen von Albert Einstein entwickelt. Er benutzte die von Carl Friedrich Gauß, Bernhard Riemann, Elwin Bruno Christoffel, Gregorio Ricci-Curbastro und Tullio Levi-Civita entwickelte Differentialgeometrie, wie er sie von Marcel Grossmann, einem befreundeten Mathematiker, gelernt hatte. Mittels dieser Differentialgeometrie formulierte er in der Raumzeit – die Hermann Minkowski für die spezielle Relativitätstheorie eingeführt hatte – die Gravitation als Eigenschaft der Maßverhältnisse. Überlegungen von Ernst Mach beeinflussten Einsteins Überzeugung, dass auch unter dem Einfluss von Gravitation nur Bewegung relativ zu anderen Körpern physikalisch erheblich sei.

Die erste Veröffentlichung, die der allgemeinen Relativitätstheorie zugerechnet werden kann, ist eine 1908 veröffentlichte Arbeit Albert Einsteins über den Einfluss von Gravitation und Beschleunigung auf das Verhalten von Licht in der speziellen Relativitätstheorie. In dieser Arbeit formuliert er bereits das Äquivalenzprinzip und sagt die gravitative Zeitdilatation und Rotverschiebung sowie die Lichtablenkung durch massive Körper vorher.[2] Der Hauptteil der Theorie wurde aber erst in den Jahren von 1911 bis 1915 von Einstein erarbeitet. Den Beginn seiner Arbeit markiert dabei eine zweite Veröffentlichung zur Wirkung der Gravitation auf Licht im Jahr 1911, in der Einstein seine Veröffentlichung von 1908 aufarbeitet.[3]

Bevor er die Arbeit abschloss, veröffentlichte Einstein 1913 einen Entwurf für die Relativitätstheorie, der bereits eine gekrümmte Raumzeit verwendete.[4] Aufgrund von Problemen mit dem Prinzip der generellen Kovarianz, das sich letztlich doch als richtig erwies, verfolgte Einstein jedoch in der Folgezeit einen falschen Ansatz, bevor er das Problem letztlich 1915 lösen konnte. Er hielt während seiner Arbeit auch Vorträge darüber und tauschte sich mit Mathematikern aus, namentlich mit Marcel Grossmann und David Hilbert.

Im Oktober 1915 veröffentlichte Einstein eine Arbeit über die Periheldrehung des Merkur,[5] in der er noch von falschen Feldgleichungen ausging, die mit der lokalen Erhaltung von Energie und Impuls nicht verträglich waren. Im November 1915 fand Einstein die richtigen Feldgleichungen und veröffentlichte sie in den Sitzungsberichten der Preußischen Akademie der Wissenschaften am 25. November 1915 zusammen mit der Berechnung der Periheldrehung des Merkurs und der Lichtablenkung an der Sonne. Zwar reichte Hilbert seine Arbeit fünf Tage zuvor der Göttinger Königlichen Gesellschaft der Wissenschaften zur Veröffentlichung ein. Allerdings enthalten die Korrekturfahnen von Hilberts Arbeit, anders als die später publizierte Version, nicht die Feldgleichungen[6] – die Korrekturfahnen sind allerdings nicht vollständig erhalten. Einen – gelegentlich behaupteten – Prioritätsstreit zwischen Hilbert und Einstein gab es jedoch nie, da Hilbert ohnehin nur einen rechnerischen Teilaspekt mit Hilfe der von ihm besser beherrschten Tensoranalysis gelöst hatte, in die sich Einstein erst einarbeiten musste.[7]

Einsteins späteren Artikel Die Grundlage der allgemeinen Relativitätstheorie kann man als ersten Übersichtsartikel der ART auffassen. Er wurde am 20. März 1916 in den Annalen der Physik veröffentlicht, zwei Monate nachdem Einstein die von Schwarzschild stammende Lösung seiner Feldgleichungen der Preußischen Akademie der Wissenschaften vorgetragen hatte.[8]

Auf Hilbert geht das Wirkungsfunktional der ART zurück, aus dem er die Feldgleichungen in seinem 1916 veröffentlichten Artikel ableitete.[9]

Grundlegende Konzepte

Die Ausgangspunkte der ART lassen sich als drei grundlegende Prinzipien formulieren: das allgemeine Relativitätsprinzip, das Äquivalenzprinzip und das Machsche Prinzip.[10]

Die Theorie folgt nicht zwingend aus diesen Prämissen, und zumindest beim Machschen Prinzip ist unklar, ob die ART es überhaupt erfüllt. Die drei Prinzipien erklären aber, welche physikalischen Probleme Einstein dazu veranlassten, die ART als neue Gravitationstheorie zu formulieren.

Die Beschreibung der Raumzeitkrümmung baut logisch auf dem Äquivalenzprinzip auf, deshalb wird sie in diesem Kapitel ebenfalls behandelt.

Relativitätsprinzip

In der allgemeinen Relativitätstheorie wird ein gegenüber der speziellen Relativitätstheorie erweitertes Relativitätsprinzip angenommen: Die Gesetze der Physik haben nicht nur in allen Inertialsystemen die gleiche Form, sondern auch in Bezug auf alle Koordinatensysteme. Dies gilt für alle Koordinatensysteme, die jedem Ereignis in Raum und Zeit vier Parameter zuweisen, wobei diese Parameter auf kleinen Raumzeitgebieten, die der speziellen Relativitätstheorie gehorchen, hinreichend differenzierbare Funktionen der dort lokal definierbaren kartesischen Koordinaten sind. Diese Forderung an das Koordinatensystem ist nötig, damit die Methoden der Differentialgeometrie für die gekrümmte Raumzeit überhaupt angewendet werden können. Eine gekrümmte Raumzeit ist dabei im Allgemeinen nicht mehr global mit einem kartesischen Koordinatensystem zu beschreiben. Das erweiterte Relativitätsprinzip wird auch allgemeine Koordinaten-Kovarianz genannt.

Die Koordinaten-Kovarianz ist eine Forderung an die Formulierung von Gleichungen (Feldgleichungen, Bewegungsgleichungen), die in der ART Gültigkeit besitzen sollen. Allerdings lässt sich auch die spezielle Relativitätstheorie bereits allgemein kovariant formulieren. So kann beispielsweise selbst ein Beobachter auf einem rotierenden Drehstuhl den Standpunkt vertreten, er selbst sei in Ruhe und der Kosmos rotiere um ihn herum. Dabei entsteht das Paradoxon, dass sich die Sterne und das von ihnen ausgesandte Licht im Koordinatensystem des rotierenden Beobachters rechnerisch mit Überlichtgeschwindigkeit bewegen, was scheinbar der speziellen Relativitätstheorie widerspricht. Die Auflösung dieses Paradoxons ist, dass die allgemein kovariante Beschreibung per Definition lokal ist. Das bedeutet, dass die Konstanz der Lichtgeschwindigkeit nur nahe der Weltlinie des Beobachters gelten muss, was für den rotierenden Beobachter ebenso erfüllt ist wie für jeden anderen Beobachter. Die kovariant, also im Sinne des allgemeinen Relativitätsprinzips, geschriebenen Gleichungen ergeben für die Sterne also überlichtschnelle Kreisbewegungen, stehen aber dennoch im Einklang mit den Prinzipien der speziellen Relativitätstheorie. Dies wird auch dadurch klar, dass es unmöglich ist, dass ein Beobachter in der Nähe eines Sterns im rotierenden Koordinatensystem ruht und also dem Stern mit Überlichtgeschwindigkeit begegnet. Dieser Beobachter hat also zwangsweise ein anderes Koordinatensystem als der rotierende Beobachter und misst die „richtige“ Lichtgeschwindigkeit.

Obwohl es möglich ist, den Kosmos aus der Sicht eines rotierenden Beobachters korrekt zu beschreiben, sind die Gleichungen eines Bezugssystems, in dem die meisten Objekte ruhen oder sich nur langsam bewegen, meist einfacher. Die Bedingung eines nichtrotierenden Koordinatensystems für Inertialsysteme und die Unterscheidung in ihrer Betrachtung, die von der klassischen Physik gefordert wird, entfällt aber prinzipiell.

Im Fall eines Mehrkörpersystems auf engem Raum ist die Raumzeit maßgeblich gekrümmt und diese Krümmung in jedem Koordinatensystem auch zeitlich veränderlich. Daher ist von vornherein kein Kandidat für ein ausgezeichnetes Koordinatensystem erkennbar, das sich zur Beschreibung aller Phänomene eignet. Das Relativitätsprinzip besagt für diesen allgemeinen Fall, dass es auch nicht nötig ist, danach zu suchen, weil alle Koordinatensysteme gleichberechtigt sind. Man kann also je nachdem, welches Phänomen man beschreiben will, verschiedene Koordinatensysteme vergleichen und das rechentechnisch einfachste Modell auswählen.

Daher kann die ART auch auf den klassischen astronomischen Begriff der Scheinbarkeit von Bewegungen verzichten, den das noch in der newtonschen Anschauung verhaftete heliozentrische Weltbild erforderte.

Machsches Prinzip

Einstein war bei der Entwicklung der Relativitätstheorie stark von Ernst Mach beeinflusst. Insbesondere die von Einstein als machsches Prinzip bezeichnete Annahme, dass die Trägheitskräfte eines Körpers nicht von dessen Bewegung relativ zu einem absoluten Raum, sondern von dessen Bewegung relativ zu den anderen Massen im Universum abhängen, war für Einstein eine wichtige Arbeitsgrundlage. Die Trägheitskräfte sind nach dieser Auffassung also Resultat der Wechselwirkung der Massen untereinander, und ein unabhängig von diesen Massen existierender Raum wird verneint. Demnach sollten beispielsweise Fliehkräfte rotierender Körper verschwinden, wenn das restliche Universum „mitrotiert“.

Diese von Einstein bevorzugte, recht allgemeine Formulierung des machschen Prinzips ist jedoch nur eine von vielen, nicht äquivalenten Formulierungen. Daher ist das machsche Prinzip und sein Verhältnis zur ART bis heute umstritten. Beispielsweise fand Kurt Gödel 1949 ein nach den Gesetzen der ART mögliches Universum, das sogenannte Gödel-Universum, das manchen spezifischen Formulierungen des machschen Prinzips widerspricht. Es gibt jedoch andere spezifische Formulierungen des Prinzips, denen das Gödel-Universum nicht zuwiderläuft. Astronomische Beobachtungen zeigen allerdings, dass sich das reale Universum stark von Gödels Modell unterscheidet.

Einstein sah den Lense-Thirring-Effekt, den die ART vorhersagte, als eine Bestätigung seiner Version des machschen Prinzips. Folge dieses Effektes ist, dass Bezugssysteme innerhalb einer rotierenden massebehafteten Hohlkugel eine Präzession erfahren, was Einstein so interpretierte, dass die Masse der Kugel Einfluss auf die Trägheitskräfte hat. Da jedoch bei der Rechnung und der Interpretation ein „ruhendes“ Bezugssystem in Form eines Fixsternhimmels angenommen wurde, ist auch diese Interpretation umstritten.

Die allgemein gehaltene Version des machschen Prinzips, die Einstein formulierte, ist also zu ungenau, um entscheiden zu können, ob sie mit der ART vereinbar ist.

Äquivalenzprinzip

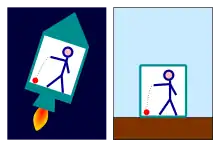
Gemäß dem Äquivalenzprinzip kann man innerhalb eines fensterlosen Raums nicht entscheiden, ob er im Gravitationsfeld eines Planeten steht, oder ob er wie eine Rakete im Weltraum beschleunigt wird.

Bereits in der klassischen Mechanik war das Prinzip der Äquivalenz von träger und schwerer Masse bekannt. Es besagt in seiner klassischen Form, die man auch als schwaches Äquivalenzprinzip bezeichnet, dass die schwere Masse, die angibt, wie stark die durch ein Gravitationsfeld an einem Körper erzeugte Kraft ist, und die träge Masse, die durch das Kraftgesetz festlegt, wie stark ein Körper durch eine Kraft beschleunigt wird, äquivalent sind. Dies bedeutet insbesondere, dass sich jeder Körper unabhängig von seiner Masse in einem Schwerefeld (bei Abwesenheit anderer Kräfte) gleich bewegt. (Geladene Körper sind davon aufgrund der Synchrotronstrahlung ausgeschlossen.) So fallen beispielsweise im Vakuum alle (ungeladenen) Körper gleich schnell, und die geostationäre Bahn ist für schwere Satelliten wie für leichte Satelliten stets dieselbe. Folge des klassischen Äquivalenzprinzips ist, dass ein Beobachter in einem geschlossenen Labor, ohne Information von außen, aus dem mechanischen Verhalten von Gegenständen im Labor nicht ablesen kann, ob er sich in Schwerelosigkeit oder im freien Fall befindet.

Dieses Prinzip wurde von Einstein verallgemeinert: Das einsteinsche starke Äquivalenzprinzip besagt, dass ein Beobachter in einem geschlossenen Labor ohne Wechselwirkung mit der Umgebung durch überhaupt kein Experiment feststellen kann, ob er sich in der Schwerelosigkeit fernab von Massen befindet oder im freien Fall nahe einer Masse. Das bedeutet insbesondere, dass auch ein Lichtstrahl für einen Beobachter im freien Fall nicht – wie in einem beschleunigten Bezugssystem – parabelförmig gekrümmt ist. Andererseits muss ein Beobachter, der im Gravitationsfeld ruht, z. B. indem er auf der Erdoberfläche steht, einen Lichtstrahl gekrümmt wahrnehmen, da er die ganze Zeit gegen den freien Fall nach oben beschleunigt wird.

Es muss allerdings beachtet werden, dass dieses Prinzip wegen der im Gravitationsfeld auftretenden Gezeitenkräfte nur lokal gilt:

So wird ein „unten“ (näher am Gravizentrum) befindliches Objekt stärker angezogen als ein weiter „oben“ befindliches. Ist der frei fallende Raum in vertikaler Richtung groß genug, so wird der Beobachter daher feststellen, dass sich Objekte, die sich weiter oben befinden, von denen, die sich weiter unten befinden, entfernen.
Umgekehrt wird sich bei ausreichender horizontaler Ausdehnung des Raumes die Richtung der Anziehungskraft auf zwei horizontal voneinander entfernte Objekte merklich unterscheiden, da sie beide in Richtung des Gravitationszentrums beschleunigt werden. Daher wird der frei fallende Beobachter feststellen, dass sich weit auseinander gelegene Körper aufeinander zubewegen. Ein ausgedehnter Körper wird also eine Kraft erfahren, die ihn in eine Richtung auseinanderzieht und in den dazu senkrechten Richtungen zusammendrückt.

In der ART folgt das Äquivalenzprinzip direkt aus der Beschreibung der Bewegung von Körpern: Da sich alle Körper entlang Geodäten der Raumzeit bewegen, kann ein Beobachter, der sich entlang einer Geodäte bewegt, nur dann eine Krümmung der Raumzeit feststellen, die er als Gravitationsfeld interpretieren könnte, wenn das von ihm beobachtbare Raumzeitstück maßgeblich gekrümmt ist. In diesem Fall beobachtet er die oben genannten Gezeitenkräfte als eine relative Annäherung oder Entfernung benachbarter frei fallender Körper. Die Krümmung sorgt auch dafür, dass geladene Körper nichtlokal mit ihrem eigenen Feld wechselwirken und daher das Äquivalenzprinzip auf diese prinzipiell nicht anwendbar ist, da ihr elektromagnetisches Feld grundsätzlich langreichweitig ist.[11]

Raumzeitkrümmung

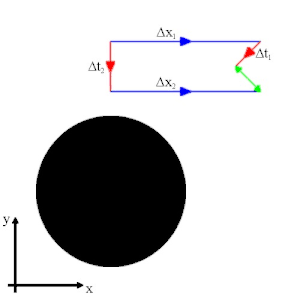
Paralleltransporte nahe einer massiven Kugel.
Blaue Pfeile stellen Paralleltransporte im Raum entlang der x-Achse dar.
Rote Pfeile stellen die Bewegung im Raum bei einem Paralleltransport entlang der Zeitachse dar, der einem freien Fall entspricht.
Die Längen der gleichartigen Paralleltransporte sind dabei jeweils gleich, also Δx₁ = Δx₂ und Δt₁ = Δt₂. Beim ersten, oberen Weg wird zuerst der Transport in x-Richtung ausgeführt und dann der Transport in Zeitrichtung. Beim zweiten, unteren Weg wird die Reihenfolge der Paralleltransporte vertauscht. Der grüne Doppelpfeil illustriert die verschiedenen Endpunkte bei Vertauschung der Paralleltransporte.

Die Krümmung der Raumzeit, die in diesem Abschnitt erläutert wird, ist kein unabhängiges Konzept, sondern eine Folgerung aus dem Äquivalenzprinzip. Mit Hilfe des Äquivalenzprinzips lässt sich daher auch der Begriff der Raumzeitkrümmung anschaulich erläutern. Dafür muss zunächst der Begriff des Paralleltransports entlang der Zeitachse erklärt werden.

Ein Paralleltransport ist eine Verschiebung in einer Richtung, bei der die Ausrichtung des zu Verschiebenden beibehalten wird, also ein lokales Koordinatensystem mitgeführt wird. Eine bloße Verschiebung in einer Raumrichtung ist in einer Raumzeit ohne Massen anschaulich verständlich. Die Definition der Zeit ist nach der speziellen Relativitätstheorie von der Bewegung des Koordinatensystems abhängig. Eine konstante Zeitrichtung ist dabei nur für unbeschleunigte Koordinatensysteme gegeben. In diesem Fall bedeutet eine Verschiebung in Zeitrichtung in einer Raumzeit ohne Massen, dass ein Gegenstand relativ zum Koordinatensystem ruht. Er bewegt sich dann entlang der Zeitachse dieses Koordinatensystems. (Verglichen werden die unbewegten Anfangs- und Endzustände.)

Nach dem Äquivalenzprinzip lässt sich damit der Paralleltransport entlang der Zeitachse in einem Gravitationsfeld verstehen. Das Äquivalenzprinzip besagt, dass ein frei fallender Beobachter in einem Gravitationsfeld äquivalent zu einem unbeschleunigten Beobachter fernab eines Gravitationsfeldes ist. Daher entspricht ein Paralleltransport entlang der Zeitachse um ein Zeitintervall t einem freien Fall der Dauer t. Das bedeutet, dass eine Parallelverschiebung in der Zeit auch eine Bewegung im Raum zur Folge hat. Da aber die Richtung des freien Falls vom Ort abhängig ist, macht es nun einen Unterschied, ob ein Beobachter zuerst im Raum und dann in der Zeit parallel verschoben wird oder umgekehrt. Man sagt, der Paralleltransport ist nicht kommutativ, das heißt, die Reihenfolge der Transporte ist bedeutsam.

Bisher wurden große Verschiebungen betrachtet, bei denen offensichtlich die Reihenfolge der Paralleltransporte bedeutend ist. Es ist jedoch sinnvoll, Aussagen über beliebig kleine Bereiche der Raumzeit machen zu können, um auch für kurze Zeiten und Strecken das Verhalten von Körpern beschreiben zu können. Wenn man die Paralleltransporte über immer kürzere Distanzen und Zeiten vornimmt, sind die Endpunkte für verschiedene Reihenfolgen der Transporte weiterhin verschieden, wobei der Unterschied sich aber entsprechend verkleinert. Mit Hilfe von Ableitungen lässt sich ein infinitesimal kleiner Paralleltransport an einem Punkt beschreiben. Das Maß für die Abweichung der Endpunkte bei Vertauschung der Reihenfolge zweier Paralleltransporte ist dann durch den sogenannten Krümmungstensor gegeben.

Durch die Raumzeitkrümmung lassen sich auch die oben erwähnten Gezeitenkräfte erklären. Zwei Kugeln im freien Fall in einem frei fallenden Labor bewegen sich beide entlang der Zeitachse, also auf zueinander parallelen Linien. Die Tatsache, dass die Paralleltransporte nicht kommutativ sind, ist äquivalent dazu, dass parallele Linien keinen konstanten Abstand haben. Die Bahnen der Kugeln können sich also einander nähern oder voneinander entfernen. Im Erdschwerefeld ist die Annäherung selbst bei sehr langem Fall nur sehr klein.

Zur Beschreibung der Krümmung ist es nicht nötig, die Raumzeit in einen höherdimensionalen Raum einzubetten. Die Krümmung ist nicht als Krümmung in eine fünfte Dimension zu verstehen oder als eine Krümmung des Raumes in die vierte Dimension, sondern als Krümmung ohne Einbettung oder eben als Nichtkommutativität von Paralleltransporten. (Eine Prämisse dieser Darstellung ist es, Raum und Zeit als vierdimensionale Raumzeit zu behandeln. Raum- und Zeitkoordinaten sind also weitgehend analog, und es besteht nur ein subtiler mathematischer Unterschied im Vorzeichen der Signatur.)

In welcher Weise die Raumzeit gekrümmt ist, wird durch die einsteinschen Feldgleichungen festgelegt.

Mathematische Beschreibung

Grundbegriffe

Die mathematische Beschreibung der Raumzeit und ihrer Krümmung erfolgt mit den Methoden der Differentialgeometrie, die die Euklidische Geometrie des uns vertrauten „flachen“ dreidimensionalen Raumes der klassischen Mechanik umfasst und erweitert. Die Differentialgeometrie verwendet zur Beschreibung gekrümmter Räume, wie der Raumzeit der ART, sogenannte Mannigfaltigkeiten. Wichtige Eigenschaften werden mit sogenannten Tensoren beschrieben, die Abbildungen auf der Mannigfaltigkeit darstellen.

Die gekrümmte Raumzeit wird als Lorentz-Mannigfaltigkeit beschrieben.
Eine besondere Bedeutung kommt dem metrischen Tensor zu. Wenn man in den metrischen Tensor zwei Vektorfelder einsetzt, erhält man für jeden Punkt der Raumzeit eine reelle Zahl. In dieser Hinsicht kann man den metrischen Tensor als ein verallgemeinertes, punktabhängiges Skalarprodukt für Vektoren der Raumzeit verstehen. Mit seiner Hilfe werden Abstand und Winkel definiert und er wird daher kurz als Metrik bezeichnet.
Ebenso bedeutend ist der riemannsche Krümmungstensor zur Beschreibung der Krümmung der Mannigfaltigkeit, der eine Kombination von ersten und zweiten Ableitungen des metrischen Tensors darstellt. Wenn ein beliebiger Tensor in irgendeinem Koordinatensystem in einem Punkt nicht null ist, kann man überhaupt kein Koordinatensystem finden, sodass er in diesem Punkt null wird. Dies gilt dementsprechend auch für den Krümmungstensor. Umgekehrt ist der Krümmungstensor in allen Koordinatensystemen null, wenn er in einem Koordinatensystem null ist. Man wird also in jedem Koordinatensystem bezüglich der Frage, ob eine Mannigfaltigkeit an einem bestimmten Punkt gekrümmt ist oder nicht, zum gleichen Ergebnis gelangen.
Die maßgebliche Größe zur Beschreibung von Energie und Impuls der Materie ist der Energie-Impuls-Tensor. Wie dieser Tensor die Krümmungseigenschaften der Raumzeit bestimmt, zeigt der folgende Abschnitt.

Einsteinsche Feldgleichungen

Die einsteinschen Feldgleichungen stellen einen Zusammenhang zwischen einigen Krümmungseigenschaften der Raumzeit und dem Energie-Impuls-Tensor her, der die lokale Massendichte beziehungsweise über $E=mc^{2}$ die Energiedichte enthält und damit die relevanten Eigenschaften der Materie charakterisiert.

Diese Grundgleichungen der allgemeinen Relativitätstheorie sind Differentialgleichungen für die 10 unabhängigen Komponenten der Metrik $g_{\mu \nu }$ :

R_{\mu \nu }-{\frac {R}{2}}\,g_{\mu \nu }+\Lambda \ g_{\mu \nu }={\frac {8\ \pi \ G}{c^{4}}}\ T_{\mu \nu }

Dabei ist $R_{\mu \nu }$ der Ricci-Krümmungstensor, $R$ der Ricci-Krümmungsskalar, $g_{\mu \nu }$ der metrische Tensor, $\Lambda$ die kosmologische Konstante, die aber auch häufig weggelassen wird (siehe unten), $c$ die Lichtgeschwindigkeit, $G$ die Gravitationskonstante und $T_{\mu \nu }$ der Energie-Impuls-Tensor. Da alle Tensoren in dieser Gleichung symmetrisch sind (z. B. $R_{\mu \nu }=R_{\nu \mu }$ ), sind nur 10 dieser 16 Gleichungen unabhängig voneinander.

Das Ziel ist es, die Komponenten des Energie-Impuls-Tensors auf der rechten Seite der Gleichungen vorzugeben und die Feldgleichungen dann zu verwenden, um die Metrik zu bestimmen. Der Ausdruck auf der linken Seite der Gleichung besteht aus Größen, die vom Krümmungstensor hergeleitet sind. Sie enthalten daher Ableitungen der gesuchten Metrik. Man erhält also 10 Differentialgleichungen für die Komponenten der Metrik. Die Metrik und ihre Ableitungen finden sich jedoch meist auch auf der rechten Seite der Gleichungen im Energie-Impuls-Tensor. Erschwerend kommt hinzu, dass die Summe zweier Lösungen im Allgemeinen keine Lösung der Feldgleichungen ist, die Lösungen sind also nicht superponierbar. Dies liegt an der Nichtlinearität der Feldgleichungen, die als ein Hauptkennzeichen der ART gilt. Aufgrund dieser Komplexität der Gleichungen ist es oft nicht möglich, exakte Lösungen für die Feldgleichungen zu finden. In solchen Fällen können zum Teil Verfahren zum Finden einer Näherungslösung verwendet werden.

In den Feldgleichungen steht nicht der Krümmungstensor, sondern nur der aus ihm abgeleitete Ricci-Krümmungstensor und der Ricci-Krümmungsskalar. Diese beiden Summanden werden zusammengefasst auch als Einsteintensor $G_{\mu \nu }$ bezeichnet, wobei dieser nicht alle Informationen über die Krümmung der Raumzeit enthält. Ein Teil der Raumzeitkrümmung, die sogenannte Weyl-Krümmung, ist also nicht direkt vom Energie-Impuls-Tensor und damit von der Massen- und Energiedichte abhängig. Allerdings ist der Weyl-Krümmungstensor nicht frei wählbar, da er aufgrund der geometrischen Bianchi-Identitäten teilweise durch den Ricci-Krümmungstensor festgelegt wird.[12]

Einstein glaubte zunächst, dass das Universum seine Größe nicht mit der Zeit ändere, daher führte er die kosmologische Konstante $\Lambda$ ein, um ein solches Universum theoretisch zu ermöglichen. Das Gleichgewicht, das er damit erreichte, erwies sich jedoch als instabiles Gleichgewicht. $\Lambda$ hat formal den Stellenwert einer Art Integrationskonstante, und hat daher zunächst keinen bestimmten Zahlenwert, der direkt aus der Theorie folgen würde. Sie muss also experimentell bestimmt werden.[13] Eine alternative Sicht auf die kosmologische Konstante fasst den entsprechenden Term als Teil des Energie-Impuls-Tensors auf und setzt $T_{\Lambda }^{\mu \nu }={\frac {c^{4}}{8\ \pi \ G}}\ \Lambda \ g^{\mu \nu }$ . Das bedeutet, dass die kosmologische Konstante sich als ideale Flüssigkeit mit negativem Druck darstellt und als außergewöhnliche Form von Materie oder Energie aufgefasst wird. In der heutigen Kosmologie hat sich in diesem Zusammenhang die Bezeichnung „Dunkle Energie“ durchgesetzt.

Die Feldgleichungen geben an, wie der Materie- und Energieinhalt sich auf die Krümmung der Raumzeit auswirkt. Sie enthalten jedoch auch alle Informationen über die Auswirkung der Raumzeitkrümmung auf die Dynamik von Teilchen und Feldern, also über die andere Richtung der Wechselwirkung. Dennoch verwendet man nicht direkt die Feldgleichungen, um die Dynamik von Teilchen oder Feldern zu beschreiben, sondern leitet dazu die Bewegungsgleichungen her. Die Bewegungsgleichungen sind also „technisch“ von Bedeutung, obwohl ihr Informationsinhalt konzeptionell bereits in den Feldgleichungen enthalten ist.

Eine besonders elegante Herleitung der einsteinschen Feldgleichungen bietet das Prinzip der kleinsten Wirkung, das auch in der newtonschen Mechanik eine wichtige Rolle spielt. Eine geeignete Formel für die Wirkung, deren Variation im Rahmen der Variationsrechnung zu diesen Feldgleichungen führt, ist die Einstein-Hilbert-Wirkung, die erstmals von David Hilbert angegeben wurde.

Bewegungsgleichungen

Um die Bewegungsgleichungen formulieren zu können, muss eine beliebige Weltlinie eines Körpers parametrisiert werden. Das kann beispielsweise geschehen, indem ein Nullpunkt und eine positive Richtung festgelegt werden und dann jedem Punkt auf der Weltlinie die Bogenlänge vom Nullpunkt bis zu diesem Punkt mit dem entsprechenden Vorzeichen zugeordnet wird. So stellt man sicher, dass jeder Punkt auf der Weltlinie eindeutig bestimmt ist. Eine sehr ähnliche Parametrisierung ist die Parametrisierung nach der Eigenzeit. Die beiden sind identisch, wenn man die Gleichungen durch Ignorieren aller Faktoren c vereinfacht, indem man also formal die Lichtgeschwindigkeit $c=1$ setzt. Die folgenden Formeln sind in Bogenlängenparametrisierung zu verstehen.

Im Folgenden bezeichnet der Begriff „Kraft“ nie die Gravitation (die als geometrischer Effekt aufgefasst wird), sondern andere Kräfte, zum Beispiel die elektromagnetische oder mechanische Kräfte. Betrachtet man nun einen Körper, auf den eine Kraft $K^{\mu }\$ wirkt, so lauten die Bewegungsgleichungen:

m\ {\ddot {x}}^{\mu }+m\ \Gamma _{\lambda \nu }^{\mu }\ {\dot {x}}^{\lambda }\ {\dot {x}}^{\nu }=K^{\mu }.

Für den Fall, dass auf einen Körper keine Kraft wirkt, wird seine Weltlinie durch die Geodätengleichungen der gekrümmten Raumzeit beschrieben. Man erhält sie, indem man im obigen Kraftgesetz die Kraft $K^{\mu }\ =0$ setzt:

{\ddot {x}}^{\mu }+\Gamma _{\lambda \nu }^{\mu }\ {\dot {x}}^{\lambda }\ {\dot {x}}^{\nu }=0.

Dabei ist m die Masse des Körpers und $\left(x^{\mu }\right)=(x^{0},\,x^{1},\,x^{2},\,x^{3})$ sind die vier Raumzeit-Komponenten der Weltlinie des Körpers; $x^{0}$ steht für die Zeit-Komponente. Punkte über den Größen sind Ableitungen nach der Bogenlänge und nicht nach der Zeitkomponente $x^{0}$ .

\textstyle \Gamma _{\lambda \nu }^{\mu }={\dfrac {g^{\mu \rho }}{2}}\left(\partial _{\lambda }\ g_{\nu \rho }+\partial _{\nu }\ g_{\lambda \rho }-\partial _{\rho }\ g_{\lambda \nu }\right)

ist ein Christoffelsymbol, das die Abhängigkeit des metrischen Tensors vom Raumzeitpunkt, also die Raumzeitkrümmung, charakterisiert. Die $g^{\mu \rho }$ sind Komponenten des kometrischen Tensors, der invers zum metrischen Tensor $g_{\nu \rho }$ ist. In der Formel werden außerdem Kurzschreibweisen verwendet: $\textstyle \partial _{\mu }:={\tfrac {\partial }{\partial x^{\mu }}}$ für die partiellen Ableitungen, ferner die Summenkonvention, die besagt, dass über Indizes, die jeweils einmal oben und einmal unten stehend auftauchen, automatisch von 0 bis 3 summiert wird.

Das Kraftgesetz ist eine Verallgemeinerung des klassischen Aktionsprinzips ( ${\vec {K}}=m\ {\ddot {\vec {x}}}$ ) auf vier Dimensionen einer gekrümmten Raumzeit. Die Gleichungen lassen sich erst lösen, wenn der metrische Tensor bekannt ist. Umgekehrt ist der metrische Tensor erst bekannt, wenn die Gleichungen für alle Bahnen gelöst sind. Diese intrinsische Forderung der Selbstkonsistenz ist ein Grund für die Schwierigkeit der Theorie.

Prinzipiell können nun die Bewegungsgleichungen für eine Teilchenwolke und die einsteinschen Feldgleichungen als Gleichungssystem betrachtet werden, das die Dynamik einer Wolke massiver Teilchen beschreibt. Aufgrund der oben erwähnten Schwierigkeiten bei der Lösung der Feldgleichungen ist dies jedoch praktisch nicht durchführbar, sodass für Mehrteilchensysteme immer mit Näherungen gerechnet wird.

Die Kräfte, die auf einen Körper wirken, berechnen sich dabei im Allgemeinen etwas anders als in der speziellen Relativitätstheorie. Da die Formeln in der ART koordinatenkovariant geschrieben werden müssen, ist in den Formeln für die Kräfte, zum Beispiel in den Maxwell-Gleichungen, anstelle der partiellen Ableitung nach Raumzeitkomponenten nun die kovariante Ableitung zu verwenden. Da die Ableitungen nach Raumzeitkomponenten die Änderungen einer Größe beschreiben, heißt das, dass die Änderungen aller Felder (also ortsabhängige Größen) nun in der gekrümmten Raumzeit beschrieben werden müssen. Die Maxwell-Gleichungen ergeben sich damit zu

D_{\mu }\ F^{\mu \nu }=4\ \pi \ J^{\nu }

und

D_{\mu }F_{\nu \rho }+D_{\nu }\ F_{\rho \mu }+D_{\rho }\ F_{\mu \nu }=\partial _{\mu }\ F_{\nu \rho }+\partial _{\nu }\ F_{\rho \mu }+\partial _{\rho }\ F_{\mu \nu }=0.

Die Verwendung der kovarianten Ableitungen $D_{\mu }\$ betrifft also nur die inhomogenen Maxwellgleichungen, während die homogenen Gleichungen sich gegenüber der klassischen Form nicht ändern. Die Definitionen der kovarianten Ableitungen von Tensoren sind dem Artikel Christoffelsymbole zu entnehmen.

Metriken

Eine „Metrik“ als kurze Bezeichnung für ein Feld metrischer Tensoren stellt eine bestimmte Geometrie der Raumzeit und Lösung der Gleichungen der Allgemeinen Relativitätstheorie dar. Die Minkowski-Metrik entspricht dem einfachsten Fall einer flachen Raum-Zeit ohne große Massen, die die Raumzeit krümmen.

Metriken Schwarzer Löcher

Ein Schwarzes Loch ist eine kompakte Zentralmasse und verursacht als einfachste Metrik ein kugelsymmetrisches Gravitationsfeld.

Schwarzschild-Metrik

Die Schwarzschild-Metrik war eine der ersten Lösungen einer Metrik, die nach der Veröffentlichung der Allgemeinen Relativitätstheorie entwickelt wurden. Karl Schwarzschild führte Polarkoordinaten als Schwarzschild-Koordinaten ein. So konnte Schwarzschild zum ersten Mal das Gravitationsfeld einer ungeladenen, nichtrotierenden Kugel beschreiben, deren Masse gleichmäßig verteilt war. Die Schwarzschild-Metrik wird somit als erste Beschreibung eines Schwarzen Loches angenommen. Schwarzschild berechnete neben der äußeren Vakuumlösung auch eine innere Lösung für eine homogene Kugel.

Es gibt diverse andere Beschreibungen für die Metrik einer Zentralmasse, z. B. Kruskal-Szekeres-Koordinaten, Eddington–Finkelstein Koordinaten, Gullstrand–Painlevé Koordinaten und Lemaître Koordinaten. Das River-Modell beschreibt das Innere eines Schwarzen Loches.

Kerr-Metrik

Die Kerr-Metrik beschreibt rotierende, ungeladene Objekte in der Raumzeit, ist also gut zur Beschreibung rotierender Schwarzer Löcher geeignet. Sie wurde nach Roy Kerr benannt, der 1963 die Lösung gefunden hatte. In dieser Metrik gibt es zwei singuläre Raumzeitregionen, in der Mitte liegt die Ergosphäre (detaillierter beschrieben in Kerr-Metrik). Das Besondere an dieser Metrik ist, dass die Singularität bei $r=0$ eines Schwarzen Loches ringförmig ist.

Reissner-Nordström-Metrik

Die Reissner-Nordström-Metrik beschreibt elektrisch geladene, statische (also nicht rotierende) Schwarze Löcher. Ihr Linienelement ähnelt dem der Schwarzschild-Metrik. Hierbei existiert ein zusätzlicher Parameter Q, der die elektrische Ladung beschreibt.

Kerr-Newman-Metrik

Die Kerr-Newman-Metrik beschreibt elektrisch geladene und rotierende Schwarze Löcher. Im Falle eines elektrisch neutralen Schwarzen Loches $(Q=0)$ vereinfachen sich die Lösungen zur simpleren Kerr-Metrik, bei fehlendem Drehimpuls $J=0$ zur Reissner-Nordström-Metrik und bei $J=0$ und $Q=0$ zur Schwarzschild-Metrik.

Gödel-Metrik

Die Gödel-Metrik wurde von Kurt Gödel im Jahr 1949 entwickelt. Sie beschreibt eine rotierende Raumzeit auf der Basis von Einsteins Feldgleichungen. Das Rotationszentrum ist an jedem Punkt der Raumzeit gleichermaßen vorhanden, dies fordert das kosmologische Prinzip. Eine Konsequenz aus seinem eher mathematischen Modell ist, dass klassische Weltlinien bei einer solchen Raumzeit auch in die Vergangenheit verlaufen können. Sein Modell erregte einiges Aufsehen, weil er bewies, dass Einsteins Feldgleichungen die mathematische Behandlung von Raumzeiten gestatten, in denen Zeitreisen möglich sind.

Kruskal-Lösung

Die Kruskal-Lösung ist eine maximale Erweiterung der Schwarzschild-Lösung. Sie weist intrinsische Singularitäten auf, weshalb sie nicht vollständig ist. Die Lösung kann als eine Beschreibung von Einstein-Rosen-Brücken bzw. Wurmlöchern angesehen werden.

Robertson-Walker-Metrik

Die Robertson-Walker-Metrik (auch „Friedmann-Lemaître-Robertson-Walker-Metrik“ genannt) beschreibt ein homogenes Universum nach dem kosmologischen Prinzip. Sie wird als Näherung in einigen Urknalltheorien verwendet. Da das exakte Modell voraussetzen würde, dass sich keine Strukturen wie Galaxien und Sterne im Universum bilden könnten, verwendet man ein Fast-FLRM-Modell, das kleine Störungen bzw. Dichteschwankungen mit einberechnen kann.

De-Sitter-Raum

Der De-Sitter-Raum ist eine maximale symmetrische Vakuumlösung der Feldgleichungen, die eine positive kosmologische Konstante beinhaltet, also ist der Raum positiv gekrümmt. Er kann als Untermannigfaltigkeit zu einem höherdimensionalen Minkowski-Raum angesehen werden.

Der De-Sitter-Kosmos ist ein Modell, das diese Überlegungen beinhaltet. Wählt man eine Friedmann-Lösung mit verschwindender Krümmung ( $k=0$ in der Robertson-Walker-Metrik) und ohne Materie, ergibt sich als Lösung ein flacher, sich ausdehnender De-Sitter-Kosmos mit Radius $R(t)\sim e^{Ht}$ und der Hubble-Konstanten $H=c\cdot {\sqrt {\Lambda /3}}.$

Daher wird von den meisten Kosmologen angenommen, dass das Universum in seiner Anfangsphase ein De-Sitter-Raum gewesen sei, der sich ausbreitete (siehe Inflation). Der Kosmos könnte sich allerdings in ferner Zukunft so einem materiefreien Zustand erneut annähern.

Anti-De-Sitter-Raum

Der Anti-de-Sitter-Raum ist das Gegenstück zum De-Sitter-Raum, hat also eine negative kosmologische Konstante und ist daher negativ gekrümmt. Der Raum ist so interessant, weil er besondere physikalische Eigenschaften besitzt und weil er oft mit dem holografischen Prinzip und der Stringtheorie in Verbindung gebracht wird.

Physikalische Effekte

Zur experimentellen Überprüfung der ART[14] reicht es nicht aus, Experimente durchzuführen, mit denen man zwischen der ART und der newtonschen Mechanik entscheiden kann, da es konkurrierende Theorien zur ART gibt. Es ist daher auch nötig, experimentell zwischen der ART und anderen Gravitationstheorien zu entscheiden. Abweichungen von den Vorhersagen der ART könnten auch ein neuer Anstoß zur Entwicklung einer schlüssigen und experimentell überprüfbaren Quantentheorie der Raumzeit sein.

Die allgemeine Relativitätstheorie sagt die experimentellen Ergebnisse im Rahmen der Messgenauigkeit richtig voraus. Das Äquivalenzprinzip ist mit einer Messgenauigkeit von bis zu 10⁻¹³ bestätigt,[15] für andere Phänomene der ART bis zu 10⁻⁵.[16] Im Folgenden werden einige physikalische Phänomene erklärt, deren genaue experimentelle Überprüfung bisher die ART gut bestätigt und den Spielraum für Alternativtheorien sehr verkleinert hat. Außerdem lassen die guten Übereinstimmungen von Experiment und Vorhersage erwarten, dass Quanteneffekte der Gravitation sehr klein sind, da sie als Abweichungen von den Vorhersagen der ART erkennbar sein müssten.

Gravitative Zeitdilatation und Rotverschiebung

Gravitative Rotverschiebung einer Lichtwelle

Die gravitative Zeitdilatation folgt bereits aus der speziellen Relativitätstheorie und dem Äquivalenzprinzip der ART. Sie wurde von Einstein 1908 vorhergesagt.[2] Wenn man eine in einem Gravitationsfeld ruhende Uhr betrachtet, muss sie durch eine Gegenkraft in Ruhe gehalten werden, wie ein Mensch, der auf der Erdoberfläche steht. Sie wird also fortwährend beschleunigt, sodass man die Formel für die Zeitdilatation in einem beschleunigten Bezugssystem aus der speziellen Relativitätstheorie benutzen kann. Dies hat zur Folge, dass der Effekt nicht symmetrisch ist, wie man es von zwei gleichförmig bewegten Bezugssystemen in der speziellen Relativitätstheorie kennt. Ein Beobachter im Weltall sieht also die Uhren auf der Erde langsamer gehen als seine eigene Uhr. Umgekehrt sieht ein Beobachter auf der Erde Uhren im Weltall schneller gehen als seine eigene Uhr. Mit sehr genauen optischen Atomuhren lässt sich die gravitative Zeitdilatation auch noch bei einem Höhenunterschied nur einiger Zentimeter messen.[17]

Eine direkte Folge der Zeitdilatation ist die gravitative Rotverschiebung. Sie wurde von Einstein bereits 1911 vor Fertigstellung der allgemeinen Relativitätstheorie vorausgesagt. Da beide Effekte bereits aus dem Äquivalenzprinzip hergeleitet werden können, ist ihre experimentelle Bestätigung für sich genommen keine Bestätigung für die Gültigkeit der ART. Würde jedoch ein von der Vorhersage abweichendes Verhalten beobachtet, würde dies die ART widerlegen. Die experimentelle Bestätigung der Effekte ist also für die Gültigkeit der Theorie notwendig, aber nicht hinreichend.

Die Rotverschiebung bedeutet, dass Licht, das von einer Lichtquelle mit einer gegebenen Frequenz nach „oben“ (also vom Gravitationszentrum weg) ausgestrahlt wird, dort mit einer geringeren Frequenz gemessen wird, ähnlich wie beim Doppler-Effekt. Demnach ist bei einem Lichtsignal mit einer bestimmten Anzahl von Schwingungen der zeitliche Abstand zwischen dem Beginn und dem Ende des Signals beim Empfänger größer als beim Sender. Die gravitative Rotverschiebung wurde erstmals 1960 im Pound-Rebka-Experiment nachgewiesen. 2018 wurde die gravitative Rotverschiebung beim Stern S2 bei dessen größter Annäherung an das schwarze Loch in Sagittarius A* im Zentrum der Milchstraße durch die Gravity Kollaboration nachgewiesen.[18]

Lichtablenkung und Lichtverzögerung

Simulation der Ablenkung des Lichts eines Sterns (rot) im Gravitationsfeld eines Neutronensterns (blau).

Licht nahe einer großen Masse bewegt sich aus Sicht eines entfernten Beobachters langsamer als mit Vakuumlichtgeschwindigkeit. Dieses Phänomen wird nach seinem Entdecker als Shapiro-Verzögerung bezeichnet. Außerdem nimmt ein entfernter Beobachter eine Ablenkung des Lichts nahe großer Massen wahr. Diese beiden Effekte gehen auf dieselbe Erklärung zurück. Die reale Zeit, die sogenannte Eigenzeit, ist nahe der Masse verschieden vom Zeitbegriff des entfernten Beobachters. Außerdem hat die Masse auch Auswirkungen auf das Verhalten des Raums, ähnlich einer Lorentzkontraktion, was sich nur im Rahmen der ART und nicht klassisch erklären lässt. Ein Beobachter, der sich selbst nahe der Masse befindet, wird dementsprechend die Vakuumlichtgeschwindigkeit als Geschwindigkeit des Lichtstrahls messen. Der entfernte Beobachter nimmt jedoch eine verringerte Geschwindigkeit wahr, die er als ortsabhängigen Brechungsindex beschreiben kann. Diese Beschreibung liefert auch eine Erklärung für die Lichtablenkung, die als eine Art Brechung interpretiert werden kann.

Die obige Erklärung beruht auf einer Analogie. Die abstrakte Interpretation im Rahmen der ART ist, dass die Nullgeodäten, auf denen sich Licht bewegt, nahe großer Massen im Raum gekrümmt erscheinen. Es ist dabei zu berücksichtigen, dass sich das Licht auch in der Zeit bewegt, sodass hier tatsächlich eine Raumzeitkrümmung und keine reine Krümmung des dreidimensionalen Raumes vorliegt.

Der Ablenkwinkel $\alpha _{\text{ablenk}}$ ist von der Masse $M$ der Sonne, dem Abstand $r$ vom sonnennächsten Punkt der Bahn zum Mittelpunkt der Sonne und der Lichtgeschwindigkeit $c$ abhängig. Er kann nach der Gleichung

\alpha _{\text{ablenk}}\,=\,{\frac {4\ G\,M}{r\ c^{2}}}\,=\,{\frac {4\ r_{G}}{r}}

berechnet werden. Darin ist $G$ die Gravitationskonstante und $r_{G}$ der Gravitationsradius.

Auf Ablenkung von Licht im Gravitationsfeld beruht auch der in der Astronomie beobachtete Gravitationslinseneffekt.

Periheldrehung

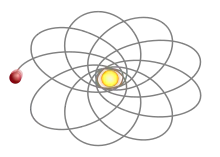
Die Periheldrehung der Bahn eines Planeten. Die Exzentrizität der Bahn und der Betrag der Drehung sind gegenüber der realen Periheldrehung des Merkur stark übertrieben.

Die Periheldrehung der Planetenbahnen – z. B. der Bahn der Erde um die Sonne – ist ein Effekt, der zum größten Teil durch die Gravitationskraft anderer Planeten (z. B. des Jupiters) entsteht. Beim Merkur misst man 571″ pro Jahrhundert, von denen 43,3″ nicht aus diesen Störungen resultieren. Die Relativitätstheorie konnte diesen Wert erklären (durch ein im Vergleich zur Newtonschen Mechanik anderes effektives Potential), was ein erster Erfolg der Theorie war. Die Periheldrehung der Erde ist mit 1161″ pro Jahrhundert noch größer als die des Merkur, der relativistische Fehlbetrag beträgt bei der Erde aber lediglich 5″. Auch die gemessenen Fehlbeiträge zur Periheldrehung anderer Planeten sowie auch des Kleinplaneten Icarus stimmen mit den Vorhersagen der Relativitätstheorie überein. Die in Planung befindliche europäisch-japanische Merkursonde BepiColombo soll es ermöglichen, die Bewegung des Merkur mit bisher unerreichter Genauigkeit zu bestimmen und damit Einsteins Theorie noch genauer zu testen.

Bei Doppelsternsystemen aus Sternen oder Pulsaren, die einander in sehr geringer Entfernung umkreisen, ist die Periheldrehung mit mehreren Grad pro Jahr deutlich größer als bei den Planeten des Sonnensystems. Auch die bei diesen Sternsystemen indirekt gemessenen Werte der Periheldrehung stimmen mit den Vorhersagen der ART überein.

Gravitationswellen

Ein Ring von Testpartikeln unter dem Einfluss einer Gravitationswelle

Zweidimensionale Darstellung von Gravitationswellen, die von zwei einander umkreisenden Neutronensternen ausgesandt werden.

Die ART ermöglicht die Beschreibung von Fluktuationen der Raumzeitkrümmung, die sich mit Lichtgeschwindigkeit ausbreiten. In erster Näherung sind diese Fluktuationen mit transversalen Wellen vergleichbar, daher werden sie als Gravitationswellen bezeichnet. Eine Beschreibung dieses Phänomens ohne Näherungen existiert bisher (2016) nicht. Gravitationswellen wären dadurch beobachtbar, dass sich quer (transversal) zu ihrer Ausbreitungsrichtung der Raum periodisch ausdehnt und zusammenzieht. Da es bei der Gravitation keine positive und negative Ladung wie beim Elektromagnetismus gibt, können Gravitationswellen nicht als Dipolstrahlung, sondern nur als Quadrupolstrahlung auftreten.[19] Außerdem ist die Kopplung der Gravitation an Materie sehr viel schwächer als beim Elektromagnetismus.

Daraus folgt eine sehr geringe Intensität der Gravitationswellen, was den Nachweis enorm erschwert. Das erwartete Verhältnis von Längenveränderung zur betrachteten Strecke liegt in der Größenordnung von 10⁻²¹, das entspricht etwa einem Tausendstel Protondurchmesser pro Kilometer. Aufgrund dieser Schwierigkeiten ist erst am 14. September 2015 der direkte Nachweis von Gravitationswellen gelungen.

Einen indirekten Nachweis von Gravitationswellen gibt es bereits länger, denn bei einander umkreisenden Sternen führen die Gravitationswellen zu einem Energieverlust des Sternensystems. Dieser Energieverlust äußert sich in einer Abnahme des gegenseitigen Abstandes und der Umlaufzeit, wie zum Beispiel am Doppelsternsystem PSR J1915+1606 beobachtet wurde.[20]

Schwarze Löcher

Eine Lösung der ART sagt voraus, dass ein äußerst kompakter Körper die Raumzeit so stark krümmt, dass sich eine Raumregion bildet, aus der kein Licht und damit auch keine Materie mehr entkommen kann. Eine solche Raumregion besitzt im Inneren eine Singularität und wurde erstmals 1916 von Karl Schwarzschild durch die Schwarzschild-Metrik beschrieben. Die Oberfläche, bei deren Überschreiten ein Lichtstrahl nicht mehr entkommen kann, wird als Ereignishorizont bezeichnet. Da ein Schwarzes Loch kein Licht aussenden oder reflektieren kann, ist es unsichtbar und kann lediglich indirekt über die Effekte der enormen Raumzeitkrümmung beobachtet werden.

Lense-Thirring-Effekt

Im Jahr 1918 wurde von dem Mathematiker Josef Lense und dem Physiker Hans Thirring der nach ihnen benannte Lense-Thirring-Effekt (auch Frame-Dragging-Effekt) theoretisch vorhergesagt. Der Effekt beschreibt die Beeinflussung des lokalen Inertialsystems durch eine rotierende Masse, was man sich vereinfacht so vorstellen kann, dass die rotierende Masse die Raumzeit um sich herum wie eine zähe Flüssigkeit geringfügig mitzieht und dadurch verdrillt.

Derzeit wird noch diskutiert, ob den Wissenschaftlern um Ignazio Ciufolini von der Universität Lecce und Erricos Pavlis von der University of Maryland in Baltimore im Jahr 2003 der experimentelle Nachweis des Effektes gelungen ist. Sie vermaßen dafür die Bahnen der geodätischen Satelliten LAGEOS 1 und 2 präzise, da deren Position und Lage von der Masse der sich drehenden Erde beeinflusst werden sollte. Aufgrund möglicher Fehlerquellen durch das uneinheitliche Schwerefeld der Erde ist umstritten, ob die zentimetergenauen Positionsbestimmungen der LAGEOS-Satelliten ausreichten, um diesen relativistischen Effekt nachzuweisen.

Der NASA-Satellit Gravity Probe B, gestartet im April 2004, ist mit mehreren präzisen Gyroskopen ausgestattet, die den Effekt sehr viel genauer vermessen können. Zur Messung des Effektes werden bei diesem Satelliten die Änderungen der Drehrichtungen von vier Gyroskopen bestimmt.

Kosmologie

Die Kosmologie ist ein Teilgebiet der Astrophysik, das sich mit dem Ursprung und der Entwicklung des Universums befasst. Da die Entwicklung des Universums maßgeblich durch die Gravitation bestimmt ist, ist die Kosmologie eines der Hauptanwendungsgebiete der ART. Im Standardmodell der Kosmologie wird das Universum als homogen und isotrop angenommen. Mit Hilfe dieser Symmetrien vereinfachen sich die Feldgleichungen der ART zu den Friedmann-Gleichungen. Die Lösung dieser Gleichungen für ein Universum mit Materie implizieren eine Phase der Expansion des Universums. Dabei ist das Vorzeichen der Skalarkrümmung auf kosmischer Skala entscheidend für die Entwicklung eines expandierenden Universums.

Bei einer positiven Skalarkrümmung wird das Universum zunächst expandieren und sich dann wieder zusammenziehen, bei verschwindender Skalarkrümmung wird die Expansionsgeschwindigkeit einen festen Wert annehmen, und bei negativer Skalarkrümmung wird das Universum beschleunigt expandieren.

Einstein fügte 1917 die kosmologische Konstante Λ ursprünglich in die Feldgleichungen ein, um ein Modell eines statischen Kosmos zu ermöglichen, was er nach Entdeckung der Expansion des Universums bedauerte. Die kosmologische Konstante kann je nach Vorzeichen die kosmische Expansion verstärken oder ihr entgegenwirken.

Astronomische Beobachtungen haben inzwischen das relativistische Weltmodell erheblich verfeinert und genaue quantitative Messungen der Eigenschaften des Universums gebracht. Beobachtungen entfernter Supernovae vom Typ 1a haben ergeben, dass das Universum beschleunigt expandiert. Messungen der räumlichen Struktur der Hintergrundstrahlung mit WMAP zeigen, dass die Skalarkrümmung innerhalb der Fehlergrenzen verschwindet. Diese und weitere Beobachtungen führen zur Annahme einer positiven kosmologischen Konstante. Die derzeitigen Erkenntnisse über die Struktur des Universums werden im Lambda-CDM-Modell zusammengefasst.

Verhältnis zu anderen Theorien

Klassische Physik

Die ART muss das newtonsche Gravitationsgesetz als Grenzfall enthalten, denn dieses ist für langsam bewegte und nicht zu große Massen gut bestätigt. Große Massen bewirken dagegen große Gravitationsbeschleunigungen an ihrer Oberfläche, die zu relativistischen Effekten wie beispielsweise der Zeitdilatation führen. Daher braucht für diese das newtonsche Gravitationsgesetz nicht zu gelten.

Auf der anderen Seite muss auch die spezielle Relativitätstheorie in Raumzeitgebieten, in denen die Gravitation vernachlässigbar ist, in der ART enthalten sein. Das bedeutet, dass für den Grenzfall einer verschwindenden Gravitationskonstanten G die spezielle Relativitätstheorie reproduziert werden muss. In der Nähe von Massen gilt sie nur noch in ausreichend kleinen Raumzeitgebieten.

Die Forderung, dass die Gleichungen der ART die beiden oben genannten Grenzfälle erfüllen müssen, bezeichnet man als Korrespondenzprinzip. Dieses Prinzip besagt, dass die Gleichungen veralteter Theorien, die in einem bestimmten Gültigkeitsbereich gute Ergebnisse liefern, für diesen Gültigkeitsbereich als Grenzfall in der neuen Theorie enthalten sein müssen. Einige Autoren gehen unter diesem Begriff in Bezug auf die ART nur auf einen der beiden Grenzfälle, meist bezüglich der newtonschen Gravitationstheorie, ein.

Die Bewegungsgleichungen klassischer, also nicht quantenmechanischer Feldtheorien ändern sich gegenüber der klassischen Mechanik, wie oben beschrieben wurde. Es ist also ohne Probleme möglich, gravitative und elektromagnetische Wechselwirkungen geladener Objekte gleichzeitig zu beschreiben. Insbesondere ist es möglich, eine nichtrelativistische (d. h. newtonsche, also naturgemäß unvollständige) optimale Näherung für die ART anzugeben. Darüber hinaus gibt es eine post-newtonsche Näherung an die Allgemeine Relativitätstheorie, die Terme für die Erzeugung der Gravitationsfelder gemäß der Einsteinschen Theorie einschließt und sich darin von den post-newtonschen Näherungen anderer metrischer Theorien der Gravitation unterscheidet und so zu deren experimenteller Unterscheidung dienen kann.[21]

Quantenphysik

Die ART ist bei sehr hohen Teilchenenergien im Bereich der Planck-Skala oder entsprechend bei sehr kleinen Raumzeitgebieten mit starker Krümmung nicht mit der Quantenphysik vereinbar. Obwohl es keine Beobachtung gibt, die der ART widerspricht und ihre Vorhersagen gut bestätigt sind, liegt es daher nahe, dass es eine umfassendere Theorie gibt, in deren Rahmen die ART ein Spezialfall ist. Dies wäre also eine Quantenfeldtheorie der Gravitation.

Die Formulierung einer Quantenfeldtheorie der Gravitation wirft jedoch Probleme auf, die mit den bisher bekannten mathematischen Methoden nicht lösbar sind. Das Problem besteht darin, dass die ART als Quantenfeldtheorie nicht renormierbar ist. Die Größen, die sich daraus berechnen lassen, sind also unendlich. Diese Unendlichkeiten können als prinzipielle Schwäche im Formalismus der Quantenfeldtheorien verstanden werden, und sie lassen sich bei anderen Theorien meist durch Renormierungsverfahren von den physikalisch sinnvollen Ergebnissen trennen. Bei der ART ist das aber mit den üblichen Verfahren nicht möglich, sodass unklar ist, wie man physikalisch sinnvolle Vorhersagen treffen soll.

Die aktuell (2015) am meisten diskutierten Ansätze zur Lösung dieses Problems sind die Stringtheorie und die Schleifenquantengravitation. Zudem existieren eine Vielzahl weiterer Modelle.

Allgemeine Relativitätstheorie und Weltformel

Das nachstehende Diagramm zeigt die Allgemeine Relativitätstheorie im Gefüge einer hypothetischen Weltformel.

Fundamentale Wechselwirkungen und ihre Beschreibungen (Theorien in frühem Stadium der Entwicklung sind grau hinterlegt.)
	Starke Wechselwirkung	Elektromagnetische Wechselwirkung		Schwache Wechselwirkung	Gravitation
klassisch		Elektrostatik	Magnetostatik		Newtonsches Gravitationsgesetz
		Elektrodynamik			Allgemeine Relativitätstheorie
quanten- theoretisch	Quantenchromodynamik (Standardmodell)	Quantenelektrodynamik		Fermi-Theorie	Quantengravitation (?)
		Elektroschwache Wechselwirkung (Standardmodell)
	Große vereinheitlichte Theorie (?)
	Weltformel („Theorie von Allem“) (?)

Literatur

Populärwissenschaftlich:

Harald Fritzsch: Die verbogene Raum-Zeit. Piper, 1997, ISBN 3-492-22546-2.
Marcia Bartusiak: Einsteins Vermächtnis. Europäische Verlagsanstalt, 2005, ISBN 3-434-50529-6.
Rüdiger Vaas: Tunnel durch Raum und Zeit. 2. Auflage. Franckh-Kosmos, 2006, ISBN 3-440-09360-3.

Lehrbücher:

Torsten Fließbach: Allgemeine Relativitätstheorie. 4. Auflage. Elsevier – Spektrum Akademischer Verlag, 2003, ISBN 3-8274-1356-7.
Charles Misner, Kip S. Thorne, John A. Wheeler: Gravitation. W. H. Freeman, San Francisco 1973, ISBN 0-7167-0344-0.
Hans Stephani: Allgemeine Relativitätstheorie. 4. Auflage. Wiley-VCH, 1991, ISBN 3-326-00083-9.
Steven Weinberg: Gravitation and Cosmology. Principles and Applications of the General Theory of Relativity. New York 1972, ISBN 0-471-92567-5.
Hermann Weyl: Raum, Zeit, Materie. Vorlesungen über Allgemeine Relativitätstheorie. 8. Auflage. Springer 1993, online (1919).
Wolfgang Rindler: Relativity. Special, General and Cosmological. 2. Auflage. Oxford University Press, 2006, ISBN 0-19-856732-4.
Robert M. Wald: General Relativity. University of Chicago Press, ISBN 0-226-87033-2.
Reinhard Meinel: Spezielle und allgemeine Relativitätstheorie für Bachelorstudenten. 2. Auflage. Springer, 2019, ISBN 978-3-662-58966-3.
Rainer Oloff: Geometrie der Raumzeit. Eine mathematische Einführung in die Relativitätstheorie. 4. Auflage. Vieweg, 2008, ISBN 978-3-8348-0468-6.
Ray d’Inverno: Einführung in die Relativitätstheorie. 2. Auflage. Wiley-VCH, 2009, ISBN 978-3-527-40912-9.
M. P. Hobson, G. P. Efstathiou, A. N. Lasenby: General Relativity. An Introduction for Physicists. Cambridge University Press, Cambridge 2006, ISBN 0-521-82951-8.
Lewis Ryder: Introduction to General Relativity. Cambridge University Press, Cambridge 2009, ISBN 978-0-521-84563-2.

Monographien:

Thomas W. Baumgarte, Stuart L. Shapiro: Numerical Relativity: Solving Einstein’s Equations on the Computer. Cambridge University Press, 2010, ISBN 978-0-521-51407-1.
Yvonne Choquet-Bruhat: General Relativity and the Einstein Equations. Oxford University Press, 2009, ISBN 978-0-19-923072-3.
Stephen W. Hawking, George F. R. Ellis: The Large Scale Structure of Space-time. Cambridge University Press, ISBN 0-521-09906-4.
Hans Stephani, Dietrich Kramer, Malcolm MacCallum, Cornelius Hoenselaers, Eduard Herlt: Exact Solutions of Einstein’s Field Equations. Cambridge University Press, ISBN 0-521-46702-0.

Geschichte der ART:

Abraham Pais: Subtle is the Lord.
- „Raffiniert ist der Herrgott…“. Albert Einstein, eine wissenschaftliche Biographie. Spektrum Akademischer Verlag, Heidelberg/ Berlin 2000, ISBN 3-8274-0529-7.
Thomas de Padova: Allein gegen die Schwerkraft. Einstein 1914–1918. Hanser, München 2015, ISBN 978-3-446-44481-2.
Jürgen Renn, Hanoch Gutfreund: Albert Einstein. Relativity. The Special & the General Theory. Princeton University Press, Princeton, New Jersey, USA 2015, ISBN 978-0-691-16633-9.
Jürgen Renn, Hanoch Gutfreund: The Road to Relativity. The History and Meaning of Einstein’s «The Foundation of General Relativity». Princeton University Press, Princeton, New Jersey, USA 2015, ISBN 978-1-4008-6576-5.

Weblinks

Commons: Allgemeine Relativitätstheorie – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Allgemeine Relativitätstheorie – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Charles W. Misner, Kip S. Thorne, John Archibald Wheeler: Gravitation. W. H. Freeman and Company, San Francisco 1973, ISBN 0-7167-0334-3, S. 315 ff. (englisch).
Albert Einstein: Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. In: Jahrbuch der Radioaktivität und Elektronik IV. 1908, S. 411–462 (Faksimile, PDF).
Albert Einstein: Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. In: Annalen der Physik. 35, 1911, S. 898–908 (Faksimile, PDF).
Albert Einstein, Marcel Grossmann: Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation. In: Zeitschrift für Mathematik und Physik. 62, 1913, S. 225–261.
Albert Einstein: Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. In: Sitzungsberichte der Preußischen Akademie der Wissenschaften. 1915, S. 831–839.
Darauf wiesen Corry, Renn, Stachel in Science. Band 278, 1997, S. 1270 hin
F. Winterberg: On “Belated Decision in the Hilbert-Einstein Priority Dispute”, published by L. Corry, J. Renn, and J. Stachel. In: Zeitschrift für Naturforschung A. 59, 2004, S. 715–719 (PDF, freier Volltext)., ausführlich in Daniela Wuensch: Zwei wirkliche Kerle. 2. Auflage. Termessos Verlag, 2007. Siehe auch Klaus P. Sommer: Wer entdeckte die Allgemeine Relativitätstheorie? Prioritätsstreit zwischen Hilbert und Einstein. In: Physik in unserer Zeit. 36, Nr. 5, 2005, S. 230–235, ISSN 0031-9252
Albert Einstein: Die Grundlage der allgemeinen Relativitätstheorie. In: Annalen der Physik. Band 354, Nr. 7, 1916, S. 769–822, doi:10.1002/andp.19163540702.
David Hilbert: Die Grundlagen der Physik. In: Königliche Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, Nachrichten (1915). S. 395–407.
Einstein sah diese selbst als Hauptgesichtspunkte der ART an: Albert Einstein: Prinzipielles zur allgemeinen Relativitätstheorie. In: Annalen der Physik. 55, 1918, S. 241–244 (Faksimile, PDF).
Øyvind Grøn, Sigurd Kirkevold Næss: An electromagnetic perpetuum mobile? In: General Relativity and Quantum Cosmology. 3. Juni 2008, arxiv:0806.0464 (Erläuterung am „freien Fall“ des Elektrons).
G. F. R. Ellis: Relativistic Cosmology. In: Proc. Int. School of Physics „Enrico Fermi“ Course XLVIII – General Relativity and Cosmology (Varena, 1969). Ed. R. K. Sachs, Academic Press, New York 1971, S. 104–182.
Nach gegenwärtigen Beobachtungen der Kosmologie scheint das Universum beschleunigt zu expandieren, was für einen positiven Wert von Λ spricht.
Zusammenfassende Übersicht: Clifford M. Will: The Confrontation between General Relativity and Experiment. In: Living Rev. Relativity. 9, Nr. 3, 2006, ISSN 1433-8351. Onlinedokument. (Memento vom 13. Juni 2007 im Internet Archive).
S. Baeßler, B. R. Heckel, E. G. Adelberger, J. H. Gundlach, U. Schmidt, H. E. Swanson: Improved Test of the Equivalence Principle for Gravitational Self-Energy. In: Physical Review Letters. Band 83, Nr. 18, 1. November 1999, S. 3585–3588, doi:10.1103/PhysRevLett.83.3585.
B. Bertotti, L. Iess, P. Tortora: A test of general relativity using radio links with the Cassini spacecraft.. In: Nature. 425, 2003, S. 374–376. (PDF, abgerufen am 23. Dezember 2009; 199 kB).
Extrem genaue optische Atomuhren messen die Zeitdilatation unter Alltagsbedingungen (2010).
Gravity Collaboration, R. Abuter u. a., Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole, Astronomy & Astrophysics, Band 615, 2018, L 15, Abstract
Ulrich E. Schröder: Gravitation: Eine Einführung in die allgemeine Relativitätstheorie. Harri Deutsch Verlag, Frankfurt am Main 2007, ISBN 978-3-8171-1798-7, S. 133 (Seite nicht mehr abrufbar, Suche in Webarchiven: @1@2Vorlage:Toter Link/books.google.deeingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 29. August 2017]).
Torsten Fließbach: Allgemeine Relativitätstheorie. 3. Auflage. ISBN 3-8274-0357-X, S. 171.
Zum Beispiel Misner, Thorne, Wheeler: Gravitation. Freeman, 1973, Kapitel 39, S. 1068.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Charles W. Misner, Kip S. Thorne, John Archibald Wheeler: Gravitation. W. H. Freeman and Company, San Francisco 1973, ISBN 0-7167-0334-3, S. 315 ff. (englisch).

[Ein1908-2] Albert Einstein: Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. In: Jahrbuch der Radioaktivität und Elektronik IV. 1908, S. 411–462 (Faksimile, PDF).

[Ein1911-3] Albert Einstein: Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. In: Annalen der Physik. 35, 1911, S. 898–908 (Faksimile, PDF).

[Ein1913-4] Albert Einstein, Marcel Grossmann: Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation. In: Zeitschrift für Mathematik und Physik. 62, 1913, S. 225–261.

[5] Albert Einstein: Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. In: Sitzungsberichte der Preußischen Akademie der Wissenschaften. 1915, S. 831–839.

[6] Darauf wiesen Corry, Renn, Stachel in Science. Band 278, 1997, S. 1270 hin

[7] F. Winterberg: On “Belated Decision in the Hilbert-Einstein Priority Dispute”, published by L. Corry, J. Renn, and J. Stachel. In: Zeitschrift für Naturforschung A. 59, 2004, S. 715–719 (PDF, freier Volltext)., ausführlich in Daniela Wuensch: Zwei wirkliche Kerle. 2. Auflage. Termessos Verlag, 2007. Siehe auch Klaus P. Sommer: Wer entdeckte die Allgemeine Relativitätstheorie? Prioritätsstreit zwischen Hilbert und Einstein. In: Physik in unserer Zeit. 36, Nr. 5, 2005, S. 230–235, ISSN 0031-9252

[Ein1916-8] Albert Einstein: Die Grundlage der allgemeinen Relativitätstheorie. In: Annalen der Physik. Band 354, Nr. 7, 1916, S. 769–822, doi:10.1002/andp.19163540702.

[Hil1915-9] David Hilbert: Die Grundlagen der Physik. In: Königliche Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, Nachrichten (1915). S. 395–407.

[Ein1918-10] Einstein sah diese selbst als Hauptgesichtspunkte der ART an: Albert Einstein: Prinzipielles zur allgemeinen Relativitätstheorie. In: Annalen der Physik. 55, 1918, S. 241–244 (Faksimile, PDF).

[11] Øyvind Grøn, Sigurd Kirkevold Næss: An electromagnetic perpetuum mobile? In: General Relativity and Quantum Cosmology. 3. Juni 2008, arxiv:0806.0464 (Erläuterung am „freien Fall“ des Elektrons).

[ellis-12] G. F. R. Ellis: Relativistic Cosmology. In: Proc. Int. School of Physics „Enrico Fermi“ Course XLVIII – General Relativity and Cosmology (Varena, 1969). Ed. R. K. Sachs, Academic Press, New York 1971, S. 104–182.

[13] Nach gegenwärtigen Beobachtungen der Kosmologie scheint das Universum beschleunigt zu expandieren, was für einen positiven Wert von Λ spricht.

[14] Zusammenfassende Übersicht: Clifford M. Will: The Confrontation between General Relativity and Experiment. In: Living Rev. Relativity. 9, Nr. 3, 2006, ISSN 1433-8351. Onlinedokument. (Memento vom 13. Juni 2007 im Internet Archive).

[15] S. Baeßler, B. R. Heckel, E. G. Adelberger, J. H. Gundlach, U. Schmidt, H. E. Swanson: Improved Test of the Equivalence Principle for Gravitational Self-Energy. In: Physical Review Letters. Band 83, Nr. 18, 1. November 1999, S. 3585–3588, doi:10.1103/PhysRevLett.83.3585.

[16] B. Bertotti, L. Iess, P. Tortora: A test of general relativity using radio links with the Cassini spacecraft.. In: Nature. 425, 2003, S. 374–376. (PDF, abgerufen am 23. Dezember 2009; 199 kB).

[scharf2010-17] Extrem genaue optische Atomuhren messen die Zeitdilatation unter Alltagsbedingungen (2010).

[18] Gravity Collaboration, R. Abuter u. a., Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole, Astronomy & Astrophysics, Band 615, 2018, L 15, Abstract

[19] Ulrich E. Schröder: Gravitation: Eine Einführung in die allgemeine Relativitätstheorie. Harri Deutsch Verlag, Frankfurt am Main 2007, ISBN 978-3-8171-1798-7, S. 133 (Seite nicht mehr abrufbar, Suche in Webarchiven: @1@2Vorlage:Toter Link/books.google.deeingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 29. August 2017]).

[20] Torsten Fließbach: Allgemeine Relativitätstheorie. 3. Auflage. ISBN 3-8274-0357-X, S. 171.

[21] Zum Beispiel Misner, Thorne, Wheeler: Gravitation. Freeman, 1973, Kapitel 39, S. 1068.