John von Neumann

John von Neumann (* 28. Dezember 1903 in Budapest, Österreich-Ungarn als János Lajos Neumann von Margitta; † 8. Februar 1957 in Washington, D.C., Vereinigte Staaten) war ein ungarisch-US-amerikanischer Mathematiker. Er leistete bedeutende Beiträge zur mathematischen Logik, Funktionalanalysis, Quantenmechanik und Spieltheorie und gilt als einer der Väter der Informatik. Später veröffentlichte er als Johann von Neumann; heutzutage ist er vor allem unter seinem in den USA gewählten Namen John von Neumann bekannt.

John von Neumann (um 1940)

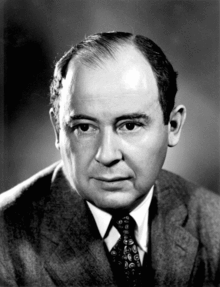
Leben und Werk

Herkunft und Anfänge der Karriere

Sein Vater, der königlich ungarische Regierungsrat Max (ungarisch Miksa) Neumann, wurde am 1. Juli 1913 in den ungarischen Adelsstand erhoben und erhielt den Adelsnamen Margittai Neumann, wobei Margittai im Ungarischen für „von Margitta“ steht.[1] Der Vater war Anwalt und zur Zeit der Geburt von John von Neumann Direktor einer der größten ungarischen Banken, der Magyar Jelzáloghitel Bank (Ungarische Hypothekenbank).[1] Die Familie war jüdisch, was der Vater auch beibehielt, als er eine Karriere im österreichisch-ungarischen Kaiserreich verfolgte, befolgte aber die jüdischen religiösen Regeln nicht streng.[1] Beispielsweise wurde in der Familie zu Weihnachten ein Baum aufgestellt und die Kinder sangen mit ihrem deutschen Kindermädchen.[2] Daneben hatte die Familie auch französische Gouvernanten. Die Mutter Margit kam aus einer gutsituierten Familie, ihr Vater Jakab Kann kam aus einfachen Verhältnissen, machte aber ein Vermögen im Handel mit landwirtschaftlichen Geräten.[1] John von Neumann, der in Kurzform in Ungarn Jancsi genannt wurde, hatte noch zwei jüngere Brüder, den 1907 geborenen Mihály (später Michael) und den 1911 geborenen Miklós (später Nicholas). Im Haus der von Neumanns wohnten auch vier der Tanten mütterlicherseits aus der Familie Kann mit ihren Töchtern.[3]

Schon als Kind zeigte John Neumann jene überdurchschnittliche Intelligenz, die später selbst Nobelpreisträger – zum Beispiel Eugene Paul Wigner – zum Staunen brachte. Als Sechsjähriger konnte er mit hoher Geschwindigkeit achtstellige Zahlen im Kopf dividieren. Er besaß ein außergewöhnliches Gedächtnis, das ihm beispielsweise erlaubte, den Inhalt einer Buchseite nach einem kurzen Blick darauf präzise wiederzugeben. Später konnte er ganze Bücher wie Goethes Faust auswendig und so zum Beispiel auch durch detailliertes historisches Wissen glänzen. Er besuchte in Budapest das humanistische deutschsprachige Lutheraner-Gymnasium, wie auch gleichzeitig Eugene Paul Wigner, mit dem Abitur 1921. Die politische Situation in Ungarn war damals sehr unsicher, da auf das Regime der Räterepublik von Béla Kun, in denen die von Neumanns als Kapitalisten von Verfolgung bedroht waren, 1919 das reaktionäre antisemitische Regime von Miklós Horthy folgte. Schon als Gymnasiast glänzte von Neumann durch mathematische Leistungen und veröffentlichte mit seinem Lehrer Michael Fekete seinen ersten mathematischen Artikel, den er konzipierte, als er noch nicht ganz 18 Jahre alt war. Dem Wunsch seiner Eltern folgend, studierte er jedoch zunächst von 1921 bis 1923 Chemieingenieurwesen in Berlin und dann bis zu seinem Diplom 1925 an der ETH Zürich. Gleichzeitig war er an der Universität Budapest eingeschrieben, absolvierte dort aber nur die Examina. Sein eigentliches Interesse galt allerdings immer der Mathematik, der er sich gewissermaßen als „Hobby“ widmete. Er besuchte Mathematikkurse in Berlin und die von Hermann Weyl und George Pólya an der ETH Zürich und machte schon bald auf sich aufmerksam. Von Neumann war von 1928 bis 1933 (jüngster) Privatdozent der Berliner Universität[4] und im Sommersemester 1929 an der Universität Hamburg. Davor arbeitete er 1926/1927 in Göttingen mit David Hilbert zusammen.

Von Neumann in den Vorlesungsverzeichnissen der Friedrich-Wilhelms-Universität zu Berlin
Die ersten drei Ausschnitte stammen aus dem Sommersemester 1928, der vierte Ausschnitt aus dem Wintersemester 1928/29.[5] Namhafte hier erwähnte Kollegen waren Georg Feigl, Issai Schur, Erhard Schmidt, Leó Szilárd, Heinz Hopf, Adolf Hammerstein und Ludwig Bieberbach.

Am Anfang seiner Karriere als Mathematiker beschäftigte sich von Neumann unter anderem mit der Entwicklung der axiomatischen Mengenlehre, für die er noch als Student einen neuen Ansatz fand (Dissertation in Budapest 1926 bei Leopold Fejér),[6] der Neumann-Bernays-Gödel-Mengenlehre (NBG), und mit der Hilbertschen Beweistheorie. Diese Themen waren damals das aktuelle Forschungsgebiet der Gruppe um Hilbert in Göttingen, damals eines der Weltzentren der Mathematik. Seine Definition der Ordinalzahlen ist heute ein Standard: Eine neue Ordinalzahl wird durch die Menge der bereits eingeführten definiert. Die Phase seiner Beschäftigung mit mathematischer Logik endete mit dem Bekanntwerden von Gödels Unvollständigkeitssatz, der Hilberts Programm einen schweren Schlag versetzte. Gödel war später ein enger Freund und Kollege von John von Neumann und Albert Einstein in Princeton.

Arbeiten zur Quantenmechanik

Von Neumann war ebenfalls Verfasser des ersten mathematisch durchdachten Buches zur Quantenmechanik, in dem er den Messprozess und die Thermodynamik der Quantenmechanik behandelte (siehe dazu Dichtematrix, von ihm 1927 eingeführt, Von-Neumann-Entropie, Von-Neumann-Gleichung). Das damals „heiße“ Thema der sich stürmisch entwickelnden Quantenmechanik war auch der Hauptgrund, warum er sich der Funktionalanalysis zuwandte und die Theorie linearer Operatoren in Hilberträumen entwickelte, genauer die der unbeschränkten selbstadjungierten Operatoren.[7] Die Mathematiker in Göttingen wandten gegen die neue Quantenmechanik ein, dass mit den bis dahin untersuchten linearen beschränkten Operatoren die kanonischen Vertauschungsrelationen nicht zu erfüllen waren. Von Neumann klärte das und lieferte gleichzeitig zahlreiche weitere Beiträge zu diesem Gebiet. Als man allerdings später Werner Heisenberg fragte, ob er von Neumann deswegen nicht dankbar sei, stellte er nur die Gegenfrage, wo denn der Unterschied zwischen beschränkt und unbeschränkt liege.[8] Von Neumanns Buch über Quantenmechanik genoss einen derartigen Ruf, dass selbst sein „Beweis“ der Unmöglichkeit von Hidden-Variable-Theorien, der zwar korrekt war, aber von falschen Voraussetzungen ausging, lange nicht hinterfragt wurde. Die Physiker bevorzugten jedoch zu von Neumanns Leidwesen die fast gleichzeitig veröffentlichten Principles of Quantum mechanics von Paul Dirac, in der das angesprochene mathematische Problem durch Einführung von Distributionen umgangen wurde, die bei den Mathematikern zunächst verpönt waren, ehe sie auch dort Ende der 1940er Jahre ihren Siegeszug antraten (Laurent Schwartz).

Mit Eugene Wigner veröffentlichte von Neumann 1928/29 eine Reihe von Arbeiten über die Anwendung der Gruppentheorie in den Atomspektren. Auch hier war die Begeisterung der Physiker gedämpft, es wurde sogar von „Gruppenpest“ gesprochen[9], die sich von Seiten der Mathematiker in der Quantenmechanik breitzumachen versuchte.

Das Stone-von-Neumann-Theorem drückt die Eindeutigkeit der kanonischen Kommutatoren von zum Beispiel Orts- und Impulsoperatoren in der Quantenmechanik aus und zeigt die Äquivalenz von deren beiden grundlegenden Formulierungen von Schrödinger (Wellenfunktion) und Heisenberg (Matrizen).

Seine Arbeiten über Quantenmechanik begründeten seinen Ruf in Amerika – und nicht zuletzt im Hinblick auf einen Wechsel auf besser bezahlte Positionen in den USA hat er sich so intensiv mit ihr beschäftigt. In Deutschland war außerdem der Wettbewerb um Professorenstellen hart (siehe dazu auch Weimarer Republik#Juden zwischen Assimilation und Ausgrenzung) und von Neumann hatte sich nach dem Tod des Vaters 1929 als Ältester um seine Familie zu kümmern.[10] Im Herbst 1929 wurde er von Oswald Veblen eingeladen, an die Princeton University in New Jersey zu kommen und Vorträge darüber zu halten, und er wechselte auch in den folgenden Jahren zwischen Princeton und Deutschland. Ab 1933 wirkte er am neu gegründeten, anspruchsvollen Institute for Advanced Study in Princeton als Professor für Mathematik. Unter seinen Kollegen dort waren Albert Einstein und Hermann Weyl. Wie diese emigrierte auch von Neumann nach der Machtergreifung Hitlers dauerhaft in die USA.

Amerika, Spieltheorie und Mathematik

John von Neumann erbrachte auf vielen Gebieten der Mathematik herausragende Beiträge. Schon 1928 hatte ihn ein Aufsatz des Mathematikers Émile Borel über Minimax-Eigenschaften zu Ideen geführt, die später auf einen seiner originellsten Entwürfe hinausliefen, die Spieltheorie. Von Neumann bewies 1928 das Min-Max-Theorem für die Existenz einer optimalen Strategie in „Nullsummenspielen“. Mit dem Wirtschaftswissenschaftler Oskar Morgenstern schrieb er 1944 das zum Klassiker gewordene Buch The Theory of Games and Economic Behavior (3. Auflage 1953), wo auch die für die Ökonomie wichtige Verallgemeinerung auf n-Personen Spiele behandelt wird. Er wurde damit zum Begründer der Spieltheorie, die er allerdings weniger auf klassische Spiele anwendet, als auf alltägliche Konflikt- und Entscheidungssituationen bei unvollkommener Kenntnis der Absichten des Gegenspielers (wie beim Pokern).[11] In den Wirtschaftswissenschaften wird auch ein Seminarvortrag von 1936 zur mathematischen Modellierung expandierender Wirtschaften häufig zitiert.[12] In der zweiten Auflage von The Theory of Games and Economic Behavior (1947) präsentierten Morgenstern und von Neumann den Von-Neumann-Morgenstern-Erwartungsnutzen und leisteten damit bedeutende Beiträge zur Nutzentheorie.

In den 1930er Jahren entwickelte von Neumann in einer Serie von Arbeiten mit Francis Murray eine Theorie von Algebren beschränkter Operatoren in Hilberträumen, die Jacques Dixmier später Von-Neumann-Algebren nannte. Diese sind heute ein aktuelles Forschungsgebiet (zum Beispiel Alain Connes, Vaughan F. R. Jones), das auch – wie von Neumann vorhersah – Anwendungen in der Physik hat, allerdings weniger in der Quantenmechanik als in der Quantenfeldtheorie und Quantenstatistik. Von Neumann und Murray bewiesen ein Klassifikationstheorem für Operatoralgebren als direkte Summe von „Faktoren“ (mit trivialem Zentrum) vom Typ I, II, III, jeweils mit Unterteilungen.

Operatoralgebren waren Teil seiner Suche nach einer Verallgemeinerung des quantenmechanischen Formalismus, denn er sagte in einem Brief an Garrett Birkhoff 1935, er würde nicht mehr an Hilberträume glauben. Weitere Versuche in dieser Richtung waren die Untersuchung der „lattice theory“ (Theorie der Verbände), zunächst als Algebra von Projektionsoperatoren im Hilbertraum (an der auch Birkhoff beteiligt war), später als Erweiterung der Logik zur „Quantenlogik“ interpretiert, und kontinuierliche Geometrien, die sich aber am Ende als kein Fortschritt gegenüber Operatoralgebren erwiesen.

Ein weiteres Arbeitsfeld der 1930er Jahre in Princeton war das berühmte Ergodenproblem, bei dem es um die mathematische Grundlegung der statistischen Mechanik in klassischen Systemen geht (Gleichverteilung der Bahnen im Phasenraum). Von Neumann hatte in Deutschland diese Fragen schon von quantenmechanischer Seite behandelt. Nachdem Bernard Koopman das Problem in Operator-Form gebracht hatte, griff von Neumann es auf und lieferte sich unfreiwillig ein „Duell“ mit dem bekannten amerikanischen Mathematiker George David Birkhoff. Wie er später sagte, hätte er eine Zusammenarbeit vorgezogen.

Manhattan-Projekt und Regierungsberater

Von Neumann arbeitete ab 1943 am Manhattan-Projekt in Los Alamos. Er war schon in den Jahren zuvor bei der Army und Navy ein gefragter Berater, etwa für Ballistikfragen, Hohlladungen, Operations Research, Bekämpfung deutscher Magnetminen oder Optimierung der Wirkung von Bomben mit „schrägen Stoßwellen“. Eines seiner Hauptarbeitsgebiete war die Theorie der Stoßwellen, die in den 50er Jahren für den Überschallflug aktuell wurde und die er unter anderem für die Entwicklung von Sprengstofflinsen für den Implosionsmechanismus der Plutoniumbombe nutzte. In diesen Zusammenhang gehört auch seine Entwicklung des ersten numerischen Verfahrens zur Lösung von hyperbolischen partiellen Differentialgleichungen, des Monte-Carlo-Verfahrens mit Stanislaw Ulam, die Von-Neumann-Stabilitätsanalyse sowie seine Pionierleistungen in der Rechnerarchitektur. Übrigens optimierte er mit seiner Expertise in der Theorie der Stoßwellen während des Zweiten Weltkriegs auch britische Luftminen über Deutschland. Auch an der Weiterentwicklung des amerikanischen Nuklearbomben-Programms bis hin zur Wasserstoffbombe war von Neumann beteiligt.

Von Neumann war einerseits geschätzt, weil er seine Ideen freigiebig weitergab und Kollegen weiterhalf (bei Besuchen in Los Alamos war er oft von einer Traube von Wissenschaftlern umgeben, die schnellen Rat wollten), andererseits gefürchtet, da er Ideen schnell aufgriff und mit atemberaubender Geschwindigkeit eigene Theorien daraus entwickelte.

Neben seinen mathematischen Leistungen war von Neumann als Regierungsberater auch politisch einflussreich. Vor dem Abwurf der Atombomben auf Japan war er ein Mitglied des Target Committee, das die genauen Ziele der Bomben mitbestimmte. Er berechnete dabei auch die optimale Detonationshöhe der Atombomben, um einen möglichst großen Schaden durch die Explosion am Boden zu erzielen. Mit dem Namen John von Neumann ist angeblich auch die Idee verbunden, die Ost-West-Konfrontation durch die Explosion einer Wasserstoffbombe über unbewohntem sowjetischem Gebiet zu beenden, die Sowjetunion von der Entwicklung einer eigenen Bombe abzuhalten und dauerhaft einzuschüchtern.[13] Ob US-Präsident Eisenhower allerdings tatsächlich durch von Neumann zu einem solchen Schritt gedrängt wurde, ist umstritten. Er war aber wesentlich daran beteiligt, das militärische Raketenprogramm der USA auf den Weg zu bringen.

Computer und Kybernetik

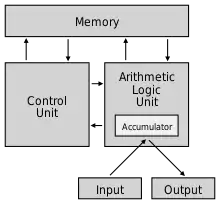
Von Neumann gilt als einer der Väter der Informatik. Nach ihm wurde die Von-Neumann-Architektur (auch Von-Neumann-Rechner) benannt, ein Computer, in dem Daten und Programm binär codiert im selben Speicher liegen. Das Programm selbst kann somit im laufenden Rechenvorgang verändert werden und durch bedingte Sprungbefehle von der festgelegten Reihenfolge der gespeicherten Anweisungen abgewichen werden. Es definiert in loser Analogie zum menschlichen Hirn (wie er im Report schreibt) eine Rechnerarchitektur aus Steuereinheit und arithmetischer Einheit sowie eine Speichereinheit. Die Befehle werden seriell abgearbeitet. Er beschrieb dieses Prinzip 1945 im First Draft of a Report on the EDVAC. Der Bericht war als Diskussionsbericht mit der ENIAC-Gruppe gedacht und blieb zunächst unveröffentlicht, kursierte jedoch schnell in wissenschaftlichen Kreisen. So gut wie alle modernen Rechner beruhen auf von Neumanns Idee.

Von Neumanns Rolle als alleiniger Erfinder der nach ihm benannten modernen Rechnerarchitektur ist bestritten worden und seit längerem Gegenstand von Auseinandersetzungen. Heutzutage wird deshalb vorzugsweise statt „Von-Neumann-Rechner“ die Bezeichnung „speicherprogrammierter Rechner“ (stored program computer) verwendet.[14] Insbesondere betrifft das die Ansprüche der eigentlichen Erbauer des ersten Röhrencomputers ENIAC und dessen Nachfolgemodells EDVAC, John Presper Eckert und John William Mauchly von der Moore School der University of Pennsylvania in Philadelphia, mit denen von Neumann und Herman Goldstine anfangs eng zusammenarbeiteten.[15] Von Neumann stieß durch eine zufällige Begegnung auf einem Bahnsteig mit dem ihm zuvor nicht bekannten Mathematiker Goldstine im August 1944 zu den Computerentwicklern der Moore School, wo Goldstine Verbindungsoffizier der US-Army war.[16] Wie Goldstine berichtete, beendete die von ihm selbst betriebene freizügige Verbreitung des Edvac-Reports die enge Beziehung von ihm und von Neumann zu Eckert und Mauchly,[17] die ihren Beitrag in dem (eigentlich nicht für die Öffentlichkeit bestimmten) Edvac-Report nicht gewürdigt sahen und für wesentliche Teile des Von-Neumann-Rechners Prioritätsansprüche geltend machten. Bei Eckert und Mauchly standen Patentüberlegungen im Vordergrund, die dazu führten, dass sie schon 1946 die Moore School verließen, um eine eigene Firma zu gründen, und die später zu einem jahrzehntelangen Streit vor Gericht führten (sie schalteten schon 1945 Patentanwälte ein). Von Neumann sah dagegen zunächst Bedarf für weitere Forschung und Entwicklung und trat für eine offene Diskussion und weite Verbreitung der Ergebnisse ein.[18] Teile des Konzepts wurden unabhängig auch von anderen Computerpionieren – darunter Konrad Zuse in Deutschland – entwickelt, u. a. die Idee der Trennung von Speicher und Prozessor, die schon in Zuses noch rein mechanischen Z1 im Jahr 1938 erfolgte. Zuses frühen Rechnern, die für Spezialaufgaben ausgelegt waren, fehlte jedoch das wesentliche Konzept der bedingten Verzweigung, obwohl es ihm bekannt war und er es in seinem Plankalkül verwendete.[19][20] Von Neumann setzte sich seinerzeit vehement für die weitere Entwicklung der Rechenmaschinen ein. Die Verdienste von Neumanns beruhen insbesondere auf der Mathematisierung und Verwissenschaftlichung der Rechenmaschinen.

Zusammen mit Norbert Wiener organisierte er gegen Ende des Winters 1943/44 in Princeton ein interdisziplinäres Treffen mit Ingenieuren, Neurowissenschaftlern und Mathematikern zu Gemeinsamkeiten zwischen dem Gehirn und Computern[21]^:147–151 und damit den Grundlagen der Kybernetik, die Wiener 1948 erstmals umfassend beschrieb.[22]

Schematische Darstellung der Von-Neumann-Architektur, 1947

Von Neumann leitete ab 1949 am Institute for Advanced Study schließlich ein eigenes Computerprojekt, den IAS-Computer, in dem er seine Ideen verwirklichen konnte, darunter auch viele Programmierkonzepte. Auf ihn gehen Unterprogramme mit Parameterübergabe über einen Verweis auf eine Speicherstelle, verschiedene Verfahren zur Erzeugung von Zufallszahlen (unter anderem die Mittquadratmethode und die Verwerfungsmethode) und der Mergesort zurück. Er trug maßgeblich zur Verwendung von Binärcodes in den Rechnersystemen bei und propagierte die Verwendung von Flussdiagrammen, in denen er auch eine Art von Assertions vorsah, die als Vorläufer für Schleifeninvarianten im Hoare-Kalkül angesehen werden können. Ein enger Mitarbeiter wurde Goldstine, den er aus der ENIAC-Gruppe übernahm. Auch die Reports aus Princeton ab 1949 ließ er frei zirkulieren, und schon bald entstanden überall in den USA und England Rechner nach diesen Vorbildern. Genutzt wurde der IAS-Rechner und der nach von Neumanns Ideen umgebaute ENIAC vor allem für militärische Berechnungen (Ballistik). Von Neumann nutzte den Princeton-Rechner allerdings auch für Pionierarbeiten in der numerischen Wettervorhersage, wie die erste rechnergestützte 24-Stunden-Wetterprognose.

1953 entwickelte er auch die Theorie der selbstreproduzierenden Automaten[23] bzw. der Selbstreplikation, für die er ein kompliziertes Beispiel angab. Heute ergeben sich viel einfachere aus der Theorie der zellulären Automaten (zum Beispiel John Horton Conways Spiel des Lebens). Ideen dafür soll er auch beim Spielen mit einem Bauklötzchen-Spiel (Tinkertoy) ausprobiert haben.[24] Science-Fiction-Autoren stellten sich die Besiedlung unserer Galaxie mit solchen Automaten vor und prägten dafür den Namen Von-Neumann-Sonden. Von Neumanns zellulare Automaten bilden eine wichtige Grundlage für die Forschungsdisziplin Artificial life und ermöglicht die Simulation biologischer Organisation, Selbstreproduktion und Evolution von Komplexität.

Würdigung und Ende

Über von Neumann kursierten zahlreiche Anekdoten (einige hat Halmos in dem in der Literatur zitierten Artikel gesammelt). Beispielsweise versuchte jemand ihn durch folgendes Rätsel zu testen: „Die Endpunkte einer Strecke $s$ bewegen sich mit der Geschwindigkeit $v$ aufeinander zu, ein Läufer flitzt zwischen den beiden Endpunkten mit einer Geschwindigkeit $w>v$ hin und her. Welche Strecke legt er zurück?“ Es gibt eine einfache und eine etwas kompliziertere Lösungsmethode (Summation der Teilstrecken). Von Neumann gab die Antwort blitzschnell und erklärte auf Nachfrage, die Reihe summiert zu haben – er hatte also den komplizierten Weg gewählt, was für ihn jedoch keinen höheren Zeitaufwand bedeutete.[25]

Wegen seiner Fähigkeit, komplexe Sachverhalte schnell in einfache Fragestellungen zu zergliedern und oft aus dem Stand einer Lösung zuzuführen, sowie seiner streng sachbezogenen, jeden unnötigen Streit vermeidenden Haltung, wurde von Neumann gerne als technischer Berater engagiert; so von IBM, Standard Oil oder der RAND Corporation. Sein Name ist deshalb auf den unterschiedlichsten Anwendungsgebieten ein Begriff. Er veröffentlichte 1952 das Von-Neumann-Gesetz, das die zeitliche Änderung der Größe von Zellen zweidimensionalen Schaumes beschreibt. Für Standard Oil half er Methoden zu entwickeln, Öl-Lagerstätten besser auszunutzen. Sein Tod verhinderte eine geplante größere Zusammenarbeit mit IBM.[26] Für die RAND Corporation wandte er die Spieltheorie auf strategische Denkspiele an, wie auch gleichzeitig andere Mathematiker wie John Nash und John Milnor. In einer unveröffentlichten Arbeit 1953 legte er auch die Prinzipien des Halbleiterlasers dar.[27]

John von Neumann war ein lebenslustiger und geselliger Mensch (Spitzname „Good Time Johnny“); er war zweimal verheiratet – mit Marietta Kövesi und Klára Dán – und hatte eine Tochter (Marina) aus erster Ehe, geboren 1935. Seine erste Frau Marietta war eine ungarische Katholikin, Tochter eines mit der Familie von Neumann befreundeten Arztes. Bei der Heirat 1929 konvertierte John von Neumann zum Katholizismus.[28] Für seine Umgebung machte er auch weiterhin eher den Eindruck eines Agnostikers[29] mit Ausnahme der letzten Tage, als er auf dem Sterbebett einen Priester kommen ließ. 1937 wurde die erste Ehe geschieden, und im November 1938 heiratete er Klara Dan in Budapest, die aus jüdischer Familie in Budapest stammte und sich vorher scheiden ließ.[30] Unmittelbar darauf emigrierte die ganze Familie (Mutter, Geschwister) in die USA. Sein Haus in Princeton war Mittelpunkt der akademischen Kreise auf den legendären Princeton-Partys. Von Neumann liebte auch schnelle Wagen wie Cadillac oder Studebaker, sein Fahrstil war aber gefürchtet, da er sich bei ruhigem Verkehr schnell langweilte und dann in Geistesabwesenheit verfiel.[31] Auch mitten aus einer Party konnte er sich plötzlich verabschieden, um ein mathematisches Problem zu durchdenken. Sein Alkoholkonsum war teilweise nur vorgetäuscht, wie das Kind eines Gastes einmal überrascht feststellte. Ein weiterer Aspekt des „Unterhaltungskünstlers“ von Neumann war sein unerschöpfliches Reservoir oft schlüpfriger Witze und seine Vorliebe für Limericks.

Von Neumann starb nach einem qualvollen Krebsleiden, das möglicherweise durch seine Teilnahme an Nukleartests verursacht worden war, im Washingtoner Walter-Reed-Militärkrankenhaus. Ein Soldat hielt vor dem Zimmer Wache, damit er im Delirium – der Krebs griff am Ende auch sein Gehirn an – keine Staatsgeheimnisse preisgab. Noch auf dem Totenbett schrieb er an seinem Buch „Die Rechenmaschine und das Gehirn“, in dem er den Besonderheiten des „Computers“ im menschlichen Kopf nachging.

Zuletzt bekannte er sich erneut zum katholischen Glauben (die Familie war 1929/30 konvertiert) und pflegte am Ende seines Lebens einen intensiven Gedankenaustausch mit einem Priester.[32] Er ist auf dem Princeton Cemetery in Princeton[33] neben seiner Mutter, seiner zweiten Ehefrau Klari (die 1963 im Meer ertrank, wahrscheinlich ein Suizid) und Karl Dan, dem Vater von Klari, der 1939 nach Übersiedlung aus Ungarn in die USA Suizid beging, begraben.

Ehrungen und Mitgliedschaften

1954 hielt er einen Plenarvortrag auf dem Internationalen Mathematikerkongress in Amsterdam (On unsolved problems in mathematics) und ebenso 1950 in Cambridge (Massachusetts) (Shock interaction and its mathematical aspects).
Colloquium Lecturer der American Mathematical Society (1937)
Bôcher Memorial Prize (1938)
Gibbs Lecturer der American Mathematical Society 1947
Präsident der American Mathematical Society 1951 bis 1953
Er war Mitglied der Accademia dei Lincei, der American Academy of Arts and Sciences (1944)[34], der National Academy of Sciences, der Königlich Niederländischen Akademie der Wissenschaften, des Istituto Lombardo in Mailand, der American Philosophical Society, der peruanischen Akademie der Wissenschaften.
1947 erhielt er die Verdienstmedaille des US-Präsidenten (Medal for Merit)
1952 Ehrenmitglied der London Mathematical Society[35]
1956 erhielt er die Freiheitsmedaille des US-Präsidenten (Medal of Freedom)
1956: Albert Einstein Commemorative Award
1956: Enrico-Fermi-Preis

Nach Neumann ist die John-von-Neumann-Medaille der IEEE, der John-von-Neumann-Theorie-Preis in Operations Research, die John von Neumann Lecture der SIAM sowie der Von-Neumann-Mondkrater benannt. Die Institute für Informatik und Mathematik der Humboldt-Universität zu Berlin sitzen im Johann von Neumann-Haus.

Zitate

Von Neumann in einer Diskussion mit Jacob Bronowski 1943 beim Studium von Bombenkratern auf Luftbildern:

„Nein, nein, du siehst das nicht richtig. Dein visualisierender Verstand kann das nicht richtig sehen. Du musst abstrakt denken. Was passiert, ist, dass der erste Differentialquotient identisch verschwindet und daher das, was sichtbar wird, die Spur des zweiten Differentialquotienten ist.“[36]

Bronowski berichtet, dass er auf diesen Rat hin das besprochene Problem neu durchdachte und spät in der Nacht von Neumanns Sicht bestätigt fand – als er ihm dies am nächsten Morgen mitteilte, bat ihn von Neumann nur, ihn doch bitte das nächste Mal zu so einer für von Neumann frühen Stunde nur zu stören, falls er falsch läge, und nicht falls er recht habe.

Das Problem der Überanpassung von mathematischen Modellen beschrieb von Neumann sehr anschaulich mit dem Beispiel eines Elefanten:[37]

“With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”

„Ich kann einen Elephanten in 4 Parameter bekommen, und mit fünf kann er noch mit den Rüssel wackeln.“

– John von Neumann, zitiert nach Freeman Dyson, zitiert nach Enrico Fermi: Nature

Auch wenn eine grobe Skizze eines Elefanten mit Hilfe von vier komplexen Zahlen tatsächlich möglich ist, zielt die Aussage wohl darauf ab, zu starke Anpassungen eines Modells an vorhandene Daten kritisch zu hinterfragen.

Schriften

Collected works, 6 Bände. Pergamon Press, ab 1961
Brody, Vamos (Hrsg.): The von Neumann compendium. World Scientific (Reprint von wichtigen Aufsätzen von Neumanns)
The computer and the brain (Silliman Lectures). Yale University Press, 2000 (deutsch Die Rechenmaschine und das Gehirn, 1958)
The mathematician. In: Heywood (Hrsg.): The works of the mind. 1948. Nachgedruckt in: Kasner, Newman (Hrsg.): The world of mathematics, Bd. 4
Mathematische Grundlagen der Quantenmechanik. 2. Auflage. Springer Verlag, 1996, ISBN 978-3-540-59207-5 (zuerst 1932)
Theory of games and economic behavior, zusammen mit Oskar Morgenstern. Princeton Univ. Press, 1944, Theory of games and economic behavior. (PDF; 57 MB). Deutsche Übersetzung: Spieltheorie und wirtschaftliches Verhalten, ISBN 3-7908-0134-8.

Einige Aufsätze und Bücher online:

Eine Axiomatisierung der Mengenlehre. In: Journal für die reine und angewandte Mathematik, Band 154, 1925, S. 219–240.
Die Axiomatisierung der Mengenlehre, Mathematische Zeitschrift, Band 27, 1928, S. 669–752 (entspricht größtenteils der Dissertation, Der axiomatische Aufbau der allgemeinen Mengenlehre (Ungarisch), Budapest 1925)
Über eine Widerspruchsfreiheitsfrage in der axiomatischen Mengenlehre In: Journal für die reine und angewandte Mathematik, 160, 1929, S. 227–241.
Zur Hilbertschen Beweistheorie, Mathematische Zeitschrift, Band 26, 1927, S. 1–46
Zur Theorie der Gesellschaftsspiele. In: Mathematische Annalen, Band 100, 1928, S. 295–320.
Mathematische Begründung der Quantenmechanik. In: Nachr.Ges.Wiss., Göttingen, 1927, S. 1–57
Thermodynamik quantenmechanischer Gesamtheiten. In: Nachr.Ges.Wiss., Göttingen, 1927, S. 237–291
Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik, Nachr. Ges. Wiss. Göttingen, 1927, S. 245–272
mit David Hilbert, Lothar Nordheim: Über die Grundlagen der Quantenmechanik, Mathematische Annalen, Band 98, 1927, S. 1–30´
Über die Definition der transfiniten Induktion und verwandte Fragen der allgemeinen Mengenlehre, Mathematische Annalen, Band 99, 1928, S. 373–391
Die Eindeutigkeit der Schrödingerschen Operatoren. In: Mathematische Annalen, Band 104, 1931, S. 570–578
Mathematische Grundlagen der Quantenmechanik. Berlin 1932
Allgemeine Eigenwerttheorie hermitescher Funktionaloperatoren. In: Mathematische Annalen, Band 102, 1930, S. 49–131
Zur Algebra der Funktionaloperatoren und Theorie der normalen Operatoren. In: Mathematische Annalen, Band 102, 1930, S. 370–427
First Draft of a Report on the EDVAC. (PDF; 411 kB) 1945 (englisch)
mit Burks, Goldstine Preliminary discussion of the logical design of an electronic computing instrument, US Army Ordonance Department Report 1946

Einige in Los Alamos entstandene Arbeiten von Neumanns (zum Beispiel über Schockwellen, Detonationswellen) sind bei der Federation of American Scientists online verfügbar.

Einige weitere Arbeiten zum Beispiel zu kontinuierlichen Geometrien, Operatorenringen oder zur Ergodentheorie sind bei der National Academy of Sciences online verfügbar.

Literatur

chronologisch

Sonderausgabe über von Neumann. Bulletin of the American Mathematical Society, Bd. 64, Nr. 3, 1958 (unter anderem Stanislaw Ulam, Garrett Birkhoff (Lattice theory), Léon Van Hove (Quantenmechanik), Francis J. Murray, Richard Kadison (Operatoralgebren), Harold W. Kuhn, Albert William Tucker (Spieltheorie), Claude Shannon (Theorie der Automaten/Computer), Paul Halmos (Maßtheorie, Ergodentheorie))
Paul Halmos: The Legend of John von Neumann. In: American Mathematical Monthly, Band 80, April 1973, S. 382–394. (JSTOR 2319080).
Herman Goldstine: The computer from Pascal to von Neumann. Princeton University Press, Princeton 1980, ISBN 0-691-08104-2.
Steve J. Heims: John von Neumann and Norbert Wiener. From mathematics to the technologies of life and death. MIT Press, Cambridge, MA 1980, 547 S., ISBN 978-0-262-08105-4.
Doppelbiographie zweier eminenter Wissenschaftler mit informativer Darstellung der Positionen beider Mathematiker in der unmittelbaren Nachkriegszeit.
Ed Regis: Who got Einsteins Office – Eccentricity and Genius at the Institute for Advanced Study. Basic Books 1988, ISBN 978-0201122787.
Ed Regis: Einstein, Gödel & Co. Genialität und Exzentrik – die Princeton-Geschichte. Aus dem Amerikanischen von Anita Ehlers. Birkhäuser, Basel u. a. 1989, ISBN 3-7643-2235-7, online-Ausschnitte.
William Aspray: John von Neumann and the origins of modern computing. MIT Press, Cambridge, Mass. 1990, ISBN 0-262-01121-2.
William Poundstone: Prisoners dilemma: John von Neumann, game theory and the puzzle of the bomb. Doubleday, New York 1992, ISBN 0-385-41567-2; Oxford University Press 1993, ISBN 0-19-286162-X (paperback).
Norman Macrae: John von Neumann. Mathematik und Computerforschung – Facetten eines Genies. Birkhäuser Verlag, Basel 1994, ISBN 3-7643-2974-2. (Das Buch des Journalisten Macrae ist leider in weiten Teilen sehr schwach und an einigen Stellen unzuverlässig, beruht aber auf vielen Interviews.)
Konrad Jacobs: Neumann, John von. In: Neue Deutsche Biographie (NDB). Band 19, Duncker & Humblot, Berlin 1999, ISBN 3-428-00200-8, S. 153 f. (Digitalisat).
Ernst Peter Fischer: Aristoteles, Einstein & Co. Piper Verlag 2000, ISBN 3-492-23045-8, S. 386–399, Kap. John von Neumann – oder: Den Planeten zum Wackeln bringen.
Miklós Rédei (Hrsg.): John von Neumann: Selected Letters. LMS/AMS History of Mathematics, 2005, ISBN 0-8218-3776-1.[38]
István Hargittai: The Martians of science – five physicists who changed the twentieth century. Oxford University Press, Oxford 2006, ISBN 978-0-19-517845-6.
Ulf Hashagen: Johann Ludwig Neumann von Margitta (1903–1957). Teil 1: Lehrjahre eines jüdischen Mathematikers während der Zeit der Weimarer Republik. Informatik-Spektrum, Bd. 29, 2006, S. 133–141, (doi:10.1007/s00287-006-0072-1); Teil 2: Ein Privatdozent auf dem Weg von Berlin nach Princeton. ibid, Bd. 29, S. 227–236, (doi:10.1007/s00287-006-0084-x).
Giorgio Israel, Ana Millán Gasca: The world as a mathematical game. John von Neumann and Twentieth Century Science. Birkhäuser, Basel u. a. 2009, ISBN 978-3-7643-9896-5, (Science Networks Historical Studies, Band 38), doi:10.1007/978-3-7643-9896-5.
Ulf Hashagen: Die Habilitation von John von Neumann an der Friedrich-Wilhelms-Universität in Berlin: Urteile über einen ungarisch-jüdischen Mathematiker in Deutschland im Jahr 1927, Historia Mathematica, Band 37, 2010, S. 242–280.
George Dyson: Turings Cathedral: the origin of the digital universe. Lane, London 2012, ISBN 978-0-7139-9750-7.[39]
Marina von Neumann Whitman: The Martians daughter: a memoir. University of Michigan Press, Ann Arbor 2012, ISBN 978-0-472-02855-9.
Ananyo Bhattacharya: The Man from the Future: The Visionary Life of John von Neumann. Allen Lane, London 2021, ISBN 978-0-241-39885-2.

Dokumentarfilme

John von Neumann. Der Denker des Computer-Zeitalters. Dokumentarfilm, Frankreich, 2014, 56:44 Min., Buch und Regie: Philippe Calderon, Produktion: arte France, BFC Productions, Erstsendung: 4. August 2015 bei arte, Inhaltsangabe von ARD, youtube.com.
Der Kampf um die Freiheit: Sechs Freunde und ihre Mission – Von Budapest nach Manhattan. Dokumentarfilm, Deutschland, 2013, 88:42 Min., Buch: Thomas Ammann und Judith Lentze, Regie: Thomas Ammann, Produktion: Prounen Film, Mythberg Films, Agenda Media, MDR, arte, Erstsendung: 17. Dezember 2013 bei arte, Inhaltsangabe von ARD.

Weblinks

Commons: János Lajos Neumann – Sammlung von Bildern, Videos und Audiodateien

Literatur von und über John von Neumann im Katalog der Deutschen Nationalbibliothek
Why not bomb them today? Studienarbeit zum politischen Wirken von Neumanns
John J. O’Connor, Edmund F. Robertson: John von Neumann. In: MacTutor History of Mathematics archive.
Kritischer Artikel zur Biografie Neumanns. In: heise.de, 28. Dezember 2003
Von Neumann, Dirac unter anderem zu Quantenmechanik in: Stanford Encyclopedia of Philosophy, 2004 (englisch)
John Von Neumann. A Register of his Papers in the The Library of Congress, 2002 (englisch)
Freeman Dyson: A walk through Johnny von Neumann’s Garden. In: Notices AMS, Februar 2013
Wolfgang Burgmer: 8. Februar 1957 - Todestag des Mathematikers John von Neumann WDR ZeitZeichen vom 8. Februar 2022. (Podcast)

Einzelnachweise

Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 1f.
Poundstone, Prisoners dilemma, S. 11.
Poundstone, Prisoners dilemma, S. 11.
Siehe Ulf Hashagens Artikel über die Habilitation in Berlin (S. 265). Sie war am 13. Dezember 1927 abgeschlossen.
Im Wintersemester 1928/29 ist Neumann von Margitta wie im Sommersemester 1928 auch beim mathematischen Kolloquium und bei der Besprechung neuerer Arbeiten zur Quantentheorie mit Leó Szilárd angegeben. Weitere Dozenten bei der Besprechung neuerer Arbeiten zur Quantentheorie waren im Wintersemester 1928/29 Hartmut Kallman und Fritz London.
John (Janos) von Neumann im Mathematics Genealogy Project (englisch)
Die in der Quantenmechanik verwendeten Operatoren für Messgrößen sind linear (Superpositionsprinzip für Lösungen zum Beispiel der linearen Schrödingergleichung) und selbst-adjungiert, da dann die Eigenwerte, die möglichen Messwerte, reell sind.
Die Anekdote stammt von Kurt Friedrichs, vgl. Peter Lax Mathematics and Physics, Bulletin American Mathematical Society, Bd. 45, 2008, S. 135–152.
Zuerst wahrscheinlich von Paul Ehrenfest in einem Brief an Wolfgang Pauli im September 1928 verwendet, siehe Martina Schneider, Zwischen zwei Disziplinen. B. L. van der Waerden und die Entwicklung der Quantenmechanik, Springer 2011, S. 63.
Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 15
Von Neumann war wie Edward Teller und eine Reihe anderer theoretischer Physiker nach Ende des Krieges in Los Alamos bei seinen Besuchen (man arbeitete an der Wasserstoffbombe) Mitglied einer Poker-Runde. Stanislaw Ulam Adventures of a Mathematician, Scribners 1976, S. 169.
Im Menger Kolloquium, übersetzt als A model of general equilibrium. In: Review of Economic Studies, Bd. 13, 1945, 1, auch in Brody, Vamos (Hrsg.): The von Neumann compendium. Neu war unter anderem die Verwendung von Ungleichungen statt nur von Gleichungen wie bei Walras, vgl. McRae, S. 217ff.
Poundstone „Prisoners dilemma“, S. 4 zitiert einen Nachruf in Life Magazin 1957, in der sich von Neumann 1950 sogar für einen vorbeugenden Atomkrieg gegen die Sowjetunion aussprach, wie etwa zur gleichen Zeit auch andere Persönlichkeiten wie der durch die Zeitgeschichte gewandelte Pazifist Bertrand Russell.
Friedrich L. Bauer: Historische Notizen zur Informatik. Springer Verlag, 2009, S. 139.
Nicholas Metropolis, J. Worlton: A trilogy on errors in the history of computing. In: IEEE Annals of the history of computing, Band 2., 1980, S. 49–55, vertreten die Ansicht, dass das Konzept stored program durch Eckert und Mauchly vor der Beteiligung von von Neumann entwickelt wurde. Siehe auch Friedrich L. Bauer: Historische Notizen zur Informatik. Springer Verlag, 2009, Kapitel Wer erfand den von Neumann Rechner? Wiederabdruck aus Informatik Spektrum, Band 21, 1998, S. 84. Auch Joel Shurkin: Engines of the Mind. The history of the computer. Norton, 1984, sieht für den Edvac die Beiträge von Eckert und Mauchly als zentral an und von Neumanns bedeutende Rolle erst mit seinem eigenen IAS-Rechner einsetzend, Goldstine: The Computer from Pascal to von Neumann. 1993, S. 186f. spricht sich dagegen für eine zentrale Rolle von Neumanns aus, der nach Goldstine schon Anfang August 1944 an den Diskussionen in der Moore School beteiligt war.
Goldstine: The Computer from Pascal to von Neumann. 1993, S. 182.
Goldstine: The Computer from Pascal to von Neumann. Princeton University Press, 1993, S. 229.
Bauer: Historische Notizen zur Informatik. S. 138.
Raúl Rojas: The architecture of Konrad Zuses early computing machines. In: Rojas, Hashagen: The first computers. MIT Press, 2000. Nach Rojas war die Z1 vom logischen Aufbau dem späteren Relais-Rechner Z3 sehr ähnlich und beide prinzipiell als universelle Rechenmaschine einsetzbar, auch wenn das nicht praktikabel war.
Raúl Rojas: Zuse und Turing. Der Draht des Mephistopheles. In: Telepolis, 21. Dezember 2011.
Thomas Rid: Maschinendämmerung. Eine kurze Geschichte der Kybernetik. Propyläen, Berlin 2016, ISBN 978-3-549-07469-5 (492 S., amerikanisches Englisch: Rise of the Machines. A Cybernetic History. New York 2016. Übersetzt von Michael Adrian, Erstausgabe: W.W. Norton & Company).
Norbert Wiener: Kybernetik. Regelung und Nachrichtenübertragung im Lebewesen und in der Maschine. Mit Ergänzung von 1961 zu lernenden und sich selbst reproduzierenden Maschinen. Zweite, revidierte und ergänzte Auflage. Econ-Verlag, Düsseldorf 1963 (287 S., amerikanisches Englisch: Cybernetics or Control and Communication in the Animal and the Machine. 1948. Übersetzt von E. H. Serr, E. Henze, Erstausgabe: MIT-Press).
John von Neumann: Theory of Self-reproducing Automata. posthum herausgegeben. Hrsg.: Arthur W. Burks. University of Illinois Press, 1967, ISBN 978-0-252-72733-7 (englisch, 388 S.).
Poundstone: Prisoner’s Dilemma. S. 24
Howard Eves: Return to Mathematical Circles, PWS-Kent Publishing, 1988, S. 140.
Stephen Dunwell von IBM berichtet darüber in seinem Oral History Interview 1989. (PDF) Babbage Institute. Nach Dunwell war seine Rolle als Berater bei IBM sehr begrenzt, man war sich aber bei IBM bewusst, dass man ihm als Vater des modernen Computers sehr viel verdankte. Das hing auch mit von Neumanns allgemeiner Einstellung zusammen – er vertrat nach Dunwell die Meinung, bei Computern wäre nicht geringer Speicherplatz das Problem, sondern einfallslose Programmierer.
Russell Dupuis: The Diode Laser – the first 30 days 40 years ago. In: Optics and Photonics News, Bd. 15, 2004, S. 30, The Diode Laser—the First Thirty Days Forty Years Ago (Memento vom 19. Juni 2010 im Internet Archive)
Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 15
Poundstone, Prisoners Dilemma, S. 11, 17 und S. 194 zu seinem Tod
Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 85
Nach anderen Aussagen pflegte er auch, laut im Auto zu singen, mit entsprechenden Lenkbewegungen. Er fuhr fast jedes Jahr ein Auto zu Schrott. Poundstone Prisoners Dilemma, S. 25.
McRae, John von Neumann, Birkhäuser, S. 328
Find a grave, John von Neumann
Members of the American Academy. Listed by election year, 1900–1949 (PDF). Abgerufen am 8. Oktober 2015
Honorary Members. London Mathematical Society, abgerufen am 22. Mai 2021.
McRae: Von Neumann, S. 186, nach Jacob Bronowski: The Ascent of man, BBC book, 1973 und in seiner gleichnamigen BBC Fernsehserie, Folge 13. Bei McRae steht „Differentialkoeffizient“, offensichtlich ein Übersetzungsfehler.
Freeman Dyson: A meeting with Enrico Fermi. In: Nature. 427, Nr. 297, 2004.
Besprechung von Neumanns Selected Letters von George Dyson: Review. In: Notices AMS, Juni/Juli 2007.
Besprechung von George Dyson, Turings Cathedral von Brian Blank: Review. In: Notices AMS, August 2014. Wie das Buch von Regis viel zur Geschichte des IAS. Er wertet Klara von Neumanns unveröffentlichte Memoiren aus.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[IsraelGasca-1] Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 1f.

[2] Poundstone, Prisoners dilemma, S. 11.

[3] Poundstone, Prisoners dilemma, S. 11.

[4] Siehe Ulf Hashagens Artikel über die Habilitation in Berlin (S. 265). Sie war am 13. Dezember 1927 abgeschlossen.

[5] Im Wintersemester 1928/29 ist Neumann von Margitta wie im Sommersemester 1928 auch beim mathematischen Kolloquium und bei der Besprechung neuerer Arbeiten zur Quantentheorie mit Leó Szilárd angegeben. Weitere Dozenten bei der Besprechung neuerer Arbeiten zur Quantentheorie waren im Wintersemester 1928/29 Hartmut Kallman und Fritz London.

[6] John (Janos) von Neumann im Mathematics Genealogy Project (englisch)

[7] Die in der Quantenmechanik verwendeten Operatoren für Messgrößen sind linear (Superpositionsprinzip für Lösungen zum Beispiel der linearen Schrödingergleichung) und selbst-adjungiert, da dann die Eigenwerte, die möglichen Messwerte, reell sind.

[8] Die Anekdote stammt von Kurt Friedrichs, vgl. Peter Lax Mathematics and Physics, Bulletin American Mathematical Society, Bd. 45, 2008, S. 135–152.

[9] Zuerst wahrscheinlich von Paul Ehrenfest in einem Brief an Wolfgang Pauli im September 1928 verwendet, siehe Martina Schneider, Zwischen zwei Disziplinen. B. L. van der Waerden und die Entwicklung der Quantenmechanik, Springer 2011, S. 63.

[10] Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 15

[11] Von Neumann war wie Edward Teller und eine Reihe anderer theoretischer Physiker nach Ende des Krieges in Los Alamos bei seinen Besuchen (man arbeitete an der Wasserstoffbombe) Mitglied einer Poker-Runde. Stanislaw Ulam Adventures of a Mathematician, Scribners 1976, S. 169.

[12] Im Menger Kolloquium, übersetzt als A model of general equilibrium. In: Review of Economic Studies, Bd. 13, 1945, 1, auch in Brody, Vamos (Hrsg.): The von Neumann compendium. Neu war unter anderem die Verwendung von Ungleichungen statt nur von Gleichungen wie bei Walras, vgl. McRae, S. 217ff.

[13] Poundstone „Prisoners dilemma“, S. 4 zitiert einen Nachruf in Life Magazin 1957, in der sich von Neumann 1950 sogar für einen vorbeugenden Atomkrieg gegen die Sowjetunion aussprach, wie etwa zur gleichen Zeit auch andere Persönlichkeiten wie der durch die Zeitgeschichte gewandelte Pazifist Bertrand Russell.

[14] Friedrich L. Bauer: Historische Notizen zur Informatik. Springer Verlag, 2009, S. 139.

[15] Nicholas Metropolis, J. Worlton: A trilogy on errors in the history of computing. In: IEEE Annals of the history of computing, Band 2., 1980, S. 49–55, vertreten die Ansicht, dass das Konzept stored program durch Eckert und Mauchly vor der Beteiligung von von Neumann entwickelt wurde. Siehe auch Friedrich L. Bauer: Historische Notizen zur Informatik. Springer Verlag, 2009, Kapitel Wer erfand den von Neumann Rechner? Wiederabdruck aus Informatik Spektrum, Band 21, 1998, S. 84. Auch Joel Shurkin: Engines of the Mind. The history of the computer. Norton, 1984, sieht für den Edvac die Beiträge von Eckert und Mauchly als zentral an und von Neumanns bedeutende Rolle erst mit seinem eigenen IAS-Rechner einsetzend, Goldstine: The Computer from Pascal to von Neumann. 1993, S. 186f. spricht sich dagegen für eine zentrale Rolle von Neumanns aus, der nach Goldstine schon Anfang August 1944 an den Diskussionen in der Moore School beteiligt war.

[16] Goldstine: The Computer from Pascal to von Neumann. 1993, S. 182.

[17] Goldstine: The Computer from Pascal to von Neumann. Princeton University Press, 1993, S. 229.

[18] Bauer: Historische Notizen zur Informatik. S. 138.

[19] Raúl Rojas: The architecture of Konrad Zuses early computing machines. In: Rojas, Hashagen: The first computers. MIT Press, 2000. Nach Rojas war die Z1 vom logischen Aufbau dem späteren Relais-Rechner Z3 sehr ähnlich und beide prinzipiell als universelle Rechenmaschine einsetzbar, auch wenn das nicht praktikabel war.

[20] Raúl Rojas: Zuse und Turing. Der Draht des Mephistopheles. In: Telepolis, 21. Dezember 2011.

[21] Thomas Rid: Maschinendämmerung. Eine kurze Geschichte der Kybernetik. Propyläen, Berlin 2016, ISBN 978-3-549-07469-5 (492 S., amerikanisches Englisch: Rise of the Machines. A Cybernetic History. New York 2016. Übersetzt von Michael Adrian, Erstausgabe: W.W. Norton & Company).

[Kybernetik-22] Norbert Wiener: Kybernetik. Regelung und Nachrichtenübertragung im Lebewesen und in der Maschine. Mit Ergänzung von 1961 zu lernenden und sich selbst reproduzierenden Maschinen. Zweite, revidierte und ergänzte Auflage. Econ-Verlag, Düsseldorf 1963 (287 S., amerikanisches Englisch: Cybernetics or Control and Communication in the Animal and the Machine. 1948. Übersetzt von E. H. Serr, E. Henze, Erstausgabe: MIT-Press).

[23] John von Neumann: Theory of Self-reproducing Automata. posthum herausgegeben. Hrsg.: Arthur W. Burks. University of Illinois Press, 1967, ISBN 978-0-252-72733-7 (englisch, 388 S.).

[24] Poundstone: Prisoner’s Dilemma. S. 24

[25] Howard Eves: Return to Mathematical Circles, PWS-Kent Publishing, 1988, S. 140.

[26] Stephen Dunwell von IBM berichtet darüber in seinem Oral History Interview 1989. (PDF) Babbage Institute. Nach Dunwell war seine Rolle als Berater bei IBM sehr begrenzt, man war sich aber bei IBM bewusst, dass man ihm als Vater des modernen Computers sehr viel verdankte. Das hing auch mit von Neumanns allgemeiner Einstellung zusammen – er vertrat nach Dunwell die Meinung, bei Computern wäre nicht geringer Speicherplatz das Problem, sondern einfallslose Programmierer.

[27] Russell Dupuis: The Diode Laser – the first 30 days 40 years ago. In: Optics and Photonics News, Bd. 15, 2004, S. 30, The Diode Laser—the First Thirty Days Forty Years Ago (Memento vom 19. Juni 2010 im Internet Archive)

[28] Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 15

[29] Poundstone, Prisoners Dilemma, S. 11, 17 und S. 194 zu seinem Tod

[30] Israel, Gasca, The world as a mathematical game, Birkhäuser 2009, S. 85

[31] Nach anderen Aussagen pflegte er auch, laut im Auto zu singen, mit entsprechenden Lenkbewegungen. Er fuhr fast jedes Jahr ein Auto zu Schrott. Poundstone Prisoners Dilemma, S. 25.

[32] McRae, John von Neumann, Birkhäuser, S. 328

[33] Find a grave, John von Neumann

[34] Members of the American Academy. Listed by election year, 1900–1949 (PDF). Abgerufen am 8. Oktober 2015

[35] Honorary Members. London Mathematical Society, abgerufen am 22. Mai 2021.

[36] McRae: Von Neumann, S. 186, nach Jacob Bronowski: The Ascent of man, BBC book, 1973 und in seiner gleichnamigen BBC Fernsehserie, Folge 13. Bei McRae steht „Differentialkoeffizient“, offensichtlich ein Übersetzungsfehler.

[37] Freeman Dyson: A meeting with Enrico Fermi. In: Nature. 427, Nr. 297, 2004.

[38] Besprechung von Neumanns Selected Letters von George Dyson: Review. In: Notices AMS, Juni/Juli 2007.

[39] Besprechung von George Dyson, Turings Cathedral von Brian Blank: Review. In: Notices AMS, August 2014. Wie das Buch von Regis viel zur Geschichte des IAS. Er wertet Klara von Neumanns unveröffentlichte Memoiren aus.