Feld (Physik)
In der Physik beschreibt ein Feld die räumliche Verteilung einer physikalischen Größe. Dabei kann es sich um ein Skalarfeld (wie z. B. die Temperatur, das Gravitationspotential oder das elektrostatische Potential), um ein Vektorfeld (wie z. B. die Strömungsgeschwindigkeit, das Gravitationsfeld oder das elektrische Feld) oder um ein höherdimensionales Tensorfeld wie den Energie-Impuls-Tensor handeln. Der Wert eines Feldes an einem bestimmten Ort wird in manchen Fällen Feldstärke genannt. Die Lehre von den physikalischen Feldern nennt man Feldtheorie.
Manche Felder sind darüber hinaus selbst physikalische Objekte:
- Sie erfüllen Bewegungsgleichungen, hier Feldgleichungen genannt. Für das elektrische und das magnetische Feld sind die Maxwell-Gleichungen die Bewegungsgleichungen.
- Wie Körper besitzen Felder Energie (die Feldenergie), Impuls und auch Drehimpuls. Die Kraftwirkung zwischen zwei Körpern im leeren Raum wird dadurch erklärt, dass ein Feld diese Größen von einem Körper aufnimmt und sie auf den anderen Körper überträgt.
In der Quantenfeldtheorie ist das Feld der fundamentale Begriff, aus dem alle Eigenschaften der Materie und Kräfte entwickelt werden. Ein Feld kann hier nur in definierten Stufen angeregt werden, die als Erzeugung einer entsprechenden Anzahl von Feldquanten beschrieben werden. Alle bekannten Materieteilchen bestehen aus solchen Feldquanten bestimmter Felder, während die Kräfte zwischen ihnen durch Austauschteilchen, d. h. Feldquanten bestimmter anderer Felder, bewirkt werden. Die einzelnen Feldquanten sind die fundamentalen Elementarteilchen.
Allgemeines
Verschiedene Auffassungen des Feldbegriffs
Felder geben einerseits die räumliche Verteilung bestimmter physikalischer Eigenschaften an: Beispielsweise kann die räumliche Verteilung der Temperatur einer Herdplatte durch ein Temperaturfeld beschrieben werden oder die räumliche Verteilung der Dichte in einem Körper durch ein Massendichtefeld. In diesem Sinne ist ein Feld ein mathematisches Hilfsmittel, das die eigentlich punktweise definierten physikalischen Eigenschaften eines ausgedehnten oder aus Untersystemen zusammengesetzten Systems in einer Größe, dem Feld, zusammenfasst.
Ein Feld kann aber auch eine eigenständige physikalische Entität sein, die nicht als zusammengesetztes System oder mathematische Hilfsgröße angesehen werden darf. Das Feld kann dann genauso wie ein Teilchen, ein starrer Körper oder ein anderes physikalisches System einen Impuls und Drehimpuls tragen, Energie enthalten und sich in angeregten Zuständen befinden. Beispielsweise ist ein Lichtstrahl, der Energie durch den leeren Raum transportiert, wie durch den Poynting-Vektor beschrieben, ein (zeitabhängiges) Feld und steht in der physikalischen Hierarchie der Entitäten auf der gleichen Ebene wie Teilchen oder andere Materie.[1]
In diesem Sinne kann z. B. das elektrische Feld einerseits einfach nur als räumliche Verteilung der elektrischen Feldstärke angesehen werden, oder aber als eigenständiges nicht reduzierbares System.
Dynamik von Feldern
Im Allgemeinen sind Felder zeitabhängig, also Funktionen von Ort und Zeit. Die Dynamik eines Teilchens wird mittels Bewegungsgleichungen beschrieben; entsprechend wird die Dynamik von Feldern, also die raum-zeitliche Änderung der Feldgröße, mittels Feldgleichungen beschrieben. Der wesentliche Unterschied zwischen Feldgleichungen und Bewegungsgleichungen von Teilchen besteht darin, dass eine Feldgleichung die Dynamik unendlich vieler Freiheitsgrade beschreibt, da ein Feld unendlich viele Freiheitsgrade besitzt (die Feldgröße an jedem Raumpunkt bildet einen Freiheitsgrad und ein Feld ist im Allgemeinen an unendlich vielen Raumpunkten definiert). Die Bewegungsgleichungen eines Teilchen beschreiben dagegen nur die Dynamik endlich vieler Freiheitsgrade (meistens die zeitliche Entwicklung der drei räumlichen Koordinaten des Teilchens).
Geschichte des Feldbegriffs
Der Ursprung des Konzeptes des Feldes liegt im 18. Jahrhundert, als in der Kontinuumsmechanik und der Fluidmechanik die räumliche Verteilung bestimmter Größen thematisiert wurde. Es wurde nicht als eigenständige Entität angesehen und die Dynamik der Felder wurde mittels der newtonschen Teilchen-Mechanik aus den Eigenschaften der dem Feld zugrundeliegenden Moleküle oder Volumenelemente abgeleitet. Eine ganz neue Bedeutung erhielt der Feldbegriff durch die aufkommende Elektrodynamik am Ende des 19. Jahrhunderts, da das elektromagnetische Feld nicht als makroskopischer Zustand aufgebaut aus mikroskopischen Untersystemen erklärt werden konnte. Das elektromagnetische Feld wurde zu einer neuen irreduziblen Entität.[2][3] Michael Faraday und James Clerk Maxwell waren noch der Meinung, dass das elektromagnetische Feld nur ein angeregter Zustand des Äthers ist und führten damit das Feld auf Bewegung oder mechanische Spannungen in einer Materieform, dem Äther, zurück. Doch das Michelson-Morley-Experiment widersprach der Äthertheorie. Die Existenz des Äthers, der den leeren Raum ausfülle, wurde fortan in der Physik verworfen. Die Beobachtung, dass das elektromagnetische Feld auch im Vakuum, ohne Trägermaterie, ohne eine unsichtbare Trägersubstanz wie den Äther existiert, führte dazu, dass das elektrische Feld als eigenständiges physikalisches System aufgefasst wurde.[1] Heute steht der Begriff des Feldes dem Begriff der Materie (mindestens) gleichberechtigt gegenüber. Der leere Raum kann sowohl Materie als auch Felder enthalten. In der Quantenfeldtheorie schließlich werden auch die Materieteilchen als Feldquanten, d. h. gequantelte Anregungen von Feldern angesehen. Die Frage, ob Teilchen oder Felder letztlich das „Fundamentalere“ in der Natur sind, wird bis heute (2018) kontrovers diskutiert. Die meisten Physiker sind allerdings der quantenfeldtheoretischen Ansicht, dass es weder lokalisierte Teilchen noch leeren Raum gibt, sondern nur Felder (und deren Quanten, die an jeder Stelle, an der das Feld nicht null ist, gefunden werden können).[4]
Das Feld als Träger von Wechselwirkungen
Die newtonsche Gravitationstheorie ist eine Fernwirkungstheorie, da in dieser Theorie nicht erklärt wird, wie ein von Körper A entfernter Körper B die Anwesenheit von A spürt, wie also die Gravitationswechselwirkung durch den leeren Raum transportiert wird. Außerdem ist die Ausbreitungsgeschwindigkeit der Wechselwirkung in dieser feldlosen Theorie unbegrenzt. Laut der Relativitätstheorie gibt es aber eine obere Grenze der Ausbreitungsgeschwindigkeit für alle Wechselwirkungen und zwar die Lichtgeschwindigkeit. Wechselwirkungstheorien müssen, um die Kausalität von Ereignissen nicht zu verletzen, lokal sein. Mit Hilfe des Feldbegriffs können Wechselwirkungen lokal beschrieben werden.[5] Der Körper A ist vom Gravitationsfeld umgeben und reagiert auf die Änderungen des Feldes in seiner Umgebung und nicht direkt auf die Verschiebung anderer Körper, die das Feld erzeugen. Das Feld ist also Träger der Wechselwirkung. Feldgleichungen beschreiben, wie und mit welcher Geschwindigkeit sich Störungen in einem solchen Wechselwirkungsfeld ausbreiten, also auch mit welcher Geschwindigkeit A von der Versetzung von B erfährt. Die Feldgleichungen der Gravitation sind die einsteinschen Feldgleichungen, die Feldgleichungen des Elektromagnetismus die Maxwell-Gleichungen.
Einteilung von Feldern

Der Feldbegriff findet in allen Zweigen der Physik Anwendung, und zur speziellen Charakterisierung haben sich viele spezielle Feldbegriffe durchgesetzt. Dabei kann dasselbe Feld unter mehrere der folgenden speziellen Feldbegriffe fallen.
Ein Kriterium zur Charakterisierung von Feldern ist die physikalische Natur der Feldgröße: Dichtefeld, Temperaturfeld, Geschwindigkeitsfeld, Gravitationsfeld, Elektrisches Feld, Magnetfeld, (Konservatives) Kraftfeld und Schallfeld.
Ein anderes Kriterium ist die mathematische Natur der Feldgröße: Skalarfelder haben Skalare als Funktionswerte, etwa die Massedichte oder die Temperatur. Ein wichtiges Skalarfeld ist das physikalische Potential. Vektorfelder haben Vektoren als Funktionswerte, etwa die Kraft oder die elektrische Feldstärke; Tensorfelder haben Tensoren als Funktionswerte, etwa die elastische Spannung; Spinorfelder haben Spinoren als Funktionswerte, etwa die Lösungen der Diracgleichung oder Weyl-Gleichung in der relativistischen Quantenmechanik. Für die Feldgröße mancher Vektorfelder ist der Name Feldstärke gebräuchlich.
Felder können zusätzlich nach ihrer zeitlichen (Un)veränderlichkeit charakterisiert werden: Statische Felder besitzen Funktionswerte, die zeitunabhängig sind, und sind damit beispielsweise Gegenstand der Statik, Elektrostatik, Magnetostatik, Hydrostatik oder Aerostatik. Stationäre Felder besitzen Funktionswerte, die zwar im Allgemeinen zeitabhängig sind, sich aber im gerade betrachteten Fall nicht zeitlich ändern. Beispiele sind hier das Magnetfeld um einen ruhenden, von einem konstanten Gleichstrom durchflossenen Leiter oder eine stationäre Strömung einer Flüssigkeit. Quasistationär nennt man Felder, deren Funktionswerte sich zwar mit der Zeit ändern, doch nur so wenig, dass diese Veränderung vernachlässigbar ist.
Felder können auch nach ihrer örtlichen (Un)veränderlichkeit eingeteilt werden. In einem homogenen Feld ist die Feldgröße an jedem Ort gleich, also ortsunabhängig. Ist dies nicht der Fall, heißt das Feld inhomogen.
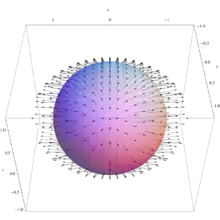
Vektorfelder können nach dem Verlauf ihrer Feldlinien charakterisiert werden. Feldlinien können von bestimmten Punkten im Raum ausgehen und in anderen Punkten verschwinden (Quelle und Senke) – Felder dieser Art heißen ganz allgemein Quellenfelder. Beispiel hierfür sind das elektrostatische Feld einer positiven und negativen elektrischen Ladung oder das Gravitationsfeld. Feldlinien können aber auch als stets in sich geschlossene Schleifen auftreten – Felder dieser Art heißen ganz allgemein Wirbelfelder. Bekanntestes Beispiel hierfür ist das Magnetfeld. Das Vektorfeld, das sich aus dem Gradienten an jedem Ort eines Potenzialfeldes ergibt, heißt Gradientenfeld.
Bildliche Darstellung von Feldern
Zweidimensionale Skalarfelder oder zweidimensionale Schnitte von höherdimensionalen Skalarfeldern können mit Hilfe von Höhenlinien oder der Höhe entsprechend eingefärbten Punkten in einer Ebene dargestellt werden (siehe oberes nebenstehendes Bild).
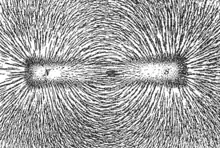
Manche zweidimensionale Vektorfelder können besonders anschaulich mit Hilfe von Feldlinien dargestellt werden (siehe unteres nebenstehendes Bild). Die Tangente einer Feldlinie gibt die Richtung der Feldgröße (Vektor) an der jeweiligen Stelle an; der Abstand der Linien voneinander ist umgekehrt proportional dem Betrag der Feldgröße.
Literatur
- Hartmann Römer, Michael Forger: Elementare Feldtheorie: Elektrodynamik, Hydrodynamik, spezielle Relativitätstheorie. VCH, Weinheim 1993, ISBN 3-527-29065-6 (uni-freiburg.de).
- Otto Nachtmann: Phänomene und Konzepte der Elementarteilchenphysik. Vieweg+Teubner, 1992, ISBN 3-528-08926-1.
Weblinks
- Lecture 1 | Quantum Entanglements, Part 1 (Stanford), Leonard Susskind, Stanford, benutzt die Temperatur, um ein Feld zu erklären (englisch). Video, 25. September 2006
Einzelnachweise
- David Bohm: Causality and chance in modern physics. University of Pennsylvania Press, 1980, ISBN 978-0-8122-1002-6, S. 42 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 29. Januar 2012]).
- Internationale Tagung Ontological Aspects of Quantum Field Theory (abgerufen am 27. Januar 2017), Zentrum für Interdisziplinäre Forschung der Universität Bielefeld, 11.–13. Oktober 1999 (geleitet von Manfred Stöckler, Andreas Bartels, Brigitte Falkenburg, Michael Drieschner und Allen Hirshfeld).
- Meinard Kuhlmann, Holger Lyre, Andrew Wayne: Ontological aspects of quantum field theory. World Scientific, 15 June 2002, ISBN 978-981-238-182-8, S. 8–.
- Art Hobson: There are no particles, there are only fields. Am.J.Phys.81,211(2013). Aus dem Amerikanischen: Es gibt keine Teilchen, es gibt nur Felder
- Marc Lange: An introduction to the philosophy of physics: locality, fields, energy and mass. Wiley-Blackwell, 24 June 2002, ISBN 978-0-631-22501-0, S. 26 ff. (Abgerufen am 30. Januar 2012).