Heuristik
Heuristik (von altgriechisch εὑρίσκω heurísko „ich finde“; von εὑρίσκειν heurískein ‚auffinden‘, ‚entdecken‘) bezeichnet die Kunst, mit begrenztem Wissen (unvollständigen Informationen) und wenig Zeit dennoch zu wahrscheinlichen Aussagen oder praktikablen Lösungen zu kommen.[1] Es bezeichnet ein analytisches Vorgehen, bei dem mit begrenztem Wissen über ein System mit Hilfe mutmaßender Schlussfolgerungen Aussagen über das System getroffen werden. Die damit gefolgerten Aussagen weichen oftmals von der optimalen Lösung ab. Durch Vergleich mit einer optimalen Lösung kann die Güte der Heuristik bestimmt werden.
Bekannte Heuristiken sind zum Beispiel Versuch und Irrtum (trial and error), statistische Auswertung von Zufallsstichproben und das Ausschlussverfahren. Heuristische Verfahren basieren auf Erfahrungen; sie können auch auf „falschen“ Erfahrungen (z. B. verzerrte Wahrnehmung, Scheinkorrelation) basieren.[2]
Begriffsunterscheidung
Der Unterschied der Heuristik zur Approximation liegt darin, dass eine Approximation eine quantifizierbare Güte (d. h. eine Aussage über den zu erwartenden Fehler) enthält.[3]
Der Übergang zwischen Heuristik und Algorithmus ist fließend. Werner Stangl definiert ihn folgendermaßen: Ein Algorithmus bezeichnet eine systematische, logische Regel oder Vorgehensweise, die zur Lösung eines vorliegenden Problems führt. Im Gegensatz dazu steht dabei die schnellere, aber auch fehleranfälligere Heuristik.[4]
Entwicklung der Heuristik
Pappos in der Antike
Erste Ansätze stammen aus dem 4. Jahrhundert vom griechischen Mathematiker Pappos von Alexandria. Pappos entwickelte folgende Methode:
Algorithmische Traditionslinie
Al-Chwarizmi
.png.webp)
Al-Chwarizmi, der um 830 lebte, beschrieb algorithmische Methoden, wie sie bereits in Persien entwickelt worden waren. Im Mittelalter wurde das Werk ins Lateinische übersetzt (algoritmi de numero Indorum). So entstand aus dem Namen al Khovarezmi der pseudogriechische Terminus algorithmos.
Raimundus Lullus und Athanasius Kircher
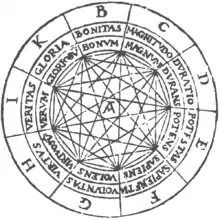
Raimundus Lullus (1235–1313), ein katalanischer Philosoph und Theologe mit arabischen Sprachkenntnissen, konstruierte eine mechanisch-kombinatorische Anordnung beweglicher Scheiben, die es ermöglichen sollte, alle möglichen Urteile und Wahrheiten zu gewinnen. Der hier in Ansatz gebrachte Lösungsstammbaum mit drei Entscheidungsstufen von jeweils neun Wahlmöglichkeiten eröffnet naturgemäß nur eine endliche Anzahl von Kombinationen. Die ars combinatoria des Lullus ist auf 93 = 729 Wahlmöglichkeiten begrenzt. (Siehe Abb.: Ramon Lull-Ars Magna, Fig.1). Eine direkte Fortsetzung fanden die Ideen Lullus’ durch den deutschen Jesuiten Athanasius Kircher in seiner Schrift Ars magna sciendi sive combinatoria (1669), um mithilfe der Kombinatorik aus einem System von Grundbegriffen alle erdenklichen und gültigen Schlussweisen und Wahrheiten auf mechanischem Wege abzuleiten. Die Kombination der gesamten Buchstaben des Alphabets mit Zahlenpermutationen ergibt andere Möglichkeiten als die nur neun symbolischen Buchstaben des Lullus: B, C, D, E, F, G, H, I, K = Bonitas, Magnitudo, Duratio, Potentia, Cognitio, Voluntas, Virtus, Veritas, Gloria. Aus der Kombination dieser principa absoluta und der principa relativa (Differenzia, Concordantia, Contrarietas, Principium, Medium, Finis, Majoritas, Aqualitas, Minoritas) sollten alle Formen des Seienden nach damaliger Auffassung Lull erfasst werden können.[5] Daher findet man bei Kircher die Permutationsreihe aus Zehn mit der Zahl 3.628.800 beim Buchstaben K.[6]
In der Literatur beschäftigte sich Stéphane Mallarmé (1842–1898), ein Kritiker und Poet des 19. Jahrhunderts, dessen Gedichte als Hauptwerke des Symbolismus gelten, mit der Kombinatorik von Wörtern. Sein fragmentarisch gebliebenes Text-Kunstwerk „Livre“, an dem er über 30 Jahre arbeitete, sollte sich für den Leser, durch die vielfältigen Kombinationsweisen des experimentell erweiterten Buches, unterschiedliche Lektüren und Lesarten bieten.[7][8][9] Aber auch diese Methode endet in einer endlichen Anzahl von Möglichkeiten. Lesenswert in diesem Zusammenhang ist der Aufsatz Einladung zu einem Poesie-Automaten von Hans Magnus Enzensberger.[10][11]
Lord Francis Bacon
Lord Francis Bacon (1561–1626) forderte in seinem Werk Novum Organon[12] eine Weiterentwicklung der Heuristik. Er beschreibt darin die Methode der Induktion als den wahren Weg, den bisher noch niemand versucht habe. Letzteres stimmt nicht: Schon Aristoteles hat die induktive Methode sehr wohl genutzt; diesem folgten Naturphilosophen in Alexandria, arabische Denker und Humanisten.[13]
Gottfried Wilhelm Leibniz
 Gottfried Wilhelm Leibniz (1646–1716)
Gottfried Wilhelm Leibniz (1646–1716) Der Ursprung der Rechenmaschine, das Sprossenrad, Handskizze von Leibniz[14]
Der Ursprung der Rechenmaschine, das Sprossenrad, Handskizze von Leibniz[14] 1990 Dresdner Nachbau der Leibniz’schen Rechenmaschine[15]
1990 Dresdner Nachbau der Leibniz’schen Rechenmaschine[15]
Gottfried Wilhelm Leibniz postulierte 1666 in Analogie zu Lullus die ars combinatoria, durch die man alle Erkenntnisse auf algorithmische Weise gewinnen kann. Im Gegensatz zu Lullus und in Anlehnung an René Descartes sind alle Begriffe auf ihren elementaren Kern zu reduzieren; dann könne man – durch ihre Kombination – alle möglichen Begriffszusammensetzungen erhalten. Aufgrund der Unzulänglichkeiten der Sprache muss zuvor eine Übersetzung in eine Kunstsprache, die Characteristica universalis, eine Weiterentwicklung der Mathesis universalis, erfolgen. Selbiges – das Übersetzen in eine künstliche universelle Plansprache, hatte Athanasius Kircher bereits 1663 in der Polygraphia nova gefordert und eine solche auch geschaffen.
Beispiel:
- Abbildung grundlegender Begriffe durch Primzahlen
- Lebewesen = 2; vernunftbegabt = 3
- Abbildung komplexer Begriffe auf Produkten von Primzahlen
- Mensch = vernunftbegabtes Lebewesen = 3 × 2 = 6
Im Gegensatz zu Descartes’ geschlossener Konzeption wurde Leibniz’ Auseinandersetzung mit der Heuristik nur fragmentarisch überliefert. Er unterschied zwischen der ars iudicandi, der Kunst, die Wahrheit von Aussagen zu beurteilen, und der ars inveniendi, der reinen Entdeckungskunst. 1673 stellte Gottfried Wilhelm Leibniz eine von ihm entwickelte Staffelwalzen-Maschine der Royal Society in London vor.[16]
Fritz Zwicky
Als Weiterentwicklung der algorithmischen Traditionslinie erdachte Fritz Zwicky (1898–1974), ein schweizerisch-amerikanischer Physiker und Astronom, neben seinen astronomischen Tätigkeiten eine Methodik, aus Ideen konkrete Produkte zu entwickeln; siehe Morphologischer Kasten.
Heuristische Traditionslinie oder Klassische Heuristik
René Descartes
René Descartes (1596–1650) entwickelte 1637 mit seinem Discours de la méthode eine frühe Methodologie, die sich mehrfach auf das Vermögen der Intuition stützt. Mit ihrer Hilfe, so Descartes, erfasst der Mensch augenblicklich die Wahrheit einfachster Aussagen wie „Ein Dreieck hat drei Seiten“. Die Methode selbst besteht im Wesentlichen darin, komplexe Probleme derart zu zerlegen, dass ihre einzelnen Elemente qua Intuition als wahr erkannt werden können.
Joachim Jungius
Joachim Jungius (1587–1657) hat wahrscheinlich erstmals den Begriff Heuristik verwandt und sah in der heuristischen Erkenntnis die höchste Stufe der Erkenntnis, da sie ungelöste Probleme und neue Verfahren zum Gegenstand habe.
Friedrich Schleiermacher
Friedrich Schleiermacher (1768–1834) postulierte erstmals die Heuristik als eigenständige Wissenschaft neben der Logik. An Stelle der abstrakten Zielsetzung sollte eine konkrete Denkpraxis treten. Schleiermacher definierte Heuristik als bewusstes, kunstmäßiges geistiges Arbeiten zum Finden neuer Erkenntnisse und Erkenntniszusammenhänge. Nach Schleiermacher zerfällt der Erkenntnisprozess bei der Heuristik in zwei Etappen:
- Konzentration auf den Problemsachverhalt.
- Bezugnahme auf den allgemeinen Zusammenhang.
Entscheidend sei hierbei die bewusste Durchführung des Verfahrens, da sich unbewusste und Zufallslösungen einer empirischen Überprüfung entziehen.
Bernard Bolzano
Bernard Bolzano (1781–1848) setzte auf die Systematisierung der Methoden, um in der jeweilig gegebenen Erkenntnissituation faktisch die zur Verfügung stehenden Möglichkeiten für die logische Inangriffnahme vorgegebener Problemstellungen herauszuarbeiten und zu begründen. Willkürliches Denken, dessen Lösungsfindung niemals vollständig von logischen Gesetzen bestimmt ist, soll durch systematisch geordnete Zusammenstellung und klare Darlegung in der Wissenschaftspraxis angewendeter Methoden gelenkt werden. Die von Bolzano beschriebene Methodenproblematik stellt die umfassendste und geschlossenste Darstellung von heuristischen Methoden in der älteren Literatur dar.[17]
Leonhard Euler
Der Mathematiker Leonhard Euler (1707–1783) schuf unter anderem die Grundlagen für die effiziente Lösung des Problems des Handlungsreisenden (TSP), siehe auch MST-Heuristik, Christofides-Heuristik, k-Opt-Heuristik.
George Pólya

Viele bekannte Aussagen zur Heuristik in der Mathematik machte insbesondere der ungarische Mathematiker und Schriftsteller George Pólya. In seiner Reihe Vom Lösen mathematischer Probleme behandelt er intensiv Problemlösungsstrategien mittels heuristischer Methoden.
Moderne Ansätze
Ab 1964 wurde in der DDR u. a. durch Johannes Müller die Entwicklung und Anwendung eines Methodensystems, der Systematischen Heuristik betrieben, um die kreative Arbeit in den Bereichen Forschung und Entwicklung zu verbessern.[18] Die russische Variante der Systematischen Heuristik nennt sich TRIZ.
Qualitative Heuristik ist eine von Gerhard Kleining entworfene sozialwissenschaftliche und psychologische Methodologie, die die „Entwicklung und Anwendung von Entdeckungsverfahren in regelgeleiteter Form“ zum Gegenstand hat.
Die Entwicklung der Lochkartentechnik von etwa 1900 bis etwa 1960 (s. u.) sowie der EDV seit den 1950er Jahren trug maßgeblich dazu bei, dass sich Wissenschaftler verschiedener Disziplinen intensiv mit dem Thema Heuristik beschäftig(t)en. Zum Beispiel versuchten Wirtschaftswissenschaftler, Techniken weiterzuentwickeln, mit denen man auf der Basis von Unternehmensdaten besser planen kann. Für dieses Forschungsgebiet bürgerte sich der Begriff Operations Research (OR) ein. Ziel von OR ist die Entwicklung und der Einsatz quantitativer Modelle und Methoden zur Entscheidungsunterstützung (siehe auch Entscheidungsunterstützungssystem). OR ist ein Querschnittsgebiet zwischen Angewandter Mathematik, Wirtschaftswissenschaften und Informatik.
Schon vor dem Ersten Weltkrieg hatten Militärs verschiedener Länder die Möglichkeiten quantitativer Planung erkannt, die die Lochkartentechnik bot:
- Die US Army setzte im Ersten Weltkrieg Lochkartenlogistik im Sanitätswesen ein.
- Österreich-Ungarn produzierte den Stahlhelm Modell 1917 bei Krupp Berndorfer Metallwarenfabrik. Zur statistischen Absicherung des Designs wurden K.u.k-Sanitätsberichte mit Hollerith-Lochkartentechnik ausgewertet.[19]
- In Polen hieß das Tochterunternehmen von IBM bis 1938 »Polski Hollerith«, es berichtete über Multitasking und hatte mit der umgekehrten polnischen Notation Potenzial für die Entwicklung von Computern.
- Es gibt Berichte über den Einsatz in Tschechien, in Holland und in Belgien im Wehrersatzwesen (Musterung, Einberufung u. ä.)
Hauptartikel: Maschinelles Berichtswesen
Anwendungsgebiete
Wirtschaftswissenschaften
Im Bereich der Operations Research werden heuristische Verfahren eingesetzt, wenn der erforderliche Rechenaufwand im Entscheidungsfindungsprozess zu umfangreich ist oder dieser den Rahmen des Möglichen sprengt (wie auch bei Schachprogrammen.[20]) Dabei wird die Anzahl der in Betracht zu ziehenden Möglichkeiten reduziert, indem man aussichtslos erscheinende Varianten von vornherein ausschließt. Anwendungsgebiete sind z. B. multiple Containerladeprobleme wie die Beladung von Containerschiffen etc.[21], oder auch Multimomentaufnahmen.
Eine Lösung mittels Heuristiken erfolgt zum Beispiel auch beim Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) oder auch beim Ameisenalgorithmus. Weitere Anwendungen finden sich in der Schwarmintelligenz und den Boids.
Die Alternative zu heuristischen Verfahren ist die Brute-Force-Methode, bei der alle in Frage kommenden Möglichkeiten ausnahmslos durchgerechnet werden. Die bekannteste und einfachste Heuristik ist die Lösung eines Problems mittels „Versuch und Irrtum“ (Englisch: by trial and error).
Gerd Gigerenzer vom Max-Planck-Institut für Bildungsforschung wies 2007 in seinem Buch Bauchentscheidungen anhand von mehrfach wiederholten Experimenten nach, dass eine Gruppe zufällig ausgewählter Straßenpassanten, die zufällig Namen von Börsenunternehmen genannt hatten, eine wesentlich höhere „Performance“ erreichten, als ein von Finanzexperten und Börsenanalytikern zusammengestelltes Portfolio. Die Faustregel „Investiere in das, was du kennst“ hat sich gegenüber einer mit großen Informationsmengen gefällten Entscheidung als überlegen erwiesen.
Siehe in diesem Zusammenhang auch Verhaltensökonomik.
Philosophie
In der Philosophie spricht man von einer heuristischen Herangehensweise insbesondere dann, wenn eine bekannte Einheit X auf Grund ihrer Ähnlichkeit genutzt wird, um das Verständnis oder das Wissen über eine unbekannte Einheit Y zu erweitern beziehungsweise zu vertiefen. In diesem Sinne können Gleichnisse, Metaphern und sogar Fabeln als heuristische Mittel angesehen werden, um den Erkenntnisprozess eines Menschen zu fördern.
So nutzt beispielsweise Platons bekanntestes Werk Politeia jene heuristischen Mittel, indem es einen idealen Staat nicht als Muster für tatsächlich existierende Staaten beschreibt. Vielmehr zeigt er schlussfolgernd auf, wie Dinge verbunden werden müssten und wie sie aufeinander wirken, wenn man bestimmte Prinzipien rigoros verfolgt.
Psychologie
In der Psychologie sind Heuristiken einfache, effiziente Regeln, die sich durch evolutionäre Prozesse gefestigt haben oder erlernt wurden. Sie werden insbesondere genutzt, um Lagebeurteilungen, Entscheidungsfindungen und Problemlösungen von Menschen in komplexen Situationen (in denen es häufig an Informationen mangelt) zu erklären.
In den meisten Fällen erbringen diese heuristischen Vorgehensweisen das erwartete Ergebnis und führen daher zu einer befriedigenden Problemlösung. Es kann bei der Anwendung jedoch zu Fehleinschätzungen kommen.
Wahrnehmungspsychologie
Die Wahrnehmungspsychologie fand zahlreiche Heuristiken, die insbesondere im Bereich der Objekterkennung bei der visuellen Wahrnehmung eine wichtige Rolle spielen. Hier werden sie vom Gehirn dazu eingesetzt, aus den zweidimensionalen Bildern auf der Netzhaut dreidimensionale Objekte zu rekonstruieren. Wie spätestens die Künstliche-Intelligenz-Forschung zeigte, ist die Rekonstruktion eine enorme Leistung, denn häufig sind die Objekte teilweise verdeckt, oder die Ursachen von Hell-Dunkel-Übergängen – sie sind für das Erkennen von Objektumrissen („Kantendetektion“) wichtig – sind mehrdeutig.
Am häufigsten werden bei der Deutung der Informationen sogenannte Top-down-Verfahren eingesetzt, bei denen fehlende Bildinformationen aus dem Gedächtnis ergänzt werden. Sie ermöglichen dem Betrachter, bekannte Objekte schnell zu erkennen und in einen passenden Zusammenhang zu stellen. Ein Beispiel dafür ist die „Licht-von-oben-Heuristik“. Hierbei nimmt das Gehirn im Zweifelsfall an, dass das Licht von oben auf die Szene fällt und die Objekte entsprechende Schatten werfen. Diese werden bei der Kantendetektion „herausgerechnet“. Weitere Beispiele liefern die Gesetze der Gestaltpsychologie.
Da die eingesetzten Verfahren lediglich Heuristiken sind, sind sie anfällig für bestimmte Fehler. Diese werden augenfällig bei optischen Täuschungen.
Denkpsychologie
Aus Sicht der Kognitionspsychologie stellen Urteilsheuristiken Handlungsmöglichkeiten zur Verfügung, und zwar nicht nur dann, wenn die Situation auf Grund fehlender Informationen schwer einschätzbar ist, sondern auch, wenn die Lagebeurteilung aus Zeit- oder Motivationsmangel unvollständig ist.
Die Forschung auf diesem Gebiet haben insbesondere die Psychologen Daniel Kahneman und Amos Tversky vorangetrieben. Von ihnen stammen bekannte Studien zu häufig angewandten Heuristiken, darunter
- die Verfügbarkeitsheuristik,
- die Repräsentativitätsheuristik und
- die Ankerheuristik.
Daniel Kahneman erhielt im Jahr 2002 "für das Einführen von Einsichten der psychologischen Forschung in die Wirtschaftswissenschaft, besonders bezüglich Beurteilungen und Entscheidungen bei Unsicherheit" den Nobelpreis im Bereich Wirtschaftswissenschaften. Seine Arbeiten erlangten durch die Publikation seines Buches Schnelles Denken, langsames Denken (englisch: Thinking, Fast and Slow) Bekanntheit auch außerhalb wissenschaftlicher Kreise.
Mathematik
Im mathematischen Sinne wird der Begriff Heuristik für zwei verschiedene Verfahrensarten zur Lösung mathematischer Probleme verwendet.
Auf der einen Seite werden besonders einfache, aber mitunter nur mit hohem Zeitaufwand zur Lösung führende Verfahren heuristisch genannt. Ein Beispiel hierfür ist das gezielte Raten von Nullstellen einer Polynomfunktion, indem die ganzzahligen Teiler des Koeffizienten vom Polynom kleinsten Grades der Funktion ausprobiert werden.
Auf der anderen Seite sind speziell in der Optimierung Eröffnungsverfahren heuristische Verfahren, jene Methoden also, die innerhalb kurzer Zeit und ohne großen Aufwand eine zulässige Lösung liefern. Diese sogenannte Basislösung kann durch mehrfaches Anwenden der Heuristik (in mehreren Iterationen) präzisiert werden. Dennoch ist die gefundene Lösung meist nicht die Optimallösung. Jedoch ist das Finden einer Optimallösung gerade bei komplexen Problemen nicht immer praktikabel oder effektiv. Ein Beispiel dafür ist das Matrixminimumverfahren zur Ermittlung einer Basislösung des Transportproblems oder der Savings-Algorithmus.
Informatik
In der Informatik kommen, ähnlich wie in der Mathematik, heuristische Methoden zum Einsatz, um mit geringem Rechenaufwand und kurzer Laufzeit zulässige Lösungen für ein bestimmtes Problem zu erhalten. Klassische Algorithmen versuchen, einerseits die optimale Rechenzeit und andererseits die optimale Lösung zu garantieren. Heuristische Verfahren dienen bei der Lösungsfindung der Laufzeitoptimierung. Suchen in großen Bäumen (Verzweigungsrate und Tiefe) werden erst durch Heuristiken möglich. So kann die Breitensuche bei einem Baum mit Tiefe 15 und Verzweigungsrate 3 sehr lange dauern. Mit einer heuristischen Suche kann diese Suche viel schneller abgearbeitet werden. Es gibt diverse heuristische Algorithmen, z. B. in der informierten Suche. Dazu wird versucht, mithilfe von Schätzungen, „Faustregeln“, intuitiv-intelligentem Raten oder unter zusätzlichen Hilfsannahmen eine gute Lösung zu erzeugen, ohne optimale Eigenschaften garantieren zu müssen. Bekannte heuristische Algorithmen sind etwa A*-Suche, Simulierte Abkühlung und Evolutionäre Algorithmen in der Optimierung. Auch Fuzzy-Regeln, die in der Fuzzylogik eine wichtige Rolle spielen, können als heuristische Regeln bezeichnet werden. Ein grundsätzliches Verfahren, das nicht an ein spezielles Problem gebunden ist, wird in diesem Zusammenhang als Metaheuristik bezeichnet.
Eine Heuristik in der Informatik ist eine Bewertung, welche durch eine Berechnung ermittelt wird. Diese Berechnung basiert auf Schätzen, Beobachten, Vermuten oder Raten. Heuristiken dienen der Problemlösung, z. B. bei der Suche wird eine Heuristik verwendet, um einen „guten“ Weg oder eine „gute“ Lösung zu finden. Die Bewertung ist nur so gut wie die „Schätzung“. Heuristiken kommen immer dann zum Einsatz, wenn eine exakte Berechnung der optimalen Lösung unmöglich ist (z. B. non-polynominales Problem, zu wenige Informationen, nicht realisierbar) oder derartig aufwendig, dass es sich nicht lohnt (z. B. alle Flugzeuge testen, um bestes Flugzeug zu finden).
Bei Virenscannern bezeichnet Heuristik die Suche nach Viren anhand von typischen Merkmalen.
Chemie
In der organischen Chemie können heuristische Methoden bei dem Verständnis und zur Klassifizierung bekannter Reaktionen helfen. Dies kann eine Hilfe sein, um neue Reaktionen und neue Substanzen vorhersagen zu können.[22]
Literatur
- Athanasius Kircher: Ars magna sciendi sive combinatoria. 1669.
- Gottfried Wilhelm Leibniz: De Arte combinatoria. 1666.
- Friedrich Schleiermacher Sämmtliche Werke. Berlin 1834–1864 (Abteilung I: Zur Theologie, 11 Bände, 1835–1864, zwei geplante Bände sind nicht erschienen; Abteilung II: Predigten, 10 Bände, 1834–1856; Abteilung III: Zur Philosophie, 9 Bände, 1835–1862) (fast vollständig bei google books, inkl. der Dialektik, hg. Jonas von 1839)
- George Pólya: Mathematik und plausibles Schliessen (= Wissenschaft und Kultur. Band 14). 3. Auflage. Band 1: Induktion und Analogie in der Mathematik. Birkhäuser Verlag, 1998, doi:10.1007/978-3-0348-9166-0.
- George Pólya: Mathematik und plausibles Schliessen (= Wissenschaft und Kultur. Band 15). 2. Auflage. Band 2: Typen und Strukturen plausibler Folgerung. Birkhäuser Verlag, 1975, doi:10.1007/978-3-0348-7671-1.
- Gerd Gigerenzer, Peter M. Todd: Simple Heuristics That Make Us Smart (Evolution and Cognition). Oxford University Press, New York 2000, ISBN 0-19-972924-7.
- Gerd Gigerenzer: Das Einmaleins der Skepsis: Über den richtigen Umgang mit Zahlen und Risiken (= BvT. Band 41). Bvt Berliner Taschenbuch Verlag, 2004, ISBN 3-8333-0041-8 (Originaltitel: How to Reckon With Risk: From Innumeracy to Insight.).
- Gerd Gigerenzer: Bauchentscheidungen: Die Intelligenz des Unbewussten und die Macht der Intuition. C. Bertelsmann Verlag, New York 2008, ISBN 978-3-570-00937-6 (Originaltitel: Gut Feelings.).
- Gottlob Frege: Begriffsschrift. und andere Aufsätze.
- Arnd Bogatzki: Fabrikplanung: Verfahren zur Optimierung von Maschinenaufstellung. Roderer, Regensburg 1998, ISBN 3-89073-234-8.
- Norbert Bischof: Struktur und Bedeutung. 2. Auflage. Huber, Bern 1998, ISBN 3-456-83080-7.
- Allen Newell: Human Problem Solving. Prentice-Hall, Englewood Cliffs, N.J 1972, ISBN 0-13-445403-0.
- Douglas B. Lenat: Automated Mathematician.
- J. Müller: Systematische Heuristik.
- Amos Tversky, Daniel Kahneman: Judgment under uncertainty – Heuristics and biases. In: Science. 185, 1974, S. 1124–1131.
- H. Streim: Heuristische Lösungsverfahren – Versuch einer Begriffserklärung. In: Zeitschrift für Operations Research. Band 19, 1975, S. 143–162.
- Lutz Jäncke: Ist das Hirn vernünftig? 2016 | 2., unveränderte Auflage. Hogrefe, vorm. Verlag Hans Huber, ISBN 978-3-456-85653-7.
Weblinks
- Materialien über Heuristik im Katalog der Deutschen Nationalbibliothek
- Suche nach Informationen über Heuristik In: Deutsche Digitale Bibliothek
- Suche nach Heuristik im Online-Katalog der Staatsbibliothek zu Berlin – Preußischer Kulturbesitz (Achtung: Die Datenbasis hat sich geändert; bitte Ergebnis überprüfen und
SBB=1setzen) - Literatur über Heuristik im Katalog der DNB
- Einträge über Heuristik in historischen Lexika bei Zeno.org
Einzelnachweise
- G. Gigerenzer und P. M. Todd mit der ABC Research Group: Simple heuristics that make us smart. Oxford University Press, New York 1999.
- Ulf Pillkahn: Innovationen zwischen Planung und Zufall: Bausteine einer Theorie der bewussten Irritation. Books on Demand 2012, ISBN 978-3-8448-1737-9, S. 170.
- Heuristiken. (PDF) In: zaik.uni-koeln.de. S. 2, abgerufen am 19. Juli 2015.
- Werner Stangl: Algorithmus. In: lexikon.stangl.eu. Abgerufen am 19. Juli 2015.
- Manierismus in der Literatur. Sprach-Alchimie und esoterische Kombinationskunst. hockebooks, 2016, ISBN 978-3-95751-119-5 (books.google.de).
- History of Computers and Computing, Dreamers, Athanasius Kircher.
- Christoph Benjamin Schulz: Poetiken des Blätterns. Georg Olms Verlag – Language Arts & Disciplines, Hildesheim 1. September 2015, S. 279 ff.
- Virginia A. La Charité: Mallarmé’s Livre: The Graphomatics of the Text. In: Symposium: A Quarterly Journal in Modern Literatures. Band 34, Nr. 3, 4. September 2013, S. 249–259, doi:10.1080/00397709.1980.10733451.
- Gustav René Hocke: Manierismus in der Literatur. Sprach-Alchimie und esoterische Kombinationskunst. Reinbek bei Hamburg 1969 (rde 82/83, zuerst 1959).
- Hans Magnus Enzensberger: Einladung zu einem Poesie-Automaten. Juni 2002, abgerufen am 6. August 2009 (It is copyright © 1974, 1999, 2002 Hans Magnus Enzensberger.): „1. Beschreibung, 2. Theorie, 3. Weiterungen, 4. Technischer Anhang“
- Siehe auch Frances A. Yates: The Art of Ramon Lull. In: Journal of the Warburg and Courtauld Institutes. Band 17, Nr. 1/2, 1954, S. 115–173.
- Deutsche Übersetzung des Novum Organon.
- Friedrich Kirchner, Carl Michaëlis et al.: Wörterbuch der Philosophischen Grundbegriffe. 1907, S. 262–263 (zeno.org [abgerufen am 6. August 2009]).
- Ludolf von Mackensen: Zur Vorgeschichte und Entstehung der ersten digitalen 4-Spezies-Rechenmaschine von Gottfried Wilhelm Leibniz. In: Studia Leibnitiana. Supplementa. 2 (1969), S. 34–68.
- Nikolaus Joachim Lehmann: Neue Erfahrungen zur Funktionstüchtigkeit von Leibniz’ Rechenmaschine. In: Studia Leibnitiana. 25 (1993), S. 174–188.
- Jan-Willem Liebezeit: Leibniz-Rechenmaschinen. Universität Jena, Juli 2004, abgerufen am 16. November 2012 (Umfassende Information zur Leibnizschen Rechenmaschinen, Funktionstüchtigkeit und Verbleib): „Person, Lebenslauf, Tätigkeitsfelder und Einige Gedanken Rechenmaschinen Historischer Abriss, Erfindungen nebenbei, Die jüngere Maschine: Wiederentdeckung, Lehmann, Funktionsweise, Standorte, Quellen“
- Bolzano’s Logic. Stanford Encyopedia of Philosophy, 23. September 2007, abgerufen am 4. August 2009 (englisch, Umfangreiche Literaturangaben).
- storyal.de.
- portal.acm.org
- turbulence.org/spotlight/thinking/chess.html.
- Artikel der Fernuniversität in Hagen (PDF als Download auf der Seite)
- Nicole Graulich, Henning Hopf, Peter R. Schreiner: Heuristic thinking makes a chemist smart. In: Chemical Society Reviews. 39, 2010, S. 1503–1512.
