Superposition (Physik)

Unter Superposition, auch Superpositionsprinzip versteht man in der Physik eine Überlagerung gleicher physikalischer Größen, die sich dabei nicht gegenseitig behindern. Dieses Überlagerungsprinzip wird bei linearen Problemen in vielen Bereichen der Physik benutzt und unterscheidet sich nur in der Art der überlagerten Größen. Oft wird die Redeweise „mehrere Größen superponieren miteinander“ gebraucht.

Wichtige Anwendungsbereiche des Superpositionsprinzips sind elektromagnetische Wellen in der Optik und in der Funktechnik, Kräfte in der klassischen Mechanik und Zustände in der Quantenmechanik.

Ein Bereich, in dem das Superpositionsprinzip aufgrund der mathematischen Struktur der Theorie nicht gilt, ist die Allgemeine Relativitätstheorie zur Beschreibung der Gravitation.

Mathematischer Hintergrund

Mathematisch lässt sich eine Superposition als Linearkombination

x(t)=\sum _{i=1}^{n}{\alpha _{i}x_{i}(t)}

darstellen. Die Summenformel sagt aus, dass beliebige Funktionen oder Größen $x_{i}(t)$ derselben Art zu einer neuen Größe $x(t)$ addiert werden können. Der Faktor $\alpha _{i}$ gibt die Gewichtung der jeweiligen Komponente an.

Die Gültigkeit des Prinzips bei vielen physikalischen Systemen ist eine Folge der Tatsache, dass sie linearen Differentialgleichungen gehorchen. Besitzt eine homogene lineare Differentialgleichung die beiden Lösungen $f_{1}$ und $f_{2}$ , so ist aufgrund der Summenregel auch ihre Summe $f_{1}+f_{2}$ eine Lösung. Allgemein formuliert ergibt sich:

Sind $f_{1}$ bis $f_{n}$ Lösungen einer homogenen linearen Differentialgleichung, dann ist auch jede Summe dieser Lösungen eine Lösung der Differentialgleichung.

Wellenlehre

Zwei Wellen durchdringen einander, ohne sich zu beeinflussen.

In der Wellenlehre bedeutet Superposition die ungestörte Überlagerung (Interferenz) mehrerer Wellen des gleichen Typs. Die relevante Größe der Überlagerung ist die Amplitude (die „Höhe“) der einzelnen Wellen. So können sich beispielsweise mehrere elektromagnetische Wellen gegenseitig überlagern, wodurch sich ihre Amplituden zur gleichen Zeit an manchen Punkten gegenseitig verstärken und an anderen gegenseitig abschwächen.

Der daraus resultierende Amplitudenverlauf wirkt jedoch – von möglichen Energieverlusten abgesehen – nicht auf die ihm zugrunde liegenden einzelnen Amplitudenverläufe zurück. Er ist lediglich das Gesamtergebnis der "übereinander gelegten" Einzelverläufe. Die Wellen durchqueren einander also, ohne sich gegenseitig zu beeinflussen. Sie beeinflussen lediglich ihr Ausbreitungsmedium.

Mathematisch ergibt sich für die resultierende Wellenfunktion $\Psi ({\vec {x}},t)$ der Zusammenhang

\Psi ({\vec {x}},t)=\sum _{i=1}^{n}\Psi _{i}({\vec {x}},t)

,

wobei die $\Psi _{i}({\vec {x}},t)$ die Wellenfunktionen der ursprünglichen einzelnen Wellen sind.

Klassische Mechanik

Kräfte

Überlagerung zweier Kräfte

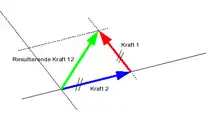
Mechanische Kräfte lassen sich ebenfalls überlagern. Man spricht in diesem Zusammenhang auch vom Prinzip der ungestörten Überlagerung der Kräfte, Prinzip der resultierenden Kraft oder vom Vierten newtonschen Gesetz.

Mathematisch formuliert ergibt sich der Zusammenhang

{\vec {F}}=\sum _{i=1}^{n}{\vec {F}}_{i}

.

Dieser Ausdruck besagt, dass verschiedene Kräfte, die alle einzeln auf den gleichen Körper wirken, dasselbe bewirken, als würde lediglich ihre Summe auf den Körper wirken.

Als Beispiel lässt sich das Schieben einer Kiste anführen: Es spielt im Hinblick auf das Endergebnis keine Rolle, ob eine Kiste erst nach vorne und dann nach links oder ob sie direkt schräg nach links-vorne geschoben wird.

Lastfälle

Mehrere Lastfälle lassen sich überlagern, jedoch bei nichtlinearen Problemen, beispielsweise in der (linearisierten) Theorie II. Ordnung ist dies nicht einfach durch Addition der einzelnen Kräfte der jeweiligen Lastfälle möglich, sondern erfordert eine Neuermittlung der Schnittgrößen unter Einwirkung sämtlicher Belastungen, da die Kräfte sich umlagern, als auch eine Verweichung (oder Versteifung) des Systems in der verformten Lage vorliegt. In der Theorie II. Ordnung, haben Belastungen auch einen Systemcharakter, da die Steifigkeiten insbesondere von der Normalkraft abhängen.

Quantenmechanik

Superposition in der Quantenmechanik ist vergleichbar mit der aus der klassischen Wellenlehre, da quantenmechanische Zustände ebenfalls durch Wellenfunktionen beschrieben werden. Zu beachten ist hierbei jedoch, dass die quantenmechanischen Wellenfunktionen, im Gegensatz zu den klassischen, noch keine „reale“ bzw. eindeutige Bedeutung haben. In der dazu äquivalenten Darstellung mit Zustandsvektoren bedeutet Superposition einfach die Addition (oder Linearkombination) von Vektoren.

Mathematisch wird dies in der Bra-Ket-Notation durch

|\psi \rangle =\sum \limits _{i=1}^{n}c_{i}|\varphi _{i}\rangle

ausgedrückt. Diese Gleichung sagt aus, dass sich der Gesamtzustand $|\psi \rangle$ durch eine Überlagerung der möglichen Einzelzustände $|\varphi _{i}\rangle$ beschreiben lässt. Er wird daher auch Überlagerungszustand genannt. Sind diese $|\varphi _{i}\rangle$ alle orthogonal zueinander (und normiert), so geben die Betragsquadrate $|c_{i}|^{2}$ der komplexen Wahrscheinlichkeitsamplituden $c_{i}$ die Wahrscheinlichkeit dafür an, den zugehörigen Zustand $|\varphi _{i}\rangle$ bei einer auf diesen Zustand spezialisierten Messung vorzufinden.

Als Beispiel wird oft Schrödingers Katze angeführt. Aber auch die Wellenfunktion eines Teilchens kann als Überlagerungszustand aufgefasst werden. Sie ist die Überlagerung von Zuständen, in denen das Teilchen an jeweils einem Ort lokalisiert ist.

Thermodynamik

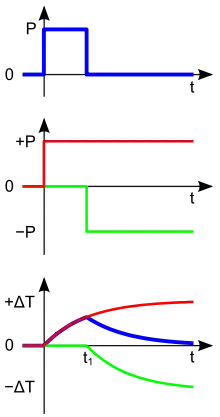
Superpositionsprinzip bei einem transienten Erwärmungsvorgang

Das Superpositionsprinzip wird in der Thermodynamik zur Berechnung von transienten Erwärmungsvorgängen angewandt. Überlagert werden dabei alle Prozesse, die zur Wärmeabfuhr und -zufuhr beitragen. Man kann so beispielsweise die Temperatur eines Leistungshalbleiters zu einem gewissen Zeitpunkt $t$ bestimmen, wenn ein Leistungsimpuls auf dieses Bauteil gewirkt hat.

Im nebenstehenden Beispiel wirkt vom Zeitpunkt $t=0$ bis $t=t_{1}$ eine Leistung, was eine Erwärmung des Bauteils bewirkt. Die Temperatur steigt nach einer Exponentialfunktion an (rote Kurve):

\Delta T=k\,\left(1-e^{-{\frac {t}{t_{1}}}}\right)

.

Um nun die Temperatur des Bauteils nach dem Ende der Erwärmung zu ermitteln, lässt man den Leistungsimpuls fortwirken und setzt zum Erwärmungsende einen gleich großen negativen Leistungsimpuls an. Daraus resultiert eine „negative“ Erwärmungskurve (grüne Kurve). Die Summe der beiden Erwärmungskurven ergibt dann die Abkühlfunktion (blaue Kurve).

Elektrotechnik

In der Elektrotechnik versteht man unter Überlagerungssatz das Überlagerungsverfahren nach Helmholtz. Es ist ein vereinfachtes Verfahren zur Berechnung linearer elektrischer Schaltungen mit mehreren Spannungs- und/oder Stromquellen. Der Überlagerungssatz besagt, dass die Berechnung für jede Quelle getrennt erfolgen kann, wobei alle anderen (idealen) Quellen auf den Wert Null gesetzt werden. Spannungsquellen werden dabei durch Kurzschlüsse ersetzt (0 V) und Stromquellen durch Unterbrechungen (0 A), die Innenwiderstände der Quellen verbleiben jedoch in der Schaltung. Am Schluss erfolgt die lineare Überlagerung durch vorzeichenrichtige Addition der errechneten Teilergebnisse.

Ursprünglich wurde der Überlagerungssatz nur für Gleichstrom bzw. Gleichspannung formuliert. Seine Gültigkeit wird jedoch im Rahmen der komplexen Wechselstromrechnung auch auf Wechselstrom und Wechselspannung übertragen. Durch Anwendung der Operatorenrechnung, beispielsweise der Laplace-Transformation, ist er sogar für beliebige Signalformen gültig. Generell gilt der Überlagerungssatz aber nur für Schaltungen aus linearen Bauelementen.

Literatur

Elektrodynamik:

J. D. Jackson: Klassische Elektrodynamik.4., überarbeitete Auflage, Walter de Gruyter, 2006, ISBN 3-11-018970-4.
E. Hecht: Optik. 4. Auflage, Oldenbourg, 2005, ISBN 3-486-27359-0.

Quantenmechanik:

Claude Cohen-Tannoudji, Bernard Diu, Frank Laloë: Quantenmechanik. Band 1. 3. Auflage, de Gruyter, 2007, ISBN 978-3-11-019324-4.

Siehe auch

Lineares System (Systemtheorie)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.