Kohärenz (Physik)

Kohärenz (von lat.: cohaerere = zusammenhängen) bezeichnet in der Physik die Eigenschaft eines ausgedehnten Wellenfelds, dass sich die momentanen Auslenkungen an verschiedenen Orten zeitlich bis auf eine konstant bleibende Phasenverschiebung auf dieselbe Weise ändern. Als Folge kann bei der Überlagerung von kohärenten Wellen eine räumlich stationäre Interferenz sichtbar werden. Das Fehlen von Kohärenz wird als Inkohärenz bezeichnet.

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Davon abgeleitet wird in der Quantenmechanik von kohärenter Überlagerung verschiedener Zustände gesprochen, wenn sie unter Beachtung ihrer quantenmechanischen Phasen addiert werden müssen wie Vektoren.

Charakteristisch für die Kohärenz zweier Wellen, die am selben Ort eintreffen, ist, dass ihre Amplituden sich addieren. Im Fall der Inkohärenz addieren sich ihre Intensitäten, also die (Absolut-)Quadrate ihrer Amplituden.

Während die häufig gewählte mathematische Beschreibung einer Welle als Sinuskurve zeitlich und räumlich unbegrenzt gedacht ist, sind reale physikalische Wellen zeitlich und räumlich begrenzt. Auch haben zwei durch verschiedene Anordnungen erzeugte Wellen meist leicht unterschiedliche Frequenzen. Das Vorhandensein von Kohärenz deutet daher meist auf eine gemeinsame oder zusammenhängende Entstehungsgeschichte der Wellen hin. Je nach Zeitdauer dieser Entstehung kann die Kohärenz somit zeitlich begrenzt sein, die dabei zurückgelegte Weglänge nennt man die Kohärenzlänge, die die räumliche Ausdehnung ihrer Kohärenz bemisst.

Kohärenz spielt eine Rolle in allen Bereichen der Physik, in denen Interferenzen beobachtet werden, insbesondere in der Laseroptik, der Spektroskopie und der Interferometrie. Dabei spielt es für die Bedeutung der Kohärenz keine Rolle, ob es sich um Lichtwellen oder um Materiewellen handelt. Da es insbesondere in der Lasertechnik möglich ist, von einzelnen Photonen zahlreiche Kopien mit zusammenhängender Entstehungsgeschichte zu erzeugen, so hat die Kohärenz insbesondere auch eine große Bedeutung in deren Anwendungsgebieten, wie der Erstellung von Hologrammen, der Quantenkryptographie oder der Signalverarbeitung.

Als Maß der Interferenzfähigkeit zweier Wellen und damit der Kohärenz der beiden dient das Korrelationsintegral.

Nähere Beschreibung

Sämtliche physikalische Wellen wie Lichtwellen, Radarwellen, Schallwellen oder Wasserwellen können auf eine bestimmte Weise kohärent zu anderen Wellen sein, oder es kann Kohärenz zwischen entsprechenden Teilwellen bestehen. Ursache der Kohärenz kann eine gemeinsame Entstehungsgeschichte der Wellen sein. Wenn beispielsweise bei der Wellenerzeugung derselbe ursächliche Mechanismus zu Grunde lag, können gleichbleibende Schwingungsmuster im Wellenzug entstehen, die später bei einem Vergleich von Teilwellen sichtbar gemacht werden können. Sind die Wellenamplituden zweier Wellen direkt miteinander korreliert, so zeigt sich dies bei der Überlagerung der Wellen am Auftreten von stationären (räumlich und zeitlich unveränderlichen) Interferenzerscheinungen. In anderen Fällen ist zum Teil ein technisch höherer Aufwand oder eine kompliziertere mathematische Betrachtung des Wellenverlaufs notwendig, um eine Kohärenz in den Wellen nachzuweisen.

In einfachen Fällen, wie bei periodischen Wellen, sind zwei Teilwellen kohärent, wenn eine feste Phasenbeziehung zueinander besteht. In der Optik bedeutet diese Phasenbeziehung häufig eine gleich bleibende Differenz zwischen den Phasen der Schwingungsperiode. Teilwellen, die sich an einem festen Ort zu einer bestimmten (zeitlich gemittelten) Intensität überlagern (zum Beispiel auf einem Beobachtungsschirm), können sich dann abhängig von der Phasenbeziehung entweder verstärken bzw. auslöschen (vollständige Kohärenz), ein wenig verstärken bzw. abschwächen (partielle Kohärenz) oder zu einer mittleren Intensität ausgleichen (Inkohärenz). Inkohärenz liegt hier vor allem bei unterschiedlichen Frequenzen vor, wenn alle Phasendifferenzen gleich häufig vorkommen und dadurch keine konstruktive oder destruktive Interferenz möglich ist.

Andererseits können auch Wellen mit unterschiedlichen Frequenzen eine Kohärenz zueinander aufweisen. Technisch spielt diese Art der Kohärenz eine Rolle beim Frequenzkamm oder in der Radartechnik. Erzeugt wird diese Kohärenz durch Modenkopplung oder Frequenzverdopplung oder -vervielfachung.

In Wellenfeldern kann man auch die Fälle einer zeitlichen und einer räumlichen Kohärenz unterscheiden, auch wenn normalerweise beide Formen der Kohärenz vorhanden sein müssen. Zeitliche Kohärenz liegt vor, wenn entlang der Zeitachse (oft bildlich gleichgesetzt mit der Raumachse parallel zur Ausbreitungsrichtung) eine feste Phasendifferenz besteht. Räumliche Kohärenz liegt vor, wenn entlang einer Raumachse (oft reduziert auf die Raumachsen senkrecht zur Ausbreitungsrichtung) eine feste Phasendifferenz besteht.

Mathematische Darstellung

Kohärenz und Korrelation

Die für Interferenzfähigkeit notwendige Kohärenz bei Wellen kann anhand der Korrelationsfunktion quantifiziert werden[1]. Diese Funktion liefert ein Maß für die Ähnlichkeit des zeitlichen Verlaufs zweier in Verbindung gebrachter Wellenamplituden.

Die Funktion

\Gamma _{\mathrm {A} \mathrm {B} }(\tau )=\langle E(\mathbf {r} _{\mathrm {A} },t)E^{*}(\mathbf {r} _{\mathrm {B} },t+\tau )\rangle =\lim \limits _{T\to \infty }{\frac {1}{T}}\int \limits _{-T/2}^{+T/2}{E(\mathbf {r} _{\mathrm {A} },t)E^{*}(\mathbf {r} _{\mathrm {B} },t+\tau ){\textrm {d}}t}

definiert zunächst die (komplexe) Kreuzkorrelationsfunktion zwischen den Zeitverläufen zweier betrachteter Amplituden. Die beiden Amplituden werden an den Ortspunkten A und B der Welle $E$ und bei einem Zeitunterschied von $\tau$ herausgegriffen und als Funktion der Zeit $t$ verglichen.

Die Kontrastfunktion für raumzeitliche Kohärenz, die durch

K_{\mathrm {A} \mathrm {B} }(\tau )=\left|{\frac {2\Gamma _{\mathrm {A} \mathrm {B} }(\tau )}{\Gamma _{\mathrm {A} \mathrm {A} }(0)+\Gamma _{\mathrm {B} \mathrm {B} }(0)}}\right|

gegeben ist, liefert nun direkt die Stärke der Kohärenz als Wert zwischen 0 und 1. Im Allgemeinen unterscheidet man drei Fälle:

	$K_{\mathrm {A} \mathrm {B} }(\tau )$	= 1	vollständige Kohärenz
0 <	$K_{\mathrm {A} \mathrm {B} }(\tau )$	< 1	partielle Kohärenz
	$K_{\mathrm {A} \mathrm {B} }(\tau )$	= 0	vollständige Inkohärenz

Im Falle rein zeitlicher Kohärenz werden nur Korrelationen mit A = B betrachtet. Hier liefert die Kontrastfunktion für zeitliche Kohärenz

K(\tau )=\left|{\frac {\Gamma (\tau )}{\Gamma (0)}}\right|

die Stärke der zeitlichen Kohärenz in Abhängigkeit vom Zeitabstand $\tau$ . $K(\tau )$ hat bei $\tau =0$ den maximalen Wert 1 und fällt je nach Kohärenz mehr oder weniger schnell auf 0 ab. Die Kohärenzzeit $\tau _{c}$ ist definiert als der Zeitabstand $\tau$ , bei dem die Kontrastfunktion auf 1/e abgefallen ist. Soll die Kohärenz zwischen verschiedenen Wellen berechnet werden, wird die Kreuzkorrelationsfunktion

\Gamma (\tau )=\langle E_{1}(t)E_{2}^{*}(t+\tau )\rangle

der Wellen $E_{1}$ und $E_{2}$ verwendet.

Im Falle rein räumlicher Kohärenz werden nur Korrelationen mit $\tau =0$ betrachtet. Hier liefert die Kontrastfunktion für räumliche Kohärenz

K_{\mathrm {A} \mathrm {B} }=\left|{\frac {2\Gamma _{\mathrm {A} \mathrm {B} }}{\Gamma _{\mathrm {A} \mathrm {A} }+\Gamma _{\mathrm {B} \mathrm {B} }}}\right|

die Stärke der räumlichen Kohärenz zwischen den Punkten A und B. Ein Volumen, in dem alle Punktepaare A, B einen Kontrast $K_{\mathrm {A} \mathrm {B} }>1/e$ aufweisen, bildet ein sogenanntes Kohärenzvolumen, innerhalb dessen räumliche Kohärenz vorliegt. Meistens wird unter dem Begriff der räumlichen Kohärenz nur die Kohärenz quer zur Ausbreitungsrichtung der Welle verstanden, was präziser mit transversal räumliche Kohärenz bezeichnet werden müsste. Die räumliche Kohärenz entlang der Ausbreitungsrichtung, also die longitudinal räumliche Kohärenz, wird dagegen oft mit der zeitlichen Kohärenz gleichgesetzt, was nur näherungsweise korrekt ist.

Vielstrahlinterferenz

Die gezeigte mathematische Definition der Kohärenz beschreibt nur die Korrelation zwischen zwei Punkten einer Welle. In vielen Anwendungen muss jedoch die Bedingung erfüllt sein, dass sich sehr viele Teilwellen zu einem gemeinsamen Interferenzmuster überlagern können. Dabei ist die paarweise Kohärenz der Teilwellen allein nicht hinreichend. Der Kohärenzbegriff muss hierfür erweitert oder mit Zusatzbedingungen verknüpft werden.

Im Beispiel eines Beugungsgitters in der Optik etwa, bei dem eine sehr große Zahl von Teilwellen interferieren muss, genügt die paarweise räumliche Kohärenz noch nicht, um scharfe Beugungsspektren sichtbar werden zu lassen. Zusätzlich muss eine simultane Korrelation zwischen den Phasen aller Teilwellen vorliegen, damit die paarweise interferenzfähigen Teilstrahlen in einem gemeinsamen Beugungsmaximum auf dem Schirm zur Deckung kommen. Diese Bedingung ist insbesondere dann erfüllt, wenn ebene Wellenfronten auf ein ebenes Beugungsgitter treffen. Zwei weitere Anwendungsfälle, bei denen Vielstrahlinterferenz eine Rolle spielt, sind die Braggreflexion und das Fabry-Pérot-Interferometer.

Kohärenz in der klassischen Optik

In der klassischen Optik wird Kohärenz mit der Interferenzfähigkeit von Licht in direkten Zusammenhang gebracht. Der Kontrast des Interferenzmusters V (engl. Visibility) ist ein Maß für die Kohärenz des Lichts. Insbesondere in der Optik spielen die beiden Spezialfälle der räumlichen und zeitlichen Kohärenz eine große Rolle.

Kohärenz und Kontrast eines Interferogramms

In der Optik bedeutet Kohärenz die Interferenzfähigkeit bezüglich eines bestimmten Experimentes und wird mit dem Kontrast $V$ des Interferenzmusters, der maximal 1 (vollständig kohärentes Licht) und minimal 0 (vollständig inkohärentes Licht) sein kann, in Verbindung gebracht. Das Interferenzmuster zweier Lichtquellen ist abhängig von ihrer komplexen gegenseitigen Kohärenzfunktion $\Gamma =\left\langle E_{1}E_{2}^{*}\right\rangle$ bzw. dem komplexen gegenseitigen Kohärenzgrad $\gamma ={\frac {\Gamma }{\sqrt {I_{1}I_{2}}}}$ bzw. vom Kontrast $V={\frac {2{\sqrt {I_{1}I_{2}}}}{I_{1}+I_{2}}}\left|\gamma \right|$

I=I_{1}+I_{2}+2Re\{\Gamma \}=I_{1}+I_{2}+2{\sqrt {I_{1}I_{2}}}Re\{\gamma \}

Für Zweistrahlinterferenz einer Welle $E_{1}=E({\vec {r}}_{1},t_{1})$ mit ihrer räumlich und zeitlich verschobenen Kopie $E_{2}=E({\vec {r}}_{2},t_{2})$ ergibt sich die Zweistrahlinterferenzformel $I=I_{0}\left(1+V\cos(\Delta \Phi )\right)$ .

Zeitliche Kohärenz

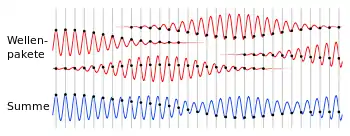
Interferenz zweier zeitlich getrennter Punkte einer Welle

Licht entsteht aus diskontinuierlichen Emissionsakten, die Photonen-Wellenzüge aussenden. Diese Wellenzüge sind jeweils mit einem regelmäßig oszillierenden Feld verbunden, das willkürlich seine Phase verändert. „Dieses Intervall, in dem die Lichtwelle eine Sinusschwingung darstellt, ist ein Maß für ihre zeitliche Kohärenz.“[2] Die Kohärenzzeit ist somit durch das mittlere Zeitintervall definiert, in dem die Lichtwelle in einer vorhersagbaren Weise schwingt. Eine höhere Kohärenzzeit entspricht einer höheren zeitlichen Kohärenz einer Licht emittierenden Quelle.

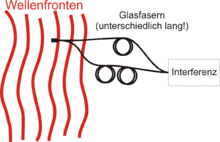
Einzelne Wellenpakete gleicher Frequenz und unterschiedlicher Phase. Das Summensignal ergibt eine Kohärenzzeit in der Größenordnung, die der Dauer der einzelnen Wellenpakete entspricht.

Zeitliche Kohärenz ist dann notwendig, wenn die Welle zu einer zeitlich verschobenen Kopie ihrer selbst kohärent sein soll. Das ist beispielsweise dann der Fall, wenn in einem Michelson-Interferometer die Weglängen im Objekt- und Referenzarm unterschiedliche Längen aufweisen. Die Zeit, nach der sich die Relativwerte von Phase und/oder Amplitude signifikant verändert haben (so dass die Korrelation in entscheidendem Maße abnimmt), wird Kohärenzzeit $\tau _{c}$ genannt. Bei $\Delta t=0$ ist die Kohärenz noch perfekt, sie hat sich aber nach der Zeit $\Delta t=\tau _{c}$ entscheidend verringert. Die Kohärenzlänge $l_{c}$ ist als die Entfernung definiert, die die Welle innerhalb der Kohärenzzeit zurücklegt.

Wiener-Chintschin-Theorem

Bei einer Lichtquelle wird die zeitliche Kohärenz durch die spektrale Zusammensetzung des Lichts bestimmt. Licht einer monochromatischen Lichtquelle ist zeitlich vollständig kohärent. Licht, das sich aus verschiedenen Wellenlängen zusammensetzt (z. B. wegen Dopplerverbreiterung), ist – je nach Art der Zusammensetzung – partiell kohärent oder inkohärent. Dieser Zusammenhang wird durch das Wiener-Chintschin-Theorem beschrieben, das besagt, dass der Kohärenzgrad (als Autokorrelationsfunktion der Feldstärke) der normierten Fouriertransformation des Lichtspektrums entspricht. Die Kohärenzlänge des Lichts ist als der Punkt definiert, an dem der Kohärenzgrad auf $1/e$ abgefallen ist.

Den Zusammenhang zwischen dem Spektrum der Lichtquelle und der zeitlichen Kohärenz kann man sich am Beispiel des Michelson-Interferometers veranschaulichen. Bei verkipptem Referenzspiegel ist der Weglängenunterschied beider Strahlen linear von der Kipprichtung abhängig. Entspricht der Weglängenunterschied einem ganzzahligen Vielfachen der Wellenlänge, so interferieren die Strahlen konstruktiv, und das Interferenzmuster hat ein Maximum. Bei monochromatischem Licht ist ein Streifenmuster auf dem Schirm sichtbar.

Hat das Licht verschiedene Wellenlängen, so sind die einzelnen Streifenmuster zueinander verschoben. Die Streifen sind umso breiter, je größer die Wellenlänge ist. Bei der Überlagerung der Streifenmuster auf einem Beobachtungsschirm löschen sich die Streifen an manchen Orten gegenseitig aus oder verstärken sich gegenseitig (partielle Kohärenz).

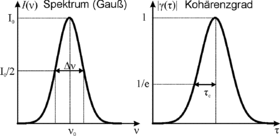
Zeitliche Kohärenz als Fouriertransformierte des Spektrums der Lichtquelle

Berechnet man nach dem Wiener-Chintschin-Theorem die Kohärenzfunktion für den Fall eines Lasers mit einem gaußförmigen Spektrum (Bandbreite FWHM = $\Delta \lambda$ , Schwerpunktwellenlänge $\lambda$ ), so erhält man eine gaußförmige Kohärenzfunktion mit der Kohärenzlänge $l_{c}={\frac {\lambda ^{2}}{\Delta \lambda }}$ .

Aus der Fouriertransformation folgt direkt, dass – je nach Form des Spektrums (im obigen Fall des gaußförmigen Spektrums beispielsweise nicht, wohl aber z. B. für eine Schwebung, bei der die Autokorrelationsfunktion periodisch ist) – auch für größere Weglängenunterschiede als $l_{c}$ wieder eine hohe Kohärenz erreicht werden kann. Diese Eigenschaft der Kohärenz lässt sich im anschaulichen Bild der endlich langen Wellenzüge (s. u.) nicht erklären.

Anschauliche Erklärung der zeitlichen Kohärenz durch endliche Wellenzüge

„Natürliches“ Licht entsteht, wenn ein Elektron in einem Atom von einem angeregten in einen weniger angeregten Zustand übergeht. Beim Zerfall des angeregten Zustandes schwingt in semiklassischer Vorstellung das Elektron eine gewisse Zeit. Während dieser Zeit (= Lebensdauer) wird es ein Photon emittieren (gedämpfte Schwingung). Typische Lebensdauern solcher atomarer Prozesse sind $\tau =10\,\mathrm {ns}$ (= Kohärenzzeit). Dieses führt zu Wellenpaketen mit Längen von $l_{c}=c\tau \approx 3\,\mathrm {m}$ (= Kohärenzlänge) mit einer Frequenzunschärfe $\Delta f={\frac {1}{\tau }}$ von etwa 100 MHz.

Das resultierende Licht setzt sich additiv aus Wellenpaketen zusammen, die von vielen unterschiedlichen Atomen ausgesandt wurden und sich in der Phase und auch in der Frequenz unterscheiden. Da die Atome meist in thermischer Bewegung sind, zeigt das von solchen Atomen emittierte Licht Dopplerverbreiterung, bei starker gegenseitiger Wechselwirkung (z. B. Stöße) der Atome auch Druckverbreiterung. Beide Effekte verkürzen die Kohärenzzeit bzw. -länge des emittierten Lichts erheblich.

Die Zerfälle durch endliche Wellenzüge zu modellieren, kann nicht alle Aspekte der zeitlichen Kohärenz erklären, dient aber als Hilfsvorstellung in einfachen Fällen.

Räumliche Kohärenz

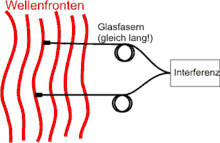
Interferenz zweier Punkte entlang einer Welle

Soll die Welle mit einer räumlich verschobenen Kopie ihrer selbst interferieren, ist räumliche Kohärenz nötig. Dieses ist beispielsweise im youngschen Doppelspaltversuch der Fall: Hier werden durch die beiden Spalte zwei Punkte aus der einfallenden Welle herausgegriffen und zur Interferenz gebracht. Wie weit diese beiden Punkte auseinanderliegen dürfen, beschreibt die Ausdehnung des Gebiets der räumlichen Kohärenz.

Van-Cittert-Zernike-Theorem

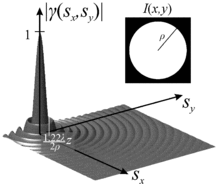
Komplexer Kohärenzgrad als Fouriertransformierte der Intensitätsverteilung der Lichtquelle für eine runde Lichtquelle

Bei einer ausgedehnten Lichtquelle mit statistischer Phasenverteilung, d. h. zutreffend für LEDs, Glühbirnen und Gasentladungslampen, jedoch nicht für Laser, wird die räumliche Kohärenz durch die Ausdehnung und die Form der Lichtquelle bestimmt. Dabei geht es mehr um die Winkelausdehnung als um die tatsächliche Ausdehnung, so dass die räumliche Kohärenz daher mit steigender Entfernung zunimmt. Eine Punktlichtquelle hat auch bei geringem Abstand eine vollständige räumliche Kohärenz. Dieser Zusammenhang wird durch das Van-Cittert-Zernike-Theorem – nach Pieter Hendrik van Cittert (1889–1959) und Frits Zernike – beschrieben, das besagt, dass der komplexe Kohärenzgrad der normierten Fouriertransformierten der Intensitätsverteilung der Lichtquelle entspricht (Bedingungen: kleine Ausdehnungen der Lichtquelle und des Beobachtungsgebiets, ausreichend großer Beobachtungsabstand). Für eine kreisförmige Lichtquelle fällt die räumliche Kohärenz schnell ab und erreicht bei $1{,}22\lambda z/2\rho$ ihr Minimum in Abhängigkeit vom Abstand $z$ des Beobachtungsschirms von der Lichtquelle. Danach ist die Kohärenz nicht verloren, sondern kommt für größere Abstände (in sehr schwacher Form) wieder.

Den Zusammenhang zwischen Ausdehnung der Lichtquelle und räumlicher Kohärenz kann man sich am Beispiel des Doppelspalt-Interferenzversuchs veranschaulichen. Am Beobachtungsschirm entsteht abhängig von den Laufzeitunterschieden der beiden Strahlen ein Interferenzmuster. Hierfür ist eine ausreichend hohe zeitliche Kohärenz der Lichtstrahlen nötig. Für den Punkt des Beobachtungsschirms, der zwischen den beiden Spalten liegt, haben die Lichtstrahlen keine Laufzeitdifferenz. Hier hat das Interferenzmuster das nullte Maximum. Bei einer ausgedehnten Lichtquelle ist der Punkt mit Laufzeitdifferenz gleich null für jeden Punkt der Lichtquelle leicht verschoben. Die einzelnen Interferenzmuster verwischen sich je nach Größe der Lichtquelle gegenseitig.

Erzeugung von kohärentem Licht

Die Wahl der Lichtquelle ist entscheidend für die Kohärenz. Allerdings ist Kohärenz keine Eigenschaft einer Lichtquelle selbst, sondern der Lichtstrahlen, da die Interferenzfähigkeit des Lichts bei der Ausbreitung verloren gehen kann.

Wenn man räumlich nicht-kohärentes Licht durch einen sehr schmalen Spalt sendet, verhält sich das Licht dahinter, als wäre der Spalt eine Punktlichtquelle (in einer Dimension), die Elementarwellen aussendet (siehe Huygenssches Prinzip). Die Größe des räumlichen Kohärenzgebiets ist im Fall eines einfachen Spaltes indirekt proportional zur Spaltgröße (van-Cittert-Zernike-Theorem, Verdetsche Kohärenzbedingung). Mit zunehmendem Abstand zur Lichtquelle nimmt die Winkelausdehnung der Lichtquelle ab und damit die räumliche Kohärenz zu.

Die zeitliche Kohärenz des Lichts kann erhöht werden, indem man einen Wellenlängenfilter einsetzt, der das Spektrum der Lichtquelle begrenzt.

Leuchtstoffröhren, Glühlampen und Gasentladungslampen sind räumlich ausgedehnte Lichtquellen (räumlich inkohärent), die weißes Licht einer großen Menge verschiedener Frequenzen (zeitlich inkohärent) erzeugen. Durch Lochblenden und Wellenlängenfilter kann daraus räumlich und zeitlich kohärentes Licht erzeugt werden, jedoch wird dabei die verbleibende Intensität des Lichts stark reduziert, so dass dieses Verfahren wenig praktikabel ist.

Laserlicht dagegen gilt als das am besten erzeugbare monochromatische Licht überhaupt und hat die größte Kohärenzlänge (bis zu mehreren Kilometern). Ein Helium-Neon-Laser kann beispielsweise Licht mit Kohärenzlängen von über 1 km produzieren. Allerdings sind nicht alle Laser monochromatisch (z. B. kann ein Titan:Saphir-Laser auch spektrale Breiten von Δλ ≈ 2 – 70 nm aufweisen). LEDs sind weniger monochromatisch (Δλ ≈ 30 nm) und haben deshalb kürzere Kohärenzzeiten als die meisten monochromatischen Laser. Da ein Laser in der Regel über seine gesamte Austrittsapertur hinweg dieselbe Phase aufweist, besitzt das emittierte Laserlicht zudem eine sehr hohe räumliche Kohärenz.

Zeitliche Kohärenz

Man kann die Kohärenzzeit bzw. Kohärenzlänge einer Lichtwelle bestimmen, indem man diese in zwei Teilstrahlen aufteilt und sie später wieder vereint – etwa in einem Michelson-Interferometer oder Mach-Zehnder-Interferometer. Man sieht Interferenzerscheinungen in einer solchen Anordnung nur dann, wenn der Laufzeitunterschied bzw. der Wegunterschied zwischen den Teilwellen kleiner bleibt als die Kohärenzzeit bzw. Kohärenzlänge der von den Atomen ausgesandten Wellenzüge.

Auch aus der Messung des Spektrums lässt sich durch Fouriertransformation die zeitliche Kohärenz bestimmen. Umgekehrt kann auch das Spektrum einer Lichtquelle bestimmt werden, indem der Interferenz-Kontrast in einem Michelson-Interferometer gemessen wird, während der Weglängenunterschied variiert wird (FTIR-Spektrometer).

Räumliche Kohärenz

Ähnlich wie im Fall der zeitlichen Kohärenz kann die räumliche Kohärenz durch Messung des Kontrastes eines Interferenzmusters bestimmt werden, wenn ein Interferometer eingesetzt wird, das empfindlich auf die räumliche Kohärenz ist (Verwandte des Doppelspaltaufbaus). Bei der Stellarinterferometrie wird durch Messung des Kontrasts über die räumliche Kohärenz die Winkelausdehnung von Sternen bestimmt.

Quellen

Die mathematische Definition folgt dem Lehrbuch Kohärente Optik von Werner Lauterborn. Der * kennzeichnet den Übergang zum Komplex-konjugierten.
Eugene Hecht: Optik. 4., überarbeitete Auflage. 2005, S. 631.

Literatur

Paul, Harry: Lexikon der Optik. Spektrum Akademischer Verlag, 2003, ISBN 3-8274-1422-9.
Lauterborn, Werner: Kohärente Optik. Grundlagen für Physiker und Ingenieure. Springer 1993, ISBN 3-540-56769-0.
Lipson; Lipson; Tannhauser: Optik. Springer 1997, ISBN 3-540-61912-7.
Goodman, Joseph: Statistical Optics. Wiley 1985, ISBN 0-471-01502-4.
Roy J. Glauber: Quantum Theory of Optical Coherence: Selected Papers and Lectures. Wiley-VCH, Weinheim 2007, ISBN 978-3-527-40687-6.

Weblinks

Commons: Coherence – Sammlung von Bildern, Videos und Audiodateien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Die mathematische Definition folgt dem Lehrbuch Kohärente Optik von Werner Lauterborn. Der * kennzeichnet den Übergang zum Komplex-konjugierten.

[2] Eugene Hecht: Optik. 4., überarbeitete Auflage. 2005, S. 631.