Magische Zahl (Physik)
Als Magische Zahlen bezeichnet man in der Kernphysik bestimmte Neutronen- und Protonenzahlen in Atomkernen, bei denen im Grundzustand des Kerns eine höhere Stabilität als bei benachbarten Nukliden beobachtet wird. Solche Kerne selbst werden auch als magische Kerne bezeichnet. Die magischen Zahlen lassen sich durch das Schalenmodell der Kernphysik erklären. Auf dieser Basis werden auch Inseln der Stabilität bei Ordnungszahlen oberhalb der natürlich vorkommenden Elemente vorhergesagt.
Stabilitätseigenschaften
Mit höherer Stabilität sind unter anderem folgende beobachteten Eigenschaften gemeint:[1]
- Elemente mit magischen Protonenzahlen sind mengenmäßig im Universum relativ stark vertreten (Helium, Sauerstoff, Calcium, Nickel).
- Die Bindungsenergie pro Nukleon ist besonders hoch. Dies zeigt sich beispielsweise in den hohen Energien von Alpha- und Beta-Zerfällen, die zu magischen Kernen führen.
- Die Anregungsenergie des ersten angeregten Zustands eines magischen Kerns ist besonders hoch.
- Bei magischer Protonenzahl existieren besonders viele stabile Isotope (Zinn hat mit 10 die meisten stabilen Isotope), bei magischer Neutronenzahl besonders viele stabile Isotone.
- Der Wirkungsquerschnitt des Kerns für Neutroneneinfang und die beim Neutroneneinfang freigesetzte Energie sind besonders klein.
- Das Quadrupolmoment des Kerns im Grundzustand hat bei magischen Zahlen ein Minimum, was auf eine relativ kugelsymmetrische Verteilung der elektrischen Ladung hinweist.
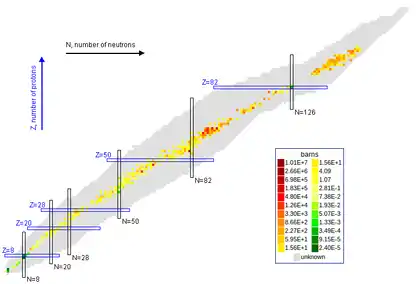
Die in dieser Weise beobachtbaren magischen Zahlen sind 2, 8, 20, 28, 50, 82, 126 und 184. Die 126 sowie die 184 sind allerdings bisher nur für Neutronen beobachtbar, da Nuklide mit so hoher Ordnungszahl (Protonenzahl) nicht in der Natur vorkommen und künstlich noch nicht hergestellt werden konnten (siehe Unbihexium).
Als Beispiel zeigt das nebenstehende Bild eine Nuklidkarte mit farblicher Kennzeichnung des Wirkungsquerschnitts für Neutroneneinfang. Die magischen Protonen- und Neutronenzahlen sind durch Doppellinien hervorgehoben. Man erkennt, dass dieser Wirkungsquerschnitt bei magischen Atomkernen meist klein, fernab von magischen Zahlen dagegen groß ist.
Doppelt magische Kerne
Doppelt magisch heißt ein Nuklid, wenn seine Protonen- und seine Neutronenzahl magisch sind. Die oben genannten Stabilitätseigenschaften sind dann besonders ausgeprägt. Vier doppelt magische Nuklide sind auch im absoluten Sinn stabil, d. h. nicht radioaktiv: Helium-4, Sauerstoff-16, Calcium-40 und Blei-208. Weitere doppelt magische Nuklide sind Calcium-48 (mit der Halbwertszeit von etwa 6 · 1018 Jahren „fast“ absolut stabil), Nickel-56, Nickel-78, Zinn-100 und Zinn-132; sie sind zwar wegen ihres zu großen oder zu kleinen Neutronenüberschusses radioaktiv, zeigen aber relativ erhöhte Stabilität verglichen mit ihren Nachbarnukliden, erkennbar z. B. an ihren Halbwertszeiten.
Erklärung durch das Schalenmodell
Natürliche Elemente
Das Schalenmodell des Atomkerns erklärt die magischen Zahlen damit, dass dort (vereinfacht gesagt) jeweils die äußerste „Schale“ vollständig besetzt, also abgeschlossen ist, ähnlich wie die chemisch stabilen Edelgase durch abgeschlossene Außenschalen ihrer Elektronenhülle gekennzeichnet sind. Solche Abschlüsse – also eine endliche Höchstzahl gleichartiger Teilchen, die ein bestimmtes Energieniveau in einem Potentialfeld besetzen können – treten in der Quantenmechanik für Fermionen als Folge des Pauli-Prinzips allgemein auf.
Künstlich erzeugte Elemente
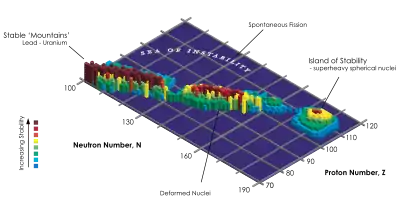
Oberhalb der natürlich vorkommenden Protonen- und Neutronenzahlen sagt die Theorie weitere Schalenabschlüsse, also magische Zahlen voraus. Für Protonen ergeben sich durch Unterschalenabschlüsse die Zahlen 114 und 120. Tatsächlich zeigen die bisher entdeckten Isotope des Elements Flerovium, das 114 Protonen enthält, auffällig lange Halbwertszeiten (mehrere Sekunden). Das doppelt magische Isotop Fl-298 mit 184 Neutronen, für das eine besonders lange Halbwertszeit zu erwarten ist, konnte noch nicht beobachtet werden. Eine ganze Insel der Stabilität (ein von Glenn Seaborg geprägter Begriff) mit diesem doppelt magischen Nuklid als Zentrum wird vermutet (siehe Abbildung). Dabei ist der Begriff Stabilität nur relativ zu den umgebenden Nukliden zu verstehen; absolut stabile Nuklide ohne jeden spontanen Zerfall, also mit der Halbwertszeit unendlich, sind jenseits von Blei kaum zu erwarten. Ähnliche „Inseln“ werden auch in der Nähe der magischen Ordnungszahlen 120 und 126 erwartet. Sie würden sich gruppieren um die noch nicht entdeckten doppelt magischen Nuklide Unbinilium-304, , bzw. Unbihexium-310, .
Experimentell hergestellt werden derartige Nuklide durch Verschmelzung schwerer Kerne mittels Schwerionenbeschleunigern. Die Hauptschwierigkeit, Nuklide wie etwa das Unbinilium zu erreichen, liegt darin, dass als Target und als Projektil Nuklide mit genügend hohem Neutronenüberschuss verwendet werden müssen; diese sind selbst im Allgemeinen instabil und nicht in großer Menge verfügbar.
Erklärung mittels Gruppentheorie
In einer 2010 veröffentlichten Arbeit[2] wird berichtet, dass die magischen Protonen- und Neutronenzahlen sich auch aus gruppentheoretischen Überlegungen ohne Annahme einer bestimmten Potentialform ergeben.
Atomkerne mit sehr großem Neutronenüberschuss
Neuere experimentelle Befunde weisen darauf hin, dass in Kernen mit besonders großem Neutronenüberschuss außer den oben genannten magischen Zahlen noch weitere auftreten, erwartet wird die 34.[3][4] Damit deutet sich an, dass das Schalenmodell für solche „exotischen“ Kerne verfeinert werden muss.
Bei leichten sehr neutronenreichen Kernen zeigen sich die für doppelt magische Nuklide typischen Eigenschaften in einigen Fällen eher an Isotopen mit nicht-magischen Neutronenzahlen; sie sind beispielsweise beim doppelt magischen Sauerstoffisotop O-28 (Protonenzahl Z = 8, Neutronenzahl N = 20) weniger ausgeprägt als bei O-24 (Z = 8, N = 16).[5][6] Das mittelschwere, doppelt magische Nuklid Ni-78 (Z = 28, N = 50) zeigt hingegen mit 2,6 MeV die typische, erwartete hohe Anregungsenergie des ersten angeregten Zustands.[7]
Literatur
Einzelnachweise
- E. B. Paul: Nuclear and Particle Physics. Amsterdam: North-Holland 1969, S. 422–423.
- Richard Herrmann: Higher dimensional mixed fractional rotation groups as a basis for dynamic symmetries generating the spectrum of the deformed Nilsson-oscillator. In: Physica A. 389, 2010, S. 693. doi:10.1016/j.physa.2009.11.016.
- Jan Oliver Löfken: Wann sind Atomkerne magisch? Pro-Physik, 2005, abgerufen am 21. September 2015.
- Holger Dambeck: Kernphysik: Forscher entdecken neue magische Zahl. In: Spiegel Online. 9. Oktober 2013, abgerufen am 21. September 2015.
- C. R. Hoffman et al., Physics Letters B672 (2009) S. 17
- R. Kanungo et al., Physical Review Letters 102 (2009) S. 152501
- R. Taniuchi et al., Nature 569 (2019) S. 53