Überlichtgeschwindigkeit

Überlichtgeschwindigkeit ist eine Geschwindigkeit, die größer als die Naturkonstante Lichtgeschwindigkeit ist. Dies wird auch superluminar genannt.

Allgemeines

Ein von einem rotierenden Spiegel auf eine ausreichend weit entfernte Wand projizierter Lichtpunkt bewegt sich dort überlichtschnell. Aber nur der beleuchtete Ort wandert, während keine Welle und keine Materie sich mit Überlichtgeschwindigkeit bewegt.[1]

Ob sich Materie oder Information im Vakuum auch überlichtschnell (superluminar, raumartig) bewegen bzw. ausbreiten kann, ist eine von der überwiegenden Mehrheit der Physiker verneinte, aber noch nicht abschließend geklärte Frage. Dabei kommt es prinzipiell nicht darauf an, ob sich ein Objekt überlichtschnell bewegt, sondern darauf, ob eine kausale Beziehung zwischen zwei Raum-Zeit-Punkten bestehen kann, die so weit räumlich bzw. so kurz zeitlich getrennt sind, dass eine Verbindung zwischen ihnen nur durch Überlichtgeschwindigkeit zu erreichen wäre. Das umfasst z. B. auch die Situation eines Objektes, das an einem Ort unvermittelt verschwindet, bevor es nach weniger als einem Jahr ein Lichtjahr entfernt wieder erscheint. In der klassischen Newtonschen Mechanik können Objekte beliebig beschleunigt werden. Da die Theorie dabei keine Grenzen setzt, könnte auch die Lichtgeschwindigkeit übertroffen werden. Allerdings gilt die Newtonsche Mechanik nur näherungsweise für hinreichend kleine Geschwindigkeiten (v ≪ c). Bei höheren Geschwindigkeiten treten dagegen relativistische Effekte auf, die ein Überschreiten der Lichtgeschwindigkeit verhindern.

In Science-Fiction-Büchern und -Filmen werden Reisen mit Überlichtgeschwindigkeit oft als Realität dargestellt, weil sonst interstellare Reisen aus dramaturgischer Sicht viel zu lange dauern würden. Dasselbe gilt für die Kommunikation zwischen zwei Stationen oder Raumschiffen. Die Datenübertragung findet in diesen Geschichten fast immer ohne Zeitverzögerung statt, auch wenn die Raumschiffe Lichtjahre voneinander entfernt sind und damit jede Information nach momentanen wissenschaftlichen Erkenntnissen also mindestens die entsprechende Zeit für die Strecke vom Sender zum Empfänger benötigen würde.

Die Fernsehbilder der Mondlandungen benötigten hingegen schon 1,3 Sekunden nur für ihren Weg zur Erde, eine Kommunikation zwischen der Erde und beispielsweise dem Mars dauert je nach Lage der beiden Planeten zueinander zwischen drei und 22 Minuten.

Die Unterscheidung zwischen Überlichtgeschwindigkeit und Unterlichtgeschwindigkeit ist im Rahmen der Relativitätstheorie absolut: Ein Vorgang, der in einem Bezugssystem mit Überlichtgeschwindigkeit stattfindet, findet in jedem Bezugssystem mit Überlichtgeschwindigkeit statt, dasselbe gilt auch für Unterlichtgeschwindigkeit. Mathematischer Hintergrund ist die Nichtexistenz einer Lorentztransformation, die zeitartige in raumartige Vektoren transformiert. So kann man z. B. nicht einfach Überlichtgeschwindigkeit gegen die Erde erreichen, indem man erst eine Rakete mit ¾ der Lichtgeschwindigkeit von der Erde abschießt und von dieser Rakete eine relativ zu ihr wiederum mit ¾ der Lichtgeschwindigkeit fliegende Rakete startet. Aufgrund der Relativität der Gleichzeitigkeit können Relativgeschwindigkeiten nicht einfach addiert werden, wie es bei den geringen Geschwindigkeiten des Alltags noch sehr genau zutrifft. Stattdessen ergibt sich für die Gesamtgeschwindigkeit nach dem relativistischen Additionstheorem für Geschwindigkeiten:

v_{\mathrm {ges} }={\frac {v_{1}+v_{2}}{1+{\frac {v_{1}\cdot v_{2}}{c^{2}}}}}

Demgemäß bewegt sich im Beispiel die zweite Rakete lediglich mit 0,96 c von der Erde weg (die 0,75 c zur ersten Rakete sind davon unberührt). Aus dem Prinzip von der Konstanz der Lichtgeschwindigkeit folgt, dass eine Beschleunigung eines massebehafteten Körpers auf Lichtgeschwindigkeit unendlich viel Energie benötigen würde.

Es gibt einige Beobachtungen, die auf den ersten Blick superluminare Bewegungen zu bestätigen scheinen:

Seit einigen Jahren werden im Universum Jets beobachtet, die sich superluminar von ihrem Ursprungsort zu entfernen scheinen. Allerdings ist dies nur ein optischer Effekt, in Wahrheit bewegen sich die Jets mit Unterlichtgeschwindigkeit.
An der Universität Köln, mittlerweile mehrfach durch andere Institutionen überprüft, wurde nachgewiesen, dass es beim quantenmechanischen Tunneln von Photonen zu Effekten kommen kann, die von einigen Forschern als superluminare Geschwindigkeiten interpretiert werden. Die Interpretationen dieser Beobachtungen werden jedoch derzeit noch kontrovers diskutiert.
Bei einer Messung an quantenmechanisch verschränkten Teilchen scheint Information zwischen den Teilchen instantan (also ohne Zeitdifferenz) übertragen zu werden (Einstein-Podolsky-Rosen-Effekt, kurz: EPR-Effekt). Es ist aber nicht möglich, diesen Effekt zur Kommunikation mit Überlichtgeschwindigkeit zu verwenden.
Im September 2011 wurde von der OPERA-Kollaboration am Gran Sasso gemeldet, man habe Hinweise darauf gefunden, dass Neutrinos sich mit Überlichtgeschwindigkeit bewegt hätten. Eine neue Messung durch ICARUS hat jedoch Übereinstimmung mit der Lichtgeschwindigkeit ergeben, wodurch das OPERA-Resultat mit großer Wahrscheinlichkeit widerlegt ist. Für mehr Details siehe Messungen der Neutrinogeschwindigkeit.

Innerhalb eines Mediums können sich Materieteilchen jedoch schneller bewegen als das Licht, das heißt schneller als elektromagnetische Wellen innerhalb des gleichen Mediums. Dabei entsteht die Tscherenkowstrahlung. Die Lichtgeschwindigkeit im Vakuum wird dabei jedoch nicht übertroffen.

Tachyonen

Superluminare Geschwindigkeiten sind durch die Gleichungen der Relativitätstheorie nicht kategorisch ausgeschlossen, lediglich der Wechsel zwischen Über- und Unterlichtgeschwindigkeit ist in keiner Richtung möglich. Theoretisch könnte ein superluminares Teilchen existieren, ein Tachyon, welches sich ausschließlich superluminar bewegt und eine imaginäre Masse hat. Es hat jedoch eine Menge paradoxer Eigenschaften, zum Beispiel beschleunigt es („Runaway Solution“), falls es durch Abstrahlung (bei geladenen beschleunigten Tachyonen) Energie verliert, so dass es schwierig ist, eine Theorie wechselwirkender Tachyonen zu konstruieren. Die Idee der Tachyonen mit formal „imaginärer Masse“ wurde erstmals in den 1960er-Jahren von George Sudarshan und anderen ausgesprochen. Betrachtet man Tachyonen jedoch quantenmechanisch, stellt man fest, dass sich selbst diese als lokale Störung nicht überlichtschnell ausbreiten können.[2]

Scheinbar überlichtschnelle Objekte in der Astronomie

Manche Jets, die etwa von Quasaren ausgesandt werden, scheinen sich mit Überlichtgeschwindigkeit zu bewegen. Beispielsweise bewegte sich ein zwischen 1977 und 1980 beobachteter Jet des Quasars 3C 273 mit scheinbar elffacher Lichtgeschwindigkeit. Dies beruht aber auf einer Täuschung, die immer dann entsteht, wenn sich das beobachtete Objekt mit einer Geschwindigkeit zwischen 70,7 % und 100 % der Lichtgeschwindigkeit nähert. Im Jahr 1970 wurde das Phänomen erstmals beobachtet, nachdem es schon 1966 von Martin Rees[3] theoretisch erörtert und erklärt worden war.

Erklärung

Ein Quasar in der Entfernung $r_{0}$ stoße zum Zeitpunkt $t=0$ einen Jet mit einem hellen Knoten aus. Der Knoten bewegt sich mit der Geschwindigkeit $v$ unter dem Winkel $\theta$ zur Richtung zur Erde.

Tatsächliche Bewegung

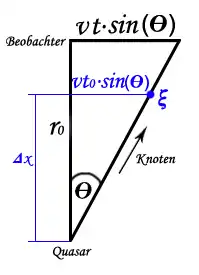
Darstellung der Bewegung eines Jets

Nach Ablauf der Zeit $t_{0}$ ist der Knoten an einem Ort $\xi$ in der Entfernung $vt_{0}$ vom Quasar.

In Erdrichtung hat er sich dann um die Strecke

\Delta x=vt_{0}\,\cos(\theta )

auf den Beobachter zubewegt. Dabei hat er transversal die Strecke

\Delta y=vt_{0}\,\sin(\theta )

zurückgelegt.

Scheinbare Bewegung Der Beobachter sieht den Knoten am Quasar entstehen, nachdem das Licht die Entfernung $r_{0}$ durchlaufen hat, also zum Zeitpunkt

t_{1}={\frac {r_{0}}{c}}

.

Der Beobachter sieht den Knoten am Ort $\xi$ , wenn das zum Zeitpunkt $t_{0}$ dort emittierte Licht noch die restliche Strecke zum Beobachter zurückgelegt hat. Da der Jet nur in nächster Nähe des Quasars beobachtet wird, liegt der Lichtweg von $\xi$ zum Beobachter praktisch parallel zur Beobachtungsrichtung des Quasars. Somit beträgt seine Entfernung zum Beobachter

R=r_{0}-\Delta x

.

Den Beobachter erreicht das Licht vom Knoten bei $\xi$ nach der Zeit

{\begin{aligned}t_{2}&=t_{0}+{\frac {R}{c}}\\&=t_{0}+{\frac {r_{0}-\Delta x}{c}}\\&=t_{0}+{\frac {r_{0}-vt_{0}\,\cos(\theta )}{c}}\end{aligned}}

.

Zwischen der Beobachtung der Emission im Nukleus und der Beobachtung des Erreichens von $\xi$ vergeht die Zeit

{\begin{aligned}\Delta t&=t_{2}-t_{1}\\&=t_{0}+{\frac {r_{0}-vt_{0}\,\cos(\theta )}{c}}-{\frac {r_{0}}{c}}\\&=t_{0}-{\frac {vt_{0}\,\cos(\theta )}{c}}\\&=t_{0}(1-\beta \,\cos(\theta ))\end{aligned}}

,

mit $\beta =v/c$ .

Für die scheinbare transversale Geschwindigkeit ${\tilde {v}}$ finden wir damit

{\begin{aligned}{\tilde {v}}&={\frac {\Delta y}{\Delta t}}\\&={\frac {vt_{0}\,\sin(\theta )}{t_{0}(1-\beta \,\cos(\theta ))}}\\&={\frac {\sin(\theta )}{1-\beta \,\cos(\theta )}}\cdot v\end{aligned}}

bzw. mit ${\tilde {\beta }}={\tilde {v}}/c$

{\tilde {\beta }}={\frac {\beta \,\sin(\theta )}{1-\beta \,\cos(\theta )}}

.

Beispiel: Für $\beta =0{,}996$ und $\theta =6^{\circ }$ ergibt sich ${\tilde {\beta }}=11$ , also scheinbar 11-fache Lichtgeschwindigkeit.

Bedingung für Beobachtung von Superluminalität

Die Bewegung erscheint superluminar, wenn ${\tilde {\beta }}>1$ ist, also wenn

{\frac {\beta \,\sin(\theta )}{1-\beta \,\cos(\theta )}}>1

.

Umstellen ergibt

{\frac {1}{\beta }}<\sin(\theta )+\cos(\theta )

,

und nach trigonometrischer Umformung der rechten Seite:

{\frac {1}{\beta }}<{\sqrt {2}}\cos(\theta -\pi /4)

.

Wegen $\beta <1$ muss gelten

{\sqrt {2}}\cos(\theta -\pi /4)>1

,

das ist der Fall für

0\leq \theta <\pi /2=90^{\circ }

.

Jeder Jet, der eine auf den Beobachter zu gerichtete Komponente hat, kann also den Eindruck erwecken, als würde er sich transversal mit Überlichtgeschwindigkeit bewegen. Die kleinste Jetgeschwindigkeit in Bezug auf seine Quelle, bei der dieser Effekt auftreten kann, ergibt sich aus dem Maximalwert von ${\sqrt {2}}\cos(\theta -\pi /4)$ . Dies ist bei einem Winkel von $\theta =45^{\circ }$ der Fall. Unter diesen Umständen reicht es aus, wenn die Jet-Geschwindigkeit $v_{\text{Jet}}$ die Bedingung erfüllt:

v_{\text{Jet}}\,\geq \,{\frac {c}{\sqrt {2}}}\,\approx \,0{,}71\,c

.

Wobei $c$ die Lichtgeschwindigkeit ist.

Überlichtschnelle Effekte in der Quantenmechanik

Superluminares Tunneln

An der Universität Köln wurde unter der Leitung von Günter Nimtz der quantenmechanische Effekt des superluminaren Tunnelns von Mikrowellen-Photonen, dem der Tunneleffekt zu Grunde liegt, zuerst nachgewiesen.[4]

Experimente vom Nimtz-Typ mit Photonen anderer Wellenlänge, insbesondere mit sichtbarem Licht, haben durch andere Gruppen stattgefunden und haben die Beobachtungen von Nimtz bestätigt (u. a. Steinberg und Raymond Chiao von der Universität Berkeley), werden von den Experimentatoren wie Chiao und Steinberg aber anders interpretiert. In allen Experimenten wird festgestellt, dass sich eine superluminare Geschwindigkeit dann einstellt, wenn sich zwischen der Quelle und dem Detektor eine Barriere befindet, welche die Photonen erst überwinden (durchtunneln) müssen.

Medienwirksam wurde dort 1994 mit frequenzmodulierten Mikrowellen ein Teil einer Mozart-Sinfonie mit übertragen, wobei Nimtz nach eigenen Angaben für das Maximum und die Anstiegsflanke des Wellenpakets[5] eine 4,7-fache Lichtgeschwindigkeit maß[6]. Nimtz behauptet, damit die Möglichkeit der Übertragung von Information mit Überlichtgeschwindigkeit gezeigt zu haben, was aber bestritten wurde. Definiert man die Geschwindigkeit der Informationsübertragung über die Ansprechzeit eines Detektors, gibt es keine Informationsübertragung mit Überlichtgeschwindigkeit: Ein Detektor auf einer gleich langen Vergleichsstrecke ohne „Tunnel“, auf der sich die gleiche Information (Pulsform) mit Lichtgeschwindigkeit ausbreitet, spricht zuerst an, da das Signal auf der Tunnelstrecke viel schwächer ist und zwar unabhängig von der Empfindlichkeit des Detektors.[7]

Diese Experimente stehen nach allgemeiner Ansicht in völliger Übereinstimmung mit einer der Grundaussagen der Relativitätstheorie, nach der keine Informationsausbreitung mit Überlichtgeschwindigkeit stattfindet. So kann man z. B. zeigen, dass ein Wellenzug beim Tunneln stärker im hinteren Teil gedämpft wird als im vorderen, so dass sich sein Intensitätsmaximum nach vorne verlagert. Definiert man die Lage des Maximums als Position des Wellenzuges, so kann man eine Überlichtgeschwindigkeit errechnen, ohne dass irgendein Teil des Wellenzuges mit Überlichtgeschwindigkeit vorangeschritten wäre.

Bei Tunnelexperimenten mit einzelnen Photonen wurde bereits überlichtschnelles Tunneln nachgewiesen, siehe zum Beispiel Experimente der Chiao-Gruppe. Da beim Tunneln jedoch ein großer Teil der tunnelnden Photonen und damit der Information verloren geht, ist auch hier die Möglichkeit einer überlichtschnellen Informationsübertragung umstritten, siehe auch diese Bibliografie.[8]

Von anderen Physikern, zum Beispiel im Überblicksartikel von Privitera et al.,[9] wird darauf hingewiesen, dass die Superluminalität des Geschehens ein Artefakt der verwendeten Definition von Geschwindigkeit ist.[10] Dass zum Beispiel die Gruppengeschwindigkeit von Pulsen in Medien mit starker Absorption und Dispersion größer als die Lichtgeschwindigkeit sein kann, jedoch keine Signalgeschwindigkeit ist, war schon Léon Brillouin und Arnold Sommerfeld bekannt.[11] Horst Aichmann und Günter Nimtz verteidigen dagegen ihre Interpretation der Experimente, dass beim Tunnelprozess tatsächlich superluminale Signalgeschwindigkeiten auftreten können, und werfen ihren Kritikern Fehlinterpretationen vor.[12]

EPR-Effekt

Ein anderes Phänomen, das auf den ersten Blick das Auftreten von Überlichtgeschwindigkeit nahelegt, ist der EPR-Effekt: Hat man zwei verschränkte Teilchen an verschiedenen Orten, so sagt die Quantenmechanik voraus, dass einerseits vor der Messung der Zustand jedes einzelnen der Teilchen unbestimmt ist (der Wert der Messgröße also nicht feststeht), andererseits nach Messung des einen Teilchens auch sofort der Zustand des anderen Teilchens festgelegt ist. Diese von Einstein als „spukhafte Fernwirkung“[13] zurückgewiesene Eigenschaft der Quantenmechanik ist experimentell bestätigt.[14] Allerdings lässt sich der EPR-Effekt nicht nutzen, um damit überlichtschnell zu kommunizieren, da die einzelnen Messergebnisse für sich genommen jeweils zufällig sind. Erst beim Vergleich der Messergebnisse an beiden Teilchen kann die Korrelation festgestellt werden. Dazu ist aber erst eine „klassische“, unterlichtschnelle Informationsübertragung notwendig. Beispielsweise beruht die Quantenteleportation auf dieser Kombination aus EPR-Effekt und anschließender klassisch übertragener Information.

Nick Herbert schlug Anfang der 1980er-Jahre ein Experiment vor, in dem in der Quantenmechanik Informationen mit Überlichtgeschwindigkeit übertragen werden können, falls es möglich wäre, perfekte Quanten-Kopierer herzustellen.[15] Wie Wojciech Zurek und William Wootters kurz darauf 1982 aber zeigten, sind solche Kopierer grundsätzlich unmöglich (No-Cloning-Theorem).

Ob beim EPR-Effekt überhaupt Information übertragen wird, ist umstritten und hängt sehr von der Interpretation der Quantenmechanik und des Informationsbegriffs ab. Eine Interpretation besagt, dass die Teilchen zusätzliche Information in verborgenen Variablen, d. h. nicht messbaren Eigenschaften, die die Korrelation steuern, mitführen. Man kann jedoch zeigen, dass die Messergebnisse dann gewissen statistischen Regeln, den Bellschen Ungleichungen, gehorchen müssten. Eine Verletzung dieser Ungleichungen wurde experimentell bestätigt.[16] Andere Erklärungsversuche ziehen auch zeitumgekehrte Kausalbeziehungen für quantenmechanische Systeme in Betracht.

Zeitreisen

Nach der speziellen Relativitätstheorie würde Überlichtgeschwindigkeit Zeitreisen oder zumindest in Form eines Antitelefons das Versenden von Nachrichten in die Vergangenheit ermöglichen. Der Zusammenhang zwischen Überlichtgeschwindigkeit und Zeitreise lässt sich aus den Eigenschaften der Lorentz-Transformation im Minkowski-Diagramm ableiten. Wegen der daraus folgenden Paradoxa wird die Möglichkeit von Zeitreisen in physikalischen Theorien meist ausgeschlossen. Ohne Zusatzannahmen verbieten die Gleichungen der Allgemeinen Relativitätstheorie allerdings Zeitreisen nicht, wie zuerst Kurt Gödel zeigte.

Überlichtgeschwindigkeit in der Kosmologie

Überlichtgeschwindigkeit durch die Expansion des Raumes

Das Lichtspektrum der meisten Galaxien weist eine Rotverschiebung auf. Edwin P. Hubble deutete diese Verschiebung zunächst als Dopplereffekt. Das heißt, die jeweilige Galaxie entfernt sich mit erheblicher Geschwindigkeit $v$ von der Erde. Beim Vergleich der Rotverschiebung von Galaxien mit bekannter Entfernung $d$ zur Erde fand Hubble einen linearen Zusammenhang. Dies ist das Hubble-Gesetz $v=H_{0}\,d$ mit der Hubblekonstante $H_{0}$ . Gemäß diesem Gesetz müssten sich Galaxien schneller als Lichtgeschwindigkeit von der Erde entfernen, wenn sie nur weit genug entfernt sind.

Die Interpretation der kosmologischen Rotverschiebung führt diese auf die Zunahme der Entfernungen infolge der Expansion des Universums zurück, nicht auf den Dopplereffekt. Das Hubble-Gesetz ist im Rahmen der relativistischen Kosmologie bei beliebigen Entfernungen gültig, wenn $d$ als physikalische Entfernung (Entfernung zu einem festen Zeitpunkt) interpretiert wird und $v$ als die zeitliche Änderung dieser Entfernung. $v={\dot {d}}$ kann größer als Lichtgeschwindigkeit werden, was gelegentlich als Widerspruch zur Relativitätstheorie gewertet und als Gegenargument zur Urknalltheorie angeführt wird. Konzeptuell darf aber die Abstandsänderungsrate ${\dot {d}}$ nicht mit einer Geschwindigkeit verwechselt werden. Geschwindigkeiten sind lokale Größen, die den Beschränkungen der speziellen Relativitätstheorie unterliegen. Abstandsänderungen unterliegen als globale Größen nicht diesen Beschränkungen und können beliebig groß werden. Echte Überlichtgeschwindigkeiten liegen also auch bei weit entfernten Galaxien nicht vor.

Kosmologische Theorien mit variabler Lichtgeschwindigkeit

Verschiedentlich wurden kosmologische Theorien mit einer variablen Lichtgeschwindigkeit (Variable Speed of Light Theories, VSL) vorgeschlagen. Bekannt wurde insbesondere ein Vorschlag von João Magueijo und Andreas Albrecht von 1999,[17] in denen das Horizontproblem und das Problem der Flachheit des Universums, die üblicherweise heute im Rahmen des Inflationären Modells der Kosmologie erklärt werden, stattdessen durch eine um bis zu 60 Größenordnungen höhere Lichtgeschwindigkeit im frühen Universum erklärt werden. Die Lichtgeschwindigkeit ist in dieser Theorie eine dynamische Variable, also zeitlich veränderlich, allerdings auf eine besondere Art und Weise, die die Form der Feldgleichungen der Allgemeinen Relativitätstheorie nicht zu stark modifiziert. Die Lorentzinvarianz der Theorie ist aber explizit gebrochen, es gibt ein ausgezeichnetes Bezugssystem (das durch die kosmologische Expansion vorgegeben wird). Nach Magueijo und Albrecht wird auch das Problem der Kosmologischen Konstante so gelöst.[18][19] Magueijo schrieb darüber auch ein populärwissenschaftliches Buch.[20] Einen ähnlichen Vorschlag machte schon 1992 der kanadische Physiker John Moffat,[21] ebenfalls mit der Absicht der Lösung kosmologischer Probleme.[22] Die Idee der variablen Lichtgeschwindigkeit wurde von Köhn aufgegriffen und mit dem Konzept mehrerer Zeitdimensionen kombiniert[23]. Er zeigte, dass die Lichtgeschwindigkeit in solch einer Raumzeit von der Zeit abhängt. Jedoch ist diese Zeitabhängigkeit für das beobachtbare Universum vernachlässigbar, so dass die Lichtgeschwindigkeit im jetzigen Universum konstant erscheint, wohingegen sie im frühen Universum variabel war, wie ursprünglich von Albrecht und Magueijo vorgeschlagen.

Die Theorie steht in der Tradition zeitlich veränderlicher fundamentaler (dimensionsloser) physikalischer Größen, die seit Dirac diskutiert werden. Dabei ist es sinnvoll, nur die Variabilität dimensionsloser Größen zu diskutieren, da die Variabilität dimensionsbehafteter Größen in der Physik von den verwendeten Maßeinheiten abhängig ist und somit keine fundamentale Bedeutung hat. Im Fall der VSL-Theorien ist die Feinstrukturkonstante veränderlich, was prinzipiell bei weit entfernten Objekten als Funktion der Rotverschiebung beobachtbar sein sollte.[24]

Das Alcubierre-Van-den-Broeck-Warpfeld

Wurmlöcher

Ein damit verwandter Effekt ist das Durchqueren sogenannter Wurmlöcher, das oft in Science-Fiction-Romanen verwendet wird. Dabei bewegt sich ein Raumschiff lokal zwar nicht schneller als mit Lichtgeschwindigkeit, es nimmt aber im gekrümmten Raum eine Abkürzung, so dass es am Ende doch schneller als das Licht am Ziel ankommt. Als zweidimensionale Analogie kann man den Weg über ein gefaltetes Blatt Papier betrachten. Statt auf dem Papier zu bleiben, kann ein Reisender auch einfach ein Loch ins Papier bohren und damit die darangefaltete andere Seite erreichen. Mit dieser Technik wären auch Zeitmaschinen denkbar. Solche Wurmlöcher können zwar in der Relativitätstheorie theoretisch konstruiert werden, es scheint aber, dass sie in der Praxis sehr instabil wären, so dass nicht einmal Informationen durch sie hindurchgeleitet werden könnten.

Hyperraum

Einen vergleichbaren Effekt bewirken würde die ebenfalls in der Science-Fiction gerne verwendete Vorstellung einer Abkürzung durch einen Hyperraum, in den unsere Raumzeit eingebettet sein könnte. Die Idee ist dabei folgende: Um den Weg vom Nordpol zum Südpol abzukürzen, reise man quer durch die Erde anstatt entlang der Oberfläche. Der Weg durch die Erde (über die dritte Dimension) ist kürzer als der Weg auf der (zweidimensionalen) Erdoberfläche. Genauso könnte man sich vorstellen, dass unsere Raumzeit auch in einen höherdimensionalen Hyperraum eingebettet ist (wie die Erdoberfläche in den Raum), und man daher durch den Hyperraum abkürzen könnte. Auch hier würde man (im Hyperraum) nicht schneller als Lichtgeschwindigkeit fliegen müssen, um schneller als das Licht im Normalraum am Ziel anzukommen.

Sonstiges

Die Verwendung des englischen Begriffs FTL (für faster than light) geht bis in die 1950er Jahre zurück. Im Breakthrough Propulsion Physics Project der NASA wurden Konzepte und Theorien für Überlichtgeschwindigkeit evaluiert.

Literatur

Kirk T. McDonald: Radiation from a superluminal Source. Princeton University, Princeton. NJ 08544, 26. November 1986, arxiv:physics/0003053.
Ernst Udo Wallenborn: Was ist das Nimtz-Experiment? theorie.gsi.de, 23. Juni 1999.
Rüdiger Vaas: Tunnel durch Raum und Zeit, Franckh-Kosmos, Stuttgart 2006 (2. Aufl.), ISBN 3-440-09360-3.
João Magueijo: Schneller als die Lichtgeschwindigkeit – der Entwurf einer neuen Kosmologie. Bertelsmann, München 2003, ISBN 3-570-00580-1.
Günter Nimtz (et al.): Zero time space – how quantum tunneling broke the light speed barrier. Wiley-VCH, Weinheim 2008, ISBN 978-3-527-40735-4.
Michio Kaku: Faster than Light; in Physics of the impossible. S. 197–215, Allen Lane, London 2008, ISBN 978-0-7139-9992-1. deutsch: Die Physik des Unmöglichen.Rowohlt, Reinbek 2008, ISBN 978-3-498-03540-2.
John G. Cramer: Faster-than-Light Implications of Quantum Entanglement and Nonlocality. S 509–529, in Marc G. Millis (et al.): Frontiers of Propulsion Science. American Inst. of Aeronautics & Astronautics, Reston 2009, ISBN 1-56347-956-7.
Moses Fayngold: Special relativity and motions faster than light. Wiley-VCH, Weinheim 2002, ISBN 3-527-40344-2.
Nick Herbert Faster than light- superluminal loopholes in physics, New American Library, 1988.
Barak Shoshany: Lectures on Faster-than-Light Travel and Time Travel, SciPost Physics Lecture Notes, 10, 2019, Arxiv

Weblinks

Wiktionary: Überlichtgeschwindigkeit – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Videos

Kann man mit Lichtgeschwindigkeit reisen? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 5. Jan. 2005.

Einzelnachweise

http://scienceblogs.de/hier-wohnen-drachen/2011/12/04/scheren-laser-und-quasare-wie-man-uberlichtgeschwindigkeit-beobachtet/
Matt Austern zu Tachyonen (Memento vom 18. Februar 2014 im Internet Archive), auch in quantenmechanischer Behandlung (englisch)
Nature, Band 211, S. 468
wissenschaft.de: Stürzt Einsteins Dogma? 1. August 1997, abgerufen am 7. September 2019., mit einer Beschreibung der Experimente von Günter Nimtz
Peak and the rising edge of a frequency band limited wave packet, gemäß W. Heitmann, G. Nimtz: On causality proofs of superluminal barrier traversal of frequency band limited wave packets, Phys. Lett. A, Bd. 196, 1994, S. 154
Ernst-Udo Wallenborn: Und Mozart? (Memento des Originals vom 5. April 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/theory.gsi.de, Wallenborn 1999 zum Experiment von Nimtz
Ernst-Udo Wallenborn: Aber ist das nicht Überlichtgeschwindigkeit? (Memento des Originals vom 5. April 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/theory.gsi.de, Wallenborn in einer Diskussion des Experiments von Nimtz, 1999
Unvollständiges kommentiertes Literaturverzeichnis zum Thema „Überlichtgeschwindigkeit durch Tunneln“, Stand 2001
G. Privitera, G. Salesi, V.S. Olkhovsky, E. Recami: Tunnelling times: An elementary introduction. In: Rivista del Nuovo Cimento vol. 26, n. 4, 2003. arxiv:quant-ph/0412146
Ernst-Udo Wallenborn: Superluminales Tunneln (Memento des Originals vom 4. August 2003 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/theory.gsi.de, Argumente gegen eine Interpretation des Tunneleffektes als überlichtschnelle Informationsausbreitung, 23. Juni 1999
Diskussion der Geschwindigkeitsdefinitionen, Duke University (Memento vom 10. Juni 2010 im Internet Archive)
H.Aichmann, G.Nimtz, On the traversal time of barriers, Foundations of Physics, Band 44, 2014, S. 678–688, Abstract
Max Born, Albert Einstein: Albert Einstein, Max Born. Briefwechsel 1916–1955. München (Nymphenburger) 1955, S. 210.
Harry Paul: Photonen, 1999, B.-G.-Teubner-Verlag, ISBN 3-519-13222-2
Herbert: FLASH – A Superluminal Communicator Based upon a New Kind of Quantum Measurement, Foundations of Physics, Bd. 12, 1982, S. 1171
Hensen et al.: Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. In: Nature. Band 526, 2015, S. 682–686, doi:10.1038/nature15759.
Albrecht, Magueijo: A time varying speed of light as a solution to cosmological puzzles, Phys. Rev. D59, 1999. arxiv:astro-ph/9811018.
Magueijo: New variable speed of light theories, Reports Progress Physics 2003. arxiv:astro-ph/0305457.
John Barrow: Cosmologies with varying light speed, 1998. arxiv:astro-ph/9811022.
Magueijo: Faster Than the Speed of Light: The Story of a Scientific Speculation. Massachusetts: Perseus Books Group, 2003.
Moffat: Superluminary Universe: A Possible Solution to the Initial Value Problem in Cosmology, International Journal Modern Physics D, Bd. 2, 2003, S. 351, Moffat Reinventing Gravity, Collins 2008
und davor 1988 der Franzose Jean-Pierre Petit, bei ihm änderte sich auch die Gravitationskonstante mit der Zeit, so dass die einsteinschen Feldgleichungen insgesamt invariant bleiben
C. Köhn: The Planck Length and the Constancy of the Speed of Light in Five Dimensional Spacetime Parametrized with Two Time Coordinates. In: J. High Energy Phys., Grav. Cosm.. 3, 2017, S. 635–650.
1999 schienen Beobachtungen von J. K. Webb und Anderen eine solche Variabilität zu zeigen, siehe: Webb, Churchill, Drinkwater, Flambaum, Barrow: Physical Review Letters, Bd. 82, 1999, S. 884

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] ttp://scienceblogs.de/hier-wohnen-drachen/2011/12/04/scheren-laser-und-quasare-wie-man-uberlichtgeschwindigkeit-beobachtet/

[2] Matt Austern zu Tachyonen (Memento vom 18. Februar 2014 im Internet Archive), auch in quantenmechanischer Behandlung (englisch)

[3] Nature, Band 211, S. 468

[4] wissenschaft.de: Stürzt Einsteins Dogma? 1. August 1997, abgerufen am 7. September 2019., mit einer Beschreibung der Experimente von Günter Nimtz

[5] Peak and the rising edge of a frequency band limited wave packet, gemäß W. Heitmann, G. Nimtz: On causality proofs of superluminal barrier traversal of frequency band limited wave packets, Phys. Lett. A, Bd. 196, 1994, S. 154

[6] Ernst-Udo Wallenborn: Und Mozart? (Memento des Originals vom 5. April 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/theory.gsi.de, Wallenborn 1999 zum Experiment von Nimtz

[7] Ernst-Udo Wallenborn: Aber ist das nicht Überlichtgeschwindigkeit? (Memento des Originals vom 5. April 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/theory.gsi.de, Wallenborn in einer Diskussion des Experiments von Nimtz, 1999

[8] Unvollständiges kommentiertes Literaturverzeichnis zum Thema „Überlichtgeschwindigkeit durch Tunneln“, Stand 2001

[9] G. Privitera, G. Salesi, V.S. Olkhovsky, E. Recami: Tunnelling times: An elementary introduction. In: Rivista del Nuovo Cimento vol. 26, n. 4, 2003. arxiv:quant-ph/0412146

[10] Ernst-Udo Wallenborn: Superluminales Tunneln (Memento des Originals vom 4. August 2003 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/theory.gsi.de, Argumente gegen eine Interpretation des Tunneleffektes als überlichtschnelle Informationsausbreitung, 23. Juni 1999

[11] Diskussion der Geschwindigkeitsdefinitionen, Duke University (Memento vom 10. Juni 2010 im Internet Archive)

[12] H.Aichmann, G.Nimtz, On the traversal time of barriers, Foundations of Physics, Band 44, 2014, S. 678–688, Abstract

[Einstein1955-13] Max Born, Albert Einstein: Albert Einstein, Max Born. Briefwechsel 1916–1955. München (Nymphenburger) 1955, S. 210.

[14] Harry Paul: Photonen, 1999, B.-G.-Teubner-Verlag, ISBN 3-519-13222-2

[15] Herbert: FLASH – A Superluminal Communicator Based upon a New Kind of Quantum Measurement, Foundations of Physics, Bd. 12, 1982, S. 1171

[16] Hensen et al.: Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. In: Nature. Band 526, 2015, S. 682–686, doi:10.1038/nature15759.

[17] Albrecht, Magueijo: A time varying speed of light as a solution to cosmological puzzles, Phys. Rev. D59, 1999. arxiv:astro-ph/9811018.

[18] Magueijo: New variable speed of light theories, Reports Progress Physics 2003. arxiv:astro-ph/0305457.

[19] John Barrow: Cosmologies with varying light speed, 1998. arxiv:astro-ph/9811022.

[20] Magueijo: Faster Than the Speed of Light: The Story of a Scientific Speculation. Massachusetts: Perseus Books Group, 2003.

[21] Moffat: Superluminary Universe: A Possible Solution to the Initial Value Problem in Cosmology, International Journal Modern Physics D, Bd. 2, 2003, S. 351, Moffat Reinventing Gravity, Collins 2008

[22] und davor 1988 der Franzose Jean-Pierre Petit, bei ihm änderte sich auch die Gravitationskonstante mit der Zeit, so dass die einsteinschen Feldgleichungen insgesamt invariant bleiben

[23] C. Köhn: The Planck Length and the Constancy of the Speed of Light in Five Dimensional Spacetime Parametrized with Two Time Coordinates. In: J. High Energy Phys., Grav. Cosm.. 3, 2017, S. 635–650.

[24] 1999 schienen Beobachtungen von J. K. Webb und Anderen eine solche Variabilität zu zeigen, siehe: Webb, Churchill, Drinkwater, Flambaum, Barrow: Physical Review Letters, Bd. 82, 1999, S. 884