Spezielle Relativitätstheorie

Die spezielle Relativitätstheorie (SRT) ist eine physikalische Theorie über die Bewegung von Körpern und Feldern in Raum und Zeit. Sie erweitert das ursprünglich in der Mechanik entdeckte galileische Relativitätsprinzip zum speziellen Relativitätsprinzip. Dem speziellen Relativitätsprinzip zufolge haben nicht nur die Gesetze der Mechanik, sondern alle Gesetze der Physik in allen Inertialsystemen dieselbe Form. Dies gilt auch für die Gesetze des Elektromagnetismus, das sind die Maxwell-Gleichungen. Aus diesen folgt, dass die Lichtgeschwindigkeit im Vakuum in jedem Inertialsystem denselben Wert hat.

Der Begründer der Relativitätstheorie Albert Einstein um 1905

Damit folgt aus dem Relativitätsprinzip, dass Längen und Zeitdauern vom Bewegungszustand des Betrachters abhängen und es keinen absoluten Raum und keine absolute Zeit gibt. Dies zeigt sich in der Lorentzkontraktion und der Zeitdilatation. Eine weitere wichtige Konsequenz der SRT ist die Äquivalenz von Masse und Energie.

Als Geburt der speziellen Relativitätstheorie wird der Artikel Zur Elektrodynamik bewegter Körper[1] angesehen, den Albert Einstein 1905 nach Vorarbeiten von Hendrik Antoon Lorentz und Henri Poincaré veröffentlichte. Da sich die Theorie mit der Beschreibung relativ zueinander bewegter Bezugssysteme und mit der Relativität von Zeitdauern und Längen befasst, wurde sie bald als „Relativitätstheorie“ bekannt. 1915 wurde sie von Einstein in spezielle Relativitätstheorie umbenannt, als er die allgemeine Relativitätstheorie (ART) veröffentlichte. Diese schließt – anders als die SRT – auch die Gravitation ein.

Die SRT erklärte das Ergebnis des Michelson-Morley-Experiments und wurde später durch das Kennedy-Thorndike-Experiment sowie eine Vielzahl weiterer Tests bestätigt.

Einführung

Die Gesetze der klassischen Mechanik haben die besondere Eigenschaft, in jedem Inertialsystem gleichermaßen zu gelten (Relativitätsprinzip). Ein Inertialsystem ist ein Bezugssystem, in dem sich jeder kräftefreie Körper geradlinig gleichförmig bewegt oder im Zustand der Ruhe verharrt. Diese Tatsache erlaubt es, auch im ICE bei voller Fahrt z. B. einen Kaffee zu trinken, ohne dass die Geschwindigkeit von 300 km/h irgendwelche Auswirkungen hat. Die Transformationen (Umrechnungsformeln), mit denen in der klassischen Mechanik von einem Inertialsystem ins andere umgerechnet wird, heißen Galileitransformationen, und die Eigenschaft, dass die Gesetze nicht vom Inertialsystem abhängen (sich bei einer Galileitransformation also nicht ändern), nennt man entsprechend Galilei-Invarianz. Die Formeln für eine Galileitransformation folgen unmittelbar aus der klassischen Vorstellung eines allen Ereignissen zugrundeliegenden dreidimensionalen euklidischen Raumes und einer davon unabhängigen (eindimensionalen) Zeit.

Ende des 19. Jahrhunderts wurde jedoch erkannt, dass die Maxwell-Gleichungen, die sehr erfolgreich die elektrischen, magnetischen und optischen Phänomene beschreiben, nicht Galilei-invariant sind. Das bedeutet, dass sich die Gleichungen in ihrer Form verändern, wenn eine Galilei-Transformation in ein relativ zum Ausgangssystem bewegtes System durchgeführt wird. Insbesondere wäre die Lichtgeschwindigkeit vom Bezugssystem abhängig, wenn man die Galilei-Invarianz als fundamental betrachtete. Die Maxwell-Gleichungen wären demnach nur in einem einzigen Bezugssystem gültig, und es sollte durch Messung der Lichtgeschwindigkeit möglich sein, die eigene Geschwindigkeit gegenüber diesem System zu bestimmen. Das berühmteste Experiment, mit dem versucht wurde, die Geschwindigkeit der Erde gegenüber diesem ausgezeichneten System zu messen, ist der Michelson-Morley-Versuch. Kein Experiment konnte jedoch eine Relativbewegung nachweisen.

Die andere Lösung des Problems ist das Postulat, dass die Maxwell-Gleichungen in jedem Bezugssystem unverändert gelten und stattdessen die Galilei-Invarianz nicht universal gültig ist. An die Stelle der Galilei-Invarianz tritt dann die Lorentz-Invarianz. Dieses Postulat hat weitreichende Auswirkungen auf das Verständnis von Raum und Zeit, weil die Lorentztransformationen, welche die Maxwell-Gleichungen unverändert lassen, keine reinen Transformationen des Raumes (wie die Galilei-Transformationen) sind, sondern dabei Raum und Zeit gemeinsam verändern. Gleichzeitig müssen auch die Grundgleichungen der klassischen Mechanik umformuliert werden, weil sie nicht Lorentz-invariant sind. Für niedrige Geschwindigkeiten sind Galileitransformationen und Lorentztransformationen jedoch so ähnlich, dass die Unterschiede nicht messbar sind. Die Gültigkeit der klassischen Mechanik widerspricht daher bei kleinen Geschwindigkeiten nicht der neuen Theorie.

Die spezielle Relativitätstheorie liefert damit ein erweitertes Verständnis von Raum und Zeit, demzufolge auch die Elektrodynamik nicht mehr vom Bezugssystem abhängt. Ihre Vorhersagen wurden experimentell vielfach erfolgreich überprüft und mit hoher Genauigkeit bestätigt.[2]

Lorentztransformationen

Die Unveränderlichkeit der physikalischen Gesetze unter Lorentztransformationen ist die zentrale Behauptung der speziellen Relativitätstheorie. Daher werden in diesem Abschnitt die physikalischen Auswirkungen der Lorentztransformationen anschaulich erklärt.

Da die Gesetze der Elektrodynamik in jedem Bezugssystem gleichermaßen gelten, gilt insbesondere auch ihre Vorhersage einer konstanten Vakuum-Lichtgeschwindigkeit. Das Licht ist also in jedem Bezugssystem gleich schnell. Dies folgt direkt aus der Lorentz-Invarianz, und es wird oft als wichtigste Eigenschaft der Lorentztransformationen betrachtet, dass sie die Lichtgeschwindigkeit unverändert lassen.

Einsteins Gedankenexperiment

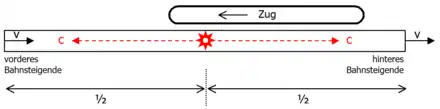
Grafische Verdeutlichung des Gedankenexperiments

Um die verschiedenen Aspekte der Lorentztransformationen zu veranschaulichen, wird ein Gedankenexperiment verwendet, das auf Albert Einstein zurückgeht: Ein Zug fährt durch einen Bahnhof mit der Geschwindigkeit $-v$ . Auf dem Bahnsteig und im Zug befinden sich verschiedene Beobachter, deren Beobachtungen und Messungen verglichen werden sollen. Sie verfügen über Uhren und Maßstäbe sowie über Blitzlichter, mit denen Lichtsignale ausgetauscht werden können. Wir nennen das in Fahrtrichtung vordere Ende des Zuges „Zuganfang“, das andere nennen wir „Zugende“. Der Zuganfang erreicht zunächst jenes Ende des Bahnsteigs, das wir als das „hintere“ bezeichnen. Später kommt er am „vorderen“ Ende an.

Für den Zugpassagier sieht es so aus, als würde er ruhen und sich der Bahnsteig mit der Geschwindigkeit $+v$ entgegen der Fahrtrichtung des Zuges bewegen. Nach dem Relativitätsprinzip ist seine Sichtweise genauso richtig wie die des Beobachters, der am Bahnhof steht. Beide Bezugssysteme sind Inertialsysteme und damit physikalisch gleichwertig.

Es ist sehr wichtig zu beachten, dass jeder Beobachter direkte Aussagen nur über Ereignisse machen kann, die unmittelbar an seinem Ort stattfinden. Will er jedoch wissen, wann ein Ereignis an einem anderen Ort stattgefunden hat, so kann er sich nur auf Lichtsignale verlassen, die von diesem Ort ausgesandt wurden. Über die Entfernung und die Lichtlaufzeit kann er dann auf den Zeitpunkt des Ereignisses schließen, denn die Lichtgeschwindigkeit ist in allen Inertialsystemen gleich.

Gleichzeitigkeit

Eine der größten Schwierigkeiten beim Verständnis der Auswirkungen der Lorentztransformationen ist der Begriff der Gleichzeitigkeit. Zum Verständnis ist es daher wichtig, sich klarzumachen, dass Gleichzeitigkeit von Ereignissen an verschiedenen Orten nicht von vornherein definiert ist. Zur Definition von Gleichzeitigkeit bedient man sich der Lichtgeschwindigkeit, da diese in allen Bezugssystemen gleich ist. Die Lichtsignale von zwei gleichzeitigen Ereignissen werden einen Beobachter zu verschiedenen Zeiten erreichen, wenn die Ereignisse sich unterschiedlich weit vom Beobachter entfernt ereignen. Wenn ein Beobachter jedoch von zwei Ereignissen gleich weit entfernt ist und Lichtsignale von diesen ihn gleichzeitig erreichen, so nennt man die beiden Ereignisse selbst gleichzeitig.

Diese Definition von Gleichzeitigkeit erscheint anschaulich verständlich, führt aber zusammen mit der Lorentz-Invarianz zu einem paradox wirkenden Effekt: Die Gleichzeitigkeit zweier Ereignisse an verschiedenen Orten ist abhängig vom Bewegungszustand des Beobachters.

Diese Tatsache lässt sich unmittelbar mit dem eingangs beschriebenen Gedankenexperiment verstehen:

In der Mitte des Bahnsteiges steht eine Lampe. Für einen Beobachter, der auf dem Bahnsteig steht, ist unmittelbar klar: Wenn die Lampe eingeschaltet wird, dann erreicht das Licht beide Enden des Bahnsteigs gleichzeitig: Es hat ja in beide Richtungen denselben Weg zurückzulegen. Betrachten wir nun die Situation aus der Sicht eines Fahrgastes des Zuges: Der Bahnsteig bewegt sich nun mit konstanter Geschwindigkeit v nach hinten. Das Licht besitzt aber auch gegenüber dem Zug in beiden Richtungen die Geschwindigkeit c. Zum Zeitpunkt des Aussendens sind beide Enden des Bahnsteigs gleich weit von der Lampe entfernt. Somit kommt das vordere Bahnsteigende dem Lichtstrahl entgegen, sodass das nach vorne laufende Licht eine kürzere Strecke zurücklegt, bis es dieses Bahnsteigende erreicht. Umgekehrt bewegt sich das hintere Bahnsteigende in Richtung des ihm nacheilenden Lichtes, sodass das Licht hier einen etwas längeren Weg zurücklegen muss, bis es dieses Ende erreicht hat. Daher wird das Licht das vordere Bahnsteigende früher erreichen als das hintere, und somit werden die beiden Enden des Bahnsteigs nicht gleichzeitig erreicht.

Der Beobachter am Bahnsteig und der Beobachter im Zug sind sich also nicht einig über die Frage, ob die beiden Ereignisse „das Licht erreicht das vordere Ende des Bahnsteigs“ und „das Licht erreicht das hintere Ende des Bahnsteigs“ gleichzeitig sind. Da beide Beobachter sich jedoch gleichförmig bewegen, ist keines der beiden Systeme ausgezeichnet: Die Sichtweisen der beiden Beobachter sind also gleichwertig. Gleichzeitigkeit ist tatsächlich für beide Beobachter verschieden.

Die Gleichzeitigkeit von Ereignissen, deren Ort sich nur senkrecht zur Bewegungsrichtung ändert, ist in beiden Bezugssystemen gleich: Wenn die Lampe auf halber Höhe des Zuges hängt, so wird das Licht sowohl für den Beobachter am Bahnsteig als auch für den Beobachter im Zug gleichzeitig die Unter- und Oberseite des Zuges erreichen.

Lorentzkontraktion

Gedankenexperiment zur Lorentzkontraktion

Aus der Relativität der Gleichzeitigkeit ergibt sich ein anderer, ebenfalls paradox wirkender Effekt:

Angenommen, der Anfang des Zuges (vgl. Einsteins Gedankenexperiment) löst beim Passieren des vorderen Bahnsteigendes einen Lichtblitz aus und das Ende des Zuges löst einen ebensolchen Lichtblitz beim Passieren des hinteren Bahnsteigendes aus.

Der Beobachter in der Mitte des Bahnsteigs sieht bei der Durchfahrt des Zuges beide Lichtblitze gleichzeitig. Daraus schließt dieser Beobachter, wenn er weiß, dass er sich in der Mitte des Bahnsteigs aufhält und was die beiden Lichtblitze auslöste, dass Zug und Bahnsteig gleich lang sind.

Für den Beobachter in der Mitte des Zuges stellt sich die Situation aber ganz anders dar: Der Lichtblitz vom Anfang des Zuges erreicht ihn früher als der Lichtblitz vom hinteren Ende des Zuges, da er dem vorderen Lichtblitz entgegen fährt und sich gleichzeitig vom hinteren Lichtblitz entfernt. Da das „hintere“ Ereignis (das Zugende passiert das hintere Bahnsteigende) für ihn später eintritt als das „vordere“ (der Zuganfang passiert das vordere Bahnsteigende), schließt er, dass der Zug länger ist als der Bahnsteig, denn schließlich war das Zugende noch gar nicht am Bahnsteig angekommen, als der Zuganfang ihn schon wieder verlassen hat.

Somit ist für den Beobachter im Zug der Bahnsteig kürzer und der Zug länger als für den Beobachter auf dem Bahnsteig.

Das Relativitätsprinzip besagt wieder, dass beide recht haben: Wenn aus Sicht des Zugfahrers der (bewegte) Bahnsteig verkürzt ist, dann muss auch aus Sicht des Bahnsteig-Beobachters der (bewegte) Zug verkürzt sein. Die Lorentzkontraktion gilt nur in Bewegungsrichtung, da ja senkrecht zur Bewegungsrichtung die Gleichzeitigkeit der Ereignisse in beiden Bezugssystemen übereinstimmt. Beide Beobachter sind sich also z. B. über die Höhe des Fahrdrahtes einig.

Ein indirekter Nachweis der Längenkontraktion ergibt sich auch aus dem Problem des elektromagnetischen Feldes einer mit hoher Geschwindigkeit bewegten elektrischen Punktladung. Das elektrische Feld dieses Objekts ist bei verschwindender oder im Vergleich zur Lichtgeschwindigkeit geringer Geschwindigkeit einfach das Coulombfeld der Ladung, d. h. mit gleichmäßiger radialer Richtungsverteilung. Mit zunehmender Annäherung an die Lichtgeschwindigkeit konzentrieren sich dagegen – wegen der Abstandskontraktion in Bewegungsrichtung – die elektrischen Felder zunehmend in den Transversalrichtungen zur Bewegung. Zusätzlich treten jetzt neben den elektrischen Feldern auch (asymptotisch gleich starke) Magnetfelder auf, die die Bewegungsachse umkreisen.

Zeitdilatation

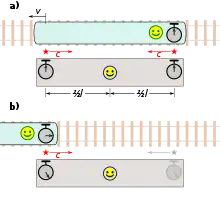
Gedankenexperiment zur Zeitdilatation. a) Uhren starten b) Uhren stoppen

Ebenso wie Distanzen von Beobachtern in verschiedenen Inertialsystemen verschieden festgestellt werden, muss auch beim Vergleich von Zeitspannen die Relativgeschwindigkeit der Inertialsysteme berücksichtigt werden: Der Beobachter im Zug (vgl. Einsteins Gedankenexperiment) stehe am hinteren Ende des Zuges und an jedem Ende des Bahnsteigs sei eine Uhr. Die Uhr am vorderen Ende des Bahnsteigs wird in Gang gesetzt, wenn der Anfang des Zuges sie passiert, und die Uhr am hinteren Ende des Bahnsteiges, wenn das Ende des Zuges sie passiert. Da der Zug für den Beobachter am Bahnsteig genauso lang ist wie der Bahnsteig, werden die Uhren also nach seinem Gleichzeitigkeitsbegriff gleichzeitig gestartet. Die Uhr am vorderen Bahnsteigende wird gestoppt, wenn das hintere Zugende sie passiert.

Der Beobachter im Zug setzt seine Uhr in Gang, wenn er das hintere Bahnsteigende passiert, also gleichzeitig mit dem Start der dortigen Bahnsteiguhr, und stoppt sie, wenn er das vordere Bahnsteigende passiert, gleichzeitig mit dem Stoppen der dortigen Bahnsteiguhr. Nach seinem Gleichzeitigkeitsbegriff geht die Uhr am vorderen Bahnsteigende gegenüber der am hinteren Bahnsteigende und damit auch gegenüber seiner Uhr vor, da nach seinem Längenbegriff der Zug länger ist als der Bahnsteig. Die Zeitspanne, die er für seine Fahrt vom hinteren bis zum vorderen Ende des Bahnsteigs misst, ist also kleiner als die Dauer, die von der Uhr am vorderen Bahnsteigende angezeigt wird, wenn er diese passiert.

Der Beobachter am Bahnsteig sieht also an den Anzeigen der Uhren, dass der Beobachter im Zug eine kürzere Zeitspanne misst als er selbst. Da nach seinem Gleichzeitigkeitsbegriff die Start- und Stoppzeitpunkte der Uhr des Beobachters im Zug und der Uhr am vorderen Bahnsteigende gleich sind, sind nach seinem Gleichzeitigkeitsbegriff auch die Zeitspannen gleich lang. Er kommt also zu dem Schluss, dass die Uhr des Beobachters im Zug zu langsam geht. Nach dem Gleichzeitigkeitsbegriff des Beobachters im Zug fallen jedoch die Startzeitpunkte der Uhren nicht zusammen, sodass er diese Beobachtung nicht macht.

Diese Betrachtung lässt sich auch umkehren, indem man je eine Uhr am Anfang und am Ende des Zuges anbringt und nach dem Gleichzeitigkeitsbegriff des Beobachters im Zug gleichzeitig startet, wenn der Anfang des Zuges das vordere Bahnsteigende passiert. Aus Sicht des Beobachters im Zug ergibt sich dann, dass die Zeit am Bahnsteig langsamer vergeht als im Zug.

Wieder lässt sich nicht entscheiden, welcher der beiden Beobachter recht hat. Beide Beobachter bewegen sich relativ zueinander unbeschleunigt und sind daher gleichberechtigt. Zeitspannen sind für beide Beobachter verschieden, und für beide Beobachter vergeht die Zeit in ihrem jeweiligen Ruhesystem am schnellsten, während sie in allen relativ bewegten Systemen langsamer vergeht. Dieser Effekt heißt Zeitdilatation. Die Zeit, die jeder Beobachter auf seiner eigenen Uhr abliest, nennt man Eigenzeit. Diese mit einer „mitgeführten Uhr“ gemessene Zeit ergibt immer den kürzestmöglichen, unveränderlichen Wert unter allen Zeitspannen, die für zwei kausal miteinander verbundene Ereignisse in relativ zueinander bewegten Inertialsystemen gemessen werden. Alle anderen Werte sind demgegenüber „zeitlich dilatiert“.

Konkret gesagt: Die mitgeführten Armbanduhren „ticken“ für die Zugpassagiere schneller (zeigen also eine größere Zeit an) als gleichartige Bahnhofsuhren, an denen der Zug mit Geschwindigkeit v vorbeirauscht. Wenn sich dessen Geschwindigkeit erhöht, wird auch die (i. A. sehr geringe) Dilatation der von der Bahnhofsuhr angezeigten Zeit immer größer, während die vom Zug aus gemessene Zeit (die Eigenzeit) immer gleich bleibt. Im Gegensatz zu dieser Zeitdilatation erscheint ein mit dem Zug mitbewegter Maßstab, dessen Länge aus Sicht der Zugpassagiere den Wert L besitzt, von der Bahnhofsuhr aus gesehen verkürzt (Längenkontraktion, siehe oben). Die Effekte sind allerdings enorm klein: Und zwar ist ein Intervall Δτ der Eigenzeit im Vergleich zur Zeitspanne Δt, die von der Bahnhofsuhr angezeigt wird, nur ganz wenig kleiner (genauer gilt bei konstanter Relativgeschwindigkeit: $\Delta \tau =\Delta t\cdot {\sqrt {1-(v/c)^{2}}},$ wobei $v$ die Zuggeschwindigkeit ist (beispielsweise 80 km/h), c dagegen die extrem viel höhere Lichtgeschwindigkeit (~ 1 Milliarde km/h).

Die Eigenzeit ist im Übrigen die den oben angegebenen Koordinatenwechsel (Lorentztransformation → Lorentzinvariante) bestimmende Invariante.

Eine unmittelbare Folge der Zeitdilatation ist, dass die verstrichene Zeitspanne vom gewählten Weg abhängt. Angenommen, jemand steigt in den Zug und fährt bis zur nächsten Station. Dort steigt er in einen Zug um, der wieder zum Ausgangspunkt zurückfährt. Ein anderer Beobachter hat in der Zwischenzeit dort am Bahnsteig gewartet. Nach der Rückkehr vergleichen sie ihre Uhren. Aus Sicht des am Bahnhof gebliebenen Beobachters hat nun der Reisende sowohl bei der Hinfahrt als auch bei der Rückfahrt eine Zeitdilatation erfahren. Somit geht die Uhr des Reisenden aus Sicht des Wartenden jetzt nach. Aus Sicht des Reisenden erfährt jedoch der Wartende eine Zeitdilatation sowohl auf dem Hinweg wie auch auf dem Rückweg, sodass auf den ersten Blick die Uhr des Wartenden aus Sicht des Reisenden nun nachgehen muss. Dieses Paradoxon heißt Zwillingsparadoxon. Tatsächlich ist die Situation in diesem Fall jedoch nicht symmetrisch, da der Reisende umgestiegen ist, also sein mitbewegtes Bezugssystem gewechselt hat. Im Gegensatz zum Beobachter am Bahnsteig bleibt der Reisende also nicht während der gesamten Reise in einem einzigen Inertialsystem, daher geht die Uhr des Reisenden tatsächlich nach.

Dieses Paradoxon wurde tatsächlich in Experimenten zur Überprüfung der speziellen Relativitätstheorie nachgewiesen. So wurden etwa im Hafele-Keating-Experiment die gemessenen Zeitspannen zweier Atomuhren verglichen, von denen eine in einem Flugzeug die Erde umkreiste, während die zweite Uhr auf dem Start- und Zielflugplatz zurückblieb. Die „zurückgebliebene“ Uhr zeigte eine geringfügige, aber präzise messbare Gang-Erhöhung an.

Relativistische Geschwindigkeitsaddition

Wenn nun im Zug der Schaffner mit konstanter Geschwindigkeit nach vorne läuft (vgl. Einsteins Gedankenexperiment), ist seine Geschwindigkeit für einen Beobachter am Bahnsteig nach der klassischen Mechanik einfach als die Summe der Laufgeschwindigkeit und der Geschwindigkeit des Zuges gegeben. In der Relativitätstheorie liefert eine solche einfache Addition nicht das richtige Ergebnis. Vom Bahnsteig aus betrachtet ist die Zeit, die der Schaffner z. B. von einem Wagen zum nächsten braucht, wegen der Zeitdilatation länger als für den Zugreisenden. Zudem ist der Wagen selbst vom Bahnsteig aus gesehen Lorentz-verkürzt. Hinzu kommt, dass der Schaffner nach vorne läuft, also das Ereignis „Erreichen des nächsten Wagens“ weiter vorne im Zug stattfindet: Aufgrund der Relativität der Gleichzeitigkeit bedeutet dies, dass das Ereignis für den Beobachter am Bahnsteig später stattfindet als für den Zugreisenden. Insgesamt ergeben also alle diese Effekte, dass die Geschwindigkeitsdifferenz des Schaffners zum Zug für den Beobachter am Bahnsteig geringer ist als für den Beobachter im Zug. Mit anderen Worten: Der Schaffner ist vom Bahnsteig aus gesehen langsamer unterwegs, als es die Addition der Geschwindigkeit des Zuges und der Geschwindigkeit des Schaffners vom Zug aus gesehen ergeben würde. Die Formel, mit der man diese Geschwindigkeit berechnet, heißt relativistisches Additionstheorem für Geschwindigkeiten.

Der Extremfall tritt auf, wenn man einen nach vorne laufenden Lichtstrahl betrachtet. In diesem Fall ist der Verlangsamungseffekt so stark, dass der Lichtstrahl auch vom Bahnsteig aus wieder Lichtgeschwindigkeit hat. Die Konstanz der Lichtgeschwindigkeit ist ja die Grundlage der Relativitätstheorie. Dies sorgt auch dafür, dass der Schaffner sich aus Sicht des Beobachters am Bahnsteig immer langsamer als mit Lichtgeschwindigkeit bewegt, sofern seine Laufgeschwindigkeit im Ruhesystem des Zuges kleiner ist als die Lichtgeschwindigkeit: Angenommen der Schaffner hält eine Taschenlampe auf einen Spiegel am Ende des Wagens und läuft langsamer als das Licht. Dann wird vom Zug aus betrachtet der Lichtstrahl reflektiert und trifft den Schaffner, bevor er das Ende des Wagens erreicht. Würde nun seine Geschwindigkeit vom Bahnsteig als Überlichtgeschwindigkeit wahrgenommen, so würde der Schaffner das Ende des Wagens vor dem Lichtstrahl erreichen und damit das Treffen mit dem Lichtstrahl nicht stattfinden. Die Tatsache, dass ein solches Treffen stattfindet, ist jedoch beobachterunabhängig und damit ergibt sich ein Widerspruch. Also liefert die relativistische Addition von zwei Geschwindigkeiten unterhalb der Lichtgeschwindigkeit immer ein Ergebnis unterhalb der Lichtgeschwindigkeit.

Nun kann der Schaffner aber im Zug nicht nur nach vorne laufen, sondern auch nach hinten. In diesem Fall findet das Ereignis „Erreichen des nächsten Wagens“ weiter hinten im Zug statt und somit für den Bahnsteig-Beobachter relativ zum Zugreisenden „verfrüht“, während die anderen Effekte immer noch „verlangsamend“ wirken. Die Effekte heben sich gerade dann auf, wenn der Schaffner mit derselben Geschwindigkeit im Zug nach hinten rennt, wie der Zug fährt: In diesem Fall kommt auch die Relativitätstheorie zu dem Ergebnis, dass der Schaffner relativ zum Bahnsteig ruht. Für höhere Geschwindigkeiten nach hinten sieht der Beobachter am Bahnsteig nun eine höhere Geschwindigkeit, als er nach der klassischen Mechanik erwarten würde. Dies geht wieder bis zum Extremfall des nach hinten gerichteten Lichtstrahls, der wiederum auch vom Bahnsteig aus gesehen exakt mit Lichtgeschwindigkeit unterwegs ist.

Impuls, Masse und Energie

Stoß zweier Kugeln mit Änderung der Bewegungsrichtung um 90°

Im Bahnhof (vgl. Einsteins Gedankenexperiment) gibt es auch einen Spielsalon mit Billardtischen. Auf einem ereignet sich, als der Zug vorbeifährt, gerade Folgendes, aus Sicht des Beobachters am Bahnsteig geschildert: Zwei Billardkugeln, die jeweils dieselbe absolute Geschwindigkeit wie der Zug haben, sich aber senkrecht zum Gleis aufeinander zubewegen, stoßen völlig elastisch zusammen, und zwar so versetzt, dass sie sich nach dem Stoß parallel zum Gleis bewegen, die Rote in Richtung des Zuges (und in dessen Bezugssystem ruhend) die Blaue in Gegenrichtung.

In der klassischen Mechanik ist der Impuls eines Objekts definiert als das Produkt aus Masse und Geschwindigkeit des Objekts. Der Gesamtimpuls, der sich durch einfaches Addieren der Einzelimpulse ergibt, ist eine Erhaltungsgröße. In der Tat ist beim obigen Stoß der so definierte Impuls aus Bahnsteig-Sicht erhalten: Da die Kugeln sich sowohl vor als auch nach dem Stoß mit gegengleicher Geschwindigkeit bewegen, ist der so definierte Impuls vor wie nach dem Stoß null.

Aus dem Zug betrachtet rollen die Kugeln vor dem Stoß schräg aufeinander zu: Parallel zum Gleis haben beide die Geschwindigkeit des Bahnsteiges (da sie sich ja mit dem Bahnsteig mitbewegen), und senkrecht zum Gleis haben sie einander entgegengesetzte Geschwindigkeiten (diese Komponente beruht auf der Bewegung der Kugeln relativ zum Bahnsteig senkrecht zum Zug). Der Gesamtimpuls der beiden Kugeln senkrecht zum Gleis ist also null, parallel zum Gleis ist der Gesamtimpuls zweimal Kugelmasse mal Bahnsteiggeschwindigkeit.

Nach dem Stoß hat nun die rote Kugel die Geschwindigkeit – und damit auch den Impuls – null (aus Bahnsteigsicht ist sie mit Zuggeschwindigkeit in Zugrichtung unterwegs gewesen), somit muss nun die blaue Kugel den gesamten Impuls tragen. Um die Geschwindigkeit der blauen Kugel zu bestimmen, muss jedoch nun die im vorigen Abschnitt betrachtete relativistische Geschwindigkeitsaddition verwendet werden, und – wie oben dargelegt – hat diese Kugel nun eine geringere Geschwindigkeit als das Doppelte der Bahnsteiggeschwindigkeit (= Zuggeschwindigkeit). Damit wird klar, dass die klassische Impulserhaltung nicht mehr gültig ist. Um den Erhaltungssatz wiederherzustellen, wird der relativistische Impuls verwendet, der stärker als linear mit der Geschwindigkeit ansteigt. Aus demselben Grund muss auch die kinetische Energie bei hohen Geschwindigkeiten schneller ansteigen, als sie es nach der klassischen Mechanik tut.

Die Äquivalenz von Masse und Energie besagt, dass die Ruheenergie $E_{\text{Ruhe}}$ jedes Teilchens, Körpers oder physikalischen Systems proportional seiner Masse $m$ ist. Der Faktor, der diese beiden Größen verbindet, ist das Quadrat der Lichtgeschwindigkeit:

E_{\text{Ruhe}}=m\ c^{2}

Weil man an der Masse die Ruheenergie ablesen kann, versteht man, warum bei radioaktivem Zerfall oder Kernspaltung die Tochterteilchen zusammen weniger Masse haben als der Ausgangskern: Ein Teil der anfänglichen Ruheenergie ist in kinetische Energie der Tochterteilchen und gegebenenfalls in andere Strahlung umgewandelt worden.

Die Äquivalenz von Masse und Energie ist experimentell mit hoher Genauigkeit bestätigt:[3]

{\frac {m\,c^{2}}{E_{\text{Ruhe}}}}-1\,\leq \,(1{,}4\pm 4{,}4)\cdot 10^{-7}

Relativistische Masse und Ruhemasse

Ordnet man durch

E(v)=m_{\text{relativistisch}}\ c^{2}

der geschwindigkeitsabhängigen Energie $E(v)$ eines Teilchens oder Körpers in Bewegung rechnerisch eine ebenfalls geschwindigkeitsabhängige Masse $m_{\text{relativistisch}}$ zu, so heißt sie relativistische Masse. Sie ist keine vom Bezugssystem unabhängige feste Eigenschaft des Teilchens, sondern hängt von seiner Geschwindigkeit (bzw. der des Beobachters) ab. Im Ruhesystem stimmt $m_{\text{relativistisch}}$ mit der Masse $m$ überein, die deshalb gelegentlich auch als Ruhemasse oder invariante Masse bezeichnet wird. Bei hinreichend starker Annäherung an die Lichtgeschwindigkeit wird $m_{\text{relativistisch}}$ beliebig groß. Mit der relativistischen Masse schreibt sich der relativistische Impuls wie in Newtons Mechanik als „Masse mal Geschwindigkeit“. Dass der Impuls eines Teilchens unbegrenzt anwachsen kann, während seine Geschwindigkeit durch die Lichtgeschwindigkeit nach oben begrenzt ist, wird in diesem Bild durch die entsprechend zunehmende relativistische Masse bewirkt. Im Bereich relativistischer Geschwindigkeiten reagiert ein Teilchen auf eine Kraft senkrecht zu seiner Flugrichtung so, dass man ihm nach der Newtonschen Mechanik gerade die relativistische Masse zuschreiben müsste. Für eine Kraft in Richtung der Geschwindigkeit müsste man allerdings wieder eine andere Masse nehmen, und für andere Richtungen ist die Beschleunigung noch nicht einmal parallel zur Kraft.

Der Begriff der relativistischen Masse wird daher in der heutigen (2017) Physik aus diesen und anderen Gründen gemieden. Die Masse ist vielmehr wie in Newtons Physik eine Eigenschaft des Teilchens, Körpers oder physikalischen Systems, die unabhängig vom Bezugssystem ist. Damit entfällt auch eine Unterscheidung zwischen „Masse“ und „Ruhemasse“. Beides sind Bezeichnungen für denselben Begriff.

Von Raum und Zeit zur Raumzeit

Angesichts der oben erläuterten relativistischen Effekte stellt sich die Frage, wie diese Effekte zu interpretieren sind. Sieht man die Zeit als vierte Dimension an, kann man zusammen mit den drei Dimensionen des Raumes die vierdimensionale Raumzeit betrachten, die aber nicht den vierdimensionalen Euklidischen Raum $\mathbb {R} ^{4}$ ergibt, sondern den sog. Minkowski-Raum $\mathbb {M} ^{4}.$ Der Unterschied ergibt sich aus einer mathematischen Besonderheit der Metrik (besser: Pseudo-Metrik) des Minkowski-Raumes – sie kann beide Vorzeichen besitzen. Dies ergibt den Unterschied von Drehungen im vierdimensionalen euklidischen Raum $\mathbb {R} ^{4}$ und den unten angegebenen „rhomboedrischen“ Koordinaten-Transformationen der vierdimensionalen Raumzeit. Zugleich ergibt sich so, dass auch in der Relativitätstheorie noch ein Unterschied zwischen raumartig und zeitartig bzw. – bei Zeitartigkeit – zwischen „Vergangenheit“ und „Zukunft“ verbleiben kann, je nach dem Vorzeichen der Metrik des betrachteten Punktes im Minkowski-Raum bzw. nach dem Vorzeichen seiner Zeitkoordinate (siehe auch: Lichtkegel).

Die Bewegung eines Beobachters wird in dieser vierdimensionalen Raumzeit zu einer Kurve (der sog. Weltlinie des Beobachters) und lässt sich in Minkowski-Diagrammen darstellen. Dabei erkennt man, dass der vorliegende Wechsel des Bezugssystems auf jeden Fall (sowohl klassisch-mechanisch als auch relativistisch) mit einem „Kippen“ der Zeitachse einhergeht. Dieses beschreibt die „Relativität der GleichORTigkeit“: Während der Beobachter im Zug feststellt, dass z. B. sein Koffer über ihm im Gepäcknetz die ganze Zeit am selben Ort bleibt, ist für den Beobachter am Bahnsteig klar, dass sich derselbe Koffer mit dem Zug mitbewegt, also gerade nicht am selben Ort bleibt. Was den Minkowski-Raum der Relativitätstheorie von Newtons Raum und Zeit unterscheidet, ist die Tatsache, dass für zueinander bewegte Bezugssysteme auch die GleichZEITigkeit relativ ist, wie oben beschrieben. Dies führt dazu, dass nach der Relativitätstheorie (im Gegensatz zur klassischen Mechanik) zusammen mit der Zeitachse auch die Ortsachse gekippt wird.

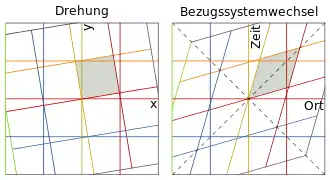
Gegenüberstellung von Drehung (links) und dem im Text beschriebenen „rhomboedrischen“ Bezugssystemwechsel (rechts)

Eine wohlbekannte Bewegung, bei der zwei Koordinatenachsen geändert werden, ist die Drehung im Raum. Das nebenstehende Bild illustriert den Unterschied zwischen der bekannten Drehung und dem angegebenen Bezugssystemwechsel: Während bei Drehungen im Raum beide Achsen in dieselbe Richtung gedreht werden, werden bei einem Bezugssystemwechsel Ortsachse und Zeitachse in entgegengesetzte Richtungen gedreht: Aus dem ursprünglichen Quadrat entsteht ein flächengleicher Rhombus, wobei die Bedingung der Flächengleichheit der Konstanz der Lichtgeschwindigkeit entspricht. Die lange Diagonale (eine Winkelsymmetrale der Achsen, die sog. 1. Mediane) bleibt unverändert. Sie beschreibt aber gerade den Weg des Lichtes, ihr Anstieg ist die Lichtgeschwindigkeit. Die Unveränderlichkeit dieser Diagonalen bei Bezugssystemwechsel bedeutet also gerade, dass die Lichtgeschwindigkeit konstant ist.

Aus diesen Betrachtungen folgt, dass es sinnvoll ist, Raum und Zeit als eine Einheit anzusehen, so wie Länge, Breite und Höhe eine Einheit bilden, nämlich den dreidimensionalen Raum. Die vierdimensionale Einheit aus Raum und Zeit nennt man Raumzeit. Es ist damit nicht mehr möglich, eine ganz bestimmte Richtung unabhängig vom Beobachter als die Zeitrichtung anzugeben, genauso wie es im Raum kein eindeutiges (beobachterunabhängiges) „Vorne“ gibt. So laufen z. B. sowohl die schwarze Zeitachse als auch die gelbe „gedrehte“ Zeitachse in Zeitrichtung. Allerdings ist es – im Unterschied zum normalen Raum – in der Raumzeit nicht möglich, die Zeitrichtung bis zur Raumrichtung zu drehen oder gar die Zeit „umzudrehen“, also Vergangenheit und Zukunft zu vertauschen. Durch die Konstanz der Diagonalen werden die von Diagonalen begrenzten Gebiete stets in sich selbst überführt. Dies entspricht der Flächengleichheit der eingezeichneten Netzwerk-Segmente.

Bei genauerer Betrachtung der Drehung (linkes Bild) sieht man, dass jedes Koordinatenquadrat wieder in ein gleich großes Quadrat überführt wird (das gedrehte Quadrat oben rechts vom Ursprung ist im Bild schraffiert). Zudem ist der Schnittpunkt der gedrehten y-Achse (gelbe Linie) mit dem Schnittpunkt der gedrehten ersten Parallelen der x-Achse (hellbraune Linie) gleich weit entfernt vom Ursprung wie der ungedrehte Schnittpunkt. Der y-Wert dieses Schnittpunktes ist hingegen kleiner als für den ungedrehten Schnittpunkt. Dies führt zum Phänomen der perspektivischen Verkürzung, wenn die Linie aus x-Richtung angeschaut wird.

Betrachtet man nun analog das rechte Bild, so sieht man, dass auch hier das Koordinatenquadrat in eine gleich große Fläche überführt wird, aber die neue Fläche ist kein Quadrat mehr, sondern rhomboedrisch. Das hat die Auswirkung, dass der Schnittpunkt der „gedrehten“ Zeitachse (gelb) mit der nächsten Parallelen der gedrehten Raumachse (hellbraun) höher, also später liegt als im ungedrehten Fall. Nehmen wir nun an, die Raumachsen werden bei jedem Tick einer Uhr „gesetzt“, so sieht man, dass die Uhr im „gedrehten“ Koordinatensystem, also die relativ zum Beobachter bewegte Uhr, anscheinend langsamer geht (zwischen zwei Ticks vergeht mehr Zeit des Beobachters). Aus der Analogie zur Drehung wird ebenfalls klar, dass es sich auch hierbei nur um einen „perspektivischen“ Effekt handelt. Damit erklärt sich ganz zwanglos der scheinbare Widerspruch, dass beide Beobachter die Uhr des jeweils anderen langsamer laufen sehen. Auch die perspektivische Verkürzung wird wechselseitig wahrgenommen, ohne dass das zu Widersprüchen führen würde.

Ein wesentlicher Unterschied des Bezugssystemwechsels zur Drehung ist jedoch, dass für die Variable „Zeit“ statt einer Verkürzung eine Verlängerung (Dehnung: Zeitdilatation) wahrgenommen wird. Dies kann man an obiger Gegenüberstellung gut erkennen: Bei der Drehung im Raum wandert der Schnittpunkt der gelben und der hellbraunen Linie nach unten (perspektivische Verkürzung), beim Bezugssystemwechsel hingegen nach oben.

Effekte

Die genannten Effekte, die nur mit der Lorentztransformation verständlich sind, lassen sich teilweise direkt beobachten. Insbesondere die Zeitdilatation wurde durch viele Experimente bestätigt (siehe z. B. Zeitdilatation bewegter Teilchen). Im Folgenden werden einige Effekte dargestellt, bei denen der Zusammenhang mit Lorentztransformationen nicht so offensichtlich ist.

Aberration

Wenn sich ein Beobachter schneller und schneller bewegt, kommen ihm die seitlichen Lichtstrahlen ähnlich wie Regentropfen mehr und mehr von vorne entgegen. Es ändert sich der Winkel, unter dem ein Lichtstrahl für einen bewegten Beobachter einfällt. Ursprünglich erklärte man dieses Phänomen, die Aberration des Lichts, mit Newtons Korpuskeltheorie des Lichtes genauso wie bei Regentropfen. In der speziellen Relativitätstheorie wird nun die klassische durch die relativistische Geschwindigkeitsaddition ersetzt. Daraus folgt, dass ein bewegter Beobachter nach der Korpuskeltheorie einen anderen Aberrationswinkel als nach der speziellen Relativitätstheorie beobachten und je nach Bewegungsgeschwindigkeit verschiedene Lichtgeschwindigkeiten des einfallenden Lichts messen würde.

Nach der Beobachtung, dass sich Licht wie eine Welle ausbreitet (Undulationstheorie), konnte man die Aberration jedoch nicht mehr verstehen. Bei einer Lichtwelle würden sich in der newtonschen Physik die Wellenfronten bei Bewegung des Beobachters nicht ändern. Erst in der speziellen Relativitätstheorie ändern sich die Wellenfronten aufgrund der Relativität der Gleichzeitigkeit so wie Teilchenbahnen, und Aberration wird verstehbar, ob sie nun bei Wellen oder bei Teilchen auftritt.

Dopplereffekt

Bei Wellen, die sich in einem Trägermedium fortpflanzen, wie den Schallwellen, kommt es bei einer Bewegung der Quelle oder des Empfängers gegenüber dem Trägermedium zu einer Veränderung der gemessenen Frequenz. Dabei ist der Effekt verschieden je nachdem, ob die Quelle oder der Empfänger gegenüber dem Trägermedium bewegt ist. Generell wird die Frequenz größer, wenn sich Quelle und Empfänger aufeinander zubewegen, weil dann vom Empfänger in derselben Zeit mehr Wellenberge wahrgenommen werden. Entsprechend wird die Frequenz kleiner, wenn sich Quelle und Empfänger auseinanderbewegen. Diese Frequenzverschiebung heißt Dopplereffekt. Bei Schallwellen kann der Empfänger schneller sein als die Wellen und ihnen ganz entkommen; entsprechend kann die Quelle ihrem eigenen Signal vorauseilen, was zum Überschallknall führt.

Bei Lichtwellen im Vakuum ist keine Relativbewegung zum Trägermedium messbar, da die Vakuumlichtgeschwindigkeit in allen Inertialsystemen gleich ist. Der Dopplereffekt des Lichts kann also nur von der Relativgeschwindigkeit von Quelle und Empfänger abhängen, das heißt, es gibt keinen Unterschied zwischen Bewegung der Quelle und des Empfängers. Da eine Relativbewegung schneller als mit Vakuumlichtgeschwindigkeit nicht möglich ist, gibt es für Licht im Vakuum kein analoges Phänomen zum Überschallknall. In Medien wie Wasser, in denen die Ausbreitungsgeschwindigkeit des Lichts geringer ist als im Vakuum, gibt es mit dem Tscherenkow-Effekt ein dem Überschallknall ähnliches Phänomen.

Es ist klar, dass die Zeitdilatation einen Einfluss auf die Frequenzen hat, die zwei relativ zueinander bewegte Beobachter messen. Daher tritt beim Licht auch ein Dopplereffekt auf, wenn sich der Beobachter senkrecht zur Richtung bewegt, in der die Quelle liegt. Dieser Effekt heißt transversaler Dopplereffekt. Die Definition des Einfallswinkels hängt aufgrund der Aberration vom Beobachter ab. Daher tritt je nachdem, in welchem Bezugssystem das Licht senkrecht einfällt, eine Frequenzerhöhung (Blauverschiebung) oder -verringerung (Rotverschiebung) auf:

Aus Sicht des Ruhesystems des Empfängers vergeht aufgrund der Zeitdilatation die Zeit im System der Quelle langsamer. Das bedeutet, dass er in seinem System eine niedrigere Frequenz misst als ein Beobachter, der relativ zur Quelle ruht, er misst also eine Rotverschiebung. Der zur Quelle ruhende Beobachter erklärt den Effekt damit, dass sich der Empfänger zum Zeitpunkt des Empfangens nicht senkrecht zur Richtung der Quelle, sondern von der Quelle weg bewegt. Der Lichtstrahl trifft den Empfänger aus seiner Sicht von hinten, womit er die Rotverschiebung erklärt.
Aus Sicht des Ruhesystems der Quelle vergeht die Zeit im Ruhesystem des Empfängers langsamer. Daher misst der Empfänger eine höhere Frequenz, also eine Blauverschiebung, wenn das Licht im Ruhesystem der Quelle senkrecht zur Bewegungsrichtung den Empfänger trifft. Der Empfänger erklärt diese Blauverschiebung wieder anders, denn aus seiner Sicht trifft ihn der Lichtstrahl nicht im rechten Winkel, sondern schräg von vorn. Er wird also die Blauverschiebung durch die Annäherung an die Quelle erklären.

Lorentzkraft

Illustration der Lorentzkraft

Die Relativitätstheorie wird nicht erst bei sehr hohen Geschwindigkeiten relevant. Die Lorentzkraft bietet ein Beispiel dafür, wie sich in der Erklärung bekannter Effekte bereits bei sehr geringen Geschwindigkeiten grundlegende Unterschiede gegenüber der klassischen Physik ergeben können.

Dazu betrachtet man eine einzelne negative elektrische Probeladung in gewissem Abstand neben einem Draht, der insgesamt elektrisch neutral ist, aber aus einem positiv geladenen, starren Grundmaterial (den Atomrümpfen) und vielen negativ geladenen, beweglichen Elektronen besteht. In der Ausgangssituation ruht die Probeladung und im Draht fließt kein Strom. Daher wirkt auf die Probeladung weder eine elektrische noch eine magnetische Kraft. Bewegen sich nun die Probeladung außerhalb und die Elektronen innerhalb des Drahtes mit gleicher Geschwindigkeit längs des Drahtes, fließt im Draht ein Strom. Dieser erzeugt ein Magnetfeld; es übt auf die Probeladung, weil sie sich bewegt, die Lorentzkraft aus, die sie radial zum Draht hinzieht. Dies ist die Beschreibung in dem Bezugssystem, in dem das positive Grundmaterial des Drahtes ruht.

Im Bezugssystem, das mit der negativen Ladung mitbewegt wird, wirkt dieselbe Kraft, muss aber ganz anders erklärt werden. Eine Lorentzkraft kann es nicht sein, denn die Geschwindigkeit der Probeladung ist ja Null. Es bewegt sich aber das positiv geladene Grundmaterial des Drahtes und erscheint nun durch die Lorentzkontraktion verkürzt. Es erhält dadurch eine vergrößerte Ladungsdichte, während die im Draht befindlichen Elektronen in diesem Bezugssystem ruhen und daher dieselbe Ladungsdichte haben wie in der Ausgangssituation. Die gesamte Ladungsdichte im Draht zeigt also einen Überschuss an positiver Ladung. Er übt auf die ruhende negative Probeladung eine elektrostatische Kraft aus, die sie radial zum Draht hinzieht. Dies ist die Beschreibung im mitbewegten Bezugssystem.

Beide Beschreibungen führen zu gleichen Voraussagen über die Kraft, die auf die Probeladung wirkt. Ohne Berücksichtigung der Lorentzkontraktion ließe sich dies nicht erklären; in beiden Bezugssystemen bliebe dann der Draht elektrisch neutral. Zwar würde vom Standpunkt des bewegten Bezugssystems aus das bewegte positive Grundmaterial des Drahtes einen Stromfluss bedeuten, der ein Magnetfeld erzeugt, dieses hätte aber auf die ruhende Probeladung keine Wirkung.

Diese Betrachtung zeigt, dass durch Lorentztransformationen Magnetfelder und elektrische Felder teilweise ineinander umgewandelt werden. Das ermöglicht es, die Lorentzkraft auf elektrostatische Anziehung zurückzuführen. Dieser Effekt hat bereits für kleine Geschwindigkeiten messbare Auswirkungen – die mittlere Elektronengeschwindigkeit in Drahtrichtung ist bei Stromfluss typischerweise unter einem Millimeter pro Sekunde, also sehr viel kleiner als Lichtgeschwindigkeit.

Indirekte Effekte

Viele direkte Effekte sind schon deshalb nicht offensichtlich, weil sie meist erst bei Annäherung an die Lichtgeschwindigkeit auftreten würden. Aber es gibt viele indirekte Effekte, darunter die folgenden:

In der gesamten Chemie ist der Elektronenspin wesentlich, der erst durch die relativistische Quantenmechanik verständlich wird (Dirac-Gleichung).
In der Elementarteilchenphysik muss die Kinematik meistens relativistisch berechnet werden.

Zu den mehr indirekten Bestätigungen gehören auch viele Bestrahlungs- und Diagnoseverfahren der Medizin, die z. B. auf Röntgen- oder Kernspin-Effekten beruhen.
Zu den sog. „ultrarelativistischen“ Effekten gehören die auf der Ausbreitung von elektromagnetischen Wellen beruhenden Verfahren der Funk-, Fernseh- und Telephonie-Technologien.
Auf der Äquivalenz von Masse und Energie beruht u. A. die gesamte Kernenergietechnik.

Alle diese Effekte können als indirekte Bestätigungen der speziellen Relativitätstheorie gewertet werden.

Verhältnis zu anderen Theorien

Klassische Mechanik

Die spezielle Relativitätstheorie tritt an die Stelle der dynamischen Gesetze der klassischen Mechanik. Allerdings sind die Gesetze der klassischen Mechanik über Jahrhunderte immer wieder sehr genau bestätigt worden. Dabei wurden jedoch immer Geschwindigkeiten betrachtet, die sehr viel kleiner waren als die Lichtgeschwindigkeit. Für solche kleinen Geschwindigkeiten sollte die spezielle Relativitätstheorie also dieselben Ergebnisse liefern wie die klassische Mechanik. Das bedeutet, dass die Lorentztransformationen für sehr kleine Geschwindigkeiten die Galilei-Transformationen ergeben müssen. Daraus ergibt sich dann sofort, dass auch der Impuls, die kinetische Energie und alle anderen Größen für kleine Geschwindigkeiten die bekannten klassischen Werte annehmen.

Wenn der Zug in den obigen Gedankenexperimenten sehr viel langsamer fährt als mit Lichtgeschwindigkeit, ist der Unterschied zwischen den Gleichzeitigkeitsbegriffen der Beobachter sehr klein. Das führt dazu, dass auch die anderen relativistischen Effekte so klein werden, dass man sie kaum beobachten kann. Wenn also die Zeitdilatation so klein ist, dass sie unbemerkt bleibt, werden durch die Lorentztransformation anscheinend nur die Raumkoordinaten transformiert. Wenn auch die Längenkontraktion unbemerkt bleibt, bleiben genau die Galilei-Transformationen übrig.

Das veranschaulicht, dass die spezielle Relativitätstheorie für sehr kleine Geschwindigkeiten dieselben Resultate wie die klassische Mechanik liefert. Die Tatsache, dass die Voraussagen einer alten, bewährten Theorie auch in einer neuen Theorie ableitbar sein müssen, wird als Korrespondenzprinzip bezeichnet. Die spezielle Relativitätstheorie erfüllt also das Korrespondenzprinzip bezüglich der klassischen Mechanik. Bei nicht-mechanischen, elektromagnetischen Prozessen ist das nicht immer so, wie durch die Erklärung der Lorentzkraft illustriert wird.

Im Physikunterricht wird oft eine Geschwindigkeit von 0,1c (10 % der Lichtgeschwindigkeit) als Faustregel verwendet; bis zu diesem Wert gelten Berechnungen nach klassischer Physik als akzeptabel, bei höheren Geschwindigkeiten ist relativistisch zu rechnen.[4] Letztlich entscheidet jedoch die konkrete Problemstellung, bei welchen Geschwindigkeiten relativistisch gerechnet werden muss.

Allgemeine Relativitätstheorie

In Raumbereichen, bei denen die Wirkung der Gravitation vernachlässigbar ist (also insbesondere weit entfernt von großen Massen), kann die SRT sämtliche Arten von Bewegungen beschreiben (entgegen einer häufigen Fehlannahme auch beschleunigte Bewegungen).[5] Dagegen tritt bei Berücksichtigung von Gravitationseffekten die allgemeine Relativitätstheorie an die Stelle der speziellen Relativitätstheorie. Insofern muss auch hier ein Korrespondenzprinzip erfüllt sein, da die Vorhersagen der speziellen Relativitätstheorie sehr genau experimentell bestätigt sind.

Im Unterschied zur speziellen Relativitätstheorie ist die Raumzeit in der allgemeinen Relativitätstheorie gekrümmt und die Theorie muss daher streng lokal formuliert werden. Für große Entfernungen können sich deshalb Abweichungen von den Aussagen der speziellen Relativitätstheorie ergeben. Durch die Berücksichtigung der Gravitation ist vor allem in der Nähe von großen Massen, allgemeiner in der Nähe großer Energien, die spezielle Relativitätstheorie nur für kleine Distanzen gültig.

Ein besonders illustrativer Effekt, der die Grenze der Gültigkeit der speziellen Relativitätstheorie zeigt, ist die Shapiro-Verzögerung: Für Licht, das nahe an einem Körper mit großer Masse, wie der Sonne, vorbeigeschickt wird, misst ein Beobachter, der weiter von dem massiven Körper entfernt ist, eine kleinere Geschwindigkeit als die erwartete Vakuumlichtgeschwindigkeit. Ein Beobachter direkt beim Lichtstrahl misst dagegen die „richtige“ Lichtgeschwindigkeit. Offensichtlich gelten also die Gesetze der speziellen Relativitätstheorie, wie die Konstanz der Lichtgeschwindigkeit, nur in kleinen Bereichen. In der allgemeinen Relativitätstheorie wird das dadurch klar, dass die Raumzeit eine sogenannte Lorentzmannigfaltigkeit bzw. ein Riemann-Raum ist, der jedoch an jedem Raumzeitpunkt lokal durch einen Minkowski-Raum – das ist die flache Raumzeit der speziellen Relativitätstheorie – beschrieben werden kann.

Quantentheorie

Im Gegensatz zur allgemeinen Relativitätstheorie, bei der nach wie vor unklar ist, wie sie mit der Quantenphysik zu einer Theorie der Quantengravitation verschmolzen werden kann, gehören speziell-relativistische Quantentheorien zu den Standardwerkzeugen der modernen Physik. Tatsächlich lassen sich viele Versuchsergebnisse gar nicht verstehen, wenn man nicht sowohl die Prinzipien der Quantentheorie als auch das Raum-Zeit-Verständnis der speziellen Relativitätstheorie berücksichtigt.

Bereits im halbklassischen Bohr-Sommerfeldschen Atommodell gelingt es erst bei Einbeziehung der speziellen Relativitätstheorie, die Feinstruktur von atomaren Energieniveaus zu erklären.

Paul Dirac entwickelte eine Wellengleichung, die Dirac-Gleichung, die das Verhalten von Elektronen unter Berücksichtigung der speziellen Relativitätstheorie in der Quantenmechanik beschreibt. Diese Gleichung führt zur Beschreibung des Spins, einer Eigenschaft des Elektrons, die durch die nichtrelativistische Quantenmechanik nur festgestellt, aber nicht erklärt werden kann, und zur Vorhersage des Positrons als Antiteilchen des Elektrons. Auch die Feinstruktur kann wie in den halbklassischen Modellen durch die nichtrelativistische Quantenmechanik nicht erklärt werden.

Allerdings: Gerade die Existenz von Antiteilchen zeigt, dass bei der Vereinigung von spezieller Relativitätstheorie und Quantentheorie nicht einfach eine relativistische Version der üblichen Quantenmechanik herauskommen kann. Stattdessen ist eine Theorie nötig, in der die Teilchenzahl variabel ist – Teilchen können vernichtet und erzeugt werden (einfachstes Beispiel: die Paarbildung von Teilchen und Antiteilchen). Dies leisten die (relativistischen) Quantenfeldtheorien, etwa die Quantenelektrodynamik als speziell-relativistische Theorie der elektromagnetischen Wechselwirkung und die Quantenchromodynamik als Beschreibung der starken Kraft, welche die Bausteine von Atomkernen zusammenhält.

In Gestalt des Standardmodells der Elementarteilchenphysik bilden relativistische Quantenfeldtheorien das Rückgrat der heutigen Physik der kleinsten Teilchen. Die Vorhersagen des Standardmodells lassen sich an Teilchenbeschleunigern mit hoher Präzision testen, und die Vereinigung von spezieller Relativitätstheorie und Quantentheorie gehört damit zu den am strengsten überprüften Theorien der modernen Physik.

Äthertheorien

Die spezielle Relativitätstheorie wird in der Literatur vielfach als Gegentheorie zum Äther aufgefasst. Die meisten Äthertheorien sind mit der speziellen Relativitätstheorie unvereinbar und werden durch die experimentellen Bestätigungen der speziellen Relativitätstheorie widerlegt.

Eine Ausnahme bildet die lorentzsche Äthertheorie, die von Hendrik Antoon Lorentz und Henri Poincaré vor und gleichzeitig mit der speziellen Relativitätstheorie entwickelt worden war. Diese Theorie ist in ihren Vorhersagen identisch mit der speziellen Relativitätstheorie, nimmt jedoch an, dass es ein absolut ruhendes Bezugssystem gibt, welches sich aber durch keine Beobachtung von jedem anderen Bezugssystem unterscheiden lässt. Diese Theorie gilt heute als veraltet, weil das Postulat des unbeobachtbaren Ruhesystems das Sparsamkeitsprinzip verletzt. Außerdem ist noch ungeklärt, ob die lorentzsche Äthertheorie mit der allgemeinen Relativitätstheorie verträglich ist.

Literatur

Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 1905, S. 891–921; Faksimile (PDF; 1,9 MB) digitalisierter Volltext – Quellen, Texte, Werke, Übersetzungen, Medien auf Wikilivres (auch bekannt als Bibliowiki). Zur Elektrodynamik bewegter Körper. Kommentare und Erläuterungen (Wikibooks).
Albert Einstein: Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? In: Annalen der Physik. 18, 1905, S. 639–643; Faksimile (PDF; 203 kB).
Albert Einstein: Über die spezielle und allgemeine Relativitätstheorie. Springer, Berlin, 2001, ISBN 978-3-540-87776-9.[6]
Hermann Bondi: Einsteins Einmaleins. Einführung in die Relativitätstheorie. Fischer, 1974, ISBN 3-436-01827-9.
Max Born: Die Relativitätstheorie Einsteins. Springer, o. J, 2003, ISBN 978-3-642-32357-7.[7]
Jürgen Freund: Spezielle Relativitätstheorie für Studienanfänger. vdf-Hochschulverlag, 2005, ISBN 3-7281-2993-3.
Domenico Giulini: Spezielle Relativitätstheorie. Fischer, 2004, ISBN 3-596-15556-8.
Hubert Goenner: Spezielle Relativitätstheorie und die klassische Feldtheorie. Elsevier – Spektrum Akademischer Verlag, München, 2004, ISBN 3-8274-1434-2.
Johann Rafelski: Spezielle Relativitätstheorie heute. Springer Spektrum, Berlin, 2019, ISBN 978-3-662-59419-3.

Weblinks

Commons: Spezielle Relativitätstheorie – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Spezielle Relativitätstheorie – Lern- und Lehrmaterialien

Interaktive Webseiten mit Animationen zur Kinematik der speziellen Relativitätstheorie.
Einstein für Einsteiger: Spezielle Relativitätstheorie. auf Einstein Online (Max-Planck-Institut für Gravitationsphysik).
Franz Embacher: Systematische Einführung in die spezielle Relativitätstheorie. Universität Wien.
Skripte zur SRT und ART.
Arthur Ruh: Einsteins Relativitätstheorie … relativ einfach erklärt. (PDF; 2,7 MB). Einführung in die SRT, erweitertes Skript eines Vortrages an der Volkshochschule Rapperswil-Jona, Schweiz.
David Eckstein: Epstein erklärt Einstein. Eine Einführung in die SRT und ART basierend auf Epstein-Diagrammen.

Relativistische Effekte

Flug durch Stonehenge bei simulierten relativistischen Geschwindigkeiten.
Fast lichtschnell durch die Stadt. Eine Spritztour durch die Tübinger Altstadt bei simulierter Beinahe-Lichtgeschwindigkeit.

Einzelnachweise und Kommentare

Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 1905, S. 891–921; Faksimile (PDF; 1,9 MB)
G. Saathoff, S. Karpuk, U. Eisenbarth et al.: Improved Test of Time Dilation in Special Relativity In: Phys. Rev. Lett., 91, 2003, 190403, doi:10.1103/PhysRevLett.91.190403 – Überprüfung der Vorhersage der speziellen Relativitätstheorie zur Zeitdilatation mit einer Genauigkeit von 2.2e^-7
Simon Rainville, James K. Thompson, Edmund G. Myers, John M. Brown, Maynard S. Dewey, Ernest G. Kessler, Richard D. Deslattes, Hans G. Börner, Michael Jentschel, Paolo Mutti, David E. Pritchard: World Year of Physics: A direct test of E=mc2. In: Nature. Band 438, Nr. 7071, 22. Dezember 2005, S. 1096–1097, doi:10.1038/4381096a.
Hanno Krieger: Grundlagen der Strahlungsphysik und des Strahlenschutzes. 5. Auflage. Springer 2017, S. 24.
Roger Penrose: The Road to Reality. New York 2005, S. 422.
Über die spezielle und die allgemeine Relativitätstheorie. Springer, Berlin / Heidelberg 2009, ISBN 978-3-540-87776-9, doi:10.1007/978-3-540-87777-6 (springer.com [abgerufen am 13. Juli 2020]).
Max Born: Die Relativitätstheorie Einsteins. Springer, Berlin / Heidelberg 2003, ISBN 978-3-642-32357-7, doi:10.1007/978-3-642-55459-9 (springer.com [abgerufen am 13. Juli 2020]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Ea-1] Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 1905, S. 891–921; Faksimile (PDF; 1,9 MB)

[2] G. Saathoff, S. Karpuk, U. Eisenbarth et al.: Improved Test of Time Dilation in Special Relativity In: Phys. Rev. Lett., 91, 2003, 190403, doi:10.1103/PhysRevLett.91.190403 – Überprüfung der Vorhersage der speziellen Relativitätstheorie zur Zeitdilatation mit einer Genauigkeit von 2.2e^-7

[Rainville_2005-3] Simon Rainville, James K. Thompson, Edmund G. Myers, John M. Brown, Maynard S. Dewey, Ernest G. Kessler, Richard D. Deslattes, Hans G. Börner, Michael Jentschel, Paolo Mutti, David E. Pritchard: World Year of Physics: A direct test of E=mc2. In: Nature. Band 438, Nr. 7071, 22. Dezember 2005, S. 1096–1097, doi:10.1038/4381096a.

[4] Hanno Krieger: Grundlagen der Strahlungsphysik und des Strahlenschutzes. 5. Auflage. Springer 2017, S. 24.

[5] Roger Penrose: The Road to Reality. New York 2005, S. 422.

[6] Über die spezielle und die allgemeine Relativitätstheorie. Springer, Berlin / Heidelberg 2009, ISBN 978-3-540-87776-9, doi:10.1007/978-3-540-87777-6 (springer.com [abgerufen am 13. Juli 2020]).

[7] Max Born: Die Relativitätstheorie Einsteins. Springer, Berlin / Heidelberg 2003, ISBN 978-3-642-32357-7, doi:10.1007/978-3-642-55459-9 (springer.com [abgerufen am 13. Juli 2020]).