Schwarzes Loch

Ein Schwarzes Loch ist ein Objekt, dessen Masse auf ein extrem kleines Volumen konzentriert ist und infolge dieser Kompaktheit in seiner unmittelbaren Umgebung eine so starke Gravitation erzeugt, dass nicht einmal das Licht diesen Bereich verlassen oder durchlaufen kann. Die äußere Grenze dieses Bereiches wird Ereignishorizont genannt. Nichts kann einen Ereignishorizont von innen nach außen überschreiten – keine Information, keine Strahlung und schon gar keine Materie. Dass ein „Weg nach außen“ nicht einmal mehr denkbar ist, beschreibt die allgemeine Relativitätstheorie schlüssig durch eine extreme Krümmung der Raumzeit.

Aus Radioaufnahmen des Event Horizon Telescope berechnete Darstellung, die das supermassereiche Schwarze Loch der Galaxie M87 zeigt. Die schwarze Scheibe in der Bildmitte ist etwa 2,5-mal so groß wie der Ereignishorizont (Schwarzschild-Durchmesser ca. 38·10¹² m) des supermassereichen Schwarzen Lochs im Zentrum.[1]

Simulation eines nichtrotierenden Schwarzen Lochs von 10 Sonnenmassen, wie es aus einer Entfernung von 600 km aussähe. Die Milchstraße im Hintergrund erscheint durch die Gravitation des Schwarzen Lochs verzerrt und doppelt. Die Bildbreite entspricht einem Blickwinkelbereich von etwa 90°.

Es gibt unterschiedliche Klassen von Schwarzen Löchern mit ihren jeweiligen Entstehungsmechanismen. Am einfachsten zu verstehen sind stellare Schwarze Löcher, die entstehen, wenn ein Stern einer bestimmten Größe seinen gesamten nuklearen Brennstoff verbraucht hat und kollabiert. Während die äußeren Hüllen dann in einer Supernova abgestoßen werden, fällt der Kern durch seinen Schweredruck zu einem extrem kompakten Körper zusammen. Für ein hypothetisches Schwarzes Loch von der Masse der Sonne hätte der Ereignishorizont einen Durchmesser von nur etwa sechs Kilometern, das entspricht dem 230.000-sten Teil des jetzigen Sonnendurchmessers. Am anderen Ende des Spektrums gibt es supermassereiche Schwarze Löcher von millionen- bis milliardenfacher Sonnenmasse, die im Zentrum von Galaxien stehen und eine wichtige Rolle in deren Entwicklung spielen.

Außerhalb des Ereignishorizonts verhält sich ein Schwarzes Loch wie ein normaler Massenkörper und kann von anderen Himmelskörpern auf stabilen Bahnen umrundet werden. Der Ereignishorizont erscheint von außen visuell als vollkommen schwarzes und undurchsichtiges Objekt, in dessen Nähe der dahinterliegende Raum wie durch eine optische Linse verzerrt abgebildet wird.

Die Bezeichnung Schwarzes Loch wurde im Jahr 1967 durch John Archibald Wheeler geprägt. Zu jener Zeit galt die Existenz der erst theoretisch beschriebenen Schwarzen Löcher zwar als sehr wahrscheinlich, war aber noch nicht durch Beobachtungen bestätigt. Später wurden zahlreiche Beispiele für Auswirkungen Schwarzer Löcher beobachtet, z. B. ab 1992 die Untersuchungen des supermassereichen Schwarzen Lochs Sagittarius A* im Zentrum der Milchstraße im Infrarotbereich. 2016 wurde die Fusion zweier Schwarzer Löcher über die dabei erzeugten Gravitationswellen durch LIGO beobachtet und 2019 gelang eine radioteleskopische Aufnahme eines Bildes des supermassereichen Schwarzen Lochs M87* im Zentrum der Galaxie M87.

Für ihre Forschungen zu Schwarzen Löchern wurde 2020 den Wissenschaftlern Roger Penrose, Reinhard Genzel und Andrea Ghez der Nobelpreis für Physik zuerkannt.[2]

Forschungsgeschichte

18. Jahrhundert

Schon 1783 spekulierte der britische Naturforscher John Michell über Dunkle Sterne, deren Gravitation ausreicht, um Licht gefangen zu halten. In einem Brief, der von der Royal Society publiziert wurde, schrieb er:

“If the semi-diameter of a sphere of the same density as the Sun were to exceed that of the Sun in the proportion of 500 to 1, a body falling from an infinite height towards it would have acquired at its surface greater velocity than that of light, and consequently supposing light to be attracted by the same force in proportion to its vis inertiae [mass], with other bodies, all light emitted from such a body would be made to return towards it by its own proper gravity. This assumes that light is influenced by gravity in the same way as massive objects.”

„Wenn der Radius einer Kugel von der gleichen Dichte wie die Sonne den der Sonne in einem Verhältnis von 500 zu 1 überstiege, hätte ein Körper, der aus unendlicher Höhe auf sie zu fiele, an ihrer Oberfläche eine höhere Geschwindigkeit als die des Lichts erlangt. Folglich – unter der Annahme, dass Licht von derselben im Verhältnis zu seiner Masse stehenden Kraft angezogen wird wie andere Körper auch – würde alles von einem solchen Körper abgegebene Licht infolge seiner eigenen Gravitation zu ihm zurückkehren. Dies gilt unter der Annahme, dass Licht von der Gravitation in der gleichen Weise beeinflusst wird wie massive Objekte.“

– John Michell[3]

Die Idee schwerer Sterne, von denen korpuskulares Licht nicht entkommen könne, wurde im Jahr 1796 auch von Pierre Simon Laplace in seiner Exposition du Système du Monde beschrieben. Er schuf dafür den Begriff „Dunkler Körper“ (corps obscur). Diese Ideen bewegten sich innerhalb der newtonschen Physik.

Erste Hälfte des 20. Jahrhunderts: Beitrag der allgemeinen Relativitätstheorie

Karl Schwarzschild

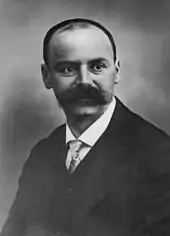
Nachdem Albert Einstein 1915 die Feldgleichungen der allgemeinen Relativitätstheorie aufgestellt hatte, gab der deutsche Astronom Karl Schwarzschild 1916 erstmals eine Metrik an, die Schwarzschild-Metrik, die dem Gravitationsfeld einer punktförmigen Masse entspricht.[4] Die Schwarzschild-Lösung beschreibt Größe und Verhalten eines nichtrotierenden und nicht elektrisch geladenen statischen Schwarzen Lochs mit dem sogenannten Ereignishorizont bei $\textstyle r=2GMc^{-2}$ und einer zentralen Singularität bei $\textstyle r=0$ . Dabei steht $G$ für die Gravitationskonstante, $M$ für die Masse des Schwarzen Lochs und $c$ für die Lichtgeschwindigkeit.

Würde zum Beispiel die Masse der Sonne zu einer Kugel mit nur drei Kilometer Radius komprimiert, dann könnte von deren Oberfläche kein Lichtstrahl nach außen gelangen. Die Masse unserer Erde ( $r\approx 6378\ {\rm {km}}$ ) würde erst bei einem Radius von unter einem Zentimeter ein Schwarzes Loch bilden.

Mit den Kruskal-Szekeres-Koordinaten in den 1950er Jahren konnte mathematisch gezeigt werden, dass ein externer Beobachter, der einen internen Beobachter auf das Schwarze Loch zustürzen sieht, den Eindruck gewinnen muss, dass sich der interne Beobachter dem Ereignishorizont nur asymptotisch annähert, mit trotz regelmäßiger Aussendung immer langsamer eintreffenden Signalen. Dagegen überquert der interne Beobachter selbst den Ereignishorizont schnell, ohne etwas Besonderes zu verspüren, obwohl er von jetzt ab nicht mehr umkehren kann und seine Signale den externen Beobachter nicht mehr erreichen können. Der interne Beobachter wird zudem sehr bald von der Singularität bei $\textstyle r=0$ verschlungen.

In den späten 1920er Jahren zeigte der indische Astrophysiker Subrahmanyan Chandrasekhar, dass für ein astrophysikalisches Objekt ohne Kernreaktionen eine gewisse Grenzmasse, die sogenannte Chandrasekhar-Grenze, existiert. Objekte oberhalb dieser Massengrenze kollabieren zu Neutronensternen oder zu Schwarzen Löchern, aber nicht wie erwartet zu Weißen Zwergen.[5] Chandrasekhars Arbeiten führten zu einer Kontroverse mit dem Astronomen Arthur Eddington. Ersterer war der Überzeugung, dass Sterne oberhalb der Massengrenze zu Objekten kollabieren könnten, deren Gravitation elektromagnetische Strahlen einfangen könnte. Eddington erwartete aber, dass es einen Mechanismus gibt, der den Zusammenbruch verhindern würde. Robert Oppenheimer wies 1939 zusammen mit Robert Serber und George Michael Volkoff anhand von Modellrechnungen nach, dass beim Kollaps eines großen Sterns ein Schwarzes Loch entstehen würde.

Zweite Hälfte des 20. Jahrhunderts: Erweiterte Theorieformung

Der Mathematiker Roy Kerr beschrieb 1963 mit der Kerr-Metrik eine Lösung für ein rotierendes Schwarzes Loch. Bis dahin wurden die Begriffe schwarze Sterne oder gefrorene Sterne verwendet – letzterer als Metapher dafür, dass nach der Theorie aufgrund der gravitativen Zeitdilatation von außen gesehen am Rand des Schwarzen Lochs die Zeit stillzustehen scheint.

Der Begriff „Schwarzes Loch“ ist erstmals 1964 nachgewiesen in einem Bericht der Wissenschaftsjournalistin Ann Ewing über ein Symposion der American Association for the Advancement of Science zu den verschiedenen Endstadien von Sternen. Die Autorin gab Hong-Yee Chiu als Organisator sowie Alastair Cameron, Charles Misner, Volker Weidemann und John Beverly Oke als Redner an, ohne den Urheber des Ausdrucks zu benennen. Etabliert wurde der Begriff 1967, nachdem John Archibald Wheeler bei einer Konferenz einen Ersatz für den langen Ausdruck „gravitationally completely collapsed object“ suchte und den Vorschlag eines unbekannt gebliebenen Zuhörers aufgriff.[6]

Im Jahr 1971 folgte mit der Entdeckung von Cygnus X-1 der erste beobachtbare Kandidat für ein Schwarzes Loch. Auf theoretischem Gebiet stellte Jacob Bekenstein Anfang der 1970er Jahre eine Thermodynamik Schwarzer Löcher auf, indem er der Oberfläche des Ereignishorizonts eine Entropie zuwies (Bekenstein-Hawking-Entropie). Das wurde unterstützt durch die Entdeckung von Stephen Hawking (1974), dass Schwarze Löcher eine Strahlung abgeben, die Hawking-Strahlung. Gleichzeitig wurde damit eine Verbindung von der allgemeinen Relativitätstheorie zur Quantenfeldtheorie geschlagen.

In den 2000er Jahren entwickelte sich ein Trend, nicht direkt der Beobachtung zugängliche Phänomene wie Hawking-Strahlung an Schwarzes-Loch-Analoga experimentell zu untersuchen, wobei es sich nicht um gravitative Systeme handelt, sondern um akustische oder elektromagnetische bzw. optische.

Physikalische Beschreibung

Entstehungsdynamik

Äußere Schwarzschildlösung

Allgemein hat die Masse eines Körpers immer Gravitationskräfte zur Folge. Wenn die Masse auf ein genügend kleines Volumen begrenzt ist, hält sich der Körper von allein zusammen: Die Gravitationskraft führt zu einer Kompression des Körpers. Normalerweise gibt es Gegenkräfte im Inneren, die eine weitere Kompression aufhalten, was zu einem Gleichgewicht zwischen Gravitation und den Gegenkräften führt. Bei den Gegenkräften kann es sich je nach Objektgröße um den Thermodynamischen Druck, um die Abstoßung zwischen den Atomen oder Nukleonen oder um den Fermi-Druck handeln. Die letzte stabile Massengrenze liegt bei etwa 1,5 bis 3,2 Sonnenmassen (Tolman-Oppenheimer-Volkoff-Grenze); bei Objekten, die leichter sind, kann der Entartungsdruck in der in entartetem Zustand vorliegenden Materie einem Gravitationskollaps erfolgreich entgegenwirken.

Wenn eine kritische Dichte überschritten wird, reichen die Gegenkräfte nicht mehr aus, um die Gravitation zu kompensieren. Ein Gravitationskollaps ist die Folge: Die Gravitationskraft steigt schneller an als die durch Abstoßung der Teilchen resultierenden Gegenkräfte. Dadurch beschleunigt sich der Prozess selbst. Die Masse fällt auf ein verschwindendes Volumen zusammen. Die immer weiter ansteigende Gravitation verzerrt lokal den Raum und den Ablauf der Zeit, und zwar derart, dass – von einer hinreichenden Entfernung aus betrachtet – der Kollaps sich verlangsamt, die vom Geschehen abgegebenen Lichtstrahlen immer energieärmer werden, und sich das Volumen nie auf einen einzelnen Punkt zusammenzieht.

Schwarze Löcher können aus massereichen Sternen am Ende ihrer Sternentwicklung entstehen. Sterne der Hauptreihe oberhalb von ca. 40 Sonnenmassen enden über die Zwischenstufen Wolf-Rayet-Stern und Supernova als Schwarzes Loch.[7] Sterne mit Massen zwischen ca. 8 und ca. 25 Sonnenmassen sowie alle massereichen Sterne mit hoher Metallizität enden als Neutronenstern.[8] Liegt ihre Masse zwischen ca. 25 und ca. 40 Sonnenmassen, können Schwarze Löcher durch Rückfall des bei der unvollständigen Supernova abgesprengten Materials entstehen.

Gravitative Auswirkungen

Da die Masse erhalten bleibt, wächst die Dichte des Körpers über alle Grenzen. Solche Körper krümmen die Raumzeit um sich herum so stark, dass man anschaulich von einem Loch im Gefüge des Raums sprechen könnte, man nennt sie jedoch exakter Singularität. Die Singularität wird von einem Raumzeitbereich umgeben, aus dem weder Materie noch Information nach außen gelangen kann. Die Grenze dieses Bereichs ist der sogenannte Ereignishorizont, die Entfernung des Ereignishorizontes von der Singularität ist der sogenannte Schwarzschildradius.

Der Ereignishorizont ist kein physisches Gebilde, er bezeichnet nur einen Ort oder genauer eine Grenzfläche. Ein Beobachter, der durch den Ereignishorizont hindurchfällt, würde daher selbst nichts davon bemerken. Relativistische Effekte (allgemeine Relativitätstheorie) führen aber dazu, dass ein von einem zweiten, weit entfernten Beobachter betrachteter Körper aufgrund der Zeitdilatation unendlich lange braucht, um den Ereignishorizont zu erreichen, wobei er zunehmend in rotverschobenem Licht erscheint und lichtschwächer wird.

Das Gravitationsfeld im Außenraum kugelförmiger, nichtrotierender und elektrisch ungeladener Körper wird durch die Schwarzschild-Metrik beschrieben. Sie gilt nicht nur für Schwarze Löcher, sondern für alle Körper mit diesen Eigenschaften und stellt für Sterne oder Planeten aufgrund deren geringer Rotationsgeschwindigkeit meist eine gute Näherung dar. Die Größe des Schwarzschildradius beträgt für ein Schwarzes Loch von einer Sonnenmasse etwa 2,9 Kilometer, für ein Objekt von einer Erdmasse etwa 9 Millimeter.

Es ist ein weitverbreiteter Irrtum, dass das Gravitationsfeld eines Schwarzen Loches beziehungsweise die von ihm hervorgerufene Krümmung von Raum und Zeit bei üblichen Entfernungen von außerordentlich großer Stärke sei. Da sowohl Schwarze Löcher als auch Sterne von derselben Metrik beschrieben werden, würde sich am Gravitationsfeld im Sonnensystem nichts ändern, wenn man die Sonne durch ein Schwarzes Loch gleicher Masse ersetzte. Abgesehen vom Fehlen des Sonnenlichts wäre lediglich in unmittelbarer Umgebung des Schwarzen Loches (innerhalb etwa des vorherigen Kernradius der Sonne) ein enormer Zuwachs der Gravitationsbeschleunigung festzustellen.

Rotation

Das rotierende Schwarze Loch ist eine allgemeinere Form dieses astrophysikalischen Phänomens. Als rotierende Schwarze Löcher werden solche bezeichnet, die einen Eigendrehimpuls besitzen. Wie alle Schwarzen Löcher verursachen auch sie, bedingt durch ihre enorme Gravitation, eine entsprechend große Veränderung der geometrischen Struktur von Raum und Zeit (siehe Raumzeitkrümmung). Bei einem rotierenden Schwarzen Loch nimmt die Singularität jedoch eine Kreis- oder Ringform an und reißt die Raumzeit um sich herum mit, anstatt sie nur zu krümmen: Der Raum wird in der Drehrichtung des Schwarzen Lochs mitgedreht. Diese Art der Raumzeitkrümmung erscheint nicht bei einem ruhenden Schwarzen Loch, sondern tritt bei rotierenden Schwarzen Löchern sozusagen zusätzlich außerhalb des Ereignishorizonts mit der Form eines an den Polen abgeplatteten Rotationsellipsoides auf. Alle Objekte um ein rotierendes Schwarzes Loch werden mitgedreht, eben weil sich auch die Raumzeit selbst mitdreht.

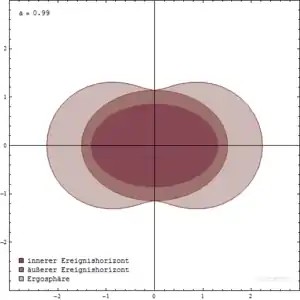
Ergosphäre und Ereignishorizonte eines rotierenden Schwarzen Loches (der innere Ereignishorizont ist nur ein mathematischer Befund; der äußere Ereignishorizont ist der physikalisch vorkommende Ereignishorizont)[9]

Einem relativ zu seiner Umgebung stillstehenden Beobachter käme es so vor, als würde sich das ganze Universum um ihn drehen. Dieser Effekt nimmt mit der Entfernung stark ab. Aber bis zu einem bestimmten Abstand (der sogenannten statischen Grenze), in einem Bereich, der „Ergosphäre“ genannt wird, ist die Drehgeschwindigkeit so hoch, dass alle Objekte (und auch Energie wie Lichtstrahlen) wiederum schneller als Licht sein müssten, um die Drehgeschwindigkeit auszugleichen, also nicht mitzurotieren. Die Winkelgeschwindigkeit eines Teilchens am eigentlichen Ereignishorizont entspricht genau der Rotationsgeschwindigkeit des Schwarzen Loches. Nach außen nimmt die Winkelgeschwindigkeit des Teilchens ab, seine Bahngeschwindigkeit hat dabei aber immer eine Komponente in Drehrichtung des Schwarzen Lochs. Das heißt nicht, dass seine Eigengeschwindigkeit größer als die Lichtgeschwindigkeit ist, sondern dass es innerhalb der Ergosphäre keine nicht mitrotierenden Teilchen geben kann. Dieses Frame-Dragging ist ein Extremfall des seit 1918 bekannten Lense-Thirring-Effekts. Eine Besonderheit der Ergosphäre ist, dass die kinetische Energie in diesem Bereich aus Sicht eines äußeren Beobachters negativ sein kann. Ein Teilchen, das sich in der Ergosphäre befindet, kann deshalb so in zwei Teilchen zerfallen, dass die kinetische Energie eines der beiden größer ist als die des ursprünglichen Teilchens. Das betreffende Teilchen kann die Ergosphäre verlassen, während sein Komplement mit negativer kinetischer Energie (ohne weitere Wechselwirkung) notwendig und in endlicher Eigenzeit den Ereignishorizont überschreitet. Die scheinbar aus dem Nichts generierte Energie wird der Rotationsenergie des Schwarzen Lochs entzogen. Dieser Mechanismus zur Energiegewinnung wurde zuerst von Roger Penrose vorgeschlagen.

Die Ausdehnung der Ergosphäre ist vom Polarwinkel (entspricht dem Komplementärwinkel der geographischen Breite auf der Erde) abhängig: An den Polen des rotierenden Schwarzen Lochs fällt die statische Grenze mit dem Ereignishorizont zusammen, in der Äquatorregion reicht sie bis in eine vom Drehimpuls des Schwarzen Lochs abhängige Entfernung von maximal dem doppelten Schwarzschildradius. Der Drehimpuls eines Schwarzen Lochs ist dabei, wie unten beschrieben wird, begrenzt.

Einige Beobachtungen, beispielsweise von extrem schnellen Materiestrahlen (Jets), die das Gebiet außerhalb des Ereignishorizonts senkrecht zur Akkretionsscheibe verlassen, werden durch Effekte beschrieben, die nur innerhalb einer Ergosphäre oder bei Vorhandensein derselben auftreten können. Aus allgemeinen Überlegungen zur Drehimpulserhaltung kann man schließen, dass alle Schwarzen Löcher rotieren, zumindest zum Zeitpunkt ihrer Entstehung. Aber natürlich zeigen nur sehr schnell rotierende Schwarze Löcher starke Auswirkungen der als Frame-Dragging bekannten Phänomene. Andererseits verdrillt jede rotierende Masse, unabhängig vom Auftreten eines Ereignishorizonts, also auch der Planet Erde, die umgebende Raumzeit. Diese Effekte bei der Erde sollten durch Messungen zum Beispiel mit Hilfe der LAGEOS-Satelliten quantifiziert werden. Erste Ergebnisse aus dem Jahr 1997 lagen noch so dicht am Bereich der Messungenauigkeit, dass sie kontrovers diskutiert wurden, erst eine Wiederholung der Messung im Jahr 2004 mit dem Satelliten Gravity Probe B bestätigte den Sachverhalt.[10]

Theoretische Betrachtungen

Mathematische Beschreibung

Ein Schwarzes Loch lässt sich durch lediglich drei physikalische Kenngrößen vollständig beschreiben (sogenannte Haarlosigkeit Schwarzer Löcher): Masse, Drehimpuls und elektrische Ladung. Die Multipolmomente entfallen. Es gibt also folgende Klassen:

Schwarze Löcher, die keine elektrische Ladung tragen ( $Q=0$ ) und nicht rotieren ( $L=0$ ), werden durch die Schwarzschild-Metrik beschrieben.
Schwarze Löcher, die keine elektrische Ladung tragen ( $Q=0$ ) und rotieren ( $L\neq 0$ ), werden durch die Kerr-Metrik beschrieben.
Schwarze Löcher, die elektrisch geladen sind ( $Q\neq 0$ ) und nicht rotieren ( $L=0$ ), werden durch die Reissner-Nordström-Metrik beschrieben.
Schwarze Löcher, die elektrisch geladen sind ( $Q\neq 0$ ) und rotieren ( $L\neq 0$ ), werden durch die Kerr-Newman-Metrik beschrieben.

Schwarze Löcher in der allgemeinen Relativitätstheorie

Formell ergibt sich ein Schwarzes Loch aus einer speziellen Vakuumlösung der allgemeinen Relativitätstheorie, der sogenannten Schwarzschild-Lösung (nach Karl Schwarzschild, der diese Lösung als erster fand), bzw. für rotierende und elektrisch geladene Schwarze Löcher aus der Kerr-Newman-Lösung. Eine „Vakuumlösung“ ist eine Lösung der Vakuumfeldgleichungen – also etwa im Außenraum um einen Stern herum, wo sich näherungsweise keine Materie aufhält und damit der Energie-Impuls-Tensor verschwindet. Im Innern des Schwarzen Lochs bildet sich, wie Stephen Hawking und Roger Penrose gezeigt haben (Singularitäten-Theorem), im Rahmen der Beschreibung durch die klassische allgemeine Relativätstheorie eine Singularität, ein Punkt mit unendlich hoher Raumkrümmung. Allerdings ist hier der Gültigkeitsbereich der allgemeinen Relativitätstheorie überschritten und zur Beschreibung dieses Ortes eine Theorie der Quantengravitation notwendig.

Die Grenze, ab der keine Information mehr zu einem im Unendlichen befindlichen Beobachter gelangen kann, heißt Ereignishorizont. Da ein nichtrotierendes Schwarzes Loch von außen gesehen kugelförmig ist, hat der Ereignishorizont die Form einer Kugeloberfläche. Der Radius dieser Kugeloberfläche ist der Schwarzschildradius. Schwarze Löcher können bei gegebener Masse weder eine beliebig große Ladung noch einen beliebig großen Drehimpuls besitzen. Setzt man nämlich in die entsprechenden Lösungen der allgemeinen Relativitätstheorie eine zu hohe Ladung und/oder einen zu hohen Drehimpuls ein, so ergibt sich statt eines Schwarzen Loches eine sogenannte nackte Singularität: Es bildet sich zwar eine zentrale Singularität aus, jedoch ist diese nicht von einem Ereignishorizont umgeben: Man kann sich vorstellen, dass durch die Drehung der Raumzeit die einfallende Materie so stark beschleunigt würde (Zentrifugalkraft), dass sie die Gravitation wieder aufhebt. Im Ergebnis würde es somit keinen Ereignishorizont geben, da die Materie wieder entkommen könnte. Allerdings kann man zeigen, dass aus einem normalen Schwarzen Loch durch Zufuhr von Ladung oder Drehimpuls keine nackte Singularität entstehen kann, denn die gleichzeitig zugeführte Energie würde seine Masse ausreichend erhöhen, sodass also stets verhindert wird, dass aus dem gewöhnlichen Schwarzen Loch eines mit einer nackten Singularität entsteht. Roger Penrose nannte dies Kosmische Zensur, der Beweis der Nichtexistenz nackter Singularitäten innerhalb der allgemeinen Relativitätstheorie ist aber offen.

Der Ereignishorizont wird bei Sternen, die zu nicht rotierenden Schwarzen Löchern kollabierten, von Lichtstrahlen begrenzt (der sogenannten Photonensphäre). Diese Lichtstrahlen sind die letzten, die noch nicht von der Gravitation des Schwarzen Loches angezogen wurden. Im Falle von rotierenden Schwarzen Löchern (siehe oben) gibt es nicht nur einen Radius, auf dem Lichtstrahlen die Singularität umkreisen können, sondern unendlich viele innerhalb der Ergosphäre. Nahe der Singularität, also deutlich innerhalb des Schwarzschildradius, ist die Verzerrung der Raumzeit so stark, dass für ein hineinfallendes Objekt auch der Empfang von Nachrichten sich auf einen schrumpfenden Horizont beschränkt. Dieses nur theoretisch zugängliche Phänomen wird asymptotisches Schweigen genannt.

Die „Hauptsätze der Schwarzloch-Dynamik“

Für Schwarze Löcher folgen aus der allgemeinen Relativitätstheorie Gesetze, die auffallend jenen der Thermodynamik gleichen. Schwarze Löcher verhalten sich ähnlich wie ein Schwarzer Strahler, sie haben also eine Temperatur. Es gelten im Einzelnen die folgenden Gesetze:

Der Erste Hauptsatz der „Schwarzloch-Dynamik“ ist, wie in der gewöhnlichen Thermodynamik, der Energieerhaltungssatz, jedoch unter Berücksichtigung der relativistischen Energie-Masse-Äquivalenz. Zusätzlich gelten die anderen Erhaltungssätze der Mechanik und Elektrodynamik: Neben der Energie bleiben Impuls, Drehimpuls und Ladung erhalten.
Der Zweite Hauptsatz der „Schwarzloch-Dynamik“ – von Stephen W. Hawking postuliert – besagt, dass die Summe der Flächen der Ereignishorizonte niemals abnehmen kann, egal was mit den Schwarzen Löchern passiert. Dies gilt nicht nur, wenn Materie in das Schwarze Loch fällt (was dessen Masse – und damit dessen Ereignishorizont – vergrößert), sondern auch für die Verschmelzung zweier Schwarzer Löcher und für jeden anderen denkbaren Prozess. Dies entspricht dem Zweiten Hauptsatz der Thermodynamik, wobei die Fläche des Ereignishorizonts die Rolle der Entropie übernimmt. Die Bekenstein-Hawking-Entropie des Schwarzen Lochs ist $S_{SL}={\frac {Ak_{\mathrm {B} }c^{3}}{4\hbar G}}$ (Erklärung der Formelzeichen: siehe unten). Schwarze Löcher haben die höchste Entropie aller bekannten physikalischen Systeme gleicher Masse.

Hawking-Strahlung

Quantentheoretische Überlegungen zeigen, dass jedes Schwarze Loch auch Strahlung abgibt. Dies scheint im Widerspruch zu der Aussage zu stehen, dass nichts das Schwarze Loch verlassen kann. Jedoch lässt sich der Vorgang als Produktion von Teilchen/Antiteilchen-Paaren nahe am Schwarzschildradius deuten, bei dem eines der Teilchen ins Zentrum des Schwarzen Lochs fällt, während das andere in die Umgebung entkommt. Auf diese Weise kann ein Schwarzes Loch Teilchen abgeben, ohne dass etwas den Ereignishorizont von innen nach außen überschreitet. Die Energie für diesen Hawking-Strahlung genannten Prozess stammt aus dem Gravitationspotential des Schwarzen Lochs. Das heißt, es verliert durch die Strahlung an Masse.

Von außen betrachtet sieht es also so aus, als würde das Schwarze Loch „verdampfen“ und somit langsam kleiner werden, je kleiner, desto schneller. Wenn es beim Urknall sehr kleine Schwarze Löcher gab, dann wären sie daher in der Zwischenzeit vollständig verdampft. Die dabei entstehende Strahlung wäre sehr charakteristisch und könnte als Nachweis solcher Löcher dienen. Diese Strahlung wurde jedoch bisher nicht gefunden. Daraus ergibt sich eine Obergrenze für die Anzahl der beim Urknall entstandenen kleinen Schwarzen Löcher.

Aus Sternen der Hauptreihe entstandene Schwarze Löcher geben nur sehr wenig Hawking-Strahlung ab, sie verdampfen auf einer Zeitskala, die das Alter des Universums um dutzende Größenordnungen übersteigt. Momentan wachsen sie allein schon durch Absorption der Hintergrundstrahlung.

Entropie und Temperatur

Hawking erkannte 1974 nach Vorarbeiten des israelischen Physikers Jacob Bekenstein, dass Schwarze Löcher eine formale Entropie und eine Temperatur $T$ haben. Die formale Entropie $S_{SL}$ eines Schwarzen Lochs ist proportional zur Oberfläche $A$ seines Horizonts und sonst nur von Naturkonstanten abhängig. Die Temperatur entspricht dem thermischen Energiespektrum der Hawking-Strahlung und ist umgekehrt proportional zur Masse des Schwarzen Lochs:

S_{\mathrm {SL} }={\frac {Ak_{\mathrm {B} }c^{3}}{4\hbar G}}

oder

S_{\mathrm {SL} }/A=1{,}321\cdot 10^{46}\,\mathrm {J} /\mathrm {m} ^{2}\mathrm {K}

T={\frac {\hbar c^{3}}{8\pi k_{\mathrm {B} }GM}}

oder

T\cdot r_{s}={\frac {\hbar c}{4\pi k_{\mathrm {B} }}}=0{,}182223\,\mathrm {mm\,K}

Dabei ist $\hbar =h/(2\pi )$ das reduzierte Plancksche Wirkungsquantum, $c$ die Lichtgeschwindigkeit, $\pi$ die Kreiszahl Pi, $k_{\mathrm {B} }$ die Boltzmannkonstante, $G$ die Gravitationskonstante, $M$ die Masse und $r_{s}=2MG/c^{2}$ der Schwarzschildradius.[11]

Aus der Gleichung lässt sich berechnen, dass ein Schwarzes Loch mit einer Masse, die 2,4 % der Erdmasse entspricht, so heiß wie die kosmische Hintergrundstrahlung (2,725 K) wäre, also das gleiche Spektrum hätte.

Lebensdauer

Da ein Schwarzes Loch stetig Energie in Form von Hawking-Strahlung verliert, wird es nach einer bestimmten Zeitspanne $\Delta t$ vollständig zerstrahlt sein, sofern es während dieser Zeitspanne keine neue Masse aufnehmen kann. Diese Zeitspanne berechnet sich durch

\Delta t={\frac {M^{3}}{3\Lambda _{t}}},

wobei $M$ die Masse des Schwarzen Loches zu Beginn der Zeitspanne und $\Lambda _{t}\approx 4\cdot 10^{15}\ {\frac {\mathrm {kg} ^{3}}{\mathrm {s} }}$ eine Konstante ist.

Das No-Hair-Theorem und das Informationsparadoxon Schwarzer Löcher

Ein Eindeutigkeits-Theorem von Werner Israel besagt, dass ein Schwarzes Loch vollständig durch Masse (siehe Schwarzschild-Metrik), elektrische Ladung (siehe Reissner-Nordström-Metrik) und Drehimpuls (siehe Kerr-Metrik) charakterisiert ist. Das veranlasste John Archibald Wheeler zur Aussage „Schwarze Löcher haben keine Haare“. Man spricht deshalb vom No-Hair-Theorem, Keine-Haare-Theorem oder Glatzensatz. Weitere Informationen aus dem Inneren seien nicht zu erhalten, auch nicht durch die Hawking-Strahlung, da sie rein thermisch sei.

Das No-Hair-Theorem legt nahe, dass Schwarze Löcher einen Verlust an Information bewirken, da die bei der Auflösung entstehende Hawking-Strahlung keine Information über die Entstehungsgeschichte des Schwarzen Lochs enthält. Das Verschwinden von Informationen widerspricht einem Grundprinzip der Quantenmechanik, dem Postulat der Unitarität der Zeitentwicklung. Das Problem wird auch als Informationsparadoxon Schwarzer Löcher bezeichnet.

Prominente Vertreter dieser Sicht waren Kip Thorne und lange Zeit auch Stephen Hawking. Stephen Hawking änderte jedoch seine Meinung und erklärte auf der 17. International Conference on General Relativity and Gravitation (18.–23. Juli 2004 in Dublin), dass Schwarze Löcher doch Haare haben könnten. Weiterhin nehmen unter anderem Roger Penrose, John Preskill und Juan Maldacena an, dass zumindest gewisse Informationen zusätzlich nach außen dringen könnten. Auch in seinem Buch Das Universum in der Nussschale äußert Stephen Hawking die Annahme, dass Schwarze Löcher bei ihrer Auflösung die gesammelte Information wieder abgäben. Das Informationsparadoxon ist von Joseph Polchinski im Feuerwand-Paradoxon verschärft worden. 2013 schlugen Juan Maldacena und Leonard Susskind eine Lösung durch die Äquivalenz von Quantenverschränkung und Wurmlöchern vor (ER-EPR-Vermutung), weiter ausgebaut durch einen expliziten Vorschlag solcher durchquerbarer Wurmlöcher durch Ping Gao, Daniel Louis Jafferis und Aron C. Wall (siehe Wurmloch). Das Gebiet ist umstritten und auch Hawking kam darauf in einer seiner letzten Veröffentlichungen zurück.

Ein neuerer Ansatz schlägt vor, das No-Hair-Theorem anhand der Präzession der Bahnellipsen zweier eng um Sagittarius A* umlaufender Sterne zu testen. Wenn das No-Hair-Theorem zutrifft, dann sollte das Verhältnis der beiden Präzessionsraten nur vom Drehimpuls des vermuteten Schwarzen Lochs Sagittarius A* abhängen. Sollte sich herausstellen, dass das Verhältnis der Präzessionsraten komplizierteren Beziehungen gehorcht, so wäre das No-Hair-Theorem widerlegt.[12][13]

Entstehung

Zwei Wege der Entstehung binärer Schwarzer Löcher werden unterschieden. Zum einen kann sie herrühren aus zwei stark wechselwirkenden Galaxien, wenn diese kollidiert sind und offenbar Swing-by-Vorgänge eine Rolle spielen.[14] Als Beispiel einer vorausgegangenen Kollision wird vermutet, dass das supermassereiche Schwarze Loch im Zentrum von M87 durch Verschmelzung entstanden ist.

Zum anderen kann ein wechselwirkender Doppelstern der Ausgangspunkt sein, wenn beide Sterne sehr massereich sind. Nach einem Wind Roche-Lobe Overflow entsteht normalerweise ein Schwarzes Loch plus ein weißer Zwerg. Alternativ kann der Overflow aber untypisch verlaufen und zwischenzeitlich eine gemeinsame Hülle entstehen, sodass sich letztlich zwei Schwarze Löcher bilden.[15]

Verschmelzen

Wenn ein Schwarzes-Loch-Paar entstanden ist, kann es nach einer Phase des Umkreisens zu einem einzigen Schwarzen Loch verschmelzen. Im 300 Millionen Lichtjahre entfernten Galaxienhaufen Abell 400 hat man Hinweise auf die bevorstehende Verschmelzung zweier Schwarzer Löcher gefunden.[16] 2015 wurde erstmals eine solche Kollision nachgewiesen, als vorhersagegemäß im letzten Sekundenbruchteil vor der Verschmelzung das Ausmaß der Beschleunigung bei gleichzeitiger Abgabe von Materie bzw. Energie derartig groß war, dass die so erzeugte Gravitationswelle in den LIGO-Observatorien gemessen werden konnte.

Klasseneinteilung

Klasseneinteilung Schwarzer Löcher
Klasse	Masse	Größe (Schwarzschildradius)
Supermassereiches Schwarzes Loch	≈ 10⁵–10¹⁰ M_☉	≈ 0,001–200 AE
Mittelschweres Schwarzes Loch	≈ 1000 M_☉	≈ 3000 km
Stellares Schwarzes Loch	≈ 10 M_☉	≈ 30 km
Primordiales Schwarzes Loch	bis zu ≈ M_Mond	bis zu ≈ 0,1 mm

Schwarze Löcher werden nach der Entstehungsweise und aufgrund ihrer Masse in nebenstehend gezeigte Klassen verteilt, auf die im Folgenden eingegangen wird:

Supermassereiche Schwarze Löcher

Sgr A* und IRS 13 im Zentrum der Milchstraße

Supermassereiche (supermassive) Schwarze Löcher (englisch supermassive black hole, SMBH) können die millionen- bis milliardenfache Sonnenmasse (M_☉) haben. Sie befinden sich in den Zentren heller elliptischer Galaxien und im Bulge der meisten oder sogar aller Spiralgalaxien. Wie sie entstanden sind und wie ihre Entstehung mit der Entwicklung der Galaxien zusammenhängt, ist Gegenstand aktueller Forschung.

So ist die starke Radioquelle Sagittarius A* (kurz Sgr A*) im Zentrum der Milchstraße ein supermassereiches Schwarzes Loch von 4,3 Millionen Sonnenmassen.[17] Vor wenigen Jahren lag die Massenabschätzung, die auf der Beobachtung von Gaswolken (z. B. der sogenannten Mini-Spirale) fußte, noch bei etwa 2,7 Mio. Sonnenmassen. Dank verbesserter Auflösung und Empfindlichkeit der Teleskope konnte die Masse für das Schwarze Loch im Zentrum der Galaxis genauer angegeben werden, indem die Bahnkurven beispielsweise von S0-102 oder S0-2 analysiert wurden.

Natarajan und Treister[18] haben ein Modell entwickelt, das eine obere Massengrenze in der Größenordnung von 10 Milliarden Sonnenmassen vorhersagt. Die Begründung liegt – anschaulich erklärt – darin, dass die hineinstürzende Materie durch die Gravitationskraft eines solchen supermassereichen Schwarzen Lochs derart beschleunigt wird, dass sich ein stabiler Orbit außerhalb des Schwarzschild-Radius ergibt. Zusätzlich wirken die elektromagnetische Strahlung und die „Materiewinde“, die von der Materie in der Akkretionsscheibe ausgestrahlt werden, als Widerstand gegen weiter einfallende Materie, sodass sich letztlich ein Gleichgewicht zwischen einfallender und abgestoßener Materie einstellt (siehe Eddington-Grenze).

Ein ungelöstes Rätsel ist die Entstehung supermassereicher Schwarzer Löcher im frühen Universum. Es ist bekannt, dass schon 700 Millionen Jahre nach dem Urknall supermassereiche Löcher von rund 2 Milliarden Sonnenmassen existierten (ULAS J1120+0641).[19] Auch das zum Stand Dezember 2017 entfernteste bekannte Objekt ULAS J1342+0928, weniger als 690 Millionen Jahre nach dem Urknall, ist bereits ein supermassereiches Schwarzes Loch.[20] Die meisten Wissenschaftler stimmen darin überein, dass sie aus kleineren Schwarzen Löchern entstanden, wobei ein Lager diese „Saat“ in Schwarzen Löchern von maximal einigen hundert Sonnenmassen sieht, das andere in solchen von tausenden bis zehntausenden Sonnenmassen.[21] Die Ersteren sind leichter herzustellen, müssen aber einen Mechanismus schnellen Wachstums besitzen, der die Eddington-Grenze umgeht. Beim zweiten Fall starten die Schwarzen Löcher mit einer größeren Anfangsmasse und können mehr Masse aus Gaswolken der Umgebung aufnehmen, bevor sie die Eddington-Grenze erreichen, es bedarf aber einer Theorie, die deren Existenz natürlich erklärt. N. Yoshida und Kollegen veröffentlichten 2017 eine Simulation des frühen Universums, in dem supermassereiche Sterne von rund 34.000 Sonnenmassen durch die Wechselwirkung sehr überschallschneller Gaswinde und der Dynamik von Klumpen dunkler Materie, die dann zu einem Schwarzen Loch kollabieren, entstehen.[22] In anderen Szenarien verhindert das intensive UV-Licht junger Sterne benachbarter Galaxien die Sternbildung in einer Gaswolke, bis sie direkt zu einem Schwarzen Loch von rund 100.000 Sonnenmassen kollabiert.[23] Mehr Aufschlüsse über Sterne und Gaswolken im frühen Universum erhofft man sich durch das James Webb Space Telescope.

2008 hat ein schweizerisches Team der Eidgenössischen Technischen Hochschule Lausanne (EPFL) um Alexander Eigenbrod ein energiereiches Ringgebilde um einen 10 Milliarden Lichtjahre entfernten Quasar, das Einsteinkreuz im Sternbild Pegasus, am VLT beobachtet und damit die Theorie der supermassereichen Löcher sehr gut bestätigt.[24]

Das größte bekannte Schwarze Loch (Stand Januar 2021) ist TON 618 (Quasar) mit schätzungsweise 66 bis 70 Milliarden Sonnenmassen, danach das zentrale Schwarze Loch der Galaxie IC 1101 mit ca. 40 Milliarden Sonnenmassen.[25] Ein weiteres Beispiel von geschätzten 21 Milliarden Sonnenmassen befindet sich im Zentrum der Galaxie NGC 4889 (2011).[26] Mit einem supermassereichen Schwarzen Loch von etwa 20 Milliarden Sonnenmassen[27] gehört der Quasar APM 08279+5255 (ca. 12 Milliarden Lichtjahre entfernt), um den 2011 enorme Mengen an Wasserdampf entdeckt wurden,[28] ebenfalls zu den massereichsten bisher bekannten Kandidaten.

Im Zentrum der relativ nahe gelegenen Galaxie M87 (ca. 55 Millionen Lichtjahre entfernt) wurde ein Schwarzes Loch mit einer Masse von 6,6 Milliarden Sonnenmassen nachgewiesen.[29][30]

Supermassereiche Schwarze Löcher wurden auch in (ultrakompakten) Zwerggalaxien gefunden (zuerst 2014 in M60-UCD 1),[31][32] was darauf hinweist, dass diese als „normale“ Galaxien entstanden, denen durch Kollisionen mit größeren Galaxien ein Großteil der Sterne entrissen wurde.

Im September 2017 wurde die Entdeckung eines doppelten supermassereichen Schwarzen Loches veröffentlicht, das mit Hilfe der Very Long Baseline Interferometry (VLBI) beobachtet werden konnte. Hierbei handelt es sich um zwei einander im Abstand von 1,1 Lichtjahren umkreisende Schwarze Löcher mit einer Gesamtmasse von 36 Millionen Sonnenmassen in der 380 Millionen Lichtjahre entfernten Spiralgalaxie NGC 7674.[33]

2015 wurde unter Mitwirkung von NuStAR und XMM-Newton entdeckt, dass supermassereiche Schwarze Löcher „Plasma-Winde“ (Gase hochenergetischer und hochionisierter Atome) in sphärisch symmetrischer Form abstrahlen und dass diese stark genug sind, Sternbildung in großen Bereichen der Wirtsgalaxie zu verhindern.[34] Durch die Kugelsymmetrie unterscheiden sie sich deutlich von Jets. 2017 wurde am Keck-Observatorium nachgewiesen, dass die Winde von Schwarzen Löchern (in diesem Fall im 9,3 Milliarden Lichtjahre entfernten Quasar 3C 298) sogar die Fähigkeit haben, die gesamte Wirtsgalaxie aktiv zu formen.[35][36][37] Die Galaxie hat nur ein Hundertstel der Masse, die aus der normalen Relation zwischen der Masse supermassereicher Schwarzer Löcher und ihrer Wirtsgalaxien zu erwarten wäre.

Mittelschwere Schwarze Löcher

Mittelschwere Schwarze Löcher (englisch intermediate-mass black hole, IMBH) von einigen hundert bis wenigen tausend Sonnenmassen entstehen möglicherweise infolge von Sternenkollisionen und -verschmelzungen. Anfang 2004 veröffentlichten Forscher Ergebnisse einer Untersuchung von Nachbargalaxien mit dem Weltraumteleskop Chandra, in der sie Hinweise auf mittelschwere Schwarze Löcher in sogenannten ultrahellen Röntgenquellen (englisch ultra-luminous X ray source, ULX) fanden. Danach gab es allerdings aufgrund von Beobachtungen mit dem VLT und dem Subaru-Teleskop starke Zweifel daran, dass ULX mittelschwere Schwarze Löcher sind.[38]

Neue Kandidaten sind die Zentren der Kugelsternhaufen Omega Centauri in der Milchstraße und Mayall II in der Andromeda-Galaxie,[39] sowie in der Spiralgalaxie Messier 82 und in einer Zwerg-Seyfert-Galaxie.[40]

Stellare Schwarze Löcher

Stellare Schwarze Löcher (englisch stellar black hole, SBH) stellen den Endzustand der Entwicklung massereicher Sterne dar. Sterne, deren Anfangsmasse kleiner als drei Sonnenmassen ist, können nicht zu einem Schwarzen Loch werden. Sie beenden ihr Leben als vergleichsweise unspektakulär auskühlender Sternenrest (Weißer Zwerg/Neutronenstern). Sterne, deren Anfangsmasse drei Sonnenmassen übersteigt (etwa Blaue Riesen), durchlaufen am Ende ihres Lebens die höheren Stufen der Nukleosynthese bis zum Siliciumbrennen. Sie explodieren in einer Kernkollaps-Supernova, wobei der übrigbleibende Sternenrest zu einem Schwarzen Loch kollabiert, sofern er noch mehr als 2,5 Sonnenmassen besitzt (Tolman-Oppenheimer-Volkoff-Grenze). Ansonsten können Sterne bis zur 15-fachen Sonnenmasse – abhängig davon, wie viel Masse sie als Supernova verlieren – auch als Neutronenstern enden, wenn die verbleibende Masse zwischen 1,5 und 2,5 Sonnenmassen liegt. Neutronensterne können sich – beispielsweise als kompakter Begleiter in einem Röntgendoppelstern – durch die Akkretion weiterer Materie noch zu Schwarzen Löchern entwickeln.

Durch die Beobachtung von Gravitationswellen konnte im September 2015 die Verschmelzung zweier stellarer Schwarzer Löcher mit etwa 36 und 29 Sonnenmassen beobachtet werden. Das resultierende Schwarze Loch hat eine Masse von etwa 62 Sonnenmassen (die Energie von 3 Sonnenmassen wurde als Gravitationswellen abgestrahlt). Dies ist das massereichste bekannte stellare Schwarze Loch (Stand: März 2016).

Ein weiteres sehr massereiches Schwarzes Loch in der Zwerggalaxie IC 10 im Sternbild Kassiopeia hat eine Masse von 24 bis 33 Sonnenmassen. Es ist Teil eines Doppelsternsystems. Das Schwarze Loch wurde indirekt durch die in ihrer Stärke schwankende Röntgenstrahlung des begleitenden Sterns entdeckt, was ein Hinweis auf ein periodisch die Quelle verdeckendes Objekt sein kann. Berechnungen aus Daten des Satelliten Swift sowie des Gemini-Teleskops auf Hawaiʻi bestätigten die Vermutungen.[41]

Als Kandidat für das kleinste Schwarze Loch galt 2008 XTE J1650-500, ebenfalls ein Röntgendoppelstern, dessen Masse inzwischen auf ca. 10,7 Sonnenmassen geschätzt wird. Seit 2011 wird IGR J17091-3624 untersucht. Es handelt sich um ein Doppelsternsystem aus einem normalen Stern und einem Schwarzen Loch, das anhand der Veränderungen seines Röntgensignals auf weniger als drei Sonnenmassen geschätzt wird.[42] Im November 2019 wurde über einen Kandidaten für ein Schwarzes Loch von nur rund 3,3 Sonnenmassen (in den Grenzen 2,6 bis 6,1) in einem Doppelsternsystem berichtet (2MASS J05215658+4359220). Das kompakte Objekt agiert nicht mit seinem Begleitstern über die Akkretion von Masse und wurde deshalb nicht an der Röntgenemission, sondern durch die Schwerkraftwirkung identifiziert, selbst emittiert es keine Strahlung.[43] Es ist entweder ein Schwarzes Loch oder ein ungewöhnlicher Neutronenstern (gewöhnlich wird die obere Grenze für die Masse von Neutronensternen auf 2,5 Sonnenmassen geschätzt). 2021 kam V723 Monocerotis hinzu, ein Doppelsystem mit einem mutmaßlichen Schwarzen Loch (inoffiziell „The Unicorn“ genannt) von etwa 2,6 Sonnenmassen hinzu. Falls sich das bestätigt, wäre es zugleich mit 1500 Lichtjahren Entfernung das sonnennächste bekannte Schwarze Loch.[44]

Primordiale Schwarze Löcher

1966 stellten Jakow Borissowitsch Seldowitsch und Igor Dmitrijewitsch Nowikow[45][46] und 1971 Stephen Hawking[47], der dies genauer behandelte, als Erste die Vermutung auf, neben den durch Supernovae entstandenen Schwarzen Löchern könnte es sogenannte primordiale Schwarze Löcher geben. Das sind Schwarze Löcher, die sich bereits beim Urknall in Raumbereichen gebildet haben, in denen die lokale Massen- und Energiedichte genügend hoch war (rechnet man die ständig abnehmende Materiedichte im Universum zurück, so findet man, dass sie in der ersten Tausendstelsekunde nach dem Urknall die Dichte des Atomkerns überstieg). Auch der Einfluss von Schwankungen der gleichmäßigen Dichteverteilung (siehe hierzu kosmische Hintergrundstrahlung) im frühen Universum war für die Bildung von primordialen Schwarzen Löchern ausschlaggebend, ebenso die beschleunigte Expansion während der Inflationsphase nach dem Urknall. Damals könnten sich kleine Schwarze Löcher u. a. mit einer Masse von etwa 10¹² Kilogramm gebildet haben. Für ein derartiges Schwarzes Loch wird ein Schwarzschild-Radius von nur ca. 10⁻¹⁵ Metern oder einem Femtometer angegeben, weniger als die klassische Größe eines Protons. Es wäre daher äußerst schwierig mit optisch basierten Methoden im Raum zu lokalisieren. Eine ähnliche Masse haben z. B. die kleinen Jupitermonde S/2003 J 9 und S/2003 J 12 mit rund 1 km Durchmesser oder ein irdischer Berg ähnlicher Größe. Seit Mitte der 1990er Jahre wird diskutiert, ob die kürzesten auf der Erde gemessenen Gammablitze von verstrahlenden primordialen Schwarzen Löchern stammen könnten, denn deren berechnete Lebensdauer liegt in der Größenordnung des Alters des heutigen Universums. Auch ein Zusammenhang mit bestimmten Fast Radio Bursts wurde diskutiert.

Aus seinen Überlegungen über kleine Schwarze Löcher folgerte Hawking im Jahre 1974 die Existenz der nach ihm benannten Hawking-Strahlung, dass also Schwarze Löcher Materie nicht nur schlucken, sondern auch wieder freisetzen können. Obwohl die Existenz von primordialen Schwarzen Löchern keineswegs gesichert ist, haben sich also allein aus hypothetischen Betrachtungen wertvolle neue Erkenntnisse im Bereich der Kosmologie, der Quantenphysik und der Relativitätstheorie ergeben.

Schwarze Mikro-Löcher

Nach einigen vereinheitlichten Theorien, wie der Stringtheorie, sollte die Mindestmasse für Schwarze Löcher weit unterhalb der Planck-Masse liegen, sodass Schwarze Mikro-Löcher beim Betrieb zukünftiger Teilchenbeschleuniger entstehen könnten.[48] In der Tat wurde aus diesem Grund seit 2008 gegen den Betrieb des LHC-Beschleunigers opponiert[49] und sogar geklagt. Die Klage wurde 2012 letztinstanzlich abgelehnt.[50] Die Kläger befürchteten, dass ein solches Mikro-Loch in den Erdkern fallen, dort wachsen und sich schließlich die ganze Erde einverleiben könnte. Dagegen spricht, dass die Theorien, die die Mikro-Löcher vorhersagen, ihnen gleichzeitig eine extrem geringe Lebensdauer zuschreiben. Außerdem ist der Erde seit Milliarden Jahren trotz permanenter Kollision mit noch viel energiereicherer kosmischer Strahlung nichts passiert.[51]

Beobachtungsmethoden

Akkretionsscheibe eines Röntgendoppelsterns

Eine Galaxie zieht hinter einem Schwarzen Loch vorbei (Simulation).

Schwarze Löcher geben weder beobachtbares Licht noch andere messbare Strahlung ab. Aktuellen Theorien zufolge sind Schwarze Löcher zwar in der Lage, Energie in Form von sogenannter Hawking-Strahlung abzugeben. Sollte dies zutreffen, würde das bedeuten, dass Schwarze Löcher allmählich „verdampfen“, wobei dieser Prozess umso schneller verläuft, je kleiner die Masse des Schwarzen Loches ist. Doch die Hawking-Strahlung wäre so energiearm, dass sie vom üblichen Hintergrund nicht zu unterscheiden wäre.

Beobachtet werden dagegen die Auswirkungen auf Materie außerhalb des Ereignishorizonts.

Insbesondere von Bedeutung für die Entdeckung von Schwarzen Löchern sind die Folgen des Hineinfallens der Materie. Da der Ereignishorizont ein für kosmische Verhältnisse sehr kleines Gebiet umschließt, unterliegt die einfallende Materie auch schon in einem Bereich vor dem Ereignishorizont einer sehr hohen optischen Verdichtung und Beschleunigung durch die Gravitationskräfte. Bei rotierenden Schwarzen Löchern geschieht dies in Form einer Akkretionsscheibe. Dort reibt die Materie aneinander und gibt große Mengen Energie frei, sowohl als elektromagnetische Strahlung als auch als Beschleunigung von Teilchen durch elektromagnetische Felder und Stoßvorgänge. Ein Resultat dieser Vorgänge sind Materiestrahlen, die senkrecht zur Akkretionsscheibe entlang einer Achse durch das Schwarze Loch ausgestoßen werden. Besonders auffällig sind diese Jets bei supermassereichen Schwarzen Löchern: Dort strömen die geladenen Teilchen unter so großen Beschleunigungen ins intergalaktische Medium, dass sie weit über ihre Ursprungsgalaxie hinausreichen. Außerdem erzeugen beschleunigte geladene Teilchen Synchrotronstrahlung, was bei solchen Jets zu starken Gammastrahlenemissionen führt. Beobachtet wurde dies z. B. Ende 2007 bei dem Schwarzen Loch im Zentrum der Galaxie 3C 321. Ein weiteres bekanntes Beispiel ist die Galaxie M 87 mit dem eindrucksvollen Jet ihres zentralen Schwarzen Lochs.

Historisch unterteilt man viele Arten von aktiven Galaxienkernen, je nach unserem Blickwinkel auf das Objekt, die Energieskalen der Prozesse und die Aktivität (wie viel Materie gerade in das Objekt strömt). Ein Beispiel sind die Quasare.

Kinematischer Nachweis

Dabei werden die Bahn und die Geschwindigkeit von Sternen, die das Schwarze Loch umkreisen, als Nachweis herangezogen. Wird eine enorm hohe Masse, die auch noch dunkel und dicht ist, berechnet, so liegt die Vermutung nahe, dass es sich um ein Schwarzes Loch handelt. Die Vermessung der Bahn des Sterns S2, der Sgr A* im Zentrum unserer Milchstraße auf einer Keplerbahn umkreist, erlaubte sehr genaue Aussagen über die Massenkonzentration im Zentralbereich von Sgr A*. Bei einer weiteren kinematischen Methode werden die Dopplerverschiebung und der Abstand zwischen dem dunklen Objekt und dem um ihn kreisenden Stern festgestellt, woraus sich die gravitative Rotverschiebung und sodann die Masse abschätzen lässt.[52]

Eruptiver Nachweis

Sterne, die dem Gezeitenradius eines Schwarzen Lochs zu nahe kommen, können durch die auftretenden Gezeitenkräfte zerrissen werden und dabei eine charakteristische, durch Geräte wie das Nuclear Spectroscopic Telescope Array nachweisbare Röntgenstrahlung freisetzen.

Aberrativer Nachweis

Schwarze Löcher besitzen die Eigenschaft, elektromagnetische Strahlung abzulenken oder zu bündeln, wodurch es möglich ist, sie zu identifizieren. Sollte beispielsweise die Form der elliptischen Bahn eines Sterns verzerrt erscheinen, liegt die Annahme nahe, dass ein Schwarzes Loch zwischen dem Beobachter und dem Stern vorhanden ist.[52]

Obskurativer Nachweis

Durch die Gravitationsrotverschiebung lässt sich eine schwarze Färbung am Rand der Schwarzen Löcher erkennen, da der relativistische Rotverschiebungsfaktor elektromagnetische Wellen beeinflusst und somit die Strahlungen in der Nähe des Ereignishorizonts unterdrückt werden, sodass ein Schwarzes Loch erkennbar wird.[52]

Temporaler Nachweis

Durch die (durch eine Analyse der Lichtkurven erkennbare) zeitliche Verzerrung (die sogenannte Zeitdilatation), die ein Schwarzes Loch bei Objekten auslöst, die es umkreisen oder sich in der Nähe befinden, ist es möglich, ein Schwarzes Loch als solches zu identifizieren.[52]

Spektroskopie

Linseneffekte und Gravitationsverschiebungen verfremden die Spektren der Sterne, die sich in der Umgebung von Schwarzen Löchern befinden.[52]

Gravitationswellen

Beschleunigte Schwarze Löcher oder Kollisionen von Schwarzen Löchern können Wellen der Raumzeit hervorrufen, die mit Gravitationswellendetektoren wie LIGO gemessen werden können. Die 2016 von LIGO vorgestellten Beobachtungen der Gravitationswellen aus der Verschmelzung zweier kleinerer Schwarzer Löcher von 29 und 36 Sonnenmassen waren der erste direkte Nachweis von Gravitationswellen (siehe Gravitationswelle#Experimenteller Nachweis).

Radioteleskopaufnahmen mit VLBI

Mit Very Long Baseline Interferometry (VLBI) können Radioteleskope eine Auflösung erreichen, die vergleichbar mit dem Radius eines Schwarzen Lochs ist. Damit ist es dem Projekt Event Horizon Telescope gelungen, Bilder der Akkretionsflüsse um das supermassereiche Schwarze Loch M87* im Zentrum der Galaxie Messier 87 aufzuzeichnen und damit erstmals direkte Bilder der Umgebung eines Schwarzen Lochs zu erhalten. Die Vorstellung im April 2019 der Resultate der koordinierten Aktion vom April 2017 gilt als wissenschaftliche Sensation, die es zum Beispiel auf die Titelseite des Nachrichtenmagazins Spiegel brachte.[53] Aufgrund gravitativer und relativistischer Effekte erscheinen die Akkretionsflüsse und Bilder der aufgeheizten Gase in der Umgebung des Schwarzen Lochs als ein Ring, der einen dunklen Bereich – den sogenannten „Schatten“ des Schwarzen Lochs – umschließt. Der Schatten ist eine durch den Gravitationslinseneffekt vergrößerte Abbildung des Bereichs, der durch den Ereignishorizont begrenzt ist. Er ist auf linearem Maßstab bis zu fünfmal größer als der Ereignishorizont und wird durch den Photonenorbit begrenzt, auf dem Licht um das Schwarze Loch zirkuliert und bei kleinen Störungen entweder im Schwarzen Loch verschwindet oder nach außen dringt.[54] Die Aufnahmen erlauben durch Vergleich mit Computersimulationen Rückschlüsse auf die Masse und die Rotation des Schwarzen Lochs, bisher aber noch nicht auf den Drehimpuls.[55] Nach dem bisherigen Stand der Technik ist nur der Schatten der supermassereichen Schwarzen Löcher in M87 und Sagittarius A* im Zentrum der Milchstraße so groß, dass sie mit dem EHT beobachtbar sind. Das EHT hat auch Aufnahmen von Sagittarius A gemacht, die aber aufgrund der viel dynamischeren Natur von Sagittarius A undeutlicher sind und demnächst vorgestellt werden sollen (Stand April 2019). Sagittarius A hat eine geringere Masse, ist aber auch näher zur Erde. Der Schatten erscheint deshalb etwa gleich groß.

Bekannte Schwarze Löcher

Sagittarius A*

Sagittarius A* ist das supermassereiche Schwarze Loch im Zentrum der Milchstraße. Seit 1992 wird seine Umgebung vor allem im infraroten Bereich von einem Team von Astronomen untersucht. Dabei wurden die Umlaufbahnen und die Geschwindigkeiten von 28 Sternen vermessen. Eingesetzt wurden Nah-Infrarot-Kameras mit adaptiver Optik beim Very Large Telescope in Cerro Paranal in Chile, der bildgebende Spektrograph Sinfoni, die Speckle-Abbildungskamera SHARP I und andere Instrumente der europäischen Südsternwarte. Außerdem wurden Beobachtungen des Keck-Teleskops auf Hawaiʻi, des New Technology Teleskops sowie Aufnahmen des Hubble-Teleskops ausgewertet.[56]

Die Untersuchungen zeigten, dass die zentrale Masse nur durch ein Schwarzes Loch erklärt werden kann und dass circa 95 % der gesamten Masse im beobachteten Sektor sich in diesem Schwarzen Loch befinden muss. Die Vermessung der Infrarot- und Röntgenemission in der Akkretionszone deutet darauf hin, dass das Schwarze Loch einen hohen Drehimpuls aufweist.[57]

Weitere Schwarze Löcher in der Milchstraße

Neben dem vermuteten zentralen Schwarzen Loch in unserer Galaxie, nämlich Sagittarius A* mit ca. 4,3 Millionen Sonnenmassen, gibt es eine Reihe weiterer vermuteter kleiner Schwarzer Löcher, die in der Milchstraße verteilt sind und eine Masse von einigen wenigen bis einem Dutzend Sonnenmassen aufweisen. Sie alle sind Bestandteile von Doppel- oder Mehrfachsternsystemen, ziehen von ihrem Partner scheinbar in einer Akkretionsscheibe Materie ab und strahlen im Röntgenbereich.[58][59]

Neueste Forschungsergebnisse zeigen, dass sich in der Sternengruppe IRS 13, die nur drei Lichtjahre von Sgr A* entfernt liegt, ein zweites Schwarzes Loch mit vergleichsweise geringen 1300 Sonnenmassen befindet. Es ist derzeit nicht geklärt, ob es sich in Zukunft mit Sgr A* vereinigen wird, ob es sich auf einer stabilen Umlaufbahn befindet oder sich sogar von ihm entfernt.

Im Januar 2005 wurden mit dem Röntgenteleskop Chandra Helligkeitsausbrüche in der Nähe von Sgr A* beobachtet, die darauf schließen lassen, dass sich im Umkreis von etwa 70 Lichtjahren 10.000 bis 20.000 kleinere Schwarze Löcher befinden, die das supermassereiche zentrale Schwarze Loch in Sgr A* umkreisen.[60] Einer Theorie zufolge sollen diese das zentrale Schwarze Loch in regelmäßigen Abständen mit Sternen aus der Umgebung „füttern“.[61]

Schwarze Löcher in der Milchstraße
Name	Masse (M_☉)	Masse Partner (M_☉)	Umlaufzeit (Tage)	Geschätzte Entfernung von der Erde (Lj)
A0620−00	≈ 11	≈ 0,7	0,33	≈ 03.500
XTE J1118+480	≈ 06–8		0,17	≈ 06.200
Cyg X-1	≈ 07–13	≈ 0,25	5,6	≈ 06.000–8.000
GRO J0422+32	≈ 03–5	≈ 1,1	0,21	≈ 08.500
GS 2000+25	≈ 07–8	≈ 4,9–5,1	0,35	≈ 08.800
V404 Cyg	≈ 09	≈ 0,5	6,5	≈ 10.000
GRO J1655-40	≈ 07,0	≈ 2,34	2,62	≈ 10.500
XTE J1650−500[62]	≈ 03,8	≈ 2,7	0,32	≈ 15.000
V4641 Sagittarii	≈ 10	≈ 7	2,82	≈ 10.000–25.000
GX 339-4		≈ 5–6	1,75	≈ 15.000
GRS 1124-683	≈ 06,5–8,2		0,43	≈ 17.000
XTE J1550−564	≈ 10–11	≈ 6,0–7,5	1,5	≈ 17.000
XTE J1819−254	≈ 10–18	≈ 3	2,8	< 25.000
4U 1543-475	≈ 08–10	≈ 0,25	1,1	≈ 24.000
Sgr A*	4,3 Mio.	≈ –	–	≈ 25.000

Sonstige

In der Galaxie NGC 6240 befinden sich zwei Schwarze Löcher, die einander im Abstand von 3000 Lichtjahren umkreisen und in einigen hundert Millionen Jahren verschmelzen werden.

Das erste Schwarze Loch außerhalb unserer Galaxie wurde 1982 in der etwa 150.000 Lichtjahre entfernten Großen Magellanschen Wolke nachgewiesen und bildet eine Komponente des Röntgendoppelsterns LMC X-3.[63]

Im Zentrum von NGC 4889 befindet sich ein Schwarzes Loch mit einer Masse von geschätzten 21 Milliarden Sonnenmassen („best fit“ aus dem Bereich 6 bis 37 Milliarden Sonnenmassen), zum Zeitpunkt der Veröffentlichung (Dezember 2011) war es das größte direkt gemessene Schwarze Loch.[26]

Das Schwarze Loch mit der Katalognummer SDSS J0100+2802 ist sehr alt, von der Erde aus wird der Zustand 875 Millionen Jahre nach dem Urknall beobachtet. Seine Masse betrug zu diesem Zeitpunkt bereits rund zwölf Milliarden Sonnenmassen. Es ist unklar, wie es so früh so massereich werden konnte.[64]

Alternative Erklärungen für ultrakompakte dunkle Objekte

Es wurden einige alternative Erklärungen für ultrakompakte dunkle Objekte vorgeschlagen, die ohne Singularitäten auskommen und kein Informationsparadoxon aufweisen. Da diese Modelle keine mit heutigen Mitteln beobachtbaren Vorhersagen machen, durch die sie sich von einem Schwarzen Loch unterscheiden ließen, ist die Akzeptanz in der Fachliteratur gering. Ein Beispiel sind die hypothetischen Gravasterne, auch „Quasi Black Hole Objects“ (QBHO) genannt. Die Erfinder der Theorie, Pawel O. Mazur und Emil Mottola, haben vorgeschlagen, dass die Theorie eine Lösung des Informationsparadoxons Schwarzer Löcher darstellt und dass Gravasterne Quellen für Gammablitze sein könnten. Die Theorie erreichte in der Öffentlichkeit nur wenig Interesse, da die Theorie keinen Vorteil gegenüber der Theorie der Schwarzen Löcher hat und rein spekulativ ist.[65] Ein weiterer Versuch, auf der Stringtheorie aufbauend das Informationsparadoxon zu lösen, stammt von Samir Mathur.[66][67] Nach diesem „Fusselknäuel-Modell“ verhüllt der Ereignishorizont ein Konglomerat aus Branen und Strings und ist selbst nicht scharf abgegrenzt.

Adaptionen in der Science Fiction

Schwarze Löcher werden in der Science-Fiction-Literatur oft als mögliches Mittel zum überlichtschnellen Transport, so etwa in Stanisław Lems Roman Fiasko, bzw. als ultimative Möglichkeit der Energiegewinnung dargestellt, wie bspw. in der Fernsehserie Stargate.

Der Film Das schwarze Loch von 1979 – mit Maximilian Schell und Anthony Perkins in den Hauptrollen –, der unter anderem die starke Gravitationskraft Schwarzer Löcher thematisiert, wurde 1980 für zwei Oscars nominiert. Der Film Interstellar aus dem Jahr 2014 von Regisseur Christopher Nolan beinhaltet ebenfalls die Thematiken vom Schwarzen Loch und seinen Gravitationskräften. In der Fernsehserie Andromeda gerät das Raumschiff Andromeda Ascendant nahe an den Ereignishorizont eines Schwarzen Lochs, wodurch Schiff und Besatzung aufgrund der Zeitdilatation bis zur Bergung und damit für 300 Jahre in der Zeit einfrieren.

Siehe auch

Weißes Loch
Spaghettisierung (extreme Verformung eines Objekts, das den Gezeitenkräften in der Nähe eines Schwarzen Loch ausgesetzt ist)

Literatur

Kip S. Thorne: Gekrümmter Raum und verbogene Zeit. Droemer Knaur, München 1996, ISBN 3-426-77240-X.
- Kip S. Thorne: Black Holes and Time Warps: Einstein’s Outrageous Legacy. W. W. Norton & Company, New York 1994, ISBN 0-393-31276-3.
Max Camenzind: Von der Rekombination zur Bildung Schwarzer Löcher. In: Sterne und Weltraum. Heidelberg 44.2005, 3, S. 28–38. ISSN 0039-1263.
Stephen W. Hawking: Eine kurze Geschichte der Zeit. Rowohlt Tb., Reinbek bei Hamburg 1988, ISBN 3-499-60555-4.
Stephen W. Hawking: Das Universum in der Nussschale. 2. Auflage. Dtv, München 2004, ISBN 3-423-34089-4.
Bernard J. Carr, Steven B. Giddings: Schwarze Löcher im Labor. In: Spektrum der Wissenschaft. Heidelberg 2005, 9, ISSN 0170-2971.
Ute Kraus: Reiseziel – Schwarzes Loch. In: Sterne und Weltraum. Heidelberg 2005, 11. ISSN 0039-1263.
Rüdiger Vaas: Tunnel durch Raum und Zeit. 6. Auflage. Franckh-Kosmos, Stuttgart 2013, ISBN 978-3-440-13431-3.
Stephen W. Hawking: Die kürzeste Geschichte der Zeit. Rowohlt Tb., Reinbek bei Hamburg 2006, ISBN 3-499-62197-5.
Mitchell Begelman, Martin Rees: Schwarze Löcher im Kosmos – Die magische Anziehungskraft der Gravitation. Spektrum Akademischer Verlag, Heidelberg 2000, ISBN 3-8274-1044-4.
Fulvio Melia: The galactic supermassive black hole. Princeton Univ. Pr., Princeton 2007, ISBN 978-0-691-09535-6.
Pietro Fré: Classical and quantum black holes. Inst. of Physics Publ., Bristol 1999, ISBN 0-7503-0627-0.
Hyun Kyu Lee u. a.: Black hole astrophysics 2002. World Scientific, Singapore 2002, ISBN 981-238-124-4.
Edwin F. Taylor, John A. Wheeler: Exploring Black Holes: Introduction to General Relativity. Addison-Wesley Longman, San Francisco 2000, ISBN 978-0-20138-423-9.
Valerij P. Frolov u. a.: Black hole physics – basic concepts and new developments. Kluwer, Dordrecht 1998, ISBN 0-7923-5146-0.

Piotr T. Chruściel, João Lopes Costa, Markus Heusler: Stationary Black Holes, Uniqueness, and Beyond. In: Living Rev. Relativity. Band 15, Nr. 7, 2012 (livingreviews.org [PDF; 1,4 MB; abgerufen am 15. Dezember 2012]).

Weblinks

Wiktionary: Schwarzes Loch – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Schwarzes Loch – Sammlung von Bildern, Videos und Audiodateien

Die bunte Welt der Schwarzen Löcher. In: Werner Kasper: Abenteuer Universum. Ausführlich, aber leicht verständlich.
The Nature of Space and Time. Vorlesungen von Stephen Hawking (Teil 2 enthält eine Karikatur des No-Hair-Theorems).

Videos

Was sind schwarze Löcher? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 3. Jan. 1999. Vom 3. Januar 1999.
Gibt es schwarze Löcher in der Milchstraße? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 9. Mai 1999. Vom 9. Mai 1999.
Wo ist das nächste Schwarze Loch? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 4. Juni 2000. Vom 4. Juni 2000.
Verschmelzen Schwarze Löcher? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 27. Mai 2001. Vom 27. Mai 2001.
Bewegen sich Schwarze Löcher im All? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 20. Jan. 2002. Vom 20. Januar 2002 (behandelt KV Ursae Majoris).
Tanzen Schwarze Löcher? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 21. Jan. 2004. Vom 21. Januar 2004.
Rotieren Schwarze Löcher? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 16. Feb. 2005. Vom 16. Februar 2005.
Gibt es ein 2. Schwarzes Loch im Galaktischen Zentrum? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 10. Mai 2006. Vom 10. Mai 2006.

Einzelnachweise und Anmerkungen

Astronomers Capture First Image of a Black Hole. Event Horizon Telescope (EHT), abgerufen am 14. April 2019 (englisch).
The Nobel Prize in Physics 2020. In: nobelprize.org. 6. Oktober 2020, abgerufen am 10. Oktober 2020.
Brief an Henry Cavendish, zitiert nach en:Dark star (Newtonian mechanics).
Karl Schwarzschild: Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. In: Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1, 189–196 (1916).
R. und H. Sexl: Weiße Zwerge, Schwarze Löcher. RoRoRo-Taschenbuch, 1979.
World Wide Words: Black Hole.
David L. Meier: Black Hole Astrophysics. The Engine Paradigm. 2009, S. 397.
John Antoniadis: Multi-Wavelength Studies of Pulsars and Their Companions. 2015, S. 4.
Matt Visser: The Kerr spacetime: A brief introduction. (PDF; 321 kB), S. 35, Fig. 3. Erstveröffentlichung: arxiv:0706.0622.
Verbogene Raumzeit. Satelliten-Messung gibt Einstein Recht. In: Spiegel.de. 15. April 2007, abgerufen am 1. September 2018.
Zur Begründung der angegebenen Formeln zwei sehr stark vereinfachende Plausibilitätsargumente:
In der Thermodynamik gilt die Formel $\mathrm {d} S=(1/T)\cdot \delta Q_{\mathrm {rev} },$ wobei $\delta Q_{\mathrm {rev} }$ für eine reversibel zugeführte Wärmeenergie steht (bei irreversibler Zuführung gilt stattdessen das Kleiner-Zeichen). $\mathrm {d} S$ ist das (vollständige) Differential der Entropie $S,$ und $T$ ist die absolute Temperatur. Die zugeführte Wärmeenergie (z. B. durch Einstrahlung von Teilchen ins Schwarze Loch) ist proportional zur Fläche $A$ des Ereignishorizonts. Der „Nutzenergie-Anteil“ ist wie in der Thermodynamik proportional zum Gewichtsfaktor $1/T$ (nicht zu $T$ ) und gegeben durch $Mc^{2},$ wobei $M$ die Masse des Schwarzen Loches und $c$ die Lichtgeschwindigkeit ist (vgl. „E=mc²“).
Clifford Will: Testing the General Relativistic “No-Hair” Theorems Using the Galactic Center Black Hole Sagittarius A*. In: Astrophysical Journal Letters. 674, 2008, S. L25–L28, doi:10.1086/528847.
Mathematisch rigorose Aussagen zur Gültigkeit bzw. Ungültigkeit des No-Hair-Theorems finden sich in einem „Living Review“ am Ende des Literaturverzeichnisses.
The LIGO Scientific Collaboration, the Virgo Collaboration: Search for gravitational waves from binary black hole inspiral, merger and ringdown. 2011, arxiv:1102.3781.
Krzysztof Belczynski, Tomasz Bulik, Bronislaw Rudak: The First Stellar Binary Black Holes: The Strongest Gravitational Wave Burst Sources. 2004, arxiv:astro-ph/0403361.
Zwei Schwarze Löcher vor Verschmelzung. In: astronews.com.
Ein Monster im Visier. Astronomen vermessen das Schwarze Loch im Milchstraßenzentrum. In: wissenschaft.de. 10. Dezember 2008, archiviert vom Original am 29. Juli 2009; abgerufen am 1. Oktober 2009.
Natarajan, Treister: Is there an upper limit to black hole masses? 2008. bibcode:2009MNRAS.393..838N.
D. Mortlock u. a.: A luminous quasar at a redshift of z=7,085. Nature, Band 474, 2011, S. 616–619.
Eduardo Bañados u. a.: An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5. In: Nature. 6. Dezember 2017. arxiv:1712.01860. bibcode:2018Natur.553..473B. doi:10.1038/nature25180. Abgerufen am 18. August 2018.
Yasemin Saplakogu: Zeroing in on how supermassive black holes formed. In: Scientific American. Online-Ausgabe, 29. September 2017.
Shingo Hirano, Takashi Hosokawa, Naoki Yoshida, Rolf Kuiper: Supersonic gas streams enhance the formation of massive black holes in the early universe. In: Science. Band 357, 2017, S. 1375–1378. Arxiv.
John Regan, John H. Wise, Greg Bryan u. a.: Rapid Formation of Massive Black Holes in close proximity to Embryonic Proto-Galaxies. In: Nature Astronomy. März 2017, Arxiv.
Theorie über Ringe um Schwarze Löcher bestätigt. In: Welt.de. 15. Dezember 2008, abgerufen am 1. Oktober 2009.
Stupendously Large Black Holes Could Be Hiding in Universe, auf: sci-news vom 22. Januar 2021
Nicholas J. McConnell: Two ten-billion-solar-mass black holes at the centres of giant elliptical galaxies. (PDF) Nature, 8. Dezember 2011, archiviert vom Original am 6. Dezember 2011; abgerufen am 6. Dezember 2011.
Spectrum of Quasar APM 08279+5255. Englisch.
12 Milliarden Lichtjahre entfernt. US-Forscher entdecken gigantisches Wasserreservoir im All. Wasserdampf bei APM 08279+5255 stellt Mengen- und Entfernungsrekord. Bei: Spiegel.de.
MPE-Astronom findet massereichstes schwarzes Loch in Galaxie M87. Max-Planck-Institut für extraterrestrische Physik (MPE), 8. Juni 2009, archiviert vom Original am 2. Januar 2010; abgerufen am 20. April 2019.
Masse-Rekord. Das schwerste Objekt im Universum. In: Spiegel Online. 17. Januar 2011, abgerufen am 20. April 2019 (Neue Massenbestimmung des Schwarzen Lochs in M87).
Harald Zaun: Im Zentrum einer Zwerggalaxie pulsiert ein Monster. In: Welt.de. 18. September 2014.
Anil Seth, Matthias Frank, Nadine Neumayer u. a.: A supermassive black hole in an ultra-compact dwarf galaxy. (Memento vom 2. Oktober 2014 im Internet Archive). In: Nature. Band 513, 2014, S. 398–400, Abstract.
Rainer Kayser: Doppeltes Schwarzes Loch beobachtet. Welt der Physik vom 18. September 2017, abgerufen am 20. September 2017.
How black hole winds blow. In: NASA.gov. 17. August 2015.
Michelle Starr: We Finally Have Evidence That Black Holes Drive Winds Shaping Their Entire Galaxy. In: ScienceAlert.com. 28. Dezember 2017.
A. Vayner, Shelley Wright u. a.: Galactic-scale Feedback Observed in the 3C 298 Quasar Host Galaxy. In: Astroph. J. Band 851, 2017, Nr. 2, Abstract.
Astronomers Shed Light on Formation of Black Holes and Galaxies. In: KeckObservatory.org. 20. Dezember 2017.
M. W. Pakull u. a.: Ultraluminous X-Ray Sources, Bubbles and Optical Counterparts. Preprint.
Ein Schwarzes Loch in Omega Centauri. In: Sterne und Weltraum. Mai 2008, S. 21. ISSN 0039-1263.
Xiaobo Dong u. a.: SDSS J160531.84+174826.1: A Dwarf Disk Galaxy With An Intermediate-Mass Black Hole. Preprint.
Massive Black Hole Smashes Record. Bei: NASA.gov.
Mikroquasare. Der Herzschlag eines Schwarzen Lochs. Bei: Astronews.com.
Todd A. Thompson u. a.: A noninteracting low-mass black hole–giant star binary system. Science, Band 366, 1. November 2019, S. 637–640, Online
T. Jayasinghe, K. Z. Stanek, Todd A. Thompson, C. S. Kochanek, D. M. Rowan, P. J. Vallely, K. G. Strassmeier, M. Weber, J. T. Hinkle, F.-J. Hambsch, D. Martin: A unicorn in monoceros: The 3 M_⊙ dark companion to the bright, nearby red giant V723 Mon is a non-interacting, mass-gap black hole candidate. In: Monthly Notices of the Royal Astronomical Society. 504, Nr. 2, 1. Januar 2021, S. 2577–2602. arxiv:2101.02212. doi:10.1093/mnras/stab907.
Zeldovich, Novikov, The Hypothesis of Cores Retarded During Expansion and the Hot Cosmological Model, Soviet Astronomy, Band 10, Heft 4, 1966, S. 602–603
M. Sasaki u. a.: Primordial Black Holes - Perspectives in Gravitational Wave Astronomy, Classical and Quantum Gravity, Arxiv 2018
Hawking: Gravitationally collapsed objects of very low mass, Mon. Not. R. Astron. Soc., Band 152, 1971, S. 75
Greg Landsberg: Black Holes at Future Colliders and Beyond. (PDF; 191 kB), Vortrag auf der 10. SUSY Konferenz, Juni 2002, DESY/Hamburg.
Felix Knoke: Schwarze Löcher in Genf. Angst vor Weltuntergang – Amerikaner klagt gegen Teilchenbeschleuniger. In: Spiegel.de. 31. März 2008.
Angst vor Weltuntergang. Klage gegen Cern endgültig gescheitert. In: Spiegel.de. 16. Oktober 2012.
Norbert Frischauf: Weltuntergang am CERN? Der Orion, 25. Oktober 2008, abgerufen am 5. Juli 2014.
Andreas Müller: Wie man ein Schwarzes Loch entdeckt. In: wissenschaft-online.de.
Am Ende von Raum und Zeit. In: Der Spiegel. Nr. 16, 13. April 2019.
Ulf von Rauchhaupt: Eine nackte Singularität ist es schon mal nicht. In: Frankfurter Allgemeine Sonntagszeitung. 14. April 2019, S. 56.
Kazunori Akiyama u. a. (Event Horizon Telescope Collaboration): First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. In: Astroph. J. Letters. 10. April 2019, IOPScience.
Galactic Black Hole disrupts Gas Cloud. In: mpe.mpg.de. Abgerufen am 28. Januar 2014.
R. Genzel u. a.: Near IR-Flares from Accreting Gas Near the last stable Orbit around the Supermassive Black Hole in the Galactic Centre. In: Nature. London 425.2003, 954.
J. Casares: Observational evidence for stellar-mass black holes. arxiv:astro-ph/0612312, Preprint.
M. R. Garcia u. a.: Resolved Jets and Long Period Black Hole Novae. arxiv:astro-ph/0302230, Preprint.
Sagittarius A* wird umschwärmt ? von 10.000 kleinen Verwandten. Bei: Bild der Wissenschaft. 2005. Nach einem Vortrag von Michael Muno.
Siehe Sagittarius A*#Weitere Schwarze Löcher.
Das kleine Schwarze. (Memento vom 6. April 2008 im Internet Archive). In: wissenschaft.de. 3. April 2008, abgerufen am 2. Februar 2019.
A. P. Cowley u. a.: Discovery of a massive unseen star in LMC X-3. In: The Astrophysical Journal. 272, 118, 1983, bibcode:1983ApJ...272..118C.
Rainer Kayser: Supermassereiches Schwarzes Loch zu massereich. Auf: weltderphysik.de. 25. Februar 2015, abgerufen am 26. Februar 2015.
P. Rocha u. a.: Bounded excursion stable gravastars and black holes. arxiv, 2008, Journal of Cosmology and Astroparticle Physics, 06, 2008, 025
Samir D. Mathur: Where are the states of a black hole? (arxiv), Talk at Quantum theory and symmetries, Cincinnati, September 2003.
NKS, Mathur states, ’t Hooft-Polyakov monopoles, and Ward-Takahashi identities. Bei: wolframscience.com.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Astronomers Capture First Image of a Black Hole. Event Horizon Telescope (EHT), abgerufen am 14. April 2019 (englisch).

[2] The Nobel Prize in Physics 2020. In: nobelprize.org. 6. Oktober 2020, abgerufen am 10. Oktober 2020.

[3] Brief an Henry Cavendish, zitiert nach en:Dark star (Newtonian mechanics).

[4] Karl Schwarzschild: Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. In: Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1, 189–196 (1916).

[5] R. und H. Sexl: Weiße Zwerge, Schwarze Löcher. RoRoRo-Taschenbuch, 1979.

[6] World Wide Words: Black Hole.

[7] David L. Meier: Black Hole Astrophysics. The Engine Paradigm. 2009, S. 397.

[8] John Antoniadis: Multi-Wavelength Studies of Pulsars and Their Companions. 2015, S. 4.

[9] Matt Visser: The Kerr spacetime: A brief introduction. (PDF; 321 kB), S. 35, Fig. 3. Erstveröffentlichung: arxiv:0706.0622.

[10] Verbogene Raumzeit. Satelliten-Messung gibt Einstein Recht. In: Spiegel.de. 15. April 2007, abgerufen am 1. September 2018.

[11] Zur Begründung der angegebenen Formeln zwei sehr stark vereinfachende Plausibilitätsargumente:
In der Thermodynamik gilt die Formel $\mathrm {d} S=(1/T)\cdot \delta Q_{\mathrm {rev} },$ wobei $\delta Q_{\mathrm {rev} }$ für eine reversibel zugeführte Wärmeenergie steht (bei irreversibler Zuführung gilt stattdessen das Kleiner-Zeichen). $\mathrm {d} S$ ist das (vollständige) Differential der Entropie $S,$ und $T$ ist die absolute Temperatur. Die zugeführte Wärmeenergie (z. B. durch Einstrahlung von Teilchen ins Schwarze Loch) ist proportional zur Fläche $A$ des Ereignishorizonts. Der „Nutzenergie-Anteil“ ist wie in der Thermodynamik proportional zum Gewichtsfaktor $1/T$ (nicht zu $T$ ) und gegeben durch $Mc^{2},$ wobei $M$ die Masse des Schwarzen Loches und $c$ die Lichtgeschwindigkeit ist (vgl. „E=mc²“).

[12] Clifford Will: Testing the General Relativistic “No-Hair” Theorems Using the Galactic Center Black Hole Sagittarius A*. In: Astrophysical Journal Letters. 674, 2008, S. L25–L28, doi:10.1086/528847.

[13] Mathematisch rigorose Aussagen zur Gültigkeit bzw. Ungültigkeit des No-Hair-Theorems finden sich in einem „Living Review“ am Ende des Literaturverzeichnisses.

[14] The LIGO Scientific Collaboration, the Virgo Collaboration: Search for gravitational waves from binary black hole inspiral, merger and ringdown. 2011, arxiv:1102.3781.

[15] Krzysztof Belczynski, Tomasz Bulik, Bronislaw Rudak: The First Stellar Binary Black Holes: The Strongest Gravitational Wave Burst Sources. 2004, arxiv:astro-ph/0403361.

[16] Zwei Schwarze Löcher vor Verschmelzung. In: astronews.com.

[17] Ein Monster im Visier. Astronomen vermessen das Schwarze Loch im Milchstraßenzentrum. In: wissenschaft.de. 10. Dezember 2008, archiviert vom Original am 29. Juli 2009; abgerufen am 1. Oktober 2009.

[18] Natarajan, Treister: Is there an upper limit to black hole masses? 2008. bibcode:2009MNRAS.393..838N.

[19] D. Mortlock u. a.: A luminous quasar at a redshift of z=7,085. Nature, Band 474, 2011, S. 616–619.

[NAT-20171206-20] Eduardo Bañados u. a.: An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5. In: Nature. 6. Dezember 2017. arxiv:1712.01860. bibcode:2018Natur.553..473B. doi:10.1038/nature25180. Abgerufen am 18. August 2018.

[21] Yasemin Saplakogu: Zeroing in on how supermassive black holes formed. In: Scientific American. Online-Ausgabe, 29. September 2017.

[22] Shingo Hirano, Takashi Hosokawa, Naoki Yoshida, Rolf Kuiper: Supersonic gas streams enhance the formation of massive black holes in the early universe. In: Science. Band 357, 2017, S. 1375–1378. Arxiv.

[23] John Regan, John H. Wise, Greg Bryan u. a.: Rapid Formation of Massive Black Holes in close proximity to Embryonic Proto-Galaxies. In: Nature Astronomy. März 2017, Arxiv.

[24] Theorie über Ringe um Schwarze Löcher bestätigt. In: Welt.de. 15. Dezember 2008, abgerufen am 1. Oktober 2009.

[sci-news-2021-01-22-25] Stupendously Large Black Holes Could Be Hiding in Universe, auf: sci-news vom 22. Januar 2021

[McConnell2011-26] Nicholas J. McConnell: Two ten-billion-solar-mass black holes at the centres of giant elliptical galaxies. (PDF) Nature, 8. Dezember 2011, archiviert vom Original am 6. Dezember 2011; abgerufen am 6. Dezember 2011.

[27] Spectrum of Quasar APM 08279+5255. Englisch.

[28] 12 Milliarden Lichtjahre entfernt. US-Forscher entdecken gigantisches Wasserreservoir im All. Wasserdampf bei APM 08279+5255 stellt Mengen- und Entfernungsrekord. Bei: Spiegel.de.

[29] MPE-Astronom findet massereichstes schwarzes Loch in Galaxie M87. Max-Planck-Institut für extraterrestrische Physik (MPE), 8. Juni 2009, archiviert vom Original am 2. Januar 2010; abgerufen am 20. April 2019.

[30] Masse-Rekord. Das schwerste Objekt im Universum. In: Spiegel Online. 17. Januar 2011, abgerufen am 20. April 2019 (Neue Massenbestimmung des Schwarzen Lochs in M87).

[31] Harald Zaun: Im Zentrum einer Zwerggalaxie pulsiert ein Monster. In: Welt.de. 18. September 2014.

[32] Anil Seth, Matthias Frank, Nadine Neumayer u. a.: A supermassive black hole in an ultra-compact dwarf galaxy. (Memento vom 2. Oktober 2014 im Internet Archive). In: Nature. Band 513, 2014, S. 398–400, Abstract.

[33] Rainer Kayser: Doppeltes Schwarzes Loch beobachtet. Welt der Physik vom 18. September 2017, abgerufen am 20. September 2017.

[34] How black hole winds blow. In: NASA.gov. 17. August 2015.

[35] Michelle Starr: We Finally Have Evidence That Black Holes Drive Winds Shaping Their Entire Galaxy. In: ScienceAlert.com. 28. Dezember 2017.

[36] A. Vayner, Shelley Wright u. a.: Galactic-scale Feedback Observed in the 3C 298 Quasar Host Galaxy. In: Astroph. J. Band 851, 2017, Nr. 2, Abstract.

[37] Astronomers Shed Light on Formation of Black Holes and Galaxies. In: KeckObservatory.org. 20. Dezember 2017.

[38] M. W. Pakull u. a.: Ultraluminous X-Ray Sources, Bubbles and Optical Counterparts. Preprint.

[39] Ein Schwarzes Loch in Omega Centauri. In: Sterne und Weltraum. Mai 2008, S. 21. ISSN 0039-1263.

[40] Xiaobo Dong u. a.: SDSS J160531.84+174826.1: A Dwarf Disk Galaxy With An Intermediate-Mass Black Hole. Preprint.

[41] Massive Black Hole Smashes Record. Bei: NASA.gov.

[42] Mikroquasare. Der Herzschlag eines Schwarzen Lochs. Bei: Astronews.com.

[43] Todd A. Thompson u. a.: A noninteracting low-mass black hole–giant star binary system. Science, Band 366, 1. November 2019, S. 637–640, Online

[Jayasinghe_et_al_2021-44] T. Jayasinghe, K. Z. Stanek, Todd A. Thompson, C. S. Kochanek, D. M. Rowan, P. J. Vallely, K. G. Strassmeier, M. Weber, J. T. Hinkle, F.-J. Hambsch, D. Martin: A unicorn in monoceros: The 3 M_⊙ dark companion to the bright, nearby red giant V723 Mon is a non-interacting, mass-gap black hole candidate. In: Monthly Notices of the Royal Astronomical Society. 504, Nr. 2, 1. Januar 2021, S. 2577–2602. arxiv:2101.02212. doi:10.1093/mnras/stab907.

[45] Zeldovich, Novikov, The Hypothesis of Cores Retarded During Expansion and the Hot Cosmological Model, Soviet Astronomy, Band 10, Heft 4, 1966, S. 602–603

[46] M. Sasaki u. a.: Primordial Black Holes - Perspectives in Gravitational Wave Astronomy, Classical and Quantum Gravity, Arxiv 2018

[47] Hawking: Gravitationally collapsed objects of very low mass, Mon. Not. R. Astron. Soc., Band 152, 1971, S. 75

[48] Greg Landsberg: Black Holes at Future Colliders and Beyond. (PDF; 191 kB), Vortrag auf der 10. SUSY Konferenz, Juni 2002, DESY/Hamburg.

[CERN1-49] Felix Knoke: Schwarze Löcher in Genf. Angst vor Weltuntergang – Amerikaner klagt gegen Teilchenbeschleuniger. In: Spiegel.de. 31. März 2008.

[CERN2-50] Angst vor Weltuntergang. Klage gegen Cern endgültig gescheitert. In: Spiegel.de. 16. Oktober 2012.

[51] Norbert Frischauf: Weltuntergang am CERN? Der Orion, 25. Oktober 2008, abgerufen am 5. Juli 2014.

[amue-52] Andreas Müller: Wie man ein Schwarzes Loch entdeckt. In: wissenschaft-online.de.

[53] Am Ende von Raum und Zeit. In: Der Spiegel. Nr. 16, 13. April 2019.

[54] Ulf von Rauchhaupt: Eine nackte Singularität ist es schon mal nicht. In: Frankfurter Allgemeine Sonntagszeitung. 14. April 2019, S. 56.

[m87-i-55] Kazunori Akiyama u. a. (Event Horizon Telescope Collaboration): First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. In: Astroph. J. Letters. 10. April 2019, IOPScience.

[56] Galactic Black Hole disrupts Gas Cloud. In: mpe.mpg.de. Abgerufen am 28. Januar 2014.

[57] R. Genzel u. a.: Near IR-Flares from Accreting Gas Near the last stable Orbit around the Supermassive Black Hole in the Galactic Centre. In: Nature. London 425.2003, 954.

[58] J. Casares: Observational evidence for stellar-mass black holes. arxiv:astro-ph/0612312, Preprint.

[59] M. R. Garcia u. a.: Resolved Jets and Long Period Black Hole Novae. arxiv:astro-ph/0302230, Preprint.

[60] Sagittarius A* wird umschwärmt ? von 10.000 kleinen Verwandten. Bei: Bild der Wissenschaft. 2005. Nach einem Vortrag von Michael Muno.

[61] Siehe Sagittarius A*#Weitere Schwarze Löcher.

[62] Das kleine Schwarze. (Memento vom 6. April 2008 im Internet Archive). In: wissenschaft.de. 3. April 2008, abgerufen am 2. Februar 2019.

[63] A. P. Cowley u. a.: Discovery of a massive unseen star in LMC X-3. In: The Astrophysical Journal. 272, 118, 1983, bibcode:1983ApJ...272..118C.

[64] Rainer Kayser: Supermassereiches Schwarzes Loch zu massereich. Auf: weltderphysik.de. 25. Februar 2015, abgerufen am 26. Februar 2015.

[65] P. Rocha u. a.: Bounded excursion stable gravastars and black holes. arxiv, 2008, Journal of Cosmology and Astroparticle Physics, 06, 2008, 025

[66] Samir D. Mathur: Where are the states of a black hole? (arxiv), Talk at Quantum theory and symmetries, Cincinnati, September 2003.

[67] NKS, Mathur states, ’t Hooft-Polyakov monopoles, and Ward-Takahashi identities. Bei: wolframscience.com.

	statisch $(J=0)$	rotierend $(J\neq 0)$
ungeladen $(Q=0)$	Schwarzschild-Metrik	Kerr-Metrik
geladen $(Q\neq 0)$	Reissner-Nordström-Metrik	Kerr-Newman-Metrik
$Q$ : Elektrische Ladung; $\ J$ : Drehimpuls