Interpretationen der Quantenmechanik

Interpretationen der Quantenmechanik beschreiben die physikalische und metaphysische Bedeutung der Postulate und Begriffe, aus welchen die Quantenmechanik aufgebaut ist. Besonderes Gewicht hat dabei die Interpretation derjenigen Konzepte, wie z. B. des Welle-Teilchen-Dualismus, die nicht nur einen Bruch mit etablierten Vorstellungen der klassischen Physik bedeuten, sondern auch der Anschauung oftmals zuwiderzulaufen scheinen.

Neben der Kopenhagener Interpretation wurden seit Entwicklung der Quantenmechanik in den 1920er Jahren eine Vielzahl alternativer Interpretationen entwickelt. Diese Interpretationen unterscheiden sich in ihren Aussagen über den Determinismus, die Kausalität, die Frage der Vollständigkeit der Theorie, die Rolle von Beobachtern und über eine Reihe weiterer metaphysischer Aspekte.

Interpretationsrelevante Aspekte

Hinsichtlich ihres empirischen Erfolges gilt die Quantenmechanik als eine der am besten gesicherten physikalischen Theorien überhaupt. Seit ihrer Formulierung in den 1920er Jahren konnte die Quantenmechanik bis heute experimentell nicht falsifiziert werden. Die Frage, wie die Quantenmechanik zu interpretieren ist, wird jedoch kontrovers diskutiert: Beschreibt die Theorie nur physikalische Phänomene oder erlaubt sie auch Rückschlüsse auf Elemente einer hinter den Phänomenen verborgenen Realität? Fragen zur Ontologie der Quantenmechanik lassen sich weder mit experimentellen noch mit theoretischen Methoden der Physik beantworten, weshalb sie von manchen Physikern als unwissenschaftlich angesehen werden.[1][2][3][4] Allerdings zeigt sich, dass sich viele fundamentale Begriffe der Theorie, wie beispielsweise „Messung“, „physikalische Eigenschaft“ oder „Wahrscheinlichkeit“, ohne interpretativen Rahmen nicht eindeutig definieren lassen. Andere Physiker und Philosophen sehen daher die Formulierung einer konsistenten Interpretation, das heißt einer semantischen Deutung des mathematischen Formalismus, als sinnvollen, wenn nicht notwendigen Bestandteil der Theorie an.[5][6]

Neben der ersten und lange Zeit dominierenden Kopenhagener Interpretation entstanden im Laufe der Zeit zahlreiche alternative Interpretationen der Quantenmechanik, die im nächsten Kapitel beschrieben werden. Im Folgenden werden zunächst einige der physikalischen und philosophischen Prinzipien und Konzepte erläutert, in welchen sich die Interpretationen der Quantenmechanik voneinander unterscheiden.

Determinismus

Die Gesetze der klassischen Physik gelten gemeinhin als deterministisch:[7] Kennt man den aktuellen Zustand eines abgeschlossenen Systems vollständig, kann man theoretisch sein Verhalten, also alle zukünftig möglichen Beobachtungen an diesem System für jeden beliebigen Zeitpunkt, exakt vorhersagen. Jegliches anscheinend zufällige Verhalten und jegliche Wahrscheinlichkeiten resultieren im Rahmen der klassischen Physik ausschließlich aus Unkenntnis, beziehungsweise in konkreten Experimenten aus der Unfähigkeit des Experimentators, den Zustand exakt zu präparieren, oder Unzulänglichkeiten des Messgerätes. Dieser prinzipielle Determinismus besteht auch zum Beispiel für die statistische Mechanik und Thermodynamik.

Viele Interpretationen der Quantenmechanik, darunter insbesondere die Kopenhagener Interpretation, gehen hingegen davon aus, dass die Annahme einer deterministischen Dynamik physikalischer Systeme nicht aufrechterhalten werden kann: Die Tatsache, dass es nicht möglich ist, beispielsweise den Zeitpunkt des Zerfalls eines radioaktiven Atoms vorherzusagen, sei demnach nicht darin begründet, dass ein Beobachter nicht genügend Informationen über etwaige innere verborgene Eigenschaften dieses Atoms besitzt. Vielmehr gäbe es keinen Grund für den konkreten Zeitpunkt des Zerfalls; der Zeitpunkt sei „objektiv zufällig“.[8]

Eine entgegengesetzte Ansicht vertreten Befürworter von Verborgene-Variablen-Interpretationen, wie der bohmschen Mechanik. Die Quantenmechanik biete demnach keine vollständige Beschreibung der Natur, sie lasse bestimmte Einflussfaktoren außer Betracht. Wüssten wir um diese, ließe sich auch ein einzelnes künftiges Messergebnis exakt und deterministisch berechnen.

Ideal des losgelösten Beobachters

Diesem Konzept[9] liegt die idealisierte Annahme zugrunde, dass bei Beobachtungen beziehungsweise Messungen zwischen einem beobachteten „Objektsystem“ und einem „Beobachter“ unterschieden werden kann, wobei zur Beschreibung der Eigenschaften des Objektsystems der Beobachter nicht mit in Betracht gezogen werden muss. Dieses Ideal lässt sich zwar aufgrund der zur Durchführung der Messung zwingend notwendigen Wechselwirkung zwischen Objektsystem und Messvorrichtung weder in der klassischen Physik noch in der Quantenmechanik vollständig erreichen, jedoch kann man in der klassischen Physik den Einfluss der Messapparatur auf das Objektsystem prinzipiell als beliebig minimierbar annehmen. In der klassischen Physik ist die Messung demnach kein grundsätzliches, sondern nur ein praktisches Problem.

In der Quantenmechanik kann die Annahme eines vernachlässigbaren Einflusses der Messvorrichtung hingegen nicht aufrechterhalten werden. Generell ist jede Wechselwirkung des Objektsystems mit der Messvorrichtung mit Dekohärenzprozessen verbunden, deren Auswirkungen nicht als „klein“ betrachtet werden können. In vielen Fällen (beispielsweise beim Nachweis eines Photons durch einen Detektor) wird das untersuchte Objekt bei der Messung sogar vernichtet. Die gegenseitige Beeinflussung zwischen Objektsystem und Umgebung beziehungsweise Messvorrichtung wird daher in allen Interpretationen der Quantenmechanik berücksichtigt, wobei sich die einzelnen Interpretationen in ihrer Beschreibung des Ursprungs und der Auswirkungen dieser Beeinflussung wesentlich unterscheiden.

Messproblem

Die von der Quantenmechanik postulierte Gesetzmäßigkeit der Zeitentwicklung des Systemzustands und das Auftreten eindeutiger Messergebnisse scheinen in direktem Widerspruch zu stehen: Einerseits erfolgt die Zeitentwicklung des Systemzustands strikt deterministisch, andererseits sind die Messergebnisse nur statistisch vorhersagbar. Einerseits sollen den Systemzuständen im Allgemeinen überlagerte Linearkombinationen von Eigenzuständen entsprechen, andererseits wird kein verwaschenes Bild mehrerer Werte gemessen, sondern stets eindeutige Werte.

Die in den meisten Lehrbüchern zugrunde gelegte orthodoxe Interpretation erklärt die Vorgänge bei der Durchführung einer quantenmechanischen Messung mit einem so genannten Kollaps der Wellenfunktion, also einem instantanen Übergang des Systemzustands in einen Eigenzustand der gemessenen Observablen, wobei dieser Übergang im Gegensatz zu sonstigen physikalischen Prozessen nicht durch die Schrödingergleichung beschrieben wird. Hierbei wird in der orthodoxen Interpretation offen gelassen, welcher Vorgang in der Messkette zu dem Kollaps führt, der Messprozess wird im Rahmen dieser Interpretation nicht genauer spezifiziert. Viele Physiker und Interpreten halten es dagegen für notwendig, in physikalischen Begriffen anzugeben, was genau eine „Messung“ ausmacht.

Die Erklärung dieses scheinbaren Widerspruchs zwischen deterministischer Systementwicklung und indeterministischen Messergebnissen ist eine der hauptsächlichen Herausforderungen bei der Interpretation der Quantenmechanik.

Erkenntnistheoretische Positionen

Ein grundsätzlicher Aspekt bei der Interpretation der Quantenmechanik ist die wissenschaftstheoretische Fragestellung, welche Art von Kenntnis über die Welt diese Theorie vermitteln kann. Die Standpunkte der meisten Interpretationen der Quantenmechanik zu dieser Frage können grob in zwei Gruppen aufgeteilt werden, die instrumentalistische Position und die realistische Position.[10]

Gemäß der instrumentalistischen Position stellen die Quantenmechanik beziehungsweise die auf Basis der Quantenmechanik ausgearbeiteten Modelle keine Abbildungen der „Realität“ dar. Vielmehr handele es sich bei dieser Theorie lediglich um einen nützlichen mathematischen Formalismus, der sich als Werkzeug zur Berechnung von Messergebnissen bewährt hat. Diese pragmatische Sicht dominierte bis in die 1960er Jahre die Diskussion um die Interpretation der Quantenmechanik und prägt bis heute viele gängige Lehrbuchdarstellungen.[11]

Neben der pragmatischen Kopenhagener Interpretation existiert heute eine Vielzahl alternativer Interpretationen, die bis auf wenige Ausnahmen das Ziel einer realistischen Deutung der Quantenmechanik verfolgen. In der Wissenschaftstheorie wird eine Interpretation als wissenschaftlich-realistisch bezeichnet, wenn sie davon ausgeht, dass die Objekte und Strukturen der Theorie treue Abbildungen der Realität darstellen und dass sowohl ihre Aussagen über beobachtbare Phänomene als auch ihre Aussagen über nicht beobachtbare Entitäten als (näherungsweise) wahr angenommen werden können.

In vielen Arbeiten zur Quantenphysik wird Realismus gleichgesetzt mit dem Prinzip der Wert-Definiertheit.[12][13] Dieses Prinzip basiert auf der Annahme, dass einem physikalischen Objekt physikalische Eigenschaften zugeordnet werden können, die es eindeutig entweder hat oder nicht hat. Beispielsweise spricht man bei der Beschreibung der Schwingung eines Pendels davon, dass das Pendel (zu einem bestimmten Zeitpunkt, und innerhalb einer gegebenen Genauigkeit) eine Auslenkung x hat.

In der orthodoxen Interpretation der Quantenmechanik wird die Annahme der Wert-Definiertheit aufgegeben. Ein Quantenobjekt hat demnach im Allgemeinen keine Eigenschaften, vielmehr entstehen Eigenschaften erst im Moment und im speziellen Kontext der Durchführung einer Messung. Die Schlussfolgerung der orthodoxen Interpretation, dass die Wert-Definiertheit aufgegeben werden muss, ist allerdings weder aus logischer noch aus empirischer Sicht zwingend. So geht beispielsweise die (empirisch von der orthodoxen Interpretation nicht unterscheidbare) De-Broglie-Bohm-Theorie davon aus, dass Quantenobjekte Teilchen sind, die sich entlang wohldefinierter Bahnkurven bewegen.

Lokalität und Kausalität

Gemäß dem Prinzip der lokalen Wirkung hat die Änderung einer Eigenschaft eines Subsystems A keinen direkten Einfluss auf ein räumlich davon getrenntes Subsystem B.[14] Einstein betrachtete dieses Prinzip als notwendige Voraussetzung für die Existenz empirisch überprüfbarer Naturgesetze. In der speziellen Relativitätstheorie gilt das Lokalitätsprinzip in einem absoluten Sinn, wenn der Abstand zwischen den zwei Subsystemen raumartig ist.

In der Quantenmechanik bewirkt die Verschränkung statistische Abhängigkeiten (so genannte Korrelationen) zwischen den Eigenschaften verschränkter, räumlich voneinander getrennter Objekte. Diese legen die Existenz gegenseitiger nicht-lokaler Beeinflussungen zwischen diesen Objekten nahe. Allerdings kann gezeigt werden, dass auch im Rahmen der Quantenmechanik keine überlichtschnelle Übertragung von Information möglich ist.

Das mit der quantenmechanischen Verschränkung verbundene Phänomen, dass die Durchführung von Messungen an einem Ort die Messergebnisse an einem (im Prinzip beliebig weit entfernten) anderen Ort zu beeinflussen scheint, war einer der Gründe, weshalb Einstein die Quantenmechanik ablehnte. In dem berühmten, gemeinsam mit Boris Podolsky und Nathan Rosen entwickelten EPR-Gedankenexperiment versuchte er, unter der Prämisse der Lokalität, nachzuweisen, dass die Quantenmechanik keine vollständige Theorie sein kann.[15] Dieses Gedankenexperiment erwies sich in seiner ursprünglichen Formulierung als nicht praktisch durchführbar, jedoch gelang es John Stewart Bell im Jahr 1964, die zentrale EPR-Prämisse des lokalen Realismus, das heißt der Existenz lokaler physikalischer Eigenschaften, in der experimentell überprüfbaren Form der Bellschen Ungleichung zu formulieren. Alle bislang vorliegenden experimentellen Untersuchungen haben die Verletzung der Bellschen Ungleichung und damit die Voraussagen der Quantenmechanik bestätigt.[16]

Allerdings sind sowohl die Bewertung der Aussagekraft der Experimente als auch die Interpretation der genauen Natur der EPR/B-Korrelationen Gegenstand einer bis heute andauernden Kontroverse. Viele Physiker leiten aus den experimentellen Ergebnissen zur Bellschen Ungleichung ab, dass das Lokalitätsprinzip nicht in der von Einstein vertretenen Form gültig sei.[17] Andere Physiker interpretieren hingegen die Quantenmechanik und die Experimente zur Bellschen Ungleichung und zur Leggettschen Ungleichung so, dass die Annahme des Realismus aufgegeben werden müsse,[18] das Lokalitätsprinzip hingegen aufrechterhalten werden könne.[19]

Die Rolle der Dekohärenz

Bei der Wechselwirkung eines Quantensystems mit seiner Umgebung (beispielsweise mit Gasteilchen der Atmosphäre, mit einfallendem Licht oder mit einer Messapparatur) kommt es unweigerlich zu Dekohärenz-Effekten. Das Phänomen der Dekohärenz lässt sich unmittelbar aus dem Formalismus der Quantenmechanik ableiten. Es stellt daher keine Interpretation der Quantenmechanik dar. Dennoch spielt Dekohärenz bei den meisten modernen Interpretationen eine zentrale Rolle, da sie einen unverzichtbaren Bestandteil bei der Erklärung des „klassischen“ Verhaltens makroskopischer Objekte darstellt und damit für jeden Versuch relevant ist, die Diskrepanz zwischen den ontologischen Aussagen der Interpretationen der Quantenmechanik und der Alltagserfahrung zu erklären.

Zu den wesentlichen Auswirkungen der Dekohärenz gehören die folgenden Phänomene:[20][21]

Dekohärenz führt zu einer irreversiblen Auslöschung der Interferenzterme in der Wellenfunktion: Bei großen Systemen (ein Fulleren ist in dieser Hinsicht bereits als „groß“ anzusehen) ist dieser Mechanismus äußerst effizient. Die Dekohärenz macht somit verständlich, warum bei makroskopischen Systemen keine Superpositionszustände beobachtet werden:
Dekohärenz verursacht eine selektive Dämpfung aller Zustände, die nicht bestimmten Stabilitätskriterien genügen, die durch die Details der Wechselwirkung zwischen dem System und seiner Umgebung definiert sind. Diese so genannte Einselection (Abkürzung für „environmentally-induced-superselection“, d. h. „umgebungsinduzierte Superselektion“) führt zur Ausprägung bevorzugter „robuster“ Zustände, d. h. von Zuständen, die nicht durch die Dekohärenz zerstört werden.
Die tatsächlich beobachtbaren Observablen sind durch diese robusten Zustände bestimmt. Modellrechnungen zeigen, dass das Coulomb-Potential, das (unter Normalbedingungen) wichtigste für den Aufbau von Materie relevante Wechselwirkungspotential, zu einer Superselektion räumlich lokalisierter Zustände führt. Das Auftreten lokalisierter makroskopischer Zustände von Alltagsgegenständen kann so auch im Rahmen der Quantenmechanik erklärt werden.
Messvorrichtungen sind immer makroskopische Objekte und unterliegen damit der Dekohärenz. Das Auftreten eindeutiger Zeigerzustände bei der Durchführung von Messungen lässt sich damit zwanglos erklären. Allerdings löst auch die Dekohärenz das Messproblem nicht vollständig, da sie nicht beschreibt, wie es zum Auftreten eines konkreten Ereignisses (z. B. des Zerfalls eines Atoms) kommt. Hierfür müssen auch im Rahmen des Dekohärenz-Programms zusätzliche Annahmen, wie z. B. das Postulat eines Kollapses oder die Annahmen der viele-Welten-Interpretation, zugrunde gelegt werden.

Interpretationen

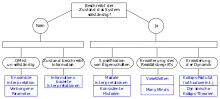
Klassifizierung der bekanntesten Interpretationen nach Bassi und Ghirardi[22]

Varianten der Kopenhagener Interpretation

Der Begriff der „Kopenhagener Interpretation“ wurde erstmals 1955 in einem Essay von Werner Heisenberg als Bezeichnung für eine vereinheitlichte Interpretation der Quantenmechanik verwendet,[23] wobei Heisenberg weder in diesem Artikel noch in späteren Veröffentlichungen eine präzise Definition dieser Interpretation formulierte.[24] Dieses Fehlen einer autoritativen Quelle und der Umstand, dass die Konzepte Heisenbergs, Bohrs und der anderen Gründungsväter der Kopenhagener Interpretation in einigen Aspekten untereinander unverträglich sind,[25][26][27][28] führten dazu, dass heute unter dem Begriff der „Kopenhagener Interpretation“ ein breites Spektrum verschiedener Interpretationsvarianten subsumiert wird.

Niels Bohr

Niels Bohr in Diskussion mit Einstein

Ein besonderes Kennzeichen von Bohrs Interpretation ist seine Betonung der Rolle der klassischen Physik bei der Beschreibung von Naturphänomenen. Demnach wird zur Beschreibung von Beobachtungsergebnissen – wie wenig der untersuchte Vorgang auch mit der klassischen Mechanik zu tun haben mag – notwendig die klassische Terminologie benutzt. So spricht man beispielsweise von Zählraten beim Nachweis von Teilchen an einem Detektor. Messvorrichtungen und Messergebnisse sind prinzipiell nur in der Sprache der klassischen Physik beschreibbar. Für eine vollständige Beschreibung eines physikalischen Phänomens muss daher die quantenmechanische Beschreibung mikroskopischer Systeme um die Beschreibung der verwendeten Messapparatur ergänzt werden. Hierbei spielt die Messapparatur nicht nur die passive Rolle eines losgelösten Beobachters (siehe oben), vielmehr ist jeder Messvorgang gemäß dem Quantenpostulat[29] unvermeidlich mit einer Wechselwirkung zwischen Quantenobjekt und Messapparatur verbunden. Je nach verwendeter Messvorrichtung weist das Gesamtsystem (Quantenobjekt + Messvorrichtung) daher unterschiedliche komplementäre Eigenschaften auf (siehe Komplementaritätsprinzip). Da z. B. die Messung der Position und die Messung des Impulses eines Teilchens unterschiedliche Messvorrichtungen erfordern, stellen Position und Impuls zwei unterschiedliche Phänomene dar, die grundsätzlich nicht in einer einheitlichen Beschreibung zusammengefasst werden können.

Bohr verneinte die Möglichkeit einer realistischen Interpretation der Quantenmechanik. Er betrachtete das Komplementaritätsprinzip als eine prinzipielle epistemologische Grenze und lehnte daher ontologische Aussagen über die „Quantenwelt“ ab.[3] Auch zum Formalismus der Quantenmechanik hatte Bohr eine rein instrumentalistische Einstellung, die Wellenfunktion war für ihn nicht mehr als ein mathematisches Hilfsmittel zur Berechnung der Erwartungswerte von Messgrößen unter wohldefinierten experimentellen Bedingungen.

Werner Heisenberg

Werner Heisenberg

Im Gegensatz zu Bohr vertrat Heisenberg eine Interpretation der Quantenmechanik mit realistischen und subjektivistischen Elementen. Gemäß Heisenberg repräsentiert die Wellenfunktion zum einen eine objektive Tendenz, die von ihm so bezeichnete „Potentia“, dass ein bestimmtes physikalisches Ereignis eintritt. Zum anderen enthält sie „Aussagen über unsere Kenntnis des Systems, die natürlich subjektiv sein müssen“. Hierbei kommt dem Messvorgang eine entscheidende Rolle zu:[30]

Die Beobachtung selbst ändert die Wahrscheinlichkeitsfunktion unstetig. Sie wählt von allen möglichen Vorgängen den aus, der tatsächlich stattgefunden hat. Da sich durch die Beobachtung unsere Kenntnis des Systems unstetig geändert hat, hat sich auch ihre mathematische Darstellung unstetig geändert, und wir sprechen daher von einem „Quantensprung“. […] Wenn wir beschreiben wollen, was in einem Atomvorgang geschieht, müssen wir davon ausgehen, dass das Wort „geschieht“ sich nur auf die Beobachtung beziehen kann, nicht auf die Situation zwischen zwei Beobachtungen. Es bezeichnet dabei den physikalischen, nicht den psychischen Akt der Beobachtung.

John von Neumann („orthodoxe Interpretation“)

Die von John von Neumann und P.A.M. Dirac erarbeiteten mathematischen Methoden bilden bis heute das formale Fundament der orthodoxen Interpretation. Charakteristische Merkmale der orthodoxen Interpretation sind die Annahme des so genannten „Eigenwert-Eigenzustand-Link“ und das Kollaps-Postulat.

Gemäß dem Eigenwert-Eigenzustand-Link hat eine Observable dann – und nur dann – einen definierten (d. h. prinzipiell vorhersagbaren) Wert, wenn sich das System in einem Eigenzustand der Observablen befindet. Wenn sich das System hingegen in einem Superpositionszustand verschiedener Eigenzustände befindet, kann der Messgröße in dieser Interpretation kein definierter Wert zugeordnet werden. Der Ausgang eines einzelnen Messvorgangs ist in diesem Fall zufällig, die Entwicklung des Systems ist bei Durchführung einer Messung nicht deterministisch.

Bei der Beschreibung des Messprozesses ging von Neumann im Unterschied zu Bohr davon aus, dass neben dem Objektsystem auch die Messvorrichtung quantenmechanisch dargestellt werden muss. Zur Vermeidung des Messproblems übernahm er Heisenbergs Konzept des „Kollapses der Wellenfunktion“.

Ensemble-Interpretationen

Gemäß der Ensemble-Interpretation beschreibt der quantenmechanische Zustand ein Ensemble ähnlich präparierter Systeme (z. B. den Zustand eines einzelnen Atoms). Sie widerspricht der Annahme der Kopenhagener Interpretation, dass die Quantenmechanik eine vollständige Beschreibung der Eigenschaften mikroskopischer Objekte darstellt und daher auch die Eigenschaften eines einzelnen Systems vollständig beschreibt. Frühe Befürworter der Ensemble-Interpretation waren unter anderen A. Einstein und K. R. Popper.[31] Heute vertritt diese Interpretation insbesondere der kanadische Physiker Leslie Ballentine.[32][33]

Bis in die 1970er Jahre gingen die meisten Vertreter der Ensemble-Interpretation davon aus, dass das Auftreten von Wahrscheinlichkeiten in der Quantenmechanik eine Folge ihrer Unvollständigkeit ist, dass mikroskopische Objekte in Wirklichkeit exakt determinierte Werte („PIVs“)[34] für alle ihre dynamischen Größen (insbesondere: Position und Impuls) haben und die Quantenmechanik nur nicht in der Lage ist, diesen Sachverhalt vollständig zu beschreiben. Damit sind diese frühen Ensemble-Interpretationen eng verwandt zu den Verborgene-Variablen-Theorien.

Durch die Bellsche Ungleichung ist der Spielraum für PIV-Ensemble-Interpretationen stark eingeschränkt. Die „minimale Ensemble-Interpretation“ verzichtet daher auf die Annahme von PIVs. Zur Determiniertheit physikalischer Größen macht sie keine Aussage.

De-Broglie-Bohm-Theorie

Abbildung 1: Simulation einiger bohmscher Trajektorien beim Doppelspalt. Die Teilchen werden durch die Wellenfunktion geleitet, die am Doppelspalt interferiert. Auf diese Weise kommt es zu dem bekannten Interferenzmuster, obwohl eine Bewegung von Teilchen beschrieben wird.

Die De-Broglie-Bohm-Theorie, häufig auch als „bohmsche Mechanik“ bezeichnet, geht davon aus, dass Quantenobjekte, wie z. B. Elektronen, Teilchen sind, die sich entlang wohldefinierter Bahnkurven bewegen. Die Bahnkurve eines solchen Teilchens lässt sich durch eine Bewegungsgleichung („Führungsgleichung“) berechnen. Eine andere (mathematisch äquivalente) Formulierung dieser Theorie führt ein so genanntes „Quantenpotential“ ein, welches aus der schrödingerschen Wellenfunktion abgeleitet wird und unter dessen Wirkung die Teilchenbewegung erfolgt.

Nach dieser Theorie ist der physikalische Zustand eines Teilchens also nicht nur durch die Wellenfunktion, sondern erst durch die Kombination aus Wellenfunktion und Teilchenposition vollständig definiert. Da diese Definition über die Zustandsdefinition der orthodoxen Interpretation hinausgeht, wird die Teilchenposition in der Terminologie der Quantenphysik als eine verborgene Variable bezeichnet, die De-Broglie-Bohm-Theorie zählt damit zur Klasse der Verborgene-Variablen-Theorien.

Die Dynamik der De-Broglie-Bohm-Theorie ist deterministisch. Wäre die Ausgangsposition eines Teilchens und die Wellenfunktion zu einem Zeitpunkt t₀ bekannt, ließe sich seine Position zu einem beliebigen späteren Zeitpunkt berechnen. Der beobachtete indeterministische Charakter von Quantenphänomenen wird in dieser Theorie auf die faktische Unmöglichkeit zurückgeführt, die Anfangswerte zu bestimmen, da im Rahmen dieser Interpretation der Versuch einer Ermittlung dieser Anfangswerte auf den Versuch einer Ermittlung der initialen Gesamtwellenfunktion des Universums hinausläuft.[35]

Eine Eigenschaft der De-Broglie-Bohm-Theorie, in der sie sich wesentlich zur klassischen Physik unterscheidet, ist ihr explizit nichtlokaler Charakter: Bei einem Mehrteilchensystem führt jede Änderung an einem Teilchen zu einer instantanen Änderung der Gesamtwellenfunktion; diese Änderung beeinflusst unmittelbar das Quantenpotential und damit die Bahnkurven aller Teilchen des Mehrteilchensystems, unabhängig vom Abstand zwischen den Teilchen.

Viele-Welten-Interpretation

Bei der Messung eines per Strahlteiler präparierten Photons entstehen gemäß der Viele-Welten-Interpretation zwei überlagerte „Welten“.

Die Viele-Welten-Interpretation entstand ausgehend von einer Veröffentlichung von Hugh Everett aus dem Jahr 1957. In dieser Arbeit hat Everett den Ansatz untersucht, wonach der physikalische Zustand des gesamten Universums mit allen darin enthaltenen Objekten durch eine einzige universale Wellenfunktion beschrieben werden soll, die sich gemäß einer durch eine Schrödingergleichung gegebenen Dynamik entwickelt.[36] Die Arbeit wirft dabei die Frage auf, ob sich die Annahme eines vermeintlichen Kollaps der Wellenfunktion nicht durch die Grundprinzipien der Quantenmechanik selbst vermeiden ließe.

Während nach der bornschen Wahrscheinlichkeitsinterpretation die Wellenfunktion die Wahrscheinlichkeiten für das Auftreten verschiedener möglicher Messergebnisse beschreibt, von welchen dann bei Durchführung einer Messung nur eines realisiert wird, entwickelten in der Folge die Autoren der Viele-Welten-Interpretation die Vorstellung, dass alle physikalisch möglichen Ereignisse auch tatsächlich realisiert werden. Um keine Widersprüche zur Realität zu erhalten, wird dabei jedoch davon ausgegangen, dass „Beobachter“ keine vollständige Sicht auf diese parallel stattfindenden Ereignisse haben können. Dabei wird auch angenommen, dass bei einer Messung oder auch allgemeiner bei jeder physikalischen Wechselwirkung an einem überlagerten Quantensystem mehrere überlagerte „Welten“ entstehen, wobei in jeder dieser Welten jeweils nur eines der verschiedenen möglichen Ergebnisse realisiert ist.

Welten, die sich in makroskopischen Größenordnungen voneinander unterscheiden, entwickeln sich aufgrund von Dekohärenzeffekten fast unabhängig voneinander, weshalb ein Beobachter im Normalfall nichts von der Existenz der anderen Welten bemerkt. Das einzige nachweisbare Indiz der Existenz der anderen Welten sind Interferenzeffekte, die sich beobachten lassen, wenn sich die Welten nur auf mikroskopischer Ebene (z. B. in den Bahnkurven einzelner Photonen beim Durchlaufen eines Interferometers) unterscheiden.

Die Viele-Welten-Interpretation wird sehr kontrovers diskutiert.[37][38] Befürworter, wie der Physiker D. Deutsch oder der Philosoph D. Wallace, betonen, dass sie die einzige realistische Interpretation sei, die das Messproblem ohne Modifikation des Formalismus der Quantenmechanik löse. Auch in der Quantenkosmologie wurde die Viele-Welten-Interpretation als konzeptioneller Rahmen zur Beschreibung der Entwicklung des Universums verwendet.[39]

Kritiker werfen ihr eine extravagante Ontologie vor. Es gibt bislang auch keinen Konsens darüber, wie in einem Multiversum, in dem alle physikalisch möglichen Ereignisse tatsächlich stattfinden, unterschiedliche Wahrscheinlichkeiten für die verschiedenen Ereignisse erklärt werden können.[40]

Konsistente-Historien-Interpretation

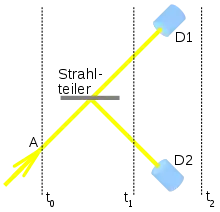
Messaufbau zum Nachweis von Photonen nach Wechselwirkung mit einem Strahlteiler. Konsistente Historien beschreiben die zeitliche Entwicklung der Photonen als Quantenereignisse zu drei Zeitpunkten t₀, t₁ und t₂.

Die konsistente-Historien-Interpretation besteht im Kern aus einem Satz an Regeln, die festlegen, wie die zeitliche Entwicklung eines physikalischen Systems in Form so genannter „konsistenter Historien“ beschrieben werden kann. Eine Historie ist hier (ähnlich den bewegten Bildern in einem Film) als zeitlich geordnete Sequenz physikalischer Ereignisse definiert. Beispielsweise können bei dem rechts dargestellten einfachen Experiment folgende zwei Historien formuliert werden:

„Ein Photon befindet sich zur Zeit t₀ in der Region A und bewegt sich auf den Strahlteiler zu. Zur Zeit t₁, nach Passieren des Strahlteilers, sind für das Photon zwei unterschiedliche Routen möglich: Entweder bewegt es sich auf den Detektor D1 zu, oder auf den Detektor D2.“

Die zwei Historien (Bewegung in Richtung D1 bzw. in Richtung D2) bilden hierbei eine so genannte „Historienfamilie“. Als konsistent gelten Historienfamilien, wenn ihre Wahrscheinlichkeit identisch zur Summe der Wahrscheinlichkeiten der einzelnen Historien der Familie ist, d. h. wenn die einzelnen Historien nicht interferieren. Inkonsistenten Historienfamilien kann keine Wahrscheinlichkeit zugeordnet werden, sie sind physikalisch nicht sinnvoll.

Die konsistenten Historienfamilien sind durch die Konsistenzbedingungen nicht eindeutig festgelegt, vielmehr lassen die Konsistenzregeln mehrere alternative inkompatible Historienfamilien zu. Beispielsweise lässt sich in dem oben beschriebenen Strahlteiler-Experiment die Bewegung eines Photons alternativ durch drei einander ausschließende konsistente Historienfamilien beschreiben, 1.) durch die oben beschriebene „Teilchen-Historienfamilie“, 2.) durch eine „Interferenz-Historienfamilie“ oder 3.) durch eine Historienfamilie mit einem makroskopischen Überlagerungszustand des Gesamtsystems.[39] Die Interpretation trifft keine Aussage, welche der alternativen Historienfamilien die „richtige“ ist.[41] Dies ist das Messproblem in der Terminologie der konsistente-Historien-Interpretation.

Die konsistente-Historien-Interpretation wurde seit ihrer Einführung im Jahr 1984 durch R. Griffiths mehrfach weiterentwickelt. Ab 1988 arbeitete R. Omnes eine explizit logische Formulierung der Quantenmechanik auf Basis konsistenter Historien aus. 1990 integrierten M. Gell-Mann und J. Hartle die Dekohärenz als Bedingung praktisch interferenzfreier Historienfamilien in die Konsistenzbedingungen.[39] Konsistente Historienfamilien werden seither auch häufig als „dekohärente Historien“ bezeichnet.

Als Vorteil der Interpretation gilt ihr Verzicht auf metaphysisches „Gepäck“, wie z. B. die Annahme der Existenz vieler unbeobachtbarer Welten, oder die Annahme einer speziellen Rolle von Beobachtern, des Bewusstseins oder des Messprozesses. Da sie auf geschlossene Systeme anwendbar ist, wird sie auch in der Quantenkosmologie als konzeptioneller Rahmen zugrunde gelegt.[41][42]

Allerdings weist auch die konsistente-Historien-Interpretation konzeptionelle Probleme auf. Insbesondere die Tatsache, dass sie keine Lösung des Messproblems anbietet, wird als Nachteil dieser Interpretation angesehen.[41][43][44]

Dynamischer-Kollaps-Theorien

Gemäß der rGRWf-Theorie besteht Materie aus räumlich und zeitlich lokalisierten Ereignissen, den so genannten „flashes“, die durch spontane Kollapsprozesse der Wellenfunktion beschrieben werden.[45]

Die Grundidee der dynamischer-Kollaps-Theorien ist die Lösung des Messproblems durch die Annahme, dass der Zustand von Quantensystemen zu zufälligen Zeitpunkten spontan in einen räumlich lokalisierten Zustand kollabiert.[46][47] Zur Beschreibung der Kollaps-Vorgänge wird die Schrödingergleichung um nichtlineare und stochastische Terme erweitert, die so gewählt sind, dass die Lokalisierungsrate bei isolierten mikroskopischen Systemen praktisch vernachlässigbar, bei makroskopischen Systemen hingegen dominant ist. Die Theorie erklärt damit, weshalb die aus der Schrödingergleichung resultierenden Überlagerungszustände nur bei mikroskopischen Systemen auftreten, während makroskopische Systeme immer in lokalisiertem Zustand vorgefunden werden.

Die älteste vollständig ausgearbeitete dynamischer-Kollaps-Theorie ist die so genannte GRW-Theorie (nach ihren Autoren Giancarlo Ghirardi, Alberto Rimini und Tullio Weber), deren Grundzüge erstmals im Jahr 1984 formuliert wurden.[48] Die ursprüngliche Fassung der GRW-Theorie wies zunächst noch einige schwerwiegende Probleme auf, unter anderem war sie nicht auf Systeme identischer Teilchen anwendbar, und es ergaben sich zunächst Schwierigkeiten beim Versuch einer relativistischen Verallgemeinerung.[49] Im Rahmen verschiedener Weiterentwicklungen konnten diese Schwierigkeiten jedoch gelöst werden. Zu den ausgereiftesten Varianten der dynamischer Kollaps-Theorien zählen heute das CSL-Modell (englische Abkürzung für „Continuous Spontaneous Localization“)[47][46], sowie R. Tumulkas rGRWf-Theorie (Abkürzung für „relativistische GRW-Theorie mit flash-Ontologie“).[45]

Die GRW-Theorie entstand zunächst als rein phänomenologischer Ansatz zur Lösung des Messproblems. Eine Reihe von Physikern, darunter T. P. Singh, R. Penrose und L. Diósi, vermuten jedoch auch aufgrund theoretischer Überlegungen zur Quantengravitation, dass die Wirkung der (Selbst-)Gravitation bei massebehafteten Quantensystemen mit nichtlinearen Effekten verbunden ist, welche zu dynamischen Kollapsprozessen führen.[50][51][52] Im nichtrelativistischen Fall wird dies durch die Schrödinger-Newton-Gleichung beschrieben.

Da sich die Grundgleichungen der dynamischer-Kollaps-Theorien von der Schrödingergleichung unterscheiden, handelt es sich bei diesen Theorien genaugenommen nicht um Interpretationen der Quantenmechanik, sondern um alternative Theorien, deren Abweichungen zur Quantenmechanik im Prinzip experimentell überprüfbar sind. Allerdings erfordert der Nachweis dieser Abweichungen die kontrollierte Erzeugung makroskopischer Quantenzustände in einer Größenordnung, die mit den heute verfügbaren technischen Mitteln nicht realisierbar ist.[53]

Informationsbasierte Interpretationsansätze

Bereits die älteste Interpretation der Quantenmechanik, die Kopenhagener Interpretation, enthält in manchen Varianten subjektivistische Elemente (siehe oben). W. Heisenberg, W. Pauli, R. Peierls und andere vertraten den Standpunkt, dass die Quantenmechanik nicht die Eigenschaften von Quantensystemen beschreibt, sondern „unsere Kenntnis ihres Verhaltens“. Allerdings wurden mögliche Zusammenhänge zwischen subjektiver Kenntnis, Information und Quantenmechanik bis in die 1980er Jahre weder in der Physik noch in der Informatik systematisch untersucht.

Mit dem Aufkommen der Quanteninformatik in den 1990er Jahren verdichteten sich die Hinweise, dass Quantenphänomene als neuartige (d. h. im Rahmen der klassischen Informatik unbekannte) Mittel zur Übertragung und Verarbeitung von Information verwendet werden können. Untersuchungen der theoretischen Grundlagen von Quantencomputern, der Quantenteleportation, der Quantenkryptografie und anderen neuen Ansätzen der Quanteninformatik zeigten eine Reihe enger Zusammenhänge und Abhängigkeiten zwischen den Konzepten der Informatik und der Quantenmechanik.

Einige Physiker und Philosophen zogen hieraus den Schluss, dass auch eine zufriedenstellende Interpretation der Quantenmechanik nur aus einer informationstheoretischen Perspektive möglich ist. Heute existieren verschiedene Varianten informationsbasierter Interpretationen, die sich unter anderem in ihrer Definition des Begriffs „Information“ unterscheiden: Bei einigen Interpretationsvarianten bezeichnet Information die (subjektive) Einschätzung eines Beobachters (siehe übernächster Abschnitt). Die im Folgenden beschriebenen informationstheoretischen Rekonstruktionen der Quantenmechanik basieren hingegen auf der technischen Definition von Information als der Größe, deren Informationsgehalt durch die von-Neumannsche Entropie bemessen ist.

Informationstheoretische Rekonstruktionen der Quantenmechanik

Gemäß A. Grinbaum gibt es zwei entgegengesetzte Ansätze zur Beschreibung des Zusammenhangs zwischen Information und Physik:[54] a) Die Verarbeitung von Information basiert auf den Gesetzen der Physik. Physik ist grundlegend, Information ist ein abgeleitetes Konzept. b) Die Prinzipien der Physik sind informationstheoretischer Natur.

Verschiedene Philosophen, wie z. B. J. Bub oder A. Grinbaum, sehen eine Ursache für viele Interpretationsprobleme in der Verwendung einer ungeeigneten Methodik:[55][56] Bei den meisten Interpretationen wird der mathematische Formalismus vorausgesetzt und dann versucht, den formalen Begriffen der Theorie, wie z. B. dem quantenmechanischen Zustand, eine semantische Bedeutung zu geben. Diese Methode habe sich jedoch nicht bewährt. Vielmehr sei analog zu Einsteins Vorgehensweise bei der Herleitung der Relativitätstheorie eine Rekonstruktion der Quantenmechanik erforderlich, d. h. ihre Ableitung aus geeignet gewählten physikalischen Prinzipien. Erst aus der Perspektive dieser Prinzipien lasse sich eine sinnvolle Interpretation der Quantenmechanik formulieren.

Es existiert eine Reihe verschiedener Vorschläge für axiomatische Rekonstruktionen der Quantenmechanik, wobei die meisten entsprechenden Ansätze seit Anfang der 1990er auf informationstheoretischen Prinzipien basieren.[56] Neben Rovellis „Relationaler Interpretation“[57][58] und Zeilingers „Grundprinzip der Quantenphysik“[59] zählt das CBH-Theorem zu den bekanntesten informationsbasierten Rekonstruktionen.

In informationstheoretischen Rekonstruktionen der Quantenmechanik hat Information den Status einer physikalischen Fundamentalgröße. Quantentheorien sind in diesen Interpretationen keine Theorien über die Eigenschaften materieller Objekte, sondern über die Darstellung und Manipulation von Information.[60] Die hier zugrundeliegende Idee, dass Physik auf Information zurückführbar ist, gewann in den letzten Jahren mit dem Aufkommen der Quanteninformatik an Bedeutung. Der bekannteste Vertreter und Vordenker dieser Denkschule, der Physiker J. A. Wheeler, formulierte 1990 seine „it from bit“-These, der zufolge alle physikalischen Objekte, wie z. B. Elementarteilchen, Kraftfelder, selbst die Raumzeit, einen informationstheoretischen Ursprung haben.[61]

Einige Interpreten, wie z. B. G. Jaeger oder A. Duwell, halten diesen Standpunkt für eine unhaltbare Extremposition: Insbesondere sei Information nicht als physikalische Substanz (d. h. als physikalische Materie) zu betrachten, Information sei daher nicht als Grundbegriff zur Beschreibung der Eigenschaften von Materie geeignet.[62][63] Andererseits bezweifelt der Philosoph C. Timpson, dass mit informationstheoretischen Interpretationen eine immaterialistische Position begründet werden kann: Letztlich liefen auch diese Interpretationen entweder auf eine instrumentalistische Position oder auf Verborgene-Variablen-Theorien hinaus.[64]

Subjektivistische Interpretationen, Quanten-Bayesianismus

Mit dem Quanten-Bayesianismus entstand in den letzten Jahren eine konsequent subjektivistische Interpretation der Quantenmechanik. Die Physiker C. Fuchs, Carlton M. Caves, R. Schack und andere zeigten, dass die Quantenmechanik in konsistenter Weise auf Basis des Bayesschen Wahrscheinlichkeitskonzeptes formuliert werden kann.[62][65][66] Demnach bezieht sich die Wellenfunktion nicht auf ein Quantensystem, sondern sie repräsentiert die Einschätzung eines rationalen Agenten über das Ergebnis einer Messung an einem System. Der Kollaps der Wellenfunktion bei der Durchführung einer Messung beschreibt im Rahmen dieser Interpretation keinen realen physikalischen Prozess, sondern die Aktualisierung der Einschätzung des Agenten über den möglichen Ausgang einer weiteren Messung an dem System.

Der Quanten-Bayesianismus enthält sowohl realistische als auch anti-realistische Elemente:[67] Physikalische Objekte, wie z. B. Elektronen, Neutrinos oder Quarks, werden als existierend angenommen. Jedoch besitzen Quantensysteme im Rahmen dieser Interpretation nur dispositionelle Eigenschaften, d. h. die Fähigkeit, im Falle von Wechselwirkungen mit anderen Quantensystemen bestimmte physikalische Ereignisse zu verursachen. Der Verlauf dieser Ereignisse ist durch kein physikalisches Gesetz bestimmt, selbst die Gültigkeit stochastischer Gesetzmäßigkeiten auf mikroskopischer Ebene wird in dieser Interpretation verneint.[67]

Als Vorteil des Quanten-Bayesianismus führen seine Anhänger an, dass viele der gängigen (scheinbaren) Paradoxien der Quantenmechanik, wie z. B. das Wigners-Freund-Paradoxon, im Rahmen dieser Interpretation vermieden werden können, da die meisten dieser Paradoxien auf einer objektiven Interpretation des quantenmechanischen Zustandes basieren.[68] Weiterhin vertreten sie in der (unabhängig von der Quantentheorie existierenden) Kontroverse um die Interpretation von Wahrscheinlichkeit den Bayesschen Standpunkt, dass nur eine subjektivistische Wahrscheinlichkeitsinterpretation ohne logische Inkonsistenzen formulierbar sei.

Andere Autoren, wie der Physiker G. Jaeger oder der Philosoph C. Timpson, kritisieren, dass der Quanten-Bayesianismus ein Defizit an Erklärungsvermögen aufweise. Die Zielsetzung von Physik sei die Beschreibung und Erklärung der Eigenschaften physikalischer Systeme, nicht die Beschreibung der Einschätzungen von Agenten.[69][70]

Weitere Interpretationen

Neben den in den letzten Abschnitten erwähnten Interpretationen entstanden im Zeitraum seit ca. 1980 eine Reihe weiterer Interpretationen mit einem etwas geringeren Bekanntheitsgrad. Hierzu zählen unter anderem die Modale Interpretation[71], die Existential Interpretation[72], die Transactional Interpretation[73], sowie die Empiricist Interpretation[74] (zu den drei letztgenannten Interpretationen sind keine deutschen Übersetzungen etabliert).

Vergleich der Interpretationen

Ein tabellarischer Vergleich der unterschiedlichen Interpretationen:

Interpretation	Autor(en)	Ist echter Zufall möglich?	Ist die Wellenfunktion real?	Eine Historie?	Keine versteckten Variablen?	Kein Kollaps der Wellenfunktion?	Beobachter nicht erforderlich?	Nichtlokal?	Keine kontrafaktische Bestimmtheit?
Ensemble- Interpretation	Max Born, 1926	k. A.	Nein	Ja	k. A.	Ja	Ja	Ja	Ja
Kopenhagener Deutung der Quantenmechanik	Niels Bohr, Werner Heisenberg, 1927	Ja	Nein[A 1]	Ja	Ja	Nein[A 2]	Kausal	Ja	Ja
de-Broglie- Bohm- Theorie	Louis de Broglie, 1927, David Bohm, 1952	Nein	Ja[A 3]	Ja[A 4]	Nein	Phänomenologisch	Ja	Ja[A 5]	Nein
Quantenlogik	Garrett Birkhoff, 1936	k. A.	k. A.	Ja[A 6]	Ja	Ja	Interpretierbar[A 7]	k. A.	Ja
Zeit- symmetrische Theorien	Satosi Watanabe, 1955	Nein	Ja	Ja	Nein	Ja	Ja	Nein	Ja
Viele-Welten Interpretation	Hugh Everett, 1957	Nein	Ja	Nein	Ja	Ja	Ja	Nein	situativ
Bewusstsein verursacht Kollaps	Eugene Wigner, 1961	Ja	Ja	Ja	Ja	Nein	Kausal	Ja	Ja
Stochastische Interpretation	Edward Nelson, 1966	Ja	Nein	Ja	Nein [A 8]	Ja	Ja	Ja	Nein[A 9]
Viele- Gedanken Interpretation	H. Dieter Zeh, 1970	Nein	Ja	Nein	Ja	Ja	Interpretierbar[A 10]	Nein	situativ
Konsistente Historien	Robert B. Griffiths, 1984	Ja	Nein	Nein	Ja	Ja	Ja	Nein	Ja
Transaktions- Interpretation	John G. Cramer, 1986	Ja	Ja	Ja	Ja	Nein [A 11]	Ja	Ja[A 12]	Nein
Objektiver- Kollaps- Theorien	Ghirardi Rimini Weber Penrose, 1986/89	Ja	Ja	Ja	Ja	Nein	Ja	Ja	Ja
Relationale Quanten- mechanik	Carlo Rovelli, 1994	k. A.	Nein	k. A.[A 13]	Ja	Nein[A 14]	Intrinsisch[A 15]	Nein	Ja
QBism	C. Fuchs, R. Schack, 2010	Ja	Nein[A 16]	k. A.[A 17]	Ja	Nein[A 18]	Intrinsisch[A 19]	Nein	Ja

Anmerkungen

Nach Bohr hat das Konzept eines physikalischen Zustands, der unabhängig von den Bedingungen seiner experimentellen Beobachtung ist, keine klar definierte Bedeutung. Nach Heisenberg stellt die Wellenfunktion eine Wahrscheinlichkeit dar, nicht aber eine objektive Realität in Raum und Zeit.
Gemäß der Kopenhagener Interpretation bricht die Wellenfunktion zusammen, wenn eine Messung durchgeführt wird.
Beide Teilchen und Führungswellenfunktion sind real.
Eindeutige Partikelhistorie, aber mehrere Wellenhistorien.
Die Art von Nichtlokalität, die von der Theorie verlangt wird, um die Bell-Ungleichungen zu verletzen, ist schwächer als die in EPR angenommene. Insbesondere ist diese Art von Nicht-Lokalität kompatibel mit keinem Signalisierungstheorem und Lorentz-Invarianz.
Aber Quantenlogik ist in ihrer Anwendbarkeit begrenzter als kohärente Historien.
Die Quantenmechanik wird als eine Art der Vorhersage von Beobachtungen oder eine Theorie der Messung angesehen.
Die Annahme der intrinsischen Periodizität ist ein Element der Nicht-Lokalität, die mit der Relativität konsistent ist, da die Periodizität kausal variiert.
In der stochastischen Interpretation ist es nicht möglich, Geschwindigkeiten für Teilchen zu definieren, d. h. die Wege sind nicht gradlinig. Um die Bewegung der Teilchen zu jedem Zeitpunkt zu kennen, muss man wissen, was der Markov-Prozess ist. Sobald wir jedoch die genauen Anfangsbedingungen und den Markov-Prozess kennen, ist die Theorie tatsächlich eine realistische Interpretation der Quantenmechanik.
Beobachter trennen die universelle Wellenfunktion in orthogonale Sätze von Erfahrungen.
Der Kollaps des Zustandsvektors wird als Abschluss der Transaktion zwischen Emitter und Absorber interpretiert.
Die transaktionale Interpretation ist explizit nicht lokal.
Der Vergleich von Historien zwischen Systemen in dieser Interpretation hat keine wohldefinierte Bedeutung.
Jede physische Interaktion wird als ein Kollaps-Ereignis relativ zu den beteiligten Systemen behandelt, nicht nur makroskopische oder bewusste Beobachter.
Der Zustand des Systems ist beobachtungsabhängig, d. H. der Zustand ist spezifisch für den Referenzrahmen des Beobachters.
Eine Wellenfunktion kodiert lediglich die Erwartungen eines Agenten für zukünftige Erfahrungen. Es ist nicht mehr real als eine Wahrscheinlichkeitsverteilung ist in der Bajian (Bajaan Wahrscheinlichkeit).
Die Quantentheorie ist ein Werkzeug, mit dem jeder Agent seine Erwartungen erfüllen kann. Die Vergangenheit kommt nur insoweit zum Tragen, als die individuellen Erfahrungen und das Temperament eines Handelnden seine Prioritäten beeinflussen.
Obwohl QBism diese Terminologie vermeiden würde. Eine Veränderung der Wellenfunktion, die ein Agent einem System als Ergebnis einer Erfahrung zuschreibt, stellt eine Veränderung seiner Überzeugungen über weitere Erfahrungen dar, die sie möglicherweise haben.
Beobachter oder, richtiger, Teilnehmer sind für den Formalismus genauso wichtig wie die Systeme, mit denen sie interagieren.

Geschichte

1927–1950: Monopolstellung der „Kopenhagener Schule“

Nachdem Mitte 1926 die Ausarbeitung des Formalismus der Quantenmechanik weitgehend abgeschlossen war, verschärfte sich unter den Quantenphysikern jener Zeit die Frage nach einer zufriedenstellenden Interpretation der Quantenmechanik. Innerhalb kurzer Zeit, bis Ende 1927, setzten sich Bohr und Heisenberg gegen die Opposition Einsteins und Schrödingers weitgehend in der wissenschaftlichen Gemeinschaft durch. Die grundsätzlichen Fragen zur Quantenmechanik wurden als geklärt angesehen, und die meisten Physiker wandten sich den vielfältigen Anwendungen der Theorie zu. Selbst spätere Kritiker der Kopenhagener Interpretation, wie z. B. Landé, Louis Victor de Broglie oder David Bohm, traten zunächst für diese Interpretation ein.[75]

1950–1970: Revision der Grundlagen der Quantenmechanik

In den 1950er Jahren wurde die Beschäftigung mit den konzeptionellen Grundlagen der Quantenmechanik von den meisten Physikern als philosophische und nicht als wissenschaftliche Aktivität betrachtet.[76] Gegen den wissenschaftlichen Mainstream befassten sich einzelne Physiker kritisch mit den Prinzipien der Kopenhagener Interpretation. Der Physiker D. Bohm bewies mit der De-Broglie-Bohm-Theorie, dass die Formulierung empirisch adäquater verborgene-Variablen-Theorien möglich ist. Bei der Analyse der grundlegenden Prämissen dieser Theorien gelang J. Bell mit der Formulierung des Bellschen Theorems ein wissenschaftlicher Durchbruch, der wesentlich dazu beitrug, dass sich Untersuchungen der Grundlagen der Quantenphysik ab Anfang der 1970er Jahre zu einem rasch wachsenden Forschungsgebiet der Physik entwickelten.

1970 bis heute: Aufschwungphase der „experimentellen Metaphysik“

Die Schwierigkeiten bei der Interpretation der Quantenmechanik, wie z. B. die vielfach als unzureichend empfundene Behandlung des Messproblems in der orthodoxen Interpretation, waren ein wesentliches Motiv für die Ausarbeitung bzw. Weiterentwicklung der im letzten Kapitel beschriebenen Alternativ-Interpretationen. Fortschritte auf experimenteller Seite, konzeptionelle Weiterentwicklungen der Theorie, wie z. B. die Ausarbeitung des Dekohärenz-Programms, sowie neue Entwicklungen auf dem Gebiet der Quanteninformatik trugen zusätzlich zu einem bis heute anhaltenden Interesse vieler Physiker und Philosophen an der Grundlagenforschung zur Quantenmechanik bei.

Experimentelle Fortschritte

Bei der experimentellen Untersuchung verschiedener grundlegender Quantenphänomene wurden in den letzten Jahrzehnten erhebliche experimentelle Fortschritte erzielt. Alle diese Experimente zeigen, dass die Prinzipien der klassischen Physik nicht auf Quantensysteme übertragbar sind, während bislang keine Abweichungen zu den theoretischen Ergebnissen der Quantenmechanik nachgewiesen werden konnten. Allerdings sind die bislang durchgeführten Experimente nicht zur Unterscheidung zwischen den verschiedenen Interpretationen der Quantenmechanik geeignet, weshalb sich der folgende Überblick auf eine kurze Aufzählung der bekanntesten Schlüsselexperimente seit 1970 beschränkt:

Experimente zum lokalen Realismus („Bell-Test-Experimente“): – Experimente zur Bellschen Ungleichung; GHZ-Experiment; Experimente zur Leggett-Ungleichung
Experimente zum Komplementaritätsprinzip: – „Welcher-Weg“-Experimente
Experimente zum Messprozess: – Delayed-Choice-Experimente; Quantenradierer; Quanten-Zeno-Effekt
Quanten-Kommunikation, Quantencomputer – Quantenteleportation; Implementierungen von Qubits

Das Dekohärenz-Programm

1970 stellte der Heidelberger Physiker Dieter Zeh fest, dass viele der (scheinbaren) Paradoxien der Quantenmechanik, wie z. B. das Wigners-Freund-Paradoxon und das Messproblem, unter anderem durch falsche Prämissen bei der Beschreibung der Messvorrichtung bzw. des Beobachters begründet sind.[77] Insbesondere zeigte er, dass makroskopische Quantensysteme aufgrund unvermeidlicher Wechselwirkungen mit der Umgebung nicht als geschlossene Systeme betrachtet werden können, und schlug daher als Lösungsansatz vor, dass die Umgebung der Messvorrichtung (bzw. des Beobachters) in der quantenmechanischen Beschreibung des Messprozesses berücksichtigt wird. Allerdings wurden Zehs Anregungen bis Anfang der 1980er Jahre kaum beachtet.

1981–1982 erfolgte die Ausarbeitung der wesentlichen Konzepte der Dekohärenz durch Wojciech Zurek.[77] 1991 veröffentlichte er einen Artikel[72] in der Zeitschrift „Physics Today“ und machte die Dekohärenz damit einer breiteren Öffentlichkeit bekannt.[77] In den Folgejahren entwickelte sich die Dekohärenz zum Gegenstand zahlreicher experimenteller und theoretischer Untersuchungen. Diese Arbeiten warfen ein neues Licht auf den quantenmechanischen Messprozess und auf den Zusammenhang zwischen Quantenmechanik und klassischer Physik, was in der Folge dazu führte, dass die Konzepte der Dekohärenz in vielen Interpretationen der Quantenmechanik als zentrale Bestandteile integriert wurden.[78]

Literatur

Bibliographien

A. Cabello: Bibliographic guide to the foundations of quantum mechanics and quantum information. In: Quantum Physics. 2000, S. 1–462, arxiv:quant-ph/0012089v12 (Umfangreiche Bibliographie über Veröffentlichungen zu den Grundlagen der Quantenmechanik, mit über 10.000 Referenzen.).

Interpretationen der Quantenmechanik

David Albert: Quantum Mechanics and Experience. Harvard University Press, Cambridge 1992. (Gut lesbare Einführung mit einfachen Modellen.)
Giorgio Auletta: Foundations and Interpretation of Quantum Theory. World Scientific, Singapore 2000, ISBN 981-02-4039-2. (Umfassende Darstellung der Grundlagen der Quantenmechanik und ihrer Interpretationen.)
K. Baumann und R.U. Sexl (Hrsg.): Die Deutungen der Quantentheorie. 3. überarbeitete Auflage, Vieweg, Braunschweig 1987, ISBN 3-528-08540-1. (Nützliche Sammlung klassischer Texte in deutscher Übersetzung.)
John Stewart Bell: Speakable and Unspeakable in Quantum Mechanics, 2. Aufl., Cambridge University Press, Cambridge 2004, ISBN 978-0-521-52338-7 (mit einer Einführung von Alain Aspect, bündelt Bells Originalaufsätze, dt. Übersetzung: Quantenmechanik, Sechs mögliche Welten und weitere Artikel, de Gruyter, Berlin 2015, ISBN 978-3-11-044790-3).
Jeffrey Bub: Interpreting the Quantum World, Cambridge University Press, Cambridge 1997.
Jeffrey Bub: The Interpretation of Quantum Mechanics, Reidel, Dordrecht 1974.
Nancy Cartwright: Another Philosopher Looks at Quantum Mechanics, or: What Quantum Theory is Not (PDF; 201 kB). (Instrumentalistische Reaktion auf Putnam 2005: Quantenmechanik kann als „lebende und arbeitende Theorie“ uninterpretiert bleiben.)
Hong Dingguo: On the Neutral Status of QM in the Dispute of Realism vs. Anti-Realism., in: Cohen, Robert S / Hilpinen, Risto / Renzong, Qiu (Hrsg.): Realism and Anti-Realism in the Philosophy of Science. Kluwer Academic Publishers, Dordrecht 1996, S. 307–316.
Peter Forrest: Quantum metaphysics. Blackwell, Oxford 1988, ISBN 0-631-16371-9. Diskussion realistischer metaphysischer Interpretationsoptionen.
Bas van Fraassen: Quantum Mechanics, An Empiricist View. Oxford University Press, Oxford 1991, ISBN 0-19-823980-7. (Ausgearbeitete antirealistische Interpretation aus der Position des konstruktiven Empirismus.)
Cord Friebe, Meinard Kuhlmann, Holger Lyre, Paul Näger, Oliver Passon, Manfred Stöckler: Philosophie der Quantenphysik. Einführung und Diskussion der zentralen Begriffe und Problemstellungen der Quantentheorie für Physiker und Philosophen. Springer Spektrum 2015, ISBN 978-3-642-37789-1
R. I. G. Hughes: The structure and interpretation of quantum mechanics. Harvard University Press, Cambridge, Massachusetts 1989, ISBN 0-674-84391-6. (Einführung in den Formalismus und verschiedene Aspekte der Interpretation der Quantenmechanik.)
Gregg Jaeger (2009) Entanglement, Information, and the Interpretation of Quantum Mechanics. Springer, ISBN 978-3-540-92127-1.
Tim Maudlin: Quantum Non-Locality and Relativity. Blackwell, Oxford U. K. and Cambridge MA 1994.
Hilary Putnam, A Philosopher Looks at Quantum Mechanics (Again). in: The British Journal for the Philosophy of Science, 56/4 (2005), S. 615–634. doi:10.1093/bjps/axi135 (Ablehnung „kopenhagener“ Interpretationen als bloßen Zurückweisungen eines wissenschaftlichen Realismus und der statistischen Interpretation (Born), Diskussion der wichtigsten verbleibenden realistischen Optionen: spontaner Kollaps (GRW) und Bohm.)
Michael Redhead: Incompleteness, nonlocality and realism: a prolegomenon to the philosophy of quantum mechanics. Clarendon Press, Oxford 1987, ISBN 0-19-824937-3. (Eines der wichtigsten weiterführenden Werke, inklusive einer knappen Darstellung der Theorie.)
Hans Reichenbach, Philosophic Foundations Of Quantum Mechanics. University Of California Press 1944, ISBN 0-486-40459-5.
John Archibald Wheeler, Wojciech Zurek (Hrsg.): Quantum theory and measurement. Princeton University Press, Princeton, NJ 1983, ISBN 0-691-08315-0. (Standard-Handbuch mit den wichtigsten Texten aus der Interpretationsgeschichte, umfangreicher und aktueller als Sexl / Baumann.)

Weblinks

Physik-Nobelpreisträger Theodor W. Hänsch über Interpretationen der Quantenmechanik Interview zur Quantenmechanik bei Drillingsraum.de, 22. Juli 2008
Das Streitgespräch, das Niels Bohr und Erwin Schrödinger am 2. Aug. 1935 über die Deutung der Quantenphänomene und über die Deutung der Quantentheorie führten. (PDF; 473 kB)
Auf der Suche nach dem Quantenmodell Allgemeinverständliche Übersicht der aktuellen Interpretationen, Oktober 2021

Originalarbeiten und Belege

C. A. Fuchs, A. Peres: Quantum Theory needs no “Interpretation”. In: Physics Today. Nr. 53(3), 2000, Seite 70 (Online).
If I were forced to sum up in one sentence what the Copenhagen interpretation says to me, it would be “Shut up and calculate!”, Zitiert in D. Mermin: Could Feynman Have Said This?. In: Physics Today. Nr. 57, 2004, Seite 10.
„There is no quantum world. There is only an abstract quantum physical description. It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature.“ Bohr-Zitat von Aage Petersen, in: The Bulletin of the atomic scientists. Nr. 19, 1963, Seite 8.
N. Cartwright: Another Philosopher Looks at Quantum Mechanics or What Quantum Theory is Not. In: Y. Ben-Menahem (Hrsg.): Hilary Putnam. Cambridge University Press, 2005, S. 188–202.
E. Dennis, T. Norsen: Quantum Theory: Interpretation Cannot be avoided. arxiv:quant-ph/0408178.
„Jedoch auch die Vorstellung, dass sich die Quantenmechanik, unsere fundamentalste Theorie, ausschließlich mit Ergebnissen von Experimenten beschäftigt, würde unbefriedigend bleiben.“ und „Die Quantenmechanik ausschließlich auf lächerliche Laboroperationen zu beschränken, heißt, das große Vorhaben zu verraten. Eine ernsthafte Formulierung wird die große Welt außerhalb des Laboratoriums nicht ausschließen.“ Zitate aus: „Wider die ,Messung'“. In J. S. Bell: Quantenmechanik, Sechs mögliche Welten und weitere Artikel, de Gruyter, Berlin 2015, ISBN 978-3-11-044790-3, S. 241–259.
Der Standpunkt, dass die klassische Mechanik wirklich deterministisch ist und Ungenauigkeiten auf die Unfähigkeit des Experimentators zurückzuführen sind, ist jedoch umstritten; entgegengesetzter Ansicht war beispielsweise Karl Popper. Karl Popper: Indeterminism in Quantum Physics and in Classical Physics I. In: The British Journal for the Philosophy of Science 1:2, 1950, S. 117–133. Karl Popper: Indeterminism in Quantum Physics and in Classical Physics II. In: The British Journal for the Philosophy of Science 1:3, 1950, 173–195.
Die Formulierung des „objektiven Zufalls“ wird beispielsweise von A. Zeilinger verwendet. Heisenberg prägte zur Bezeichnung der Verwirklichungstendenz quantenmechanischer Systeme beim Messprozess den Begriff der „Potentia“. Auch Poppers Propensitäten-Interpretation liegt ein ähnliches Konzept von Wahrscheinlichkeit zugrunde.
Die Formulierung geht auf Pauli zurück, der damit die Haltung Einsteins zusammenfasste: „Es erscheint mir durchaus angebracht, die konzeptive Beschreibung der Natur in der klassischen Physik, die Einstein so emphatisch beibehalten möchte, das Ideal des losgelösten Beobachters zu nennen. In drastischen Worten hat der Beobachter nach diesem Ideal gänzlich in diskreter Weise als versteckter Zuschauer (spectator) aufzuscheinen, niemals als Handelnder (actor), die Natur wird dabei in ihrem vorbestimmten Lauf der Ereignisse allein gelassen, unabhängig davon, auf welche Weise die Phänomene beobachtet werden.“ W. Pauli, Letter PLC 0014.51, veröffentlicht in K. V. Laurikainen: Wolfgang Pauli and the Copenhagen Philosophy. In: P. Lahti und P. Mittelstaedt (Hrsg.): Symposium on the Foundation of Modern Physics. World Scientific, Singapore 1985, S. 273–287.
Die Gruppierung in Instrumentalismus versus Realismus ist eine starke Vereinfachung der tatsächlich vorhandenen Vielfalt verschiedener Positionen der Wissenschaftstheorie. Ein ausführlicher Überblick über die wichtigsten erkenntnistheoretischen Positionen in der Physik findet sich zum Beispiel in B. d’Espagnat: Reality and the Physicist: Knowledge, Duration and the Quantum World. Cambridge University Press, 1989, ISBN 0-521-33846-8.
H. P. Stapp: The Copenhagen Interpretation. In: American Journal of Physics. Band 40, 1972, S. 1098, doi:10.1119/1.1986768.
In der englischsprachigen Literatur findet sich eine Vielzahl verschiedener Bezeichnungen für die Wert-Definiertheit: „value-definiteness“, „intrinsic property“, „pre-assigned initial values“ (Home und Whitaker), „precise value principle“ (Hughes), „classical principle C“ (Feyerabend), sowie Bells „beables“. Auch das in der Messtechnik verwendete Konzept des „wahren Wertes“ setzt Wert-Definiertheit voraus.
Zur erkenntnistheoretischen Einordnung der Wert-Definiertheit gibt es unterschiedliche Auffassungen. Feyerabend bezeichnete sie als ein „klassisches Prinzip“, und d’Espagnat ordnet sie dem physikalischen Realismus zu. Für den Physiker T. Norsen lässt sich das Prinzip der Wert-Definiertheit hingegen keiner der gängigen realistischen Positionen der Erkenntnistheorie zuordnen, weshalb er die Verwendung des Begriffes „Realismus“ in diesem Zusammenhang ablehnt: T. Norsen: Against ‘realism’. In: Foundations of Physics. Band 37, 2007, S. 311, doi:10.1007/s10701-007-9104-1, arxiv:quant-ph/0607057v2.
The following idea characterises the relative independence of objects far apart in space (A and B): external influence on A has no direct influence on B; this is known as the Principle of Local Action, which is used consistently only in field theory. If this axiom were to be completely abolished, the idea of the existence of quasienclosed systems, and thereby the postulation of laws which can be checked empirically in the accepted sense, would become impossible., aus A. Einstein: Quantenmechanik und Wirklichkeit. In: Dialectica 2. 1948, S. 320–324.
A. Einstein, B. Podolsky, N. Rosen: Can quantum-mechanical description of physical reality be considered complete?. In: Physical Review. Band 47, 1935, S. 777–780 (Online).
A. Aspect et al.: Experimental Tests of Realistic Local Theories via Bell’s Theorem. In: Physical Review Letters. Band 47, 1981, S. 460. A. Aspect et al.: Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. In: Physical Review Letters. Band 49, 1982, S. 91. A. Aspect et al.: Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. In: Physical Review Letters. Band 49, 1982, S. 1804. M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe, D. J. Wineland: Experimental violation of Bell’s inequalities with efficient detection. In: Nature. Band 409, 2001, S. 791–794.
Thus, a wide consensus has it that the quantum realm involves some type of non-locality. J. Berkovitz: Action at a Distance in Quantum Mechanics. Eintrag in der Stanford Encyclopedia of Philosophy, 2007 (Online).
S. Gröblacher et al.: An experimental test of non-local realism. In: Nature. Band 446, 2007, S. 871 (doi:10.1038/nature05677).
J. Berkovitz: Action at a Distance in Quantum Mechanics. Eintrag in der Stanford Encyclopedia of Philosophy, 2007, Kapitel 9 (Online)
E. Joos et al.: Decoherence and the Appearance of a Classical World in Quantum Theory. Springer, 2003, ISBN 3-540-00390-8.
Schlosshauer, Maximilian: Decoherence, the Measurement Problem, and Interpretations of Quantum Mechanics. In: Reviews of Modern Physics. Band 76, 2004, S. 1267–1305, arxiv:quant-ph/0312059v4, doi:10.1103/RevModPhys.76.1267.
A. Bassi, G.C. Ghirardi, Dynamical reduction models, Physics Reports 379 (2003) 257–426; G.C. Ghirardi, in: L. Accardi (Hrsg.): The Interpretation of Quantum Theory: Where Do We Stand?, Istituto dell’Enciclopedia Italiana, 1994.
The Development of the Interpretation of the Quantum Theory, in Wolfgang Pauli (Hrsg.), Niels Bohr and the Development of Physics. London: Pergamon (1955), 12–29.
“Despite an extensive literature which refers to, discusses, and criticizes the Copenhagen interpretation of quantum mechanics, nowhere [in the writings of the founders of quantum mechanics] does there seem to be any concise statement which defines the full Copenhagen interpretation”, aus “The Transactional Interpretation of Quantum Mechanics”, Cramer, J., Reviews of Modern Physics 58, (1986), 647–687.
J. Faye, Copenhagen Interpretation of Quantum Mechanics, Stanford Encyclopedia of Philosophy (2008), (Online)
Howard, D. Who Invented the “Copenhagen Interpretation”? A Study in Mythology. Philosophy of Science (2004), 71, 669–682. doi:10.1086/425941.
R. Gomatam, Niels Bohr’s Interpretation and the Copenhagen Interpretation – Are the two incompatible?, Philosophy of Science 74 (2007), S. 736. (Online) (Memento vom 5. Juli 2008 im Internet Archive) (PDF; 118 kB).
Beller, M. (1999). Quantum Dialogue: The Making of a Revolution. Chicago: University of Chicago Press
N. Bohr, Das Quantenpostulat und die neuere Entwicklung der Atomistik, Die Naturwissenschaften 15 (1928), S. 245–257 doi:10.1007/BF01504968.
W. Heisenberg, Quantentheorie und Philosophie, Reclam, 1979, S. 55–56. (Online, englische Übersetzung).
„Einstein [7] was an early supporter of the view, which he maintained until the end of his life, that quantum theory represented a correct and complete statistical theory of ensembles, but not a theory of elementary processes. […] In the early days of the quantum theory, ensemble interpretations had other strong advocates — Slater [9], Kemble [10], Popper [11], Langevin [12],and Margenau [13], but the very great influence of Bohr meant that, at the very least till the 1950s, such views remained peripheral.“: D. Home, M.A.B. Whitaker, Ensemble Interpretations of Quantum Mechanics. A Modern Perspective, Physics Reports 210 (1992), S. 223.
Einen Überblick über verschiedene Varianten der Ensemble-Interpretation bietet der Review-Artikel von Home und Whitaker: D. Home, M.A.B. Whitaker, Ensemble Interpretations of Quantum Mechanics. A Modern Perspective, Physics Reports 210 (1992), 223–317.
Eine allgemeinverständliche Beschreibung der Ensemble-Interpretation findet sich in P. Gibbins, Particles and Paradoxes, Cambridge University Press, 1987, S. 75ff.
Die determinierten Werte werden in der englischsprachlichen Literatur oft als „pre-assigned initial values“ (PIVs) bezeichnet (siehe z. B. Home und Whitaker). Hughes bezeichnet die Annahme determinierter Werte als „precise value principle“ (PVP).
D. Dürr, S. Goldstein, N. Zanghi, Quantum equilibrium and the origin of absolute uncertainty, Journal of Stat. Phys. 67 (1992), S. 843–907. arxiv:quant-ph/0308039v1
Hugh Everett III: “Relative State” Formulation of Quantum Mechanics. In: Reviews of modern physics. Vol. 29, 1957, S. 454–462, doi:10.1103/RevModPhys.29.454.
L. Vaidman, Many-Worlds Interpretation of Quantum Mechanics, Eintrag in der Stanford Encyclopedia of Philosophy, 2002, Kap. 6. (Online)
J. Barrett, Everett’s Relative-State Formulation of Quantum Mechanics, Eintrag in der Stanford Encyclopedia of Philosophy, 2008. (Online)
J. Baggott, Beyond measure: Modern physics, philosophy, and the meaning of quantum theory, Oxford University Press, 2004, S. 276–281
L. Vaidman, Many-Worlds Interpretation of Quantum Mechanics, Eintrag in der Stanford Encyclopedia of Philosophy, 2002, Kap. 4. (Online)
A. Whitaker, Einstein, Bohr and the Quantum Dilemma, Cambridge University Press, 2006, S. 316 ff.
J. B. Hartle, The quasiclassical realms of this quantum universe, in Many Quantum Worlds, editiert von A. Kent und S. Saunders, Oxford University Press, Oxford, 2009 (in Kürze erscheinend). arxiv:0806.3776v3.
D. Home, A. Whitaker, Einstein’s Struggles with Quantum Theory, Springer (2007), S. 259 ff.
A. Kent, Quantum Histories and Their Implications, Lect.Notes Phys. 559 (2000) 93–115. arxiv:gr-qc/9607073v4.
Ein aktueller Überblick über die rGRWf-Theorie findet sich in der Habilitationsarbeit des Physikers R. Tumulka:R. Tumulka: The Point Processes of the GRW Theory of Wave Function Collapse. In: Reviews in Mathematical Physics. Band 21, 2009, doi:10.1142/S0129055X09003608, arxiv:0711.0035.
G. Ghirardi: Collapse Theories. In: Stanford Encyclopedia of Philosophy. 2007 (stanford.edu).
A. Bassi, G. Ghirardi: Dynamical reduction models. In: Physics Reports. Band 379, Nr. 5-6, 2003, S. 257–426, doi:10.1016/S0370-1573(03)00103-0.
G. C. Ghirardi, A. Rimini und T. Weber: Unified dynamics for microscopic and macroscopic systems. In: Phys. Rev. D. Band 34, 1986, S. 470–491, doi:10.1103/PhysRevD.34.470.
Siehe z. B. A. Whitaker: Einstein, Bohr and the Quantum Dilemma: From Quantum Theory to Quantum Information. Cambridge University Press, 2006, ISBN 0-521-67102-7, S. 329 ff.
T. P. Singh: The inevitable nonlinearity of quantum gravity falsifies the many-worlds interpretation of quantum mechanics. In: Int. J. Mod. Phys. D. Band 17, 2008, S. 611–615, doi:10.1142/S0218271808012346, arxiv:0705.2357.
R. Penrose: On Gravity’s role in Quantum State Reduction. In: General Relativity and Gravitation. Band 28, Nr. 5, 1996, S. 581–600, doi:10.1007/BF02105068.
L. Diósi: Models for universal reduction of macroscopic quantum fluctuations. In: Phys. Rev. A. Band 40, 1989, S. 1165–1174, doi:10.1103/PhysRevA.40.1165.
Für einen Überblick über den aktuellen Stand der Technik zur experimentellen Untersuchung spontaner Kollapsprozesse sei auf den aktuellen Artikel von Kleckner et al. verwiesen: D. Kleckner, I. Pikovski, E. Jeffrey, L. Ament, E. Eliel, J. van den Brink und D. Bouwmeester: Creating and Verifying a Quantum Superposition in a Micro-optomechanical System. In: New J. Phys. Band 10, 2008, S. 095020, doi:10.1088/1367-2630/10/9/095020, arxiv:0807.1834.
A. Grinbaum, The Significance of Information in Quantum Theory, Doktorarbeit (2004), Kap. 2.2. arxiv:quant-ph/0410071v1.
C.G. Timpson, Philosophical Aspects of Quantum Information Theory, in D. Rickles (Hrsg.): The Ashgate Companion to the New Philosophy of Physics (Ashgate 2008), Kap. 5.2. arxiv:quant-ph/0611187.
A. Grinbaum, Reconstruction of Quantum Theory, Brit. J. Phil. Sci. 8 (2007), S. 387–408.
C. Rovelli, Relational Quantum Mechanics, International Journal of Theoretical Physics 35 (1996), S. 1637–1678. arxiv:quant-ph/9609002v2.
C. Rovelli, Relational Quantum Mechanics, Stanford Encyclopedia of Philosophy, 2008. (Online).
A. Zeilinger, A foundational principle for quantum mechanics, Found. Phys. 29 (1999), S. 631–643.
„Assuming that the information-theoretic constraints are in fact satisfied in our world, no mechanical theory of quantum phenomena that includes an account of measurement interactions can be acceptable, and the appropriate aim of physics at a fundamental level then becomes the representation and manipulation of information.“, in J. Bub, Why the Quantum?, Studies in History and Philosophy of Modern Physics 35B (2004), S. 241. arxiv:quant-ph/0402149v1.
“Every 'it', every particle, every field of force, even the spacetime continuum itself, derives its way of action and its very existence entirely, even if in some contexts indirectly, from the detector-elicited answers to yes-or-no questions, binary choices, bits. Otherwise stated, all things physical, all its … must in the end submit to an informationtheoretic description.” aus J.A. Wheeler, “Sakharov revisited; It from bit”, in L. V. Keldysh and V. Yu. Fainberg (Eds.), Proceedings of the first international Sakharov conference on physics, Vol. 2 (Nova Science Publishers; New York, 1991), S. 751.
G. Jaeger, Entanglement, Information, and the Interpretation of Quantum Mechanics, Springer (2009), Kap. 3.7, S. 188 und S. 234 ff.
A.Duwell, Quantum information does exist, Studies in History and Philosophy of Modern Physics 39 (2008), S. 195.
C. Timpson, Information, Immaterialism, Instrumentalism: Old and New in Quantum Information, in A. Bokulich und G. Jaeger (Editoren), Philosophy of Quantum Information and Entanglement. Cambridge University Press 2010, ISBN 978-0-521-89876-8. Online Preview (PDF; 196 kB)
C. Caves, C. A. Fuchs, and R. Schack, “Quantum probabilities as Bayesian probabilities,” Phys. Rev. A 65 (2002), S. 022305. arxiv:quant-ph/0106133v2.
A. Fuchs, R. Schack, Unknown Quantum States and Operations, a Bayesian View, Lecture Notes in Physics, Springer (2004), S. 147. arxiv:quant-ph/0404156v1.
C. Timpson, Quantum Bayesianism: A Study, Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), Kap. 4.1. arxiv:0804.2047v1.
C. Timpson, Quantum Bayesianism: A Study, Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), Kap. 2.1. arxiv:0804.2047v1.
„The question is what physical insight into the quantum world is gained from this interpretation other than, to borrow a phrase from Einstein, a “gentle pillow for the true believer in the information age”?“, in G. Jaeger, Entanglement, Information, and the Interpretation of Quantum Mechanics, Springer (2009), S. 179.
C. Timpson, Quantum Bayesianism: A Study, Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), S. 579. arxiv:0804.2047v1.
M. Dickson, D. Dieks, Modal Interpretations of Quantum Mechanics, Stanford Encyclopedia of Philosophy, 2007. (Online).
W. Zurek, Decoherence and the Transition from Quantum to Classical–Revisited, 2003. arxiv:quant-ph/0306072v1.
J. Cramer, Rev. Mod. Phys. 58 (1986), 647. (Online) (Memento vom 16. Juli 2012 im Internet Archive)
W.M. de Muynck, Foundations Of Quantum Mechanics: An Empiricist Approach, Springer, 2007.
„… In any case, all texts written between 1930 and 1950 – and this includes the books by Landé, de Broglie and Bohm, who later all turned against the Copenhagen view – espoused the complementarity principle even if they did not name it. In fact, it would be difficult to find a textbook of that period which denied that “the numerical value of a physical quantity has no meaning whatsoever until an observation upon is performed". M. Jammer: „The Philosophy of Quantum Mechanics“, Wiley, 1974, S. 247 ff.
O. Freire, The Historical Roots of “Foundations of Quantum Physics” as a Field of Research (1950–1970), Foundations of Physics, 34 (2004), 1741 doi:10.1007/s10701-004-1314-1.
M. Schlosshauer, Decoherence and the Quantum-to-Classical Transition, Springer 2007, ISBN 3-540-35773-4, Kap. 1, S. 10 ff.
G. Bacciagaluppi, The Role of Decoherence in Quantum Mechanics, Stanford Encyclopedia of Philosophy, 2007. (Online).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[75] Nach Bohr hat das Konzept eines physikalischen Zustands, der unabhängig von den Bedingungen seiner experimentellen Beobachtung ist, keine klar definierte Bedeutung. Nach Heisenberg stellt die Wellenfunktion eine Wahrscheinlichkeit dar, nicht aber eine objektive Realität in Raum und Zeit.

[76] Gemäß der Kopenhagener Interpretation bricht die Wellenfunktion zusammen, wenn eine Messung durchgeführt wird.

[77] Beide Teilchen und Führungswellenfunktion sind real.

[78] Eindeutige Partikelhistorie, aber mehrere Wellenhistorien.

[79] Die Art von Nichtlokalität, die von der Theorie verlangt wird, um die Bell-Ungleichungen zu verletzen, ist schwächer als die in EPR angenommene. Insbesondere ist diese Art von Nicht-Lokalität kompatibel mit keinem Signalisierungstheorem und Lorentz-Invarianz.

[80] Aber Quantenlogik ist in ihrer Anwendbarkeit begrenzter als kohärente Historien.

[81] Die Quantenmechanik wird als eine Art der Vorhersage von Beobachtungen oder eine Theorie der Messung angesehen.

[82] Die Annahme der intrinsischen Periodizität ist ein Element der Nicht-Lokalität, die mit der Relativität konsistent ist, da die Periodizität kausal variiert.

[83] In der stochastischen Interpretation ist es nicht möglich, Geschwindigkeiten für Teilchen zu definieren, d. h. die Wege sind nicht gradlinig. Um die Bewegung der Teilchen zu jedem Zeitpunkt zu kennen, muss man wissen, was der Markov-Prozess ist. Sobald wir jedoch die genauen Anfangsbedingungen und den Markov-Prozess kennen, ist die Theorie tatsächlich eine realistische Interpretation der Quantenmechanik.

[84] Beobachter trennen die universelle Wellenfunktion in orthogonale Sätze von Erfahrungen.

[85] Der Kollaps des Zustandsvektors wird als Abschluss der Transaktion zwischen Emitter und Absorber interpretiert.

[86] Die transaktionale Interpretation ist explizit nicht lokal.

[87] Der Vergleich von Historien zwischen Systemen in dieser Interpretation hat keine wohldefinierte Bedeutung.

[88] Jede physische Interaktion wird als ein Kollaps-Ereignis relativ zu den beteiligten Systemen behandelt, nicht nur makroskopische oder bewusste Beobachter.

[89] Der Zustand des Systems ist beobachtungsabhängig, d. H. der Zustand ist spezifisch für den Referenzrahmen des Beobachters.

[90] Eine Wellenfunktion kodiert lediglich die Erwartungen eines Agenten für zukünftige Erfahrungen. Es ist nicht mehr real als eine Wahrscheinlichkeitsverteilung ist in der Bajian (Bajaan Wahrscheinlichkeit).

[91] Die Quantentheorie ist ein Werkzeug, mit dem jeder Agent seine Erwartungen erfüllen kann. Die Vergangenheit kommt nur insoweit zum Tragen, als die individuellen Erfahrungen und das Temperament eines Handelnden seine Prioritäten beeinflussen.

[92] Obwohl QBism diese Terminologie vermeiden würde. Eine Veränderung der Wellenfunktion, die ein Agent einem System als Ergebnis einer Erfahrung zuschreibt, stellt eine Veränderung seiner Überzeugungen über weitere Erfahrungen dar, die sie möglicherweise haben.

[93] Beobachter oder, richtiger, Teilnehmer sind für den Formalismus genauso wichtig wie die Systeme, mit denen sie interagieren.

[Fuchs_2000-1] C. A. Fuchs, A. Peres: Quantum Theory needs no “Interpretation”. In: Physics Today. Nr. 53(3), 2000, Seite 70 (Online).

[Mermin_shut_up-2] If I were forced to sum up in one sentence what the Copenhagen interpretation says to me, it would be “Shut up and calculate!”, Zitiert in D. Mermin: Could Feynman Have Said This?. In: Physics Today. Nr. 57, 2004, Seite 10.

[Bohr-Zitat_Petersen-3] „There is no quantum world. There is only an abstract quantum physical description. It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature.“ Bohr-Zitat von Aage Petersen, in: The Bulletin of the atomic scientists. Nr. 19, 1963, Seite 8.

[Cartwright_2005-4] N. Cartwright: Another Philosopher Looks at Quantum Mechanics or What Quantum Theory is Not. In: Y. Ben-Menahem (Hrsg.): Hilary Putnam. Cambridge University Press, 2005, S. 188–202.

[Norsen_2006-5] E. Dennis, T. Norsen: Quantum Theory: Interpretation Cannot be avoided. arxiv:quant-ph/0408178.

[Bell_1990-6] „Jedoch auch die Vorstellung, dass sich die Quantenmechanik, unsere fundamentalste Theorie, ausschließlich mit Ergebnissen von Experimenten beschäftigt, würde unbefriedigend bleiben.“ und „Die Quantenmechanik ausschließlich auf lächerliche Laboroperationen zu beschränken, heißt, das große Vorhaben zu verraten. Eine ernsthafte Formulierung wird die große Welt außerhalb des Laboratoriums nicht ausschließen.“ Zitate aus: „Wider die ,Messung'“. In J. S. Bell: Quantenmechanik, Sechs mögliche Welten und weitere Artikel, de Gruyter, Berlin 2015, ISBN 978-3-11-044790-3, S. 241–259.

[7] Der Standpunkt, dass die klassische Mechanik wirklich deterministisch ist und Ungenauigkeiten auf die Unfähigkeit des Experimentators zurückzuführen sind, ist jedoch umstritten; entgegengesetzter Ansicht war beispielsweise Karl Popper. Karl Popper: Indeterminism in Quantum Physics and in Classical Physics I. In: The British Journal for the Philosophy of Science 1:2, 1950, S. 117–133. Karl Popper: Indeterminism in Quantum Physics and in Classical Physics II. In: The British Journal for the Philosophy of Science 1:3, 1950, 173–195.

[Potentia_Propensity-8] Die Formulierung des „objektiven Zufalls“ wird beispielsweise von A. Zeilinger verwendet. Heisenberg prägte zur Bezeichnung der Verwirklichungstendenz quantenmechanischer Systeme beim Messprozess den Begriff der „Potentia“. Auch Poppers Propensitäten-Interpretation liegt ein ähnliches Konzept von Wahrscheinlichkeit zugrunde.

[PauliRolleBeobachter-9] Die Formulierung geht auf Pauli zurück, der damit die Haltung Einsteins zusammenfasste: „Es erscheint mir durchaus angebracht, die konzeptive Beschreibung der Natur in der klassischen Physik, die Einstein so emphatisch beibehalten möchte, das Ideal des losgelösten Beobachters zu nennen. In drastischen Worten hat der Beobachter nach diesem Ideal gänzlich in diskreter Weise als versteckter Zuschauer (spectator) aufzuscheinen, niemals als Handelnder (actor), die Natur wird dabei in ihrem vorbestimmten Lauf der Ereignisse allein gelassen, unabhängig davon, auf welche Weise die Phänomene beobachtet werden.“ W. Pauli, Letter PLC 0014.51, veröffentlicht in K. V. Laurikainen: Wolfgang Pauli and the Copenhagen Philosophy. In: P. Lahti und P. Mittelstaedt (Hrsg.): Symposium on the Foundation of Modern Physics. World Scientific, Singapore 1985, S. 273–287.

[EspagnatInstrumentalismus-10] Die Gruppierung in Instrumentalismus versus Realismus ist eine starke Vereinfachung der tatsächlich vorhandenen Vielfalt verschiedener Positionen der Wissenschaftstheorie. Ein ausführlicher Überblick über die wichtigsten erkenntnistheoretischen Positionen in der Physik findet sich zum Beispiel in B. d’Espagnat: Reality and the Physicist: Knowledge, Duration and the Quantum World. Cambridge University Press, 1989, ISBN 0-521-33846-8.

[Stapp_1972-11] H. P. Stapp: The Copenhagen Interpretation. In: American Journal of Physics. Band 40, 1972, S. 1098, doi:10.1119/1.1986768.

[Value-Definiteness-12] In der englischsprachigen Literatur findet sich eine Vielzahl verschiedener Bezeichnungen für die Wert-Definiertheit: „value-definiteness“, „intrinsic property“, „pre-assigned initial values“ (Home und Whitaker), „precise value principle“ (Hughes), „classical principle C“ (Feyerabend), sowie Bells „beables“. Auch das in der Messtechnik verwendete Konzept des „wahren Wertes“ setzt Wert-Definiertheit voraus.

[AgainstRealism-13] Zur erkenntnistheoretischen Einordnung der Wert-Definiertheit gibt es unterschiedliche Auffassungen. Feyerabend bezeichnete sie als ein „klassisches Prinzip“, und d’Espagnat ordnet sie dem physikalischen Realismus zu. Für den Physiker T. Norsen lässt sich das Prinzip der Wert-Definiertheit hingegen keiner der gängigen realistischen Positionen der Erkenntnistheorie zuordnen, weshalb er die Verwendung des Begriffes „Realismus“ in diesem Zusammenhang ablehnt: T. Norsen: Against ‘realism’. In: Foundations of Physics. Band 37, 2007, S. 311, doi:10.1007/s10701-007-9104-1, arxiv:quant-ph/0607057v2.

[Einstein_1948-14] The following idea characterises the relative independence of objects far apart in space (A and B): external influence on A has no direct influence on B; this is known as the Principle of Local Action, which is used consistently only in field theory. If this axiom were to be completely abolished, the idea of the existence of quasienclosed systems, and thereby the postulation of laws which can be checked empirically in the accepted sense, would become impossible., aus A. Einstein: Quantenmechanik und Wirklichkeit. In: Dialectica 2. 1948, S. 320–324.

[EPR1935-15] A. Einstein, B. Podolsky, N. Rosen: Can quantum-mechanical description of physical reality be considered complete?. In: Physical Review. Band 47, 1935, S. 777–780 (Online).

[Bell-Experimente-16] A. Aspect et al.: Experimental Tests of Realistic Local Theories via Bell’s Theorem. In: Physical Review Letters. Band 47, 1981, S. 460. A. Aspect et al.: Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. In: Physical Review Letters. Band 49, 1982, S. 91. A. Aspect et al.: Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. In: Physical Review Letters. Band 49, 1982, S. 1804. M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe, D. J. Wineland: Experimental violation of Bell’s inequalities with efficient detection. In: Nature. Band 409, 2001, S. 791–794.

[SEP_Lokalität-17] Thus, a wide consensus has it that the quantum realm involves some type of non-locality. J. Berkovitz: Action at a Distance in Quantum Mechanics. Eintrag in der Stanford Encyclopedia of Philosophy, 2007 (Online).

[Gröblacher_2007-18] S. Gröblacher et al.: An experimental test of non-local realism. In: Nature. Band 446, 2007, S. 871 (doi:10.1038/nature05677).

[SEP_LokaleQuantentheorie-19] J. Berkovitz: Action at a Distance in Quantum Mechanics. Eintrag in der Stanford Encyclopedia of Philosophy, 2007, Kapitel 9 (Online)

[Joos2003-20] E. Joos et al.: Decoherence and the Appearance of a Classical World in Quantum Theory. Springer, 2003, ISBN 3-540-00390-8.

[Schlosshauer2004-21] Schlosshauer, Maximilian: Decoherence, the Measurement Problem, and Interpretations of Quantum Mechanics. In: Reviews of Modern Physics. Band 76, 2004, S. 1267–1305, arxiv:quant-ph/0312059v4, doi:10.1103/RevModPhys.76.1267.

[Bassi2003-22] A. Bassi, G.C. Ghirardi, Dynamical reduction models, Physics Reports 379 (2003) 257–426; G.C. Ghirardi, in: L. Accardi (Hrsg.): The Interpretation of Quantum Theory: Where Do We Stand?, Istituto dell’Enciclopedia Italiana, 1994.

[Heisenberg1955-23] The Development of the Interpretation of the Quantum Theory, in Wolfgang Pauli (Hrsg.), Niels Bohr and the Development of Physics. London: Pergamon (1955), 12–29.

[Cramer1986-24] “Despite an extensive literature which refers to, discusses, and criticizes the Copenhagen interpretation of quantum mechanics, nowhere [in the writings of the founders of quantum mechanics] does there seem to be any concise statement which defines the full Copenhagen interpretation”, aus “The Transactional Interpretation of Quantum Mechanics”, Cramer, J., Reviews of Modern Physics 58, (1986), 647–687.

[Faye_2008-25] J. Faye, Copenhagen Interpretation of Quantum Mechanics, Stanford Encyclopedia of Philosophy (2008), (Online)

[Howard2004-26] Howard, D. Who Invented the “Copenhagen Interpretation”? A Study in Mythology. Philosophy of Science (2004), 71, 669–682. doi:10.1086/425941.

[Gomatam2007-27] R. Gomatam, Niels Bohr’s Interpretation and the Copenhagen Interpretation – Are the two incompatible?, Philosophy of Science 74 (2007), S. 736. (Online) (Memento vom 5. Juli 2008 im Internet Archive) (PDF; 118 kB).

[Beller1999-28] Beller, M. (1999). Quantum Dialogue: The Making of a Revolution. Chicago: University of Chicago Press

[Bohr1928-29] N. Bohr, Das Quantenpostulat und die neuere Entwicklung der Atomistik, Die Naturwissenschaften 15 (1928), S. 245–257 doi:10.1007/BF01504968.

[Heisenberg_1958-30] W. Heisenberg, Quantentheorie und Philosophie, Reclam, 1979, S. 55–56. (Online, englische Übersetzung).

[Home_1992_Advocates_EI-31] „Einstein [7] was an early supporter of the view, which he maintained until the end of his life, that quantum theory represented a correct and complete statistical theory of ensembles, but not a theory of elementary processes. […] In the early days of the quantum theory, ensemble interpretations had other strong advocates — Slater [9], Kemble [10], Popper [11], Langevin [12],and Margenau [13], but the very great influence of Bohr meant that, at the very least till the 1950s, such views remained peripheral.“: D. Home, M.A.B. Whitaker, Ensemble Interpretations of Quantum Mechanics. A Modern Perspective, Physics Reports 210 (1992), S. 223.

[Home_1992-32] Einen Überblick über verschiedene Varianten der Ensemble-Interpretation bietet der Review-Artikel von Home und Whitaker: D. Home, M.A.B. Whitaker, Ensemble Interpretations of Quantum Mechanics. A Modern Perspective, Physics Reports 210 (1992), 223–317.

[Gibbins_1987-33] Eine allgemeinverständliche Beschreibung der Ensemble-Interpretation findet sich in P. Gibbins, Particles and Paradoxes, Cambridge University Press, 1987, S. 75ff.

[PIV-34] Die determinierten Werte werden in der englischsprachlichen Literatur oft als „pre-assigned initial values“ (PIVs) bezeichnet (siehe z. B. Home und Whitaker). Hughes bezeichnet die Annahme determinierter Werte als „precise value principle“ (PVP).

[Dürr1992-35] D. Dürr, S. Goldstein, N. Zanghi, Quantum equilibrium and the origin of absolute uncertainty, Journal of Stat. Phys. 67 (1992), S. 843–907. arxiv:quant-ph/0308039v1

[Everett_1957-36] Hugh Everett III: “Relative State” Formulation of Quantum Mechanics. In: Reviews of modern physics. Vol. 29, 1957, S. 454–462, doi:10.1103/RevModPhys.29.454.

[Vaidman_2002_Kritik-37] L. Vaidman, Many-Worlds Interpretation of Quantum Mechanics, Eintrag in der Stanford Encyclopedia of Philosophy, 2002, Kap. 6. (Online)

[Barrett_2008-38] J. Barrett, Everett’s Relative-State Formulation of Quantum Mechanics, Eintrag in der Stanford Encyclopedia of Philosophy, 2008. (Online)

[Baggott_2004-39] J. Baggott, Beyond measure: Modern physics, philosophy, and the meaning of quantum theory, Oxford University Press, 2004, S. 276–281

[Vaidman_2002_Wahrscheinlichkeit-40] L. Vaidman, Many-Worlds Interpretation of Quantum Mechanics, Eintrag in der Stanford Encyclopedia of Philosophy, 2002, Kap. 4. (Online)

[Whitaker_CH_2006-41] A. Whitaker, Einstein, Bohr and the Quantum Dilemma, Cambridge University Press, 2006, S. 316 ff.

[Hartle_2008-42] J. B. Hartle, The quasiclassical realms of this quantum universe, in Many Quantum Worlds, editiert von A. Kent und S. Saunders, Oxford University Press, Oxford, 2009 (in Kürze erscheinend). arxiv:0806.3776v3.

[Home_2007-43] D. Home, A. Whitaker, Einstein’s Struggles with Quantum Theory, Springer (2007), S. 259 ff.

[Kent_2000-44] A. Kent, Quantum Histories and Their Implications, Lect.Notes Phys. 559 (2000) 93–115. arxiv:gr-qc/9607073v4.

[Tumulka_2007-45] Ein aktueller Überblick über die rGRWf-Theorie findet sich in der Habilitationsarbeit des Physikers R. Tumulka:R. Tumulka: The Point Processes of the GRW Theory of Wave Function Collapse. In: Reviews in Mathematical Physics. Band 21, 2009, doi:10.1142/S0129055X09003608, arxiv:0711.0035.

[Ghirardi_2007-46] G. Ghirardi: Collapse Theories. In: Stanford Encyclopedia of Philosophy. 2007 (stanford.edu).

[Bassi_2003-47] A. Bassi, G. Ghirardi: Dynamical reduction models. In: Physics Reports. Band 379, Nr. 5-6, 2003, S. 257–426, doi:10.1016/S0370-1573(03)00103-0.

[Ghirardi_1986-48] G. C. Ghirardi, A. Rimini und T. Weber: Unified dynamics for microscopic and macroscopic systems. In: Phys. Rev. D. Band 34, 1986, S. 470–491, doi:10.1103/PhysRevD.34.470.

[Probleme_GRW0-49] Siehe z. B. A. Whitaker: Einstein, Bohr and the Quantum Dilemma: From Quantum Theory to Quantum Information. Cambridge University Press, 2006, ISBN 0-521-67102-7, S. 329 ff.

[Singh-50] T. P. Singh: The inevitable nonlinearity of quantum gravity falsifies the many-worlds interpretation of quantum mechanics. In: Int. J. Mod. Phys. D. Band 17, 2008, S. 611–615, doi:10.1142/S0218271808012346, arxiv:0705.2357.

[Penrose_1996-51] R. Penrose: On Gravity’s role in Quantum State Reduction. In: General Relativity and Gravitation. Band 28, Nr. 5, 1996, S. 581–600, doi:10.1007/BF02105068.

[Diosi_1989-52] L. Diósi: Models for universal reduction of macroscopic quantum fluctuations. In: Phys. Rev. A. Band 40, 1989, S. 1165–1174, doi:10.1103/PhysRevA.40.1165.

[Kleckner_2008-53] Für einen Überblick über den aktuellen Stand der Technik zur experimentellen Untersuchung spontaner Kollapsprozesse sei auf den aktuellen Artikel von Kleckner et al. verwiesen: D. Kleckner, I. Pikovski, E. Jeffrey, L. Ament, E. Eliel, J. van den Brink und D. Bouwmeester: Creating and Verifying a Quantum Superposition in a Micro-optomechanical System. In: New J. Phys. Band 10, 2008, S. 095020, doi:10.1088/1367-2630/10/9/095020, arxiv:0807.1834.

[Grinbaum_COE-54] A. Grinbaum, The Significance of Information in Quantum Theory, Doktorarbeit (2004), Kap. 2.2. arxiv:quant-ph/0410071v1.

[Timpson_2008-55] C.G. Timpson, Philosophical Aspects of Quantum Information Theory, in D. Rickles (Hrsg.): The Ashgate Companion to the New Philosophy of Physics (Ashgate 2008), Kap. 5.2. arxiv:quant-ph/0611187.

[Grinbaum_2007-56] A. Grinbaum, Reconstruction of Quantum Theory, Brit. J. Phil. Sci. 8 (2007), S. 387–408.

[Rovelli_1996-57] C. Rovelli, Relational Quantum Mechanics, International Journal of Theoretical Physics 35 (1996), S. 1637–1678. arxiv:quant-ph/9609002v2.

[Rovelli_SEP-58] C. Rovelli, Relational Quantum Mechanics, Stanford Encyclopedia of Philosophy, 2008. (Online).

[Zeilinger_1999-59] A. Zeilinger, A foundational principle for quantum mechanics, Found. Phys. 29 (1999), S. 631–643.

[Bub_2004-60] „Assuming that the information-theoretic constraints are in fact satisfied in our world, no mechanical theory of quantum phenomena that includes an account of measurement interactions can be acceptable, and the appropriate aim of physics at a fundamental level then becomes the representation and manipulation of information.“, in J. Bub, Why the Quantum?, Studies in History and Philosophy of Modern Physics 35B (2004), S. 241. arxiv:quant-ph/0402149v1.

[Wheeler1990-61] “Every 'it', every particle, every field of force, even the spacetime continuum itself, derives its way of action and its very existence entirely, even if in some contexts indirectly, from the detector-elicited answers to yes-or-no questions, binary choices, bits. Otherwise stated, all things physical, all its … must in the end submit to an informationtheoretic description.” aus J.A. Wheeler, “Sakharov revisited; It from bit”, in L. V. Keldysh and V. Yu. Fainberg (Eds.), Proceedings of the first international Sakharov conference on physics, Vol. 2 (Nova Science Publishers; New York, 1991), S. 751.

[Jaeger_2009b-62] G. Jaeger, Entanglement, Information, and the Interpretation of Quantum Mechanics, Springer (2009), Kap. 3.7, S. 188 und S. 234 ff.

[Duwell_2008b-63] A.Duwell, Quantum information does exist, Studies in History and Philosophy of Modern Physics 39 (2008), S. 195.

[Timpson_2007-64] C. Timpson, Information, Immaterialism, Instrumentalism: Old and New in Quantum Information, in A. Bokulich und G. Jaeger (Editoren), Philosophy of Quantum Information and Entanglement. Cambridge University Press 2010, ISBN 978-0-521-89876-8. Online Preview (PDF; 196 kB)

[Caves_2002-65] C. Caves, C. A. Fuchs, and R. Schack, “Quantum probabilities as Bayesian probabilities,” Phys. Rev. A 65 (2002), S. 022305. arxiv:quant-ph/0106133v2.

[Fuchs_QB_2004-66] A. Fuchs, R. Schack, Unknown Quantum States and Operations, a Bayesian View, Lecture Notes in Physics, Springer (2004), S. 147. arxiv:quant-ph/0404156v1.

[Timpson_2009_DispProp-67] C. Timpson, Quantum Bayesianism: A Study, Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), Kap. 4.1. arxiv:0804.2047v1.

[Timpson_2009_QB_Vorteile-68] C. Timpson, Quantum Bayesianism: A Study, Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), Kap. 2.1. arxiv:0804.2047v1.

[Jaeger_2009_Kritik_an_KI-69] „The question is what physical insight into the quantum world is gained from this interpretation other than, to borrow a phrase from Einstein, a “gentle pillow for the true believer in the information age”?“, in G. Jaeger, Entanglement, Information, and the Interpretation of Quantum Mechanics, Springer (2009), S. 179.

[Timpson_2009_ExpDef-70] C. Timpson, Quantum Bayesianism: A Study, Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), S. 579. arxiv:0804.2047v1.

[Dickson_SEP-71] M. Dickson, D. Dieks, Modal Interpretations of Quantum Mechanics, Stanford Encyclopedia of Philosophy, 2007. (Online).

[ZurekPTrevisited-72] W. Zurek, Decoherence and the Transition from Quantum to Classical–Revisited, 2003. arxiv:quant-ph/0306072v1.

[Cramer_1996-73] J. Cramer, Rev. Mod. Phys. 58 (1986), 647. (Online) (Memento vom 16. Juli 2012 im Internet Archive)

[MuynckInstrumentalismusPro-74] W.M. de Muynck, Foundations Of Quantum Mechanics: An Empiricist Approach, Springer, 2007.

[JammerDominanzKI-94] „… In any case, all texts written between 1930 and 1950 – and this includes the books by Landé, de Broglie and Bohm, who later all turned against the Copenhagen view – espoused the complementarity principle even if they did not name it. In fact, it would be difficult to find a textbook of that period which denied that “the numerical value of a physical quantity has no meaning whatsoever until an observation upon is performed". M. Jammer: „The Philosophy of Quantum Mechanics“, Wiley, 1974, S. 247 ff.

[Freire2004-95] O. Freire, The Historical Roots of “Foundations of Quantum Physics” as a Field of Research (1950–1970), Foundations of Physics, 34 (2004), 1741 doi:10.1007/s10701-004-1314-1.

[Schlosshauer2007-96] M. Schlosshauer, Decoherence and the Quantum-to-Classical Transition, Springer 2007, ISBN 3-540-35773-4, Kap. 1, S. 10 ff.

[Bacciagaluppi_SEP-97] G. Bacciagaluppi, The Role of Decoherence in Quantum Mechanics, Stanford Encyclopedia of Philosophy, 2007. (Online).