Atomkern

Der Atomkern ist der positiv geladene innere Teil eines Atoms. Die Unterteilung eines Atoms in Atomkern und Atomhülle geht auf Ernest Rutherford zurück, der 1911 in Streuexperimenten zeigte, dass Atome aus einem winzigen, kompakten Kern in einer leichten Hülle bestehen müssen. Dabei hat der Atomkern zwar einen 20.000 bis 150.000 Mal kleineren Durchmesser als die Atomhülle, beherbergt aber mehr als 99,9 Prozent der Masse des gesamten Atoms. Der Atomkern besteht aus Protonen und (außer bei ¹H) Neutronen. Der Atomkern bestimmt durch seine Protonenzahl (auch Kernladungszahl, Ordnungszahl) die Anzahl der Elektronen eines elektrisch neutralen Atoms, dadurch auch die Struktur der Elektronenhülle und somit die chemischen Eigenschaften des Atoms. Protonen und Neutronen werden im Kern durch Kernkräfte zusammengehalten. Ändert sich der Aufbau oder Zustand eines Kerns, wie z. B. durch Radioaktivität, kann die umgesetzte Energie millionenfach größer sein als bei einer chemischen Reaktion der Hülle.

Schematische Darstellung des Atoms (nicht maßstäblich, sonst wäre der untere Pfeil ca. 100 m lang).

Das Teilgebiet der Physik, das sich mit Atomkernen beschäftigt, heißt Kernphysik. In Begriffen, die den Atomkern betreffen, wurde in der Anfangszeit meist der Vorsatz „Atom-“ verwendet. Später wurde das weitgehend abgelöst durch Kern- oder Nuklear-, nach dem lateinischen Wort nucleus für Kern. Nuklear bezeichnet Dinge oder Wirkungen, die mit Eigenschaften oder mit Reaktionen von Atomkernen zusammenhängen, beispielsweise Nuklearmedizin.

Die einzelnen Atomsorten werden nach dem Aufbau ihrer Atomkerne als Nuklide bezeichnet.

Kenntnisse über die Eigenschaften von Atomkernen sind notwendig u. a. zum Verstehen der Radioaktivität, der Kernspaltung (Kernkraftwerk, Kernreaktor, Kernwaffe) und der Kernfusion (Kernfusionsreaktor, Wasserstoffbombe, Leuchten der Sterne), aber auch der Magnetresonanztomographie (MRT) in der Medizin sowie der Hyperfeinstruktur in der Spektroskopie.

Zur Geschichte der Forschung an Atomkernen siehe Kernphysik#Geschichte

Aufbau des Atomkerns

Größe, Dichte, Bestandteile, Bezeichnungen

Der Atomkern befindet sich, anschaulich gesprochen, im Zentrum des Atoms; sein Durchmesser beträgt etwa ¹⁄_20.000 bis ¹⁄_150.000 des Durchmessers der Elektronenhülle. Ein Atomkern hat z. B. bei Helium rund 1 fm (Femtometer) Durchmesser, beim Uran etwa 16 fm. Der Atomkern stellt aber, je nach Element, 99,95 bis 99,98 Prozent der Masse des gesamten Atoms.

Die Dichte des Kerns (das Verhältnis von Kernmasse zu Kernvolumen) ist für alle Kerne annähernd gleich und beträgt rund 2·10¹⁷ kg/m³.[1] Materie in dieser Dichte heißt Kernmaterie. Um diese Dichte zu erreichen, müsste man beispielsweise die Cheops-Pyramide auf die Größe eines Pfefferkorns zusammendrücken.

Der Kern ist aufgebaut aus Protonen und Neutronen, die etwa gleiche Masse haben und zusammen auch Nukleonen genannt werden. Die Zahl der Protonen wird Kernladungszahl genannt und in aller Regel mit $Z$ bezeichnet. Die Gesamtzahl der Nukleonen wird Massenzahl $A$ genannt, die Zahl der Neutronen wird mit $N$ bezeichnet, so dass $A=Z+N$ (für Genaueres zur Masse des Kerns siehe Kernmasse oder Massendefekt). Die Massenzahlen der auf der Erde natürlich vorkommenden Atome reichen von $A=1$ (normaler Wasserstoff ¹H) bis 244 (Plutonium ²⁴⁴Pu). Die makroskopische Dichte der kondensierten Materie dagegen steigt nicht proportional zur Atommasse, weil auch der Atomradius im Mittel ums 3–4-fache ansteigt (neben starken periodischen Schwankungen, siehe Abb. in Atomradius).

Protonen sind elektrisch positiv geladen, Neutronen neutral. Daher ist der Atomkern positiv geladen und kann durch die Coulombkraft negativ geladene Elektronen an sich binden. Da die Ladungen von Elektron und Proton entgegengesetzt gleich ist, hat ein nach außen hin elektrisch neutrales Atom ebenso viele Elektronen in der Atomhülle wie Protonen im Kern. Da die Atomhülle weitestgehend die chemischen Eigenschaften bestimmt, legt die Kernladungszahl damit auch fest, zu welchem Element das Atom gehört, sie ist die chemische Ordnungszahl.

Die Zahl der Neutronen hat nur geringen Einfluss auf die chemischen Eigenschaften des Atoms, ist aber entscheidend für die Stabilität oder Instabilität (Radioaktivität) des Kerns. Abgesehen vom radioaktiven Zerfall – der spontan eintritt – kann sich die Zahl der Protonen oder Neutronen im Kern nur durch eine Kernreaktion ändern, also infolge eines Zusammenstoßes des Kerns mit einem anderen Kern oder mit anderen Teilchen.

Eine durch Ordnungszahl und Massenzahl festgelegte Atom- oder Atomkernsorte wird Nuklid genannt. Bei einem gg-Kern sind $Z$ und $N$ geradzahlig, bei einem uu-Kern sind beide ungerade, und bei einem ug- oder gu-Kern ist entweder $Z$ oder $N$ gerade. Als Isomere werden Atomkernsorten in langlebigen Anregungsstufen des Kerns (siehe unten) bezeichnet; sie zählen als eigene Nuklide.[2] Unterscheidet man Kerne (oder ganze Atome) desselben Elements, also mit gleicher Protonenzahl, nach ihrer Anzahl von Neutronen, spricht man von den Isotopen des betreffenden Elements. Bezeichnet werden Nuklide mit dem chemischen Elementsymbol und der Massenzahl, wie z. B. das häufigste Kohlenstoffisotop ¹²C oder das häufigste Eisenisotop ⁵⁶Fe (bei Isomeren noch mit einem Zusatz wie „m“ für „metastabil“). Weniger üblich ist die Schreibweise C-12 bzw. Fe-56, oder die redundante zusätzliche Angabe der Ordnungszahl: ${}_{26}^{56}\mathrm {Fe}$ .

Nuklidkarte

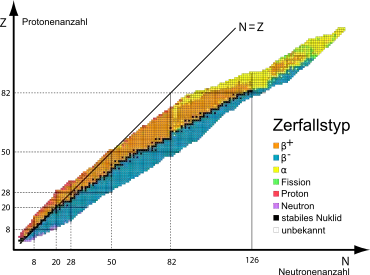
Es sind (Stand von 2003) insgesamt etwa 3200 langlebige Nuklide bekannt,[3] die sich auf etwa 2700 Isotope[4] und 118 bekannte Elemente von Wasserstoff bis zum Oganesson verteilen. Darunter gibt es ca. 250 stabile Isotope. Die Stabilität eines Nuklids hängt von der Zahl der Protonen und der Neutronen ab. Liegt das Verhältnis beider Zahlen außerhalb eines bestimmten Bereichs, ist der Kern instabil, d. h. radioaktiv, und wandelt sich in einen stabileren Kern um. Zu den Protonenzahlen 43, 61, oder größer als 82, gibt es gar kein stabiles Nuklid.

Die Nuklide werden zur Übersicht in einer Nuklidkarte oder „Isotopenkarte“ durch kleine Quadrate grafisch dargestellt. Die Abbildung zeigt 1500 Nuklide (Stand 2010). Die Abszisse gibt die Neutronenzahl an, die Ordinate die Protonenzahl. Stabile Nuklide haben schwarze Quadrate, links unten beginnend mit ¹H, rechts oben endend mit ²⁰⁸Pb. Die Schmalheit des schwarzen Bandes zeigt, wie genau die Abstimmung von Protonen- und Neutronenzahl für einen stabilen Kern sein muss. Bis A=40 müssen beide Zahlen nahezu gleich sein, darüber müssen die Neutronen zunehmend im Überschuss vorhanden sein (bis ca. 1,6:1). Die übrigen Kerne sind sämtlich instabil, wobei die Farbe des Quadrats die radioaktiven Umwandlungsarten anzeigt.

Kernspin und Kernmomente

Dass Protonen den Spin 1/2 besitzen, wurde 1927 durch David Dennison gezeigt, der aus dieser Eigenschaft erstmals die ungewöhnliche Temperaturabhängigkeit der spezifischen Wärme von Wasserstoffgas theoretisch ableiten konnte. Diese ist bei tiefen Temperaturen verschieden, je nachdem ob die beiden Protonen ihre Spins parallel oder antiparallel ausrichten, weil jeweils bestimmte Rotationsniveaus des Moleküls aus Gründen der Vertauschungssymmetrie dann nicht vorkommen. Die Messwerte zeigten, dass im normalen Wasserstoffgas 3/4 der Moleküle die Parallelstellung hatten (Orthowasserstoff) und 1/4 die Antiparallelstellung (Parawasserstoff). Dies Mengenverhältnis passt nur zum Protonenspin 1/2.

Dass alle Kerne, deren Nukleonenzahl $A$ ungerade ist, Drehimpuls (Kernspin $I$ ) und magnetisches Dipolmoment besitzen, wurde aus der Hyperfeinaufspaltung der Spektrallinien gezeigt, die aus der Wechselwirkung mit dem Magnetfeld der Hülle resultiert. Daraus wurde durch Auszählen der Komponenten einer Spektrallinie 1928 zum ersten Mal ein Kernspin bestimmt (Kern Bi-219, Spin 9/2). Andere Kernspins konnten in den 1930er Jahren aus den Rotationsbanden in den Spektren symmetrischer Moleküle wie N₂ ermittelt werden. Sie zeigen, wenn beide Atome zum gleichen Isotop gehören, einen für den Kernspin charakteristischen periodisch wiederholten Intensitätswechsel der Linien, der mit dem Symmetriecharakter des Moleküls bei Spiegelung erklärt wird.

Weiter zeigten sich bei Kernen mit $I\geq 1$ ab den 1940er Jahren in der Hyperfeinstruktur kleine Unregelmäßigkeiten, die als zusätzliche Wechselwirkung des elektrischen Quadrupolmoments mit dem inhomogenen elektrischen Feld der Elektronenhülle gedeutet wurden. Das deutete darauf hin, dass diese Kerne nicht genau kugelförmig, sondern elliptisch deformiert sind.

Kernkraft, Coulombkraft

Alle Nukleonen ziehen sich gegenseitig durch die Kernkräfte an. Diese sind eine Restwechselwirkung der Starken Wechselwirkung und haben daher nur kurze Reichweite. Ab einer größeren Entfernung als etwa ein Nukleondurchmesser (etwa 1 fm = 10⁻¹⁵ m) überwiegt zwischen je zwei Protonen die Abstoßung durch die langreichweitige Coulombkraft. Die lange Reichweite der Coulombkraft gegenüber der kurzen Reichweite der Kernkraft begrenzt die Größe der Atomkerne und damit auch Anzahl chemischer Elemente, die stabile Isotope haben können. Denn auch in einem großen Kern spürt ein Proton nur die Anziehung seiner nächsten Nachbar-Nukleonen, die Coulomb-Abstoßung hingegen von allen anderen Protonen des Kerns. Oberhalb der Protonenzahl 82 (Blei) ist die Abstoßung so stark, dass alle weiteren Kerne instabil sind, d. h. radioaktiv.

Unter diesen gibt es Nuklide mit Halbwertszeiten bis zu 14 Mrd. Jahren (Thorium ${}_{\ 90}^{232}\mathrm {Th}$ ), weshalb sie auf der Erde auch in natürlichen Vorkommen noch zu finden sind. Als Nuklid mit der höchsten natürlich vorkommenden Protonenzahl wurde in Spuren ${}_{\ 94}^{244}\mathrm {Pu}$ gefunden. Gewöhnlich werden nur Nuklide bis ${}_{\ 92}^{238}\mathrm {U}$ (Uran) als natürlich vorkommend gezählt. Kerne mit noch mehr Protonen (Transurane) „leben“ nicht lange genug, um als primordiale Nuklide vorzukommen; sie können nur nach künstlicher Herstellung in Kernreaktionen beobachtet werden.

Bindungsenergie

Mittlere Bindungsenergie pro Nukleon in Abhängigkeit von der Anzahl der Nukleonen im Atomkern.[5] Stabile Nuklide schwarz, instabile rot

Die Bindungsenergie entspricht der Energie, die zugeführt werden müsste, um den Kern in seine einzelnen Nukleonen zu zerlegen. Umgekehrt würde diese Bindungsenergie freigesetzt, wenn es gelänge, einen Atomkern aus freien Protonen und Neutronen zusammenzusetzen. Wegen der Äquivalenz von Masse und Energie führt die Bildung des Kerns zu einem Massendefekt. Das heißt, jeder Atomkern (außer ¹H) hat eine geringere Masse, als sich beim Addieren der ihn bildenden – ungebundenen – Nukleonen ergibt. Der Massendefekt liegt zwischen 0,1 % (Deuteron) und 0,9 % (Ni-62). Aus einer genauen Bestimmung der Masse $M(A,Z)$ eines Atoms mit A Nukleonen, darunter Z Protonen, lässt sich daher die Bindungsenergie $E_{\text{B}}$ des Kerns ableiten:

E_{\text{B}}(Z,A)=\left[Z\cdot m_{\text{p}}+Z\cdot m_{\text{e}}+(A-Z)\cdot m_{\text{n}}-m(A,Z)\right]\cdot c^{2}

Dabei ist

m_{\text{p}}

die Masse eines freien Protons,

m_{\text{e}}

die Masse eines Elektrons,

m_{\text{n}}

die Masse eines freien Neutrons,

c

die Lichtgeschwindigkeit.

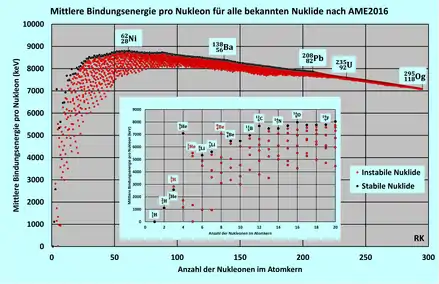
Die Bindungsenergie kurzlebiger Kerne lässt sich beispielsweise durch Messung der Energien ihrer Zerfallsprodukte bestimmen. Gemessene Werte für die mittlere Bindungsenergie pro Nukleon sind in vorstehender Abbildung dargestellt, wobei die Bindungsenergie pro Nukleon für eine Auswahl von Nukleonen in der kleineren Abbildung herausgehoben dargestellt ist.

Die Bindungsenergie der Kerne nimmt in etwa proportional zur Nukleonenzahl $A$ zu. Entsprechend bleibt die mittlere Bindungsenergie pro Nukleon (siehe Abbildung) in einem weiten Bereich in etwa bei ungefähr 8 MeV. Beginnend mit 1,1 MeV pro Nukleon bei $A=2$ steigt sie bis $A\approx 16$ auf Werte um 8 MeV. Ihr Maximum erreicht sie bei Ni-62 mit 8,8 MeV pro Nukleon. Anschließend nimmt sie allmählich bis auf etwa 7 MeV ab, verursacht durch die zunehmende elektrostatischen Abstoßung aller Protonen untereinander.

Aufgrund der unterschiedlichen Bindungsenergie pro Nukleon bei verschiedenen Kernen können Kernreaktionen, bei denen sich hinterher die Nukleonen anders gruppieren als vorher, ein erheblicher Energiegewinn ergeben. Eine Erhöhung der Bindungsenergie pro Nukleon tritt bei der Fusion zweier leichterer Kerne, aber auch bei der Spaltung eines schweren Kerns ein. Bei der Fusion von He-4 aus kleineren Kernen ist die Freisetzung besonders hoch, was für die technische Kernfusion ausgenutzt werden kann. Die Spaltung schwerer Atomkerne (ab U-235) wird in Kernkraftwerken seit den 1950er Jahren zur Energiegewinnung ausgenutzt. Beide Arten der Energiefreisetzung werden auch in Kernwaffen realisiert.

Die Bindungsenergie von Atomkernen kann im Rahmen des Tröpfchenmodells mit der Bethe-Weizsäcker-Formel mit etwa 1%iger Genauigkeit abgeschätzt werden.

Von der mittleren Bindungsenergie pro Nukleon zu unterscheiden ist die Ablösearbeit, das ist die Energie, die zur Ablösung eines einzigen Nukleons nötig ist. Sie variiert bei stabilen Kernen zwischen 1,1 MeV (Deuteron H-2) und 16,9 MeV (Ne-20). Maxima liegen bei den „magischen Zahlen“ und sind, wie die Ionisierungsenergie bei den Atomen, ein Charakteristikum von Schalenabschlüssen.

Energieniveaus

Atomkerne haben wie die Elektronenhülle diskrete Energieniveaus, typische Abstände zwischen ihnen betragen aber nicht einige eV wie bei Atomen, sondern 100 keV bis einige MeV. Die Folge dieser Niveaus setzt sich, wie bei Atomen auch, im Kontinuum fort, also oberhalb der Energie, die die Ablösung eines Teilchens ermöglicht (sie werden dann als Resonanz bezeichnet). Ein ungestörter Kern befindet sich normalerweise in seinem tiefsten Energieniveau, dem Grundzustand. Die höheren Niveaus (angeregte Zustände) sind nicht stabil, vielmehr geht der Kern früher oder später spontan in einen stabileren Zustand über, wobei die Energiedifferenz in den allermeisten Fällen als Photon (Gammastrahlung) oder an ein Elektron der K-Schale abgegeben wird (Innere Konversion). Die seltenen anderen Möglichkeiten sind die Emission eines Hüllenelektrons aus einer anderen Schale und die Paarerzeugung von Elektron und Positron. Jedes Niveau hat einen bestimmten Drehimpuls (Kernspin) und wohldefinierte Parität (bis auf eine winzige Beimischung aufgrund der Paritätsverletzung durch die Schwache Wechselwirkung). Der Zerfall der angeregten Zustände folgt dem exponentiellen Zerfallsgesetz mit meist sehr kurzen Halbwertszeiten (10⁻¹⁴s sind nicht selten); besonders langlebige (metastabile) angeregte Zustände (Halbwertszeiten von Nanosekunden bis Millionen Jahre) werden als Isomere bezeichnet. Oft verdanken sie ihre lange Lebensdauer einem Kernspin, der einige $\hbar$ größer ist als bei allen durch einen spontanen Übergang erreichbaren Zuständen.

Bei der Folge der Energieniveaus lassen sich einige Grundtypen der Anregungsformen unterscheiden:

Kollektive Rotation

Ein von der Kugelform abweichender Kern kann als ganzes zu Rotation angeregt werden. In einfachen Fällen (gg-Kerne) haben die Niveaus den geradzahligen Kernspin $I=0,2,4,\dots$ und, wie mit den Formeln der klassischen Mechanik, die Anregungsenergie

E={\frac {\hbar ^{2}}{2\Theta }}I(I+1)

,

wobei $\Theta$ das Trägheitsmoment ist. Die Abstände zwischen aufeinanderfolgenden Niveaus wachsen regelmäßig an und bilden eine Rotationsbande, wie sie auch aus den optischen Spektren 2-atomiger Moleküle bekannt ist. Dieses Bild kommt bei vielen Kernen vor, vor allem bei großen Kernen weitab von abgeschlossenen Schalen, wenn sie eine stabile ellipsoide Deformation aufweisen.

Kollektive Schwingung

In Kernen können die Protonen kollektiv gegenüber den Neutronen schwingen. Die Schwingungsfrequenz liegt oberhalb von etwa $\omega =10^{22}\,\mathrm {s^{-1}}$ , die Energie also im Bereich $E=\hbar \omega =25\,\mathrm {MeV}$ . Die Anregung heißt Riesenresonanz, weil sie sich in allen nicht zu kleinen Kernen durch einen erhöhten Wirkungsquerschnitt der Wechselwirkung mit Gammaquanten der entsprechenden Energien bzw. Frequenzen zeigt.

Daneben sind für kugelförmige Kerne, wenn sie auf der Isotopenkarte nahe bei den Gebieten mit deformierten Kernen liegen, Formschwingungen der Oberfläche bei konstantem Volumen möglich (analog den Formschwingungen von großen Seifenblasen). Das Energiespektrum $E_{n}\approx n\hbar \omega$ ist eine Vibrationsbande. Es zeigt (näherungsweise) äquidistante Anregungsenergien, deren Grundschwingung $\hbar \omega$ im Bereich von 1 MeV Anregungsenergie liegt. Die höheren Niveaus sind leicht aufgespalten und lassen sich theoretisch als Anregung mit mehreren gleichen Schwingungsquanten deuten. An der Anzahl der aufgespaltenen Niveaus und den dabei vorkommenden Kernspins zeigt sich, dass die Anregungsquanten sich wie identische Bosonen verhalten. Bei Schwingungen mit elliptischer Deformation haben sie den Spin $I=2$ , bei birnenförmiger Schwingung $I=3$ .

Außerdem gibt es bei kugelförmigen Kernen Kompressionsschwingungen. Diese sind kugelförmig, haben den Kernspin $I=0$ und eine Energie über 100 MeV. Daraus kann man den Kompressionsmodul von Kernmaterie bestimmen.

Einzelteilchenanregung

Bei Kernen nahe an abgeschlossenen Schalen für Protonen und/oder Neutronen zeigen sich Anregungsspektren, die nach Energie und Kernspin durch die Eigenschaften einzelner Orbitale bestimmt sind. Diese Spektren haben bei verschiedenen Kernen je nachdem, welches Orbital beteiligt ist, sehr unterschiedliche Folgen von Energie und Kernspin. Da die Drehimpulse benachbarter Orbitale sich in manchen Fällen stark unterscheiden, ergeben sich hier die Bedingungen für metastabile Zustände (auf der Nuklidkarte „Isomerieinseln“).

Radioaktivität

Der Begriff Radioaktivität bezeichnet die Eigenschaft instabiler Nuklide, sich spontan unter Energieabgabe umzuwandeln. Von den meisten Elementen existieren nur wenige stabile Isotope oder sogar nur eins; bei den Ordnungszahlen 43 (Technetium), 61 (Promethium) und allen oberhalb 82 (Blei) gibt es keine stabilen Isotope. Im Allgemeinen wird bei der Umwandlung ionisierende Strahlung ausgesandt.

Bei den instabilen Atomkernen werden im Wesentlichen drei Zerfallsarten unterschieden:

Zerfall unter Aussendung von Nukleonen (z. B. Alphazerfall),
Umwandlung unter Aussendung von Elektronen oder Positronen (Betazerfälle) und
Übergang zwischen zwei Zuständen ein und desselben Nuklids unter Emission von Gammastrahlung.

Alphazerfall tritt nur bei hohen Massenzahlen auf, wenn die mittlere Bindungsenergie pro Nukleon sich durch die Abgabe von zwei Protonen und zwei Neutronen genügend erhöht. Das ist theoretisch ab etwa $A=140$ gegeben. Bei großem $A$ , etwa ab 230, tritt auch spontane Kernspaltung auf.

Beim Betazerfall wird aus dem Kern eines Radionuklids ein Elektron oder Positron abgegeben. Dieses entsteht, indem sich im Kern eines der Neutronen in ein Proton, ein Elektron-Antineutrino und ein Elektron (Beta-Minus-Zerfall) bzw. eines der Protonen in ein Neutron, ein Elektron-Neutrino und ein Positron (Beta-Plus-Zerfall) umwandelt. Die Summe der elektrischen Ladungen und die Anzahl der Nukleonen bleibt dabei erhalten, aber die Mischung aus Protonen und Neutronen wird energetisch günstiger. Die chemische Ordnungszahl ändert sich um ±1. Betazerfall tritt bei allen Massenzahlen auf.

Die Abgabe von Gammastrahlung setzt voraus, dass der Kern in einem angeregten Zustand ist (vgl. Abschnitt Energieniveaus) und tritt daher hauptsächlich unmittelbar nach einem Alpha- oder Betazerfall auf, sofern dieser nicht direkt zum Grundzustand des Tochterkerns führt. Deshalb wird auch die Gamma-Emission analog den anderen Prozessen der Radioaktivität manchmal als Gamma„zerfall“ bezeichnet.

Kernmodelle

In der Kernphysik existiert kein einheitliches Modell zur umfassenden Beschreibung aller Vorgänge im Atomkern. Im Vergleich zu der Atomphysik mit dem erfolgreichen quantenmechanischen Atommodell fehlt im Kern ein besonderes, massives Kraftzentrum, und die Kräfte zwischen den Nukleonen sind um vieles komplizierter als die rein elektromagnetische Wechselwirkung im Atom. Daher werden verschiedene Kernmodelle für unterschiedliche Fragestellungen benutzt. Die wichtigsten sind:

Das Tröpfchenmodell (Carl Friedrich von Weizsäcker 1935, Niels Bohr 1936) beschreibt den Atomkern als kugelrundes Tröpfchen einer elektrisch geladenen Flüssigkeit und ergibt eine Formel für seine gesamte Bindungsenergie. Mit diesem fast klassischen Modell kann gut erklärt werden, welche Isotope stabil sind und welche sich noch durch Energieabgabe in ein fester gebundenes umwandeln können, etwa durch α-Zerfall, β-Zerfall, Kernspaltung. Damit findet u. a. auch die Anzahl der stabilen chemischen Elemente auf der Erde eine Begründung.
Das Schalenmodell für Kerne (Maria Goeppert-Mayer, J. Hans D. Jensen, 1949) führt den Aufbau der Atomkerne in Analogie zum Schalenmodell der Atomphysik rein auf quantenmechanische Gesetzmäßigkeiten (Orbitale in einem Potentialtopf, Pauli-Prinzip) zurück. Die Wechselwirkung zwischen je zwei Nukleonen wird erst in einer weiteren Verfeinerung berücksichtigt. Das Schalenmodell kann bei der Bindungsenergie der Kerne die Abweichungen vom Tröpfchenmodell erklären, insbesondere die hohe Stabilität bei bestimmten, sogenannten magischen Protonen- und Neutronenanzahlen. Es liefert auch detaillierte Erklärungen für Energieniveaus, Kernspins, magnetische Momente, Mechanismen von Kernreaktionen, soweit sie von der Bewegung eines einzigen oder nur sehr weniger Nukleonen des Kerns herrühren. Häufig werden aber angeregte Zustände eines Atomkerns unter Beteiligung vieler oder sogar aller Nukleonen gebildet.
Das Kollektivmodell (Aage Niels Bohr, Ben Mottelson, 1953) dient bei deformierten Kernen der Beschreibung kollektiver Anregungen (Vibrationen und Rotationen). Diese Kerne haben keine exakte Kugelgestalt, sondern sind in einer Richtung leicht abgeplattet oder etwas gestreckt, was sich zum Beispiel an den elektrischen Quadrupolmomenten dieser Kerne zeigt. Folge ist ein charakteristisches Niveauschema der angeregten Zustände in Form der Vibrationsbande bzw. Rotationsbande.
Im vereinheitlichten Modell (unified model, James Rainwater 1957) werden Schalenmodell und Kollektivmodell verbunden.

Weitere teils sehr vereinfachte Modelle bzw. für Spezialzwecke betrachtete Modelle sind zum Beispiel:

Fermigas-Modell (auch uniformes Modell). Hier werden die Nukleonen trotz ihrer starken Wechselwirkungen als frei beweglich angenommen und unterliegen nur dem Pauli-Prinzip. Diese Vorstellung wird im Tröpfchenmodell zur Bindungsenergie benutzt, um die Asymmetrie-Energie, die den Einfluss des Verhältnisses von Neutronen- zu Protonenzahl beschreibt, zu begründen.
Alphateilchen-Modell. Alphateilchen sind hier stabile Untereinheiten innerhalb des Kerns, was z. B. für die Kerne C-12, O-16, Ne-20 eine nützliche Modellvorstellung abgibt.
Potentialtopf-Modell. Hier wird in Analogie zum Atom ein bestimmtes Potential vorgegeben und daraus das Spektrum der Energieeigenzustände eines einzelnen Nukleons ermittelt. Es ist die Grundlage des Schalenmodells und des räumlich beschränkten Fermigas-Modells. Als Formen des Potentials kommen vor allem das einfache Kastenpotential, das Oszillatorpotential sowie das erheblich realistischere Woods-Saxon-Potential vor.
Optisches Modell. Hier werden Kernreaktionen dadurch modelliert, dass das einfliegende Projektil durch den Targetkern so beeinflusst wird wie eine Lichtwelle durch eine absorbierende („trübe“) Linse. Das Modell eignet sich gut für die elastische Streuung sowie für Reaktionen, in denen dem Targetkern lediglich ein Teilchen entrissen oder ihm hinzugefügt wird.
Interacting Boson Model. Hier werden die Nukleonen außerhalb einer abgeschlossenen Schale zunächst zu Paaren von Protonen bzw. Neutronen zusammengefasst, und im nächsten Schritt deren Wechselwirkung untereinander modelliert.

An den Modellen des Atomkerns zeigen sich zwei stark vereinfachende, aber entgegengesetzte Ausgangspunkte:

Modell starker Korrelation: Der Atomkern wird als Ansammlung von eng gepaarten Nukleonen oder Nukleonengruppen verstanden (z. B. Tröpfchenmodell, Alphateilchen-Modell, Berücksichtigung von Pairing in Kernen ähnlich wie bei der Supraleitung);
Modelle unabhängiger Teilchen: Die Nukleonen bewegen sich relativ frei im Kern (Fermigas-Modell, optisches Modell, Schalenmodell, Potentialtopf-Modell).

Realistische Modelle zeichnen sich durch eine geeignete Kombination beider Ansätze aus.

Jedes der genannten Modelle ist nur für einen bestimmten Bereich der nuklearen Phänomene anwendbar, eine widerspruchsfreie und umfassende Theorie konnte noch nicht formuliert werden.

Siehe auch

Literatur

Klaus Bethge, Gertrud Werner, Bernhard Wiedemann: Kernphysik. Eine Einführung, 3. Auflage, Springer 2008
Theo Mayer-Kuckuk, Kernphysik. 6. durchgesehene Auflage. B.G. Teubner, Stuttgart 1994, ISBN 3-519-03223-6.
B. Povh, K. Rith, C. Scholz, F. Zetsche, W. Rodejohann: Teilchen und Kerne: Eine Einführung in die physikalischen Konzepte. 9. Auflage. Springer, 2014, ISBN 978-3-642-37821-8.

Videos

Was ist ein Atomkern? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 18. Mär. 2001.
Einfache Erklärung von „Anderthalb“ (langsame Verbindung)
Einfache Erklärung von „Anderthalb“ (schnelle Verbindung)

Weblinks

Wiktionary: Atomkern – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Animierte Seite zu Kernmodellen (Potentialtopf-, Tröpfchen-) (LEIFI)
Umfangreiche Nuklidliste
Paul, Weise: Teilchen und Kerne. Skript, TU München
An den Grenzen der Nuklidkarte - wo existieren gebundene Kerne?

Einzelnachweise

D. Meschede: Gerthsen Physik. 22. Auflage, 2004, S. 630.
nuclide. In: Alan D. McNaught, Andrew Wilkinson, IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. 2. Auflage. Blackwell Scientific Publications, Oxford 1997, ISBN 0-9678550-9-8, doi:10.1351/goldbook.N04257 (englisch, korrigierte Fassung – erstellt von M. Nic, J. Jirat, B. Kosata; mit Aktualisierungen von A. Jenkins [2006–]).
G. Audi, O. Bersillon, J. Blachot, A. H. Wapstra: The NUBASE evaluation of nuclear and decay properties. In: Nuclear Physics. A 729, 2003, S. 3–128, doi:10.1016/j.nuclphysa.2003.11.001 (englisch, in2p3.fr [PDF; abgerufen am 22. November 2015]). „Langlebig“ bedeutet hier eine Halbwertzeit von mindestens 100 ns.
Eintrag zu Isotope. In: Römpp Online. Georg Thieme Verlag, abgerufen am 26. Mai 2014.
M. Wang et al.: The AME2016 atomic mass evaluation (II). Tables, graphs and references. In: Chinese Physics C. Band 41, Nr. 3, 2017, S. 30003 (nds.iaea.org [PDF; abgerufen am 11. März 2018]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] D. Meschede: Gerthsen Physik. 22. Auflage, 2004, S. 630.

[2] uclide. In: Alan D. McNaught, Andrew Wilkinson, IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. 2. Auflage. Blackwell Scientific Publications, Oxford 1997, ISBN 0-9678550-9-8, doi:10.1351/goldbook.N04257 (englisch, korrigierte Fassung – erstellt von M. Nic, J. Jirat, B. Kosata; mit Aktualisierungen von A. Jenkins [2006–]).

[nubase-3] G. Audi, O. Bersillon, J. Blachot, A. H. Wapstra: The NUBASE evaluation of nuclear and decay properties. In: Nuclear Physics. A 729, 2003, S. 3–128, doi:10.1016/j.nuclphysa.2003.11.001 (englisch, in2p3.fr [PDF; abgerufen am 22. November 2015]). „Langlebig“ bedeutet hier eine Halbwertzeit von mindestens 100 ns.

[Römpp-Isotope-4] Eintrag zu Isotope. In: Römpp Online. Georg Thieme Verlag, abgerufen am 26. Mai 2014.

[AME2016-b.pdf-5] M. Wang et al.: The AME2016 atomic mass evaluation (II). Tables, graphs and references. In: Chinese Physics C. Band 41, Nr. 3, 2017, S. 30003 (nds.iaea.org [PDF; abgerufen am 11. März 2018]).