Boson

Bosonen (nach dem indischen Physiker Satyendranath Bose) sind alle Teilchen, die sich gemäß der Bose-Einstein-Statistik verhalten, in der u. a. mehrere ununterscheidbare Teilchen den gleichen Zustand einnehmen können. Dem Spin-Statistik-Theorem zufolge haben sie einen ganzzahligen Eigendrehimpuls (Spin) in Einheiten des reduzierten Planckschen Wirkungsquantums $\hbar$ . Daran kann man sie unterscheiden von den Fermionen mit halbzahligem Spin und den Anyonen mit beliebigem (auch gebrochenzahligem) Spin; beide Typen haben damit einhergehend andere statistische Eigenschaften.

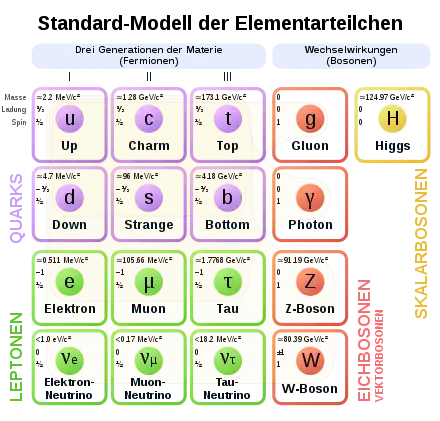
Standardmodell mit den Eichbosonen (rot) und den Skalarbosonen (gelb)

Im Standardmodell der Teilchenphysik sind die Austauschteilchen, die die Kräfte zwischen den Fermionen vermitteln, elementare Bosonen mit einem Spin von 1, wie z. B. das Photon als Überträger der elektromagnetischen Kraft. Auch das hypothetische Graviton als Träger der Gravitation ist ein Boson, allerdings mit einem Spin von 2. Darüber hinaus existiert mit dem Higgs-Boson im Standardmodell ein Boson mit einem Spin von 0.

Andere Bosonen sind aus mehreren Teilchen zusammengesetzt wie z. B. die Cooper-Paare aus Elektronen und Phononen als Ladungsträger im Supraleiter, Atomkerne mit einer geraden Nukleonenzahl oder die Mesonen, also subatomare Quark-Antiquark-Paare. Des Weiteren können auch Quasiteilchen bosonische Eigenschaften zeigen, wie die bereits erwähnten Phononen oder die Spinonen.

Einteilung nach dem Spin

Die elementaren Bosonen werden je nach Spin verschieden bezeichnet. Grundlage dieser Bezeichnung ist ihr Transformationsverhalten unter den „eigentlichen orthochronen Lorentz-Transformationen“. Elementarteilchen können, außer in einer nichtlokalen oder einer Stringtheorie, maximal einen Spin von 2 aufweisen, denn masselose Teilchen unterliegen dem Low-Energy-Theorem[1], das die Kopplung von hohen Spins an Ströme anderen Spins ausschließt, sowie einem Verbot für Selbstwechselwirkungen[2] und für massive Teilchen wurde die generelle Nichtexistenz 2017 gezeigt.[3] Bosonen mit höherem Spin sind daher physikalisch weniger relevant, da sie nur als zusammengesetzte Teilchen auftreten.

Spin	Bosontyp	Vertreter
Spin	Bosontyp	elementar	zusammengesetzt
0	Skalarboson	Higgs-Boson	Pionen, ⁴He-Kern
1	Vektorboson	Photon, W-Bosonen, Z-Boson, Gluonen	J/ψ-Meson, ¹⁴N-Kern
2	Tensorboson	Graviton (hypothetisch)	³⁶Cl-Kern, ⁶⁰Co-Kern
3	–	–	¹⁰B-Kern

Makroskopische Quantenzustände

Eine besondere Eigenschaft der Bosonen ist, dass sich bei Vertauschung zweier gleicher Bosonen die quantenmechanische Wellenfunktion nicht ändert (Phasenfaktor +1). Im Gegensatz dazu ändert sich bei einer Vertauschung zweier gleicher Fermionen das Vorzeichen der Wellenfunktion. Die Begründung für die Invarianz der Wellenfunktion bei Bosonen-Vertauschung erfolgt über das relativ komplizierte Spin-Statistik-Theorem. Anschaulich erhält man nach zweimaligem Vertauschen (d. h. einer Spiegelung bzw. Anwendung des Paritätsoperators) wieder den ursprünglichen Zustand; einmaliges Vertauschen kann also nur einen Faktor vom Betrag 1 erzeugen, der quadriert 1 ergibt – also entweder 1 oder −1 –, wobei die 1 den Bosonen entspricht.

Eine Konsequenz ist, dass sich gleichartige Bosonen zur selben Zeit am selben Ort (innerhalb der Unschärferelation) befinden können; man spricht dann von einem Bose-Einstein-Kondensat. Mehrere Bosonen nehmen dann den gleichen Quantenzustand ein, sie bilden makroskopische Quantenzustände. Beispiele sind:

die Supraleitung, die durch bosonische Cooper-Paare beschrieben wird,
der Laser, bei dem Photonen denselben Zustand einnehmen,
die Suprafluidität, bei der bosonisches ⁴He oder ⁶Li kondensieren, oder bosonische Paare des fermionischen ³He.

Zusammengesetzte Teilchen

Fermionisches oder bosonisches Verhalten zusammengesetzter Teilchen kann nur aus größerer Entfernung (verglichen mit dem betrachteten System) beobachtet werden. Bei näherer Betrachtung (in einer Größenordnung, in der die Struktur der Komponenten relevant wird) zeigt sich, dass ein zusammengesetztes Teilchen sich entsprechend den Eigenschaften (Spins) der Bestandteile verhält. Beispielsweise können zwei Helium-4-Atome (Bosonen) nicht denselben Raum einnehmen, wenn der betrachtete Raum vergleichbar mit der inneren Struktur des Heliumatoms (≈10⁻¹⁰ m) ist, da die Bestandteile des Helium-4-Atoms selbst Fermionen sind. Dadurch hat flüssiges Helium ebenso eine endliche Dichte wie eine gewöhnliche Flüssigkeit.

Supersymmetrische Bosonen

In dem Modell der Elementarteilchen, das um die Supersymmetrie erweitert ist, existieren weitere elementare Bosonen. Auf jedes Fermion kommt rechnerisch ein Boson als supersymmetrisches Partnerteilchen, ein so genanntes Sfermion, so dass sich der Spin jeweils um ±1/2 unterscheidet. Die Superpartner der Fermionen werden allgemein durch ein zusätzliches vorangestelltes S- benannt, so heißt z. B. das entsprechende Boson zum Elektron dann Selektron.

Genau genommen wird zunächst im Wechselwirkungsbild jedem fermionischen Feld ein bosonisches Feld als Superpartner zugeordnet. Im Massebild ergeben sich die beobachtbaren oder vorhergesagten Teilchen jeweils als Linearkombinationen dieser Felder. Dabei muss die Zahl und der relative Anteil der zu den Mischungen beitragenden Komponenten auf der Seite der bosonischen Superpartner nicht mit den Verhältnissen auf der ursprünglichen fermionischen Seite übereinstimmen. Im einfachsten Fall (ohne oder mit nur geringer Mischung) kann jedoch einem Fermion (wie dem Elektron) ein bestimmtes Boson bzw. Sfermion (wie das Selektron) zugeordnet werden.

Darüber hinaus benötigt bereits das minimale supersymmetrische Standardmodell (MSSM) im Unterschied zum Standardmodell (SM) mehrere bosonische Higgs-Felder inklusive ihrer Superpartner.

Bisher wurde keines der postulierten supersymmetrischen Partnerteilchen experimentell nachgewiesen. Sie müssten demnach eine so hohe Masse haben, dass sie unter normalen Bedingungen nicht entstehen. Man hofft, dass die neue Generation der Teilchenbeschleuniger zumindest einige dieser Bosonen nachweisen kann. Anzeichen sprechen dafür, dass die Masse des leichtesten supersymmetrischen Teilchens (LSP) im Bereich einiger hundert GeV/c² liegt.

Weblinks

Wiktionary: Boson – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Was sind Bosonen? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 1. Okt. 2003.
Was sind W&Z-Bosonen? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 2. Aug. 2006.

Einzelnachweise

Steven Weinberg: Photons and Gravitons in S-Matrix Theory: Derivation of Charge Conservation and Equality of Gravitational and Inertial Mass. In: Phys. Rev. Band 135, 4B, S. B1049–B1056, doi:10.1103/PhysRev.135.B1049 (englisch).
Paolo Benincasa und Eduardo Conde: Exploring the S-matrix of Massless Particles. In: Phys. Rev. D. Band 86, Nr. 2, 2012, doi:10.1103/PhysRevD.86.025007 (englisch).
Nima Arkani-Hamed et al.: Scattering Amplitudes For All Masses And Spins. 2017, arxiv:1709.04891 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Steven Weinberg: Photons and Gravitons in S-Matrix Theory: Derivation of Charge Conservation and Equality of Gravitational and Inertial Mass. In: Phys. Rev. Band 135, 4B, S. B1049–B1056, doi:10.1103/PhysRev.135.B1049 (englisch).

[2] Paolo Benincasa und Eduardo Conde: Exploring the S-matrix of Massless Particles. In: Phys. Rev. D. Band 86, Nr. 2, 2012, doi:10.1103/PhysRevD.86.025007 (englisch).

[3] Nima Arkani-Hamed et al.: Scattering Amplitudes For All Masses And Spins. 2017, arxiv:1709.04891 (englisch).