Korrespondenzprinzip
Mit Korrespondenzprinzip wurde ursprünglich eine Beziehung zwischen Termini der klassischen Physik und der Quantenmechanik bezeichnet. Der Ausdruck wurde 1920 von Niels Bohr im Kontext der älteren Quantentheorie geprägt.[1] Es wird in diesem Zusammenhang auch als Bohrsches Korrespondenzprinzip bezeichnet.
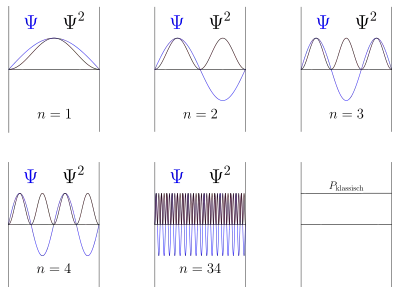
Bohr ging in seinem Atommodell von 1913 noch von einem klassischen Modell aus, war aber gezwungen, sehr einschränkende Bedingungen für die vorkommenden Elektronenbahnen zu formulieren, um die beobachteten diskreten optischen Spektren zu erklären. Trotzdem konnte die so formulierte „ältere Quantentheorie“ keine vollständige Theorie der Spektren liefern. Für große Quantenzahlen ergaben sich jedoch asymptotische Formeln, die denen der klassischen Physik entsprachen und diese Erklärungslücken teilweise füllen konnten. Das Korrespondenzprinzip diente in diesem Sinn in der älteren Quantentheorie als heuristisches Prinzip, um den Übergang zur klassischen Physik (in diesem Fall Elektrodynamik) für große Quantenzahlen zu beschreiben.
Auch in der ab 1925 entstandenen Quantenmechanik diente das Korrespondenzprinzip zur Beschreibung einer heuristischen Methode, quantenmechanische Operatoren und ihre Vertauschungsrelationen mit denen der klassischen Mechanik in Verbindung zu bringen.
In der Wissenschaftstheorie wird (angeregt durch das Beispiel der Quantentheorie) unter Korrespondenzprinzip die Beziehung verschiedener Theorien, in der Regel einer älteren und einer neueren, zum selben Phänomenbereich verstanden.[2] Es geht damit um das grundlegende Konzept einer Theorienhierarchie und -entwicklung in den Naturwissenschaften. Auch in weiteren Wissenschaften wie der Kristallographie wird in diesem Sinn von Korrespondenzprinzipien gesprochen. Es besteht ein großer Zusammenhang zur Ergodenhypothese, die Aussagen über das zeitliche Verhalten eines Systems und dessen Grundgesamtheit (Erwartungswert) macht und damit etwas über das asymptotische Grenzverhalten der Mittelung über eine unendlich lange Beobachtungszeit aussagt.
Das Korrespondenzprinzip als Konzept zur Theorienhierarchie
Das Korrespondenzprinzip beschreibt ein bestimmtes Verhältnis zwischen einer älteren naturwissenschaftlichen Theorie und einer neueren mit größerem Gültigkeitsbereich. Es liegt vor, wenn die neuere Theorie auf dem Gültigkeitsbereich der älteren zu denselben Ergebnissen kommt wie diese. Diese Art der Theorienentwicklung ist in den Naturwissenschaften typisch und erstrebenswert. In den Sozialwissenschaften war dies Gegenstand umfangreicher epistemologischer Positionskämpfe, die wissenschaftstheoretisch von Imre Lakatos und Thomas S. Kuhn begründet wurden.
Die neuere Theorie enthält in diesem Fall die ältere als Grenzfall und erklärt so ihren früheren Erfolg. Ferner gerät die neue Theorie nicht in Konflikt mit den älteren experimentellen Befunden. Dabei kann sich die neuere Theorie strukturell und begrifflich komplett von der älteren unterscheiden. Die ältere Theorie ist damit zwar im Prinzip widerlegt, sie bleibt jedoch in ihrem begrenzten Gültigkeitsbereich weiterhin nützlich.
Im Folgenden werden einige bedeutende wissenschaftsgeschichtliche Beispiele für Erfüllungen dieses Korrespondenzprinzips erläutert.
Newtonsche Physik und die Relativitätstheorie
Obwohl die Relativitätstheorie völlig neue Vorstellungen von Raum und Zeit einführt, gehen ihre Vorhersagen in die der newtonschen Physik über, wenn man sie auf unseren Alltagsbereich anwendet.
In der speziellen Relativitätstheorie hängen räumliche und zeitliche Distanzen vom Bewegungszustand des Beobachters ab. Sind die entsprechenden Geschwindigkeiten hinreichend klein gegen die Lichtgeschwindigkeit, so geraten die Differenzen dieser Distanzen unter die experimentelle Nachweisgrenze, so dass die an sich überholten Konzepte von Raum und Zeit der newtonschen Physik angewendet werden können. Ebenso ist die Krümmung des Raumes durch die Anwesenheit von Massen und die Abhängigkeit des Ganges von Uhren von ihrer Position im Gravitationsfeld, wie sie in der allgemeinen Relativitätstheorie vorhergesagt werden, für hinreichend kleine Raumgebiete wie beispielsweise innerhalb unseres alltäglichen Aktionsradius experimentell kaum feststellbar. Auch das Verhältnis zwischen spezieller und allgemeiner Relativitätstheorie entspricht dem Korrespondenzprinzip.
Newtonsche Physik und die Quantenphysik
Die Gesetze der newtonschen Physik lassen sich als Grenzfall aus denen der Quantenphysik herleiten, obwohl letztere auf völlig andersartigen und nicht mehr anschaulich zugänglichen Konzepten von Materie und Bewegung beruhen und obwohl es in der Quantenmechanik Größen gibt (z. B. den Spin), die in der klassischen Mechanik nicht vorkommen.
Die Quantenphysik erlaubt in der Regel lediglich Wahrscheinlichkeitsprognosen für den Wert einer Messgröße wie beispielsweise den Ort, an dem sich ein Objekt befinden wird. Sie ist daher nicht mehr bezüglich jeder Fragestellung deterministisch. Berechnet man den so genannten Erwartungswert, das heißt den Mittelwert dieser Messgröße im Grenzfall unendlich häufiger Wiederholung des Experiments, so stellt sich bei Existenz der Größe in der klassischen Physik heraus, dass dieser den bekannten Gleichungen der newtonschen Physik gehorcht (Ehrenfest-Theorem). Wendet man die Regeln der Quantenphysik auf makroskopische mechanische Systeme an, so wird die statistische Streuung der Messergebnisse nahezu unmessbar klein. Dabei entsprechen solche Systeme i. a. einem statistischen Ensemble aus einer großen Zahl von sogenannten reinen Quantenzuständen mit großen Quantenzahlen. Damit folgt der deterministische Charakter der klassischen Physik für den makroskopischen Grenzfall aus der Quantenphysik, obwohl letztere selbst nicht deterministisch ist.
Relativitätstheorie, Quantenphysik und Quantengravitation
Eines der großen Probleme des Theoriengebäudes der Physik besteht derzeit darin, dass seine beiden Säulen, die allgemeine Relativitätstheorie und die Quantenphysik, in ihrer Beziehung zueinander das Korrespondenzprinzip nicht erfüllen. Beide Theorien haben daher nur einen begrenzten Gültigkeitsbereich, so dass die heutige Physik keine abgeschlossene Beschreibung der Natur liefern kann. Es wird daher nach einer Theorie der so genannten Quantengravitation gesucht, die die Relativitätstheorie und die Quantenphysik vereinigt, indem sie beide als Grenzfall im Sinne des Korrespondenzprinzips enthält.
Das Korrespondenzprinzip in der älteren Quantentheorie
Die ältere Quantentheorie kombiniert die klassische Mechanik quasiperiodischer Systeme mit zusätzlichen Annahmen, deren wichtigste die Einschränkung der zulässigen Bahnen im Phasenraum ist auf solche, für die die Quantisierung des Bahndrehimpulses gilt:[3]
mit
- dem generalisierten Impuls
- der generalisierten Koordinate
- der Hauptquantenzahl
- dem Plancksches Wirkungsquantum
bzw.
mit
- dem Bahndrehimpuls
- dem reduzierten Planckschen Wirkungsquantum
Das Korrespondenzprinzip fordert nun einen Zusammenhang zwischen den Koeffizienten der Fourierentwicklung der Ortskoordinaten nach der Zeit
und den quantentheoretisch möglichen Strahlungsübergängen, sowie der Intensität und Polarisation des dabei ausgesandten Lichts. So lassen sich u. a. die spektroskopischen Auswahlregeln ableiten, indem vom Verschwinden der n-ten Fourierkomponente auf die Unmöglichkeit des korrespondierenden Quantensprungs um n Einheiten geschlossen wird.
Eine Bedingung, die Bohr an diese Korrespondenz stellt, ist die der näherungsweisen Übereinstimmung mit der klassischen Elektrodynamik für große Quantenzahlen. Dies stellt somit eines der oben beschriebenen wissenschaftstheoretischen Korrespondenzprinzipien dar.
Das Korrespondenzprinzip in der modernen Quantenmechanik
Im Anschluss an Heisenberg wird die Zuordnung klassischer Observablen zu ihren Entsprechungen in der mathematischen Formulierung der Quantenmechanik, den Operatoren auf Hilbert-Räumen, als Korrespondenz bezeichnet. Damit dient die klassische Theorie in der Anwendung des Korrespondenzprinzips in dieser Bedeutung dazu, die physikalisch sinnvollen Gleichungen der Quantenmechanik zu finden – eben durch Übernahme der algebraischen Form der Gleichungen, wobei bestimmte klassische Observablen durch die ihnen korrespondierenden quantenmechanischen Operatoren ersetzt werden. Beispielsweise entsteht durch die Ersetzung der Impulsvariable durch die entsprechenden Impulsoperatoren (und entsprechend für die Ortsvariable) aus der klassischen Energiegleichung die Schrödingergleichung. Diese Zuordnung wurde früher gelegentlich auch als Jordan’sche Regel bezeichnet.
Korrespondenz in der Kristallographie
Paul Niggli formulierte die Korrespondenz zwischen Kristallstruktur und Morphologie. Zum einen ist die Symmetrie der äußeren Kristallflächen (s. Punktgruppe) höher oder gleich der Symmetrie der Kristallstruktur (s. Raumgruppe). Zum anderen verläuft jede äußere Kristallfläche parallel zu einer Schar von Netzebenen. Ebenso verläuft eine Kristallkante parallel zu einer Schar von Gittergeraden.
Diese morphologisch-strukturelle Korrespondenz gilt auch für alle anderen Eigenschaften des Kristalls und ist als Neumann’sches Prinzip von Woldemar Voigt 1910 formuliert worden. Die Symmetrie einer Eigenschaft ist höher oder gleich der Symmetrie der Kristallstruktur.
Weblinks
- Alisa Bokulich: Bohr’s Correspondence Principle. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- mikomma.de: Korrespondenzprinzip – Animationen zu Elektronen in Rydberg-Zuständen.
Einzelnachweise
- Niels Bohr: Über die Serienspektra der Elemente. In: Zeitschrift für Physik. Bd. 2, Nr. 5, 1920, S. 423–469, doi:10.1007/BF01329978.
- Karl Popper: Die Zielsetzung der Erfahrungswissenschaft. In: Hans Albert (Hrsg.): Theorie und Realität. Ausgewählte Aufsätze zur Wissenschaftslehre der Sozialwissenschaften (= Die Einheit der Gesellschaftswissenschaften. 2, ISSN 0424-6985). J. C. B. Mohr (Paul Siebeck), Tübingen 1964, S. 75–86, hier S. 84.
- Max Jammer: The Conceptual Development of Quantum Mechanics. McGraw-Hill, New York NY u. a. 1966, S. 109.