Trajektorie (Physik)
Eine Trajektorie [tʁajɛkˈtoːʁiə], auch Bahnkurve, ein Pfad oder Weg (manchmal auch nach dem Englischen: Orbit), ist in der Physik der Verlauf der Raumkurve, entlang der sich ein Körper oder ein Punkt, beispielsweise der Schwerpunkt eines starren Körpers, bewegt. Bei einem makroskopischen Körper, etwa einem Geschoss oder einem Ball, spricht man auch von der Flugbahn. Im erweiterten Sinn ist die Trajektorie eine Kurve im n-dimensionalen Phasenraum.[1]
Bei Körpern, die Zwangsbedingungen unterliegen, wird die Form der Trajektorie mathematisch durch die Kinematik beschrieben; z. B. beschreibt ein Pendel einen Kreisbogen. Bei Körpern, die nur äußeren Kräften ausgesetzt sind, ergeben sich die Trajektorien als Lösungen von Differentialgleichungssystemen. Die Untersuchung der Trajektorie als des zeitabhängigen Verlaufs des Ortes in einem Bezugssystem ist Gegenstand der Kinetik.
Beispiele

- Die Flugbahn einer vom Boden aus abgeschossenen Kanonenkugel oder einer ballistischen Rakete nennt man ballistische Kurve.
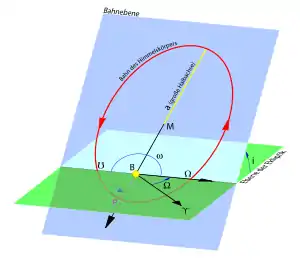
- Die Trajektorie eines natürlichen oder künstlichen Himmelskörpers im Schwerefeld eines Zentralkörpers oder im freien Weltraum verläuft auf einer Keplerbahn. Bei geschlossenen Bahnen im Sonnensystem oder in der Galaxis spricht man eher von Umlaufbahn. In jedem Zentralfeld ist die Bahn eines Körpers nach dem Drehimpulserhaltungssatz eine ebene Kurve.
- In einem homogenen magnetischen Feld beschreiben geladene Teilchen spiralförmige Bahnen (Schraubenlinien) um die Magnetfeldlinien.
- Aufgrund des Trägheitsgesetzes verläuft die Trajektorie eines Körpers gerade, wenn auf ihn keine Kraft wirkt beziehungsweise ein Kräftegleichgewicht vorliegt.
- Im Straßenbau wird der Übergang zwischen Gerade und Kreis in Form einer Klothoide ausgeführt.
- Im Rennsport ist die Ideallinie die Trajektorie eines fahrzeugfesten Punkts, auf der ein Streckenabschnitt mit der größten Geschwindigkeit befahren werden kann.
- Das bohrsche Atommodell beschreibt die Flugbahn der Elektronen um den Atomkern als geschlossene Kreisbahnen.
- Die Meteorologie kennt die Trajektorie eines (hypothetischen) Luftpartikels. Es wird zwischen Rückwärts- und Vorwärtstrajektorien unterschieden. Erstere geben an, woher die Luft gekommen ist, letztere, wohin sie sich bewegt. Von der Trajektorie ist die Stromlinie zu unterscheiden; nur in einer stationären Strömung fallen Trajektorien und Stromlinien zusammen.
- In der Objektverfolgung wird eine Trajektorie als der Bewegungspfad eines Objektes dargestellt durch die zeitliche Sequenz von Koordinaten während der Laufzeit.
- In der technischen Chemie werden Trajektorien zur Beschreibung des dynamischen Verhaltens einer chemischen Reaktion verwendet. Hierzu werden Darstellungen in der sogenannten Zustands- oder Phasenebene genutzt, bei denen die augenblickliche Konzentration über der Temperatur aufgetragen wird. Die Trajektorien zeigen dann die gleichzeitige Veränderung von Konzentration und Temperatur während eines Übergangsvorganges. Entlang der Trajektorie verläuft die Zeit.[2] Dabei können die Graphen z. B. (abhängig von den Startbedingungen und natürlich weiteren Variablen) eine spiralförmige Form aufweisen.
- Räuber-Beute Beziehungen: Lotka-Volterra-Gleichungen
Praktische Bestimmung
Bei sichtbaren Objekten kann die Trajektorie meist mit fotografischen Mitteln ermittelt werden, z. B. mit Photogrammetrie.
Die Trajektorie eines atomaren oder subatomaren Teilchens gibt es nur als anschauliche Hilfsvorstellung, da diese Teilchen durch die Quantenmechanik beschrieben werden müssen. Näherungsweise lassen sich solche Teilchenbahnen in Blasen- oder Nebelkammern sichtbar machen oder indirekt mit Hodoskopen oder Drahtkammern ermitteln.
Einzelnachweise
- Gerthsen: Physik. 18. Auflage. Springer, 1995, ISBN 978-3-662-07467-1, S. 968 (eingeschränkte Vorschau in der Google-Buchsuche).
- Manfred Baerns, Arno Behr, Axel Brehm, Jürgen Gmehling, Hanns Hofmann, Ulfert Onken: Technische Chemie. Wiley-VCH, 2006, ISBN 3-527-31000-2, S. 158.