Gravitation

Die Gravitation (von lateinisch gravitas für „Schwere“)[1], auch Massenanziehung oder Gravitationskraft, ist eine der vier Grundkräfte der Physik. Sie äußert sich in der gegenseitigen Anziehung von Massen. Sie nimmt mit zunehmender Entfernung der Massen ab, besitzt aber unbegrenzte Reichweite. Im Gegensatz zu elektrischen oder magnetischen Kräften lässt sie sich nicht abschirmen.

Ein schräg nach oben gerichteter Strahl eines Springbrunnens verformt sich auf der Erde unter dem Einfluss der Gravitation zu einer Parabel.

Zwei Spiralgalaxien, die sich unter dem Einfluss der Gravitation der jeweils anderen verformen

Auf der Erde bewirkt die Gravitation (Erdanziehungskraft), dass alle Körper nach „unten“, d. h. in Richtung Erdmittelpunkt fallen, sofern sie nicht durch andere Kräfte daran gehindert werden. Im Sonnensystem bestimmt die Gravitation die Bahnen der Planeten, Monde, Satelliten und Kometen und im Kosmos die Bildung von Sternen und Galaxien sowie dessen Entwicklung im Großen.

Gravitation wird oft mit Schwerkraft gleichgesetzt. Allerdings umfasst die vom lokal herrschenden Schwerefeld bestimmte Kraft auf einen Körper (das Gewicht des Körpers) nicht nur die Gravitationskraft, sondern auch die auf den Körper wirkenden Trägheitswirkungen (insbesondere durch die Rotation des Bezugssystems).

Im Rahmen der klassischen Physik wird die Gravitation mit dem Newtonschen Gravitationsgesetz beschrieben, d. h. als eine instantan, also unmittelbar und ohne Zeitverlust durch den leeren Raum wirkende Fernwirkungskraft. Ein grundlegend anderes Verständnis der Gravitation ergibt sich aus der allgemeinen Relativitätstheorie nach Albert Einstein. Hierbei wirkt die Gravitation nicht in Form einer Kraft auf die Körper, sondern entspricht einer Krümmung der vierdimensionalen Raumzeit, wobei die Bahnen der Körper, auf die keine weiteren Kräfte wirken, einer kürzesten Linie im gekrümmten Raum, d. h. einer Geodäte, entsprechen.

Geschichtlicher Überblick

Antike

Der griechische Philosoph Aristoteles beschrieb in der Antike im Rahmen seiner Kosmologie die Schwere als diejenige Eigenschaft der sublunaren Elemente (Erde, Wasser, Luft, Feuer), die alle aus diesen Elementen bestehenden Körper zum Mittelpunkt der Welt streben lässt. Diese Vorstellung war lange das physikalische Hauptargument für das geozentrische Weltbild.

Orient

Altindische Autoren führten den freien Fall auf eine Kraft zurück, die proportional zur Masse eines Objektes ist und in Richtung des Erdmittelpunkts wirkt. Der persische Astronom Muhammad ibn Musa erklärte im 9. Jahrhundert die Bewegungen der Himmelskörper durch eine Anziehungskraft. Al-Biruni übersetzte im 11. Jahrhundert die Werke der indischen Autoren ins Arabische und ins Persische. Sein Zeitgenosse Alhazen formulierte eine Theorie der Massenanziehung. Der Perser Al-Khazini stellte im 12. Jahrhundert die Vermutung auf, dass die Stärke der Erdanziehung abhängig vom Abstand zum Erdmittelpunkt ist, und unterschied zwischen Masse, Gewicht und Kraft.

Spätscholastik

Ein bedeutender Kritiker der peripatetischen (aristotelischen) Physik und Vorbereiter des kopernikanischen Weltbildes ist der Spätscholastiker Nikolaus von Oresme. Er hielt im 14. Jahrhundert die Erdrotation für wahrscheinlich und beschrieb die Möglichkeit vieler Welten sowie vieler gravitativer Zentren[2] – im Gegensatz zu einer ruhenden, im Mittelpunkt des Universums liegenden und alles Schwere anziehenden Erde.

Kopernikus

Nikolaus Kopernikus ging 1543 in De revolutionibus orbium coelestium davon aus, dass außer der Erde auch alle anderen Himmelskörper Gravitation ausüben:

„… Ich bin wenigstens der Ansicht, dass die Schwere nichts Anderes ist, als ein von der göttlichen Vorsehung des Weltenmeisters den Theilen eingepflanztes, natürliches Streben, vermöge dessen sie dadurch, dass sie sich zur Form einer Kugel zusammenschließen, ihre Einheit und Ganzheit bilden. Und es ist anzunehmen, dass diese Neigung auch der Sonne, dem Monde und den übrigen Planeten innewohnt …“[3]

Kepler

Johannes Kepler veröffentlichte 1609 in seiner Astronomia nova folgende Axiome:[4]

Jede körperliche Substanz ist, insofern sie körperlich ist, von Natur aus dazu geneigt, an jedem Ort zu ruhen, an dem sie sich allein befindet, außerhalb des Kraftbereichs eines verwandten Körpers.
Die Schwere besteht in dem gegenseitigen körperlichen Bestreben zwischen verwandten Körpern nach Vereinigung oder Verbindung (von dieser Ordnung ist auch die magnetische Kraft), so dass die Erde viel mehr den Stein anzieht; als der Stein nach der Erde strebt.
Das Schwere wird […] nicht zum Weltmittelpunkt als solchen hingetrieben, sondern als den Mittelpunkt eines verwandten runden Körpers …
Wäre die Erde nicht rund, so würde das Schwere nicht überall geradlinig auf den Mittelpunkt der Erde zu, sondern von verschiedenen Seiten aus nach verschiedenen Punkten hingetrieben.
Wenn man zwei Steine an einen beliebigen Ort der Welt versetzen würde, nahe beieinander außerhalb des Kraftbereichs eines dritten verwandten Körpers, dann würden sich jene Steine ähnlich wie zwei magnetische Körper an einem zwischenliegenden Ort vereinigen, wobei sich der eine dem andern um eine Strecke nähert, die der Masse des andern proportional ist.
Der Bereich der Anziehungskraft des Mondes erstreckt sich bis zur Erde.

17. Jahrhundert

Ebenfalls Anfang des 17. Jahrhunderts beschrieb Galileo Galilei den freien Fall eines Körpers als gleichmäßig beschleunigte Bewegung, die unabhängig von seiner Masse oder sonstigen Beschaffenheit ist.

In seinem 1636 erschienenen Werk „Traité de mécanique des poids soutenus par des puissances sur des plans inclinés à l'horizontale“ entwickelte Gilles Personne de Roberval die Idee einer Gravitationskraft, also Jahre vor entsprechenden Veröffentlichungen von Robert Hooke und Isaac Newton.[5] René Descartes erklärte die Schwerkraft als Folge seiner Wirbeltheorie. 1644 veröffentlichte er die Principia Philosophiae, welche großen Einfluss hatten – auch auf die Kritik durch Isaac Newton – denn die Kometen konnten offensichtlich nicht mit Descartes’ Modell erklärt werden. Dass Kometen die Sphären bzw. die Bahnen der Planeten durchdringen bzw. kreuzen, war seit Tycho Brahe und dem Kometen von 1577 die vorherrschende Meinung.[6]

Der englische Gelehrte Robert Hooke erklärte um 1670 die Wirkung der Gravitation mit „Gravitationstrichtern“. Er erklärte, dass die Gravitation eine Eigenschaft aller massebehafteten Körper sei und umso größer, je näher sich zwei Körper zueinander befänden. Die Theorie, dass die Schwerkraft umgekehrt proportional zum Quadrat des Abstands vom Massezentrum ist, taucht 1680 in einem Brief Hookes an seinen Landsmann Newton erstmals auf.

Newton

Isaac Newton beschrieb in seinen Principia (1687) als erster die Gravitation mithilfe einer mathematischen Formel. Dieses von ihm formulierte Gravitationsgesetz ist eine der Grundgleichungen der klassischen Mechanik, der ersten physikalischen Theorie, die sich auch in der Astronomie anwenden ließ. Ihr zufolge ist die Gravitation eine Kraft zwischen zwei Körpern, die diese zu ihrem gemeinsamen Schwerpunkt hin beschleunigt, wobei ihre Stärke proportional zum Quadrat des Abstandes der Körper abnimmt. Die Newtonsche Theorie, vollendet um 1800 von Pierre-Simon Laplace, liefert ein grundlegendes Verständnis der Dynamik des Sonnensystems mit der Möglichkeit präziser Vorhersagen der Bewegung von Planeten, Monden und Kometen. Sie bestätigt die keplerschen Gesetze der Planetenbewegung für einzelne Planeten, lässt aber darüber hinaus den störenden Einfluss der anderen Planeten und Monde ermitteln. Die danach berechneten Werte stimmten lange Zeit mit den entsprechenden astronomischen und irdischen Beobachtungen und Experimenten vollkommen überein. Die erste so nicht erklärbare Diskrepanz wurde Mitte des 19. Jahrhunderts an der Periheldrehung der Bahn des Merkur entdeckt.

Alternative Theorien im 18. und 19. Jahrhundert

Zur Erklärung der Gravitation im Sinne eines Prozessgeschehens wurden weiterhin bis zur Entwicklung der allgemeinen Relativitätstheorie im frühen 20. Jahrhundert eine Reihe mechanischer, kinetischer Erklärungen vorgeschlagen (siehe Mechanische Erklärungen der Gravitation). Eine der bekanntesten ist die von Fatio und Le Sage entwickelte Theorie der Le-Sage-Gravitation. Diese argumentiert, dass die Gravitationsanziehung zweier Körper auf der Abschirmung des aus Richtung des jeweils anderen wirkenden Drucks beruht. Im Zusammenhang hiermit stehen die Theorien eines Äthers als Vermittler von Wechselwirkungen (anstelle einer Fernwirkung) wie etwa der elektromagnetischen Wechselwirkung. Einige der letzten dieser Theorien waren die um 1900 entstandene Lorentzsche Äthertheorie, die schließlich von dem neuartigen Ansatz der einsteinschen Relativitätstheorie verdrängt wurde und die Gerbersche Gravitation, welche zwar in erster Näherung die Periheldrehung des Merkur richtig voraussagt, aber die Lichtablenkung an Massen nicht.

Einstein

„Newtons Apfel krümmt die Raumzeit,“ anschaulich. William Stukeley berichtet, Newton sei auf die Gravitation durch einen herabfallenden Apfel gekommen, siehe Memoirs of Sir Isaac Newton's life

In der 1916 von Albert Einstein aufgestellten allgemeinen Relativitätstheorie (ART) wird die Gravitation auf eine geometrische Eigenschaft der Raumzeit zurückgeführt.[7] Er nimmt an, dass die Raumzeit durch die Anwesenheit von Masse und jeder Form von Energie gekrümmt wird. Das ermöglicht, die Gravitation grundsätzlich anders zu interpretieren als die anderen Kräfte, nämlich als Trägheitskraft. Nach dem Äquivalenzprinzip kann die Wirkung der Gravitation nicht von der Auswirkung einer Beschleunigung des Bezugssystems unterschieden werden; insbesondere heben sich in einem frei fallenden Bezugssystem die Wirkungen von Gravitation und Beschleunigung exakt auf. Man sagt, die Gravitation sei durch den Übergang zu den neuen Koordinaten „wegtransformiert“. Allerdings gilt dies jeweils nur für einen Ort (lokal), weil jedes reale Gravitationsfeld für benachbarte Orte verschiedene Beschleunigungen bewirkt, die nicht zugleich „wegtransformiert“ werden können. In der allgemeinen Relativitätstheorie wird jedem Punkt im Raum ein eigenes, lokales Inertialsystem zugeordnet, in dem es keine Gravitation gibt und wo die spezielle Relativitätstheorie mit ihrer vierdimensionalen, flachen Raumzeit gilt. Analog dazu, dass nach Galilei kräftefreie Bewegungen geradlinig und gleichförmig verlaufen, bewegen sich in der allgemeinen Relativitätstheorie Körper ohne nichtgravitative Kräfte auf Geodäten in einem „gekrümmten“ Raum mit riemannscher Geometrie. Zur Bestimmung der an einem Punkt herrschenden Krümmung der Raumzeit dienen die einsteinschen Feldgleichungen. Sie wurden so formuliert, dass im Grenzfall schwacher Gravitation die nach ihnen berechneten Ergebnisse mit denen übereinstimmen, die nach der Newtonschen Gleichung berechnet werden. Die allgemeine Relativitätstheorie behandelt die Gravitation also als Trägheitskraft und stellt sie mit Zentrifugalkraft, Corioliskraft oder der Kraft, die man in einem Fahrzeug beim Anfahren oder Abbremsen spürt, auf eine Stufe.

Innerhalb des Sonnensystems, wo schwache Felder bzw. eine geringe Krümmung der Raumzeit vorherrschen, ergeben sich nur geringe Abweichungen von den Vorhersagen des Newtonschen Gravitationsgesetzes. Das erste erfolgreiche Anwendungsbeispiel der allgemeinen Relativitätstheorie war die Erklärung der kleinen Abweichung zwischen der beobachteten Periheldrehung der Bahn des Merkur und dem Wert, der nach der Newtonschen Theorie aufgrund der Bahnstörungen durch die anderen Planeten vorhergesagt wird.

Bei starker Krümmung, wie sie durch die Konzentration einer großen Masse auf kleinem Raum hervorgerufen wird, werden völlig neue Phänomene wie z. B. Schwarze Löcher vorhergesagt.

Als Quelle wie auch als Angriffspunkt der Gravitation gilt in der Newtonschen Mechanik allein die Masse. Ausgehend von dem ursprünglich ungenauen Begriff einer gegebenen Materiemenge erfuhr die Masse hier ihre erste präzise physikalische Definition. In der allgemeinen Relativitätstheorie ist die Gravitation Ausdruck der Krümmung der Raumzeit, die ihrerseits nicht nur von der Anwesenheit von Materie, sondern auch von Energie in jeder Form, auch der Gravitationsenergie selbst, und darüber hinaus von Massen- und Energieströmen beeinflusst ist. Alle der Beobachtung zugänglichen Vorhersagen der allgemeinen Relativitätstheorie wurden durch Messungen bestätigt.

In der Newtonschen Gravitation ging man noch von einer instantanen oder augenblicklichen Ausbreitung der Gravitationswirkung aus, das heißt, dass die Wirkung auch über große Entfernungen sofort erfolgt. Innerhalb der einsteinschen Sichtweise gilt jedoch, dass sich keine Wirkung, also auch nicht die Gravitationswirkung, schneller als mit Lichtgeschwindigkeit ausbreitet. Durch eine schnelle Veränderung der Position von Massen, wie zum Beispiel bei schnell kreisenden Doppelsternen oder beim Kollaps eines Sternes werden vielmehr Gravitationswellen erzeugt, die sich mit Lichtgeschwindigkeit ausbreiten.

Quantengravitation

Experimentell nicht zugänglich sind extrem hohe Konzentrationen von Masse bzw. Energie auf engstem Raum, für deren Beschreibung neben der Gravitation auch Quanteneffekte berücksichtigt werden müssen. Versuche einer Quantenfeldtheorie der Gravitation gibt es in Ansätzen. Es mangelt allerdings an Vorhersagen, die sowohl berechenbar als auch beobachtbar wären. Das Grundproblem dabei ist, dass sich bei solchen Konzentrationen schnell Schwarze Löcher bilden, in deren Innerem sich Quanteneffekte abspielen, die sich einer Beobachtung entziehen.

Modifizierte Newtonsche Dynamik (MOND)

Das Phänomen „Dunkle Materie“ steht für die Differenz zwischen den beobachteten und den nach den Modellen von Kepler, Newton und Einstein zu erwartenden Massen beim Rotationsverhalten von Galaxien und Galaxienhaufen. Statt zusätzlicher, nicht sichtbarer Masse schlug Mordehai Milgrom 1983 vor, dass eine Änderung der Newtonschen Bewegungsgesetze die Ursache für die beobachteten Rotationskurven sein könnte. Gemäß der „MOND-Hypothese“ hat die Änderung nur bei sehr kleinen Beschleunigungen, wie sie im astronomischen Maßstab auftreten, einen relevanten Einfluss auf die Bewegungen.

Befürworter der „Modifizierten Newtonschen Dynamik“ führen an, dass die Newtonsche Gravitationstheorie von 1686 bereits drei Modifikationen erfahren hat. Bei sehr kleinen Abständen verwenden Physiker ausschließlich die Quantenmechanik, bei sehr großen Geschwindigkeiten Einsteins spezielle Relativitätstheorie und nahe sehr großer Massen seine allgemeine Relativitätstheorie.

Gravitation in der klassischen Mechanik

Newtonsches Gravitationsgesetz

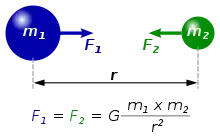
In der klassischen Mechanik ist die Gravitation oder allgemeine Massenanziehung eine Eigenschaft aller Materie, die nur von deren Masse abhängt, nicht aber von deren Art oder Bewegung. Die Gravitation drückt sich in der Gravitationskraft oder dem Gravitationsfeld aus, das von jeder Masse erzeugt wird, auf jede andere Masse anziehend wirkt und unendliche Ausbreitungsgeschwindigkeit und Reichweite besitzt. Das Newtonsche Gravitationsgesetz gibt die momentane Kraft $F_{\mathrm {G} }$ an, mit der zwei punktförmig gedachte Körper mit den Massen $m_{1}$ und $m_{2}$ im Abstand $r$ einander anziehen ( $G$ ist die universelle Gravitationskonstante):

F_{\mathrm {G} }=G{\frac {m_{1}m_{2}}{r^{2}}}

Diese Kraft ist für beide Körper gleich groß, jedoch entgegengesetzt gerichtet. Wenn keine weiteren Kräfte wirken, erfährt jeder der beiden Körper eine Beschleunigung zum anderen hin. Diese Momentanbeschleunigung $a$ kann mithilfe des zweiten Newtonschen Gesetzes $F=ma$ berechnet werden. Es ergibt sich beispielsweise für den Körper 1:

a_{1}={\frac {F_{1}}{m_{1}}}=G{\frac {m_{2}}{r^{2}}}

Die Momentanbeschleunigung des Körpers 1 hängt also nicht von seiner Masse $m_{1}$ ab, sondern von der Masse $m_{2}$ des anderen Körpers. Der Körper 2 erteilt somit in einem bestimmten Abstand jedem anderen Körper, unabhängig von dessen Masse, die gleiche Beschleunigung. Umgekehrt gilt das Gleiche für die Beschleunigung, die Körper 1 jedem anderen Körper im Abstand $r$ erteilt:

a_{2}={\frac {F_{2}}{m_{2}}}=G{\frac {m_{1}}{r^{2}}}

Die Beschleunigungen sind daher indirekt proportional zu den beschleunigten Massen: $a_{2}/a_{1}=m_{1}/m_{2}$ . Nimmt man für den Körper 2 die Erde und für den Körper 1 einen beliebigen Gegenstand des täglichen Lebens, so bedeutet dies, dass die Erde aufgrund ihrer viel größeren Masse nur eine unmessbar kleine Beschleunigung durch Körper 1 erfährt. Sie kann deshalb als ruhend angenommen werden. Körper 1 erfährt von ihr jedoch eine Beschleunigung, die zwar vom Abstand vom Erdmittelpunkt abhängt, nicht jedoch von der Masse $m_{1}$ . Dies erklärt die von Galileo Galilei zuerst ausgesprochene Tatsache, dass im leeren Raum (also ungehindert durch andere Kräfte oder Widerstände) alle Körper unabhängig von ihrer Masse die gleiche Fallbeschleunigung erfahren. Die Gleichheit der Fallbeschleunigung wird auch als das Prinzip der Äquivalenz von träger und schwerer Masse (in seiner schwachen Formulierung) bezeichnet.

Sind die Massen der beiden Körper nicht so stark voneinander verschieden wie in dem vorangehenden Beispiel, so führen beide Körper beschleunigte Bewegungen aus, wobei der Gesamtschwerpunkt zwischen den beiden Massen als ruhender Bezugspunkt gewählt werden kann (siehe Schwerpunktsatz). Wenn beide Körper aus der Ruhe starten, so stürzen sie auf gerader Strecke aufeinander zu, bis sie sich treffen. (In der Abstraktion als Punktmassen würde dies im Gesamtschwerpunkt geschehen.)

Wenn sie jedoch jeweils eine Anfangsgeschwindigkeit im Schwerpunktsystem haben, so führen sie Bewegungen aus, deren Bahnkurven in einer gemeinsamen Ebene liegen; das verlangt der Drehimpulserhaltungssatz. Welche Form diese Bahnkurven haben, hängt von den Geschwindigkeiten der beiden Körper ab (siehe Zweikörperproblem). Eine mögliche Lösung sind Ellipsenbahnen, wobei der Schwerpunkt jeweils einen Brennpunkt der beiden Ellipsen bildet. Ein Beispiel dafür ist das System Erde-Mond, bei dem die Masse der Erde so groß ist, dass der gemeinsame Schwerpunkt sogar im Inneren der Erde liegt.

Systeme, die aus drei oder mehr Körpern bestehen, die sich gegenseitig anziehen, verhalten sich oft chaotisch und sind mit analytischen Methoden nicht berechenbar (siehe Drei-Körper-Problem). Es gibt jedoch hilfreiche Näherungen. Im Sonnensystem beispielsweise ist die Masse der Planeten im Vergleich zur Sonnenmasse sehr gering. Wenn man davon ausgeht, dass die Sonne deshalb von den Planeten nicht beeinflusst wird und dass die Planeten untereinander nicht wechselwirken, dann ergeben Berechnungen mit dem Newtonschen Gravitationsgesetz die Keplerschen Bahnellipsen der Planeten.

Die klassische Beschreibung der Gravitation ist also für viele Anwendungsfälle hinreichend genau. Abweichungen treten allerdings im Zusammenhang mit sehr präzisen Messungen auf, z. B. bei der Periheldrehung des Merkur, und die klassische Beschreibung versagt völlig bei extremen Bedingungen, die z. B. bei Schwarzen Löchern vorliegen.

Die Gewichtskraft eines Körpers auf der Erdoberfläche wird maßgeblich durch die Gravitation bestimmt. Weiter tragen Trägheitskräfte zur Gewichtskraft bei; z. B. wirkt die Fliehkraft, die sich aus der Erdrotation ergibt, der Gravitation etwas entgegen. Gravitation und Trägheitskräfte zusammen bilden das Schwerefeld.

Gravitationskonstante

Die Gravitationskonstante $G$ ist eine Fundamentalkonstante der Physik. Ihre genaue Bestimmung ist sehr schwierig, denn zwischen zwei Körpern, deren Masse durch direkte Wägung bestimmt werden kann, ist die Gravitationskraft äußerst gering. Ihr Wert ist daher nur auf vier Dezimalstellen bekannt, im Unterschied zu den mindestens acht Dezimalstellen anderer Fundamentalkonstanten.[8]

Die erste Bestimmung gelang 1798 Henry Cavendish. Das in seinem Labor durchgeführte, von John Michell erdachte Experiment (Gravitationswaage) hat historische Bedeutung für die Entwicklung der experimentellen und theoretischen Grundlagen der Gravitation.

Allgemeine Relativitätstheorie

Das Licht einer weit entfernten Galaxie kann durch die Gravitation eines sehr massereichen Körpers so abgelenkt werden, dass es auf der Erde als Einstein-Ring erscheint

In der allgemeinen Relativitätstheorie (ART) wird die Gravitation nicht wie eine Kraft im Sinne der klassischen Physik behandelt. Im Unterschied zu den gewöhnlichen klassischen Feldtheorien, in denen die Koordinaten für Ort und Zeit in einer festen Struktur vorgegeben werden, betrachtet die ART diese Struktur selbst als veränderlich. Als Grundlage nutzt sie die aus der speziellen Relativitätstheorie bekannte Raumzeit, in der Orts- und Zeitkoordinaten in einer vierdimensionalen pseudo-riemannschen Mannigfaltigkeit zusammengefasst sind. Diese Raumzeit ist in der ART aber nicht mehr „flach“ wie in der Euklidischen Geometrie, sondern wird durch das Auftreten von Masse oder Energie „gekrümmt“. Die Krümmung ergibt sich an jedem Punkt der Raumzeit aus der Metrik, die den vierdimensionalen Abstand zwischen zwei Punkten der Raumzeit, also zwischen zwei Ereignissen, definiert. Dabei wird der zeitliche Abstand mit positivem, der räumliche Abstand aber mit negativem Vorzeichen gewertet (gelegentlich auch mit umgekehrtem Vorzeichen, siehe Vorzeichenkonventionen). Ein Körper, auf den außer der Gravitation keine weiteren Kräfte wirken, bewegt sich nun zwischen zwei Ereignissen (z. B. Abfahrt und Ankunft) stets entlang derjenigen Verbindungslinie, die nach dieser raumzeitlichen Metrik die längste ist (Geodäte), was wegen der erwähnten Vorzeichenwahl die räumlich kürzeste Strecke bedeutet. Dort wo die Raumzeit flach ist, ist die Geodäte die gerade Verbindungslinie der beiden Punkte. Umgerechnet in die üblichen Koordinaten für Ort und Zeit entspricht dies einer gleichförmigen Bewegung auf dem räumlich kürzesten Weg, also längs der räumlichen Verbindungsgeraden, analog zum Trägheitsgesetz der klassischen Mechanik für den völlig kräftefreien Körper. Bei einer gekrümmten Raumzeit dagegen entspricht eine Geodäte im Allgemeinen einer beschleunigten Bewegung längs einer räumlich gekrümmten Bahn. Die durch die Anwesenheit von Masse oder Energie verursachte Krümmung der Raumzeit wird durch die einsteinschen Feldgleichungen gerade so festgelegt, dass die Geodäte eine Bewegung wiedergibt, die genau der Bewegung des ansonsten kräftefreien Körpers im herrschenden Gravitationsfeld entspricht (also freier Fall, Wurfparabel, Planetenbahn etc.). Da die Masse des betrachteten Körpers dabei gar nicht einfließt, gilt für Körper mit verschiedener Masse dieselbe Geodäte, d. h., sie bewegen sich in einem gegebenen Gravitationsfeld gleich. Damit ist auch das Äquivalenzprinzip erklärt, das in der klassischen Physik die Gleichheit von schwerer und träger Masse feststellt. Die Gravitation tritt demnach nicht wie in der klassischen Physik als eine bestimmte Kraft auf, die auf den Körper wirkt und eine Beschleunigung verursacht, sondern als eine Eigenschaft der Raumzeit, in der der Körper sich kräftefrei bewegt. Gravitation wird auf diese Weise als ein rein geometrisches Phänomen gedeutet.

In diesem Sinne reduziert die allgemeine Relativitätstheorie die Gravitationskraft auf den Status einer Scheinkraft: Wenn man auf einem Stuhl sitzend fühlt, wie man durch eine „Gravitationskraft“ zur Erde hin gezogen wird, deutet die ART dies so, dass man von der Stuhlfläche fortwährend daran gehindert wird, der Geodäte durch die von der Erdmasse gekrümmte Raumzeit zu folgen, was der freie Fall wäre. Dabei ist die Kraft, mit der die Stuhlfläche auf die Sitzfläche des Beobachters einwirkt, keineswegs eine Scheinkraft. Sie geht letztlich zurück auf die elektrostatische Abstoßung bei der Berührung der Atome der Stuhlfläche durch die Atome des Beobachters. Nach der Sichtweise der allgemeinen Relativitätstheorie verschiebt sich also die Interpretation der Ereignisse. Während nach der klassischen Mechanik die Erde ein Inertialsystem darstellt, in dem die nach unten gerichtete Schwerkraft auf den Beobachter durch die nach oben gerichtete Stützkraft des Stuhls ausgeglichen wird, so dass der Beobachter in Ruhe bleiben kann, stürzt das nach der allgemeinen Relativitätstheorie richtige Inertialsystem mit Erdbeschleunigung $g$ nach unten. Doch in diesem Inertialsystem übt der Stuhl eine Kraft auf den Beobachter aus, die ihn konstant mit $-g$ nach oben beschleunigt.

Senkrecht frei fallende Körper hingegen, aber auch Satelliten, Planeten, Kometen oder Parabelflüge folgen einer Geodäte durch die Raumzeit. Ihre Bewegungen werden in der allgemeinen Relativitätstheorie als (netto) kräftefrei angesehen, da die Erdmasse (oder Sonnenmasse) durch die Raumzeitkrümmung die Definition davon beeinflusst, was im Sinne der Trägheit von Körpern „geradeaus“ bedeutet. Direkter (d. h. dem üblichen Krümmungsbegriff eher entsprechend) tritt die Raumzeitkrümmung z. B. in astronomischen Beobachtungen in Erscheinung, in denen nachgewiesen werden konnte (s. Abb.), dass große Massen die Krümmung von Lichtstrahlen bewirken.

Aufgrund des Relativitätsprinzips und der daraus folgenden Invarianz gegenüber Lorentztransformationen trägt nicht nur Masse, sondern auch jede Form von Energie zur Krümmung der Raumzeit bei. Dies gilt einschließlich der mit der Gravitation selbst verbundenen Energie. Daher sind die einsteinschen Feldgleichungen nichtlinear. Sie lassen sich jedoch im Bereich schwacher Krümmung durch lineare Gleichungen annähern, in denen sich das Newtonsche Gravitationsgesetz wiederfinden lässt. Gegenüber den nach dem Newtonschen Gesetz berechneten Phänomenen ergeben sich aber kleine Korrekturen, die durch genaue Beobachtungen sämtlich bestätigt werden konnten (siehe Tests der allgemeinen Relativitätstheorie). Völlig neue Phänomene jedoch ergeben sich bei starker Krümmung der Raumzeit, hier insbesondere bei Schwarzen Löchern.

Gravitation und Quantentheorie

Quantengravitation

Im Rahmen einer Quantenfeldtheorie wird die Gravitation in linearer Näherung durch den Austausch eines als Graviton bezeichneten masselosen Teilchens beschrieben, das den Spin 2 hat. Darüber hinaus führt schon die Formulierung einer Quantentheorie der Gravitation zu prinzipiellen Problemen, die bisher ungelöst sind. Auch die supersymmetrische Erweiterung führte bisher nicht zu einer konsistenten Theorie. Als derzeit aussichtsreichste Kandidaten gelten die Stringtheorie und die Schleifenquantengravitation. Ein wesentliches Ziel ist dabei, die Gravitation mit den übrigen Wechselwirkungen zu einer „Theorie von Allem“ zu vereinen, die alle Naturkräfte auf einmal beschreiben kann. Das bedeutet, dass die Gravitation, welche die Effekte der Quantenfeldtheorie nicht berücksichtigt, um diese erweitert würde. Ein Ansatz dafür ist die M-Theorie, nach der unser Universum mit seiner vierdimensionalen Raumzeit in ein elfdimensionales Universum eingebettet ist (siehe Branenkosmologie).

Fundamentale Wechselwirkungen und ihre Beschreibungen (Theorien in frühem Stadium der Entwicklung sind grau hinterlegt.)
	Starke Wechselwirkung	Elektromagnetische Wechselwirkung		Schwache Wechselwirkung	Gravitation
klassisch		Elektrostatik	Magnetostatik		Newtonsches Gravitationsgesetz
		Elektrodynamik			Allgemeine Relativitätstheorie
quanten- theoretisch	Quantenchromodynamik (Standardmodell)	Quantenelektrodynamik		Fermi-Theorie	Quantengravitation (?)
		Elektroschwache Wechselwirkung (Standardmodell)
	Große vereinheitlichte Theorie (?)
	Weltformel („Theorie von Allem“) (?)

Quantenphysikalische Wirkungen des Gravitationsfelds

Die Wirkung des Gravitationspotentials auf die quantenmechanische Phase der Wellenfunktion wurde 1975 durch ein Interferenzexperiment an freien Neutronen nachgewiesen.[9] Die Wellenfunktion und Energie von Neutronen, die einen im Gravitationsfeld gebundenen Zustand besetzen, konnte 2012 ausgemessen werden.[10] In beiden Fällen bestätigen die Messergebnisse die aufgrund der Quantenmechanik berechneten Voraussagen.

Gravitation auf der Erde

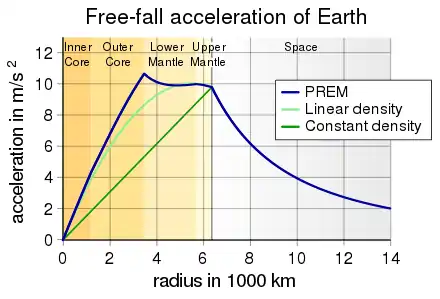
Gravitation (genauer: Erdbeschleunigung) im Erdinnern nach dem seismischen PREM-Erdmodell, sowie Näherungen durch konstante und linear nach innen zunehmende Gesteinsdichte.

Die Erde hat eine Masse von 5,9724·10²⁴ kg. Ihr Radius beträgt an den Polen 6357 km und, wegen der Erdabplattung, 6378 km am Äquator. Daraus ergibt sich mithilfe des Gravitationsgesetzes von Newton, dass die Gravitationsbeschleunigung zwischen $9{,}801\,\mathrm {m} \,\mathrm {s} ^{-2}$ (am Äquator) und $9{,}867\,\mathrm {m} \,\mathrm {s} ^{-2}$ (an den Polen) beträgt. Die tatsächlich wirksame Fallbeschleunigung weicht jedoch von dem auf diese Weise berechneten Wert ab, man spricht deshalb auch vom Ortsfaktor. Diese Ortsabhängigkeit, die auch die Richtung der Fallbeschleunigung betrifft, hängt mit der Zentrifugalwirkung, die durch die Erdrotation hervorgerufen wird, mit der Höhe des Standorts und mit lokalen Schwereanomalien zusammen. Dementsprechend ist die Gewichtskraft im Schwerefeld der Erde nicht nur eine reine Gravitationskraft im Sinne des Gravitationsgesetzes.

Schwerelosigkeit

Wenn von „Schwerelosigkeit“ gesprochen wird, ist oft nicht die Abwesenheit von Gravitation gemeint, sondern lediglich die Abwesenheit einer der Gewichtskraft entgegengerichteten Haltekraft. Ein Körper, auf den lediglich die Gravitationskraft wirkt, befindet sich in einem Zustand des freien Falls. In diesem Sinne befindet sich auch eine Raumstation im Erdorbit im freien Fall, wobei wegen genügend großer horizontaler Bahngeschwindigkeit die Flugbahn nicht an der Erdoberfläche endet, sondern um die Erde herum führt. In einem frei fallenden Bezugssystem sind keine Gravitationswirkungen bemerkbar. Folglich wird dieser Zustand als Schwerelosigkeit bezeichnet. Dies gilt unter der Bedingung, dass das Gravitationsfeld zumindest lokal näherungsweise homogen ist. Geringe Abweichungen davon führen zu Phänomenen der Mikrogravitation.

Lagrange-Punkte

In einem System aus zwei umeinander kreisenden Himmelskörpern (z. B. Erde und Sonne) gibt es konstant mitrotierende Punkte, an denen weitere Himmelskörper eine Bahn haben könnten, auf der sich alle Kräfte aufheben – die sogenannten Lagrange-Punkte. Dort heben sich die Gravitationskräfte der Himmelskörper und die Zentrifugalkraft der Bahnbewegung gegenseitig auf. Eine entsprechende Bahn, die einen Lagrange-Punkt verfolgt, kann stabil oder instabil sein – ein leichtes Abweichen vom Lagrange-Punkt kann eine korrigierende Kraft zurück zu dem Punkt bewirken (stabil) oder zum Ausbrechen führen (instabil). Das Planck-Weltraumteleskop war in einem Lagrange-Punkt stationiert.

Gravisphäre

Nahe Massen haben mehr Einfluss auf die Gravitationsbeschleunigung als ferne Massen. Daher sind auch um relativ kleine Körper im Schwerefeld großer Körper Satellitenbahnen möglich. Der Raumbereich, in dem dies der Fall ist, ist die Gravisphäre des jeweiligen Himmelskörpers.[11] Aus dem gleichen Grund ist die Gravitationsbeschleunigung eines unregelmäßig geformten Körpers nicht an allen Raumpunkten auf sein Baryzentrum ausgerichtet.

Abschirmung der Gravitation und Antigravitation

Im Bereich der Science-Fiction und Grenzwissenschaften gibt es zahlreiche Konzepte einer gravitativen Abschirmung oder einer Antigravitation. Relative Bekanntheit haben Experimente von Quirino Majorana, der um 1920 eine abschirmende Wirkung durch schwere Elemente gefunden haben will[12] (entkräftet u. a. durch Henry Norris Russell[13]), und von Jewgeni Podkletnow, der 1995 bei rotierenden Supraleitern eine Abnahme der Gewichtskraft behauptete,[14] was allerdings ebenfalls nicht bestätigt werden konnte.[15][16][17]

Literatur

Charles W. Misner, Kip S. Thorne, John A. Wheeler: Gravitation, Princeton University Press, 2017, ISBN 978-0-691-17779-3.
Gravitation; In: Sterne und Weltraum, Special 6, 2001 ISSN 1434-2057
Claus Kiefer: Gravitation, Fischer, Frankfurt am Main 2003, ISBN 3-596-15357-3.
Ephraim Fischbach, Carrick L. Talmadge: The search for non-Newtonian gravity, Springer, New York 1999, ISBN 0-387-98490-9.
Torsten Fließbach: Allgemeine Relativitätstheorie, Springer Spektrum, Heidelberg 2016, ISBN 978-3-662-53105-1.
Gilles Clément, Angie Bukley (Hrsg.): Artificial gravity, Springer, New York 2007, ISBN 978-0-387-70712-9.
David Darling: Gravity's arc-the story of gravity from Aristotle to Einstein and beyond, Wiley, Hoboken N. J. 2006, ISBN 978-0-471-71989-2.
Richard L. Amoroso: Gravitation and cosmology – from the Hubble radius to the Planck scale, Kluwer Academic, Dordrecht 2002, ISBN 1-4020-0885-6.
Roberto de Andrade Martins: The search for gravitational absorption in the early 20th century; In: H. Goenner, J. Renn, J. Ritter (Hrsg.): The Expanding Worlds of General Relativity, Einstein Studies, Band 7, Birkhäuser, Boston 1999, S. 3–44.
Roman Sexl, Helmuth Urbantke: Gravitation und Kosmologie: eine Einführung in die Allgemeine Relativitätstheorie, Spektrum Akademischer Verlag, 2008, ISBN 978-3-8274-2109-8.
Ulrich E. Schröder: Gravitation: Einführung in die Allgemeine Relativitätstheorie. Verlag Harri Deutsch, Frankfurt am Main 2011, 5. überarbeitete und erweiterte Auflage, ISBN 978-3-817-11874-8.

Weblinks

Commons: Gravitation – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Gravitation – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wiktionary: Schwerkraft – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

PONS Deutsch – Latein, Erstbedeutungen von gravitas
Edward Grant: The Nature of Natural Philosophy in the Late Middle Ages. Washington 2010, S. 63; Planets, Stars, and Orbs: The Medieval Cosmos, 1200–1687. 1994/96, S. 165; A Source Book in Medieval Science, Band 1. Zusammengestellt von Edward Grant, 1974, S. 551; Paul S. Agutter, Denys N. Wheatley: Thinking about Life: The history and philosophy of biology and other sciences. 2008, S. 59
zitiert nach: Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper. (Deutsche Übersetzung von C. L. Menzzer, 1879.), S. 23@wikisource; Original: „Equidem existimo, gravitatem non aliud esse, quam appetentiam quandam naturalem partibus inditam a divina providentia opificis universorum, ut in unitatem integritatemque suam sese conferant in formam globi coeuntes. Quam affectionem credibile est etiam Soli, Lunae, caeterisque errantium fulgoribus inesse …“ Lib. I, Cap. IX@wikisource; s. a. Johann Samuel Traugott Gehler: Physikalisches Wörterbuch. Band 2, Leipzig 1789, S. 519
Astronomia nova. Neue ursächlich begründete Astronomie (Übersetzung von Max Caspar, 1929 und Fritz Krafft, Wiesbaden 2005.), S. 28–29; Original: Scan des Druckexemplars der ETH-Bibliothek Zürich (abgerufen 24. März 2014); s. a. Johann Samuel Traugott Gehler: Physikalisches Wörterbuch. Band 2, Leipzig 1789, S. 519 und Florian Freistetter: Johannes Kepler: Astronomia Nova – Die Einleitung (3)@scienceblogs.de/astrodicticum-simplex (abgerufen 24. März 2014)
Heinz Klaus Strick: Gilles Personne Roberval (1602–1675): Entdecker der Schwerkraft. Spektrum.de-Artikel
Harry Nussbaumer: Revolution am Himmel: wie die kopernikanische Wende die Astronomie veränderte. Zürich 2011, S. 237; Eberhard Knobloch: Das Weltbild in den Wissenschaften – Geschichte einer Konzeption. in: Christoph Markschies, Johannes Zachhuber (Hrsg.): Die Welt als Bild: Interdisziplinäre Beiträge zur Visualität von Weltbildern. Berlin 2008, S. 227–246, S. 242
Albert Einstein: Die Grundlagen der Allgemeinen Relativitätstheorie. In: Annalen der Physik. 4, 49. PDF
CODATA Recommended Values. National Institute of Standards and Technology, abgerufen am 26. Juli 2015. Relative Unsicherheit 4,7·10⁻⁵
H. Colella, A. W. Overhauser, S. A. Werner: Observation of Gravitationally Induced Quantum Interference, Phys. Rev. Lett. 34 (1975) S. 1472
Hartmut Abele, Helmut Leeb: Gravitation and quantum interference experiments with neutrons, New Journal of Physics 14 (2012) 055010, doi:10.1088/1367-2630/14/5/055010.
M. D. Kislik: Spheres of Influence of Large Planets and the Moon, Cosmic Research, Vol 2, 1964, S. 853–858.
Q. Majorana: On gravitation. Theoretical and experimental researches. In: Philosophical Magazine. Band 39, 1920. S. 488–504.
H. N. Russell: On Majorana’s theory of gravitation. In: Astrophysical Journal. Band 54, 1921. S. 334–346. bibcode:1921ApJ....54..334R.
arxiv:physics/0108005 Podkletnov's Originalveröffentlichung
N. Li, D. Noever, T. Robertson, R. Koczor, W. Brantley: Static Test for a Gravitational Force Coupled to Type II YBCO Superconductors; In: Physica C, Band 281, 1997, S. 260–267.
C. Woods, S. Cooke, J. Helme, C. Caldwell: Gravity Modification by High Temperature Superconductors; In: Joint Propulsion Conference, AIAA 2001-3363, 2001.
Hathaway, Cleveland, Bao: Gravity modification experiment using a rotating superconducting disk and radio frequency fields; In: Physica C, Band 385, 2003, S. 488–500.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] PONS Deutsch – Latein, Erstbedeutungen von gravitas

[2] Edward Grant: The Nature of Natural Philosophy in the Late Middle Ages. Washington 2010, S. 63; Planets, Stars, and Orbs: The Medieval Cosmos, 1200–1687. 1994/96, S. 165; A Source Book in Medieval Science, Band 1. Zusammengestellt von Edward Grant, 1974, S. 551; Paul S. Agutter, Denys N. Wheatley: Thinking about Life: The history and philosophy of biology and other sciences. 2008, S. 59

[3] zitiert nach: Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper. (Deutsche Übersetzung von C. L. Menzzer, 1879.), S. 23@wikisource; Original: „Equidem existimo, gravitatem non aliud esse, quam appetentiam quandam naturalem partibus inditam a divina providentia opificis universorum, ut in unitatem integritatemque suam sese conferant in formam globi coeuntes. Quam affectionem credibile est etiam Soli, Lunae, caeterisque errantium fulgoribus inesse …“ Lib. I, Cap. IX@wikisource; s. a. Johann Samuel Traugott Gehler: Physikalisches Wörterbuch. Band 2, Leipzig 1789, S. 519

[4] Astronomia nova. Neue ursächlich begründete Astronomie (Übersetzung von Max Caspar, 1929 und Fritz Krafft, Wiesbaden 2005.), S. 28–29; Original: Scan des Druckexemplars der ETH-Bibliothek Zürich (abgerufen 24. März 2014); s. a. Johann Samuel Traugott Gehler: Physikalisches Wörterbuch. Band 2, Leipzig 1789, S. 519 und Florian Freistetter: Johannes Kepler: Astronomia Nova – Die Einleitung (3)@scienceblogs.de/astrodicticum-simplex (abgerufen 24. März 2014)

[5] Heinz Klaus Strick: Gilles Personne Roberval (1602–1675): Entdecker der Schwerkraft. Spektrum.de-Artikel

[6] Harry Nussbaumer: Revolution am Himmel: wie die kopernikanische Wende die Astronomie veränderte. Zürich 2011, S. 237; Eberhard Knobloch: Das Weltbild in den Wissenschaften – Geschichte einer Konzeption. in: Christoph Markschies, Johannes Zachhuber (Hrsg.): Die Welt als Bild: Interdisziplinäre Beiträge zur Visualität von Weltbildern. Berlin 2008, S. 227–246, S. 242

[7] Albert Einstein: Die Grundlagen der Allgemeinen Relativitätstheorie. In: Annalen der Physik. 4, 49. PDF

[8] CODATA Recommended Values. National Institute of Standards and Technology, abgerufen am 26. Juli 2015. Relative Unsicherheit 4,7·10⁻⁵

[9] H. Colella, A. W. Overhauser, S. A. Werner: Observation of Gravitationally Induced Quantum Interference, Phys. Rev. Lett. 34 (1975) S. 1472

[10] Hartmut Abele, Helmut Leeb: Gravitation and quantum interference experiments with neutrons, New Journal of Physics 14 (2012) 055010, doi:10.1088/1367-2630/14/5/055010.

[11] M. D. Kislik: Spheres of Influence of Large Planets and the Moon, Cosmic Research, Vol 2, 1964, S. 853–858.

[12] Q. Majorana: On gravitation. Theoretical and experimental researches. In: Philosophical Magazine. Band 39, 1920. S. 488–504.

[13] H. N. Russell: On Majorana’s theory of gravitation. In: Astrophysical Journal. Band 54, 1921. S. 334–346. bibcode:1921ApJ....54..334R.

[14] rxiv:physics/0108005 Podkletnov's Originalveröffentlichung

[15] N. Li, D. Noever, T. Robertson, R. Koczor, W. Brantley: Static Test for a Gravitational Force Coupled to Type II YBCO Superconductors; In: Physica C, Band 281, 1997, S. 260–267.

[16] C. Woods, S. Cooke, J. Helme, C. Caldwell: Gravity Modification by High Temperature Superconductors; In: Joint Propulsion Conference, AIAA 2001-3363, 2001.

[17] Hathaway, Cleveland, Bao: Gravity modification experiment using a rotating superconducting disk and radio frequency fields; In: Physica C, Band 385, 2003, S. 488–500.