Schalenmodell (Kernphysik)
Das Schalenmodell in der Kernphysik ist ein Modell des Aufbaus von Atomkernen. Es stützt sich auf quantenmechanische Gesetzmäßigkeiten, vor allem auf die Drehimpuls-Quantisierung und das Pauli-Prinzip, und erklärt so z. B. erfolgreich die magischen Zahlen.
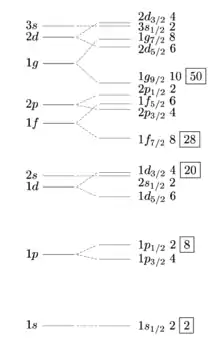
Die Nummern rechts neben den Niveaus geben die Multiplizität (2j+1) an. Die Zahlen in Kästen sind die „magischen Zahlen“.
Beschreibung
Während das Tröpfchenmodell den Atomkern mit einem Wassertropfen vergleicht, dessen Verhalten im Wesentlichen mit der klassischen Mechanik beschrieben werden kann, betrachtet das Schalenmodell die einzelnen Nukleonen und ihre Bewegung in einem Potentialfeld nach den Regeln der Quantenmechanik, ähnlich wie das Schalenmodell für Elektronen in der Atomhülle. Proton und Neutron haben wie das Elektron die Spinquantenzahl 1/2. Jedoch gibt es wichtige Unterschiede zur Atomhülle:
- der Atomkern besteht aus zwei verschiedenen Teilchenarten,
- es gibt kein gemeinsames Kraftzentrum des Potentials, sondern das Feld, das auf ein einzelnes Teilchen wirkt, wird von den übrigen Teilchen erzeugt,
- zwischen den Nukleonen wirken viel stärkere Kräfte.
Gut geeignet zur Beschreibung erscheint ein Woods-Saxon-Potential. Da sich dieses aber nur numerisch behandeln lässt, wählt man zur analytischen Behandlung beispielsweise ein ähnlich verlaufendes modifiziertes Potential eines harmonischen Oszillators. Notwendig ist auch die Berücksichtigung einer Spin-Bahn-Kopplung. Man erhält als Lösungen der Schrödingergleichung diskrete Energieniveaus, die je nach Quantenzahlen bestimmte Anzahlen von Teilchen aufnehmen können; sie werden – in Anlehnung an die Beschreibung der Atomhülle – als „Schalen“ bezeichnet.
Die Niveaus für Protonen und Neutronen sind nicht die gleichen, denn die elektrische Ladung der Protonen sorgt durch die gegenseitige Abstoßung dafür, dass die Protonen-Niveaus etwas höher liegen als die der Neutronen. Bei den meisten Nukliden (bis hinauf zu etwa 80 Protonen) sind die Abstände der Niveaus untereinander aber für Protonen und Neutronen annähernd gleich, die beiden Niveauschemata sind also im Wesentlichen nur gegeneinander verschoben. Dies lässt sich an Spiegelkernen bestätigen.[1][2] Dieser Verschiebung entspricht im Tröpfchenmodell der Coulomb-Anteil.
Die magischen Zahlen
Die Anzahl gleicher Teilchen, die sich auf einer Schale befinden können, wird begrenzt durch das Pauli-Prinzip. Die 1s-Schale z. B. ist mit zwei Nukleonen bereits voll besetzt, und ein hinzukommendes Nukleon „muss“ die 1p-Schale mit entsprechend höherer Energie besetzen.
Wenn in einem Kern alle Protonen- oder Neutronenschalen entweder vollständig gefüllt oder leer sind, ist dies eine besonders stabile Konfiguration, vergleichbar den Edelgasen in der Chemie; die besondere Stabilität zeigt sich in vielen Eigenschaften und Messgrößen. Solche Kerne werden auch magische Kerne genannt. Die magischen Zahlen, die an natürlich vorkommenden Nukliden beobachtet werden, sind:
| 2 | 8 | 20 | 50 | 82 | 114 | 126 | 164 | Protonen | ||||||
| 2 | 8 | 20 | 28 | 50 | 82 | 126 | 184 | 196 | 228 | 272 | 318 | Neutronen |
Fett hervorgehoben sind diejenigen magischen Protonen- und Neutronen-Zahlen, die zusammen im gleichen Kern vorkommen können; solche Kerne heißen doppelt magisch.
Die magischen Zahlen unterscheiden sich von den entsprechenden Zahlen in der Atomhülle. Der Grund ist die im Atomkern stärker wirkende Spin-Bahn-Kopplung. Der Energieabstand zwischen erlaubten Zuständen entsteht bei insgesamt 28 Teilchen einer Art nicht durch volle Besetzung einer Schale, sondern durch die Spin-Bahn-Kopplung des 1f-Niveaus. f-Niveau bedeutet wie bei den Elektronen, dass die Nebenquantenzahl (Bahndrehimpulsquantenzahl) l=3 ist. Mit der Spinquantenzahl s=±0,5 ergeben sich daher als mögliche Gesamtdrehimpulse j=l+s die Werte 3,5 und 2,5, wobei j=3,5 energetisch tiefer liegt als j=2,5. Sind alle Zustände mit j=3,5 besetzt, so erhält man ein stabileres Niveau bei der magischen Zahl 28.
Die Spin-Bahn-Kopplung ähnelt grundsätzlich der Feinstrukturaufspaltung der Elektronenniveaus im Atom. Jedoch tritt im Atomkern die starke Kernkraft an die Stelle der elektromagnetischen Wechselwirkung; die Aufspaltung der Nukleonen-Orbitale ist dadurch sowohl absolut als auch relativ viel größer als bei Hüllenelektronen, und der Zustand mit j=3,5 liegt hier energetisch günstiger (tiefer) als der mit j=2,5. Anschaulich ausgedrückt: Elektronen „wollen“ den Gesamtdrehimpuls j minimieren, Nukleonen „wollen“ ihn maximieren.
Entsprechend sind die magischen Zahlen 50, 82 und 126 auf die Spin-Bahn-Kopplungen der 1g-, 1h- und 1i-Orbitale zurückzuführen.
Kernspin und Parität
Das Schalenmodell sagt auch den Kernspin und die positive oder negative Parität für den Grundzustand der meisten Nuklide richtig voraus. Zum Beispiel haben alle gg-Kerne im Grundzustand den Spin Null und positive Parität.[3]
Restwechselwirkung
Kerne mit Valenznukleonen außerhalb geschlossener Schalen werden mit einem Hamiltonoperator mit einer effektiven Nukleon-Nukleon-Restwechselwirkung zwischen den Valenznukleonen beschrieben, die über die Beschreibung durch ein mittleres Potential wie im ursprünglichen Schalenmodell hinausgeht. Die Restwechselwirkung ist angelehnt an die Wechselwirkung freier Nukleonen (mit realistischen Wechselwirkungspotentialen), aber nicht mit ihr identisch, da der Zustandsraum der Valenznukleonenkonfigurationen, in denen der Hamiltonoperator diagonalisiert wird, beschränkt ist.[4][5] Schalenmodellberechnungen mit Berücksichtigung der Restwechselwirkung angelehnt an ein realistisches Nukleon-Nukleon-Potential führten Thomas Kuo und Gerald „Gerry“ Brown 1966[6] erstmals erfolgreich für die Kerne O-18 und F-18 aus; diese Kerne können als bestehend aus dem doppelt magischen Kern O-16 mit zwei zusätzlichen Valenznukleonen angesehen werden. Dies war der erste Versuch, Kernstruktureigenschaften mit einer aus der freien Nukleon-Nukleon-Wechselwirkung abgeleiteten realistischen Potentialform (Hamada-Johnston-Potential) zu berechnen. Für die effektive Restwechselwirkung benutzten sie den Formalismus der G-Matrix von Keith Brueckner.
Verzichtet man auf die Beschreibung durch ein mittleres Feld aller Nukleonen, auch derer in abgeschlossenen Schalen, so erhält man die ab initio-Methode des Schalenmodells „ohne Kern“ (No-core shell model). Auch hier werden effektive, an realistische Potentiale freier Nukleonen (wie das Bonn-Potential) angelehnte Zweiteilchenwechselwirkungspotentiale verwendet, es müssen aber zusätzlich Dreiteilchenwechselwirkungen berücksichtigt werden.[7]
Geschichte
Das Schalenmodell wurde erstmals 1932 von Dmitri Iwanenko und Jewgeni Gapon vorgeschlagen.[8] 1949 wurde es von Maria Goeppert-Mayer und unabhängig im gleichen Jahr von J. Hans D. Jensen und seinen Mitarbeitern Otto Haxel und Hans E. Suess ausgearbeitet. Goeppert-Mayer und Jensen erhielten dafür 1963 den Nobelpreis für Physik. Dass das Schalenmodell trotz der starken Nukleon-Nukleon-Kraft (s. oben) sinnvoll anwendbar ist, wurde erst ab 1955 durch Keith Brueckner u. M. verständlich gemacht, die Näherungslösungen für das Vielkörperproblem entwickelten.[9]
Schon in den 1950er Jahren wurden kollektive Effekte wie die rotierender Kerne berücksichtigt mit einem in Ellipsenform deformierten Potential für das Schalenmodell (Nilsson-Modell, nach Sven Gösta Nilsson). Aage Bohr und Ben Mottelson erhielten vor allem dafür den Nobelpreis.
Einzelnachweise
- Bethge/Walter/Wiedemann: Kernphysik. 3. Aufl., Berlin: Springer 2008, S. 92. ISBN 978-3-540-74566-2
- B. Povh, K. Rith, C. Scholz, F. Zetsche, W. Rodejohann: Teilchen und Kerne: Eine Einführung in die physikalischen Konzepte. 9. Auflage, Springer, 2014, ISBN 978-3-642-37821-8
- E. B. Paul: Nuclear and Particle Physics. Amsterdam: North-Holland, 1969, S. 266
- E. Caurier, G. Martínez-Pinedo, F. Nowacki, A. Poves, A. P. Zuker, The shell model as a unified view of nuclear structure, Reviews of Modern Physics, Band 77, 2005, S. 427–488. Arxiv
- L. Coraggio, A. Covello, A. Gargano, N.Itaco, T. T. S. Kuo, Shell-model calculations and realistic effective interactions, Progress in Particle and Nuclear Physics, Band 62, 2009, S. 135–182, Arxiv
- T. T. S. Kuo, G. E. Brown, Structure of finite nuclei and the free nucleonnucleon interaction: An application to 18O and 18F, Nucl. Phys., Band 85, 1966, S. 40–86
- B. R. Barrett, P. Navrátil, J. P. Vary, Ab initio no core shell model, Progress in Particle and Nuclear Physics, Band 69, 2013, S. 131–181. Arxiv
- Gapon, Iwanenko Zur Bestimmung der Isotopenzahl, Naturwissenschaften, Bd. 20, 1932, S. 792.
- Bernard L. Cohen: Concepts of Nuclear Physics. New York: McGraw-Hill, 1971, S. 65
Literatur
Originalarbeiten:
- Maria Goeppert-Mayer: On closed shells in nuclei. Phys. Rev. 74: 235 (1948).
- Maria Goeppert-Mayer: On closed shells in nuclei II. Phys. Rev. 75: 1969 (1949).
- Maria Goeppert-Mayer: Nuclear configurations in the spin-orbit coupling model.
- I. Empirical evidence. Phys. Rev. 78: 16 (1950).
- II. Theoretical considerations. Phys. Rev. 78: 22 (1950).
- Maria Goeppert-Mayer, J.H.D. Jensen: Elementary Theory of Nuclear Shell Structure. New York: John Wiley & Sons, 1955
- Otto Haxel, J.H.D. Jensen, H. E Suess: On the ‘magic numbers’ in nuclear structure. Phys. Rev. 75 (1949), 1766
- Haxel, Jensen, Suess: Zur Interpretation der ausgezeichneten Nukleonenzahlen im Bau des Atomkerns, Naturwissenschaften, Band 35, 1949, S. 376, Band 36, 1949, S. 153, 155
- Haxel, Jensen, Suess: Modellmäßige Deutung der ausgezeichneten Nukleonenzahlen im Kernbau, Zeitschrift für Physik, Band 128, 1950, S. 295–311
- Haxel, Jensen, Suess: Das Schalenmodell des Atomkerns, Ergebnisse der exakten Naturwissenschaften 26, 1952, S. 244–290
Neuere Literatur:
- Amos de Shalit, Igal Talmi: Nuclear Shell Theory, Academic Press 1963, Reprint bei Dover
- Xing-Wang Pan, Da Hsuan Feng, Michel Vallières (Hrsg.): Contemporary Shell Models, Proc. Int. Workshop Philadelphia 1996, Springer, Lecture notes in physics 482, 1997
- Xing-Wang Pan, T. T. S. Kuo, Michel Vallières, Da Hsuan Feng: Nuclear shell model calculations with fundamental nucleon-nucleon interactions, Physics Reports, Band 164, 1996, S. 311–323, Arxiv
- E. Caurier, G. Martinez-Pinedo, F. Nowacki, A. Poves, A. P. Zuker: The shell model as unified view of nuclear structure, Reviews of Modern Physics, Band 77, 2005, S. 427–488, Arxiv
- L. Coraggio u. a.: From Kuo-Brown to today's realistic shell model calculations, Nucl. Phys. A, Band 928, 2014, S. 43, Arxiv