Elektrodynamik

Die klassische Elektrodynamik (auch Elektrizitätslehre) ist das Teilgebiet der Physik, das sich mit bewegten elektrischen Ladungen und mit zeitlich veränderlichen elektrischen und magnetischen Feldern beschäftigt. Die Elektrostatik als Spezialfall der Elektrodynamik beschäftigt sich mit ruhenden elektrischen Ladungen und ihren Feldern. Die zugrundeliegende Grundkraft der Physik heißt elektromagnetische Wechselwirkung.

Visualisiertes Magnetfeld einer Zylinderspule

Als Entdecker des Zusammenhangs von Elektrizität und Magnetismus gilt Hans Christian Ørsted (1820), obwohl er in Gian Domenico Romagnosi (1802) einen damals kaum beachteten Vorläufer hatte. Die Theorie der klassischen Elektrodynamik wurde von James Clerk Maxwell Mitte des 19. Jahrhunderts mithilfe der nach ihm benannten Maxwell-Gleichungen formuliert. Die Untersuchung der Maxwellgleichungen für bewegte Bezugssysteme führte Albert Einstein 1905 zur Formulierung der speziellen Relativitätstheorie. Im Laufe der 1940er Jahre gelang es, die Quantenmechanik und Elektrodynamik in der Quantenelektrodynamik zu kombinieren; deren Vorhersagen stimmen mit Messergebnissen sehr genau überein.

Eine wichtige Form von elektromagnetischen Feldern sind die elektromagnetischen Wellen, zu denen als bekanntester Vertreter das sichtbare Licht zählt. Dessen Erforschung bildet ein eigenes Gebiet der Physik, die Optik. Die physikalischen Grundlagen der Beschreibung elektromagnetischer Wellen liefert jedoch die Elektrodynamik.

Klassische Elektrodynamik

Grundlegende Gleichungen

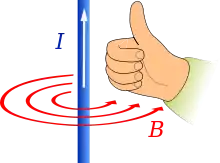Ein durch einen Leiter fließender Strom $\textstyle I$ erzeugt um den Leiter ein magnetisches Wirbelfeld $\textstyle B.$
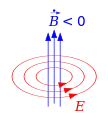Zeitliche Änderungen des magnetischen Flusses $\textstyle B$ erzeugen ein elektrisches Wirbelfeld $\textstyle E.$
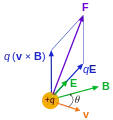Lorentzkraft $\textstyle F$ auf eine in einem elektrischen Feld $\textstyle E$ und einem magnetischen Feld $\textstyle B$ mit der Geschwindigkeit $\textstyle v$ bewegte Ladung $\textstyle +q.$

Das Zusammenspiel von elektromagnetischen Feldern und elektrischen Ladungen wird grundlegend durch die mikroskopischen Maxwell-Gleichungen

{\begin{aligned}\operatorname {div} {\vec {B}}&=0,&\operatorname {rot} {\vec {E}}+{\frac {\partial {\vec {B}}}{\partial t}}&=0\,,\\\operatorname {div} {\vec {E}}&={\frac {\rho }{\varepsilon _{0}}}\,,&\operatorname {rot} {\vec {B}}-\mu _{0}\,\varepsilon _{0}\,{\frac {\partial {\vec {E}}}{\partial t}}&=\mu _{0}\,{\vec {j}}.\end{aligned}}

und die Lorentzkraft

{\vec {F}}=q({\vec {E}}+{\vec {v}}\times {\vec {B}})

bestimmt.

Daraus ergeben sich mit Hilfe der Materialgleichungen der Elektrodynamik die makroskopischen Maxwell-Gleichungen. Diese sind Gleichungen für die effektiven Felder, die in Materie auftreten.

Weiter spielen (daraus ableitbar) eine wichtige Rolle:

die Kontinuitätsgleichung ${\frac {\partial \rho }{\partial t}}+\operatorname {div} {\vec {j}}=0$ , die besagt, dass die Ladung erhalten bleibt,
der Satz von Poynting, der besagt, dass die Energie von Teilchen und Feldern insgesamt erhalten bleibt.

Potentiale und Wellengleichung

Die homogenen Maxwellgleichungen

{\text{div}}\,{\vec {B}}=0

und

\operatorname {rot} \,{\vec {E}}+{\frac {\partial {\vec {B}}}{\partial t}}=0

können durch die Einführung der elektromagnetischen Potentiale gemäß

{\vec {B}}=\operatorname {rot} \,{\vec {A}}

und

{\vec {E}}=-{\text{grad}}\,\phi -{\frac {\partial {\vec {A}}}{\partial t}}

in einem sternförmigen Gebiet identisch gelöst werden (Poincaré-Lemma). Dabei bezeichnet $\phi$ das sogenannte skalare Potential und ${\vec {A}}$ das Vektorpotential. Da die physikalischen Felder nur durch Ableitungen der Potentiale gegeben sind, hat man gewisse Freiheiten, die Potentiale abzuändern und trotzdem dieselben physikalischen Felder zurückzuerhalten. Beispielsweise ergeben ${\vec {A}}'$ und ${\vec {A}}$ dasselbe $B$ -Feld, wenn man sie durch

{\vec {A}}'={\vec {A}}+{\text{grad}}\,\Lambda

miteinander in Beziehung setzt. Fordert man auch, dass sich bei einer solchen Transformation dasselbe $E$ -Feld ergibt, muss sich $\phi$ wie

\phi '=\phi -{\frac {\partial \Lambda }{\partial t}}

transformieren. Eine solche Transformation wird Eichtransformation genannt. In der Elektrodynamik werden zwei Eichungen oft verwendet. Erstens die sogenannte Coulomb-Eichung oder Strahlungseichung

{\text{div}}\,{\vec {A}}=0

und zweitens die Lorenz-Eichung

{\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}+{\text{div}}\,{\vec {A}}=0

.

Die Lorenz-Eichung hat dabei den Vorteil relativistisch invariant zu sein und sich bei einem Wechsel zwischen zwei Inertialsystemen strukturell nicht zu ändern. Die Coulomb-Eichung ist zwar nicht relativistisch invariant, aber wird eher bei der kanonischen Quantisierung der Elektrodynamik verwendet.

Setzt man die $E$ - und $B$ -Felder und die Vakuum-Materialgleichungen in die inhomogenen Maxwellgleichungen ein und eicht die Potentiale gemäß der Lorenz-Eichung, entkoppeln die inhomogenen Maxwellgleichungen und die Potentiale erfüllen inhomogene Wellengleichungen[1]

\Box \phi =-{\frac {\rho }{\varepsilon _{0}}}\,,\,\Box {\vec {A}}=-\mu _{0}{\vec {j}}\,.

Hierbei bezeichnet $\Box$ den D’Alembert-Operator.

Spezialfälle

Die Elektrostatik ist der Spezialfall unbewegter elektrischer Ladungen und statischer (sich nicht mit der Zeit ändernder) elektrischer Felder. Sie kann in Grenzen auch verwendet werden, solange die Geschwindigkeiten und Beschleunigungen der Ladungen und die Änderungen der Felder klein sind.

Die Magnetostatik beschäftigt sich mit dem Spezialfall konstanter Ströme in insgesamt ungeladenen Leitern und konstanter Magnetfelder. Sie kann für hinreichend langsam veränderliche Ströme und Magnetfelder verwendet werden.

Die Kombination aus beiden, Elektromagnetismus, kann beschrieben werden als Elektrodynamik der nicht zu stark beschleunigten Ladungen. Die meisten Vorgänge in elektrischen Schaltkreisen (z. B. Spule, Kondensator, Transformator) lassen sich bereits auf dieser Ebene beschreiben. Ein stationäres elektrisches oder magnetisches Feld bleibt nahe seiner Quelle, wie zum Beispiel das Erdmagnetfeld. Ein sich veränderndes elektromagnetisches Feld kann sich jedoch von seinem Ursprung entfernen. Das Feld bildet eine elektromagnetische Welle im Zusammenspiel zwischen magnetischem und elektrischem Feld. Diese Abstrahlung elektromagnetischer Wellen wird in der Elektrostatik vernachlässigt. Die Beschreibung des elektromagnetischen Feldes beschränkt sich hier also auf das Nahfeld.

Elektromagnetische Wellen hingegen sind die einzige Form des elektromagnetischen Feldes, die auch unabhängig von einer Quelle existieren kann. Sie werden zwar von Quellen erzeugt, können aber nach ihrer Erzeugung unabhängig von der Quelle weiterexistieren. Da Licht sich als elektromagnetische Welle beschreiben lässt, ist auch die Optik letztlich ein Spezialfall der Elektrodynamik.

Elektrodynamik und Relativitätstheorie

Im Gegensatz zur klassischen Mechanik ist die Elektrodynamik nicht Galilei-invariant. Das bedeutet, wenn man, wie in der klassischen Mechanik, einen absoluten, euklidischen Raum und eine davon unabhängige absolute Zeit annimmt, dann gelten die Maxwellgleichungen nicht in jedem Inertialsystem.

Einfaches Beispiel: Ein mit konstanter Geschwindigkeit fliegendes, geladenes Teilchen ist von einem elektrischen und einem magnetischen Feld umgeben. Ein zweites, mit gleicher Geschwindigkeit fliegendes und gleich geladenes Teilchen erfährt durch das elektrische Feld des ersten Teilchens eine abstoßende Kraft, da sich gleichnamige Ladungen gegenseitig abstoßen; gleichzeitig erfährt es durch dessen Magnetfeld eine anziehende Lorentzkraft, die die Abstoßung teilweise kompensiert. Bei Lichtgeschwindigkeit wäre diese Kompensation vollständig. In dem Inertialsystem, in dem beide Teilchen ruhen, gibt es kein magnetisches Feld und damit keine Lorentzkraft. Dort wirkt nur die abstoßende Coulombkraft, so dass das Teilchen stärker beschleunigt wird als im ursprünglichen Bezugssystem, in dem sich beide Ladungen bewegen. Dies widerspricht der newtonschen Physik, bei der die Beschleunigung nicht vom Bezugssystem abhängt.

Diese Erkenntnis führte zunächst zu der Annahme, dass es in der Elektrodynamik ein bevorzugtes Bezugssystem gäbe (Äthersystem). Versuche, die Geschwindigkeit der Erde gegen den Äther zu messen, schlugen jedoch fehl, so zum Beispiel das Michelson-Morley-Experiment. Hendrik Antoon Lorentz löste dieses Problem mit einer modifizierten Äthertheorie (Lorentzsche Äthertheorie), die jedoch von Albert Einstein mit seiner speziellen Relativitätstheorie abgelöst wurde. Einstein ersetzte Newtons absoluten Raum und absolute Zeit durch eine vierdimensionale Raumzeit. In der Relativitätstheorie tritt an die Stelle der Galilei-Invarianz die Lorentz-Invarianz, die von der Elektrodynamik erfüllt wird.

In der Tat lässt sich die Verringerung der Beschleunigung und damit die magnetische Kraft im obigen Beispiel als Folge der Längenkontraktion und Zeitdilatation erklären, wenn man die im bewegten System gemachten Beobachtungen in ein ruhendes System zurücktransformiert. In gewisser Weise lässt sich daher die Existenz von magnetischen Phänomenen letztlich auf die Struktur von Raum und Zeit zurückführen, wie sie in der Relativitätstheorie beschrieben wird. Unter diesem Gesichtspunkt erscheint auch die Struktur der Grundgleichungen für statische Magnetfelder mit ihren Kreuzprodukten weniger verwunderlich.

In der manifest Lorentz-forminvarianten Beschreibung der Elektrodynamik bilden das skalare Potential und das Vektorpotential einen Vierervektor, analog zum Vierervektor von Raum und Zeit, so dass die Lorentz-Transformationen analog auch auf die elektromagnetischen Potentiale angewendet werden können. Bei einer speziellen Lorentz-Transformation mit der Geschwindigkeit $v$ in $z$ -Richtung gelten für die Felder im gebräuchlichen SI-Einheitensystem die Transformationsgleichungen:

$E'_{x}={\frac {E_{x}-vB_{y}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$	$B'_{x}={\frac {B_{x}+{\frac {v}{c^{2}}}E_{y}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$
$E'_{y}={\frac {E_{y}+vB_{x}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$	$B'_{y}={\frac {B_{y}-{\frac {v}{c^{2}}}E_{x}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$
$E'_{z}=E_{z}\,$	$B'_{z}=B_{z}\,$

(In cgs-Einheiten sind diese Gleichungen nur unwesentlich modifiziert: Man muss formal nur ${\vec {B}}$ bzw. ${\vec {B}}'$ durch ${\vec {B}}/c$ bzw. ${\vec {B}}'/c$ substituieren.)

Erweiterungen

Jedoch liefert die klassische Elektrodynamik keine widerspruchsfreie Beschreibung bewegter Punktladungen, auf kleinen Skalen ergeben sich Probleme wie das der Divergenz aufgrund Strahlungsrückwirkung. Im Kleinen ist die Elektrodynamik quantenmechanisch zu beschreiben, was durch die Quantenelektrodynamik (QED) geschieht. Diese ist eine abelsche Eichfeldtheorie (Eichgruppe ist die unitäre Gruppe U(1)). Die Theorie der elektroschwachen Wechselwirkung vereinigt die QED mit der schwachen Wechselwirkung und ist Teil des Standardmodells der Elementarteilchenphysik. Diese ist auch eine Eichfeldtheorie, aber mit nichtabelscher Eichgruppe SU(2)x U(1), und auch die starke Wechselwirkung, die dritte Wechselwirkung des Standardmodells, wird in der Quantenchromodynamik durch eine nichtabelsche Eichtheorie beschrieben.

Es wurden auch Versuche der Vereinheitlichung der Elektrodynamik mit der allgemeinen Relativitätstheorie (Gravitation) als klassische Feldtheorien unternommen, bekannt unter dem Namen Kaluza-Klein-Theorien. Sie erlebten eine Wiederbelebung im Rahmen der Stringtheorie.

Siehe auch

Literatur

Geburt der klassischen Elektrodynamik

James Clerk Maxwell: On Physical Lines of Force, 4 Teile, Teil 1 The theory of molecular vortices applied to magnetic phenomena, in: Philosophical Magazine, Band 21 der 4. Folge, 1861, S. 161–175, Teil 2 The theory of molecular vortices applied to electric currents, ibid., S. 281–291, 338–348, Teil 3 The theory of molecular vortices applied to statical electricity, in: Phil. Mag., Band 23 der 4. Folge, 1862, S.. 12–24, Teil 4 The theory of molecular vortices applied to the action of magnetism on polarized light, ibid., 1862, S.. 85–95 (Volltext bei Wikisource).
James Clerk Maxwell: Eine dynamische Theorie des elektromagnetischen Feldes, 1864
James Clerk Maxwell: A Treatise on Electricity and Magnetism, 1873

Aktuelle Lehrbücher

John David Jackson: Klassische Elektrodynamik. Walter de Gruyter, Berlin 2006, ISBN 3-11-018970-4.
Torsten Fließbach: Elektrodynamik. 6. Auflage. Springer Spektrum, Berlin / Heidelberg 2012, ISBN 978-3-8274-3035-9.
Walter Greiner: Klassische Elektrodynamik. 7. Auflage. Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8085-5560-6.
Wolfgang Demtröder: Experimentalphysik. Band 2: Elektrizität und Optik. Springer, Berlin 2006, ISBN 3-540-65196-9.
Pascal Leuchtmann: Einführung in die elektromagnetische Feldtheorie. Pearson Studium, München 2005, ISBN 3-8273-7144-9.

Weblinks

Commons: elektromagnetisches Feld – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Elektrodynamik – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Versuche und Aufgaben zur Elektrodynamik (LEIFI)

Einzelnachweise

Wolfgang Nolting: Grundkurs Theoretische Physik 3 (= Springer-Lehrbuch). Springer Berlin Heidelberg, Berlin, Heidelberg 2013, ISBN 978-3-642-37904-8, doi:10.1007/978-3-642-37905-5.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Wolfgang Nolting: Grundkurs Theoretische Physik 3 (= Springer-Lehrbuch). Springer Berlin Heidelberg, Berlin, Heidelberg 2013, ISBN 978-3-642-37904-8, doi:10.1007/978-3-642-37905-5.