Welle-Teilchen-Dualismus
Der Welle-Teilchen-Dualismus ist eine Erkenntnis der Quantenphysik, wonach den Objekten der Quantenphysik gleichermaßen die Eigenschaften von klassischen Wellen wie die von klassischen Teilchen zugeschrieben werden müssen. Klassische Wellen breiten sich im Raum aus. Sie schwächen oder verstärken sich durch Überlagerung und können gleichzeitig an verschiedenen Stellen präsent sein und dabei auch verschieden stark einwirken. Ein klassisches Teilchen kann zu einem Zeitpunkt nur an einem bestimmten Ort anwesend sein. Beide Eigenschaften scheinen sich gegenseitig auszuschließen. Trotzdem wurde in mehreren Schlüsselexperimenten für verschiedene Quantenobjekte belegt, dass beide Eigenschaften vorliegen, so dass man jedem Körper eine Materiewelle zuschreibt.
Die Frage, ob Elektronen oder Lichtquanten Teilchen oder Wellen seien, lässt sich nicht beantworten. Sie sind vielmehr Quantenobjekte, die je nach der Art der Messung, die man an ihnen durchführt, unterschiedliche Eigenschaften in Erscheinung treten lassen. Dieses Problem wurde in der Quantenmechanik in der Kopenhagener Deutung (1927) mit dem dort formulierten Komplementaritätsprinzip zunächst dahingehend gelöst, dass die Festlegung der jeweils beobachteten Eigenschaft nicht allein dem Quantenobjekt zuzuordnen sei, sondern ein Phänomen der gesamten Anordnung aus Quantenobjekt und Messapparatur darstelle. Später entstanden eine Reihe weiterer Interpretationen der Quantenmechanik mit alternativen Erklärungsansätzen.
In der Alltagswelt taucht der Welle-Teilchen-Dualismus nicht auf, weil die Wellenlänge der Materiewelle bei makroskopischen Körpern um vieles zu klein ist, um Phänomene hervorzurufen, die eindeutig nur mit wellenartigem Verhalten zu erklären sind. Bei sehr kleinen Wellenlängen stimmen Wellenbild und Teilchenbild nämlich trotz der verschiedenen Ansätze in ihren beobachtbaren Konsequenzen überein, wie aus dem Verhältnis von Strahlenoptik und Wellenoptik schon früher bekannt war. Andererseits ist der Welle-Teilchen-Dualismus keineswegs auf die kleinsten Quantenobjekte beschränkt. Er wurde im Experiment auch schon für große Moleküle aus über 800 Atomen nachgewiesen.
Die Quantenfeldtheorie versteht sowohl Teilchen als auch Wechselwirkungen als diskrete Anregungen von Feldern. Damit gibt es auf der formalen Ebene keinen Unterschied zwischen diesen beiden Kategorien. Für die Anschauung allerdings bleibt das Problem, dass die zwei gegensätzlichen Bilder hier beide gelten.
Geschichte
Die Vorgeschichte der Entdeckung des Welle-Teilchen-Dualismus bei elektromagnetischer Strahlung reicht ins 17. Jahrhundert zurück, als die Gesetze der geometrischen Optik für Reflexion und Brechung von Lichtstrahlen näher erforscht wurden. Dabei entstanden zwei konkurrierende Theorien:
- Christiaan Huygens (1629–1695) konnte die optischen Gesetze mithilfe der Wellenvorstellung deuten und gilt deshalb als Begründer der Wellenoptik. Das von ihm entwickelte huygenssche Prinzip wird heute noch unverändert angewendet.
- Isaac Newton (1643–1727) deutete dieselben Gesetze mithilfe der Korpuskelvorstellung, nach der das Licht einen Strom schneller leichter Teilchen darstellt.
Beide Theorien stimmten mit den damaligen Beobachtungen gleich gut überein, obwohl ihre Ausgangspunkte unvereinbar erschienen. In Ermangelung experimenteller Möglichkeiten der Unterscheidung setzte sich, vor allem dank der größeren Autorität Newtons, zunächst die Korpuskeltheorie durch. Doch 1802 wies Thomas Young den Wellencharakter des Lichts nach. Young demonstrierte mit dem Doppelspaltexperiment, dass Licht sich durch Interferenz auslöschen kann, was für Teilchenstrahlen undenkbar ist. Allgemein anerkannt wurde die Wellennatur des Lichts erst spät im 19. Jahrhundert, nachdem weitere Entdeckungen gemacht worden waren, die nicht zur Korpuskeltheorie passten: Polarisation (François Arago u. a.), Beugung (theoretische Vorhersage durch Augustin Jean Fresnel, u. a. experimenteller Nachweis des Poisson-Flecks durch Arago 1821), geringere Fortpflanzungsgeschwindigkeit in optisch dichteren Medien (Léon Foucault 1853), der Zusammenhang von Lichtgeschwindigkeit und Elektrodynamik (James C. Maxwell 1867) und die elektromagnetischen Wellen (Heinrich Hertz 1886).
1900 entdeckte Max Planck bei der Analyse des thermodynamischen Gleichgewichts zwischen den elektromagnetischen Wellen der Wärmestrahlung und den umgebenden Wänden, dass der Energieübertrag zwischen Strahlung und Materie nur in Quanten der Größe
stattfinden kann ( Plancksches Wirkungsquantum, Frequenz der Welle). Planck nahm erstmals eine Quantisierung von Energiewerten des harmonischen Oszillators an (siehe Quantenhypothese). Dies geschah zunächst rein aus mathematischen Erwägungen.
1905 wies Albert Einstein nach, dass auch beim photoelektrischen Effekt der Energieübertrag an die Elektronen nicht mit Lichtwellen zu erklären ist, dafür aber mit Lichtquanten mit der von Planck angegebenen Energie.
wobei die Lichtgeschwindigkeit und die Wellenlänge des Photons sind. Diese Beziehung gilt auch für mechanische Wellen, wie etwa für Gitterschwingungen in einem Festkörper. Die Quanten werden in diesem Fall Phononen genannt.
Schließlich zeigte Einstein 1909, dass die Wärmestrahlung statistische Fluktuationen zeigen muss, deren Größe man nur dadurch interpretieren kann, dass die Strahlung selber aus Wellen und Quanten besteht. Er forderte die Entwicklung einer Theorie, in der die Strahlung sowohl Teilchencharakter als auch Wellencharakter hat, und gilt damit als Urheber des Prinzips des Welle-Teilchen-Dualismus. Die Lösung vermutete er allerdings irrtümlich in der Richtung, dass die stetig veränderliche elektromagnetische Welle durch die Überlagerung der Felder vieler eng benachbarter „singulärer Punkte“ entstehen würde.[1] Auch andere namhafte Physiker, darunter Max Planck und Niels Bohr, bezweifelten, dass dem Photon alle Eigenschaften eines Teilchens zugeschrieben werden müssten. Diese Erkenntnis setzte sich erst mit der Entdeckung des Compton-Effekts und seiner Deutung als elastischer Stoß zwischen einem Quant der elektromagnetischen Strahlung und einem Elektron durch Arthur Compton 1922 allgemein durch.[2]
Louis de Broglie postulierte im Jahre 1924, dass auch massebehaftete Teilchen einen Wellencharakter besitzen. Er gab für ein Teilchen mit dem Impuls eine Wellenlänge von
an. Mit Hilfe von de Broglies Formel konnte ein Beugungsverhalten von Teilchen vorhergesagt werden, welches 1927 experimentell durch Beugung eines Elektronenstrahls an einem Nickel-Kristall durch Davisson und Germer und schließlich durch das Elektronen-Doppelspaltexperiment von Claus Jönsson im Jahre 1961 bestätigt wurde. Der Wellencharakter der Materie ist durch Interferenzexperimente heute auch für weitaus größere Teilchen, beispielsweise komplexe Moleküle wie Fullerene, nachgewiesen.
Das Doppelspaltexperiment
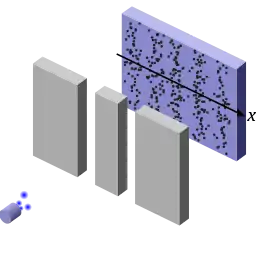




Besonders eindrücklich zeigt sich das Verhalten von Quantenobjekten im sogenannten Doppelspaltexperiment. Thomas Young konnte mit diesem Experiment erstmals die Wellennatur des Lichts nachweisen. Die auf Newton zurückgehende Korpuskeltheorie schien damit zunächst widerlegt.
Versuchsaufbau
Von einer Quelle gehen „Strahlen“ aus – es kann sich dabei um elektromagnetische Wellen oder Materieteilchen handeln – und treffen auf eine Blende mit zwei sehr feinen, eng beieinander liegenden Schlitzen. Diese Blende wird „Doppelspalt“ genannt. Hinter der Blende befindet sich ein Schirm. Die Strahlen, die durch den Doppelspalt gelangen, treffen auf den Schirm und werden dort in geeigneter Weise registriert.
Klassische Wellen
Handelt es sich bei den Strahlen um klassische Wellen, so zeigen sie ein typisches Beugungsmuster, wie es in der nebenstehenden Abbildung 1 zu sehen ist: Je nach Wellenlänge der Strahlung und Geometrie des Doppelspalts erscheinen Bereiche auf dem Schirm streifenförmig hell oder dunkel. Die hellsten Stellen befinden sich dort, wo die beiden vom Doppelspalt ausgehenden Elementarwellen einen Wegunterschied aufweisen, der ein ganzzahliges Vielfaches der Wellenlänge ist, denn dann sind die beiden Wellen „in Phase“ und interferieren konstruktiv. In der Mitte zwischen zwei solchen Stellen sind die beiden Wellen gegenphasig und löschen sich durch destruktive Interferenz gegenseitig aus.
Abgesehen von seinem streifenförmigen Aufbau erscheint das Beugungsmuster kontinuierlich. Die Helligkeit an einem Ort kann jeden beliebigen Wert zwischen völliger Dunkelheit und maximaler Beleuchtung annehmen.
Klassische Teilchen
Klassische Teilchen (also einzelne Massepunkte) zeigen keine Interferenz (siehe Abbildung 2). Sie gelangen entweder durch den linken oder den rechten Spalt und treffen dann jeweils innerhalb eines klar abgegrenzten Bereichs auf den Schirm. Folglich erscheinen auf dem Schirm genau zwei helle Streifen (je einer für einen der beiden Spalte). Bei genauerer Betrachtung fällt die körnige Struktur der beiden Streifen auf. Jedes Teilchen trifft an genau einer Stelle auf und hinterlässt dort einen hellen Punkt. Es gibt keinen kontinuierlichen Helligkeitsverlauf. Ein Ort ist entweder hell oder dunkel markiert, denn entweder wurde er von einem Teilchen getroffen oder nicht.
Quantenobjekte
Die Objekte der Quantenphysik verhalten sich hingegen so, wie es die dritte und vierte Abbildung veranschaulichen: Wie bei den klassischen Wellen zeigt die Intensitätsverteilung auf dem Schirm ein typisches Beugungsmuster. Es muss also Interferenz auftreten. Andererseits ist der Intensitätsverlauf nicht kontinuierlich. Es erscheinen helle Punkte, jedoch in unterschiedlicher Dichte. Jedem Quantenobjekt kann also (zumindest nachträglich) ein bestimmter Ort zugewiesen werden, an dem es auf den Schirm getroffen ist. Es handelt sich daher eindeutig um ein zählbares, punktförmiges Objekt.
Diskussion
Die Quantenobjekte zeigen also offensichtlich Eigenschaften beider klassischen Modelle: Sie interferieren miteinander, was typisch für Wellen ist. Andererseits sind sie zählbar und punktförmig, was der Wellennatur gänzlich widerspricht und eher auf eine Teilchennatur hinweist. Es gelingt nicht, eines der beiden Modelle widerspruchsfrei so zu modifizieren, dass es alle Aspekte des Versuchsergebnisses erklären könnte. Beispielsweise kann ein Teilchen nur durch einen der beiden Spalte gehen, jedoch nicht durch beide gleichzeitig. Wenn man abwechselnd einen der beiden Spalte abdeckt, so erhält man die Verteilung von Teilchen, die entweder durch den rechten oder durch den linken Spalt gegangen sind. Dies entspricht näherungsweise der Verteilung aus Abbildung 2, wenn man über die Beugungserscheinungen an den Kanten hinwegsieht, die bei Quantenobjekten immer auftreten. Öffnet man wieder beide Spalte, so erscheint das Beugungsmuster aus Abbildung 3 bzw. 4. Daraus folgt, dass man das Verteilungsmuster der Quantenobjekte auf dem Schirm nicht erklären kann, wenn man davon ausgeht, dass das einzelne Quantenobjekt entweder den Weg durch den einen oder durch den anderen Spalt nimmt. Trotzdem muss es sich um einzelne, unteilbare, punktförmige Teilchen handeln, denn als solche werden sie am Schirm räumlich und zeitlich getrennt voneinander registriert, wie man besonders deutlich in Abb. 4(b) sieht. Die Vorstellung einer räumlich ausgedehnten Welle, die gleichzeitig durch beide Spalte gehen und danach mit sich selbst interferieren kann, ist daher ebenso falsch.
Quantenobjekte zeigen also ein Verhalten, das weder mit dem klassischen Wellenbild noch mit dem klassischen Teilchenbild befriedigend erklärt werden kann.
Schlüsselexperimente
Zunächst stützte sich der Welle-Teilchen-Dualismus auf Untersuchungen zum Spektrum der Wärmestrahlung (Planck), zum photoelektrischen Effekt und zur statistischen Schwankung der Wärmestrahlung (Einstein) und theoretische Überlegungen zur Möglichkeit der Materiewelle (de Broglie). Er war also eher indirekt entdeckt worden, spielte aber in der Wellenmechanik (Schrödinger) eine zentrale Rolle. Daher war es das Ziel weiterer Experimente, den Welle-Teilchen-Dualismus auf wesentlich direktere Weise zu prüfen.
Compton-Effekt
Arthur Compton konnte 1923 nachweisen, dass elektromagnetische Wellen sich bei der Streuung an Elektronen genau so verhalten wie ein Strom einzelner Teilchen, die die Energie und den Impuls eines Photons besitzen und einen elastischen Stoß mit einem Elektron ausführen. Damit zeigte Compton überzeugend den Teilchencharakter der Quanten der Röntgenstrahlen im Experiment, und zwar ausgerechnet mithilfe ihres Wellencharakters. Dieser wurde dazu benutzt, um in derselben Apparatur durch ein Interferenzphänomen, nämlich die Braggsche Beugung an einem Kristall, die Wellenlänge jedes gestreuten Photons vor und nach dem Stoß festzustellen. 1925 konnte Compton zudem zeigen, dass das gestoßene Elektron gleichzeitig mit einem gestreuten Photon wegfliegt, welches die zum Ablenkwinkel passende Energie hat. Andere Erklärungsversuche waren damit widerlegt.[3]
Elektronenbeugung am Kristallgitter
Clinton Davisson und Lester Germer konnten 1927 zeigen, dass ein Strahl von Elektronen teilweise ohne Energieverlust von einer Kristalloberfläche zurückgeworfen wird und dann Interferenzphänomene zeigt wie Röntgenstrahlung bei der Braggschen Beugung. Das kann physikalisch nur mit einer Ausbreitung jedes Elektrons in Form einer Welle beschrieben werden. Dass die Elektronen andererseits auch Teilchen sind, wird im selben Experiment darin deutlich, dass ein anderer Teil der einfallenden Elektronen jeweils mit einem Elektron des Kristalls elastisch zusammengestoßen war und dadurch Energie verloren hatte. Die so gestreuten Elektronen bilden kein Interferenzmuster.[4] Sie sind durch die zufällige Energieabgabe nun inkohärent.
Interferenz größerer Moleküle
Um zu klären, ob der Welle-Teilchen-Dualismus nur elementaren Teilchen wie Photonen und Elektronen zukommt oder auch zusammengesetzten Systemen, wurden Atome und Moleküle untersucht. Entsprechende Interferenzmuster wurden erstmals 1930 von Immanuel Estermann und Otto Stern mit H2-Molekülen nach Reflexion an einer Kristalloberfläche von LiF nachgewiesen. Sie entsprachen genau den für die Moleküle vorhergesagten Materiewellen. Auf dem Weg zu Teilchen mit immer größerer Masse gelang es in Wien 1999, Interferenzmuster an C60 zu erzeugen[5]. Diese auch „Buckyballs“ genannten Moleküle bestehen aus 60 Kohlenstoffatomen, die in Form eines Fußballs zusammengesetzt sind und insgesamt 360 Protonen, 360 Neutronen und 360 Elektronen enthalten. Sie sind etwa 1 nm groß und unter dem Raster-Tunnel-Mikroskop schon gut als kleine „Materieklumpen“ zu sehen[6]. Ihre de Broglie-Wellenlänge betrug etwa 3 pm und war damit vier bis fünf Größenordnungen kleiner als die Gitterkonstante von 100 nm – die derzeit kleinste technisch realisierbare. Die Interferenzmaxima auf dem Schirm in etwa 1 m Entfernung hatten daher einen Abstand von nur 0,03 mm. Im Beugungsexperiment wurde der Teilchencharakter der Buckyballs auch dadurch deutlich, dass sie nach Durchgang durch das Beugungsgitter einzeln gezählt wurden.[7][8] Das größte Molekül, mit dem bis 2016 solche Beugungsbilder erzeugt werden konnten, ist Meso-tetra(pentafluorophenyl)porphyrin (TPPF20, C284H190F320N4S12) mit einer Molekülmasse von 10123 amu.[9]
Neuere Experimente
2005 entwickelten Pariser Physiker um Yves Couder mit einem Öltröpfchenexperiment ein makroskopisches System zum Test von de Broglies Ansatz. Öltröpfchen, welche auf den Wellen eines Ölbades surfen, könnten quantenartige Verhaltensweisen zeigen. „Zum Beispiel folgten sie nur bestimmten, »quantisierten« Bahnen, die um das Zentrum der Flüssigkeitsbäder verliefen. Und manchmal sprangen die Tröpfchen zufällig zwischen den Bahnen hin und her, so ähnlich, wie es Elektronen in Atomen tun.“ Neue Experimente von 2015 deuten jedoch darauf hin, dass Couders Demonstration quantenähnlicher Phänomene nicht den strengen Bedingungen des Doppelspaltexperiments standhält. Gleichzeitig bringen diese Experimente auch de Broglies Pilotwellen-Theorie zu Fall. Wenn man nämlich senkrecht zu den Spalten eine Trennwand einfügt, welche die Pilotwelle bzw. die Teilchen, die den einen oder den anderen Spalt passieren werden, schon weit vor dem Durchtritt trennt, verlieren die Teilchen „den Kontakt mit der Pilotwelle auf der anderen Seite der senkrecht zum Schirm angebrachten Barriere. Ohne Kontakt zum Teilchen beziehungsweise Öltropfen geht der Wellenfront jedoch rasch die Puste aus; sie kommt lange vor Erreichen des Spalts zum Erliegen.“ Dadurch kann sich hinter dem Doppelspalt auch kein Interferenzmuster mehr bilden.[10]
Auflösung des Welle-Teilchen-Dualismus in der Quantenmechanik
Jedes Teilchen wird in der Quantenmechanik durch eine Wellenfunktion beschrieben. Die Wellenfunktion eines Teilchens ist komplexwertig und somit keine Messgröße. Lediglich ihr Betragsquadrat kann als Aufenthaltswahrscheinlichkeit (genauer: als Volumendichte der Aufenthaltswahrscheinlichkeit) des Teilchens gedeutet und im Experiment bestimmt werden. Die zeitliche Entwicklung der Wellenfunktion des Teilchens und somit die Veränderung seiner Aufenthaltswahrscheinlichkeit wird durch die Schrödingergleichung beschrieben.
Quantenmechanik und statistische Physik
Im mikroskopischen Bereich dient der Welle-Teilchen-Dualismus als heuristische Erklärung für einige physikalische Phänomene. So hängt nach de Broglie die Wellenlänge eines Teilchens von seiner Geschwindigkeit und somit auch von seiner Temperatur ab. Bei niedrigen Temperaturen können die De-Broglie-Wellenlängen von Atomen größer werden als der Atomdurchmesser und sich überlappen, wodurch teilweise die Effekte der Suprafluidität von Helium-3 und Helium-4 erklärt werden können. Für eine vollständige und quantitative Behandlung dieser Themen muss jedoch die Quantenmechanik herangezogen werden.
Makroskopische Betrachtung
Der Wellencharakter der Teilchen zeigt sich nicht bei makroskopischen Gegenständen, was zwei prinzipielle Ursachen hat:
- Selbst bei langsamer Bewegung haben makroskopische Gegenstände aufgrund ihrer großen Masse eine Wellenlänge, die erheblich kleiner ist als die Abmessungen des Gegenstandes. In diesem Fall kann man nicht mehr den gesamten Gegenstand als ein quantenmechanisches Objekt behandeln, sondern muss seine Bestandteile separat beschreiben.
- In makroskopischen Gegenständen laufen permanent thermodynamisch irreversible Prozesse ab und es werden Photonen (Wärmestrahlung) mit der Umgebung ausgetauscht. Beides führt zur Dekohärenz des Systems, was bedeutet, dass ein anfangs möglicherweise interferenzfähiger Zustand sich sehr schnell in einen nicht interferenzfähigen umwandelt, der sich dann wie ein klassisches Teilchen, also nicht wie eine Welle verhält.
Anwendungsbeispiel Röntgenspektroskopie
In der Röntgenspektroskopie macht man sich die Eigenschaften der charakteristischen Röntgenstrahlung zunutze. Das Röntgenspektrum eines Stoffes gibt Aufschluss über den inneren Aufbau seiner Atome und kann daher für die Analytik verwendet werden. Die Messung kann entweder wellenlängen- oder energiedispersiv erfolgen. Bei der energiedispersiven Methode werden direkt die Energien der einzelnen Photonen bestimmt (also in der klassischen Sprechweise eine „Teilcheneigenschaft“), aus denen sich die atomaren Energieniveaus berechnen lassen. Zum selben Zweck kann man aber auch die Wellenlänge der Röntgenstrahlen messen (also eine „Welleneigenschaft“). Beide – Energie und Wellenlänge – sind charakteristische Eigenschaften der Röntgenquanten, die folglich weder klassische Wellen noch klassische Teilchen sein können.
Literatur
- Richard P. Feynman: QED. Die seltsame Theorie des Lichts und der Materie. Piper, München 2018, ISBN 978-3-492-31316-2 (englisch: QED. The strange theory of light and matter. Princeton 1985. Übersetzt von Siglinde Summerer, Gerda Kurz).
- Karl Mütze, Leonhard Foitzik, Wolfgang Krug, Günter Schreiber (Hrsg.): ABC der Optik. VEB F. A. Brockhaus Verlag, Leipzig 1961.
- Wilhelm Westphal (Hrsg.): Physikalisches Wörterbuch. Springer, Berlin, Göttingen, Heidelberg 1952.
Einzelnachweise
- Albert Einstein: Über die Entwickelung unserer Anschauungen über das Wesen und die Konstitution der Strahlung, in: 81. Versammlung Deutscher Naturforscher und Ärzte zu Salzburg, 1909
- Jörn Bleck-Neuhaus: Elementare Teilchen. Von den Atomen über das Standard-Modell bis zum Higgs-Boson. 2. Auflage. Springer, Heidelberg 2013, ISBN 978-3-642-32578-6, doi:10.1007/978-3-642-32579-3. Kap. 6.4.3
- Arthur H. Compton: A Quantum Theory of the Scattering of X-rays by Light Elements. In: Phys. Rev. Band 21, 1923, S. 483–502.
- Davisson, C. and Germer, L. H.: Diffraction of Electrons by a Crystal of Nickel. In: Phys. Rev. Band 30, 1927, S. 705–740.
- Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand van der Zouw and Anton Zeilinger: Wave–particle duality of C60 molecules. In: Nature. Band 401, Nr. 6754, 14. Oktober 1999, ISSN 0028-0836, S. 680–682, doi:10.1038/44348 (nature.com [abgerufen am 4. Oktober 2016]).
- Thomas Juffmann, Stefan Truppe, Philipp Geyer, András G. Major, Sarayut Deachapunya, Hendrik Ulbricht, and Markus Arndt: Wave and Particle in Molecular Interference Lithography. In: Physical Review Letters. Band 103, Nr. 26, 29. Dezember 2009, S. 263601, doi:10.1103/PhysRevLett.103.263601.
- Immanuel Estermann, Otto Stern: Beugung von Molekularstrahlen. In: Zeitschrift für Physik. Band 61, 1930, S. 95–125.
- Olaf Nairz, Markus Arndt, Anton Zeilinger: Quantum interference experiments with large molecules. In: American Journal of Physics. Band 71, 2003, S. 319, doi:10.1119/1.1531580.
- Christian Brand, Sandra Eibenberger,Ugur Sezer, Markus Arndt: Matter-wave physics with nanoparticles and biomolecules. In: Les Houches Summer School, Session CVII–Current Trends in Atomic Physics. 2016, S. 13 (online [PDF; abgerufen am 13. März 2019]).
- Natalie Wolchover: Öltröpfchen-Experiment: Aus für analoge Quantentheorie. In: Spektrum.de. 21. Februar 2019 (spektrum.de [abgerufen am 27. Februar 2019]).