Drehimpuls

Der Drehimpuls (in der Mechanik auch Drall oder veraltet Schwung oder Impulsmoment, in der Quantenmechanik in manchen Fällen auch Spin) ist eine physikalische Erhaltungsgröße. Ein System hat beispielsweise dann einen Drehimpuls, wenn es sich um seinen Massenschwerpunkt dreht, wie bspw. ein Kreisel, ein Sportler bei einer Pirouette oder ein Planetensystem.

Physikalische Größe

Name

Drehimpuls

Größenart

Wirkung

Formelzeichen

${\vec {L}},{\vec {J}}$

Größen- und Einheitensystem	Einheit	Dimension
SI	N·m·s = kg·m²·s⁻¹	M·L²·T⁻¹

Der Drehimpuls ist eine vektorielle Größe, und zwar – wie das Drehmoment und die Winkelgeschwindigkeit – ein Pseudovektor. Seine Dimension ist das Produkt aus Masse, Länge und Geschwindigkeit. Im SI-Einheitensystem wird er in Newtonmetersekunden ( $\mathrm {N\,m\,s}$ ) gemessen.[A 1] Sein Formelzeichen ist ${\vec {L}}$ oder ${\vec {J}}$ .

Der Drehimpuls eines Systems ist die Summe der Drehimpulse seiner Komponenten. Der Drehimpuls einer Komponente des Systems setzt sich im Allgemeinen aus zwei Komponenten zusammen (s. #Der Drehimpuls eines starren Körpers):

dem Bahndrehimpuls, als dem Anteil, der aufgrund einer Bewegung eines massebehafteten Körpers bezüglich eines Bezugspunkts entsteht, sofern der Körper sich nicht direkt auf den Bezugspunkt zu oder von ihm weg bewegt.
dem Eigendrehimpuls, als dem Anteil, der nicht Bahndrehimpuls ist. In der Mechanik wird dieser Anteil von der Rotation um den Massenschwerpunkt des Körpers hervorgerufen. In der Quantenmechanik ist es der Spin.

Der Drehimpuls bezieht sich immer auf den Punkt im Raum, der als Bezugspunkt der Drehbewegung gewählt wird. Bei einem frei rotierenden System wird als Bezugspunkt oft der Schwerpunkt festgelegt, in der Astronomie meist der Schwerpunkt des Zentralgestirns. Wenn die Rotation durch ein Lager vorgegeben ist, wird meist ein Punkt auf der Achse gewählt.

Der Drehimpuls lässt sich allgemein als Vektorprodukt aus dem Ortsvektor ${\vec {r}}$ und dem Impuls ${\vec {p}}$ des Körpers berechnen:

{\vec {L}}={\vec {r}}\times {\vec {p}},

oder mit Hilfe des Trägheitstensors $\mathbf {\Theta }$ und der Winkelgeschwindigkeit $\omega$ zu:

{\vec {L}}=\mathbf {\Theta } \cdot {\vec {\omega }}.

In der Quantenmechanik wird der Drehimpuls durch den Drehimpulsoperator beschrieben. Dabei zeigt sich, dass er eine quantisierte Größe ist. Der Betrag des Drehimpulses ist stets ein ganz- oder halbzahliges Vielfaches des reduzierten Planckschen Wirkungsquantums. Die Ausrichtung des Drehimpulses ist ebenfalls gequantelt. Sie unterliegt der Richtungsquantelung in Bezug auf die Quantisierungsachse. Die Rolle des Eigendrehimpulses wird vom Spin wahrgenommen, der nicht mit einer räumlichen Bewegung verbunden ist. Somit setzt sich der Drehimpulsoperator aus den Komponenten Bahndrehimpulsoperator ${\hat {\mathbf {L} }}={\hat {\mathbf {r} }}\times {\hat {\mathbf {p} }}$ und Spinoperator zusammen.

Leonhard Euler führte 1775 den Drallsatz als ein fundamentales von den Newton’schen Gesetzen unabhängiges Prinzip in der Mechanik ein.[1] Er besagt, dass ein Drehmoment auf das System einwirken muss, um den Drehimpuls zu ändern. Die Drehimpulserhaltung lässt sich im Alltag an vielen Stellen erfahren (siehe Video, oder Pirouetteneffekt).

Definition und Veranschaulichung

Mit der Rechte-Hand-Regel kann die Richtung des Drehimpulsvektors als Daumenrichtung bestimmt werden.

Für einen Massenpunkt, der sich am Ort ${\vec {r}}$ mit dem Impuls ${\vec {p}}=m{\vec {v}}$ bewegt, wird der Drehimpuls durch das Kreuzprodukt

{\vec {L}}={\vec {r}}\times {\vec {p}}

definiert. Bezugspunkt ist dabei der Ursprung ${\vec {r}}={\vec {0}}$ . Für den Drehimpuls um einen anderen Bezugspunkt ${\vec {r}}_{0}$ muss man ${\vec {r}}$ durch ${\vec {r}}'=({\vec {r}}-{\vec {r}}_{0})$ ersetzen.

Zur Veranschaulichung geeignet ist der Fall, dass der Massenpunkt eine ebene Kreisbewegung um den Ursprung ausführt. Dann liegt der Drehimpulsvektor senkrecht zur Kreisebene, also in Richtung der Achse der Kreisbewegung, und hat den Betrag

L=mrv=mr^{2}\omega

.

Der Drehimpuls wächst mit

höherer Winkelgeschwindigkeit $\omega$ proportional,
größerer Masse $m$ ebenfalls proportional,
größerem Abstand $r$ dieser Masse zur Drehachse jedoch in quadratischem Verhältnis.

Der Drehimpulsvektor zeigt in die Richtung, in der sich bei gleichem Drehsinn eine Rechtsschraube voranbewegen würde. Es gilt die Korkenzieherregel oder Rechte-Faust-Regel: Wenn die gekrümmten Finger der rechten Hand die Richtung der Drehbewegung angeben, so zeigt der Daumen in Richtung des Drehimpulses (siehe Bild). Dass die rechte Hand für diese Regel verwendet werden muss und nicht die linke, liegt an der Definition des Kreuzprodukts zweier Vektoren.

Den Drehimpuls eines ausgedehnten Körpers zu einem bestimmten Bezugspunkt erhält man, in dem man die Drehimpulse seiner Massenpunkte zu diesem Bezugspunkt bildet und vektoriell addiert.

Auch wenn die Bezeichnung anderes vermuten lässt, haben auch solche Körper einen Drehimpuls, die anschaulich gesehen gar keine Drehung ausführen. Selbst ein geradlinig bewegter, nicht um sich selbst rotierender Körper besitzt einen Drehimpuls, wenn man den Bezugspunkt so wählt, dass er nicht auf der Bahn des Massenmittelpunkts des Körpers liegt. Der Drehimpuls berechnet sich dann einfach aus dem Produkt von Masse, Geschwindigkeit und senkrechtem Abstand des Bezugspunktes von der Bahn. Es lassen sich daher auch stets Bezugssysteme finden, in denen zur Bewegung des Massenmittelpunktes kein Drehimpuls gehört. Der Drehimpuls eines um seinen Massenmittelpunkt rotierenden Körpers hingegen verschwindet nur in einem mitrotierenden, also beschleunigten Bezugssystem.

Drehimpulserhaltung

Erfahrungsgemäß bleibt der Drehimpuls eines isolierten physikalischen Systems nach Betrag und Richtung unverändert, gleichgültig, welche inneren Kräfte und Wechselwirkungen zwischen den Bestandteilen des Systems wirken. Dies wird als Drehimpulserhaltung bezeichnet. Nahezu perfekt isolierte Systeme sind z. B. die Atomkerne, die Moleküle in verdünnten Gasen und astronomische Objekte im Weltall. Das zweite Keplersche Gesetz, nach dem ein Planet sich auf seiner exzentrischen Umlaufbahn umso schneller bewegt, je näher er der Sonne ist, lässt sich aus der Drehimpulserhaltung herleiten.

Die Drehimpulserhaltung gilt auch in Anwesenheit äußerer Kräfte, wenn diese Kräfte insgesamt kein Drehmoment auf das System ausüben. In einem homogenen Schwerefeld gilt das z. B. für den Drehimpuls jedes Körpers um seinen eigenen Schwerpunkt. Sind die äußeren Kräfte auf verschiedene Teile eines Systems parallel zueinander, so bleibt jedenfalls die zu den Kräften parallele Komponente des Drehimpulses erhalten.

Die Drehimpulserhaltung zeigt sich beispielsweise bei Spielzeugkreiseln, beim Diskuswurf und beim Pirouetteneffekt.

Die Drehimpulserhaltung gilt für beliebige physikalische Systeme (z. B. auch elektromagnetische Felder) und kann mithilfe des Noether-Theorems daraus hergeleitet werden, dass die physikalischen Gesetze nicht von der Orientierung des betrachteten Systems im Raum abhängen.

Verschiebung, Drehung, Spiegelung

Während Ortsvektor

{\vec {r}}

und Impuls

{\vec {p}}=m{\vec {v}}

bei einer Punktspiegelung um den Koordinatenursprung ihre Richtung umkehren, bleibt die des Drehimpulses bezüglich der Scheibenmitte

{\vec {L}}=m{\vec {r}}\times {\vec {v}}

unverändert. (Im Bild sind die Vektoren in Fettdruck und nicht mit Pfeil gezeichnet.)

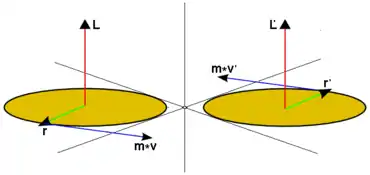
Betrag und Richtung des Drehimpulses einer Punktmasse hängen davon ab, welchen Punkt man als Bezugspunkt wählt. Bei Verschiebung des Bezugspunkts ändert sich der Vektor jedes Ortes in ${\vec {x}}^{\,\prime }={\vec {x}}+{\vec {a}}$ und der Drehimpuls in

{\vec {L}}^{\prime }={\vec {L}}+{\vec {a}}\times {\vec {p}}.

Oft wählt man als Bezugspunkt den Massenmittelpunkt oder einen Punkt, der bei den betrachteten Drehungen ruht, also auf der Drehachse liegt.

Das Kreuzprodukt zweier Vektoren steht stets senkrecht auf der von ihnen aufgespannten Ebene, eine Drehung des betrachteten Systems aber dreht sowohl die Ortsvektoren als auch die Bahngeschwindigkeiten um denselben Betrag, wodurch auch der Drehimpuls in gleicher Weise mitgedreht wird.

Bei einer Punktspiegelung am Bezugspunkt geht der Ort in den gegenüber liegenden Ort über. Auch das Vorzeichen der Geschwindigkeit in Bezug auf diesen Punkt kehrt sich um. Bei der Bildung des Kreuzprodukts kompensieren sich diese beiden Vorzeichenwechsel, sodass sich bei einer Punktspiegelung der Drehimpuls nicht ändert. Damit unterscheidet er sich vom Verhalten der Geschwindigkeit oder des Ortsvektors: Der Drehimpuls gehört zur Klasse der Pseudovektoren.

Eulerscher Drehimpulssatz

Um den Impuls eines Körpers zu ändern, muss eine Kraft wirken. Genauer gesagt ist die zeitliche Änderung des Impulses die Kraft:

{\frac {\mathrm {d} {\vec {p}}}{\mathrm {d} t}}={\vec {F}}.

Ganz analog formulierte 1754 Leonhard Euler den Eulerschen Drehimpulssatz, nach dem die zeitliche Änderung des Drehimpulses bezüglich des Ursprungs gleich dem angreifenden Drehmoment ${\vec {M}}$ um den Ursprung ist:

{\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\vec {M}}.

Um den Drehimpuls eines Körpers zu ändern, muss ein Drehmoment auftreten. Ein Drehmoment ist das Kreuzprodukt von Abstandsvektor ${\vec {r}}$ und Kraft ${\vec {F}}$ :

{\vec {M}}={\vec {r}}\times {\vec {F}}.

Der Drehimpulssatz ergibt sich, wenn man den Drehimpuls nach der Zeit ableitet, beispielsweise bei einer Punktmasse am Ort ${\vec {x}}$ :

{\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\dot {\vec {L}}}={\frac {\mathrm {d} }{\mathrm {d} t}}[{\vec {x}}\times {\vec {p}}]={\underline {{\dot {\vec {x}}}\times {\vec {p}}}}+{\vec {x}}\times {\dot {\vec {p}}}={\vec {x}}\times {\vec {F}}={\vec {M}}.

Da die Geschwindigkeit und der Impuls parallel sind, entfällt ihr Kreuzprodukt im unterstrichenen Term. Um den (Bahn-)Drehimpuls einer Punktmasse zu verändern, bedarf es also eines Moments ${\vec {M}}$ , das dem Moment der an der Punktmasse angreifenden Kraft ${\vec {F}}$ entspricht. Bei einem ausgedehnten Körper vermag auch ein Kräftepaar mit resultierender Kraft ${\vec {F}}={\vec {0}}$ eine Änderung des Drehimpulses auszulösen, was den Eigendrehimpuls betrifft, siehe unten. Der Eigendrehimpuls entfällt freilich bei einer Punktmasse.

Handelt es sich bei der Kraft um eine Zentralkraft ${\vec {F}}=f{\tfrac {\vec {x}}{|{\vec {x}}|}}$ , so bleibt der Drehimpuls um das Zentrum erhalten, denn die zeitliche Änderung des Drehimpulses – das angreifende Moment der Zentralkraft – verschwindet:

{\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\vec {x}}\times \left(f{\frac {\vec {x}}{|{\vec {x}}|}}\right)={\frac {f}{|{\vec {x}}|}}\underbrace {{\vec {x}}\times {\vec {x}}} _{={\vec {0}}}={\vec {0}}.

Folglich ist der Drehimpuls um das Zentrum über die Zeit konstant. Dies betrifft insbesondere Planetenbewegungen um ein Zentralgestirn.

Ebene Bahn, Flächensatz

Behält der Drehimpuls einer Punktmasse (beispielsweise die Erde, die die Sonne umläuft) jederzeit den anfänglichen Wert, dann verläuft die Bahn der Punktmasse in einer Ebene.

Denn das Kreuzprodukt steht senkrecht auf seinen Faktoren und zu allen Zeiten $t$ gilt für den Drehimpuls bezüglich des Koordinatenursprungs

{\vec {x}}(t)\cdot {\vec {L}}(t)={\vec {x}}(t)\cdot {\bigl (}{\vec {x}}(t)\times m{\vec {v}}(t){\bigr )}=0,

wenn $m$ die Masse und ${\vec {v}}$ die Bahngeschwindigkeit der Punktmasse sind. Wenn nun der Drehimpuls zeitunabhängig ist, ${\vec {L}}(t)={\vec {L}}(0),$ dann erfüllt jeder Bahnpunkt die Ebenengleichung

{\vec {x}}(t)\cdot {\vec {L}}(0)=0.

Es handelt sich also um eine Bewegung in der Ebene durch den Massenmittelpunkt des Systems senkrecht zum Drehimpuls.

Dann gilt das zweite Keplersche Gesetz (auch Flächensatz genannt): Der Fahrstrahl zum Planeten überstreicht in gleichen Zeiten gleich große Flächen.

Denn in einer kurzen Zeit $\mathrm {d} t$ ändert sich der Fahrstrahl ${\vec {x}}$ um ${\vec {v}}\mathrm {d} t$ und überstreicht dabei die Fläche des Dreiecks mit diesen beiden Seiten. Das Dreieck ist halb so groß wie das von beiden Vektoren aufgespannte Parallelogramm, dessen Inhalt durch den Betrag des Kreuzprodukts gegeben ist. In der Zeit $\mathrm {d} t$ überstreicht der Fahrstrahl folglich die Fläche

\mathrm {d} F={\frac {1}{2}}\left|{\vec {x}}(t)\times {\vec {v}}(t)\,\right|\,\mathrm {d} t={\frac {1}{2\,m}}{\bigl |}{\vec {L}}{\bigr |}\mathrm {d} t.

Wenn der Drehimpuls sich nicht mit der Zeit ändert, ist folglich die Flächengeschwindigkeit konstant. Dieser Sachverhalt lässt sich auch auf Situationen verallgemeinern, in denen sich der Drehimpuls ändert, siehe Drallsatz#Flächensatz.

Der Flächensatz gilt auch in relativistischer Physik, wenn zudem die Energie $E$ erhalten ist. Denn in relativistischer Physik ist

{\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}={\frac {\vec {p}}{E}}\,c^{2}

und

\mathrm {d} F={\frac {c^{2}}{2\,E}}{\bigl |}{\vec {L}}{\bigr |}\mathrm {d} t.

Für ebene Bahnen gibt es einen Zusammenhang zwischen Drehimpuls ${\vec {L}}$ und Winkelgeschwindigkeit ${\vec {\omega }}$ , der für den Runge-Lenz-Vektor relevant ist:

{\vec {L}}=mr^{2}{\vec {\omega }}.

Zum Beweis zerlegt man die Geschwindigkeit in eine radiale und eine azimutale Komponente (siehe Polarkoordinaten/Geschwindigkeit), ${\dot {\vec {r}}}={\dot {r}}{\vec {e}}_{r}+r{\dot {\varphi }}{\vec {e}}_{\varphi }$ . Im Kreuzprodukt mit ${\vec {r}}=r{\vec {e}}_{r}$ fällt die Radialgeschwindigkeit weg, und man erhält

{\vec {L}}={\vec {r}}\times m{\dot {\vec {r}}}=mr^{2}{\dot {\varphi }}\,{\vec {e}}_{r}\times {\vec {e}}_{\varphi }=mr^{2}{\dot {\varphi }}{\vec {e}}_{z}=mr^{2}{\vec {\omega }}.

Der Drehimpuls eines starren Körpers

Der Drehimpuls eines Körpers ist die Summe der Drehimpulse seiner Komponenten:

{\vec {L}}=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {x}}}_{n}

bzw. für einen Körper mit kontinuierlicher Masseverteilung das Integral:

{\vec {L}}=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times {{\vec {v}}({\vec {x}})}

$m_{1\ldots N}$ … die Massen der Massepunkte des Körpers mit diskreter Masserverteilung
$\rho ({\vec {x}})$ … die Massendichte der kontinuierlichen Masseverteilung
${\vec {x}}_{1\ldots N}$ und ${\dot {\vec {x}}}_{1\ldots N}$ … die Orte und Geschwindigkeiten der Massepunkte des Körpers mit diskreter Masseverteilung
${\vec {v}}({\vec {x}})$ … das Geschwindigkeitsfeld, das angibt, mit welcher Geschwindigkeit sich die Masse am Ort ${\vec {x}}$ bewegt

Mit Hilfe des Massenmittelpunkts eines Körpers und dessen Ortskoordinate ${\vec {s}}$ sowie seiner Schwerpunktsgeschwindigkeit ${\dot {\vec {s}}}$ können darauf bezogene Ortskoordinaten ${\vec {\chi }}:={\vec {x}}-{\vec {s}}$ und die Winkelgeschwindigkeiten der Massepunkte ${\vec {\omega }}_{n}$ definiert werden. Dann lassen sich die Geschwindigkeiten ausdrücken als:

{\begin{aligned}{\dot {\vec {x}}}_{n}&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}_{n}\\{{\vec {v}}({\vec {x}}})&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}.\end{aligned}}

Bei einem starren Körper, dessen Ausrichtung zum Bezugspunkt konstant ist, sind zudem alle Winkelgeschwindigkeiten gleich groß $(\forall n:{\vec {\omega }}_{n}\equiv {\vec {\omega }})$ . Damit ergibt sich der Drehimpuls zu:

{\begin{aligned}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right){\text{ bzw.}}\\{\vec {L}}&=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\int \mathrm {d} ^{3}\chi \rho ({\vec {\chi }})\,{\vec {\chi }}\times \left({\vec {\omega }}\times {\vec {\chi }}\right){\text{ oder verallgemeinert}}\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\mathbf {\Theta } _{s}\cdot {\vec {\omega }}.\end{aligned}}

Hier sind zusätzlich

$M=\sum _{n}m_{n}$ die Gesamtmasse des Körpers und
$\mathbf {\Theta } _{s}=\int \mathrm {d} ^{3}x\rho ({\vec {x}})\,[({\vec {x}}\cdot {\vec {x}})\,\mathbf {1} -{\vec {x}}\otimes {\vec {x}}]$ der Trägheitstensor des Körpers bezogen auf seinen Massenmittelpunkt.

Herleitung

Herleitung

Bei der Herleitung kommen verschiedene Umstellungen, die Graßmann-Identität (BAC-CAB-Formel), und die Definition des Massenmittelpunkts zum Einsatz:

{\begin{array}{lllll}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|+{\vec {0}}={\vec {s}}-{\vec {s}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}+{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\vec {x}}_{n}-{\vec {s}}={\vec {\chi }}_{n}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\text{Graßmann-Identität}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,\left({\vec {\omega }}\left({\vec {s}}\cdot {\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)\right)&\left|{\text{Summe in die Klammer}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+{\vec {\omega }}\left({\vec {s}}\cdot \sum _{n}m_{n}{\vec {\chi }}_{n}\right)-\sum _{n}m_{n}{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)&\left|\sum _{n}m_{n}\chi _{n}={\vec {0}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+0\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Graßmann-Identität}}\right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\omega }}\left({\vec {\chi }}_{n}{\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {\omega }}{\vec {\chi }}_{n}\right)&&\left|{\text{Dyadisches Produkt}}\otimes \right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left(({\vec {\chi }}_{n}{\vec {\chi }}_{n})\mathbf {1} -{\vec {\chi }}_{n}\otimes {\vec {\chi }}_{n}\right){\vec {\omega }}\end{array}}

Der erste Term $M{\vec {s}}\times {\dot {\vec {s}}}$ wird Bahndrehimpuls genannt, der zweite Term ist der Eigendrehimpuls.

Der Eigendrehimpuls

Der Eigendrehimpuls eines starren Körpers ist der Anteil seines Drehimpulses, der durch die Rotation um seinen Massenmittelpunkt ${\vec {s}}$ darstellbar ist. Mit Hilfe der Winkelgeschwindigkeit ${\vec {\omega }}_{s}$ und des Trägheitstensors $\mathbf {\Theta } _{s}$ , jeweils auf den Massenmittelpunkt ${\vec {s}}$ bezogen, lässt er sich als deren Matrixprodukt berechnen:

{\vec {L}}_{s}=\mathbf {\Theta } _{s}\cdot {\vec {\omega }}_{s}.

Im Allgemeinen zeigen ${\vec {\omega }}$ und ${\vec {L}}_{s}$ nicht in die gleiche Richtung – ein rotierender Körper „eiert“, wenn er sich frei bewegen kann, oder zeigt Unwucht, wenn die Richtung der Achse festgehalten wird. Nur bei Rotation um eine der Hauptträgheitsachsen des Körpers sind ${\vec {\omega }}$ und ${\vec {L}}_{s}$ parallel, sodass die Erhaltung des Drehimpulses auch gleichbleibende Richtung der Drehachse und damit die Konstanz des Trägheitsmoments bewirkt. Der Trägheitstensor ist symmetrisch und deshalb sind die Hauptträgheitsachsen paarweise orthogonal. Aus dem Trägheitstensor kann man zu jeder beliebigen Drehachse das Trägheitsmoment und die Hauptträgheitsachsen durch Lösung des Eigenwertproblems berechnen.

Drehimpuls in der Relativitätstheorie

In der Relativitätstheorie kann der Drehimpuls nicht in einen Vierervektor eingebettet werden. Dies wird bereits dadurch offensichtlich, dass $L_{i}=\varepsilon _{ijk}x_{j}p_{k}$ unter Lorentztransformationen wie $L'_{i}=\varepsilon _{ijk}\Lambda ^{\mu j}x_{\mu }\Lambda ^{\nu k}p_{\nu }$ transformiert. Dieses Problem wird dadurch umgangen, dass der Drehimpulstensor $M^{\mu \nu }$ eingeführt wird. Dieser ist definiert als

M_{\mu \nu }=x_{\mu }p_{\nu }-p_{\mu }x_{\nu }

und seine Einträge sind

\left(M_{\mu \nu }\right)={\begin{pmatrix}0&-N_{x}&-N_{y}&-N_{z}\\N_{x}&0&L_{z}&-L_{y}\\N_{y}&-L_{z}&0&L_{x}\\N_{z}&L_{y}&-L_{x}&0\end{pmatrix}}

mit $N_{i}=\gamma mcx_{i}-cp_{i}t.$

Siehe auch

Spezifischer Drehimpuls
Galilei-Transformation als Grundlage der klassischen Mechanik

Literatur

Dieter Meschede: Gerthsen Physik. 24., überarbeitete Auflage. Springer, Heidelberg Dordrecht London New York 2010, ISBN 978-3-642-12893-6, S. 32–33, 40, 81–98, doi:10.1007/978-3-642-12894-3.
Florian Scheck: Theoretische Physik 1. 8. Auflage. Springer, Berlin Heidelberg New York 2007, ISBN 978-3-540-71377-7, S. 13–18, 20, 184–185.

Weblinks

Commons: Drehimpuls – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Drehimpuls – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Video: Drehstuhlexperimente zur Erhaltung des Drehimpulses. Institut für den Wissenschaftlichen Film (IWF) 2003, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.3203/IWF/C-14826.
Video: Zur Vektornatur des Drehimpulses. Institut für den Wissenschaftlichen Film (IWF) 2003, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.3203/IWF/C-14827.

Anmerkungen

Die formal identische Einheit Joulesekunde sollte nicht verwendet werden, weil das Joule für die Energie, eine skalare Größe, reserviert ist.

Einzelnachweise

Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 149–158, doi:10.1002/zamm.19640440402 (wiley.com).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Die formal identische Einheit Joulesekunde sollte nicht verwendet werden, weil das Joule für die Energie, eine skalare Größe, reserviert ist.

[2] Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 149–158, doi:10.1002/zamm.19640440402 (wiley.com).