BCS-Theorie

Die BCS-Theorie ist eine Vielteilchentheorie zur Erklärung der Supraleitung in Metallen, die 1957 von John Bardeen, Leon Neil Cooper und John Robert Schrieffer entwickelt wurde. Sie erhielten dafür 1972 den Nobelpreis für Physik.

Inhalt

Die Grundlage der BCS-Theorie war die experimentelle Beobachtung, dass die Supraleitung vieler Metalle eine relativ starke Abhängigkeit der Sprungtemperatur $T_{C}$ von der Masse $M$ des untersuchten Metallisotops zeigt:

T_{C}\propto {\frac {1}{\sqrt {M}}}

Dies legte nahe, dass ein Mechanismus der Supraleitung die Wechselwirkung mit den masseabhängigen, quantisierten Gitterschwingungen (deren Quanten Phononen genannt werden) sein müsse.

Dies kann man sich folgendermaßen vorstellen: Ein erstes Elektron verändert das Gitter (respektive eine Gitterschwingung) durch Energieabgabe derart, dass ein zweites Elektron (z. B. durch Veränderung seiner Bahn oder Aufnahme eines Phonons) einen gleich großen Energiegewinn erzielt. Dies ist nur möglich, falls die Gitterbausteine und die Elektronen sich langsam genug (daher nur unterhalb einer kritischen Stromdichte) bewegen.

Die Idee der BCS-Schöpfer besteht darin, die Bildung von Cooper-Paaren aus je zwei Elektronen durch eine schwache anziehende Wechselwirkung zu postulieren. Elektronen sind aufgrund ihres Spins (s_e = 1/2) Fermionen und können als solche nicht den gleichen Zustand besetzen (Pauli-Prinzip). Im Gegensatz dazu sind die Cooper-Paare mit ganzzahligem Spin (Singulett-Zustand s=0 (antiparallele Anordnung der Elektronenspins) oder Triplett-Zustand s=1 (parallele Anordnung der Elektronenspins)) Bosonen und können daher gleichzeitig den gleichen Zustand, und somit auch alle den Grundzustand annehmen. Dies ist nicht nur energetisch günstiger, sondern äußert sich auch in einer, den ganzen Festkörper überspannenden, Bose-Einstein-Wellenfunktion.

Diese Wellenfunktion kann von lokalen Hindernissen (Atomkernen und Störstellen des Gitters allgemein) nicht mehr beeinflusst werden und garantiert somit einen widerstandslosen Ladungstransport. Dadurch wird eine Wechselwirkung mit dem Rest des Metalls verhindert und die typischen Eigenschaften eines Supraleiters wie der verschwindende elektrische Widerstand begründet.

Zusammenbrechen der Supraleitung

Bildet sich ein Cooper-Paar, so wird die Energiemenge $\Delta$ freigesetzt.

Bei zu großer Energieeinwirkung von außen, sei es durch Wärmezufuhr, eine zu große Stromdichte, Bestrahlung oder dergleichen, werden die Paare allerdings wieder aufgebrochen, und die Elektronen gehen wieder ihre normale Wechselwirkung mit dem übrigen Metall ein. Das erklärt, warum Supraleitung nur bei tiefen Temperaturen, kleinen Strömen und geringen Magnetfeldern auftreten kann.

Dabei ist dies relativ zu sehen: Aktuelle Forschungsergebnisse von MgB₂-Supraleitern zeigen, dass bei ausgeschaltetem Magnetfeld schon Stromdichten von 85 kA/cm² gemessen wurden.

Grenzen der BCS-Theorie

Die BCS-Theorie erklärt ursprünglich nur die konventionelle Supraleitung bei Temperaturen nahe dem absoluten Temperaturnullpunkt. Diese auch weiche oder ideale genannten Typ-I-Supraleiter zeigen einen vollständigen Meißner-Ochsenfeld-Effekt und eine gute Übereinstimmung zwischen Theorie und Experiment.

Die 1986 durch Bednorz und Müller entdeckte Hochtemperatursupraleitung, wie sie etwa in einigen Keramiken auftritt, kann entgegen anderslautenden Behauptungen ebenfalls durch die BCS-Theorie erklärt werden: es wurde nachgewiesen, dass auch bei Hochtemperatursupraleitern Cooper-Paare den Ladungstransport übernehmen. Jedoch ist der Mechanismus der Paarbildung nach wie vor ungeklärt; über die direkte Elektron-Phonon-Wechselwirkung kommt er nicht in Frage.

Festkörperphysikalische Details

Deformationsspur als Verdichtung der positiv geladenen Rümpfe (Netzebenen)

Die Eigenschaft der Supraleitung setzt voraus, dass es sich um eine neue Phase des Elektronengases im Metall handelt. Der Grundzustand (T=0) eines Elektronengases bricht zusammen, wenn eine auch noch so kleine attraktive Wechselwirkung zwischen zwei Elektronen zugelassen wird. Cooper benutzte in seiner Theorie den Ansatz, dass ein Elektron auf seinem Weg durch den Festkörper aufgrund seiner negativen Ladung eine Deformationsspur der Ionen rümpfe hinterlässt. Die Anhäufung positiv geladener Ionenrümpfe wirkt attraktiv auf ein zweites Elektron. Somit ziehen sich die beiden Elektronen über die Gitterdeformation an – ähnlich wie zwei Kugeln in einem Trichter.

Im Moment des Vorbeifliegens eines Elektrons erhalten die Ionen einen Kraftstoß, der erst nach dem Passieren des Elektrons zu einer Bewegung der Ionen und damit zu einer Polarisation des Gitters führt (siehe Bild).

Gegenüber der hohen Elektronengeschwindigkeit $v_{e}\sim 10^{6}\,{\frac {\mathrm {m} }{\mathrm {s} }}$ folgt das Gitter nur sehr langsam, es erreicht seine maximale Deformation bei einer Entfernung

s={\frac {v_{e}2\pi }{\omega _{\mathrm {D} }}}

hinter dem Elektron, mit der Debyefrequenz $\omega _{\mathrm {D} }$ der Phononen des Kristallgitters.

Wegen ${\frac {2\pi }{\omega _{\mathrm {D} }}}\sim 10^{-13}\,\mathrm {s}$ erfahren die beiden Elektronen eine Kopplung über eine Entfernung von mehr als 100 nm. Das impliziert u. a., dass die Coulomb-Abstoßung weitgehend abgeschirmt ist.

Quantenmechanische Interpretation

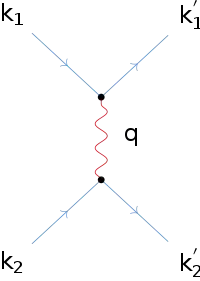
Feynman-Diagramm der Wechselwirkung zweier Elektronen mit den Wellenvektoren k1 und k2 respektive via ein Phonon des Wellenvektors q zur Cooper-Paar-Bildung im Rahmen der BCS-Theorie

Dieses Modell lässt sich auch quantenmechanisch beschreiben, indem man die Gitterdeformation als die Überlagerung der Phononen versteht, die das Elektron durch seine Wechselwirkung mit dem Gitter ständig emittiert und absorbiert.

Betrachten wir zunächst ein nicht wechselwirkendes Fermi-Gas (siehe Fermi-Dirac-Statistik) der Elektronen. Der Grundzustand im Potentialtopf ist dann dadurch gegeben, dass alle Einelektronenzustände mit Wellenvektor ${\vec {k}}$ bis zur Fermi-Kante (T=0) $E_{\mathrm {F} }={\frac {\hbar ^{2}k_{\mathrm {F} }^{2}}{2m}}$ aufgefüllt sind und alle Zustände mit $E>E_{F}$ unbesetzt bleiben. Wir fügen jetzt diesem System zwei Elektronen mit den Wellenvektoren ${\vec {k}}_{1}$ , ${\vec {k}}_{2}$ und den entsprechenden Energien $E({\vec {k}}_{1})$ und $E({\vec {k}}_{2})$ auf Zuständen oberhalb von $E_{\mathrm {F} }$ hinzu und nehmen an, dass die beiden Elektronen über die soeben beschriebene attraktive Wechselwirkung gekoppelt sind. Alle anderen Elektronen im Fermi-See sollen weiterhin nicht miteinander wechselwirken und wegen des Pauli-Prinzips eine weitere Besetzung der Zustände $|{\vec {k}}|<k_{\mathrm {F} }$ verhindern. Beim Phononenaustausch wechseln die beiden Elektronen ihre Wellenzahlvektoren, wobei der Erhaltungssatz gelten muss:

{\vec {k}}_{1}+{\vec {k}}_{2}={\vec {k}}'_{1}+{\vec {k}}'_{2}={\vec {K}}

Wir erinnern uns, dass die Wechselwirkung im ${\vec {k}}$ -Raum auf eine Schale der Energiebreite $\hbar \omega _{\mathrm {D} }$ beschränkt ist, die wie schon erwähnt oberhalb von $E_{\mathrm {F} }$ liegen muss. In der Abbildung sieht man, dass alle Paare, für die der obige Erhaltungssatz gilt, im blau schattierten Volumen (rotationssymmetrisch um die durch ${\vec {K}}$ gegebene Achse) enden.

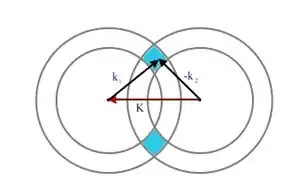
Veranschaulichung von Elektron-Paarstößen im reziproken Raum der Wellenzahlen

Dieses Volumen hängt unmittelbar mit der Anzahl der die Energie absenkenden Phononenaustauschprozesse zusammen. Das heißt, die Stärke der anziehenden Wechselwirkung wird genau dann maximal, wenn dieses Volumen maximal wird. Das ist dann der Fall, wenn die beiden Kugelschalen sich überlagern, was wiederum nur durch ${\vec {K}}=0$ realisierbar ist. Somit muss gelten:

{\vec {k}}_{1}=-{\vec {k}}_{2}

Betrachten wir im Folgenden Elektronenpaare mit entgegengesetztem Wellenzahlvektor. Die zugehörige Zweiteilchenwellenfunktion muss der Schrödinger-Gleichung genügen:

\left(-{\frac {\hbar ^{2}}{2m}}\left(\Delta _{1}+\Delta _{2}\right)+V({\vec {r}}_{1},{\vec {r}}_{2})\right)\psi ({\vec {r}}_{1},{\vec {r}}_{2})=(\varepsilon +2E_{\mathrm {F} })\psi ({\vec {r}}_{1},{\vec {r}}_{2})

Dabei ist $\varepsilon$ die Energie des Elektronenpaares bezogen auf den wechselwirkungsfreien Zustand. Man erhält folgenden Zusammenhang:

\varepsilon \approx -2\hbar \omega _{\mathrm {D} }e^{-2/V_{0}Z(E_{\mathrm {F} })}

Z ist dabei die halbe Zustandsdichte, $\omega _{\mathrm {D} }$ die Debye-Abschneidefrequenz und $V_{0}$ das attraktive Potential.

Es existiert also ein gebundener Zweielektronenzustand, dessen Energie gegenüber dem voll besetzten Fermi-See um $\varepsilon =E-2E_{\mathrm {F} }<0$ abgesenkt ist. Wird also eine noch so kleine attraktive Wechselwirkung zwischen den Elektronen eingeschaltet, so wird der Grundzustand des nicht-wechselwirkenden freien Elektronengases instabil. Diese Instabilität führt in Wirklichkeit dazu, dass sich eine hohe Dichte solcher Elektronenpaare, die auch Cooper-Paare genannt werden, bildet. Dieser neue Grundzustand ist identisch mit der supraleitenden Phase. Es sollte noch erwähnt werden, dass für beide Elektronen in Bezug auf die Zustände in der Fermi-Kugel das Pauli-Prinzip gilt. Da der Ansatz für die Zweiteilchenwellenfunktion symmetrisch gegenüber einer Vertauschung der Elektronen ist, die Gesamtwellenfunktion einschließlich der Spins jedoch antisymmetrisch sein muss, müssen die beiden Elektronen entgegengesetzten Spin haben.

Die eigentliche Ursache für den Suprastrom ist jedoch, dass der Spin eines Cooper-Paares ganzzahlig ist. Das heißt, dass Cooper-Paare nicht mehr durch die Fermi-, sondern durch die Bose-Einstein-Statistik wechselwirkungsfreier Teilchen beschrieben werden und dass sie insbesondere nicht mehr dem Pauli-Prinzip unterliegen. Sie können damit alle gleichzeitig einen quantenmechanischen Zustand einnehmen.

Es ist also möglich die Gesamtheit der Cooper-Paare im Gitter durch eine einzige Wellenfunktion zu beschreiben. Wie schon gezeigt, befinden sich alle Cooper-Paare gemeinsam in einem tiefer gelegenen Energieniveau. Diese Energiedifferenz wird zur Spaltung der Cooper-Paare benötigt und ist größer als jede durch Gitterstreuung vermittelbare Energie. Somit entsteht im Bändermodell um die Fermi-Energie $E_{\mathrm {F} }$ eine Energielücke der Breite $\Delta$ (siehe Bild), die dem Aufbrechen eines Cooper-Paares entspricht. Für potentielle Streuzentren im Gitter existiert nun, statt einzelner Cooper-Paare oder gar einzelner Elektronen, ein Kontinuum, das sich erst mit entsprechend größerem Energieaufwand auf ein höheres Niveau heben ließe. Da damit keine Energie durch Streuprozesse verloren gehen kann, ist der Stromfluss verlustfrei.

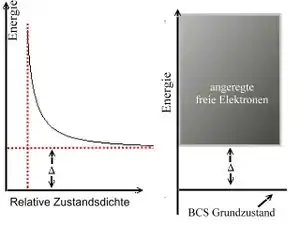
Vereinfachte Darstellung des Anregungsspektums eines Supraleiters

Man beachte, dass die Bindung ein dynamisches Gleichgewicht ist: Cooper-Paare zerfallen ständig und werden ständig neu gebildet. Die Bindungsenergie eines Cooper-Paares beträgt etwa 1 meV, ist also gegenüber der metallischen Bindung von 1 … 10 eV sehr klein. Eine Bindung von Elektronen zu Cooper-Paaren kann in metallischen Supraleitern nur stattfinden, wenn die thermische Energie des Gitters klein gegenüber dieser Bindungsenergie ist.

Bei Temperaturen dicht unterhalb der Sprungtemperatur ist nur ein kleiner Teil der Leitungselektronen zu Cooper-Paaren kondensiert. Je tiefer die Temperatur sinkt, desto größer wird dieser Anteil, bis bei T=0 alle Elektronen im Wechselwirkungsbereich (um die Fermikante) zu Cooper-Paaren verbunden sind.

Weblinks

M. Kathke: Supraleitung, eine Einführung. (PDF; 365 kB) Aachen, 7. Juni 1999, abgerufen am 29. November 2012 (Eine Ausarbeitung zum Seminarvortrag im Seminar Festkörperphysik WS 1997/98).

Literatur

J. Bardeen, L. N. Cooper und J. R. Schrieffer, Phys. Rev. 108, 1175 - 1204 (1957)
'Bardeen-Cooper-Schrieffer theory' auf Scholarpedia'
Ibach, Lüth Festkörperphysik, Kapitel Supraleitung, Springer Verlag

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.