Enigma (Maschine)
Die Enigma (griechisch αἴνιγμα aínigma, deutsch ‚Rätsel‘, Eigenschreibweise auch: ENIGMA) ist eine Rotor-Schlüsselmaschine, die im Zweiten Weltkrieg zur Verschlüsselung des Nachrichtenverkehrs der Wehrmacht verwendet wurde. Auch Polizei, Geheimdienste, diplomatische Dienste, SD, SS, Reichspost und Reichsbahn setzten sie zur geheimen Kommunikation ein. Trotz mannigfaltiger vor und während des Krieges eingeführter Verbesserungen der Verschlüsselungsqualität gelang es den Alliierten mit hohem personellen und maschinellen Aufwand, die deutschen Funksprüche nahezu kontinuierlich zu entziffern.

.jpg.webp)

Geschichte


_at_Discovery_Park_of_America.jpg.webp)
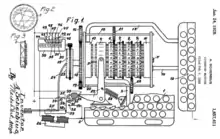
Noch während der Zeit des Ersten Weltkriegs (1914–1918) suchten die deutschen Militärs nach einem Ersatz für die inzwischen veralteten, umständlichen und unsicheren manuellen Verschlüsselungsverfahren, wie ÜBCHI, ABC-Chiffre und ADFGX, die bis dahin verwendet wurden. Hierfür kamen maschinelle Verfahren in Betracht, weil sie eine einfachere Handhabung und eine verbesserte kryptographische Sicherheit versprachen. Mit der Einführung der elektrischen Schreibmaschine und des Fernschreibers zu Beginn des 20. Jahrhunderts kamen zum Teil unabhängig voneinander und nahezu gleichzeitig mehrere Erfinder auf die Idee des Rotor-Prinzips zur Verschlüsselung von Texten. Die ersten waren 1915 in Batavia (damals Hauptstadt von Niederländisch-Ostindien, heute Jakarta, Hauptstadt von Indonesien) die beiden niederländischen Marineoffiziere Theo van Hengel und Rudolf Spengler.[1][2] Ihnen wurde jedoch nicht gestattet, ihre Erfindung zum Patent anzumelden.[3] Der nächste war im Jahr 1917 der Amerikaner Edward Hugh Hebern (Patentanmeldung 1921). Im Jahr 1918 folgte der Deutsche Arthur Scherbius (Bild) und schließlich 1919 der Niederländer Hugo Alexander Koch und der Schwede Arvid Gerhard Damm, die alle ihre Ideen zu Rotor-Chiffriermaschinen zum Patent anmeldeten.[4][5]
Erfinder der Enigma war Arthur Scherbius (1878–1929), ein promovierter Elektroingenieur und erfolgreicher Unternehmer, dessen erstes Patent[6] hierzu vom 23. Februar 1918 stammt (siehe auch: Enigma-Patente). Noch im selben Jahr am 15. April[7][8] bot er seine neue Erfindung der Kaiserlichen Marine an,[3] die eine erste „Probemaschine“ testete und deren „gute Schlüsselsicherheit“ lobte. Des Weiteren kam das Reichsmarineamt zu dem Schluss, dass „vorläufig bei der Art des Marine-Schlüsselverkehrs die Anwendung von Maschinen nicht lohnen würde“.[9]
Nach dem Krieg beschloss Scherbius, die Maschine für zivile Anwendungen zu vermarkten. Zur Fertigung wurde am 9. Juli 1923[10] die Chiffriermaschinen-Aktiengesellschaft (ChiMaAG) in Berlin (W 35, Steglitzer Str. 2, heute Pohlstraße in Berlin-Tiergarten) gegründet. Das erste Modell der Enigma (1923) war die „Handelsmaschine“ (Bild). Ihr folgte schnell die „Schreibende Enigma“ (1924). Die neuen Chiffriermaschinen wurden kommerziell auf Messen zum Kauf angeboten, wie 1923 in Leipzig und Bern[4] und 1924 auf dem internationalen Postkongress des Weltpostvereins in Stockholm.[11]
Dies weckte das Interesse auch des deutschen Militärs, das inzwischen durch Veröffentlichungen, wie Winston Churchills „The World Crisis“[12] und Julian Corbetts „Naval Operations“,[13] von den alliierten Entzifferungserfolgen erfahren hatte. Dazu gehörte die britische Entzifferung der deutschen Marinefunksprüche, was mithilfe des durch verbündete russische Taucher vom gestrandeten Kreuzer Magdeburg geborgenen deutschen Signalbuchs (Codebuch) gelang, die französische Entzifferung von ÜBCHI, einer frühen Handschlüsselmethode des Kaiserlichen Heers, sowie deren Nachfolgerinnen, der ABC- und ABCD-Chiffre, ferner die britische Entzifferung der Zimmermann-Depesche, worauf der Kriegseintritt der USA erfolgte, und die französische Entzifferung der ADFGX- sowie ADFGVX-Chiffre, was im Radiogramme de la Victoire (deutsch „Funkspruch des Sieges“) gipfelte.
Da die deutschen Militärs eine Wiederholung dieser kryptographischen Katastrophe des Ersten Weltkriegs unbedingt vermeiden wollten, erkannten sie die neue Art der maschinellen Verschlüsselung als sicherste Lösung.[14] Im Jahr 1926 wurde die Enigma zunächst von der Reichsmarine unter dem Namen „Funkschlüssel C“, zwei Jahre später auch vom Heer versuchsweise eingesetzt und verschwand daraufhin vom zivilen Markt. Kurz nach Beginn der Serienfertigung verunglückte Scherbius im Jahr 1929 tödlich.[15] Im Jahr 1934 übernahmen Rudolf Heimsoeth und Elsbeth Rinke die ChiMaAG. Unter der neuen Firma „Heimsoeth & Rinke“ (H&R)[16] setzten sie Entwicklung und Produktion der Maschine in Berlin fort. Die Zeit des Nationalsozialismus hatte bereits begonnen. Im Zuge der Aufrüstung der Wehrmacht wurde ein zuverlässiges Verschlüsselungssystem benötigt, und so stand dem Erfolg der Enigma nichts mehr im Wege.
Man schätzt, dass etwa 40.000 Maschinen hergestellt wurden.[17][18] Der norwegische Historiker und Kryptologe Frode Weierud ermittelte im Jahr 2021 die Anzahl der an die Wehrmacht ausgelieferten Enigma-Maschinen (mit Steckerbrett) zu 35.636 Stück.[19] Im Laufe der Zeit bis zum Kriegsende 1945 und noch darüber hinaus, so 1965 in Korea,[20] kamen viele verschiedene Modelle und Varianten der Enigma zum Einsatz. Die meistgebrauchte war die Enigma I (sprich: „Enigma eins“), die ab 1930 von der Reichswehr und später von der Wehrmacht eingesetzt wurde und die während des Zweiten Weltkriegs das auf deutscher Seite am häufigsten benutzte Maschinenschlüsselverfahren verkörperte. Auf amerikanischer Seite war es die vom Schweden Boris Hagelin entwickelte M‑209 (Bild) mit etwa 140.000 Stück.
Prinzip


Die Enigma I besteht im Wesentlichen aus der Tastatur zur Buchstabeneingabe, einem Walzensatz von drei austauschbaren Walzen und einem Glühlampenfeld zur Anzeige.[21] Der Walzensatz ist das Herzstück zur Verschlüsselung. Die drei Walzen sind nebeneinander unabhängig drehbar angeordnet. Jede von ihnen weist auf beiden Seiten 26 elektrische Kontakte auf. Jeder Kontakt ist einem der 26 Großbuchstaben des lateinischen Alphabets zugeordnet. Jeweils ein Kontakt auf der einen Seite einer Walze ist durch einen isolierten Draht im Inneren der Walze mit einem Kontakt auf der anderen Seite der Walze verbunden. Insgesamt sind so, für jede Walze unterschiedlich, alle 26 Kontakte auf der einen Seite einer Walze paarweise und unregelmäßig mit den 26 Kontakten auf der anderen Seite elektrisch verbunden (siehe auch: Verdrahtungstabelle im folgenden Kapitel).
Drückt man eine Buchstabentaste, so fließt elektrischer Strom von einer in der Enigma befindlichen 4,5‑Volt-Batterie über die gedrückte Taste durch den Walzensatz und lässt eine Anzeigelampe aufleuchten.[22] Der aufleuchtende Buchstabe entspricht der Verschlüsselung des gedrückten Buchstabens. Da sich bei jedem Tastendruck die Walzen ähnlich wie bei einem mechanischen Kilometerzähler weiterdrehen, ändert sich das geheime Schlüsselalphabet nach jedem Buchstaben.
Gibt man „OTTO“ ein, so leuchten nacheinander beispielsweise die Lampen „PQWS“ auf. Wichtig und kryptographisch stark ist, dass aufgrund der Rotation der Walzen jeder Buchstabe auf eine andere Weise verschlüsselt wird, im Beispiel das vordere O von OTTO zu P, das hintere aber zu S. Man spricht von vielen unterschiedlichen (Geheim-) „Alphabeten“, die zur Verschlüsselung benutzt werden, und bezeichnet dies als polyalphabetische Substitution. Im Gegensatz dazu verwendet eine monoalphabetische Substitution nur ein einziges Geheimalphabet, und ein Klartextbuchstabe wird stets in denselben Geheimtextbuchstaben verwandelt („OTTO“ beispielsweise in „GLLG“). Würden sich die Walzen der Enigma nicht drehen, so bekäme man auch bei ihr nur eine einfache monoalphabetische Verschlüsselung.
Aufbau
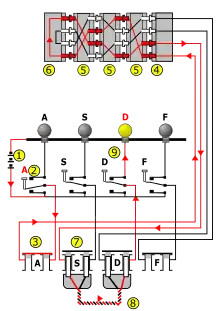
Batterie (1),
Tastatur (2),
Steckerbrett (3, 7) mit
Steckkabel (8),
Walzensatz (5) mit
Eintrittswalze (4) und Umkehrwalze (6) sowie
dem Lampenfeld (9)


Die Enigma inklusive Holzgehäuse wiegt rund 12 kg und die äußeren Abmessungen (L×B×H) betragen etwa 340 mm × 280 mm × 150 mm[23] (Daten ohne Gehäuse: 10,35 kg und 310 mm × 255 mm × 130 mm). Ihr Erfinder sagt: „Die Maschine ist ganz ähnlich einer Schreibmaschine gebaut und wird auch genau wie diese bedient.“[24]
Im Unterschied zu einer Schreibmaschine verfügt die Chiffriermaschine Enigma jedoch über einen Walzensatz aus drei drehbaren Rotoren (mit einem Durchmesser von etwa 100 mm).[25] Rechts der drei drehbaren Walzen (5) (siehe gelb hinterlegte Zahlen in der Prinzipskizze) befindet sich die Eintrittswalze (4) (Stator), die sich nicht dreht und deren Kontakte über 26 Drähte (hier sind nur vier davon gezeichnet) mit den Buchstabentasten (2) verbunden sind. Links des Walzensatzes befindet sich die Umkehrwalze (6) (UKW), die bei der Enigma I ebenfalls feststeht. Bei der Umkehrwalze (auch genannt: Reflektor), handelt es sich um eine Erfindung (patentiert am 21. März 1926) von Willi Korn (1893–1972), einem Mitarbeiter von Scherbius.[26] Sie weist nur auf ihrer rechten Seite 26 Kontakte auf (in der Skizze sind wieder nur vier davon eingezeichnet), die paarweise miteinander verbunden sind. Die Umkehrwalze bewirkt, dass der Strom, der den Walzensatz zunächst von rechts nach links durchläuft, umgelenkt wird und ihn noch einmal durchfließt, nun von links nach rechts. Der Strom verlässt den Walzensatz, wie er gekommen ist, wieder über die Eintrittswalze.
Die Tabelle[27] zeigt das als „Geheime Kommandosache!“[28] eingestufte damals streng geheime Verdrahtungsschema der bei der Enigma I verfügbaren fünf drehbaren Walzen I bis V und der Umkehrwalzen A (bis 1937 gebraucht),[29] B (ab 1937 im Einsatz)[30] und C (1940 und 1941 sporadisch verwendet):[29]
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z I E K M F L G D Q V Z N T O W Y H X U S P A I B R C J II A J D K S I R U X B L H W T M C Q G Z N P Y F V O E III B D F H J L C P R T X V Z N Y E I W G A K M U S Q O IV E S O V P Z J A Y Q U I R H X L N F T G K D C M W B V V Z B R G I T Y U P S D N H L X A W M J Q O F E C K
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z UKW A E J M Z A L Y X V B W F C R Q U O N T S P I K H G D UKW B Y R U H Q S L D P X N G O K M I E B F Z C W V J A T UKW C F V P J I A O Y E D R Z X W G C T K U Q S B N M H L
An der Gerätefront ist ein Steckerbrett mit doppelpoligen Steckbuchsen für jeden der 26 Buchstaben angebracht. Der Strom von der Buchstabentaste (2) wird, bevor er die Eintrittswalze (4) erreicht, über dieses Steckerbrett (3) geführt. Nach Durchlaufen des Walzensatzes fließt er ein zweites Mal über das Steckerbrett (7, 8) und bringt schließlich eine der 26 Buchstabenlampen (9) zum Aufleuchten. Die Buchstabenlampen sowie die Tastatur und die Steckbuchsen sind ähnlich wie bei einer deutschen Schreibmaschinentastatur angeordnet:
Q W E R T Z U I O A S D F G H J K P Y X C V B N M L
Funktion

Bei einer gedrückten Buchstabentaste, beispielsweise A, wird der Batteriestrom über die Taste A zur gleichnamigen Buchse im Steckerbrett durchgeschaltet. Ist dort die Buchse A mit einer anderen Buchse durch ein von außen angebrachtes Kabel verbunden („gesteckert“), so wird A mit einem anderen Buchstaben, beispielsweise J, vertauscht. Ist kein Kabel gesteckt („ungesteckert“), dann gelangt der Strom direkt zum Kontakt A der Eintrittswalze.
Bei der weiteren Beschreibung der Funktion wird auf das Bild „Stromfluss“ (zunächst nur obere Hälfte) Bezug genommen. Es dient nur zur Illustration und ist eine vereinfachte Darstellung des rotierenden Walzensatzes (mit linkem, mittlerem und rechtem Rotor) und der statischen Umkehrwalze (englisch: Reflector). Aus Übersichtlichkeitsgründen wurde in der Skizze die Anzahl der Buchstaben von 26 auf 8 (nur A bis H) verringert.
Angenommen der Buchstabe A sei ungesteckert, dann wird der Strom über die Eintrittswalze (sie ist in der Skizze nicht eingezeichnet) zum Eingangskontakt A der rechten Walze geleitet. Deren Verdrahtung bewirkt eine Substitution (Ersetzung) des Buchstabens durch einen anderen. Der Strom, der am Eingangskontakt A von rechts eintritt, verlässt hier die Walze auf deren linken Seite am Ausgangskontakt B. So wird durch die rechte Walze A durch B ersetzt.
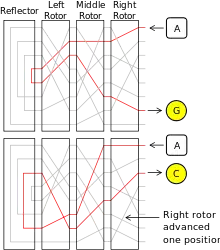
Obere Hälfte: A wird in G verschlüsselt
Untere Hälfte: A wird in C verschlüsselt
Der Strom gelangt nun über den Kontakt B in die mittlere Walze. Da es bei der Verdrahtung einer Walze durchaus möglich ist, dass (wie im Bild) ein Eingangskontakt mit dem gleichnamigen Ausgangskontakt verbunden ist, bleibt B hier unverändert. Der Strom verlässt über Kontakt B die mittlere Walze und tritt in die linke Walze ein. Deren Verdrahtung sorgt dafür, dass der Strom vom Eingangskontakt B zum Ausgangskontakt D geleitet wird. Der Strom hat nun alle drei (drehbaren) Walzen einmal durchlaufen und die Umkehrwalze erreicht. Sie hat nur Kontakte auf der rechten Seite und verbindet die Buchstaben paarweise, beispielsweise D mit E.
Nun fließt der Strom ein zweites Mal durch den Walzensatz, jetzt aber von links nach rechts. Durch die Umkehrwalze gelangt er über den Kontakt E in die linke Walze. Hier ist beispielsweise E mit C verdrahtet. Folglich fließt der Strom weiter über Kontakt C in die mittlere Walze, verlässt sie wieder über den Kontakt F und fließt in die rechte Walze. Der Strom verlässt die rechte Walze schließlich am Kontakt G.
Der weitere Stromfluss geht aus der Skizze nicht hervor, ist aber leicht erklärt. Nach Austritt aus dem Walzensatz wird der Strom über die Eintrittswalze zurück zum Steckerbrett geleitet. Ist hier der Buchstabe G mit einem anderen Buchstaben gesteckert, dann findet eine letzte Permutation statt. Ist G ungesteckert, leuchtet die Lampe G auf. Sie leuchtet nur solange auf, wie die Taste A gedrückt gehalten wird, da nur bei gedrückter Taste der Umschaltkontakt auf die Batterie umgeschaltet ist. Lässt man sie los, erlischt die Lampe. Im geschilderten Beispiel wird somit der Buchstabe A, dessen Taste eingangs gedrückt wurde und noch immer gedrückt ist, als Buchstabe G verschlüsselt.
Falls der zu verschlüsselnde Text „AACHENISTGERETTET“ lautet, ist erneut ein A einzugeben. Also wird die Taste A losgelassen und zum zweiten Mal gedrückt. Wichtig ist, dass mit dem mechanischen Druck auf die Taste mithilfe eines Fortschaltmechanismus gleichzeitig die rechte Walze um eine Position rotiert wird. Die mittlere Walze rotiert erst nach 26 Schritten der rechten Walze. In der unteren Hälfte des Bildes „Stromfluss“ ist die Situation skizziert, nachdem die rechte Walze sich um eine Position (nach unten) weitergedreht hat.
Wie man an der Skizze erkennen kann, hat sich der Pfad für den erneut am Kontakt A der rechten Walze eintretenden Strom radikal geändert. Er nimmt jetzt auch bei der mittleren und linken Walze sowie der Umkehrwalze einen völlig anderen Weg als zuvor, obwohl sich diese Walzen nicht gedreht haben. Das Ergebnis ist eine andere Verschlüsselung des Buchstabens A, der nun in C umgewandelt wird.
Bedienung


.jpg.webp)
Bei der Enigma I standen zunächst drei, ab 1939 fünf unterschiedliche Walzen zur Verfügung, die mit römischen Zahlen (I, II, III, IV und V) durchnummeriert waren. Der Benutzer wählte nach Vorgabe einer geheimen Schlüsseltabelle, die für jeden Tag wechselnde Einstellungen vorsah, drei der fünf Walzen aus und setzte diese nach der im Tagesschlüssel unter der Überschrift „Walzenlage“ vorgeschriebenen Anordnung ein.[31]
Die „Schlüsseltafel“[32] stellte tabellarisch für einen kompletten Monat die jeweils gültigen Tagesschlüssel dar, die um Mitternacht gewechselt wurden (Ausnahmen: Bei der Luftwaffe geschah der Wechsel um 3 Uhr nachts.[33] Für die Kriegsmarine siehe Enigma‑M4). Unten sind beispielhaft nur drei Monatstage dargestellt, wobei, wie damals üblich, die Tage absteigend sortiert sind. Dies erlaubt es dem Verschlüssler, die verbrauchten Codes der vergangenen Tage abzuschneiden und zu vernichten.[34]
Beispiel für den 29. des Monats: Walzenlage I IV III bedeutet, dass Walze I links (als langsamer Rotor), Walze IV in der Mitte und Walze III rechts (als schneller Rotor) einzusetzen ist. (Als Umkehrwalze wurde mit wenigen Ausnahmen stets die UKW B benutzt.) Die Ringe, die außen am Walzenkörper angebracht sind und den Versatz zwischen der internen Verdrahtung der Walzen und dem Buchstaben bestimmen, zu dem der Übertrag auf die nächste Walze erfolgt, sind auf den 16., 26. beziehungsweise 8. Buchstaben des Alphabets einzustellen, also auf P, Z und H.
Tag Walzenlage Ringstellung ---- Steckerverbindungen ---- 31 III I IV 01 17 22 AH BL CX DI ER FK GU NP OQ TY 30 II V I 18 24 11 BN DZ EP FX GT HW IY OU QV RS 29 I IV III 16 26 08 AD CN ET FL GI JV KZ PU QY WX
Die Ringstellung wurde oft (wie hier) numerisch und nicht alphabetisch verzeichnet, vermutlich um Verwechslungen mit den anderen Teilschlüsseln vorzubeugen. Als Hilfe für den Bediener „zum Umsetzen der Zahlen in Buchstaben oder umgekehrt“ ist innen im Gehäusedeckel der Enigma als Teil der Hinweisplakette „Zur Beachtung!“ eine Umsetzungstabelle angebracht.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Schließlich sind die doppelpoligen Steckbuchsen an der Frontplatte mit entsprechenden doppelpoligen Kabeln zu beschalten. In der Regel wurden genau zehn Kabel eingesteckt. Die jeweils obere Buchse eines Buchsenpaars hat einen etwas größeren Durchmesser (4 mm) als die untere (3 mm), so dass die Stecker nur in einer Orientierung eingesteckt werden können. So wurde sicher die gewünschte elektrische Überkreuzung und damit die Vertauschung der beiden Buchstaben erreicht. Sechs Buchstaben blieben ungesteckert. (Diese feste Regel der Six self-steckered letters[35] war für die Codeknacker eine Hilfe.)
Um die Gefahr des Erratens von Schlüsseln zu reduzieren, wurden von den deutschen Stellen einige Regeln für die Aufstellung der Schlüsseltabellen erfunden.[36] So war es (zeitweise) verboten, dass eine Walzenlage, die an einem Monatstag bereits benutzt wurde, sich an einem anderen Monatstag wiederholte. (Die Briten erkannten dies und nannten es die non-repeating rule.) Auch durfte sich eine Walze an zwei aufeinanderfolgenden Monatstagen nicht an derselben Stelle im Walzensatz befinden (non-clashing rule).[37] Eine dritte Regel sollte das Erraten von naheliegenden Steckerkombinationen verhindern. So war es verboten, dass zwei im Alphabet aufeinanderfolgende Buchstaben miteinander gesteckert wurden. (Auch dies nutzten die britischen Codebreakers zu ihren Gunsten und nannten es Consecutive Stecker Knock-Out CSKO.)[38][39]
All diese Vorschriften bewirkten das Gegenteil, nämlich eine Schwächung der Verschlüsselung.[40] Sie führten zu einer Arbeitserleichterung für die Codeknacker, die aufgrund der genannten Regeln insbesondere mit Fortschreiten eines Monats immer mehr Schlüsselkombinationen ausschließen konnten.[41]
Nach Einlegen der drei Walzen und Einstellen der Ringe sowie Stecken der zehn Steckerverbindungen entsprechend der Schlüsseltafel schloss der Bediener die oberhalb des Walzensatzes angebrachte Klappe und die Frontklappe. Letzteres bewirkte ein festes Andrücken der Stecker und eine sichere Kontaktgabe sowie einen Schutz vor Ausspähen des Schlüssels. Damit war die Enigma zur Verschlüsselung oder auch Entschlüsselung bereit, vorausgesetzt der Benutzer drehte nun noch die drei (rotierenden) Walzen in die korrekte Anfangsstellung.
Funkspruch
_booklet.jpg.webp)
Um sicherzustellen, dass nicht alle Funksprüche eines Schlüsselnetzes mit identischen Schlüsseln verschlüsselt werden, was die Texte angreifbar machen würde, war vorgeschrieben, für jeden Spruch eine individuelle Anfangsstellung der drei Walzen einzustellen, „Spruchschlüssel“ genannt. Die Prozeduren hierzu änderten sich von Zeit zu Zeit und waren auch nicht bei allen Wehrmachtteilen gleichartig.[43] Bei Heer und Luftwaffe galt ab dem 1. Mai 1940[44][17] (neun Tage vor Beginn des Westfeldzugs) das folgende in der „Schlüsselanleitung zur Schlüsselmaschine Enigma“[32] beschriebene Schema, wenn beispielsweise der folgende Klartext übermittelt werden soll:
„Das Oberkommando der Wehrmacht gibt bekannt: Aachen ist gerettet. Durch gebündelten Einsatz der Hilfskräfte konnte die Bedrohung abgewendet und die Rettung der Stadt gegen 18:00 Uhr sichergestellt werden.“
Da die Enigma nur Großbuchstaben und keine Ziffern oder Satzzeichen verschlüsseln kann und auch kein Leerzeichen kennt, muss der oben dargestellte Klartext vor der Verschlüsselung zunächst entsprechend aufbereitet werden. Dabei werden Satzzeichen durch „X“ ersetzt, Eigennamen verdoppelt und in „X“ eingeschlossen und Zahlen ziffernweise ausgeschrieben. Ferner war es üblich, (außer bei Eigennamen) das „ch“ und das „ck“ durch „Q“ zu ersetzen und den Text anschließend in Fünfergruppen aufzuteilen.[45][46] Man erhält somit den folgenden für die Verschlüsselung vorbereiteten Klartext:
DASOB ERKOM MANDO DERWE HRMAQ TGIBT BEKAN NTXAA CHENX AACHE NXIST GERET TETXD URQGE BUEND ELTEN EINSA TZDER HILFS KRAEF TEKON NTEDI EBEDR OHUNG ABGEW ENDET UNDDI ERETT UNGDE RSTAD TGEGE NXEIN SXAQT XNULL XNULL XUHRS IQERG ESTEL LTWER DENX
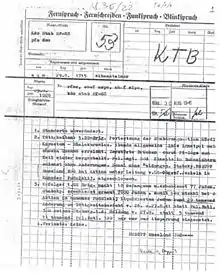
Der Verschlüssler hat seine Enigma I, wie weiter oben beschrieben, nach dem Tagesschlüssel beispielsweise für den 29. des Monats eingestellt. (Walzenlage B I IV III, Ringstellung 16 26 08 und Steckerverbindungen AD CN ET FL GI JV KZ PU QY WX. Sowohl dieser als auch die im Folgenden beschriebenen Schritte können mithilfe frei erhältlicher Computersimulationen realitätsnah nachvollzogen werden, siehe auch: Enigma-Simulationen sowie Simulationen unter Weblinks.) Der Bediener denkt sich nun eine zufällige Grundstellung aus, beispielsweise „QWE“, und stellt die drei Walzen so ein, dass genau diese drei Buchstaben in den Anzeigefenstern sichtbar werden. Nun lässt er sich einen zufälligen Spruchschlüssel ebenfalls mit drei Buchstaben einfallen, beispielsweise „RTZ“. Diesen verschlüsselt er mit seiner Enigma und beobachtet, wie nacheinander die Lampen „EWG“ aufleuchten. Den so verschlüsselten Spruchschlüssel teilt er dem Empfänger zusammen mit der zufällig gewählten Grundstellung als Indikator sowie der Uhrzeit und der Anzahl der Buchstaben des Textes als „Spruchkopf“ offen mit.
Laut damals geltender H.Dv.g.14 (= Heeres-Dienstvorschrift, geheim, Nr. 14)[32] enthält der Spruchkopf die Uhrzeit als vierstellige Zahl, die Buchstabenanzahl des Spruchs einschließlich der fünf Buchstaben der Kenngruppe sowie die gewählte Grundstellung und den verschlüsselten Spruchschlüssel (Beispiel: 2220 – 204 – qweewg). Im Allgemeinen wurden alle Buchstaben handschriftlich kleingeschrieben, da sie so schneller notiert werden konnten als bei Gebrauch von Großbuchstaben. Ein authentisches Spruchformular mit dem Spruchkopf „kr – 2300 – 182 – zzxprq –“, wobei „kr“ (Abkürzung für „kriegswichtig“ oder „Kriegsnotmeldung“[47] mit dem auffälligen Morsezeichen − · − · − ·) als Symbol für „Dringend“ steht, ist unter Weblinks als „Spruch Nr. 233“ zu sehen. Es handelt sich um eine Anfrage nach Munition für die schwere Feldhaubitze (sFH).[48]

Als Nächstes wählt der Bediener noch drei für diesen Tag gültige Kenngruppenbuchstaben anhand einer Kenngruppentabelle aus, beispielsweise „NOW“. Die Kenngruppe hat keine kryptologische Bedeutung,[49] sie dient dem Empfänger der Nachricht nur dazu, zu erkennen, dass die Nachricht wirklich für ihn bestimmt ist und auch befugt entschlüsselt werden kann. Zur Verschleierung der Kenngruppe werden die drei Buchstaben vom Absender beliebig permutiert und um zwei für jeden Spruch zufällig zu wechselnde „Füllbuchstaben“,[32] beispielsweise „XY“, ergänzt. Aus „NOW“ wird so zunächst etwa „OWN“ und schließlich „XYOWN“. Diese fünf Buchstaben werden unverschlüsselt als erste Fünfergruppe dem Geheimtext vorangestellt.[50]
Der Verschlüssler stellt nun die drei Walzen seiner Enigma auf den von ihm gewählten Spruchschlüssel „RTZ“ ein und verschlüsselt den obigen Klartext, das heißt, er gibt jeden einzelnen Buchstaben des Klartextes über die Tastatur der Enigma ein und liest die jeweils aufleuchtende Lampe als Geheimtextbuchstaben ab und notiert ihn. Zusammen mit dem Spruchkopf und der getarnten Kenngruppe ergibt sich der folgende Funkspruch:
Kopf: 2220 – 204 – QWE EWG -
XYOWN LJPQH SVDWC LYXZQ FXHIU VWDJO BJNZX RCWEO TVNJC IONTF QNSXW ISXKH JDAGD JVAKU KVMJA JHSZQ QJHZO IAVZO WMSCK ASRDN XKKSR FHCXC MPJGX YIJCC KISYY SHETX VVOVD QLZYT NJXNU WKZRX UJFXM BDIBR VMJKR HTCUJ QPTEE IYNYN JBEAQ JCLMU ODFWM ARQCF OBWN

Kopf und Geheimtext werden als Morsezeichen gefunkt und vom Empfänger aufgenommen. Dieser prüft als erstes, ob die Anzahl der Buchstaben (hier: 204) korrekt ist und der Spruch unverstümmelt empfangen wurde. Dann betrachtet er die Kenngruppe, also die erste Fünfergruppe, ignoriert die ersten beiden Buchstaben und sieht „OWN“. Er sortiert die drei Buchstaben in alphabetischer Reihenfolge, erhält so „NOW“, schaut in seine Kenngruppentabelle, entdeckt dort diese Kenngruppenbuchstaben und kann nun sicher sein, dass der Spruch für ihn bestimmt ist und er ihn entschlüsseln kann. Seine Enigma ist bereits bezüglich Walzenlage, Ringstellung und Steckerverbindungen entsprechend dem auch ihm bekannten Tagesschlüssel identisch mit der des Absenders eingestellt. Es fehlt ihm noch der Spruchschlüssel, also die richtige Anfangsstellung der Walzen zur Entschlüsselung des Spruchs. Diese Information erhält er aus dem Indikator „QWE EWG“ im Spruchkopf, den er wie folgt interpretiert: Stelle die Walzen auf die Grundstellung „QWE“ ein und taste dann „EWG“. Nun kann er beobachten, wie nacheinander die Lampen „RTZ“ bei seiner Enigma aufleuchten. Dies ist der einzustellende Spruchschlüssel.
Er dreht nun die Walzen auf die Anfangsstellung „RTZ“ und beginnt, den Geheimtext, angefangen mit der zweiten Fünfergruppe „LJPQH“, in seine Enigma einzugeben. Nun leuchten nacheinander die Lampen auf, und der folgende Text erscheint
dasoberkommandoderwehrmaqtgibtbekanntxaachenxaache nxistgerettetxdurqgebuendelteneinsatzderhilfskraef tekonntediebedrohungabgewendetunddierettungderstad tgegenxeinsxaqtxnullxnullxuhrsiqergestelltwerdenx
Kryptographische Stärken
Als die Enigma im Jahr 1918 durch Scherbius zum Patent angemeldet wurde, also noch während der Zeit des Ersten Weltkriegs, war sie eine kryptographisch äußerst starke Maschine und durfte zu Recht als „unknackbar“ bezeichnet werden.[51] Innovativ war, im Gegensatz zu den damals noch gebräuchlichen manuellen Verschlüsselungsverfahren (beispielsweise ADFGVX), die Einführung einer maschinellen Verschlüsselung. Sie war durch die damals allein üblichen manuellen, hauptsächlich linguistisch gestützten, Entzifferungsmethoden unangreifbar und blieb es auch noch bis in die 1930er-Jahre, also mehr als zehn Jahre lang.
Während dieser Zeit erhielt das damals neu etablierte teilstreitkräfteübergreifende kryptographische Büro (niederländisch Cryptographisch Bureau) der niederländischen Streitkräfte von der Chiffriermaschinen AG eine Enigma‑D (Bild) zur Ansicht und Erprobung. Nach zweimonatiger Analyse gab der Chef des Büros, Hauptmann Henri Koot, die folgende Einschätzung ab:
“I dare say that it satisfies all requirements, be they ever so high even the possession of an equal machine with the same electrical connections both in the ciphering cylinders and in the other parts of the machine will not enable an unauthorized person to find out its solution.”
„Ich wage zu behaupten, dass sie alle Anforderungen erfüllt, egal wie hoch. Selbst der Besitz einer gleichwertigen Maschine mit denselben elektrischen Verbindungen sowohl in den Chiffrierzylindern als auch in den anderen Teilen der Maschine wird eine unbefugte Person nicht dazu in die Lage versetzen, eine Lösung zu finden.“
Die kryptographischen Stärken der Enigma sind im Wesentlichen durch den rotierenden Walzensatz gegeben. Durch die Drehung der Walzen wird erreicht, dass jeder Buchstabe des Textes mit einem neuen Alphabet verschlüsselt wird (polyalphabetische Verschlüsselung). Auf diese Weise wird das bei den monoalphabetischen Verfahren so verräterische Häufigkeitsgebirge bis zur Unkenntlichkeit abgeschliffen und klassische Angriffe zur Entzifferung des Geheimtextes, wie statistische Analysen, Doppler- oder Mustersuche, sind zum Scheitern verurteilt. Auch die Periodensuche mithilfe des Koinzidenzindexes, als übliche Angriffsmethode auf polyalphabetische Verschlüsselungen, wie beispielsweise der Vigenère-Chiffre, ist ebenso aussichtslos, denn im Vergleich zur Periodenlänge (von 16.900, siehe auch: Verbesserungspotenzial) der Enigma war eine vergleichsweise winzige Höchstlänge der Funksprüche von 250 Buchstaben vorgeschrieben.[53]

Entscheidend für die Sicherheit der Verschlüsselung gegen unbefugte Entzifferung sind die Geheimhaltung der Walzenverdrahtung sowie die Anzahl der im Walzensatz verwendeten Walzen. Letzteres ist ein wichtiger Faktor, der die wesentlich stärkere Verschlüsselung der bei den deutschen U‑Booten eingesetzten Vierwalzen-Enigma‑M4 im Vergleich zur Enigma I (mit nur drei Walzen) erklärt. Es sind drei mit einer M4-Maschine verschlüsselte Funksprüche öffentlich bekannt, deren Inhalt bis zum Jahr 2006 nicht enträtselt werden konnte. Erst dann gelang es dem Hobby-Kryptologen Stefan Krah, zwei der Nachrichten, die vom U‑Boot U 264 beziehungsweise U 623 im Jahr 1942 gefunkt wurden, durch verteiltes Rechnen (distributed computing) und Zusammenschluss von mehreren tausend Computern im Internet innerhalb eines Monats zu entziffern. Der dritte Funkspruch schließlich widerstand weitere sieben Jahre und wurde erst im Januar 2013 entziffert.[54][55] Dies zeigt eindrucksvoll, dass die Enigma, deren Patentierung sich am 23. Februar 2018 zum hundertsten Mal jährte, auch mit modernen kryptanalytischen Angriffsmethoden und der heutigen weit fortentwickelten Rechnertechnik nicht einfach zu knacken ist, sondern noch immer eine „harte Nuss“ darstellt.
Die Ringe (Ringstellung), ursprünglich erfunden bereits 1928 von Willi Korn,[56] und nicht, wie vielfach falsch publiziert, von seinem Kollegen Paul Bernstein,[57][58][59] bestimmen den Versatz zwischen der inneren Verdrahtung der Walzen und dem Buchstaben, zu dem der Übertrag auf die nächste Walze erfolgt. Außerdem dienten sie zum Schutz vor Spionage. So wurde verhindert, dass durch Ablesen der von außen sichtbaren Walzenstellung auf die interne Drehposition der Walzen geschlossen werden konnte.
Mithilfe der „Doppelsteckerschnüre“,[60] die von vorne in das Steckerbrett gesteckt werden können, lassen sich Buchstaben vor und nach Durchlaufen des Walzensatzes paarweise involutorisch vertauschen. Diese Maßnahme diente zur weiteren Stärkung der kryptographischen Sicherheit der Enigma. Tatsächlich wird hierdurch der Schlüsselraum beträchtlich erweitert.
Schlüsselraum


Die Größe des Schlüsselraums der Enigma lässt sich aus den vier einzelnen Teilschlüsseln sowie der Anzahl der jeweils möglichen unterschiedlichen Schlüsseleinstellungen berechnen. Der gesamte Schlüsselraum der Enigma I (für M4 siehe Enigma‑M4) ergibt sich aus den folgenden vier Faktoren:
- a) Die Walzenlage
- Drei von fünf Walzen (I bis V) werden ausgewählt. (Als Umkehrwalze wurde fast immer nur die UKW B benutzt.) Dies ergibt 5·4·3 = 60 mögliche Walzenlagen (entspricht einer „Schlüssellänge“ von etwa 6 bit).
- b) Die Ringstellung
- Es gibt jeweils 26 verschiedene Ringstellungen (01 bis 26) für die mittlere und die rechte Walze. Der Ring der linken Walze trägt nicht zur Vergrößerung des Schlüsselraums bei, da seine Übertragskerbe kein Fortschalten einer noch weiter links befindlichen Walze bewirkt. Insgesamt sind 26² = 676 Ringstellungen relevant (entspricht etwa 9 bit).
- c) Die Walzenstellung
- Es gibt für jede der drei (rotierenden) Walzen 26 Möglichkeiten, sie einzustellen (A bis Z). Die Umkehrwalze kann nicht verstellt werden. Insgesamt sind somit 26³ = 17.576 Walzenstellungen verfügbar. Setzt man die Ringstellung als bekannt voraus, so sind davon aufgrund einer unwichtigen Anomalie des Fortschaltmechanismus 26² = 676 Anfangsstellungen als kryptographisch redundant zu eliminieren. Als relevant übrig bleiben dann 26·25·26 = 16.900 Walzenstellungen (entspricht etwa 14 bit).
- d) Die Steckerverbindungen
- Es können bis zu 13 Steckerverbindungen zwischen den 26 Buchstaben hergestellt werden. Ausgehend vom Fall des ungesteckerten Steckerbretts (in der Tabelle unten als Nummer 0 berücksichtigt), gibt es für die erste Steckerverbindung 26 Auswahlmöglichkeiten für das eine Ende und dann noch 25 für das andere Ende des Kabels. Somit gibt es für das erste Kabel 26·25 unterschiedliche Möglichkeiten, es einzustecken. Da es aber keine Rolle spielt, in welcher Reihenfolge die beiden Kabelenden gesteckt werden, entfallen davon die Hälfte der Möglichkeiten. Es bleiben also 26·25/2 = 325 Möglichkeiten für die erste Verbindung. Für die zweite erhält man analog 24·23/2 = 276 Möglichkeiten. Allgemein gibt es (26−2n+2)·(26−2n+1)/2 Möglichkeiten für die n‑te Steckerverbindung (siehe auch: Gaußsche Summenformel).
Nummer der ---- Möglichkeiten für ---- Möglichkeiten für Steckverbindung erste Seite zweite Seite Steckverbindung 0 1 1 1 1 26 25 325 2 24 23 276 3 22 21 231 4 20 19 190 5 18 17 153 6 16 15 120 7 14 13 91 8 12 11 66 9 10 9 45 10 8 7 28 11 6 5 15 12 4 3 6 13 2 1 1
- Die Gesamtzahl der möglichen Steckkombinationen bei Verwendung von mehreren Steckern ergibt sich aus dem Produkt der Möglichkeiten für die einzelnen Steckerverbindungen. Da aber auch hier die Reihenfolge der Durchführung keine Rolle spielt (es ist kryptographisch gleichwertig, wenn beispielsweise zuerst A mit X gesteckert wird und danach B mit Y oder umgekehrt zuerst B mit Y und dann A mit X), dürfen die entsprechenden Fälle nicht als Schlüsselkombinationen berücksichtigt werden. Dies sind bei zwei Steckerverbindungen genau die Hälfte der Fälle. Das vorher ermittelte Produkt ist also durch 2 zu dividieren. Bei drei Steckerverbindungen gibt es sechs mögliche Reihenfolgen für die Durchführung der Steckungen, die alle sechs kryptographisch gleichwertig sind. Das Produkt ist also durch 6 zu dividieren. Im allgemeinen Fall, bei n Steckerverbindungen, ist das Produkt der vorher ermittelten Möglichkeiten durch n! (Fakultät) zu dividieren. Die Anzahl der Möglichkeiten für genau n Steckerverbindungen ergibt sich als
_-_Museo_scienza_e_tecnologia_Milano.jpg.webp)
Stecker -------------- Möglichkeiten für ----------------
n Steckver- genau n Steck- bis zu n Steck–
bindung verbindungen verbindungen
0 1 1 1
1 325 325 326
2 276 44850 45176
3 231 3453450 3498626
4 190 164038875 167537501
5 153 5019589575 5187127076
6 120 100391791500 105578918576
7 91 1305093289500 1410672208076
8 66 10767019638375 12177691846451
9 45 53835098191875 66012790038326
10 28 150738274937250 216751064975576
11 15 205552193096250 422303258071826
12 6 102776096548125 525079354619951
13 1 7905853580625 532985208200576
- Nachdem in den ersten Jahren nur sechs und später zwischen fünf und acht Verbindungskabel gesteckt wurden, galt ab August 1939 die feste Regel, stets genau zehn Steckerverbindungen durchzuführen. Für diese ergeben sich nach der obigen Tabelle 150.738.274.937.250 (mehr als 150 Billionen) Steckmöglichkeiten (entspricht etwa 47 bit).
Der gesamte Schlüsselraum einer Enigma I mit drei aus einem Vorrat von fünf ausgewählten Walzen und einer Umkehrwalze sowie bei Verwendung von zehn Steckern lässt sich aus dem Produkt der in den obigen Abschnitten a) bis d) ermittelten 60 Walzenlagen, 676 Ringstellungen, 16.900 Walzenstellungen und 150.738.274.937.250 Steckermöglichkeiten berechnen. Er beträgt:
60 · 676 · 16.900 · 150.738.274.937.250 = 103.325.660.891.587.134.000.000
Das sind etwa 10²³ Möglichkeiten und entspricht einer Schlüssellänge von ungefähr 76 bit. Die gelegentlich zu hörenden „150 Millionen Millionen Millionen“ Kombinationen,[61] beispielsweise in den Spielfilmen „Enigma – Das Geheimnis“ und „The Imitation Game – Ein streng geheimes Leben“, basieren auf dem Weglassen der Ringstellungen.[62] Die genaue Rechnung ergibt in diesem Fall 60 · 16.900 · 150.738.274.937.250 oder 152.848.610.786.371.500.000 unterschiedliche Fälle, wobei die Briten zumeist statt 16.900 alle 26³ oder 17.576 mögliche Walzenstellungen berücksichtigten und als Produkt dann 158.962.555.217.826.360.000 erhielten.
Der Schlüsselraum war für die damalige Zeit enorm groß und hält sogar einem Vergleich mit moderneren Verfahren stand. Beispielsweise verfügt das über mehrere Jahrzehnte gegen Ende des 20. Jahrhunderts zum Standard erhobene Verschlüsselungsverfahren DES (Data Encryption Standard) über eine Schlüssellänge von genau 56 bit, also deutlich weniger als die Enigma. Eine Exhaustion (vollständiges Durchsuchen) des Schlüsselraums der Enigma ist selbst mit modernen Mitteln kaum möglich und war mit der damaligen Technologie vollkommen illusorisch.
Die Größe des Schlüsselraums ist jedoch nur eine notwendige, aber keine hinreichende Bedingung für die Sicherheit eines kryptographischen Verfahrens. Selbst eine so simple Methode wie die einfache monoalphabetische Substitution verfügt (bei Verwendung eines Alphabets aus 26 Buchstaben wie die Enigma) über 26! (Fakultät) mögliche Schlüssel. Das sind grob 4000·10²³ Schlüssel (ungefähr 88 bit) und ist verglichen mit der Zahl 10²³ der Enigma I sogar noch um etwa den Faktor 4000 größer. Dennoch ist eine monoalphabetische Substitution sehr unsicher und kann leicht gebrochen (entziffert) werden.

Auch bei der Enigma ähnelt die wesentlich zur Größe des Schlüsselraums beitragende konstruktive Komponente, nämlich das Steckerbrett, einer einfachen monoalphabetischen Substitution, denn die Steckerung bleibt schließlich während der gesamten Verschlüsselung unverändert. Das Steckerbrett kann folglich mithilfe einer intelligenten kryptanalytischen Angriffsmethode (Turing-Bombe) überwunden und praktisch gänzlich eliminiert werden. Damit kann der Faktor 150.738.274.937.250 bei der Berechnung des Schlüsselraums effektiv wieder gestrichen werden.
Ebenso bewirken die Ringe nur eine geringe kryptographische Stärkung des Verfahrens. Bei falscher Ringstellung der rechten Walze und ansonsten korrektem Schlüssel sind periodisch (Periodenlänge = 26 Buchstaben) bereits Klartextpassagen lesbar, die jeweils nach einigen Buchstaben immer wieder abreißen. Noch weniger wirkt der Ring der mittleren Walze, wobei hier die Periodenlänge 650 Buchstaben (25·26) beträgt. Die mittlere Ringstellung trägt somit zumeist überhaupt nicht zur Größe des Schlüsselraums bei, immer dann nämlich, wenn während des Spruchs kein Übertrag auf die linke Walze erfolgt, der aufgrund der vorgeschriebenen Spruchlänge von höchstens 250 Buchstaben nur selten passierte. Die Ringstellung der linken Walze ist aus kryptanalytischer Sicht völlig bedeutungslos. Insgesamt stellt die Feinjustierung der Ringe keine größere Schwierigkeit mehr dar. Damit kann man bei der Berechnung der Größe des Schlüsselraums auch den Faktor 676 getrost wieder streichen.
Als kryptographisch wirksam übrig bleiben nur die 60 Walzenlagen und die (bei unbekannter Ringstellung) 17.576 zu berücksichtigenden Walzenstellungen. So schrumpft der vorher noch so gigantisch erscheinende Schlüsselraum auf vergleichsweise winzige 60·17.576 = 1.054.560 (gut eine Million) Möglichkeiten (etwa 20 bit), eine Zahl, die auch bereits zu Zeiten des Zweiten Weltkriegs mithilfe der damaligen elektromechanischen Technik exhaustiv (erschöpfend) abgearbeitet werden konnte.
Kryptographische Schwächen

Scherbius’ Mitarbeiter Willi Korn erreichte durch die Umkehrwalze, dass das Schlüsselverfahren involutorisch wird, das heißt, wenn bei einer bestimmten Stellung der Walzen ein U in ein X verschlüsselt wird, dann wird bei dieser Stellung auch ein X in ein U verschlüsselt. So vereinfachte er Bedienung und Konstruktion der Maschine, denn man muss nicht mehr zwischen Verschlüsselung und Entschlüsselung unterscheiden. Darüber hinaus erhoffte er sich auch eine Steigerung der Sicherheit, denn der Strom durchfließt die Walzen ja nun zweimal:
„Durch diesen Rückgang des Stromes durch den Chiffrierwalzensatz findet eine weitere Verwürfelung statt. Infolge dieser Anordnung ist es möglich, mit verhältnismäßig wenig Chiffrierwalzen auszukommen und trotzdem eine große Chiffriersicherheit aufrechtzuerhalten.“
Mit diesen Worten erläutert Korn die Vorteile seiner Umkehrwalze in der Patentschrift (DRP Nr. 452 194).[63] Dies war jedoch ein Trugschluss mit weitreichenden Konsequenzen.
Zum einen bewirkt die Umkehrwalze, dass nun kein Buchstabe mehr in sich selbst verschlüsselt werden kann, denn der Strom kann ja in keinem Fall genau den Weg durch den Walzensatz wieder zurücknehmen, den er gekommen ist. Er wird stets auf einem anderen Weg zurückgeleitet, als er zur Umkehrwalze hingeflossen ist. Mathematisch spricht man hier von fixpunktfreien Permutationen. Diese Einschränkung mag als unwesentliche Kleinigkeit erscheinen, denn es bleiben ja noch 25 weitere Buchstaben des Alphabets zur Verschlüsselung, tatsächlich bedeutet dies jedoch eine drastische Reduzierung der zur Verschlüsselung verfügbaren Alphabete und darüber hinaus eine neue Angreifbarkeit des Geheimtextes. Zum anderen verursacht die Umkehrwalze dadurch, dass die Permutation und damit die Verschlüsselung involutorisch wird, eine weitere Verringerung der Alphabetanzahl.
Die durch die Umkehrwalze eingefügten kryptographischen Schwächen, insbesondere die Reduzierung der Anzahl der zur Verfügung stehenden Alphabete, lassen sich leicht klarmachen, wenn man statt von 26 Buchstaben vereinfacht von beispielsweise nur vier Buchstaben ausgeht. Mit vier Buchstaben lassen sich 4! = 24 unterschiedliche Alphabete (damit meint der Kryptograph unterschiedliche Anordnungen der Buchstaben) erzeugen, nämlich
ABCD ABDC ACBD ACDB ADBC ADCB BACD BADC BCAD BCDA BDAC BDCA CABD CADB CBAD CBDA CDAB CDBA DABC DACB DBAC DBCA DCAB DCBA
Beschränkt man sich hier, statt auf alle 24 möglichen, nur auf die fixpunktfreien Permutationen, so fallen alle Alphabete weg, bei denen ein Buchstabe in sich selbst verschlüsselt wird, also auf seinem gewohnten alphabetischen Platz steht. Aus der obigen Liste sind damit die folgenden fünfzehn Alphabete zu streichen, da sie einen oder mehrere Fixpunkte aufweisen (unten rot und unterstrichen).
ABCD ABDC ACBD ACDB ADBC ADCB BACD BCAD BDCA CABD CBAD CBDA DACB DBAC DBCA |
Übrig bleiben nur die folgenden neun fixpunktfreien Permutationen:
---- ---- ---- ---- ---- ---- ---- BADC ---- BCDA BDAC ---- ---- CADB ---- ---- CDAB CDBA DABC ---- ---- ---- DCAB DCBA
Berücksichtigt man jetzt noch, dass die Umkehrwalze nicht nur alle Permutationen mit Fixpunkten eliminiert, sondern auch alle nichtinvolutorischen Permutationen, so müssen aus der obigen Tabelle noch weitere sechs Fälle gestrichen werden, nämlich die, bei denen die zweifache Anwendung der Permutation nicht wieder zum ursprünglichen Buchstaben führt. Übrig bleiben von allen möglichen 24 Permutationen eines Alphabets aus vier Buchstaben lediglich die drei fixpunktfreien und involutorischen Fälle. Sie werden als „echt involutorische Permutationen“ bezeichnet.[64]
---- ---- ---- ---- ---- ---- ---- BADC ---- ---- ---- ---- ---- ---- ---- ---- CDAB ---- ---- ---- ---- ---- ---- DCBA

Bei der Enigma mit ihren 26 Buchstaben bewirkt diese Beschränkung, dass statt der 26! (Fakultät), also ungefähr 4·1026 insgesamt möglichen permutierten Alphabete lediglich die 25·23·21·19···7·5·3·1 = 25!! (Doppelfakultät), also etwa 8·1012 echt involutorisch permutierten Alphabete genutzt werden können. Durch die Umkehrwalze verschenkt man so den Faktor von etwa 5·1013 an Möglichkeiten – eine gigantische Schwächung der kombinatorischen Komplexität der Maschine. Übrig bleibt weniger als die Quadratwurzel der ursprünglich möglichen Permutationen.
Kryptographisch noch katastrophaler als diese drastische Reduktion der Alphabetanzahl ist jedoch, dass durch die Vermeidung von Fixpunkten Aussagen über den Text möglich sind wie „Nichts ist jemals es selbst“,[61] die bei der Entzifferung eine ganz wesentliche Hilfe waren. Weiß der Angreifer, dass niemals ein Buchstabe die Verschlüsselung seiner selbst ist, dann eröffnet ihm diese Kenntnis Abkürzungen, und er muss nicht mehr mühsam jeden einzelnen Fall abarbeiten, wie an folgendem Beispiel illustriert wird.
Ein seit Jahrhunderten bekanntes und bewährtes Entzifferungsverfahren ist die „Methode des wahrscheinlichen Wortes“.[65][66] Hierbei errät, vermutet oder weiß der Angreifer, dass im Text eine bestimmte Phrase (englisch Crib, französisch Mot probable) auftritt, beispielsweise „OBERKOMMANDODERWEHRMACHT“. Liegt dem Angreifer zum Beispiel ein mit der Enigma verschlüsseltes Geheimtextfragment wie das folgende vor, so kann er ganz leicht ermitteln, an welcher Stelle im Text das vermutete wahrscheinliche Wort sich nicht befinden kann, indem er für jede mögliche Lage prüft, ob ein Zeichen in sich selbst verschlüsselt würde, was, wie er von der Enigma weiß, unmöglich ist. Dazu schreibt er das wahrscheinliche Wort in den verschiedenen Lagen unter den Geheimtext und prüft auf Kollisionen (englisch Crash),[67] die im unteren Beispiel rot und unterstrichen hervorgehoben sind:
BHNCXSEQKOBIIODWFBTZGCYEHQQJEWOYNBDXHQBALHTSSDPWGW 1 OBERKOMMANDODERWEHRMACHT 2 OBERKOMMANDODERWEHRMACHT 3 OBERKOMMANDODERWEHRMACHT 4 OBERKOMMANDODERWEHRMACHT 5 OBERKOMMANDODERWEHRMACHT 6 OBERKOMMANDODERWEHRMACHT 7 OBERKOMMANDODERWEHRMACHT 8 OBERKOMMANDODERWEHRMACHT 9 OBERKOMMANDODERWEHRMACHT 10 OBERKOMMANDODERWEHRMACHT 11 OBERKOMMANDODERWEHRMACHT 12 OBERKOMMANDODERWEHRMACHT 13 OBERKOMMANDODERWEHRMACHT 14 OBERKOMMANDODERWEHRMACHT 15 OBERKOMMANDODERWEHRMACHT 16 OBERKOMMANDODERWEHRMACHT 17 OBERKOMMANDODERWEHRMACHT 18 OBERKOMMANDODERWEHRMACHT 19 OBERKOMMANDODERWEHRMACHT 20 OBERKOMMANDODERWEHRMACHT 21 OBERKOMMANDODERWEHRMACHT 22 OBERKOMMANDODERWEHRMACHT 23 OBERKOMMANDODERWEHRMACHT 24 OBERKOMMANDODERWEHRMACHT 25 OBERKOMMANDODERWEHRMACHT 26 OBERKOMMANDODERWEHRMACHT 27 OBERKOMMANDODERWEHRMACHT BHNCXSEQKOBIIODWFBTZGCYEHQQJEWOYNBDXHQBALHTSSDPWGW |
Die Anzahl der durch Kollisionen auszuschließenden Lagen lässt sich nach folgender Überlegung abschätzen: Bei einem wahrscheinlichen Wort der Länge 1 (also nur ein einzelner wahrscheinlicher Buchstabe) ist die Wahrscheinlichkeit für eine Kollision 1/26. Folglich ist die Wahrscheinlichkeit für keine Kollision 1−1/26. Bei einem wahrscheinlichen Wort wie oben mit der Länge 24 ist dann die Wahrscheinlichkeit für keine Kollision (1−1/26)24, das sind etwa 39 %. Das heißt, bei 27 untersuchten Lagen erwartet man im Mittel für 27·(1−1/26)24 der Fälle keine Kollisionen. Der Ausdruck ergibt etwa den Wert 10,5 und stimmt recht gut mit den im Beispiel beobachteten (und grün gekennzeichneten) acht kollisionsfreien Crib-Lagen überein.
Mithilfe dieser äußerst simplen kryptanalytischen Angriffsmethode lassen sich so von den 27 möglichen Lagen des wahrscheinlichen Worts hier 19, also mehr als zwei Drittel, als unmöglich eliminieren – eine erhebliche Arbeitsvereinfachung für den Angreifer.
Entzifferung


Die Betreiber der Schlüsselmaschine Enigma waren der Meinung, dass die durch sie maschinell verschlüsselten Texte im Gegensatz zu fast allem, was bis 1918 gebräuchlich war, mit manuellen Methoden nicht zu knacken sind. Übersehen wurde, dass einer maschinellen Verschlüsselung durch maschinelle Entzifferung begegnet werden kann.
Die Geschichte der Entzifferung der Enigma beginnt im Jahr 1932, als der für Frankreich unter dem Decknamen HE (Asché) spionierende Deutsche Hans-Thilo Schmidt geheime Schlüsseltafeln für die Monate September und Oktober 1932[69] sowie die Gebrauchsanleitung (H.Dv.g.13)[70] und die Schlüsselanleitung (H.Dv.g.14)[32] an den französischen Geheimdienstmitarbeiter Capitaine (deutsch: Hauptmann) und späteren Général Gustave Bertrand gegen Geld verriet.[71] Zu dieser Zeit waren erst drei Walzen (I bis III) im Einsatz und die Walzenlage wurde nur vierteljährlich und noch nicht, wie dann ab Oktober 1936, täglich gewechselt. Das Deuxième Bureau des französischen Geheimdienstes leitete die Unterlagen an britische und polnische Stellen weiter.
Während es Franzosen und Briten nicht gelang, in die Verschlüsselung einzubrechen und sie die Enigma als „unknackbar“ einstuften,[72] glückte dem 27‑jährigen polnischen Mathematiker Marian Rejewski bei seiner Arbeit in dem für Deutschland zuständigen Referat BS4 des Biuro Szyfrów (deutsch: „Chiffrenbüro“) bereits im Jahr 1932 der erste Einbruch in die Enigma.[73] Dabei nutzte er eine legal gekaufte kommerzielle Maschine (vermutlich Modell C),[74] bei der – anders als bei der ihm noch unbekannten militärischen Enigma I – die Tastatur mit der Eintrittswalze in der üblichen QWERTZ-Reihenfolge (Buchstabenreihenfolge einer deutschen Tastatur, beginnend oben links) verbunden war. Rejewski erriet die von den Deutschen für die militärische Variante gewählte Verdrahtungsreihenfolge,[75] die den britischen Codebreaker Dillwyn „Dilly“ Knox selbst noch 1939 fast zur Verzweiflung brachte.[76] Anschließend schaffte es Marian Rejewski mithilfe seiner exzellenten Kenntnisse der Permutationstheorie (siehe auch: Enigma-Gleichung), die Verdrahtung der drei Walzen (I bis III) sowie der Umkehrwalze (A) (siehe auch: Enigma-Walzen) zu erschließen[77] – eine kryptanalytische Meisterleistung, die ihn mit den Worten des amerikanischen Historikers David Kahn „in das Pantheon der größten Kryptoanalytiker aller Zeiten erhebt“ (im Original: „[…] elevates him to the pantheon of the greatest cryptanalysts of all time“).[78] Der englische Codeknacker Irving J. Good bezeichnete Rejewskis Leistung als „The theorem that won World War II“[79] (deutsch: „Das Theorem, das den Zweiten Weltkrieg gewann“).
Die nächste Aufgabe, die gelöst werden musste, war, jeweils die richtige Walzenlage und Walzenstellung zu erschließen. Dazu nutzte Rejewski zusammen mit seinen 1932 hinzugekommenen Kollegen Jerzy Różycki und Henryk Zygalski einen schwerwiegenden verfahrenstechnischen Fehler aus, der den Deutschen unterlief: Um eine sichere Übertragung zu gewährleisten, wurde zu dieser Zeit der Spruchschlüssel noch zweimal hintereinandergestellt und verschlüsselt an den Anfang einer Nachricht geschrieben („Spruchschlüsselverdopplung“).[80] Somit war der erste und vierte, der zweite und fünfte sowie der dritte und sechste Geheimtextbuchstabe jeweils demselben Klartextbuchstaben zuzuordnen. Mithilfe zweier, durch ihren Kollegen Antoni Palluth von der Firma AVA speziell zu diesem Zweck gebauter Maschinen,[81] genannt Zyklometer und Bomba, die zwei beziehungsweise dreimal zwei hintereinandergeschaltete und um jeweils drei Drehpositionen versetzte Enigma-Maschinen verkörperten, konnten die polnischen Kryptoanalytiker für jede der sechs möglichen Walzenlagen feststellen, bei welchen Walzenstellungen die beobachtete Zuordnung der Buchstabenpaare möglich war, und so den Suchraum erheblich einengen. Nach Analyse mehrerer Funksprüche war der korrekte Spruchschlüssel gefunden.[82]
Nachdem die Deutschen, die von alledem nichts wussten, am 15. September 1938 ihre Verfahrenstechnik änderten[83] und drei Monate später mit Einführung der Walzen IV und V die Anzahl der möglichen Walzenlagen von sechs (= 3·2·1) auf sechzig (= 5·4·3) erhöhten,[84] konnten die Polen nicht mehr mithalten und die Enigma war wieder sicher.[85] Angesichts der drohenden Gefahr übergaben sie kurz vor dem deutschen Überfall auf Polen ihr gesamtes Wissen an ihre Verbündeten. Am 26. und 27. Juli 1939[86] kam es zum legendären Geheimtreffen französischer, britischer und polnischer Codeknacker im Kabaty-Wald von Pyry, knapp 20 km südlich von Warschau, bei dem sie den verblüfften Briten und Franzosen ihre Enigma-Nachbauten und ihre kryptanalytischen Maschinen präsentierten und ihre Methodiken offenbarten.[86] Die erste Frage, die Dilly Knox bei diesem Treffen (laut Mavis Batey auf Französisch)[87] gestellt hat, war: „Quel est le QWERTZU?“[88] (deutsch: „Was ist der QWERTZU?“; also sinngemäß: „Wie lautet die Verdrahtungsreihenfolge der Eintrittswalze?“).[89] Dies hatte ihn schon lange gequält.[90] Rejewskis Antwort war genial einfach: „ABCDEFG…“.[76] Ein Gedanke, der Knox so abstrus erschien, dass er es nicht fassen konnte. Marian Rejewski hingegen kannte die „Tugend der Deutschen: den Ordnungssinn“,[91] und dies hatte ihn bereits sieben Jahre zuvor die von den deutschen Kryptographen gewählte, denkbar simpelste aller Permutationen erkennen lassen – den Trivialfall der Identität. Daraus resultierte die für ihn leicht zu erratende gewöhnliche alphabetische Reihenfolge der Verdrahtung der Eintrittswalze.



Mit diesem Anschub, vor allem mit den nun endlich bekannten Walzenverdrahtungen,[94] konnten die britischen Kryptoanalytiker mit Ausbruch des Krieges im etwa 70 km nordwestlich von London gelegenen Bletchley Park (B.P.)[95] einen erneuten Angriff auf die Enigma starten. Das wichtigste Hilfsmittel dabei war – neben ihrer intellektuellen Leistungsfähigkeit und dem hohen Personaleinsatz von später zehntausend[96] bis vierzehntausend[97] Frauen und Männern – vor allem eine spezielle elektromechanische Maschine, genannt die Turing-Bombe, die als Nachfolgerin auf der polnischen Bomba aufbaute und vom englischen Mathematiker Alan Turing ersonnen wurde. Turings Idee zur Schlüsselsuche bestand darin, durch ringförmige Verkettung von mehreren, meist zwölf, Enigma-Walzensätzen die Wirkung des Steckerbretts komplett abzustreifen.[98] Dadurch gelang es ihm, die praktisch unüberschaubare Anzahl von mehr als 200 Trilliarden Verschlüsselungsmöglichkeiten, auf die die deutschen Kryptographen ihre Hoffnungen setzten, drastisch zu reduzieren.
Das Grundprinzip geht von der Enigma I aus, bei der drei Walzen aus einem Sortiment von fünf Walzen eingesetzt werden und nur die Umkehrwalze B zur Verfügung steht. Eine andere Umkehrwalze (UKW C), von den Briten lautmalerisch Uncle Walter genannt, tauchte kurzzeitig auf und verschwand schnell wieder.[99] Für jede der 60 verschiedenen Walzenlagen gibt es 26³, also 17.576 Walzenstellungen. Wenn man bei der Schlüsselsuche von den Ringstellungen und vom Steckerbrett absehen kann, was mithilfe der durch die Bombe realisierten kryptanalytischen Angriffsmethode ermöglicht wurde, dann bleiben „nur“ noch 60·17.576, also 1.054.560 Möglichkeiten übrig. Diese etwa eine Million unterschiedlichen Fälle sind von Hand in vernünftiger Zeit praktisch nicht durchzuprobieren. Mithilfe der Turing-Bombe jedoch, die motorbetrieben mit 64 Umdrehungen pro Minute[100] während jeder Umdrehung 26 Fälle abarbeiten konnte, brauchte man nur noch 1.054.560/(26·64) Minuten, also etwas mehr als zehn Stunden, um sämtliche Möglichkeiten durchzutesten. Hinzu kommt noch die Zeit zum Einstellen und Umrüsten der Maschine auf die sechzig verschiedenen Walzenlagen, wodurch die Zeit auf rund zwanzig Stunden verdoppelt wird.[101] Leistet man sich den Aufwand, sechzig Bombes einzusetzen, jeweils eine für jede Walzenlage, dann schrumpft die Zeit für einen Durchlauf von etwas mehr als zehn Stunden auf gut zehn Minuten[102] – eine durchaus erträgliche Zeit. Tatsächlich waren Anfang 1944 mehr als 330 Bombes im Vereinigten Königreich und den Vereinigten Staaten in Betrieb,[103] nachdem sich die Briten noch Ende 1941 mit nur zwölf Bombes begnügen mussten.[104]
Entscheidend wichtig für die Funktion der Bombe sind wahrscheinliche Wörter (Cribs),[105] deren Auftreten man im Text erwarten kann. Fehlen diese, dann scheitert die Entzifferung. Beispielsweise gelang den Briten der Einbruch in zwei Schlüsselkreise der Deutschen Reichsbahn nicht,[106] die in Bletchley Park nach der frühen Dampflokomotive Rocket als Rocket II und Rocket III bezeichnet wurden.[107] Grund war, wie sie nach dem Krieg zu ihrer Überraschung feststellten, nicht eine besonders sichere Enigma-Variante, sondern die ungewohnte Eisenbahnersprache und die Art der Transportmeldungen, die ihnen das Erraten von wahrscheinlichen Wörtern nicht erlaubten. Militärische Meldungen hingegen waren häufig stereotyp abgefasst und enthielten viele leicht zu erratende Cribs wie OBERKOMMANDODERWEHRMACHT, die die britischen Codeknacker zur Entzifferung nutzen konnten.
Darüber hinaus profitierten sie von der deutschen Gründlichkeit bei der Abfassung von Routinemeldungen, wie Wetterberichte, die jeden Morgen pünktlich zur selben Zeit und vom selben Ort gesendet wurden. Zwar verbot die deutsche Dienstvorschrift „Allgemeine Schlüsselregeln für die Wehrmacht“ (H.Dv.g.7) ausdrücklich „Regelmäßigkeiten im Aufbau, gleichlautende Redewendungen und Wiederholungen im Text“[108] und warnte eindringlich „Es muß auf jeden Fall vermieden werden, daß durch flüchtig ausgebildetes Personal Schlüsselfehler gemacht werden, die […] der feindlichen Nachrichtenaufklärung die Entzifferung ermöglichen“,[109] dennoch passierten genau diese Fehler, die die Codeknacker wahrnehmen und ausnutzen konnten. Aus britischer Sicht war eine täglich frisch verschlüsselte Enigma-Meldung, die stets mit den Worten „WETTERVORHERSAGEBEREICHSIEBEN“ begann, ähnlich wertvoll wie es eine direkte öffentliche Bekanntgabe des jeweils gültigen Tagesschlüssels gewesen wäre. So wurde beispielsweise der Enigma-Schlüssel vom D‑Day, also dem Tag der Landung der Alliierten in der Normandie (Operation Overlord), durch den Crib „WETTERVORHERSAGEBISKAYA“, den die britischen Kryptoanalytiker leicht erraten konnten und korrekt vermuteten, in weniger als zwei Stunden nach Mitternacht gebrochen.[110]
Nicht selten provozierten die Briten sogar bewusst Vorfälle, nur um die darauf prompt zu erwartenden deutschen Funksprüche mit bekanntem Inhalt (und mit aktuellem Tagesschlüssel verschlüsselt) zu erhalten, und nannten diese Technik gardening (deutsch: „Gärtnern“).[111] Der britische Codebreaker Rolf Noskwith aus Baracke 8 beschrieb sie folgendermaßen: „Die RAF warf an bestimmten Stellen in der Nordsee Minen ab, so daß die Minenwarnung der Deutschen uns als Crib diente. Die Stellen waren sorgfältig ausgewählt, um bestimmte Ziffern, wie insbesondere 0 und 5, [als Koordinaten] zu vermeiden, für die die Deutschen unterschiedliche Buchstaben benutzten.“[112] Die Briten konnten sich so, unter Vermeidung der Fallunterscheidungen für „NULL“ und „NUL“ sowie „FUENF“ und „FUNF“, die Arbeit etwas erleichtern. Außer im Fall „ZWEI“ und „ZWO“ gab es für die übrigen Ziffern nur eine Schreibweise. Auch entzifferte Botschaften von kleineren Marineeinheiten, wie Hafenschiffen, die nicht über die Enigma verfügten und stattdessen Handschlüsselverfahren (Werftschlüssel oder Reservehandverfahren) benutzten, dienten den Briten als Cribs beim Bruch der Enigma. Die Deutschen versendeten nämlich viele Funksprüche, wie Minenwarnungen, wortgleich sowohl als Enigma-Geheimtexte als auch mit den Handverfahren verschlüsselt.[113] Die Briten waren dankbar für diese „Geheimtext-Geheimtext-Kompromisse“ und nannten sie Kisses.



So gelang es unter dem Decknamen „Ultra“, beginnend mit Januar 1940 zunächst die von der Luftwaffe und später auch die vom Heer mit der Enigma I verschlüsselten Nachrichten nahezu während des gesamten Zweiten Weltkriegs kontinuierlich zu brechen.[115] Im Jahr 1943 beispielsweise wurden mehr als 80.000 Funksprüche pro Monat abgefangen und entziffert, also durchschnittlich mehr als 2500 jeden Tag,[116] während des Krieges insgesamt waren es über zweieinhalb Millionen.[117]
Hartnäckiger zeigten sich die Verschlüsselungsverfahren der deutschen Kriegsmarine, die eine Variante (Enigma‑M3) mit drei aus acht Walzen (I bis VIII) sowie eine ausgeklügelte Spruchschlüsselvereinbarung nutzte. Hier gelang den Briten der Einbruch erst im Mai 1941 nach Kaperung des deutschen U‑Boots U 110 und Erbeutung einer intakten M3-Maschine und sämtlicher Geheimdokumente (Codebücher inklusive der entscheidend wichtigen „Doppelbuchstabentauschtafeln“)[118] durch den britischen Zerstörer HMS Bulldog am 9. Mai 1941.[119] Eine für die Briten schmerzliche Unterbrechung (Black-out) gab es dann, als am 1. Februar 1942 die M3 (mit drei Walzen) bei den U‑Booten durch die M4 (mit vier Walzen) abgelöst wurde.[120] Dieses von den Deutschen „Schlüsselnetz Triton“ und von den Briten Shark (deutsch: „Hai“) genannte Verfahren konnte zehn Monate lang nicht gebrochen werden, eine Zeit, von den U‑Boot-Fahrern die „zweite glückliche Zeit“ genannt, in der die deutsche U‑Bootwaffe erneut große Erfolge verbuchen konnte. Der Einbruch in Shark gelang erst am 12. Dezember 1942,[121][122] nachdem der britische Zerstörer HMS Petard am 30. Oktober 1942 im Mittelmeer das deutsche U‑Boot U 559 aufbrachte.[123] Ein Prisenkommando, bestehend aus Lieutenant Tony Fasson (1913–1942), Able Seaman Colin Grazier (1920–1942) und dem jungen Tommy Brown (1926–1945), enterte das Boot und erbeutete wichtige streng geheime Schlüsselunterlagen, wie Kurzsignalheft und Wetterkurzschlüssel, mit deren Hilfe es die Kryptoanalytiker in Bletchley Park schafften, auch die Enigma‑M4 zu überwinden.[124]

Nun kamen auch die Amerikaner zu Hilfe. Unter Federführung von Joseph Desch[125] produzierten sie ab April 1943 im United States Naval Computing Machine Laboratory (NCML), das seinen Sitz in der National Cash Register Company (NCR) in Dayton (Ohio) hatte, mehr als 120 Stück[126] Hochgeschwindigkeitsvarianten der Turing-Bombe. Diese sogenannten Desch-Bombes waren speziell gegen die M4 gerichtet.[127] In schneller Folge kamen weitere amerikanische Behörden unterstützend hinzu, wie etwa die Signal Security Agency (SSA), die Communications Supplementary Activity (CSAW), und die United States Coast Guard Unit 387 (USCG Unit 387). Die Personalstärke wuchs schnell von wenigen Hundert auf mehr als zehntausend Mitarbeiterinnen und Mitarbeiter an, die täglich Tausende von Funksprüchen entzifferten.[128]
Danach waren die deutschen U‑Boote nie mehr sicher (siehe auch: U‑Boot-Krieg). Unmittelbare Folge der amerikanischen Entzifferungen war, beginnend mit U 463 am 16. Mai 1943, einem U‑Tanker vom Typ XIV („Milchkuh“), bis U 220 am 28. Oktober 1943, einem zur Versorgung eingesetzten Minenleger vom Typ XB,[129] die Versenkung von elf der achtzehn deutschen Versorgungs-U‑Boote innerhalb weniger Monate im Jahr 1943.[130] Dies führte zu einer Schwächung aller Atlantik-U‑Boote, die nun nicht mehr auf See versorgt werden konnten, sondern dazu die lange und gefährliche Heimreise durch die Biskaya zu den U‑Boot-Stützpunkten an der französischen Westküste antreten mussten.
Geschichtliche Konsequenzen

Es gilt als unbestritten, dass die Kompromittierung der Enigma von enormer strategischer Bedeutung für den Verlauf des Zweiten Weltkriegs war. Einige Geschichtswissenschaftler gehen davon aus, dass, falls die Enigma nicht hätte gebrochen werden können, sich am Ausgang des Krieges zwar nichts geändert hätte, er aber wesentlich länger gedauert hätte und noch weitaus blutiger verlaufen wäre. So äußerte sich der englische Historiker Sir Harry Hinsley, der in Bletchley Park mitgearbeitet hatte, zur Bedeutung von Ultra mit den Worten „shortened the war by not less than two years and probably by four years“ (deutsch „[Ultra] verkürzte den Krieg um nicht weniger als zwei Jahre und vermutlich um vier Jahre“). Die Vermutung erscheint gerechtfertigt, dass es den polnischen, britischen und amerikanischen Kryptoanalytikern und ihrer Leistung bei der Entzifferung der deutschen Maschine zu verdanken ist, dass der Zweite Weltkrieg erheblich verkürzt werden konnte und damit unzähligen Menschen auf allen Seiten das Leben gerettet wurde.[132][133]
Es gibt aber auch Historiker, Politiker und Militärs, die die nachrichtendienstlichen Erkenntnisse als „entscheidend“[131] für den Sieg der Alliierten ansehen. So äußerte sich beispielsweise der amerikanische Historiker Harold Deutsch, der im Zweiten Weltkrieg Leiter der Analyse beim Amt für strategische Dienste im Kriegsministerium der Vereinigten Staaten, dem OSS war:
“I feel that intelligence was a vital factor in the Allied victory – I think that without it we might not have won, after all.”
„Ich glaube, dass die nachrichtendienstlichen Erkenntnisse ein lebenswichtiger Faktor für den Sieg der Alliierten waren – Ich meine, dass wir ohne sie schließlich doch nicht gewonnen hätten.“[134]
Experten, die Deutschs Ansicht teilen, berücksichtigen die Tatsache, dass die Entzifferungen nicht nur auf militärisch-taktischer Ebene (Heer, Luftwaffe und Marine) eine große Hilfe waren, sondern aufgrund der nahezu vollständigen Durchdringung des deutschen Nachrichtenverkehrs auf allen Ebenen (Polizei, Geheimdienste, diplomatische Dienste, SD, SS, Reichspost, Reichsbahn und Wehrmacht) auch einen äußerst genauen Einblick in die strategischen und wirtschaftlichen Planungen der deutschen Führung erlaubten. Speziell schätzten die Alliierten die Authentizität der aus Enigma-Funksprüchen gewonnenen Informationen, die aus anderen Quellen, wie Aufklärung, Spionage oder Verrat, nicht immer gegeben war. So konnten die Briten ihre zu Beginn des Krieges noch sehr begrenzten Ressourcen deutlich besser koordinieren und viel gezielter gegen die erkannten deutschen Schwächen einsetzen, als es ohne die Entzifferung der Enigma möglich gewesen wäre. Im späteren Verlauf des Krieges nutzten sie dann zusammen mit ihren amerikanischen Verbündeten die Ultra-Informationen, um die gemeinsame Überlegenheit noch besser auszuspielen.
Einer der führenden ehemaligen Codebreaker aus Bletchley Park, der britische Schachmeister Stuart Milner-Barry, schrieb: „Mit Ausnahme vielleicht der Antike wurde meines Wissens nie ein Krieg geführt, bei dem die eine Seite ständig die wichtigen Geheimmeldungen von Heer und Flotte des Gegners gelesen hat.“[135] Ein ähnliches Fazit zieht ein nach dem Krieg verfasster amerikanischer Untersuchungsbericht: „Ultra schuf in der Militärführung und an der politischen Spitze ein Bewusstsein, das die Art und Weise der Entscheidungsfindung veränderte. Das Gefühl, den Feind zu kennen, ist höchst beruhigend. Es verstärkt sich unmerklich im Laufe der Zeit, wenn man regelmäßig und aufs genaueste seine Gedanken und Gewohnheiten und Handlungsweisen beobachten kann. Wissen dieser Art befreit das eigene Planen von allzu großer Vorsicht und Angst, man wird sicherer, kühner und energischer.“[136]
„In Europa ließ die Fähigkeit der Alliierten, die deutschen Verschlüsselungssysteme zu knacken und alle Botschaften mitzulesen (Codename ULTRA), die Alliierten von Sieg zu Sieg eilen. In der „Schlacht im Atlantik“, der fundamentalsten Auseinandersetzung des ganzen Zweiten Weltkriegs, konnten die Alliierten ihre Konvois an den deutschen U‑Booten vorbeisteuern, weil sie wussten, wo diese wie Wolfsrudel lauerten. So ließen sich lähmende Verluste weitgehend vermeiden und Menschen wie Güter konnten sicher nach Großbritannien gebracht werden. Später, bei ihrer großen Invasion in Europa, die zum Sieg über Hitlers Reich führte, half die Decodierung deutscher Botschaften den Alliierten dabei, Gegenangriffe vorherzusehen und abzuwehren. Auf diese Weise konnten sie deutsche Schwachstellen besser erkennen und ins Ruhrgebiet und nach Berlin vorstoßen. Auch sowjetische Codebrecher konnten die geheimen Informationen der Deutschen entziffern, was zu ihrem Sieg an der Ostfront beitrug.“
Der ehemalige Sicherheitsberater von US-Präsident Jimmy Carter, der polnisch-amerikanische Politikwissenschaftler Zbigniew Brzeziński zitierte den Oberbefehlshaber der alliierten Streitkräfte General Dwight D. Eisenhower, der Ultra als decisive (deutsch „entscheidend“) für den Sieg bezeichnete.[138] Die polnischen Historiker Władysław Kozaczuk und Jerzy Straszak schrieben „it is widely believed that Ultra saved the world at least two years of war and possibly prevented Hitler from winning“.[139] (deutsch „es wird weithin angenommen, dass Ultra der Welt mindestens zwei Jahre Krieg erspart hat und möglicherweise verhinderte, dass Hitler ihn gewann“).

Der renommierte britische Historiker und Kryptologe Ralph Erskine sagte einfach und klar: Der Einbruch in die Marine-Enigma „rettete Großbritannien vor der Niederlage im U‑Boot-Krieg“.[140] Auch Stuart Milner-Barry vertrat die Ansicht, dass „had we not at the most crucial times and for long periods read the U‑boat ciphers, we should have lost the war“ (deutsch „hätten wir nicht zur entscheidenden Zeit und für lange Zeiträume die U‑Boot-Chiffren lesen können, dann hätten wir den Krieg verloren“).[141] In einer Ausstellung über den Secret War (deutsch „Geheimer Krieg“), die im Jahr 2003 in einem der bedeutendsten Kriegsmuseen weltweit, dem Imperial War Museum (deutsch „Kriegsmuseum des britischen Weltreichs“) in London stattfand, wurde der ehemalige britische Premierminister Winston Churchill zitiert, der seinem König George VI. gesagt hatte: „It was thanks to Ultra that we won the war.“ (deutsch „Es war Ultra zu verdanken, dass wir den Krieg gewonnen haben“).
In seinem Buch The Hut Six Story beschreibt Gordon Welchman, der neben Alan Turing einer der führenden Köpfe der britischen Codebreaker in Bletchley Park war, die Gratwanderung, die die alliierten Kryptoanalytiker zu vollbringen hatten, um nicht den Anschluss an die von den Deutschen immer wieder neu eingeführten kryptographischen Komplikationen zu verlieren. Mehrfach stand die Entzifferungsfähigkeit auf des Messers Schneide, und immer wieder senkte sich die Waagschale zugunsten der Codeknacker, oft auch mit viel Glück, wie Welchman in seinem Buch einräumt: „We were lucky“ (deutsch „Wir hatten Glück“).[142]
„Der Erfolg der Codeknacker beruhte letztlich auf einigen genialen Ideen […] Hätten Marian Rejewski 1931 in Polen und Alan Turing und Gordon Welchman 1939 in England nicht diese Ideen gehabt, wäre die »Enigma« möglicherweise nicht geknackt worden. Somit ist die Vorstellung, es hätte den Alliierten misslingen können, diese Chiffriermaschine zu knacken, keine Spekulation im luftleeren Raum, sondern es sprach tatsächlich einiges für diese Annahme.“
In seinem 2018 erschienenen Buch X, Y & Z – The Real Story of how Enigma was Broken (deutsch „X, Y & Z – Die wahre Geschichte, wie die Enigma gebrochen wurde“) fordert der Autor Sir Dermot Turing, Neffe von Alan Turing, den Leser auf:
“Imagine a counterfactual history in which the British had not been able to decipher Enigma messages during the Battle of Britain, the naval war in the Mediterranean, the early years of the Battle of the Atlantic, or in the campaign in the Western Desert. Such a scenario is frightening, as it would be a history that depicts not just a longer, drawn-out war but potentially one with a quite different outcome.”
„Stellen Sie sich eine kontrafaktische Geschichte vor, in der die Briten die Enigma-Sprüche während der [Luft-]Schlacht um England, des Seekriegs im Mittelmeer, der frühen Jahre der Atlantik-Schlacht oder im [Afrika-]Feldzug in der [Libyschen] Westlichen Wüste nicht hätten entziffern können. Ein solches Szenario ist beängstigend, denn es wäre eine Geschichte, die nicht nur einen längeren, langwierigen Krieg darstellt, sondern möglicherweise einen Krieg mit einem ganz anderen Ergebnis.“
Die Betrachtung alternativer Geschichtsverläufe ist zwangsläufig höchst spekulativ. Entscheidend ist natürlich auch der Zeitpunkt, zu dem die Enigma möglicherweise einbruchssicher gemacht worden wäre. Falls dies erst im Jahr 1945 geschehen wäre, hätte es vermutlich nur geringe Konsequenzen auf den Kriegsverlauf gehabt. Im Jahr 1944 dagegen wären die alliierten Invasionspläne der Operation Overlord („D‑Day“) behindert worden. Wie man heute weiß, war aus entzifferten Enigma-Funksprüchen nicht nur die gesamte deutsche Gefechtsaufstellung in der Normandie detailliert bekannt,[145] sondern die alliierten Befehlshaber wurden dank Ultra auch jeden Tag äußerst präzise über die deutschen Pläne und Gegenmaßnahmen auf dem Laufenden gehalten.[146] In den Jahren ab 1941 wären die deutschen U‑Boote nicht mehr so leicht zu finden gewesen, deren Positionen und Pläne die Alliierten aus entzifferten Funksprüchen genau verfolgen konnten.[147]
Was aber wäre gewesen, wenn die Enigma von Anfang an unknackbar geblieben wäre? Im Jahr 1940 beispielsweise setzte die Royal Air Force ihre letzten Reserven ein,[148] um schließlich die Luftschlacht um England (Battle of Britain) zu gewinnen. Auch hierbei waren entzifferte Funksprüche, insbesondere über die Angriffspläne der deutschen Luftwaffe, eine große Hilfe.[149][150] Ohne diese Hilfe wäre die Luftschlacht eventuell verloren worden und das Unternehmen Seelöwe, also die deutsche Invasion Englands, hätte stattfinden können.[148] Wie es ausgegangen wäre, darüber lässt sich nur spekulieren: Denkbar wäre, dass nach einer deutschen Besetzung der britischen Inseln noch im Jahr 1940 der Krieg beendet gewesen wäre,[151] denn zu diesem Zeitpunkt befanden sich weder die Sowjetunion noch die Vereinigten Staaten im Krieg. (Der deutsche Überfall auf die Sowjetunion begann am 22. Juni 1941. Der japanische Angriff auf Pearl Harbor fand am 7. Dezember 1941 statt und die Kriegserklärung Deutschlands an die USA erfolgte am 11. Dezember 1941.) Wie sich die Weltgeschichte in einem solchen Fall weiterentwickelt hätte, kann niemand sagen, denn die Geschichte verrät uns ihre Alternativen nicht. In einem Essay, das David Kahn als kontrafaktische Geschichte unter der Annahme verfasste, den Alliierten sei es nicht gelungen, die Enigma zu knacken, führt es zu einem weiteren Siegeszug der Wehrmacht, der schließlich durch eine Atombombe abrupt beendet wird.[152] Das alles sind Spekulationen – deutlich wird allerdings die enorme Bedeutung der Kryptographie und der Kryptanalyse der Schlüsselmaschine Enigma für den Verlauf der Geschichte.
Besonders bemerkenswert ist die Tatsache der perfekt funktionierenden Geheimhaltung der in Bletchley Park durchgeführten Enigma-Entzifferungen und der daraus gewonnenen Ultra-Informationen. Churchill selbst würdigte seine verschwiegenen Codebreakers mit den Worten „My geese that laid the golden eggs and never cackled“ (deutsch „Meine Gänse, die die goldenen Eier legten und niemals gackerten“).[153] Dieses „Enigma-Geheimnis“ wurde während des gesamten Krieges und selbst danach bis in die 1970er-Jahre gehütet (Britain’s best kept secret, deutsch „Britanniens bestgehütetes Geheimnis“).[154] Die Deutschen hatten keinerlei Ahnung von Ultra.[155] In Bletchley Park gab es keinen Maulwurf – mit einer Ausnahme, John Cairncross,[156] aber der spionierte für die Sowjetunion.[157]
Aufgrund verschiedener verdächtiger Ereignisse wurden auf deutscher Seite zwar mehrfach Untersuchungen angestellt, ob die Enigma wirklich sicher sei, hier wurden jedoch die falschen Schlussfolgerungen gezogen und die Fachleute mit der richtigen Einschätzung setzten sich nicht durch.[158][159] Auch die Zersplitterung der deutschen Dienste – im Gegensatz zu der in B.P. konzentrierten Kompetenz – ist sicherlich ein Grund für das Nichterkennen der Sicherheitslücken der Maschine.[160] Nebeneinander existierten in Deutschland die teilweise rivalisierenden kryptologischen Dienststellen, wie die Chiffrierabteilung des Oberkommandos der Wehrmacht (OKW/Chi), der General der Nachrichtenaufklärung (OKH/GdNA) im Oberkommando des Heeres, der B‑Dienst (Beobachtungsdienst) der Kriegsmarine, das Forschungsamt (FA) der Luftwaffe sowie das Amt IV E im Reichssicherheitshauptamt (RSHA).
Ein kurz nach dem Krieg verfasster Bericht der amerikanischen Army Security Agency erwähnt, dass der deutsche Befehlshaber der U‑Boote (BdU) Admiral Karl Dönitz den wahren Grund für den noch vor Juli 1942 zum Greifen nahen Sieg[147] und der nur wenige Monate darauf verlorenen Schlacht im Atlantik niemals verstanden hat:
“It was never realized that cryptanalysis, rather than radar and direction finding, disclosed the positions and intentions of the German submarines.”
„Es wurde zu keinem Zeitpunkt erkannt, dass die Kryptanalyse und nicht die Radartechnik oder die Funkortung die Positionen und Absichten der deutschen U‑Boote aufdeckte.“[147]

Dabei wäre es für die Deutschen durchaus nicht schwierig gewesen, die Sicherheit ihrer Maschine zu überprüfen. So schlägt der britische Historiker Hugh Sebag-Montefiore als Test vor, eine mit der Enigma wie üblich verschlüsselte Nachricht zu versenden, in der als Täuschungsmanöver beispielsweise ein Treffen deutscher U‑Boot-Tanker an einem entlegenen Ort auf See vereinbart wird, der normalerweise nicht von alliierten Schiffen aufgesucht wird. Falls nun zu dem im Funkspruch angegebenen Zeitpunkt plötzlich alliierte Kriegsschiffe am vereinbarten Treffpunkt erscheinen sollten, hätte es den Deutschen ziemlich schnell klar werden können, dass ihre Maschine tatsächlich kompromittiert war.[161]
Gegen Kriegsende wurden Tausende von Enigma-Maschinen zerstört, vergraben oder versenkt, um zu verhindern, dass sie „in Feindeshand“ gerieten. Gemäß dem „Regenbogen-Befehl“ der Kriegsmarine waren beispielsweise sogar U‑Boote selbstzuversenken, um sie nicht dem Feind übergeben zu müssen. Von Zeit zu Zeit werden solche Relikte gefunden. Beispielsweise wurde Ende 2020 berichtet, dass ein Enigma-Exemplar vom Meeresgrund der Geltinger Bucht geborgen werden konnte,[162] und im Januar 2021 wurden in der Nähe von Schleimünde gleich sechs beschädigte Exemplare ebenfalls aus der Ostsee gehoben.[163][164]
Nach dem Krieg wurden die in Stückzahlen von mehreren Hunderten,[165] möglicherweise Tausenden,[166] erbeutete und auch nachgebaute Enigma-Maschinen vor allem von den Westmächten an Verbündete oder befreundete Nationen verkauft oder verschenkt. So boten die Briten dem im Jahr 1948 neu gegründeten Staat Israel 30 Stück der zu dieser Zeit allgemein noch als „hochsicher“ und „unknackbar“ geltenden deutschen Verschlüsselungsmaschine an. Die Israelis waren hocherfreut über dieses wertvolle Geschenk und begannen, die deutschen Maschinen für ihre Zwecke zu modifizieren. Sie verbesserten die kryptographische Sicherheit und kombinatorische Komplexität der Enigma und ersetzten bei Tastatur, Lampenfeld, Steckerbrett und Walzensatz das lateinische Alphabet durch hebräische Buchstaben. Sie verzichteten jedoch schließlich auf den Einsatz dieser nun israelischen Enigma-Maschinen, nachdem sie durch den britisch-jüdischen Mathematiker Joseph Gillis (1911–1993), der in Bletchley Park mitgearbeitet hatte, einen subtilen Hinweis erhalten hatten.[167] In Korea,[168] in ehemaligen britischen Kolonien und Protektoraten sowie einigen afrikanischen Staaten wurden Enigmas teilweise noch bis 1975 genutzt,[169] wodurch es den Westmächten gelang, deren Nachrichtenverkehr mitzulesen.[166] Die wenigen heute noch existierenden intakten Exemplare – man schätzt, dass es noch rund 400 Exponate[170] in Museen oder bei privaten Sammlern gibt – werden zu Liebhaberpreisen im fünf- und sogar sechsstelligen[171] Bereich gehandelt. Im Jahr 2017 wurde bei Christie’s, einem der weltweit führenden Auktionshäuser für Kunst und Antiquitäten, eine aus dem Kriegsjahr 1944 stammende Enigma‑M4 für die rekordverdächtige Summe von 547.500 $ (rund 500.000 €) versteigert.[172]
Verbesserungspotenzial

Schon 1883 formulierte der niederländische Kryptologe Auguste Kerckhoffs unter der später (1946) explizit von Shannon angegebenen Annahme „the enemy knows the system being used“ (deutsch „Der Feind kennt das benutzte System“)[174] seine für seriöse Kryptographie bindende Maxime.[175]
- Kerckhoffs’ Prinzip: Die Sicherheit eines Kryptosystems darf nicht von der Geheimhaltung des Algorithmus abhängen. Die Sicherheit gründet sich nur auf die Geheimhaltung des Schlüssels.
Die kryptographische Sicherheit der Enigma hing – im Widerspruch zu Kerckhoffs’ Maxime – wesentlich von der Geheimhaltung ihrer Walzenverdrahtung ab. Diese war vom Benutzer nicht veränderbar, somit ein Teil des Algorithmus und nicht des Schlüssels. Bemerkenswert ist, dass die Walzenverdrahtung seit den Anfängen in den 1920er-Jahren bis 1945 bis auf ganz wenige Ausnahmen, genannt „Sonderschaltungen“,[176] nicht verändert wurde. Unter den üblichen Einsatzbedingungen einer so weit verbreiteten Schlüsselmaschine wie der Enigma darf man nicht annehmen, dass deren algorithmische Bestandteile auf Dauer geheimgehalten werden können, auch wenn die Deutschen es versucht haben.
Eine erste Möglichkeit zur Verbesserung der Enigma wäre somit das beispielsweise jährliche vollständige Auswechseln des Walzensortiments, mit jeweils radikal geänderter Verdrahtung, gewesen, ähnlich wie es die Schweizer mit ihrem Modell K machten.[177] Noch wesentlich wirkungsvoller wären Walzen, deren innere Verdrahtung schlüsselabhängig variabel gestaltet werden könnte. Interessanterweise gab es hierzu einen Ansatz, nämlich die Umkehrwalze D (britischer Spitzname: Uncle Dick),[178] die genau diese Eigenschaft aufwies, jedoch erst spät (Jan. 1944)[29] und nur vereinzelt zum Einsatz kam. Diese „stöpselbare Umkehrwalze Dora“, wie sie von deutscher Seite mithilfe des damals gebräuchlichen Buchstabieralphabets bezeichnet wurde, ermöglichte eine frei wählbare Verdrahtung zwischen den Kontaktstiften und somit eine variable Verbindung zwischen Buchstabenpaaren.

Wesentliche kryptographische Stärkungen der Enigma wären im Konstruktionsstadium leicht möglich gewesen. In erster Linie hätte man die Beschränkung auf fixpunktfreie Permutationen vermeiden müssen. Auch die Involutorik (Verschlüsseln = Entschlüsseln), zwar bequem für die Bedienung, schwächte die Maschine enorm. Beides wäre vermieden worden, hätte man auf die Umkehrwalze verzichtet.
Bereits eine frühe Vorläuferin der Enigma I, gemeint ist die aus dem Jahr 1929 stammende Enigma‑H, die von der Reichswehr und später auch von der Wehrmacht als Enigma II bezeichnet wurde, verfügte über acht nebeneinander fest angeordnete (nicht austauschbare) Walzen und einen allein durch die Walzenstellung einstellbaren Schlüsselraum von mehr als 200 Milliarden.[179] Verglichen mit den nur 17.576 Walzenstellungen der Enigma I bietet sie eine erheblich größere kombinatorische Komplexität. Zudem verfügte dieses frühe Enigma-Modell über keine Umkehrwalze, hatte also auch nicht deren Schwächen. Hätte man diese Grundkonstruktion mit acht (statt nur drei) Walzen auf die Enigma I übertragen und zusätzlich wie dort die Lage der Walzen austauschbar gestaltet, hätte dies bei acht Walzen 8! = 40.320 (statt nur 60) Walzenlagen und in Kombination mit den Walzenstellungen einen kryptographisch wirksamen Schlüsselraum von 8.419.907.243.704.320 (mehr als acht Billiarden oder knapp 53 bit) ergeben. Im Vergleich zu den nur gut eine Million (etwa 20 bit) kryptographisch wirksamen Möglichkeiten der tatsächlich realisierten Enigma wäre so eine deutlich stärkere Maschine entstanden, die trotz der vielen Fehler auf deutscher Seite und des gigantischen Aufwands auf britischer Seite vermutlich nicht hätte gebrochen werden können. Allerdings wäre eine solche Maschine mit acht Walzen weniger handlich gewesen als die Enigma mit nur drei Walzen.
Scherbius hatte in seinem grundlegenden Patent vom 23. Februar 1918 sogar schon zehn Walzen und die (bereits ohne Austauschen) daraus resultierenden rund 100 Billionen Schlüssel angegeben,[180] außerdem keine Umkehrwalze, sondern einen Umschalter zur Einstellung von Ver- und Entschlüsselung, sowie eine über Getriebe einstellbare unregelmäßige Weiterbewegung der Walzen vorgeschlagen – sämtlich gute Ideen und kryptographisch starke Konstruktionsmerkmale, die jedoch im Laufe der Zeit in Vergessenheit gerieten. Der Gründungspräsident des Bundesamts für Sicherheit in der Informationstechnik (BSI), der promovierte Mathematiker und Kryptologe Otto Leiberich meinte im Jahr 2001, mit vier Walzen „und mit einem ungleichförmigen Antrieb wäre die Enigma nie entziffert worden.“[181]
_4.jpg.webp)
Ein Beispiel für die Stärke dieser Ideen ist die Schlüsselmaschine Sigaba. Dabei handelt es sich um eine amerikanische Rotor-Maschine ähnlich wie die Enigma und ebenso aus dem Zweiten Weltkrieg, die jedoch über keine Umkehrwalze, sondern fünf Chiffrierwalzen (cipher rotor bank, deutsch „Chiffrierwalzensatz“) verfügt und zusätzlich zweimal fünf weitere Walzen (control rotor bank und index rotor bank, deutsch „Steuerwalzensatz“ und „Indexwalzensatz“) aufweist, die allein zur Erzeugung einer unregelmäßigen Fortschaltung der Chiffrierwalzen dienen. Die Sigaba erzeugt sowohl Fixpunkte als auch nichtinvolutorische Permutationen und konnte zu keinem Zeitpunkt, weder von deutschen noch von japanischen Kryptoanalytikern, noch von den Amerikanern selbst, die dies probeweise versuchten,[182] gebrochen werden.[49]
Eine sehr einfache Möglichkeit, die Enigma sicherer zu gestalten, ist die Verwendung von mehr als einer Übertragskerbe. Diese Kerben sind Bestandteil jeder Walze und bewirken den Übertrag auf die nächste, im Walzensatz weiter links liegende Walze und sorgen so für die Fortschaltung der Rotoren. Den Codeknackern kam es sehr gelegen, dass sie 26 Buchstaben lang davon ausgehen konnten, dass allein die rechte Walze rotierte und erst dann eine Fortschaltung auf den mittleren Rotor passierte. Für relativ lange Textpassagen besteht die Enigma somit aus Sicht des Kryptoanalytikers nur aus einer einzigen sich drehenden (rechten) Walze und einer, aus mittlerer und linker Walze sowie der Umkehrwalze bestehenden, sozusagen besonders dicken (feststehenden) Umkehrwalze. Erst der Übertrag auf die mittlere Walze stört dies. Hätten die Walzen der Enigma über mehr als nur eine einzige Übertragskerbe verfügt, beispielsweise neun, wie bei der britischen Schlüsselmaschine Typex,[183] so hätte sich für den Anwender praktisch nichts geändert, die Kryptanalyse jedoch wäre durch das dann häufigere Weiterschalten der mittleren und der linken Walze stark gestört worden.

Peter Twinn, einer der Mitarbeiter Turings in Bletchley Park, kommentierte es mit den Worten „they certainly missed a trick in not combining multiple-turnover wheels with Steckerverbindungen“ (deutsch „sie [die Deutschen] verpassten sicherlich einen Kniff dadurch, dass sie nicht Walzen mit mehreren Übertragskerben und die Steckerverbindungen kombinierten“).[184] Gordon Welchman unterstrich die Folgen dieses deutschen Fehlers: „We would have been in grave trouble if each wheel had had two or three turnover positions instead of one“ (deutsch „Wir hätten gravierende Probleme bekommen, wenn jede Walze zwei oder drei Übertragskerben gehabt hätte statt [nur] eine“).[51] Die Typex erwies sich nicht zuletzt auch durch ihre im Vergleich zur Enigma größeren Anzahl an Übertragskerben für OKW/Chi, die Chiffrierabteilung des OKW, als unknackbar.[185]
Vielleicht fürchteten die Entwickler der Enigma eine Reduzierung der Periode, das ist die Anzahl der Zeichen, nach der sich das zur Verschlüsselung verwendete Alphabet wiederholt. Die Periode beträgt bei der Enigma I 26·25·26 = 16.900,[186] wobei der Faktor 25 bei der mittleren Walze durch die bereits erwähnte (unwichtige) Anomalie des Fortschaltmechanismus verursacht wird.[187] Bei Verwendung einer geraden Anzahl oder von dreizehn Übertragskerben statt nur einer würde die Periode tatsächlich drastisch absinken, da diese Zahlen gemeinsame Teiler mit 26 aufweisen. Bei zum Beispiel drei, fünf, sieben, neun oder elf Kerben hingegen besteht diese Gefahr nicht, da diese Zahlen zu 26 teilerfremd sind. Interessanterweise wurden bei der Marine, in Ergänzung zu den von der Enigma I bekannten fünf Walzen, drei weitere Walzen eingesetzt (VI, VII und VIII), die mehr als eine, nämlich zwei Übertragskerben aufweisen. Die exklusiv von der Marine verwendeten drei Walzen vermieden außerdem einen weiteren Fehler der fünf Walzen der Enigma I, denn sie hatten ihre Übertragskerben alle bei identischen Buchstaben. Nicht so die Walzen I bis V, die sich durch den bei unterschiedlichen Buchstaben erfolgenden Übertrag verrieten. Die Codeknacker hatten sich dafür den (sprachlich unsinnigen) Merkspruch „Royal Flags Wave Kings Above“ gebildet, der für die Walzen I bis V in dieser Reihenfolge den jeweiligen Buchstaben nennt, der stets im Sichtfenster erscheint, nachdem ein Übertrag auf die nächste Walze erfolgt ist.[188]
Eine bedeutende Innovation, die die kryptographische Sicherheit der Enigma erheblich verbessert hätte, die aber zu spät kam, um während des Krieges noch eingesetzt werden zu können, waren die sogenannten „Lückenfüllerwalzen“ (Foto siehe unter Weblinks). Diese neuartigen Rotoren erlaubten es „an jeder Walze Schaltlücken beliebig nach Art und Zahl einzustellen“.[189] Die Einstellungen hätten schlüsselabhängig verändert werden können und so wesentlich zur kryptographischen Stärkung der Maschine beigetragen. Im Juli 1944 erhielt das Ertel-Werk in München einen Fertigungsauftrag über 8000 Stück Lückenfüllerwalzen, der kurz darauf auf 12.000 Stück erhöht wurde.[190] Kriegsbedingt konnten jedoch nur wenige hergestellt und keine mehr ausgeliefert werden. Das amerikanische Target Intelligence Committee (TICOM) konfiszierte gegen Ende des Krieges sämtliche Informationen über die Lückenfüllerwalze und hielt sie für viele Jahre sorgsam unter Verschluss.[191] Falls sie in ausreichender Stückzahl hätte gefertigt und eingesetzt werden können, so wären die britischen Codeknacker vermutlich aus dem Rennen gewesen, insbesondere, wenn es, wie geplant, gelungen wäre, die Lückenfüllerwalze in Kombination mit der Umkehrwalze D einzusetzen.[192]

Die deutsche Abwehr (Geheimdienst) verwendete ein Enigma-Modell (G), das über einen exklusiven Walzensatz verfügte, bei dem die (drei) Walzen tatsächlich mehrere Übertragskerben aufwiesen, nämlich 11, 15 beziehungsweise 17 Kerben.[25] Selbst die Umkehrwalze war – im Unterschied zu den anderen Enigma-Modellen – drehbar und rotierte mit. Dies stärkte die Verschlüsselung und sorgte sicher auch dafür, dass andere deutsche Stellen nicht mitlesen konnten. Allerdings verzichtete die Abwehr bei dieser besonders kompakten (äußere Abmessungen 270 mm × 250 mm × 165 mm) und handwerklich hervorragend gebauten Enigma auf ein Steckerbrett.[193] Die Folge war, dass es den Codebreakers von Bletchley Park, an der Spitze „Dilly“ Knox und seine Mitarbeiterinnen Margaret Rock und Mavis Lever, in B.P. als „Dilly’s girls“ hochgeachtet,[194] am 8. Dezember 1941 gelang, auch diese Verschlüsselung zu überwinden[195][196] und so dazu beizutragen, dass deutsche Agenten bereits bei ihrer Einreise „in Empfang genommen“ werden konnten. Diese wurden anschließend nicht einfach nur eliminiert, sondern es gelang dem britischen Inlandsgeheimdienst MI5, viele von ihnen „umzudrehen“ und im Rahmen des Systems Double Cross (deutsch „Doppelkreuz“, aber auch: „Doppelspiel“) als Doppelagenten einzusetzen.[197] Zusammen mit den aus Enigma‑G-Sprüchen entzifferten Informationen erhielt der MI5 ein so detailliertes und zutreffendes Bild über die Pläne und den Wissensstand der Abwehr, dass jeder einzelne noch in Großbritannien operierende deutsche Agent genau bekannt war und gezielt kontrolliert und manipuliert werden konnte. Dies wurde auch zur Desinformation der deutschen Führung genutzt (siehe auch: Operation Fortitude).
Zusammenfassend können folgende Punkte zur kryptographischen Stärkung der Enigma festgehalten werden, deren Umsetzung noch vor oder während des Krieges möglich gewesen wäre und die leicht dazu hätten führen können, dass die Enigma sich plötzlich „außerhalb der Reichweite der bereits stark gedehnten anglo-amerikanischen kryptanalytischen Finger befunden hätte, was möglicherweise den Verlauf des Krieges verändert hätte“ (englisch „Improvement in anyone of the foregoing particulars could easily have pushed the plug-board Enigma beyond the reach of already-straining Anglo-American cryptanalytic fingers, and possibly altered the course of the war“):[198]

- identische Verschlüsselung zulassen
- Involutorik vermeiden
- mehrere (z. B. neun) Übertragskerben anbringen
- Übertragskerben für alle Walzen identisch anordnen
- einstellbare Übertragskerben verwenden (Lückenfüllerwalzen)
- mehr als drei Walzen einbauen (z. B. sechs wie beim SG‑41)
- Walzensortiment erweitern (z. B. zehn statt nur fünf)
- frei verdrahtbare stöpselbare Umkehrwalze (UKW Dora)
- Walzenverdrahtung gelegentlich radikal ändern
- nicht involutorische Stecker verwenden

Eine verblüffend einfache und dabei durchschlagend wirksame Maßnahme, die laut Gordon Welchman zu jedem beliebigen Zeitpunkt ganz leicht hätte eingeführt werden können und die er während des Krieges am meisten befürchtet hatte, ist die Verwendung von einpoligen Steckerverbindungen anstelle der doppelpoligen involutorischen Kabel.[51] Dann könnte man beispielsweise X mit U steckern und U nun aber nicht notwendigerweise mit X, sondern mit irgendeinem anderen beliebigen Buchstaben. So hätte schlagartig die Involutorik des Steckerbretts – wenn auch nicht der ganzen Maschine – beseitigt werden können. Dies hätte nach Welchman katastrophale Auswirkungen für die Codeknacker in Bletchley Park gehabt. Ein Großteil der dort erarbeiteten Methodik inklusive des von Welchman selbst erfundenen diagonal board (deutsch Diagonalbrett) wäre nutzlos geworden.[199][200] Er schreibt „the output of Hut 6 Ultra would have been reduced to at best a delayed dribble, as opposed to our up-to-date flood.“[142] (deutsch „der Ertrag der Ultra-Informationen aus Baracke sechs hätte sich im besten Fall auf ein verspätetes Tröpfeln reduziert, im Gegensatz zu unserer tagesaktuellen Flut.“)
Modelle



Eine grobe Übersicht der verwirrenden Modellvielfalt der Enigma[201] zeigt die folgende Tabelle (siehe auch: Stammbaum der Enigma unter Weblinks). Neben dem Modellnamen ist das Jahr der Indienststellung, die Walzenanzahl sowie die daraus resultierende Anzahl der möglichen Walzenlagen angegeben. Ferner ist die Anzahl und die Art der Umkehrwalze (UKW) notiert, wobei zwischen fest eingebauten UKW sowie manuell einstellbaren, also „setzbaren“ UKW und rotierenden UKW unterschieden werden muss, also UKW, die während des Verschlüsselungsvorgangs weiterrotieren. Ein Beispiel dafür ist die (weiter oben) beschriebene Enigma‑G der Abwehr. Einige frühe Maschinen, wie die „Handelsmaschine“ von 1923 und die „Schreibende Enigma“ von 1924, verfügten über keine UKW. Ferner ist die Anzahl der Übertragskerben angegeben sowie eine Literaturstelle als Referenz und für weitere Informationen.
| Modell | Jahr | Walzen | Lagen | UKW | Kerben | Ref |
|---|---|---|---|---|---|---|
| Enigma I | 1930 | 3 aus 3 (5) | 6 (60) | 1 (3) fest | 1 | Kruh 11[202] |
| Enigma II | 1929 | 8 | 1 | 1 fest | siehe Enigma H | |
| Enigma-A | 1924 | 2 | 1 | 1 rotiert | Crypto Museum[203] | |
| Enigma-B | 1924 | 2 bzw. 3 | 1 | 1 fest | Crypto Museum[204] | |
| Enigma-C | 1925 | 3 | 1 | 1 fest | 1 | Kruh 5ff[205] |
| Enigma-D | 1926 | 3 | 1 | 1 setzbar | 1 | Bauer 114[206] |
| Enigma-G | 1936 | 3 aus 3 | 6 | 1 rotiert | 11, 15, 17 | Hamer[207] |
| Enigma-H | 1929 | 8 | 1 | keine | Crypto Museum[208] | |
| Enigma-K | 1936 | 3 aus 3 | 6 | 1 setzbar | 1 | Hamer 10ff[209] |
| Enigma-M1 | 1934 | 3 aus 6 | 120 | 1 fest | 1 | Pröse 50[210] |
| Enigma-M2 | 1938 | 3 aus 7 | 210 | 1 fest | 1 | Pröse 50[210] |
| Enigma-M3 | 1939 | 3 aus 8 | 336 | 1 fest | 1 (2) | – |
| Enigma-M4 | 1942 | 4 aus 8+2 | 1344 | 2 setzbar | 1 (2) | Erskine & Weierud 50[211] |
| Enigma-T | 1942 | 3 aus 8 | 336 | 1 setzbar | 5 | Girard[212] |
| Enigma-Z | 1931 | 3 aus 3 | 6 | 1 rotiert | 1 | Wik[213] |
| Handelsmaschine | 1923 | 4 | 1 | keine | Getriebe | Kruh 2[179] |
| Probemaschine | 1918 | 2 bis 7 | 1 | keine | Getriebe | Scherbius[6] |
| Schreibende Enigma | 1924 | 2 mal 4 | 1 | keine | Getriebe | Pröse 50[210] |
Neben den meistverwendeten Modellen Enigma I, Enigma‑M3 und Enigma‑M4 sowie deren Vorläuferinnen Enigma‑A bis Enigma‑D und den bereits genannten Enigma‑G und Enigma‑K ist noch die Enigma‑T erwähnenswert, die speziell für den Nachrichtenverkehr der beiden Kriegsverbündeten Deutschland und Japan konzipiert war. Sie wurde nach dem deutschen Großadmiral der früheren Kaiserlichen Marine Alfred von Tirpitz (1849–1930) auch als „Tirpitz-Maschine“ bezeichnet und verfügte über kein Steckerbrett, aber über eine „setzbare“ (einstellbare, jedoch nicht rotierende) Umkehrwalze und insgesamt acht Walzen mit jeweils fünf Übertragskerben (siehe auch: Enigma-Walzen), von denen drei ausgewählt wurden.[212] Die Enigma‑T kam kaum zum Einsatz.[214] Nicht verwechselt werden darf sie mit dem in Japan entwickelten Enigma-Nachbau, der San-shiki Kaejiki.
Ein Kuriosum stellt die Enigma-Z dar, die dem spanischen Außenministerium im Jahr 1931 zum Kauf angeboten wurde. Bei ihr handelt es sich um eine Variante ähnlich der Enigma‑D, die jedoch keinerlei Buchstabentasten, sondern allein zehn Zifferntasten („1“ bis „0“) und entsprechend (kleinere) Walzen mit nur zehn Kontakten und zehn Glühlampen für „1“ bis „0“ aufweist.[213] Sie war also nicht zur Verschlüsselung von Texten, sondern nur von Zahlen gedacht, wie zur Überschlüsselung von diplomatischen Codes. So konnte beispielsweise die Ziffernfolge „25183 91467“ als „38760 15924“ verschlüsselt werden. Die Spanier verzichteten damals auf den Erwerb der Enigma‑Z und entschieden sich stattdessen für die noch weniger sichere Kryha.[215]
Anomalie
Der Fortschaltmechanismus der Walzen weist eine konstruktive Besonderheit auf,[187][216] die zur Folge hat, dass sich die Walzen der Enigma nicht immer so weiterdrehen, wie es bei einem mechanischen Kilometerzähler der Fall wäre. Diese Besonderheit äußert sich so, dass die linke (langsame) Walze bei ihrem Fortschalten stets die mittlere Walze „mitnimmt“. Dies lässt sich an einem Beispiel illustrieren.

Bei beispielsweise Walzenlage B I II III, Ringstellung 01 01 01 und der Walzenstellung ADU dreht sich der Walzensatz mit dem ersten Tastendruck auf ADV weiter. Das ist eine ganz normale Weiterdrehung nur der rechten Walze, ohne Weiterschaltung der mittleren oder der linken Walze. Nach der bekannten Merkregel „Royal Flags Wave Kings Above“ ist für Walze III mit dem nächsten Tastendruck, also wenn sie von V auf W weiterrotiert, mit einem Übertrag auf die mittlere Walze zu rechnen. Dann wird nicht nur die rechte Walze normal weiterrotieren, sondern gleichzeitig auch die mittlere Walze von D auf E umschalten. Die nächste Walzenstellung ist somit AEW.
Nun jedoch hat die mittlere Walze (hier: Walze II) den Buchstaben erreicht, nämlich E, der nach der Merkregel unmittelbar vor ihrem Umschaltbuchstaben F liegt. Damit ist jetzt der Moment gekommen, zu dem die mittlere Walze ihrerseits einen Übertrag auf die linke Walze bewirkt. Mit dem nächsten Tastendruck wird sich also die linke Walze von A auf B weiterdrehen. Aufgrund der erwähnten konstruktiven Besonderheit führt dieses Weiterdrehen jedoch dazu, dass sie die mittlere Walze mitnimmt und sich diese noch einmal weiterdreht, also von E auf F. Folglich werden mit dem nächsten Tastendruck alle drei Walzen gleichzeitig weitergeschaltet und nach der vorherigen Walzenstellung AEW sind nun unmittelbar die Buchstaben BFX in den Anzeigefenstern der Enigma zu sehen. Nach diesem etwas fremdartig erscheinenden Ereignis kehrt die Maschine wieder in den regulären Fortschaltmodus zurück, bis dann nach 650 Tastendrücken erneut die mittlere Walze den Buchstaben E erreicht. Unter Weblinks ist ein Video zu finden, das anhand eines Holzmodells die Walzenfortschaltung illustriert, insbesondere auch den anomalen Doppelschritt der mittleren Walze.
Zusammenfassend noch einmal das Weiterschalten des Walzensatzes. Man erkennt hier die Anomalie beim dritten Tastendruck, die sich als „Doppelschritt“ der mittleren Walze äußert (hier: D → E → F).
Anfangsstellung ADU 1. Tastendruck ADV 2. Tastendruck AEW 3. Tastendruck BFX ← Anomalie 4. Tastendruck BFY
In Summe führt dieser durch die Anomalie des Fortschaltmechanismus hervorgerufene Effekt des Doppelschritts der mittleren Walze dazu, dass von den theoretisch möglichen 26³ = 17.576 Walzenstellungen der Enigma I 26² = 676 ausgelassen werden und nur 26·25·26 = 16.900 übrig bleiben.
Authentische Funksprüche


Mit der Enigma verschlüsselte Nachrichten wurden im Regelfall per Funk übermittelt, nur selten als Fernschreiben oder telefonisch als „Fernspruch“ oder per Signallampe als „Blinkspruch“. Der Absender füllte ein Formular mit dem Klartext aus, das vom Verschlüssler als Grundlage für den mithilfe der Enigma-Maschine erzeugten Geheimtext diente. Diesen übertrug er Buchstaben für Buchstaben in ein entsprechendes Funkspruchformular (siehe auch: Dokumente unter Weblinks), das wiederum dem Funker als Basis für den im Morsecode übermittelten Funkspruch diente. Verfasser, Verschlüssler und Funker der Nachricht konnten drei verschiedene Personen sein oder auch ein und dieselbe.
Eine wichtige Kennzeichnung des Funkspruchs, die im Spruchzettel mit einem Buntstift besonders hervorgehoben wurde, war die „Spruchnummer“. Durch farbige Angabe der Nummer unterschieden die Deutschen zwischen „abgegangenen“, also den zu sendenden oder bereits gesendeten Funksprüchen, bei denen die Spruchnummer mit einem blauen Farbstift in das Formular eingetragen wurde, und „angekommenen“, also empfangenen Funksprüchen, bei denen die Nummer in Rot geschrieben wurde. Nur wenige der unzählig vielen während der Zeit des Krieges ausgefüllten Spruchzettel sind erhalten geblieben. Die überwiegende Mehrzahl wurde nach Empfang und Entschlüsselung der Nachrichten vernichtet.
Die zweite sehr wichtige Quelle für authentische Enigma-Sprüche stellen die reichhaltigen Aufzeichnungen der Alliierten dar. Insbesondere die Archive des damals weltweit arbeitenden britischen Y Service (deutsch: „Y‑Dienst“) sind prall gefüllt, bisher jedoch leider nur zu einem kleinen Teil öffentlich zugänglich. Das Bild zeigt eine der raren Ausnahmen aus dem Archiv des Dienstes in Bletchley Park. Das „Y“ steht im Englischen hier lautmalerisch für die Anfangssilbe des Wortes wireless (deutsch wörtlich: „drahtlos“, mit der Bedeutung: „Funk“). Eine sinngemäße Übersetzung von Y Service wäre somit „Funkabhördienst“.
Die unten wiedergegebenen Enigma-Funksprüche stammen aus freien Quellen. Die Geheimtexte sind inzwischen mithilfe moderner kryptanalytischer Methoden und Rechnertechnik entziffert worden.[217] Zu beachten ist, dass dies keine fiktiven Funksprüche sind, wie sie der Wettbewerb Enigma Cipher Challenge (siehe auch: Entzifferungen unter Weblinks) bietet, sondern dass es sich um Originalfunksprüche handelt, die im Zweiten Weltkrieg wirklich so aufgezeichnet worden sind. Es ist deshalb durchaus möglich (und hier auch der Fall), dass Verstümmelungen auftreten. Das bedeutet, dass einige Zeichen nicht korrekt sind oder fehlen. Dies betrifft sowohl die Buchstaben als auch die Zahlen. Letzteres kann sehr leicht gesehen werden. Dazu ist nur die Geheimtextlänge zu zählen und mit der im Spruchkopf angegebenen Zahl zu vergleichen. Gründe für in der Praxis kaum vermeidbare Verstümmelungen, die auch durch die kriegsbedingten besonderen Rahmenbedingungen erklärt werden können, sind Schreibfehler, Tastfehler, atmosphärische Störungen wie beispielsweise Gewitterblitze während der Funkübertragung, Hörfehler oder schlicht Flüchtigkeitsfehler. Ausgehende Funksprüche, die man auch durch den Eintrag im Feld „Befördert am…“ (und nicht „Aufgenommen am…“) identifizieren kann, sind naturgemäß weniger verstümmelt als die eingehenden und daher (bei gleicher Textlänge) zumeist einfacher zu knacken.
- 83 - ADJ JNA - LMHNX WEKLM UERDS EVHLC JSQQK VLDES ANEVT YEDGI ZQDOD RMDKG SXGSQ SHDQP VIEAP IENLI CLZCL LAGWC BJZD |
- 149 - TLS CMU - FTMKV DRJMG FBUDK LZCTR FLTUU IWVJL OYKYX GDCKJ TMDFB WNLZQ JAXHP GGKFG SBZOQ KQKUK TINMH BAJOO AUILA QVFTK LSTMM XGAQL CNHUW LFHKA ULTXT BIVIF EWWDY PUCNS TPJHR OBWHE KYUSB CANYC W |
- 167 - MRJ LLT - KLIBM ERJAR WMMHJ STHOY OOIQB HSSZU EOOKF TASXN XVYWE SCTCH NRNBL ZPEBH XPAQE DFNYS XHMNI HRARO UNBMD ZRZDN WTGUI UCBZN ZTFJA EKOMJ AZILN RKVFD UNIEW ILZVL KQYYJ ANKXG NNNHT EMAVD FXKAY MLWCV QDFWX LO |
- 186 - DOQ VHZ - PBNXA SMDAX NOOYH RCZGV VZCBI GIBGW HMXKR RVQCF JCZPT UNSWA DDSTI GQQCS AGPKR XXLOM GFXAP HHMRF SDKYT MYPMV ROHAS QYRWF WVAVG CCUDB IBXXD YZSAC JSYOT MWUCN WOMHH JPYWD CCLUP GSWCL MBCZS SYXPG MGMQX AUFUL NOZEQ ENHEI ZZAKL C |
- 195 - EHW TNH - ABTWU GWDMP OGKMQ KBHGK HROUP RMYQY INHSA MWFBP CDQRG LDBFK YNXPP DIQHE AOIFQ AOLRZ ZFPDJ MCGEC TAHHQ MVUYA JIAWM WSOYU UTLEP AVZKG HJWCD LOQHW IMSTC LQDNP VCFCN FRUYR GSSJH ORQMU IFFYU WYNTA XPYIX MYTEE FTDCV EHUOA DCPLM APCAU JJYUK |
- 232 - KPL ZFT - IKPKE WZVTB TXWID JCJAN MPWQZ RKUGF TBBAL IERPD BCDVM ARZEL XXWKF ABVKI WFXDV HJGRR CUCQN YQGAE PNOYN LIYLC DGKYL TXTYP IVDGP YMZLY UXWQS FQLCB DELAN PXXWH TDMNQ ENFWA TJVHO EUPGO CQJCF WSLJR EJJFL TJFJT UIYKT |
- 241 - SDV RUD - TAZUK DVNNF AZOUV YYSXO ZLRJO TMMXK AWPVU TTUXS LAQOX GQUKX XKXAL URHGR SUOHD FJTRE TLFKD MGDXE MWIXX INTLG EDKVL RTJFX RFOIE NNIRR WFKTI BVFVE LLAWR GJNVB YHBZS CJVTZ PDBGV PBNNA LNAKX OUOJG WLJXO UXHDS HXJOU HVBVF DOLMN LYNVC MRGKK YTOCP DUEVN FMIPT GGJYA YBDES P |
- 272 - PPS QJH - QSDCK HQOGN OSAIC GADNM PJIAI NPWBM VLTKQ YUDII GWSHT TZEYE CCHFJ CNYBC HXZNE KOOMV SOLLS NDDGR RXPMS GFOPY SJFSY SBYBS CSKDP IOBQM HSFKV MCSMD HYJNO CHB |
Filmische Rezeption



Die Enigma ist in einigen Spielfilmen zu sehen, die vor dem Hintergrund des U‑Boot-Krieges spielen. Im deutschen Kinoklassiker „Das Boot“ nach dem gleichnamigen Roman[218] wird sie zur Entschlüsselung empfangener Funksprüche benutzt. Man hört die Stimme von Herbert Grönemeyer sagen „Erst durch die Schlüsselmaschine ergibt sich aus wirren Buchstabenfolgen ganz langsam ein Sinn“, während in Großaufnahme die Enigma im Einsatz zu sehen und auch zu hören ist. Historisch nicht ganz korrekt ist hier die Verwendung einer M4, da sie erst am 1. Februar 1942 in Dienst gestellt wurde, während das Boot in Roman und Film seine Feindfahrt im Herbst und frühen Winter des Jahres 1941 durchführt. Somit hätte korrekterweise eine M3 gezeigt werden müssen.
Im amerikanischen Film „U‑571“ wird eine Enigma durch amerikanische Seeleute von einem deutschen U‑Boot erbeutet. Speziell von britischer Seite wurde kritisiert, dass, in Verkennung der geschichtlichen Realität, hier Amerikaner als Helden bei der Erbeutung einer Enigma dargestellt werden, während es in Wirklichkeit Briten waren, denen dies gelang.[219]
Die britisch-amerikanische Gemeinschaftsproduktion „The Imitation Game – Ein streng geheimes Leben“ illustriert das Leben und die Beiträge von Alan Turing als Codeknacker in Bletchley Park. Auch hier spielt die Enigma eine zentrale Rolle. Auf Kosten der historischen Korrektheit werden im Film viele Fakten verdreht oder dramatisch überhöht dargestellt.[220] Beispielsweise wird Turings Romanze mit seiner Kollegin Joan Clarke intensiver dargestellt als sie tatsächlich war. Turings Nichte Inagh Payne kritisierte das Drehbuch mit den Worten: „You want the film to show it as it was, not a lot of nonsense“[221][222] (deutsch: „Man will doch, dass der Film es so darstellt, wie es war, und nicht einen Haufen Unsinn“). Im Film findet Turing heraus, dass Cairncross ein Spion ist. Diesem gelingt es jedoch, Turing mit seiner damals strafbaren Homosexualität zu erpressen. So decken sie gegenseitig das Geheimnis des anderen. Diese Falschdarstellung wurde heftig kritisiert, denn so wird Turing im Film faktisch als „Landesverräter“ dargestellt. Tatsächlich stand er niemals unter diesem Verdacht. Bei aller Sympathie für Überhöhungen aus dramaturgischer Sicht wurde diese Darstellung als Herabwürdigung Turings energisch zurückgewiesen und der Film daher als untragbar eingestuft.[223]
Im britischen Spielfilm Enigma – Das Geheimnis, der auf dem Roman Enigma[224] basiert, wird die Entzifferungsarbeit der britischen Codebreaker in Bletchley Park thematisiert. Bemerkenswert sind die vielen authentischen Requisiten im Film, bei denen es sich um Original-Schaustücke aus dem Bletchley-Park-Museum handelt. Die diversen Funksprüche sind speziell für den Film nach den Original-Vorschriften und Verfahren wirklichkeitsgetreu erzeugt und verschlüsselt worden.[225] Gegen Ende des Films entpuppt sich ein polnischer Codeknacker als Verräter, der versucht, das „Enigma-Geheimnis“ an die Deutschen zu verraten. Dies entspricht in zweierlei Hinsicht nicht den historischen Tatsachen. Zum einen gab es – wie bereits dargelegt – keine Verräter in Bletchley Park, die für die Deutschen spioniert hätten. Zum anderen hat dort nicht ein einziger polnischer Kryptoanalytiker mitgearbeitet, denn aus Geheimhaltungsgründen verwehrten die Briten fast allen Ausländern, selbst Marian Rejewski, den Zutritt und erst recht die Mitarbeit.[226] Somit ist die filmische Darstellung in diesem Punkt historisch verfehlt. Kritisiert wurde insbesondere, ausgerechnet einen Polen im Film als Verräter darzustellen,[227] obwohl es ja gerade polnische Kryptoanalytiker wie Marian Rejewski, Jerzy Różycki und Henryk Zygalski waren, die bereits vor dem Krieg die entscheidenden Grundlagen für den Einbruch in das Rätsel der Enigma schufen,[228] ohne die es den britischen Codeknackern vermutlich nicht gelungen wäre, deutsche Funksprüche zu entziffern[229] und der Zweite Weltkrieg einen anderen Verlauf genommen hätte.[230]
Chronologie

_-_National_Cryptologic_Museum_-_DSC07787.JPG.webp)
Im Folgenden sind einige wichtige Zeitpunkte zur Geschichte der Enigma aufgelistet
(spezielle Zeitpunkte zur Marine-Version siehe M4):
| Datum | Ereignis |
|---|---|
| 23. Feb. 1918 | Erstes Patent zur Enigma[6] |
| 15. Apr. 1918 | Probemaschine |
| 9. Juli 1923 | Gründung der Chiffriermaschinen AG[4] |
| 21. März 1926 | Patentierung der Umkehrwalze (UKW)[26] |
| 15. Juli 1928 | Die Reichswehr führt eine Vorläuferversion der Enigma ein[231] |
| 9. Aug. 1928 | Das Steckerbrett wird von der Reichswehr exklusiv für die militärisch genutzten Maschinen eingeführt[232] |
| 1. Juni 1930 | Indienststellung der Enigma I (sechs Stecker und quartalsweise wechselnde Walzenlage)[231] |
| 1. Feb. 1936 | Monatlicher Wechsel der Walzenlage[233][29] |
| 1. Okt. 1936 | Täglicher Wechsel der Walzenlage und statt sechs nun fünf bis acht Stecker[29] |
| 1. Nov. 1937 | Ablösung der UKW A durch die UKW B[234][30] |
| 15. Sep. 1938 | Neues Indikatorverfahren (frei wählbare Grundstellung für die Spruchschlüsselverschlüsselung)[235] |
| 15. Dez. 1938 | Inbetriebnahme der Walzen IV und V[235] |
| 1. Jan. 1939 | Sieben bis zehn Stecker[236] |
| 26. Juli 1939 | Zweitägiges alliiertes Treffen bei Pyry[86] |
| 19. Aug. 1939 | Zehn Stecker[237] |
| 1. Mai 1940 | Fallenlassen der Spruchschlüsselverdopplung[44][17] |
| 1940/41 | Zeitweise Benutzung der UKW C (alternativ zur UKW B)[29] |
| 5. Okt. 1941 | Einführung des Schlüsselnetzes „Triton“ für die U‑Boote zunächst noch mit der M3 |
| 15. Okt. 1941 | Einführung des Schlüsselnetzes „Neptun“ für die Schlachtschiffe bereits mit der M4[238] |
| 8. Dez. 1941 | Erster Bruch der Abwehr-Enigma durch Dilly Knox[196] |
| 1. Feb. 1942 | Indienststellung der M4 nun auch für die U‑Boote[29] |
| 1. Sep. 1943 | Fallenlassen der Kenngruppe[43] |
| 1. Jan. 1944 | Vereinzelte Benutzung der steckbaren UKW D[239] |
| 10. Juli 1944 | Die Luftwaffe führt die „Uhr“ ein[240] |
| 15. Sep. 1944 | Beim Heer wird das CY-Verfahren eingeführt[241][242] |
Glossar
Im Zusammenhang mit der Arbeitsweise der Enigma und deren Kryptanalyse wird die folgende Fachterminologie verwendet:
- Alphabet – Eine in der Reihenfolge permutierte geordnete Anordnung von Symbolen, speziell der 26 lateinischen Großbuchstaben (Beispiel: E K M F L G D Q V Z N T O W Y H X U S P A I B R C J)
- B-Dienst – (Abkürzung für Beobachtungsdienst): Nachrichtendienst der deutschen Kriegsmarine im Zweiten Weltkrieg, der sich mit dem Abhören und Aufzeichnen sowie der Entzifferung und Deutung des feindlichen, insbesondere des britischen Funkverkehrs befasste
- Biuro Szyfrów – (Abkürzung: BS): Polnische Bezeichnung für das in Warschau gelegene „Chiffrenbüro“, in dem polnische Kryptoanalytiker ab 1932 die Enigma-Verschlüsselung brachen
- Bletchley Park – (Abkürzung: B.P.): Landsitz in der englischen Ortschaft Bletchley, der im Zweiten Weltkrieg die Zentrale der britischen Codebreaker war und heute ein Museum ist
- Bomba – (Plural: Bomby): Polnischer Name für die 1938 von Rejewski entwickelte kryptanalytische Maschine, mit der der Fehler der Spruchschlüsselverdopplung ausgenutzt wurde, um die Walzenlage und den Spruchschlüssel zu erschließen
- Bombe – (Plural: Bombes): Englischer Name für die 1939 von Turing ersonnene und von Welchman verbesserte kryptanalytische Maschine, durch die mithilfe von Cribs und unter Umgehung des Steckerbretts der Tagesschlüssel ermittelt wurde
- Chi – Kurzbezeichnung für die Chiffrierabteilung des Oberkommandos der Wehrmacht, also der Dienststelle, die sich mit der Entzifferung des gegnerischen Nachrichtenverkehrs und mit der Sicherheitskontrolle eigener Schlüsselverfahren befasste
- Chiffrat – Anderer Ausdruck für Geheimtext
- Chiffrieren – Anderer Ausdruck für Verschlüsseln
- Chi-Text – Anderer Ausdruck für Geheimtext
- Cillis – (nicht authentisch auch als „sillies“ (deutsch: „Dummchen“) bezeichnet):[243] Englischer Spitzname für die fehlerhafte Wahl der Grundstellung und des Spruchschlüssels aus benachbarten Buchstaben auf der Tastatur (Beispiel: QWE RTZ, siehe auch: Funkspruch und fehlerhafter Spruchkopf)
- Clash – (deutsch: Zusammenstoß): Englischer Fachbegriff für das wiederholte Auftreten derselben Walze in derselben Lage (am selben Platz) im Walzensatz an zwei aufeinanderfolgenden Tagen.[244]
- Click – Wiederholtes Auftreten von identischen Geheimtextzeichen
- Confirmation – (deutsch: Bestätigung): Von den britischen Codeknackern insbesondere bei der Steckersuche benutzter englischer Fachbegriff.[245] (Beispiel: Der Stecker WF wird ermittelt, nachdem zuvor bereits FW erkannt worden war, siehe auch: Contradiction)
- Consecutive Stecker Knock-Out – siehe: CSKO
- Constatation – (deutsch: Relation): Englischer Fachbegriff für das an einer bestimmten Position im Kryptogramm und im Crib gebildete Buchstabenpaar.[246]
- Contradiction – (deutsch: Widerspruch): Von den britischen Codeknackern insbesondere bei der Steckersuche benutzter englischer Fachbegriff.[245] (Beispiel: Der Stecker WX wird ermittelt, nachdem zuvor bereits FW erkannt worden war, siehe auch: Confirmation)
- Crab – (deutsch: Krabbe): Englischer Spitzname für einen Rotationsschritt der mittleren Walze bei der Abwehr-Enigma
- Crash – (deutsch: Kollision): Englischer Fachbegriff für das gleichzeitige Auftreten ein und desselben Buchstabens an derselben Position im Kryptogramm und im Crib. Da dies bei der Enigma bekanntermaßen unmöglich war, diente es zum Ausschluss der angenommenen Crib-Lage.
- Crib – (deutsch: Eselsbrücke, hier treffender: Wahrscheinliches Wort): Englischer Begriff für ein Textfragment, dessen Auftreten im Klartext erwartet wird (deutscher Fachbegriff auch: „Klartext-Geheimtext-Kompromiss“).
- CSKO – Abkürzung von „Consecutive Stecker Knock-Out“ (deutsch: „Niederschlagung aufeinanderfolgender Stecker“). Britische Methode und Vorrichtung, die die häufig praktizierte fehlerhafte Eigenart der deutschen Schlüsseltafeln ausnutzte, im Alphabet benachbarte Buchstaben nicht miteinander zu steckern (Beispiele: Nicht AB, PQ oder XY).
- CY-Verfahren – Ab 15. Sep. 1944 beim Heer eingeführte Prozedur, bei der etwa in der Mitte eines Spruchs die linke Walze von Hand verstellt wurde.[241][247]
- Dechiffrat – Anderer Ausdruck für Klartext
- Depth – (von engl. wörtlich „Tiefe“): Zwei oder mehrere Geheimtexte, die mit demselben Schlüssel verschlüsselt worden sind (deutscher Fachbegriff: „Klartext-Klartext-Kompromiss“).[248]
- Doppelbuchstabentauschtafel – Bei den U‑Booten verwendete Codetafeln zur geheimen Übermittlung des Spruchschlüssels
- Doppelsteckerschnüre – (kurz: Stecker): Verbindungskabel zwischen den Frontplattenbuchsen
- Dud – (deutsch wörtlich: Blindgänger): Englischer Fachausdruck für einen Spruch, bei dem zwar Walzenlage, Ringstellung und Steckerung bekannt waren, aber nicht die Walzenanfangsstellung.[249]
- Dud-buster – (deutsch etwa: Blindgänger-Meister): Englischer Fachausdruck für Verfahren zum Lösen eines Dud.[250]
- Eintrittswalze – Feststehende Walze am Anfang des Walzensatzes
- Entschlüsseln – (englisch: to decipher):[251] Umwandlung des Geheimtextes in den Klartext mithilfe des Schlüssels
- Entziffern – (englisch: to decrypt):[252] Brechen des Geheimtextes ohne vorherige Kenntnis des Schlüssels
- Female – (im polnischen Original: samica oder umgangssprachlich: samiczkami, deutsch wörtlich: „Weibchen“, deutscher Fachbegriff: „Einerzyklus“,[253] gelegentlich auch, aber weniger präzise: „Fixpunkt“): Wiederholtes Auftreten eines identischen Geheimtext-Klartext-Buchstabenpaars, das zur Entzifferung ausgenutzt werden kann
- Füllbuchstaben – Zur Tarnung zufällig zu wählende Buchstaben, insbesondere die ersten zwei Buchstaben der Kenngruppe
- Geheimtext – Durch Verschlüsselung aus dem Klartext erzeugter Text
- Gesteckert – Zwei Buchstaben werden mithilfe eines in die Frontplatte gesteckten Kabels vertauscht
- Grundstellung – (englisch: initial position): Walzenstellung zur Schlüsselung des Spruchschlüssels
- JABJAB – Von Dennis Babbage geprägter englischer Spitzname für die fahrlässige Wahl der Grundstellung auch als Spruchschlüssel[254][255]
- Kenngruppe – (auch: Buchstabenkenngruppe, engl.: discriminant, kurz auch: disc): Fünf Buchstaben (zwei Füllbuchstaben und drei Kenngruppenbuchstaben) am Anfang eines Spruchs zur Kennzeichnung des Schlüssels
- Kenngruppenbuch – Bei den U‑Booten verwendetes Codebuch zur geheimen Übermittlung des Spruchschlüssels
- Kenngruppenbuchstaben – Die letzten drei Buchstaben der Kenngruppe
- Kenngruppenheft – Bei den U‑Booten in Zusammenhang mit Kurzsignalen verwendetes Codebuch
- Kenngruppentafel – Die Schlüsseltafel ergänzende Liste mit täglich wechselnden Kenngruppenbuchstaben
- Kiss – (deutsch wörtlich: Kuss): Englischer Ausdruck für zwei unterschiedliche Geheimtexte, denen derselbe Klartext zugrunde liegt (deutscher Fachbegriff: „Geheimtext-Geheimtext-Kompromiss“).[256]
- Kryptogramm – Anderer Ausdruck für Geheimtext
- Kurzsignalheft – Bei den U‑Booten zur Verkürzung der Funksprüche verwendetes Codebuch
- Letchworth-Enigma – Von Alan Turing ersonnenes Modell des Walzensatzes mit dem Zweck der vorteilhaften Kryptanalyse
- Lobster – (deutsch: Hummer): Englischer Spitzname für einen gleichzeitigen Rotationsschritt aller Walzen inklusive der Umkehrwalze bei der Abwehr-Enigma
- Lückenfüllerwalze – Innovative Walze mit frei einstellbaren Übertragskerben
- Non-clashing rule – (deutsch: Nichtzusammenstoß-Regel): Englischer Spitzname für den fehlerhaften deutschen Usus bei Schlüsseltafeln für benachbarte Monatstage die Wiederverwendung einer Walze an selbem Platz im Walzensatz zu vermeiden
- Non-repeating rule – (deutsch: Nichtwiederhol-Regel): Englischer Spitzname für den fehlerhaften deutschen Usus bei Schlüsseltafeln die Wiederverwendung einer Walzenlage innerhalb eines Monats zu vermeiden
- Periode – Anzahl der Buchstaben, nach der sich das zur Verschlüsselung verwendete Alphabet wiederholt (16.900 bei der Enigma I)
- QWERTZU – Von Dilly Knox geprägter Begriff für die Verdrahtungsreihenfolge der einzelnen Buchstabentasten der Tastatur mit den Austrittskontakten der Eintrittswalze
- Ringstellung – Drehposition der Ringe, die den Versatz zwischen der inneren Verdrahtung der Walzen und dem Buchstaben bestimmt, zu dem der Übertrag auf die nächste Walze erfolgt
- Schlüssel – Geheime Einstellung der Schlüsselmaschine
- Schlüsselmaschine – Zusammenfassender Begriff für Ver- und Entschlüsselungsmaschine
- Schlüsseln – Zusammenfassender Begriff für Verschlüsseln und Entschlüsseln
- Schlüsselraum – Menge aller möglichen Schlüssel (siehe auch andere Bedeutung unten)
- Schlüsselraum – Zimmer, in dem „geschlüsselt“ wird, oft der Funkraum (siehe auch andere Bedeutung oben)
- Schlüsseltafel – Liste der Tagesschlüssel
- Schlüsseltext – Anderes Wort für Geheimtext[257]
- Schlüssler – Person, die Nachrichten ver- oder entschlüsselt[258]
- Six self-steckered letters – (deutsch: Sechs ungesteckte Buchstaben): Englische Bezeichnung für die (fehlerhafte) deutsche Regel bei Schlüsseltafeln genau sechs Buchstaben ungesteckt („selbstgesteckert“) zu lassen und nur zehn Paare (statt alle dreizehn) miteinander zu vertauschen
- Sonderschaltung – In seltenen Fällen hergestellte besondere Verdrahtung der rotierenden Walzen[259]
- Spruch – Geheimtext, der meist per Funk übermittelt wird
- Spruchkopf – (englisch: preamble): Erster Teil des Funkspruchs mit unverschlüsselter Angabe der Uhrzeit, der Buchstabenanzahl, der Grundstellung sowie dem verschlüsselten Spruchschlüssel (wie QWE EWG, englisch: indicator)
- Spruchnummer – Laufende Nummer eines Funkspruchs, wobei farblich zwischen abgehenden (blau) und eingehenden (rot) unterschieden wurde
- Spruchschlüssel – (englisch: message setting oder indicator):[260] Individueller Schlüssel für einen Funkspruch
- Spruchschlüsselverdopplung – Im Mai 1940 abgeschafftes (fehlerhaftes) Verfahren der zweimaligen Übertragung des Spruchschlüssels, das den polnischen Kryptoanalytikern in den 1930er-Jahren den Einbruch ermöglichte
- Stecker – Kabelverbindungen zwischen den Frontplattenbuchsen
- Steckerbrett – An der Frontseite der Enigma angebrachte Buchsenplatte
- Tagesschlüssel – Täglich wechselnder Schlüssel
- Uhr – Zusatzgerät zur Erzeugung nichtinvolutorischer Steckerverbindungen
- Umkehrwalze – (Zumeist) feststehende Walze am Ende des Walzensatzes (Abkürzung: UKW)
- Umkehrwalze D – Innovative Umkehrwalze mit wählbarer Verdrahtung (auch genannt: UKW Dora)
- Uncle Charlie – (deutsch: Onkel Charlie): Englischer Spitzname für die Umkehrwalze C
- Uncle Dick – (deutsch: Onkel Dick): Englischer Spitzname für die Umkehrwalze D
- Uncle Walter – (deutsch: Onkel Walter): Englische lautmalerische Umschreibung des deutschen Begriffs „Umkehrwalze“
- Ungesteckert – (englisch: self-steckered):[261] Buchstaben, die aufgrund eines nicht gesteckten Kabels nicht vertauscht werden
- Verschlüsseln – Umwandlung von Klartext in Geheimtext
- Wahlwort – (englisch: wahlwort):[262] Zufällig zu wählendes Wort, das am Anfang oder Ende des Klartextes eines Funkspruchs eingefügt wird, um diesen „auf unterschiedliche Länge“ zu bringen.[263]
- Walze – (englisch: wheel): Rotor, der sich während des Schlüsselvorgangs dreht
- Walzenlage – (englisch: wheel order): Schlüsselabhängige Platzierung der Walzen im Walzensatz
- Walzensatz – (englisch: wheel set oder scrambler): Zusammenfassender Begriff für alle Walzen
- Walzenstellung – (englisch: wheel setting): Von Hand einstellbare und während des Schlüsselvorgangs sich verändernde Rotationsposition der Walzen
- Wetterkurzschlüssel – Bei der Kriegsmarine zur Verkürzung von Wettermeldungen verwendetes Codebuch
- Y Service – (deutsch: „Y‑Dienst“): Englischer Name des britischen Funkabhördienstes, dessen Hauptaufgabe während des Zweiten Weltkriegs es war, den feindlichen, insbesondere den deutschen Funkverkehr abzufangen und aufzuzeichnen
- Zyklometer – (im polnischen Original: Cyklometr): Name für das 1934 von Rejewski entworfene kryptanalytische Gerät, mit dem der Fehler der Spruchschlüsselverdopplung ausgenutzt wurde, um die Walzenlage und den Spruchschlüssel zu erschließen
Siehe auch
Literatur
- Primärliteratur
- Allgemeine Schlüsselregeln für die Wehrmacht. H.Dv.g. 7, M.Dv.Nr. 534, L.Dv.g. 7, vom 1. April 1944, Books on Demand, Nachdruck 2019. ISBN 978-37431-9385-7.
- Signalschlüssel für den Funksignaldienst (Funksignalschlüssel) – Geheim. M.Dv.Nr. 114, vom Oktober 1939, Books on Demand, Nachdruck 2019. ISBN 978-37494-6791-4.
- Gustave Bertrand: Énigma ou la plus grande énigme de la guerre 1939–1945. Librairie Plon, Paris 1973.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, ISBN 0-19-280132-5.
- Marian Rejewski: An Application of the Theory of Permutations in Breaking the Enigma Cipher. Applicationes Mathematicae, 16 (4), 1980, S. 543–559. cryptocellar.org (PDF; 1,6 MB).
- Marian Rejewski: How Polish Mathematicians Deciphered the Enigma. Annals of the History of Computing, 3 (3), Juli 1981, S. 213–234.
- Arthur Scherbius: „Enigma“ Chiffriermaschine. Elektrotechnische Zeitschrift, November 1923, S. 1035–1036, cdvandt.org (PDF; 1 MB), abgerufen am 21. Februar 2019.
- Frederick William Winterbotham: The Ultra Secret. Weidenfeld and Nicolson, London 1974.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, ISBN 0-947712-34-8.
- Sekundärliteratur
- Arthur O. Bauer: Funkpeilung als alliierte Waffe gegen deutsche U‑Boote 1939–1945. Wie Schwächen und Versäumnisse bei der Funkführung der U‑Boote zum Ausgang der „Schlacht im Atlantik“ beigetragen haben. Arthur O. Bauer Selbstverlag, Diemen, Niederlande 1997, ISBN 3-00-002142-6.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-67931-6.
- Ralph Erskine: Der Krieg der Code-Brecher. Bayerische Akademie der Wissenschaften, Akademie aktuell, München, November 2002, S. 5–11. badw.de (PDF; 995 kB)
- David Kahn: The Code Breakers – The Story of Secret Writing. Macmillan USA, Reissue 1974, ISBN 0-02-560460-0.
- David Kahn: Seizing the Enigma – The Race to Break the German U‑Boat Codes, 1939–1943. Naval Institute Press, Annapolis, MD, USA, 2012, ISBN 978-1-59114-807-4.
- Rudolf Kippenhahn: Verschlüsselte Botschaften, Geheimschrift, Enigma und Chipkarte. Rowohlt, Reinbek bei Hamburg 1999, ISBN 3-499-60807-3.
- Władysław Kozaczuk, Jerzy Straszak: Enigma – How the Poles Broke the Nazi Code. Hippocrene Books, 2004, ISBN 0-7818-0941-X.
- Władysław Kozaczuk: Geheimoperation Wicher. Bernard u. Graefe, Koblenz 1989, Karl Müller, Erlangen 1999, ISBN 3-7637-5868-2, ISBN 3-86070-803-1.
- Władysław Kozaczuk: Im Banne der Enigma. Militärverlag, Berlin 1987, ISBN 3-327-00423-4.
- Jürgen Rohwer: Der Einfluss der alliierten Funkaufklärung auf den Verlauf des Zweiten Weltkrieges. Vierteljahrshefte für Zeitgeschichte, Jahrgang 27, Heft 3, IfZ München 1979, ifz-muenchen.de (PDF 1,8 MB), abgerufen am 24. April 2019.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, ISBN 0-304-36662-5.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, ISBN 3-446-19873-3.
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, ISBN 3-453-17285-X.
- Geoff Sullivan, Frode Weierud: Breaking German Army Ciphers. Cryptologia, Vol XXIX (3), Juli 2005, S. 193–232 tandf.co.uk (PDF; 6,1 MB)
- Dermot Turing: X, Y & Z – The Real Story of how Enigma was Broken. The History Press, Stroud 2018, ISBN 978-0-75098782-0.
- Heinz Ulbricht: Die Chiffriermaschine Enigma – Trügerische Sicherheit. Ein Beitrag zur Geschichte der Nachrichtendienste. Dissertation Braunschweig 2005. tu-bs.de (PDF; 4,7 MB), abgerufen am 18. Mai 2016.
Weblinks
Details
- Website Bletchley Park, englisch
- Website Breaking German Navy Ciphers, speziell Bruch der M4, englisch
- Website Cipher Machines and Cryptology, Simulationsprogramme und Challenges, englisch
- Website Crypto Cellar, viele Original-Dokumente, englisch
- Website Crypto Museum, viele Detailinformationen zu den diversen Enigma-Modellen, englisch
- Website Enigma Museum, viele Fotos originaler Enigma-Maschinen, englisch
- Enigma Family Tree Stammbaum der Enigma, englisch
- Geheimoperation Wicher des polnischen Geheimdienstes
- The pinch from U 559, Bericht über die Erbeutung des Wetterkurzschlüssels und des Kurzsignalheftes, englisch
- Funkpeilung als alliierte Waffe gegen deutsche U‑Boote 1939–1945, Webseite mit Auszügen aus dem Buch von Arthur O. Bauer
- Die goldene Gans, die niemals schnattert von André Schulz
- Abwehrfunk – Funkabwehr. Technik und Verfahren der Spionagefunkdienste. Überarbeitete Fassung eines unveröffentlichten Manuskripts, 2018, von Rudolf Staritz

Dokumente
- Die schreibende Enigma-Chiffriermaschine Verkaufsprospekt (Vorderseite), ca. 1924.[264]
- Die schreibende Enigma-Chiffriermaschine Verkaufsprospekt (Rückseite), ca. 1924.
- Kurze Beschreibung der schreibenden „ENIGMA“-Chiffriermaschine (PDF; 1,8 MB), Scan der Produktbroschüre von 1931.
- Der Schlüssel M (PDF; 3,3 MB), Scan der Originalvorschrift von 1940.
- Spruch Nr. 233 (PDF; 201 kB), authentisches Spruchformular mit empfangenem Funkspruch.
- Luftwaffen-Maschinenschlüssel Nr. 619 (PDF; 316 kB), authentische Schlüsseltafel.
- Doppelbuchstabentauschtafeln (PDF; 2,9 MB), Scan der Originaltafeln „Kennwort: Quelle“.
- Funkspruchformulare
- The Enigma Collection von Frode Weierud (englisch).
Entzifferungen
- Breaking German Wehrmacht Ciphers von Frode Weierud (englisch).
- Breaking German Navy Ciphers, moderne Entzifferung der M4, englisch
- M4 Message Breaking Project, moderne Entzifferung der M4, englisch
- Enigma Cipher Challenge Wettbewerb: Knacke zehn (fiktive) Enigma-Funksprüche, englisch
Exponate
Fotos, Videos und Audios
- Fotos der Enigma-Maschine
- Historische Fotos zur Schlüsselarbeit mit der Enigma
- Fotos von Arthur Scherbius, Hans-Thilo Schmidt, Alan Turing und der „Lückenfüllerwalze“
- Lehrvideos zur Enigma im Videoportal YouTube, englisch
- Audio-Interview mit dem deutschen Kryptologen Friedrich L. Bauer über die Enigma (etwa 19 Minuten)
- Video bei YouTube, das anhand eines Holzmodells die Walzenfortschaltung illustriert, insbesondere auch den Doppelschritt der mittleren Walze.
Nachbauprojekte
- Nachbau einer Enigma I
- Nachbau einer Enigma I
- Nachbau einer M4
- Nachbau einer M4, englisch
- Elektronischer Nachbau „Enigma-E“ im Crypto Museum, englisch
- Elektronischer Nachbau „meinEnigma“, englisch
- 3D-gedruckter Nachbau „ENIGMA R.D.E.“
Simulationen der Maschine
- Windows, Enigma I, M3 und M4 realitätsnah visualisiert, englisch.
- Windows, weitere Varianten wie Enigma‑G und Enigma‑T sowie Nema und Sigaba, englisch.
- Android „EnigmAndroid“, freie App für Android, englisch.
- Android „Enigma Simulator APK“, freie App für Android, englisch.
- MAC OS, englisch.
- RISC OS, englisch.
Simulationen der Verschlüsselung
- Papier-Enigma (Memento vom 30. März 2017 im Internet Archive) (PDF; 84 kB), Papier-Version der Enigma-Verschlüsselung
- Die Enigma auf Papier (PDF; 210 kB), Unterlage zum Selbstbau einer Papier-Enigma
- Universal Enigma, JavaScript, browserübergreifend
- Cryptii, JavaScript, browserübergreifend
Einzelnachweise
- Karl de Leeuw und Jan Bergstra (Hrsg.): The History of Information Security – A Comprehensive Handbook. Elsevier B.V., Amsterdam, Niederlande, 2007, S. 389. ISBN 978-0-444-51608-4.
- Tom Perera, Dan Perera: Inside Enigma. 2. Auflage, Radio Society of Great Britain (RSGB) 2019, S. 19, ISBN 9781-9101-9371-6.
- Karl de Leeuw: The Dutch Invention of the Rotor Machine, 1915–1923. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 27.2003,1 (January), S. 73–94. ISSN 0161-1194.
- Louis Kruh, Cipher Deavours: The Commercial Enigma – Beginnings of Machine Cryptography. Cryptologia, Vol. XXVI, Nr. 1, Januar 2002, S. 1. apprendre-en-ligne.net (PDF; 0,8 MB) Abgerufen: 4. Nov. 2013.
- Friedrich L. Bauer: An error in the history of rotor encryption devices. Cryptologia, Juli 1999.
- Patentschrift Chiffrierapparat DRP Nr. 416 219. Abgerufen: 4. Nov. 2013. cdvandt.org (PDF; 0,4 MB)
- David Kahn: Seizing the Enigma – The Race to Break the German U‑Boat Codes, 1939–1943. Naval Institute Press, Annapolis, MD, USA, 2012, S. 35. ISBN 978-1-59114-807-4.
- David Kahn: An Enigma Chronology. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 17.1993, 3, S. 239, ISSN 0161-1194.
- Friedrich L. Bauer: Historische Notizen zur Informatik. Springer, Berlin 2009, S. 49. ISBN 3-540-85789-3.
- Louis Kruh, Cipher Deavours: The commercial Enigma – Beginnings of machine cryptography. Cryptologia, Rose-Hulman Institute of Technology, Taylor & Francis, Philadelphia PA 26.2002,1 (Januar), S. 1. ISSN 0161-1194 Abgerufen: 18. Oktober 2016. apprendre-en-ligne.net (PDF; 0,8 MB)
- Anders Wik: The First Classical Enigmas – Swedish Views on Enigma Development 1924–1930. Proceedings of the 1st International Conference on Historical Cryptology, PDF; 12,5 MB 2018, S. 83–88.
- Winston Churchill: The World Crisis – 1911–1918. 4 Bände, 1923 bis 1929, ISBN 978-0-7432-8343-4.
- Julian Corbett: Naval Operations. 1923, ISBN 1-84342-489-4.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, S. 177. ISBN 3-446-19873-3.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, S. 178. ISBN 3-446-19873-3.
- José Ramón Soler Fuensanta, Francisco Javier López-Brea Espiau und Frode Weierud: Spanish Enigma: A History of the Enigma in Spain. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 34.2010,4 (Oktober), S. 309. ISSN 0161-1194.
- Friedrich L. Bauer: Decrypted Secrets, Methods and Maxims of Cryptology. Springer, Berlin 2007 (4. Aufl.), S. 123, ISBN 3-540-24502-2.
- Reichswehr and Wehrmacht Enigma Orders in Frode Weierud’s CryptoCellar (englisch), abgerufen am 5. April 2021.
- Enigma Production at Konski & Krüger in Frode Weierud’s CryptoCellar (englisch), abgerufen am 4. April 2021.
- Max Rüegger: Erinnerungen eines Korea-Funkers – Die Arbeit mit der Chiffriermaschine ENIGMA. 2016. PDF; 4,7 MB (Memento vom 25. August 2016 im Internet Archive) Abgerufen: 24. August 2018.
- Arthur O. Bauer: Funkpeilung als alliierte Waffe gegen deutsche U‑Boote 1939–1945. Selbstverlag, Diemen Niederlande 1997, S. 31. ISBN 3-00-002142-6.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 85. ISBN 0-19-280132-5.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 83. ISBN 0-19-280132-5.
- Arthur Scherbius: „Enigma“ Chiffriermaschine. Elektrotechnische Zeitschrift, 1923, S. 1035.
- David H. Hamer: G-312. An Abwehr Enigma. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 24.2000,1 (Januar), S. 46. ISSN 0161-1194. Abgerufen: 4. Nov. 2013. PDF-Scan als ZIP; 1,1 MB (Memento vom 11. Juni 2007 im Internet Archive)
- Patentschrift Elektrische Vorrichtung zum Chiffrieren und Dechiffrieren DRP Nr. 452 194. cdvandt.org (PDF; 404 kB) Abgerufen: 4. Nov. 2013.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 119.
- Oberkommando der Kriegsmarine: Der Schlüssel M – Verfahren M Allgemein. Berlin 1940. Abgerufen: 4. Nov. 2013, S. 23. cdvandt.org (PDF; 0,7 MB)
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 115.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, ISBN 0-947712-34-8, S. 213.
- Louis Kruh: How to Use the German Enigma Cipher Machine -A Photographic Essay. Cryptologia, Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 29.2005,3, S. 193–232.
- OKW: Schlüsselanleitung zur Schlüsselmaschine Enigma. H.Dv.g. 14, Reichsdruckerei, Berlin 1940. (Abschrift des Original-Handbuchs mit einigen kleinen Tippfehlern.) Abgerufen: 24. August 2018. PDF; 0,1 MB (Memento vom 24. September 2015 im Internet Archive)
- Philip Marks: Umkehrwalze D: Enigma’s rewirable reflector – Part 1. Cryptologia, Volume XXV, Nummer 2, April 2001, S. 117.
- The US 6812 Bombe Report 1944. 6812th Signal Security Detachment, APO 413, US Army. Publikation, Tony Sale, Bletchley Park, 2002. S. 2. codesandciphers.org.uk (PDF; 1,3 MB) Abgerufen: 4. Nov. 2013.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 107. ISBN 0-19-280132-5.
- John Jackson: Solving Enigma’s Secrets – The Official History of Bletchley Park’s Hut 6. BookTower Publishing 2014, S. 96–100. ISBN 978-0-9557164-3-0.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 57. Abgerufen am 30. März 2017. codesandciphers.org.uk (PDF; 0,4 MB)
- C.H.O’D. Alexander: Stecker Knock-Out. Publikation, Bletchley Park, März 1944. Editiert und herausgegeben von Frode Weierud, Juli 1998. Abgerufen: 24. August 2018. PDF; 0,1 MB (Memento vom 2. Juli 2007 im Internet Archive)
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 459.
- Derek Taunt: Hut Six in Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 100. ISBN 0-19-280132-5.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 314. ISBN 0-304-36662-5.
- Oberkommando der Kriegsmarine: Der Schlüssel M – Verfahren M Allgemein. Berlin 1940. Abgerufen: 4. Nov. 2013, S. 23. cdvandt.org (PDF; 0,7 MB)
- Dirk Rijmenants: Enigma Message Procedures Used by the Heer, Luftwaffe and Kriegsmarine. Cryptologia, 34: 4, 2010, S. 329 ff.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 357. ISBN 0-304-36662-5.
- Oberkommando der Wehrmacht: Allgemeine Schlüsselregeln für die Wehrmacht. H.Dv.g. 7, Reichsdruckerei, Berlin 1944, S. 13. cdvandt.org (PDF; 0,9 MB) Abgerufen: 4. Nov. 2013.
- Oberkommando der Kriegsmarine: Der Schlüssel M – Verfahren M Allgemein. Berlin 1940, S. 25 ff. cdvandt.org (PDF; 0,7 MB) Abgerufen: 4. Nov. 2013.
- David H. Hamer, Geoff Sullivan, Frode Weierud: Enigma Variations – An Extended Family of Machines. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 22.1998,1 (Juli), S. 214, ISSN 0161-1194. cryptocellar.org (PDF; 80 kB) Abgerufen: 15. Februar 2016.
- Modern breaking of Enigma ciphertexts Abgerufen: 4. April 2021.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 117.
- Oberkommando der Kriegsmarine: Der Schlüssel M – Verfahren M Allgemein. Berlin 1940, S. 26. cdvandt.org (PDF; 0,7 MB) Abgerufen: 4. Nov. 2013.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 168. ISBN 0-947712-34-8.
- Louis Kruh, Cipher Deavours: The commercial Enigma – Beginnings of machine cryptography. Cryptologia, Rose-Hulman Institute of Technology, Taylor & Francis, Philadelphia PA 26.2002,1 (Januar), S. 10. ISSN 0161-1194, abgerufen am 14. März 2019. apprendre-en-ligne.net (PDF; 0,8 MB)
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 404 ISBN 0-304-36662-5.
- M4 Message Breaking Project. Abgerufen: 4. Nov. 2013. (Achtung: Die Seite scheint ab 2009 nicht mehr aktualisiert worden zu sein!)
- M4 Project 2006, Third Message (auf hoerenberg.com) Abgerufen: 4. Nov. 2013.
- US1905593 Coding Machine. 5 claims Application date 12. November 1929 and in Germany 16. November 1928 (PDF; 487 kB). Granted 25 April 1933. Applicant: Willi Korn of Berlin-Friedenau, Germany, abgerufen am 5. Juni 2019.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 117.
- Colleen Carper: Bletchley’s Secret War – British Code Breaking in the Batlle of the Atlantic. Ashbrook Statesmanship Thesis, 2009, S. 3, PDF
- Louis Kruh, Cipher Deavours: The Commercial Enigma – Beginnings of Machine Cryptography. Cryptologia, Vol. XXVI, Nr. 1, Januar 2002, S. 11. apprendre-en-ligne.net (PDF; 0,8 MB), abgerufen am 18. Februar 2019.
- OKW: Schlüsselanleitung zur Schlüsselmaschine Enigma. H.Dv.g. 14, Reichsdruckerei, Berlin 1940, S. 6. (Abschrift des Original-Handbuchs mit einigen kleinen Tippfehlern.) Abgerufen: 24. August 2018. PDF; 0,1 MB (Memento vom 24. September 2015 im Internet Archive)
- Robert Harris: Enigma. Roman. Weltbild, Augsburg 2005, S. 71. ISBN 3-89897-119-8.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 86. ISBN 0-19-280132-5.
- Patentschrift Elektrische Vorrichtung zum Chiffrieren und Dechiffrieren DRP Nr. 452 194, S. 1. cdvandt.org (PDF; 404 kB) Abgerufen: 4. Nov. 2013.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 49.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 276.
- Claude Shannon: Communication Theory of Secrecy Systems. Bell System Technical Journal, Vol 28, 1949 (Oktober), S. 710 f. netlab.cs.ucla.edu (PDF; 0,6 MB) Abgerufen: 4. Nov. 2013.
- David Kahn: Seizing the Enigma – The Race to Break the German U‑Boat Codes, 1939–1943. Naval Institute Press, Annapolis, MD, USA, 2012, S. 131. ISBN 978-1-59114-807-4.
- Krzysztof Gaj: Polish Cipher Machine –Lacida. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 16.1992,1, ISSN 0161-1194, S. 74.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 210. ISBN 0-947712-34-8.
- OKW: Gebrauchsanleitung für die Chiffriermaschine Enigma. H.Dv.g. 13, Reichsdruckerei, Berlin 1937. Online (PDF; 1,8 MB) Abgerufen: 4. Nov. 2013.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 22. ISBN 0-304-36662-5.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, S. 199. ISBN 3-446-19873-3.
- Marian Rejewski: An Application of the Theory of Permutations in Breaking the Enigma Cipher. Applicationes Mathematicae, 16 (4), 1980, S. 543–559. Abgerufen: 24. August 2018. PDF; 1,6 MB (Memento vom 21. Dezember 2015 im Internet Archive)
- Friedrich L. Bauer: Historische Notizen zur Informatik. Springer, Berlin 2009, S. 295. ISBN 3-540-85789-3.
- Marian Rejewski: How Polish Mathematicians Broke the Enigma Cipher. IEEE Annals of the History of Computing, Vol. 03, Nr. 3, S. 221, Juli 1981, S. 229 f.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 42. ISBN 0-304-36662-5.
- Frank Carter: The Polish Recovery of the Enigma Rotor Wiring. Publikation, Bletchley Park, März 2005.
- David Kahn: Seizing the Enigma – The Race to Break the German U‑Boat Codes, 1939–1943. Naval Institute Press, Annapolis, MD, USA, 2012, S. 76. ISBN 978-1-59114-807-4.
- I. J. Good, Cipher A. Deavours, Nachwort zu Marian Rejewski: How Polish Mathematicians Broke the Enigma Cipher. IEEE Annals of the History of Computing, Vol. 03, Nr. 3, S. 213–234, Juli 1981, S. 229 f.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 412.
- Chris Christensen: Review of IEEE Milestone Award to the Polish Cipher Bureau for “The First Breaking of Enigma Code”. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 39.2015,2, S. 180. ISSN 0161-1194.
- Tadeusz Lisicki: Die Leistung des polnischen Entzifferungsdienstes bei der Lösung des Verfahrens der deutschen »Enigma«-Funkschlüsselmaschine in J. Rohwer und E. Jäkel: Die Funkaufklärung und ihre Rolle im Zweiten Weltkrieg, Motorbuch Verlag, Stuttgart, 1979, S. 66–81. fgcu.edu (PDF; 1,7 MB) Abgerufen am 16. Mai 2017.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 207. ISBN 0-947712-34-8.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 16. ISBN 0-947712-34-8.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 49. ISBN 0-304-36662-5.
- Ralph Erskine: The Poles Reveal their Secrets – Alastair Dennistons’s Account of the July 1939 Meeting at Pyry. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 30.2006,4, S. 294.
- Mavis Batey: Dilly -The Man Who Broke Enigmas. Dialogue 2011, ISBN 1-906-44715-2, S. 76.
- Mavis Batey: Dilly Knox – A Reminiscence of this Pioneer Enigma Cryptanalyst. Cryptologia, Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 32.2008,2, S. 104–130.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 126. ISBN 0-19-280132-5.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 412.
- Friedrich L. Bauer: Historische Notizen zur Informatik. Springer, Berlin 2009, S. 207. ISBN 3-540-85789-3.
- The Alan Turing Internet Scrapbook (englisch). Abgerufen: 17. Juni 2016.
- The US 6812 Bombe Report 1944. 6812th Signal Security Detachment, APO 413, US Army. Publikation, Tony Sale, Bletchley Park, 2002. S. 9. codesandciphers.org.uk (PDF; 1,3 MB) Abgerufen: 4. Nov. 2013.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 219. ISBN 0-947712-34-8.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 11. ISBN 0-947712-34-8.
- David Kahn: Das nicht geknackte Rätsel. In Robert Cowley (Hrsg.) Was wäre geschehen wenn? Knaur, 2006, S. 395. ISBN 3-426-77887-4 (Kontrafaktische Geschichte unter der Annahme, den Alliierten gelingt es nicht, die Enigma zu knacken).
- John A. N. Lee, Colin Burke, Deborah Anderson: The US Bombes, NCR, Joseph Desch, and 600 WAVES – The first Reunion of the US Naval Computing Machine Laboratory. IEEE Annals of the History of Computing, 2000. S. 35. thecorememory.com (PDF; 0,5 MB) Abgerufen: 4. Nov. 2013.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 381f. ISBN 0-304-36662-5.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 113. ISBN 0-947712-34-8.
- The US 6812 Bombe Report 1944. 6812th Signal Security Detachment, APO 413, US Army. Publikation, Tony Sale, Bletchley Park, 2002. S. 59. codesandciphers.org.uk (PDF; 708 kB) Abgerufen: 7. Januar 2014.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 235. ISBN 0-304-36662-5.
- Michael Miller: Symmetrische Verschlüsselungsverfahren – Design, Entwicklung und Kryptoanalyse klassischer und moderner Chiffren. Teubner, April 2003, S. 70. ISBN 3-519-02399-7.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 344. ISBN 0-304-36662-5.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 345. ISBN 0-304-36662-5.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 22. codesandciphers.org.uk (PDF; 0,4 MB) Abgerufen am 30. März 2017.
- Michael Pröse: Chiffriermaschinen und Entzifferungsgeräte im Zweiten Weltkrieg – Technikgeschichte und informatikhistorische Aspekte. Dissertation Technische Universität Chemnitz, Leipzig 2004, S. 46.
- David H. Hamer, Geoff Sullivan, Frode Weierud: Enigma Variations – An Extended Family of Machines. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 22.1998,1 (Juli), S. 2 ff, ISSN 0161-1194. cryptocellar.org (PDF; 80 kB) Abgerufen: 15. Februar 2016.
- Oberkommando der Wehrmacht: Allgemeine Schlüsselregeln für die Wehrmacht. H.Dv.g. 7, Reichsdruckerei, Berlin 1944, S. 10. cdvandt.org (PDF; 0,9 MB) Abgerufen: 4. Nov. 2013.
- Oberkommando der Wehrmacht: Allgemeine Schlüsselregeln für die Wehrmacht. H.Dv.g. 7, Reichsdruckerei, Berlin 1944, S. 6. cdvandt.org (PDF; 844 kB) Abgerufen: 4. Nov. 2013.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 121. ISBN 0-19-280132-5.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 400.
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, S. 107. ISBN 3-453-17285-X.
- Christopher Morris: Navy Ultra’s Poor Relations in Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 235. ISBN 0-19-280132-5.
- Impact Of Bombe On The War Effort, abgerufen am 23. Mai 2018.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 230. ISBN 0-947712-34-8.
- Jack Copeland: Enigma. S. 256.Abgerufen: 4. Nov. 2013. canterbury.ac.nz (PDF; 0,8 MB)
- Stephen Pincock und Mark Frary: Geheime Codes – Die berühmtesten Verschlüsselungstechniken und ihre Geschichte. Bastei Lübbe, 2007, ISBN 3-431-03734-8, S. 109.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 136. ISBN 0-304-36662-5.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 149 ff. ISBN 0-304-36662-5.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 225. ISBN 0-304-36662-5.
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, S. 181. ISBN 3-453-17285-X.
- Rudolf Kippenhahn: Verschlüsselte Botschaften, Geheimschrift, Enigma und Chipkarte. Rowohlt, Reinbek bei Hamburg 1999, S. 247. ISBN 3-499-60807-3.
- Stephen Harper: Kampf um Enigma – Die Jagd auf U‑559. Mittler, Hamburg 2001, S. 50 ff. ISBN 3-8132-0737-4.
- Stephen Harper: Kampf um Enigma – Die Jagd auf U‑559. Mittler, Hamburg 2001, S. 66 ff. ISBN 3-8132-0737-4.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 311. ISBN 0-304-36662-5.
- Jennifer Wilcox: Solving the Enigma – History of the Cryptanalytic Bombe. Center for Cryptologic History, NSA, Fort Meade (USA) 2001, S. 52. Abgerufen: 4. Nov. 2013. PDF; 0,6 MB (Memento vom 15. Januar 2009 im Internet Archive)
- John A. N. Lee, Colin Burke, Deborah Anderson: The US Bombes, NCR, Joseph Desch, and 600 WAVES – The first Reunion of the US Naval Computing Machine Laboratory. IEEE Annals of the History of Computing, 2000, S. 27 ff.
- The Achievements of the Signal Security Agency (SSA) in World War II. NSA, Fort Meade, 2010, S. 4.
- Erich Gröner: Die deutschen Kriegsschiffe 1815–1945;- Band 3: U‑Boote, Hilfskreuzer, Minenschiffe, Netzleger, Sperrbrecher. Bernard & Graefe, Koblenz 1985, ISBN 3-7637-4802-4, S. 118f
- Nach Eberhard Rössler: Geschichte des deutschen U‑Bootbaus. Band 1. Bernard & Graefe, Bonn 1996, ISBN 3-86047-153-8, S. 248–251 gingen von Mai bis Oktober 1943 die folgenden Boote vom Typ XB (4 von 8) beziehungsweise Typ XIV (7 von 10) verloren:
- am 15. Mai; jedoch lt. Wikipedia am 16. Mai U 463 (Typ XIV),
- am 12. Juni U 118 (Typ XB),
- am 24. Juni U 119 (Typ XB),
- am 13. Juli U 487 (Typ XIV),
- am 24. Juli U 459 (Typ XIV),
- am 30. Juli U 461 (Typ XIV),
- am 30. Juli U 462 (Typ XIV),
- am 04. Aug. U 489 (Typ XIV),
- am 07. Aug. U 117 (Typ XB),
- am 04. Okt. U 460 (Typ XIV),
- am 28. Okt. U 220 (Typ XB).
- am 15. Mai; jedoch lt. Wikipedia am 16. Mai U 463 (Typ XIV),
- Frederick William Winterbotham: The Ultra Secret – The Inside Story of Operation Ultra, Bletchley Park and Enigma. Orion, 2000, S. 16–17, ISBN 0-7528-3751-6.
- Craig P. Bauer: Secret History – The Story of Cryptology. CRC Press, Boca Raton 2013, S. 285. ISBN 978-1-4665-6186-1.
- Ralph Erskine: Der Krieg der Code-Brecher. Bayerische Akademie der Wissenschaften, Akademie aktuell, München, November 2002, S. 11.
- David Kahn: The Significance of Codebreaking and Intelligence in Allied Strategy and Tactics. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 1.1977,3, S. 221. ISSN 0161-1194.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, S. 229. ISBN 3-446-19873-3.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, S. 229f. ISBN 3-446-19873-3.
- David Kahn: Das nicht geknackte Rätsel. In Robert Cowley (Hrsg.) Was wäre geschehen wenn? Knaur, 2006, S. 398. ISBN 3-426-77887-4. (Kontrafaktische Geschichte unter der Annahme, den Alliierten gelingt es nicht, die Enigma zu knacken)
- Zbigniew Brzeziński: The Unknown Victors. S. 15–18 in Jan Stanisław Ciechanowski (Hrsg.): Marian Rejewski, 1905–1980 – Living with the Enigma Secret, 1. Aufl., Bydgoszcz, Bydgoszcz City Council, 2005, S. 18, ISBN 83-7208-117-4.
- Władysław Kozaczuk, Jerzy Straszak, Enigma: How the Poles Broke the Nazi Code. Hippocrene Books, 2004, S. 74. ISBN 0-7818-0941-X.
- Ralph Erskine: Der Krieg der Code-Brecher. Bayerische Akademie der Wissenschaften, Akademie aktuell, München, November 2002, S. 5.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 96. ISBN 0-19-280132-5.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, ISBN 0-947712-34-8, S. 169.
- David Kahn: Das nicht geknackte Rätsel. In Robert Cowley (Hrsg.) Was wäre geschehen wenn? Knaur, 2006, S. 400. ISBN 3-426-77887-4. (Kontrafaktische Geschichte unter der Annahme, den Alliierten gelingt es nicht, die Enigma zu knacken)
- Dermot Turing: X, Y & Z – The Real Story of how Enigma was Broken. The History Press, 2018, ISBN 978-0-75098782-0, S. 20.
- David Kenyon: Bletchley Park and D‑Day. Yale University Press, New Haven und London 2019 (englisch), ISBN 978-0-300-24357-4.
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, S. 252f. ISBN 3-453-17285-X.
- Army Security Agency: Notes on German High Level Cryptography and Cryptanalysis. European Axis Signal Intelligence in World War II, Vol 2, Washington (D.C.), 1946 (Mai), S. 2. 24. August 2018. PDF; 7,5 MB (Memento vom 11. Juni 2014 im Internet Archive)
- Stephen Harper: Kampf um Enigma – Die Jagd auf U‑559. Mittler, Hamburg 2001, S. 24. ISBN 3-8132-0737-4
- Rudolf Kippenhahn: Verschlüsselte Botschaften, Geheimschrift, Enigma und Chipkarte. Rowohlt, Reinbek bei Hamburg 1999, S. 244. ISBN 3-499-60807-3.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, S. 202. ISBN 3-446-19873-3.
- Diana Payne: The bombes. In Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 137. ISBN 0-19-280132-5.
- David Kahn: Das nicht geknackte Rätsel. In Robert Cowley (Hrsg.) Was wäre geschehen wenn? Knaur, 2006, S. 411. ISBN 3-426-77887-4. (Kontrafaktische Geschichte unter der Annahme, den Alliierten gelingt es nicht, die Enigma zu knacken)
- James W. Mc Lendon: Information Warfare – Impact an Concerns. Forschungsbericht, Maxwell Air Force Base, Alabama 1994, S. 8. iwar.org.uk (PDF; 0,2 MB) Abgerufen: 4. Nov. 2013.
- Ted Enever: Britain’s Best Kept Secret – Ultra’s Base at Bletchley Park. Sutton Publishing Ltd, Januar 1994. ISBN 0-7509-2355-5.
- Army Security Agency: Notes on German High Level Cryptography and Cryptanalysis. European Axis Signal Intelligence in World War II, Vol 2, Washington (D.C.), 1946 (Mai), S. 5. Abgerufen: 24. August 2018. PDF; 7,5 MB (Memento vom 11. Juni 2014 im Internet Archive)
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, S. 241. ISBN 3-453-17285-X.
- BBC News: The Cambridge spy ring. Abgerufen: 4. Nov. 2013.
- TICOM I-38: Report on Interrogation of Lt. Frowein of OKM/4 SKL III, on his Work on the Security on the German Naval Four-Wheel Enigma. Marinenachrichtenschule, Flensburg-Mürwik, Juni 1945, (englisch).
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 222.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3. Auflage. S. 447. Springer, Berlin u. a. 2000, ISBN 3-540-67931-6, doi:10.1007/978-3-642-58345-2.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 4. ISBN 0-304-36662-5.
- Geltinger Bucht – Taucher finden "Enigma" auf Ostseegrund. NDR vom 4. Dezember 2020, abgerufen am 9. Dezember 2020.
- Sechs Enigma-Chiffriermaschine in Ostsee geborgen bei orf.at vom 21. Januar 2021, abgerufen 21. Januar 2021.
- Schleimünde: Taucher findet sechs weitere Enigma-Chiffriermaschinen vom 21. Januar 2021, abgerufen am 6. März 2021
- Als die Briten unsichere Enigmas nach Israel verschenkten Klausis Krypto-Kolumne. Abgerufen: 9. November 2016.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, S. 231. ISBN 0-89006-161-0.
- Nazi Enigma encryption machine may have been used by Britain to spy on Israel (englisch). Abgerufen: 9. November 2016.
- Max Rüegger: Erinnerungen eines Korea-Funkers – Die Arbeit mit der Chiffriermaschine ENIGMA. 2016.
- Cipher A. Deavours, Louis Kruh: Machine Cryptography and Modern Cryptanalysis. Artech House, 1985, S. 40. ISBN 0-89006-161-0.
- David Hamer’s List of Surviving Enigma Machines XLS-Datei; 110 kB, abgerufen am 6. Juni 2018.
- Enigma Museum (Memento vom 12. Juli 2017 im Internet Archive) SPECIAL NOTE ABOUT PRICES Abgerufen: 10. Juli 2017.
- ArtDaily.org (Memento vom 17. Juni 2017 im Internet Archive) Christie’s sets world auction record for an Enigma Machine sold to online bidder – “World auction records were set for A Four-Rotor Enigma Cipher Machine, 1944, which sold above the high estimate for $547,500 to an online bidder”, abgerufen am 25. Oktober 2020.
- Army Security Agency: Notes on German High Level Cryptography and Cryptanalysis. European Axis Signal Intelligence in World War II, Vol 2, Washington (D.C.), 1946 (Mai), S. 76. Abgerufen: 24. August 2018. PDF; 7,5 MB (Memento vom 11. Juni 2014 im Internet Archive)
- Claude Shannon: Communication Theory of Secrecy Systems. Bell System Technical Journal, Vol 28, 1949 (Oktober), S. 662. netlab.cs.ucla.edu (PDF; 0,6 MB) Abgerufen: 4. Nov. 2013.
- Auguste Kerckhoffs: La cryptographie militaire. Journal des sciences militaires. Bd. 9, S. 5–38 (Jan. 1883) und S. 161–191 (Feb. 1883). petitcolas.net (PDF; 0,5 MB) Abgerufen: 4. Nov. 2013.
- José Ramón Soler Fuensanta, Francisco Javier López-Brea Espiau und Frode Weierud: Spanish Enigma: A History of the Enigma in Spain. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 34.2010,4 (Oktober), S. 325–326. ISSN 0161-1194.
- David H. Hamer, Geoff Sullivan, Frode Weierud: Enigma Variations – An Extended Family of Machines. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 22.1998,1 (Juli), S. 11, ISSN 0161-1194. cryptocellar.org (PDF; 80 kB) Abgerufen: 15. Februar 2016.
- C.H.O'D. Alexander: Method for testing „Holmes Hypothesis“ for U.D. Publikation, Bletchley Park 1998, S. 14. PDF; 0,1 MB (Memento vom 11. Juni 2007 im Internet Archive)
- Louis Kruh, Cipher Deavours: The commercial Enigma – Beginnings of machine cryptography. Cryptologia, Rose-Hulman Institute of Technology, Taylor & Francis, Philadelphia PA 26.2002,1 (Januar), S. 2. ISSN 0161-1194 Abgerufen: 24. August 2018. PDF; 0,8 MB (Memento vom 13. April 2006 im Internet Archive)
- Patentschrift Chiffrierapparat DRP Nr. 416 219, S. 1. cdvandt.org (PDF; 0,4 MB) Abgerufen: 4. Nov. 2013.
- Otto Leiberich: Vom Diplomatischen Code zur Falltürfunktion. Spektrum der Wissenschaft, Dossier Kryptographie, 4/2001, S. 15.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 221.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 143.
- Peter Twinn: The Abwehr Enigma in Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 125. ISBN 0-19-280132-5.
- Army Security Agency: Notes on German High Level Cryptography and Cryptanalysis. European Axis Signal Intelligence in World War II, Vol 2, Washington (D.C.), 1946 (Mai), S. 77. Abgerufen: 24. August 2018. PDF; 7,5 MB (Memento vom 11. Juni 2014 im Internet Archive)
- Alan Stripp: The Enigma machine in Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 86. ISBN 0-19-280132-5.
- David H. Hamer: Enigma – Actions involved in the ’double stepping’ of the middle rotor. Publikation. intelligenia.org (PDF; 0,1 MB) Abgerufen: 4. Nov. 2013.
- Jack Good: Enigma and fish. In Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 158. ISBN 0-19-280132-5.
- Michael Pröse: Chiffriermaschinen und Entzifferungsgeräte im Zweiten Weltkrieg – Technikgeschichte und informatikhistorische Aspekte. Dissertation Technische Universität Chemnitz, Leipzig 2004, S. 43f.
- When the Russians Visited the Enigma Firm (englisch). Abgerufen: 14. Oktober 2016.
- Report on Berlin Targets by Major Heller. TICOM Report I-104 vom 17. September 1945 (englisch), S. 200, abgerufen in Frode Weierud’s CryptoCellar am 4. April 2021.
- Army Security Agency: Notes on German High Level Cryptography and Cryptanalysis. European Axis Signal Intelligence in World War II, Vol 2, Washington (D.C.), 1946 (Mai), S. 2. Abgerufen: 24. August 2018. PDF; 7,5 MB (Memento vom 11. Juni 2014 im Internet Archive)
- David H. Hamer: G-312. An Abwehr Enigma. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 24.2000,1 (Januar), S. 42. ISSN 0161-1194.
- Mavis Batey: Dilly Knox – A Reminiscence of this Pioneer Enigma Cryptanalyst. Cryptologia, Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 32.2008,2, S. 104–130.
- Frank Carter: The Abwehr Enigma Machine. Publikation, Bletchley Park. bletchleypark.org.uk (PDF; 0,1 MB) Abgerufen: 4. Nov. 2013.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 129. ISBN 0-304-36662-5.
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, S. 190 ff. ISBN 3-453-17285-X.
- Army Security Agency: Notes on German High Level Cryptography and Cryptanalysis. European Axis Signal Intelligence in World War II, Vol 2, Washington (D.C.), 1946 (Mai), S. 12. Abgerufen: 24. August 2018. PDF; 7,5 MB (Memento vom 11. Juni 2014 im Internet Archive)
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 81. ISBN 0-947712-34-8.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 384. ISBN 0-304-36662-5.
- Manufacture of Enigma Machines by Heimsoeth and Rinke, Berlin. TICOM-Report M-13 (englisch) vom 17. November 1945, abgerufen am 4. April 2021 in Frode Weierud’s CryptoCellar.
- Louis Kruh, Cipher Deavours: The commercial Enigma – Beginnings of machine cryptography. Cryptologia, Rose-Hulman Institute of Technology, Taylor & Francis, Philadelphia PA 26.2002,1 (Januar), S. 11. ISSN 0161-1194 Abgerufen: 24. August 2018. PDF; 0,8 MB (Memento vom 13. April 2006 im Internet Archive)
- Enigma A im Crypto Museum (englisch) abgerufen am 20. Februar 2019.
- Enigma B im Crypto Museum (englisch) abgerufen am 20. Februar 2019.
- Louis Kruh, Cipher Deavours: The commercial Enigma – Beginnings of machine cryptography. Cryptologia, Rose-Hulman Institute of Technology, Taylor & Francis, Philadelphia PA 26.2002,1 (Januar), S. 5. ISSN 0161-1194 Abgerufen: 24. August 2018. PDF; 0,8 MB (Memento vom 13. April 2006 im Internet Archive)
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 114.
- David H. Hamer: G-312. An Abwehr Enigma. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 24.2000,1 (Januar). ISSN 0161-1194.
- Enigma‑H im Crypto Museum (englisch). Abgerufen: 11. Februar 2016.
- David H. Hamer, Geoff Sullivan, Frode Weierud: Enigma Variations – An Extended Family of Machines. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 22.1998,1 (Juli), S. 10 ff., ISSN 0161-1194. cryptocellar.org (PDF; 80 kB) Abgerufen: 15. Februar 2016.
- Michael Pröse: Chiffriermaschinen und Entzifferungsgeräte im Zweiten Weltkrieg – Technikgeschichte und informatikhistorische Aspekte. Dissertation Technische Universität Chemnitz, Leipzig 2004, S. 50
- Ralph Erskine, Frode Weierud: Naval Enigma – M4 and its Rotors. Cryptologia, 11:4, 1987, S. 237, doi:10.1080/0161-118791862063.
- Daniel J. Girard: Breaking “Tirpitz” – Cryptanalysis of the Japanese German Joint Naval Cipher, Cryptologia, 2016. doi:10.1080/01611194.2015.1087073
- Anders Wik: Enigma Z30 retrieved. In: Cryptologia. Taylor & Francis, 14. Dezember 2015, S. 1–6, doi:10.1080/01611194.2015.1055387.
- Frode Weierud: Tirpitz and the Japanese-German naval war communication agreement. Cryptolog, Vol. 20, Nr. 3, Sommer 1999. cryptocellar.org (PDF; 0,1 MB) Abgerufen: 15. Februar 2016.
- Arturo Quirantes: Model Z, a numbers-only Enigma version. Cryptologia, Rose-Hulman Institute of Technology, Taylor & Francis, Philadelphia PA 26.2002, April 2004. ISSN 0161-1194 Abgerufen: 4. Nov. 2013. Enigma-Z
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 142.
- Geoff Sullivan, Frode Weierud: Breaking German Army Ciphers. Cryptologia, Vol XXIX (3), Juli 2005, S. 193–232.
- Lothar-Günther Buchheim: Das Boot. Roman. dtv, München 1976. ISBN 3-423-01206-4.
- Kritik der Rhein-Zeitung. Abgerufen: 4. Nov. 2013.
- Chris Christensen: Review of The Imitation Game, Cryptologia, 2016. doi:10.1080/01611194.2016.1236639
- Benedict Cumberbatch and Keira Knightleys Imitation Game romance labelled inaccurate. Abgerufen: 9. Februar 2015.
- Don’t turn my uncle’s life into a romance, says Alan Turing’s niece. Abgerufen: 9. Februar 2015.
- Alex von Tunzelmann The Imitation Game: inventing a new slander to insult Alan Turing in: The Guardian, 20. November 2014. Abgerufen: 9. Februar 2015.
- Robert Harris: Enigma. Roman. Weltbild, Augsburg 2005. ISBN 3-89897-119-8.
- Tony Sale: Making the Enigma ciphers for the film „Enigma“. Abgerufen: 4. Nov. 2013.
- Polnische Proteste gegen den Film „Enigma“. Abgerufen: 4. Nov. 2013.
- Polnische Proteste gegen die Darstellung eines „polnischen Verräters“. Abgerufen: 4. Nov. 2013.
- Polnische Beiträge zum Bruch der Enigma. Abgerufen: 4. Nov. 2013.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 204. ISBN 0-947712-34-8.
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 11 ff. ISBN 0-19-280132-5.
- Louis Kruh, Cipher Deavours: The Commercial Enigma – Beginnings of Machine Cryptography. Cryptologia, Vol. XXVI, Nr. 1, Januar 2002, S. 11. apprendre-en-ligne.net (PDF; 0,8 MB) Abgerufen: 4. Nov. 2013.
- Craig P. Bauer: Secret History – The Story of Cryptology. CRC Press, Boca Raton 2013, S. 248. ISBN 978-1-4665-6186-1.
- David Kahn: Seizing the Enigma – The Race to Break the German U‑Boat Codes, 1939–1943. Naval Institute Press, Annapolis, MD, USA, 2012, S 83. ISBN 978-1-59114-807-4.
- Rudolf Kippenhahn: Verschlüsselte Botschaften, Geheimschrift, Enigma und Chipkarte. Rowohlt, Reinbek bei Hamburg 1999, S.. 226. ISBN 3-499-60807-3.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 355. ISBN 0-304-36662-5.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 214. ISBN 0-947712-34-8.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 50.
- Scan eines (damals) geheimen Schreibens des OKM vom 15. Oktober 1941 an den Befehlshaber der Schlachtschiffe mit Eingangsstempel vom 23. Oktober 1941, abgerufen im Crypto Museum am 21. Dezember 2020.
- Philip Marks: Umkehrwalze D: Enigma’s rewirable reflector – Part 1. Cryptologia, Volume XXV, Nummer 2, April 2001, S. 107.
- Michael Pröse: Chiffriermaschinen und Entzifferungsgeräte im Zweiten Weltkrieg – Technikgeschichte und informatikhistorische Aspekte. Dissertation Technische Universität Chemnitz, Leipzig 2004, S. 40.
- Heinz Ulbricht: Die Chiffriermaschine Enigma – Trügerische Sicherheit. Ein Beitrag zur Geschichte der Nachrichtendienste. Dissertation Braunschweig 2005, S. 22.
- Michael Pröse: Chiffriermaschinen und Entzifferungsgeräte im Zweiten Weltkrieg – Technikgeschichte und informatikhistorische Aspekte. Dissertation 2004, S. 143.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 220. ISBN 0-947712-34-8.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 16. codesandciphers.org.uk (PDF; 0,4 MB) Abgerufen am 19. Oktober 2017.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 108. ISBN 0-947712-34-8.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 20. codesandciphers.org (PDF; 0,4 MB) Abgerufen am 30. März 2017.
- Geoff Sullivan, Frode Weierud: Breaking German Army Ciphers. Cryptologia, Vol XXIX (3), Juli 2005, S. 212–214.
- James A. Reeds, Whitfield Diffie, J. V. Field: Breaking Teleprinter Ciphers at Bletchley Park: An edition of I. J. Good, D. Michie and G. Timms: General Report on Tunny with Emphasis on Statistical Methods (1945). Wiley-IEEE Press, 2015, S. 396 (englisch). ISBN 978-0-470-46589-9.
- Dermot Turing: The American Army Bombe. In: HistoCrypt 2021 – Proceedings of the 4th International Conference on Historical Cryptology. S. 139.
- Dermot Turing: The American Army Bombe. In: HistoCrypt 2021 – Proceedings of the 4th International Conference on Historical Cryptology. S. 139–140.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 26. codesandciphers.org.uk (PDF; 0,4 MB) Abgerufen am 30. März 2017.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 27. codesandciphers.org.uk (PDF; 0,4 MB) Abgerufen am 30. März 2017.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 49.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 102. ISBN 0-947712-34-8.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 426.
- David Kahn: Seizing the Enigma – The Race to Break the German U‑Boat Codes, 1939–1943. Naval Institute Press, Annapolis, MD, USA, 2012, S. 139. ISBN 978-1-59114-807-4.
- Oberkommando der Wehrmacht: Allgemeine Schlüsselregeln für die Wehrmacht. H.Dv.g. 7, Reichsdruckerei, Berlin 1944, S. 5. cdvandt.org (PDF; 0,9 MB) Abgerufen: 4. Nov. 2013.
- OKW: Schlüsselanleitung zur Schlüsselmaschine Enigma. H.Dv.g. 14, Reichsdruckerei, Berlin 1940, S. 7. (Abschrift des Original-Handbuchs mit einigen kleinen Tippfehlern.) Abgerufen am 28. November 2018. PDF; 0,1 MB (Memento vom 24. September 2015 im Internet Archive)
- José Ramón Soler Fuensanta, Francisco Javier López-Brea Espiau und Frode Weierud: Spanish Enigma: A History of the Enigma in Spain. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 34.2010,4 (Oktober), S. 313. ISSN 0161-1194.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 45, abgerufen am 14. Dezember 2018. codesandciphers.org.uk (PDF; 0,4 MB)
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 422. ISBN 0-304-36662-5.
- John Jackson: Solving Enigma’s Secrets – The Official History of Bletchley Park’s Hut 6. BookTower Publishing 2014, S. 211. ISBN 978-0-9557164-3-0.
- OKM: Der Schlüssel M – Verfahren M Allgemein. Berlin 1940, S. 9.
- Louis Kruh, Cipher Deavours: The Commercial Enigma – Beginnings of Machine Cryptography. Cryptologia, Vol. XXVI, Nr. 1, Januar 2002, S. 11. apprendre-en-ligne.net (PDF; 0,8 MB)


