Produkt (Mathematik)

Unter einem Produkt versteht man das Ergebnis einer Multiplikation sowie auch einen Term, der eine Multiplikation darstellt. Die verknüpften Elemente heißen Faktoren.

In diesem Sinne ist ein Produkt eine Abbildung der Form

\cdot \;:\;A\times B\;\rightarrow \;C

wobei man das Produkt von $a\in A$ und $b\in B$ meist als $a\cdot b$ notiert.

Abgeleitet vom lateinischen Wort producere in der Bedeutung (her-)vorbringen ist „Produkt“ ursprünglich die Bezeichnung des Ergebnisses einer Multiplikation zweier Zahlen (von lat.: multiplicare = vervielfachen).[1] Die Verwendung des Malpunktes $\;\cdot \;$ geht auf Gottfried Wilhelm Leibniz zurück, das alternative Symbol $\times$ auf William Oughtred.[2]

Produkte zweier Zahlen

Hier ist stets $A=B=C$ , d. h., das Produkt zweier Zahlen ist wieder eine Zahl. Produkte werden hier zusätzlich als assoziativ vorausgesetzt, d. h.

(a\cdot b)\cdot c=a\cdot (b\cdot c)\quad {\text{für alle }}a,b,c\in A

Produkt zweier natürlicher Zahlen

3 mal 4 ergibt 12

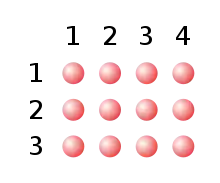
Ordnet man etwa Spielsteine in einem rechteckigen Schema in r Reihen zu je s Steinen an, so benötigt man dafür

r\cdot s=\sum _{i=1}^{s}r=\sum _{j=1}^{r}s

Spielsteine. Die Multiplikation ist hier eine Kurzschreibweise für die mehrfache Addition von r Summanden (entsprechend den r Reihen), die sämtliche den Wert s tragen (in jeder Reihe stehen s Steine). Man kann die Gesamtzahl aber auch dadurch berechnen, dass man die Zahl s (entsprechend der Anzahl der hintereinander in einer Spalte stehenden Steine) insgesamt r Mal (entsprechend der Anzahl r solcher nebeneinander angeordneter Spalten von Steinen) addiert (man benötigt hierfür r-1 Pluszeichen). Damit ist bereits die Kommutativität der Multiplikation zweier natürlicher Zahlen gezeigt.

Zählt man die Zahl 0 zu den natürlichen Zahlen, so bilden diese einen Halbring. Zu einem Ring fehlen die inversen Elemente bzgl. der Addition: Es gibt keine natürliche Zahl x mit der Eigenschaft 3+x=0.

Ein Produkt, bei dem die Zahl 0 als ein Faktor auftritt, hat stets den Wert Null: Eine Anordnung von Null Reihen von Spielsteinen umfasst unabhängig von der Zahl der Steine pro Reihe keinen einzigen Stein.

Produkt zweier ganzer Zahlen

Durch Hinzufügen der negativen ganzen Zahlen erhält man den Ring $\mathbb {Z}$ der ganzen Zahlen. Zwei ganze Zahlen werden multipliziert, indem man ihre jeweiligen Beträge multipliziert und mit folgendem Vorzeichen versieht:

{\begin{array}{|c|c  c|}\hline \cdot &-&+\\\hline -&+&-\\+&-&+\\\hline \end{array}}

In Worten ausgedrückt besagt diese Tabelle:

Minus mal Minus ergibt Plus
Minus mal Plus ergibt Minus
Plus mal Minus ergibt Minus
Plus mal Plus ergibt Plus

Für eine streng formale Definition über Äquivalenzklassen von Paaren natürlichen Zahlen vergleiche man den Artikel über ganze Zahlen.

Produkt zweier Brüche

In den ganzen Zahlen kann man uneingeschränkt addieren, subtrahieren und multiplizieren. Die Division durch eine von Null verschiedene Zahl ist nur möglich, falls der Dividend ein Vielfaches des Divisors ist. Diese Einschränkung lässt sich mit dem Übergang zum Körper der rationalen Zahlen, also zur Menge $\mathbb {Q}$ aller Brüche, aufheben. Das Produkt zweier Brüche erfordert im Gegensatz zu ihrer Summe nicht die Bildung eines Hauptnenners:

{\frac {z}{n}}\cdot {\frac {z'}{n'}}={\frac {z\cdot z'}{n\cdot n'}}

Gegebenenfalls lässt sich das Ergebnis noch kürzen.

Produkt zweier reeller Zahlen

Wie bereits Euklid nachweisen konnte, gibt es keine rationale Zahl, deren Quadrat Zwei ergibt. Ebenso ist das Verhältnis von Kreisumfang zu Kreisdurchmesser, also die Kreiszahl π, nicht als Quotient zweier ganzer Zahlen darstellbar. Beide „Lücken“ werden durch eine sogenannte Vervollständigung im Übergang zum Körper der reellen Zahlen $\mathbb {R}$ geschlossen. Da eine exakte Definition des Produktes in der hier gebotenen Kürze nicht möglich erscheint, sei nur kurz die Idee skizziert:

Jede reelle Zahl lässt sich als ein unendlicher Dezimalbruch auffassen. So sind etwa ${\sqrt {2}}=1{,}4142\ldots$ und $\pi =3{,}1415\ldots$ Die rationalen Näherungswerte – etwa 1,41 und 3,14 – lassen sich problemlos miteinander multiplizieren. Durch sukzessive Erhöhung der Anzahl der Nachkommastellen erhält man – in einem nicht in endlicher Zeit durchführbaren Prozess – eine Folge von Näherungswerten für das Produkt ${\sqrt {2}}\cdot \pi =4{,}4428\ldots$

Produkt zweier komplexer Zahlen

Selbst über der Menge der reellen Zahlen gibt es unlösbare Gleichungen wie etwa $x^{2}=-1$ . Sowohl für negative wie auch für positive Werte von $x$ ist das Quadrat auf der linken Seite stets eine positive Zahl. Durch den Übergang zum Körper $\mathbb {C}$ der komplexen Zahlen, der oft auch als Adjunktion, also Hinzufügen von $\mathrm {i} ={\sqrt {-1}}$ bezeichnet wird, entsteht aus der reellen Zahlengerade die sogenannte gaußsche Zahlenebene. Zwei Punkte dieser Ebene, also zwei komplexe Zahlen, werden unter Beachtung von $\mathrm {i} ^{2}=-1$ formal multipliziert:

{\begin{aligned}(a+b\,\mathrm {i} )\cdot (c+d\,\mathrm {i} )&=a\cdot c+a\cdot d\,\mathrm {i} +b\cdot c\,\mathrm {i} +b\cdot d\cdot \mathrm {i} ^{2}\\&=(a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)\,\mathrm {i} \end{aligned}}

Geometrische Deutung

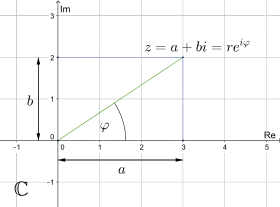
Eine komplexe Zahl in Polarkoordinaten

Eine komplexe Zahl lässt sich auch in ebenen Polarkoordinaten schreiben:

a+b\,\mathrm {i} =r\cdot (\cos(\varphi )+\mathrm {i} \sin(\varphi ))=r\cdot \mathrm {e} ^{\mathrm {i} \varphi }

Ist ferner

c+d\,\mathrm {i} =s\cdot (\cos(\psi )+\mathrm {i} \sin(\psi ))=s\cdot \mathrm {e} ^{\mathrm {i} \psi }

so gilt aufgrund der Additionstheoreme für Sinus und Cosinus

(a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)\,\mathrm {i} =r\cdot s\cdot (\cos(\varphi +\psi )+\mathrm {i} \sin(\varphi +\psi ))=r\cdot s\cdot \mathrm {e} ^{\mathrm {i} (\varphi +\psi )}

Geometrisch bedeutet das: Multiplikation der Längen bei gleichzeitiger Addition der Winkel.

Produkt zweier Quaternionen

Selbst die komplexen Zahlen lassen sich noch algebraisch erweitern. Es entsteht ein reell vierdimensionaler Raum, die sogenannten hamiltonschen Quaternionen $\mathbb {H}$ . Die zugehörigen Multiplikationsregeln werden im Artikel Quaternion ausführlich dargestellt. Im Gegensatz zu den obigen Zahlbereichen ist die Multiplikation von Quaternionen nicht kommutativ, d. h., $a\cdot b$ und $b\cdot a$ sind allgemein verschieden.

Weitere Beispiele für kommutative Ringe

Restklassen ganzer Zahlen

Dass das Produkt zweier Zahlen genau dann ungerade ist, wenn beide Faktoren ungerade sind, ist eine weithin bekannte Tatsache. Ähnliche Regeln gelten auch bezüglich der Teilbarkeit durch eine ganze Zahl N größer als Zwei. Die geraden Zahlen entsprechen hierbei den Vielfachen von N; eine gerade Zahl ist ohne Rest durch Zwei teilbar. Bei den ungeraden Zahlen sollte man unterscheiden, welcher Rest bei der ganzzahligen Division dieser Zahl durch N übrig bleibt. Modulo 3 – so die Sprechweise – gibt es drei Restklassen ganzer Zahlen: Solche, die Vielfache von Drei sind, solche mit Rest 1 und solche mit Rest 2. Das Produkt zweier solcher Zahlen hat stets Rest Eins modulo Drei.

Die Menge dieser Restklassen, $\mathbb {Z} /N\mathbb {Z}$ geschrieben, besitzt genau N Elemente. Ein typisches Element hat die Form $a+N\mathbb {Z}$ und steht für die Menge aller ganzen Zahlen, die bei Division durch N denselben Rest ergeben wie die Zahl a. Auf der Menge aller solcher Restklassen wird durch

(a+N\mathbb {Z} )+(b+N\mathbb {Z} )=a+b+N\mathbb {Z}

eine Addition und durch

(a+N\mathbb {Z} )\cdot (b+N\mathbb {Z} )=a\cdot b+N\mathbb {Z}

eine Multiplikation erklärt. Der so entstehende Ring heißt der Restklassenring modulo N. Genau dann, wenn N eine Primzahl ist, handelt es sich hierbei sogar um einen Körper. Beispiel: modulo 5 ist die Restklasse von 2 invers zu der von 3, da 6 modulo 5 Eins ist. Das systematische Auffinden von multiplikativen Inversen modulo N erfolgt mittels des Euklidischen Algorithmus.

Funktionenringe

Ist der Ring R kommutativ, so bildet die Menge $\mathbb {F$ (die Menge aller Funktionen von einer nichtleeren Menge M mit Werten in R) ebenfalls einen kommutativen Ring, wenn man Addition und Multiplikation in $\mathbb {F}$ komponentenweise definiert. Das heißt, wenn man

(f+g)(m):=f(m)+g(m)

(f\cdot g)(m):=f(m)\cdot g(m)

für alle $m\in M$ erklärt.

Wählt man als Ring R die reellen Zahlen $\mathbb {R}$ mit den üblichen Addition und Multiplikation, und als M etwa eine offene Teilmenge von $\mathbb {R}$ oder allgemeiner von $\mathbb {R} ^{n}$ , so sind die Begriffe Stetigkeit und Differenzierbarkeit von Funktionen sinnvoll. Die Menge der stetigen bzw. differenzierbaren Funktionen $f:M\to R$ bildet dann einen Unterring des Funktionenringes, der trivialerweise wieder kommutativ sein muss, wenn $\mathbb {F}$ bzw. R kommutativ ist.

Faltungsprodukt

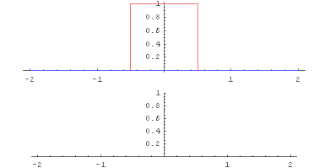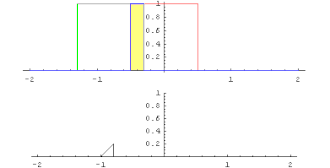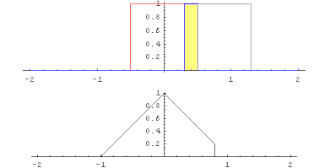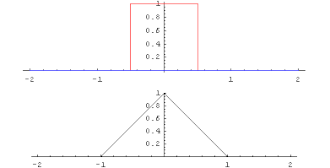
Faltung der Rechteckfunktion mit sich selbst ergibt die Dreiecksfunktion

Seien $f,g\colon \mathbb {R} \rightarrow \mathbb {R} \,$ zwei integrierbare reelle Funktionen, deren Beträge ein endliches uneigentliches Integral besitzen:

\int \limits _{-\infty }^{\infty }|f(t)|\,\mathrm {d} \,t\;<\;\infty \quad {\text{und }}\int \limits _{-\infty }^{\infty }|g(t)|\,\mathrm {d} \,t\;<\;\infty

Dann ist das uneigentliche Integral

(f*g)(t)\;:=\int \limits _{-\infty }^{\infty }f(\tau )\cdot g(t-\tau )\,\mathrm {d} \tau

für jede reelle Zahl t ebenfalls endlich. Die dadurch definierte Funktion f*g heißt das Faltungsprodukt oder die Konvolution von f und g. Dabei ist f*g wieder integrierbar mit endlichem uneigentlichem Betragsintegral. Ferner gilt f*g=g*f, d. h., die Faltung ist kommutativ.

Nach Fourier-Transformation ist das Faltungsprodukt bis auf einen konstanten Normierungsfaktor das punktweise definierte Produkt (sog. Faltungstheorem). Das Faltungsprodukt spielt eine wichtige Rolle in der mathematischen Signalverarbeitung.

Die gaußsche Glockenkurve lässt sich dadurch charakterisieren, dass ihre Faltung mit sich selbst wieder eine etwas in die Breite gezogene Glockenkurve ergibt (vgl. hier). Genau diese Eigenschaft liegt dem zentralen Grenzwertsatz zugrunde.

Polynomringe

Die Menge $\mathbb {R} [X]$ aller Polynome in der Variablen X mit reellen Koeffizienten bildet ebenfalls einen sogenannten Polynomring. Das Produkt wird hierbei wie folgt berechnet:

\left(\sum _{i=0}^{n}a_{i}X^{i}\right)\cdot \left(\sum _{j=0}^{m}b_{j}X^{j}\right)=\sum _{k=0}^{n+m}c_{k}X^{k}

mit

c_{k}=\sum _{i+j=k}a_{i}\cdot b_{j}

Diese Ringe spielen in vielen Bereichen der Algebra eine große Rolle. So lässt sich etwa der Körper der komplexen Zahlen formal elegant als Faktorring $\mathbb {R} [X]/(X^{2}+1)$ definieren.

Beim Übergang von endlichen Summen zu absolut-konvergenten Reihen bzw. formalen Potenzreihen wird aus dem hier besprochenen Produkt das sog. Cauchy-Produkt.

Produkte in der linearen Algebra

Die lineare Algebra beschäftigt sich mit Vektorräumen und linearen Abbildungen zwischen solchen. In diesem Zusammenhang treten verschiedenartige Produkte auf. Im Folgenden wird zur Vereinfachung als Grundkörper zumeist der Körper der reellen Zahlen verwendet.

Skalares Produkt

Bereits in der Definition eines Vektorraums V taucht der Begriff der Skalarmultiplikation auf. Damit lassen sich Vektoren ganz allgemein um einen reellen Faktor „strecken“, wobei im Falle der Multiplikation mit einem negativen Skalar auch noch die Richtung des Vektors umgedreht wird.

Das Skalare Produkt ist eine Abbildung $\mathbb {R} \times V\rightarrow V$

Skalarprodukt

Davon strikt zu unterscheiden ist der Begriff eines Skalarprodukts. Dabei handelt es sich um eine bilineare Abbildung

\cdot :V\times V\rightarrow \mathbb {R}

mit der zusätzlichen Forderung, dass $v\cdot v>0$ für alle $0\not =v\in V$ ist.

Daher ist der Ausdruck $\|v\|:={\sqrt {v\cdot v}}$ stets berechenbar und liefert den Begriff der Norm (Länge) eines Vektors.

Ebenso gestattet das Skalarprodukt die Definition eines Winkels zwischen zwei von Null verschiedenen Vektoren v und w:

\cos \angle (v,w)={\frac {v\cdot w}{\|v\|\cdot \|w\|}}

Die Polarisationsformel zeigt, dass ein solcher Längenbegriff umgekehrt stets zu einem Skalarprodukt und somit auch zu einem Winkelbegriff führt.

In jedem n-dimensionalen Euklidischen Raum lässt sich durch Orthonormalisierung eine Orthonormalsystem finden. Stellt man alle Vektoren als Linearkombination bezüglich einer Orthonormalbasis $e_{1},\ldots e_{n}$ dar, so lässt sich das Skalarprodukt zweier solcher Koordinatentupel als Standardskalarprodukt berechnen:

\left(\sum _{i=1}^{n}\alpha _{i}e_{i}\right)\cdot \left(\sum _{i=1}^{n}\beta _{i}e_{i}\right)=\sum _{i=1}^{n}\alpha _{i}\,\beta _{i}

Kreuzprodukt im dreidimensionalen Raum

Im $\mathbb {R} ^{3}$ , als dem Standardmodell eines 3-dimensionalen Euklidischen Raums, lässt sich ein weiteres Produkt, das sogenannte Kreuzprodukt definieren. Es leistet hervorragende Dienste bei diversen Problemen der analytischen Geometrie im Raum.

Beim Kreuzprodukt handelt es sich um eine Abbildung

{\displaystyle \times

Wie jedes Lie-Produkt ist es antikommutativ: $v\times w=-w\times v$ Insbesondere ist $v\times v=0$

Spatprodukt

Beim sogenannten Spatprodukt – ebenfalls nur im $\mathbb {R} ^{3}$ erklärt – handelt es sich nicht um ein Produkt zweier, sondern dreier Vektoren. In moderner Sprechweise stimmt es mit der Determinante von drei nebeneinander geschriebener Spaltenvektoren überein und lässt sich wohl am einfachsten nach der Regel von Sarrus berechnen. Formal liegt eine Abbildung

{\displaystyle \det

vor, die wohl nur aus historischen Gründen noch heute als ein Produkt bezeichnet wird. Anschaulich misst das Spatprodukt das Volumen eines Spates im Raum.

Komposition linearer Abbildungen

Sind f: U → V und g: V → W zwei lineare Abbildungen, so ist ihre Hintereinanderausführung

g\circ f:U\ni u\mapsto g(f(u))\in W

linear. Bezeichnet man die Menge aller linearen Abbildungen von U nach V mit $\operatorname {Hom} (U,V)$ , so liefert die Komposition von Abbildungen ein Produkt

{\displaystyle \circ

Im Spezialfall U = V = W erhält man so den sogenannten Endomorphismenring $\operatorname {End} (V)=\operatorname {Hom} (V,V)$ von V.

Produkt zweier Matrizen

Gegeben seien zwei Matrizen $A=(a_{i,j})_{i=1\ldots s;j=1\ldots r}\in \mathbb {R} ^{s\times r}$ und $B=(b_{j,k})_{j=1\ldots r;k=1\ldots t}\in \mathbb {R} ^{r\times t}$ . Da die Anzahl der Spalten von A mit der Anzahl der Zeilen von B übereinstimmt, lässt sich das Matrizenprodukt

A\cdot B=\left(\sum _{j=1}^{r}a_{i,j}\cdot b_{j,k}\right)_{i=1\ldots s;k=1\ldots t}\;\in \mathbb {R} ^{s\times t}

bilden. Im Spezialfall r = s = t quadratischer Matrizen entsteht hierdurch der Matrizenring $\mathbb {R} ^{r\times r}$ .

Komposition linearer Abbildungen als Matrizenprodukt

Zwischen der Komposition linearer Abbildungen und dem Produkt zweier Matrizen besteht ein enger Zusammenhang. Seien dazu r = dim(U), s = dim(V) und t = dim(W) die (endlichen) Dimensionen der beteiligten Vektorräume U, V und W. Seien ferner ${\mathcal {U}}=\{u_{1},\ldots u_{r}\}$ eine Basis von U, ${\mathcal {V}}=\{v_{1},\ldots v_{s}\}$ eine Basis von V und ${\mathcal {W}}=\{w_{1},\ldots w_{t}\}$ eine Basis von W. Bezüglich dieser Basen seien $A=M_{\mathcal {V}}^{\mathcal {U}}(f)\in \mathbb {R} ^{s\times r}$ die darstellende Matrix von f: U → V und $B=M_{\mathcal {W}}^{\mathcal {V}}(g)\in \mathbb {R} ^{r\times t}$ die darstellende Matrix von g: V → W. Dann ist

B\cdot A=M_{\mathcal {W}}^{\mathcal {U}}(g\circ f)\in \mathbb {R} ^{s\times t}

die darstellende Matrix von $g\circ f:U\rightarrow W$ .

Mit anderen Worten: das Matrizenprodukt liefert die koordinatenabhängige Beschreibung der Komposition zweier linearer Abbildungen.

Tensorprodukt von Vektorräumen

Das Tensorprodukt $V\otimes W$ zweier reeller Vektorräume V und W ist eine Art Produkt zweier Vektorräume. Es ähnelt daher dem weiter unten besprochenen mengentheoretischem Produkt. Im Gegensatz zu diesem handelt es sich aber nicht um das kategorielle Produkt in der Kategorie der reellen Vektorräume. Es lässt sich dennoch über eine universelle Eigenschaft bezüglich bilinearer Abbildungen kategoriell fassen. Danach ist die kanonische Einbettung

V\times W\ni (v,w)\mapsto v\otimes w\in V\otimes W

sozusagen die „Mutter aller auf V und W definierbaren Produkte“. Jedes andere reell-bilineare Produkt

B:V\times W\rightarrow Y

mit Werten in irgendeinem Vektorraum Y kommt nämlich durch Nachschalten einer eindeutig bestimmten linearen Abbildung

{\tilde {B}}:V\otimes W\rightarrow Y

zustande.

Abbildungsmatrizen als Tensoren zweiter Stufe

Der Vektorraum Hom(V,W) aller linearen Abbildungen zwischen zwei Vektorräumen V und W lässt sich auf (bifunktoriell) natürliche Weise als Tensorprodukt des Dualraums V^* von V mit W auffassen:

V^{*}\otimes W\rightarrow \operatorname {Hom} (V,W)

Hierbei wird einem zerlegbaren Tensor $f\otimes w\in V^{*}\otimes W\,$ , also einem Funktional f: V → R und einem Vektor w in W, die lineare Abbildung g: V → W mit

g(v)=f(v)\cdot w\,

zugeordnet. Lässt sich so jede lineare Abbildung von V nach W erhalten? Nein, ebenso ist aber auch nicht jeder Tensor zerlegbar. Wie jeder Tensor sich als Summe zerlegbarer Tensoren schreiben lässt, so lässt sich auch jede lineare Abbildung von V nach W als Summe von Abbildungen wie dem oben definierten g erhalten.

Dass Hom(V,W) in natürlicher Weise zum Tensorprodukt des Dualraums von V mit W isomorph ist, bedeutet gleichzeitig, dass es sich bei der darstellenden Matrix einer linearen Abbildung g: V → W um einen einfach kontravarianten und einfach kovarianten Tensor handelt. Dies drückt sich auch im Transformationsverhalten von darstellenden Matrizen bei einem Basiswechsel aus.

Mengentheoretisches Produkt

Das kartesische Produkt M × N zweier Mengen M und N fügt sich auf den ersten Blick nicht zwanglos in den hier vorgestellten Produktbegriff ein. Dennoch besteht nicht nur im Wort „Produkt“ eine Verbindung: Das Produkt zweier natürlicher Zahlen m und n wurde weiter oben als die Kardinalität des kartesischen Produkt einer m-elementigen mit einer n-elementigen Menge erklärt. Weiterhin gelten bestimmte Formen des Distributivgesetzes.

Das kartesische Produkt ist gleichzeitig das kategorielle Produkt in der Kategorie der Mengen.

Endliche und unendliche Produkte

Endliche Produkte mit vielen Faktoren

Die Produktschreibweise

Die Fakultät einer natürlichen Zahl n (geschrieben als n!) beschreibt die Anzahl der möglichen Anordnungen von n unterscheidbaren Objekten in einer Reihe:

n!=1\cdot 2\cdot \ldots \cdot (n-1)\cdot n=\prod _{i=1}^{n}i

Das Produktzeichen $\textstyle \prod$ ist in Anlehnung an den ersten Buchstaben des Wortes Produkt der griechischen Majuskel Pi nachempfunden;[3] ebenso wird $\textstyle \sum$ angelehnt an das Sigma als Summenzeichen verwendet.

Da das Produkt natürlicher Zahlen kommutativ ist, kann man auch eine Indexmenge verwenden (und damit die Reihenfolge der Faktoren unbestimmt lassen)

n!=\prod _{i\in \{1,\ldots ,n\}}i

Hier eine Animation zur Produktschreibweise:

Das leere Produkt

Das leere Produkt hat den Wert Eins (das neutrale Element der Multiplikation) – ebenso wie die leere Summe stets Null (das neutrale Element der Addition) ergibt.

Unendliche Produkte

John Wallis entdeckte 1655 die verblüffende Tatsache, dass

{\frac {\pi }{2}}=\prod _{i=1}^{\infty }{\frac {(2i)(2i)}{(2i-1)(2i+1)}}

gilt (vergleiche Wallissches Produkt). Was genau ist aber unter dem unendlichen Produkt auf der rechten Seite zu verstehen? Man betrachtet dazu die Folge der endlichen Teilprodukte

P_{n}:=\prod _{i=1}^{n}{\frac {(2i)(2i)}{(2i-1)(2i+1)}}

Falls diese Folge gegen eine reelle Zahl P konvergiert, so definiert man

\prod _{i=1}^{\infty }{\frac {(2i)(2i)}{(2i-1)(2i+1)}}\;:=P

Genauer sei $(a_{n})_{n\in \mathbb {N} }$ eine Folge von Zahlen. Das unendliche Produkt

\prod _{n=1}^{\infty }a_{n}

heißt genau dann konvergent, wenn die folgenden Bedingungen erfüllt sind:

Fast alle $a_{n}$ sind von Null verschieden, d. h., es gibt ein $n_{0}\in \mathbb {N}$ , so dass $a_{n}\neq 0$ für alle $n>n_{0}$ gilt,
der Grenzwert $\lim _{N\to \infty }\prod _{n=n_{0}+1}^{N}a_{n}$ existiert und
dieser Grenzwert ist von Null verschieden.

(Die Gültigkeit der letzten beiden Bedingungen ist unabhängig davon, welches $n_{0}$ man in der ersten gewählt hat). In diesem Fall setzt man

\prod _{n=1}^{\infty }a_{n}:=\lim _{N\to \infty }\prod _{n=1}^{N}a_{n}

.

Dieser Grenzwert existiert, denn entweder ist mindestens ein Faktor $a_{n}=0$ und ab dann sind alle Partialprodukte null oder man kann in der zweiten Bedingung o. B. d. A. $n_{0}=0$ wählen.

Kernreihenkriterium (Konvergenzkriterium für unendliche Produkte): Folgende Aussagen sind äquivalent:

Ein unendliches Produkt $\textstyle P=\prod \limits _{k=1}^{\infty }a_{k}=\prod \limits _{k=1}^{\infty }(1+h_{k})$ mit positiven Kernen $h_{k}$ konvergiert absolut.
Die Kernreihe $\textstyle S=\sum \limits _{n=1}^{\infty }h_{n}$ konvergiert absolut.[4]

Eigenschaften

Ein konvergentes unendliches Produkt ist genau dann null, wenn einer der Faktoren null ist. Ohne die dritte Bedingung wäre diese Aussage falsch.
Die Faktoren eines konvergenten Produktes konvergieren gegen 1 (notwendiges Kriterium).

Beispiele zu fehlender Konvergenz

Obwohl die Folge der Teilprodukte (gegen Null) konvergiert, werden unendliche Produkte wie die folgenden nicht als konvergent bezeichnet:

$\prod \limits _{n=1}^{\infty }0$ : Unendlich viele Faktoren sind Null, die erste Bedingung ist verletzt.
$\prod \limits _{n=1}^{\infty }(n-1)$ : Man muss $n_{0}\geq 1$ wählen. Wenn aber der erste Faktor weggelassen wird, konvergiert die Teilproduktfolge nicht (divergiert bestimmt gegen $+\infty$ ). Die zweite Bedingung ist verletzt.
$\prod \limits _{n=1}^{\infty }{\tfrac {1}{n}}$ : Die Folge der Teilprodukte konvergiert, allerdings gegen Null, so dass die dritte Bedingung verletzt ist.

Diese drei Beispiele erfüllen auch nicht das o. g. notwendige Kriterium. Das Produkt $\textstyle \prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)$ erfüllt zwar das notwendige Kriterium, die Folge der Teilprodukte konvergiert aber nicht: Das Produkt der ersten $N$ Faktoren ist $N+1$ .

Literatur

Aufbau des Zahlensystems. In: dtv-Atlas zur Mathematik, Bd. 1, 2. Auflage 1976, S. 52ff.
Heinz-Dieter Ebbinghaus et al.: Zahlen. Springer, Berlin 1992, ISBN 3-540-55654-0. (Google Books)

Umfangreiche Literaturangaben zur linearen Algebra finden sich dort.

Weblinks

Wiktionary: Produkt – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Mathe für Nicht-Freaks: Summe und Produkt – Lern- und Lehrmaterialien

Einzelnachweise

Auftreten in Albertus Magnus' Metaphysicorum in der Form productum, so Jeff Miller: Earliest Known Uses of Some of the Words of Mathematics (P) mit Verweis auf The Oxford English Dictionary, Second Edition (abgerufen am 10. August 2009.)
Steven Schwartzman: The words of mathematics: an etymological dictionary of mathematical terms used in English. Verlag MAA, 1994. ISBN 0-88385-511-9. Google Books.
Produktzeichen. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
Alexander Hölzle: Unendliche Produkte. (PDF; 80 kB) 2. Mai 2005, abgerufen am 26. Dezember 2012.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Auftreten in Albertus Magnus' Metaphysicorum in der Form productum, so Jeff Miller: Earliest Known Uses of Some of the Words of Mathematics (P) mit Verweis auf The Oxford English Dictionary, Second Edition (abgerufen am 10. August 2009.)

[2] Steven Schwartzman: The words of mathematics: an etymological dictionary of mathematical terms used in English. Verlag MAA, 1994. ISBN 0-88385-511-9. Google Books.

[3] Produktzeichen. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.

[4] Alexander Hölzle: Unendliche Produkte. (PDF; 80 kB) 2. Mai 2005, abgerufen am 26. Dezember 2012.