Polyalphabetische Substitution
Polyalphabetische Ersetzungschiffren (von altgriechisch πολύς polýs „viel“ und ἀλφάβητος alphábetos „Alphabet“) bezeichnen in der Kryptographie Formen der Textverschlüsselung, bei der einem Buchstaben bzw. Zeichen jeweils ein anderer Buchstabe bzw. Zeichen zugeordnet wird. Im Gegensatz zur monoalphabetischen Substitution werden zur Erzeugung des Geheimtextes aus dem Klartext viele („poly“) Geheimalphabete verwendet.
Caesar-Verschlüsselung mit fortschreitender Quelle
Diese Verschlüsselungsmethode arbeitet ähnlich wie die Caesar-Verschlüsselung, aber mit dem Unterschied, dass das aktuelle Klartextzeichen je nach dessen Position im Klartextstrang im Alphabet verschoben wird, wobei man gegebenenfalls wieder am Anfang beginnt. So einfach, wie dieses Verfahren ist, lässt sich auch der Geheimtext schnell entschlüsseln, indem man die Zeichen je nach ihrer Position in die andere Richtung im Alphabet verschiebt.
Beispiel:
Klartext: i n t e r n e t Positionen: 1 2 3 4 5 6 7 8 Geheimtext: J P W I W T L B
Vigenère-Verschlüsselung
Die im 16. Jahrhundert entstandene Vigenère-Verschlüsselung (nach Blaise de Vigenère) galt lange als sicherer Chiffrieralgorithmus („Le Chiffre indéchiffrable“, deutsch: „Die unentzifferbare Verschlüsselung“).[1] Ein Schlüsselwort bestimmt, wie viele und welche Alphabete genutzt werden. Die Alphabete leiten sich aus der Caesar-Substitution ab.
Dem britischen Mathematiker Charles Babbage gelang um das Jahr 1854 erstmals die Entzifferung einer Vigenère-Chiffre. Diese Entdeckung wurde jedoch damals nicht öffentlich bekannt gemacht. Der preußische Infanteriemajor Friedrich Kasiski veröffentlichte im Jahr 1863 seine Lösung (vgl. Kasiski-Test) und ging damit in die Geschichte ein.
Beispiele
Das Schlüsselwort sei „AKEY“, der Text „geheimnis“. Vier Caesar-Substitutionen verschlüsseln den Text. Die erste Substitution ist eine Caesar-Verschlüsselung mit dem Schlüssel „A“. „A“ ist der erste Buchstabe im Alphabet. Er verschiebt den ersten Buchstaben des zu verschlüsselnden Textes, das „g“, um 0 Stellen, es bleibt „G“. Der zweite Buchstabe des Schlüssels, das „K“, ist der elfte Buchstabe im Alphabet, er verschiebt das zweite Zeichen des Textes, das „e“, um zehn Zeichen. Aus „e“ wird ein „O“ (siehe Tabelle). Das dritte Zeichen des Schlüssels („E“) verschiebt um 4, „Y“ um 24 Stellen. Die Verschiebung des nächsten Buchstabens des Textes beginnt wieder bei „A“, dem ersten Buchstaben des Schlüssels:
Text: geheimnis Schlüssel: AKEYAKEYA Geheimtext: GOLCIWRGS
| Text | |||
|---|---|---|---|
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | |||
S c h l ü s s e l |
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
G e h e i m t e x t |
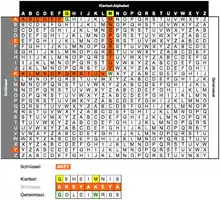
Mithilfe des Vigenère-Quadrats gelingt die Verschlüsselung noch einfacher: Wieder seien das Schlüsselwort „AKEY“ und der Text „geheimnis“. Damit ist jedem Buchstaben des Texts ein Buchstabe des Schlüssels zugeordnet, etwa dem „G“ des Texts das „A“ des Schlüssels. Nun sucht man die Reihe des Schlüssel-Buchstabens (hier die A-Reihe) und die Spalte des zu verschlüsselnden Buchstabens (hier die G-Spalte) auf, man erhält „G“. Beim zweiten Buchstaben des Texts, dem E, sucht man die K-Reihe (Schlüssel) und die E-Spalte (Text) auf und erhält ein „O“. Auf diese Weise dient das Quadrat als optische Hilfe, um die Verschlüsselung zu vereinfachen.
Kryptoanalyse
Schlüsselwörter, die im Verhältnis zum Text relativ kurz sind, bieten kaum Sicherheit. Die Länge des Schlüssels lässt sich herausfinden, indem der Text mit sich selbst (um n Stellen verschoben) korreliert und das n mit dem größten Korrelationswert ermittelt wird. Ist somit die Schlüssellänge (Periode) n bekannt, reduziert sich die Kryptoanalyse der Vigenère-Verschlüsselung auf die der Caesar-Verschlüsselung: Alle ersten, zweiten, …, n-ten Buchstaben einer Periode gehören jeweils zur selben Caesar-Verschlüsselung, und eine Häufigkeitsanalyse verrät die Buchstabenzuordnung.
Bei einem Text, der nur aus der Wiederholung eines Zeichens besteht, zeigt sich die Periode unmittelbar im Geheimtext. Ein normaler Text weist ausreichend Redundanzen auf, so dass ab einer gewissen Länge des Textes im Vergleich zum Schlüssel auch hier die Periode abgeleitet werden kann (Kasiski-Test, Friedman-Test).
Text: eeeeeeeeeeeee Schlüssel: AKEYAKEYAKEYA Geheimtext: eoiceoiceoice
Auf diese Weise bekommt man recht schnell die Schlüssellänge des verschlüsselten Textes heraus. Jetzt muss nur noch der Geheimtext spaltenweise zerlegt werden. Die Spalten, welche mit demselben Buchstaben verschlüsselt wurden, werden zusammengefasst. Die entsprechende Alphabetverschiebung der einzelnen Teiltexte löst man nun mittels Häufigkeitsanalyse.
Weist der Text keine oder nur wenige Redundanzen auf, beispielsweise weil er kurz ist, lässt sich die Schlüssellänge nicht mit dem Kasiski-Test herausfinden. Unter der Voraussetzung, dass es sich bei dem Schlüssel um ein Wort aus einem Wörterbuch handelt und auch der Text mit einem Wort beginnt, lässt sich jedoch durch geschicktes Aussortieren unwahrscheinlicher N-Gramm-Paare in vielen Fällen der Schlüssel finden. Dazu werden zuerst Text/Schlüssel-Kombinationen bewertet, ohne dass es eine Rolle spielt, was davon Klartext bzw. Schlüssel ist. Die Anzahl der Möglichkeiten wird so bereits im ersten Schritt von 26 auf 13 halbiert (N/E→R und E/N→R). Alle dann noch verbleibenden N-Gramm-Paare werden nun gemäß ihrer Wahrscheinlichkeit, am Anfang eines Wortes zu stehen, gewichtet. Ist mindestens eines der N-Gramme äußerst unwahrscheinlich an einem Wortanfang, wird das ganze Paar verworfen.
Beispiel: EIN/TKX und alle diesem Zweig folgenden 4-Gramme können verworfen werden, da TKX als Beginn einer Nachricht oder eines Schlüssels als extrem unwahrscheinlich erachtet wird.
Meist zeigt sich bereits ab Tetragrammen, dass die Anzahl der übrig gebliebenen Paare so stark reduziert wurde, dass eine Überprüfung aller restlichen Möglichkeiten machbar ist. Es bleiben statt 456.976 (= 26^4 bei Tetragrammen) meist nur ca. einhundert sinnvolle Möglichkeiten übrig. Anhand eines Wörterbuches können nun alle Wörter, die mit diesen Tetragrammen beginnen, als Schlüssel ausprobiert werden, bis sich ein schlüssiger Klartext ergibt. Eine ausführliche Beschreibung wurde 2008 veröffentlicht[2] und ist in CrypTool v1.4.30 implementiert.
Einzig ein Klartext aus statistisch gleich verteilten, unsinnigen Buchstabenfolgen wäre einem Ciphertext-only-Angriff nicht ohne weiteres zugänglich.
Autokey-Verschlüsselung
Die Autokey-Vigenère-Verschlüsselung (auch als Vigenère-Selbstschlüssel-Verfahren bekannt), ebenfalls von Blaise de Vigenère in „Le Chiffre indéchiffrable“ veröffentlicht[1], vermeidet die Periodizität des Schlüsselwortes, indem sie den Schlüssel durch Anhängen des Klartextes verlängert:
Text: geheimnis Schlüsselwort: AKEY Schlüssel: AKEYGEHEI Geheimtext: GOLCOQUMA
Gegen Known-Plaintext-Angriffe ist das Verfahren natürlich ebenso anfällig wie die Standard-Vigenère-Verschlüsselung. Bei Ciphertext-only-Angriffen gestaltet sich die Kryptoanalyse allerdings aufwendiger als beim Standardverfahren. Es gibt dazu aber trotzdem verschiedene Ansätze. So macht man sich zu Nutze, dass bestimmte N-Gramme in der natürlichen Sprache gehäuft auftreten. Diese versucht man nun als Schlüssel an allen möglichen Stellen einzusetzen. Erhält man dadurch sinnvoll klingende Klartextsilben, hat man zum einen den wahrscheinlichen Klartext an dieser Stelle, damit aber auch den Schlüssel für eine Folgestelle und aus der eingesetzten Schlüsselsilbe selbst den Klartext einer vorherigen Stelle gefunden. Es ist dann nur noch die Länge der Verschiebung (Schlüsselwortlänge) zu ermitteln, um die passenden Stellen zum Einsetzen zu finden. Damit kann man dann wiederum weitere Teile des Schlüssels und des Klartextes generieren usw.[3] Eine andere Möglichkeit ist das Ausnutzen verschiedener Häufigkeiten für die einzelnen Buchstaben in der natürlichen Sprache. Wenn man einen Buchstaben des Geheimtextes betrachtet, so kann dieser aus verschiedenen Kombinationen von Buchstaben im Klartext und Schlüssel gebildet worden sein. Allerdings sind nicht alle diese Kombinationen in der natürlichen Sprache gleich wahrscheinlich. Falls man die passende Kombination so errät, hat man im Abstand der Schlüsselwortlänge wieder Teile des vorhergehenden Klartextes bzw. des nachfolgenden Schlüsseltextes zu Verfügung, um weitere Buchstaben des Geheimtextes zu entschlüsseln usw.[4]
Vernam
Der Spezialfall, dass der Schlüssel genauso lang ist wie der zu verschlüsselnde Text, heißt Vernam-Chiffre. Handelt es sich bei dem Schlüssel um eine zufällige Folge von Buchstaben und wird der Schlüssel nur ein einziges Mal verwendet, nennt man das Verfahren auch One-Time-Pad. Bei diesem ist eine korrekte Dechiffrierung ohne Kenntnis des Schlüssels unmöglich, und es bietet perfekte Sicherheit, was durch Claude Elwood Shannon gezeigt werden konnte.
Rotor-Maschinen
Bei der Vigenère-Verschlüsselung bestimmt das Schlüsselwort die Zahl und Auswahl der Chiffrier-Alphabete. Gleiches leisten Walzen oder Räder, auf die die Buchstaben des Alphabets eingraviert sind. Richtig zueinander orientiert, liest man an ihnen unmittelbar den chiffrierten Text ab.
Kommt man überein, bei jedem Buchstaben die Stellung der Walzen zueinander zu verändern, lässt sich die Zahl der zur Verfügung stehenden Alphabete um ein Vielfaches erhöhen (siehe Enigma, Fialka).
Siehe auch
- Homophone Verschlüsselung
- Kryptologie
- CrypTool – Freie Lernsoftware zum Thema Kryptographie und Kryptoanalyse, Open-Source
Literatur
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-67931-6, S. 46.
- Simon Singh: Geheime Botschaften. die Kunst der Verschlüsselung von der Antike bis in die Zeiten des Internet, München, Hanser, 2000, ISBN 978-3-446-19873-9
Weblinks
Belege
- Jörn Müller-Quade: Hieroglyphen, Enigma, RSA - Eine Geschichte der Kryptographie. Fakultät für Informatik der Universität Karlsruhe, S. 36. Abgerufen: 28. Mai 2008. PDF; 2,1 MB
- Cryptologia (Volume 32, Issue 4, Oktober 2008)
- Vigenère-Autokey-Verfahren (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. . Stina Bridgeman: Code Making and Code Breaking. Abgerufen am 21. Dezember 2009. PDF, 88 kB, eng.
- Klassische Kryptographie. Hans Werner Lang: Kryptografie. Abgerufen am 21. Dezember 2009.