QWERTZU
QWERTZU ist ein spezieller Begriff, der vor und während des Zweiten Weltkriegs von den britischen Codeknackern in Bletchley Park (B.P.)[1] bei ihrer Entzifferungsarbeit an der deutschen Schlüsselmaschine Enigma verwendet wurde. Er bezeichnet die für die Kryptanalyse wichtige Information der genauen Verdrahtung der Eintrittswalze, also des Verbindungsgliedes zwischen Tastatur und Walzensatz der Maschine.

Hintergrund
Während des Zweiten Weltkriegs wurde das Rückgrat der deutschen Kryptographie durch die Enigma gebildet, die von allen drei Wehrmachtteilen, Heer, Luftwaffe und Kriegsmarine, zur Verschlüsselung ihres geheimen Nachrichtenverkehrs eingesetzt wurde. Bereits lange vor dem Krieg, noch im Jahr 1932, war polnischen Kryptoanalytikern um den jungen Marian Rejewski bei ihrer Arbeit in der polnischen Dechiffrierstelle, dem Biuro Szyfrów (deutsch: „Chiffrenbüro“), der erste Einbruch in das Enigma-System gelungen.[2] Nachdem die Polen im Juli 1939 beim legendären Geheimtreffen von Pyry ihr gesamtes Wissen an ihre Verbündeten weitergegeben hatten, gelang es britischen Codebreakers im etwa 70 km nordwestlich von London gelegenen englischen Bletchley Park ab Januar 1940 mit der Enigma I verschlüsselte deutsche Funksprüche, zunächst von der Luftwaffe und kurz darauf auch vom Heer, zu entziffern. Auch die von der deutschen Marine mithilfe der Enigma M3 und – besonders kriegswichtig – die mit der von den deutschen U-Booten eingesetzten Maschine Enigma M4 verschlüsselten Funksprüche blieben, im Gegensatz zu den deutschen Hoffnungen und Annahmen, für die Briten kein Geheimnis. Ihnen gelang es vielmehr, mithilfe besonderer kryptanalytischer Geräte, wie der Turing-Bombe, den verschlüsselten Nachrichtenverkehr der Wehrmacht nahezu während des gesamten Zweiten Weltkriegs kontinuierlich zu brechen und die daraus gewonnenen Informationen unter dem Decknamen „Ultra“ gewinnbringend zu nutzen.[3]
Technik
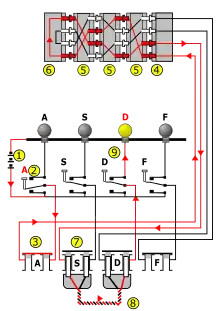
Batterie (1),
Tastatur (2),
Steckerbrett (3, 7) mit
Steckkabel (8),
Walzensatz (5) mit
Eintrittswalze (4) und Umkehrwalze (6) sowie
dem Lampenfeld (9)
Prinzip und grundlegender Aufbau der Enigma ist im Übersichtsartikel beschrieben. Rechts der drei drehbaren Walzen (5) des Walzensatzes (siehe gelb hinterlegte Zahlen in der Prinzipskizze) befindet sich die Eintrittswalze (4) (Stator), die sich nicht dreht und deren Kontakte über 26 Drähte (hier sind nur vier davon gezeichnet) mit den Buchstabentasten (2) verbunden sind. Links des Walzensatzes befindet sich die Umkehrwalze (6) (UKW), die ebenfalls feststeht. Bei ihr handelt es sich um eine Erfindung (patentiert am 21. März 1926) von Willi Korn (1893–1972), einem Mitarbeiter von Scherbius.[4] Sie weist nur auf ihrer rechten Seite 26 Kontakte auf (in der Skizze sind wieder nur vier davon eingezeichnet), die paarweise miteinander verbunden sind. Die Umkehrwalze bewirkt, dass der Strom, der den Walzensatz zunächst von rechts nach links durchläuft, umgelenkt wird und ihn noch einmal durchfließt, nun von links nach rechts. Der Strom verlässt den Walzensatz, wie er gekommen ist, wieder über die Eintrittswalze.
Die Eintrittswalze (4) stellt somit das wichtige Verbindungsglied zwischen einerseits dem Eingabeelement, also der Tastatur (2), und dem kryptographischen Herzstück der Enigma, nämlich dem Walzensatz dar, und bildet andererseits auch die Verbindung zwischen dem Walzensatz und dem Ausgabeelement, nämlich dem Lampenfeld (9). Neben der Kenntnis der Verdrahtung der in der Enigma eingesetzten drei drehbaren Walzen und der UKW (siehe auch: Enigma-Walzen) ist für die Kryptanalyse der Maschine die Kenntnis der Verdrahtung der Eintrittswalze essentiell, denn ohne Aufklärung der Verdrahtungen bliebe die Maschine „unknackbar“.
Geschichte
Lange vor dem Zweiten Weltkrieg, noch zu Beginn der 1930er Jahre, kannten die Kryptoanalytiker bereits den prinzipiellen Aufbau und die Funktionsweise einer Enigma-Maschine, denn zu dieser Zeit waren Vorläufermodelle der später militärisch genutzten Enigma I kommerziell erhältlich, die sich prinzipiell nur wenig voneinander unterschieden.[5] Die Codeknacker verfügten somit bereits über viele grundlegende Informationen, die zum erfolgreichen „Bruch“ der Enigma unbedingt erforderlich waren. Was ihnen noch fehlte, war „the all-important internal wiring of the wheels“[6] (deutsch: „die entscheidend wichtige innere Verdrahtung der Walzen“). Und ein wichtiges Element davon war die Verdrahtung der Eintrittswalze.
Die Eintrittswalze verbindet die über die Tastatur der Enigma gegebenen 26 Großbuchstaben des lateinischen Alphabets über 26 elektrisch isolierte Drähte mit 26 Kontakten, die sich auf der linken Seite der Eintrittswalze befinden, und die die Verbindungsstellen zum (während des Verschlüsselungsvorgangs rotierenden) Walzensatz bilden. Für die Verbindung der Buchstabentasten mit den Ausgangskontakten der Eintrittswalze gibt es eine nahezu unüberschaubare Anzahl von Möglichkeiten, die sich rechnerisch mithilfe der Fakultät bestimmen lässt. Es sind 26! mögliche Verdrahtungskonfigurationen denkbar, also 26·25·24···3·2·1 Fälle. Das sind exakt 403.291.461.126.605.635.584.000.000 Möglichkeiten für die Verdrahtung, von denen die deutschen Kryptographen irgendeine beliebige für die militärische Enigma aussuchen konnten.
Die Briten kannten die entsprechende Verdrahtung für die kommerziellen Maschinen. Es war schlicht die Identität, also die Verbindung der Tasten, beginnend oben links, mit den Ausgangskontakten der Eintrittswalze (auf deren linker Seite) in der Reihenfolge der 26 Buchstaben auf der Tastatur der Enigma.
Q W E R T Z U I O A S D F G H J K P Y X C V B N M L

Für die militärische Enigma hingegen galt, wie sie schnell erkannten, diese Verdrahtung jedoch nicht und die Deutschen hatten sich offensichtlich für eine andere Verdrahtungsreihenfolge entschieden. Die große Frage war, für welche? Da dieses Problem von überragender Bedeutung für die angestrebte Entzifferung der Enigma war, prägte der britische Codeknacker Dillwyn „Dilly“ Knox, der bei seinen Kollegen in Bletchley Park dafür bekannt war, wunderliche aber prägnante Begriffe zu kreieren, als abkürzende Bezeichnung für die unbekannte Verdrahtungsreihenfolge der Eintrittswalze der militärisch genutzten Enigma I den Namen „QWERTZU“.
Als Synonym für QWERTZU wurde in B.P. auch der Begriff „diagonal“ (englisch für „Diagonale“) benutzt.[8] Damit war ebenso die Buchstabenreihenfolge gemeint, in der die einzelnen Buchstabentasten der Enigma I mit der Eintrittswalze verbunden waren.
Dilly Knox selbst arbeitete für viele Jahre, wenn auch nicht ausschließlich, bis hinein ins Jahr 1939 an diesem Problem, ohne eine Lösung zu finden. Ebenso wenig kamen seine B.P.-Kollegen Tony Kendrick, Peter Twinn und selbst der große Alan Turing auf die von den Deutschen gewählte Verdrahtung, was angesichts der immens großen Zahl von Möglichkeiten für den QWERTZU auch niemand verwunderte. Keiner der genannten Kryptoanalytiker stand auch nur im Entferntesten im Verdacht, ein „phantasieloser Dummkopf“ (englisch: „unimaginative dullard“)[9] zu sein. Im Gegenteil, sie alle wurden in B.P. als äußerst intelligente und kreative Köpfe hoch geschätzt. Dennoch fand keiner von ihnen den richtigen QWERTZU.
Diese wichtige Information erlangten die Briten erst am 26. und 27. Juli 1939,[10] als es zu einem legendären Treffen französischer, britischer und polnischer Codeknacker im Kabaty-Wald von Pyry etwa 20 km südlich von Warschau kam, bei dem sie den verblüfften Briten und Franzosen ihre Enigma-Nachbauten überreichten und ihre gesammelten Erkenntnisse und erarbeiteten kryptanalytischen Methodiken offenbarten.[11] Die erste Frage, die Dilly Knox bei diesem Treffen (laut Mavis Batey auf Französisch) gestellt hat, war: „Quel est le QWERTZU?“[12] (deutsch: „Was ist der QWERTZU?“; also sinngemäß: „Wie lautet die Verdrahtungsreihenfolge der Eintrittswalze?“).[6] Dies hatte ihn schon so lange gequält.[13] Rejewskis Antwort war genial einfach: „ABCDEFG...“[14]
Der Codeknacker Peter Twinn, der ebenfalls in B.P. arbeitete, berichtet, dass Dilly Knox, nachdem er vom Pyry-Treffen gemeinsam mit dem Franzosen Gustave Bertrand ins Hotel Bristol nach Warschau zurückfuhr, wo er zusammen mit seinem Chef „Alastair“ Denniston während ihres Polen-Aufenthaltes wohnte, im Taxi begeistert auf Französisch gesungen hat: „Nous avons le QWERTZU, nous marchons ensemble“[9] (deutsch: „Wir haben den QWERTZU, wir werden vereint marschieren.“).[15]
Rückblickend erscheint die Lösung natürlich lächerlich einfach, aber aus Sicht der britischen Spezialisten war es auch die dümmste aller Möglichkeiten, für die sich die Deutschen entschieden hatten.[16] Bei einer astronomisch großen Anzahl von mehr als 400 Quadrillionen Möglichkeiten hatten die deutschen Kryptographen tatsächlich einfach nur die gewöhnliche alphabetische Reihenfolge als QWERTZU ausgewählt. Dies war aus Sicht der Briten so abstrus und so dumm und damit auch so wenig naheliegend, dass sie diesen Fall niemals ernsthaft in Betracht gezogen hatten. Marian Rejewski hingegen hatte diese Reihenfolge bereits im Jahr 1932 intuitiv richtig erraten, und damit die Grundlage geschaffen für die geschichtlich so bedeutsamen alliierten Enigma-Entzifferungen (Deckname: „Ultra“) während des Zweiten Weltkriegs.
Literatur
- Kris Gaj, Arkadiusz Orłowski: Facts and myths of Enigma: breaking stereotypes. Eurocrypt, 2003, S. 121ff. Abgerufen: 6. Februar 2012. PDF; 0,1 MB
- Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993. ISBN 0-19-280132-5
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 22. Abgerufen: 24. Jan. 2012. PDF; 0,4 MB
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, ISBN 0-304-36662-5
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000. ISBN 3-453-17285-X
Einzelnachweise
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 11. ISBN 0-947712-34-8
- Marian Rejewski: An Application of the Theory of Permutations in Breaking the Enigma Cipher. Applicationes Mathematicae, 16 (4), 1980, S. 543–559, PDF; 1,6 MB (englisch), abgerufen in Frode Weierud’s CryptoCellar am 5. April 2021.
- Gordon Welchman: The Hut Six Story – Breaking the Enigma Codes. Allen Lane, London 1982; Cleobury Mortimer M&M, Baldwin Shropshire 2000, S. 230. ISBN 0-947712-34-8
- Patentschrift Elektrische Vorrichtung zum Chiffrieren und Dechiffrieren DRP Nr. 452 194. Abgerufen: 6. Februar 2012. PDF; 0,5 MB
- Louis Kruh, Cipher Deavours: The commercial Enigma – Beginnings of machine cryptography. Cryptologia, Rose-Hulman Institute of Technology, Taylor & Francis, Philadelphia PA 26.2002,1 (Januar). ISSN 0161-1194 Abgerufen: 6. Februar 2012. PDF; 0,8 MB (Memento vom 13. April 2006 im Internet Archive)
- Peter Twinn: The Abwehr Enigma in Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 126. ISBN 0-19-280132-5
- Krzysztof Gaj: Polish Cipher Machine –Lacida. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 16.1992,1, ISSN 0161-1194, S. 74.
- Tony Sale: The Bletchley Park 1944 Cryptographic Dictionary. Publikation, Bletchley Park, 2001, S. 28. Abgerufen: 6. Februar 2012. PDF; 0,4 MB
- Peter Twinn: The Abwehr Enigma in Francis Harry Hinsley, Alan Stripp: Codebreakers – The inside story of Bletchley Park. Oxford University Press, Reading, Berkshire 1993, S. 127. ISBN 0-19-280132-5
- Ralph Erskine: The Poles Reveal their Secrets – Alastair Dennistons's Account of the July 1939 Meeting at Pyry. Cryptologia. Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 30.2006,4, S. 294
- Kris Gaj, Arkadiusz Orłowski: Facts and myths of Enigma: breaking stereotypes. Eurocrypt, 2003, S. 121ff. Abgerufen: 6. Februar 2012. PDF; 0,1 MB
- Mavis Batey: Dilly Knox – A Reminiscence of this Pioneer Enigma Cryptanalyst. Cryptologia, Rose-Hulman Institute of Technology. Taylor & Francis, Philadelphia PA 32.2008,2, S. 104–130.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-67931-6, S. 412.
- Hugh Sebag-Montefiore: Enigma – The battle for the code. Cassell Military Paperbacks, London 2004, S. 42. ISBN 0-304-36662-5
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, S. 40. ISBN 3-453-17285-X
- Michael Smith: Enigma entschlüsselt – Die „Codebreakers“ von Bletchley Park. Heyne, 2000, S. 39. ISBN 3-453-17285-X
