Thermodynamik

Die Thermodynamik (von altgriechisch θερμός thermós, deutsch ‚warm‘, sowie altgriechisch δύναμις dýnamis, deutsch ‚Kraft‘[1]) oder Wärmelehre ist eine natur- und ingenieurwissenschaftliche[2] Disziplin. Sie hat ihren Ursprung im Studium der Dampfmaschinen und ging der Frage nach, wie man Wärme in mechanische Arbeit umwandeln kann. Dazu beschreibt sie Systeme aus hinreichend vielen Teilchen und deren Zustandsübergänge anhand von makroskopischen Zustandsgrößen, die statistische Funktionen der detaillierten Vielteilchenzustände darstellen. Als Ingenieurwissenschaft hat sie für die verschiedenen Möglichkeiten der Energieumwandlung Bedeutung und in der Verfahrenstechnik beschreibt sie Eigenschaften und das Verhalten von Stoffen, die an Prozessen beteiligt sind. Als Begründer gilt der französische Physiker Sadi Carnot, der 1824 seine wegweisende Arbeit schrieb.

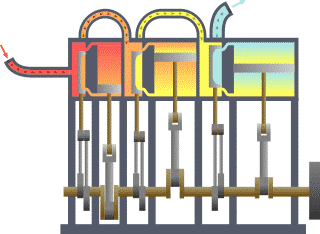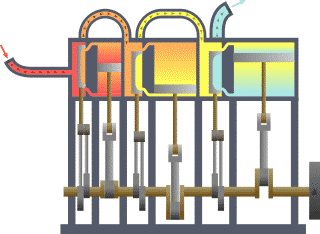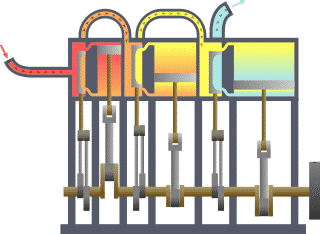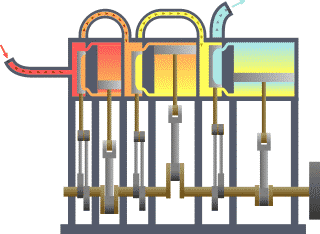
Typischer thermodynamischer Vorgang am Beispiel der prinzipiellen Wirkungsweise eines durch Dampf betriebenen Motors (rot = sehr heiß, gelb = weniger heiß, blau = Endtemperatur des Mediums)

Eine große Bedeutung haben die Hauptsätze der Thermodynamik, die eine ähnliche Stellung einnehmen wie die Newtonschen Axiome in der klassischen Mechanik oder die Maxwell-Gleichungen in der Elektrodynamik. Der erste Hauptsatz besagt, dass die gesamte Energie in einem abgeschlossenen System konstant ist und hat als Energieerhaltung in der gesamten Physik Gültigkeit. Der zweite Hauptsatz drückt aus, in welcher Richtung Energieumwandlungen möglich sind. So ist es beispielsweise möglich, mechanische, elektrische oder chemische Energie vollständig in Wärmeenergie (thermische Energie) umzuwandeln. Wärmeenergie dagegen lässt sich nur teilweise und nur mit hohem technischen Aufwand in diese Energien umwandeln.

In der Thermodynamik gibt es zwei verschiedene Herangehensweisen, die sich darin unterscheiden, ob Stoffe als Kontinuum betrachtet werden, die sich beliebig teilen lassen, oder ob sie als Ansammlung von Teilchen wie Atomen oder Molekülen gesehen werden:[3][4][5]

Die ältere Herangehensweise betrachtet Stoffe als Kontinuum und wird als klassische, phänomenologische oder Technische Thermodynamik (auch Technische Wärmelehre) bezeichnet und benutzt Begriffe wie Wärme, Druck, Volumen und Temperatur. Sie ist Teil der Klassischen Physik und vieler Ingenieurwissenschaften. Wenn die betrachteten Systeme aus mindestens $10^{22}$ Teilchen bestehen, was bei technischen Systemen immer der Fall ist, so ist dies eine sehr gute Näherung.
Die statistische Thermodynamik dagegen geht von einzelnen Teilchen aus und beschreibt sie wegen ihrer großen Anzahl mit statistischen Methoden und der kinetischen Gastheorie. Sie ist daher Teil der Statistischen Physik und erklärt beispielsweise, wie der Druck eines Gases auf den Behälter durch Stöße der einzelnen Moleküle des Gases entsteht oder wie die Temperatur mit der kinetischen Energie der Teilchen zusammenhängt. Diese Herangehensweise dient somit als Erklärung für verschiedene Phänomene und als theoretisches Fundament für die Hauptsätze, bietet aber für die Analyse oder Berechnung in den Ingenieurwissenschaften keine Vorteile, sodass sie dort nicht verfolgt wird.

Die Thermodynamik befasst sich einerseits mit verschiedenen Prozessen, wenn daran Wärme beteiligt ist, ohne auf die Besonderheiten der daran beteiligten Stoffe einzugehen. Von besonderer Bedeutung sind Kreisprozesse, die in der Technik häufig vorkommen. Andererseits macht sie Aussagen über Stoffe wie die verschiedenen Aggregatzustände und ihren Wechsel (schmelzen, sieden, verdampfen …) oder chemische Reaktionen, die sehr stark von den jeweiligen Stoffen abhängen.[6][7]

Bedeutung

Innerhalb der Naturwissenschaften hat die Thermodynamik große Bedeutung, da bei sämtlichen in der Natur ablaufenden Prozessen auch Energie beteiligt ist. Dies schließt auch Lebewesen mit ein. Zudem bietet sie einen tieferen Einblick in die Eigenschaften der Materie, was einerseits für das Verständnis physikalischer Eigenschaften oder Änderungen von Aggregatszuständen hilfreich ist und andererseits wichtig ist, um zu verstehen, welche chemischen Reaktionen ablaufen können und welche nicht. Innerhalb der Physik wird auch betont, dass die Thermodynamik verschiedene unabhängig entstandene Fachgebiete wie die klassische Mechanik oder die Quantenmechanik miteinander verbinden kann, was insbesondere über den universellen Begriff der Energie möglich wird.[8]

In den Ingenieurwissenschaften ist die Thermodynamik wichtig für die Konstruktion, Berechnung und Analyse von zahlreichen Maschinen oder Anlagen. Dazu zählen die verschiedenen Wärmekraftmaschinen (Dampfmaschine, Gas- oder Dampfturbine, Dieselmotor), die Arbeitsmaschinen[9] (Pumpen, Verdichter, …), Klima- und Kältetechnik, Wärme- und Stoffübertragung, Industrieöfen, Ver- und Entsorgungstechnik oder Energietechnik (Kraftwerke).[10][11]

Geschichte

Skizze Carnots zu seiner hypothetischen Maschine. Der mittig dargestellte Zylinder kann mit der Wärmequelle links unten oder der Kältequelle rechts unten verbunden werden, was jeweils zur Ausdehnung oder zum Zusammenziehen des Zylinderinhalts führt. Die Bewegung des Kolbens kann dabei als mechanisches Maß für die durch den Wärmefluss verrichtete Arbeit herangezogen werden.

Der französische Physiker Nicolas Léonard Sadi Carnot untersuchte die Wärmemengen einer Dampfmaschine (1824). Er stellte fest, dass heißer Wasserdampf ein kälteres Wasserreservoir erwärmt und dabei mechanische Arbeit geleistet wird. Carnot vermutete, dass bei diesem Prozess keine Wärme verloren geht. Carnot beschrieb die Vorgänge in der Dampfmaschine als Kreisprozess, der in späteren Jahren von Émile Clapeyron in mathematischer Form dargestellt wurde (Carnotscher Kreisprozess).[12]

Der deutsche Arzt Julius Robert Mayer formulierte (1841) die These, dass Energie in einem abgeschlossenen System eine konstante Größe sein sollte. Energie kann nicht verschwinden, sondern nur in eine andere Form umgewandelt werden. Diese Erkenntnis ist als Energieerhaltungssatz bekannt. Mayer machte Berechnungen zur Umwandlung von Wärme in mechanische Energie. Er gab an, wie viel Energie der Temperaturerhöhung von 1 g Wasser um 1 °C entspricht und berechnete, dass diese Energiemenge einer mechanischen Energie entspricht, die 1 g Materie 367 Meter in die Höhe heben könnte (tatsächlich sind es 426 Meter). Diese Berechnungen bildeten die Grundlage zum Ersten Hauptsatz der Thermodynamik.[13] James Prescott Joule bestimmte im Jahr 1844 noch genauer das mechanische Wärmeäquivalent.

Im Jahr 1840 veröffentlichte der schweizerisch-russische Chemiker Hermann Heinrich Hess eine Abhandlung mit dem Titel Thermochemische Untersuchungen, die auf dem Satz von der Erhaltung der Energie bei Molekülen bzw. Atomen aufgrund von chemischen Reaktionswärmen basierte.

Während Carnot noch vermutete, dass die Wärmemengen bei einer Dampfmaschine vollständig erhalten bleiben, nahm Mayer eine Umwandelbarkeit von Energieformen ineinander an. Der deutsche Physiker Rudolf Clausius verknüpfte 1854 die Ideen von Mayer und Carnot. Er zeigte, dass beim Betreiben einer Dampfmaschine immer Wärme von einem wärmeren Reservoir in ein kälteres Reservoir fließt und damit die Grundthese von Carnot korrekt ist. Jedoch bleibt die Wärmeenergie nicht – wie Carnot annahm – konstant, sondern sie wird zum Teil in mechanische Arbeit umgewandelt. Clausius stellte fest, dass die Wärmeenergie einer Maschine (Dampfmaschine) immer nur zu einem Teil in mechanische Arbeit umgewandelt werden kann; der andere Teil der Energie wird an die Umgebung abgegeben. Der Wirkungsgrad einer Maschine gibt das Umwandlungsverhältnis von gewonnener mechanischer Energie zur zugeführten Wärme an. Clausius Erkenntnis bildet den Zweiten Hauptsatz der Thermodynamik: „Es gibt keine periodisch arbeitende funktionierende Maschine, die nichts anderes tut, als Wärme in mechanische Arbeit zu verwandeln.“[14] Die Wärmemenge, die nicht zur mechanischen Arbeit genutzt werden kann, wird an die Umgebung abgegeben. Diese nicht nutzbare Wärmemenge verknüpfte Clausius mit der entsprechenden Temperatur zu einer neuen Funktion, der Entropie. Alle natürlichen Energieumwandlungsprozesse enthalten einen irreversiblen Entropieanteil, bei dem nicht genutzte Wärme an die Umgebung abgegeben wird. Entropie bedeutet eine „nach innen gekehrte, d. h. nicht mehr verwandlungsfähige oder nutzbare Energie.“[15] Später fasste Boltzmann, recht anschaulich, die Entropie als Maß der Unordnung der Bewegungen eines Systems auf.[16] Nur in einem abgeschlossenen System und bei einer reversiblen Zustandsänderung bleibt die Entropiedifferenz zwischen Anfangs- und Endzustand gleich Null.

Der französische Chemiker Marcelin Berthelot nahm als Triebkraft für eine chemische Reaktion die sich dabei entwickelnde Wärme an (1862).

Hermann Helmholtz verknüpfte die elektrische Energie bei Batterien mit der chemischen Energie und der Wärmeenergie. Er entwickelte in seiner Abhandlung Ueber die Erhaltung der Kraft unabhängig von Mayer den Energieerhaltungssatz.

Helmholtz befasste sich in späteren Jahren mit energetischen Fragen bei chemischen Reaktionen. Helmholtz gab Berthelot recht, dass bei vielen chemischen Umwandlungen Wärme frei wird; es gab jedoch auch Umwandlungen, bei denen Kälte erzeugt wurde. Helmholtz unterteilte in seiner Abhandlung Die Thermodynamik chemischer Vorgänge[17] die Energie bei Stoffumwandlungen in freie und gebundene Energie.[18] Die innere Energie und die Freie Energie verknüpfte Helmholtz mit dem Produkt aus Entropie und Temperatur. Stoffumwandlungen sind nach Helmholtz nur möglich, wenn die Freie Energie abnimmt. Auch der amerikanische Physikochemiker Josiah Willard Gibbs kam nahezu gleichzeitig zwischen 1875 und 1878 zu ähnlichen Überlegungen wie Helmholtz. Die Beziehung zwischen Enthalpiedifferenz abzüglich des Produkts aus Entropiedifferenz und Temperatur bezeichnet man als Differenz der Freien Enthalpie. Die Beziehung heißt zu Ehren der beiden Wissenschaftler Gibbs-Helmholtz-Gleichung. Mit dieser Gleichung kann der Chemiker Aussagen über eine stoffliche Umsetzung von Molekülen treffen und die nötigen Temperaturen und Konzentrationen von chemischen Umsetzungen berechnen.

Neben der klassischen Thermodynamik wurde die kinetische Gastheorie entwickelt. Gase bestehen danach aus Teilchen, Atomen oder Molekülen, die sich zwischen relativ seltenen Stößen frei im leeren Raum bewegen. Bei Temperaturerhöhung bewegen sich die Teilchen schneller und üben durch häufigere und heftigere Stöße einen stärkeren Druck auf die Gefäßwände aus. Wichtige Vertreter dieser Theorie waren August Krönig, Rudolf Clausius, James Clerk Maxwell und Ludwig Boltzmann.[19] Maxwell und Boltzmann nutzten die Wahrscheinlichkeitsrechnung, um thermodynamische Größen auf molekularer Basis zu beschreiben.

Im Jahre 1999 wurde von den Physikern Elliott Lieb und Jakob Yngvason eine axiomatische Systematik vorgestellt, bei der die Definition der Entropie auf dem Konzept der adiabatischen Erreichbarkeit beruht und auf einer streng mathematischen Basis in Form von 15 Axiomen steht. Dabei ist die Temperatur nur noch eine aus der Entropie als Grundgröße abgeleitete Größe. Das Konzept der adiabatischen Erreichbarkeit basiert auf einer axiomatischen Begründung von Constantin Carathéodory aus dem Jahr 1909. Da diese Theorie auf die Ergebnisse keine Auswirkungen hat, hat sie in die Praxis bisher keinen – und in die Lehre nur ausnahmsweise – Eingang gefunden.

Aufgrund der relativ langen Historie der Thermodynamik und der breiten Anwendungsgebiete verwenden die Beschreibungen in der technischen Thermodynamik (z. B. bei der Beschreibung eines Verbrennungsmotors oder eines Kühlschranks), der chemischen Thermodynamik (z. B. bei der Beschreibung einer chemischen Reaktion) und der statistischen Thermodynamik (z. B. bei der Beschreibung von geordneten Quantenzuständen in Festkörpern) oft deutlich unterschiedliche Formalismen.

Chronologie

Die folgende chronologische Abfolge zeigt wesentliche theoretische Erkenntnisse und die sich daraus ergebenden technische Entwicklungen:

1. Jh. n. Chr.: Heron von Alexandria baut eine erste Wärmekraftmaschine, den rotierenden Heronsball, und einen Öffner für Tempeltüren (Automat Nr. 37).
1613: Das Thermometer wird erfunden, aber wann genau und von wem ist nicht klar. So schreibt sich Galileo Galilei diese Erfindung zu und 1613 bestätigt ihm sein Schüler Gianfrancesco Sagredo, dass er Galileis Thermometer erfolgreich einsetzen konnte.[20]
1669: Richard Towneley[21] erkannte bei barometrischen Höhenmessungen den Zusammenhang zwischen Druck und Volumen bei konstanter Temperatur. Das Gesetz wurde von Robert Boyle zwar als Townley’s hypothesis bekannt gemacht, heute ist es nur als Boyle-Mariottsches Gesetz bekannt, da es Edme Mariotte unabhängig entdeckte und 1676 publizierte.
1690: Denis Papin beschreibt das Prinzip einer ersten, einfachen Dampfmaschine. Fünf Jahre später baut er eine Dampfdruckpumpe und Thomas Savery entwickelte mit Papins Ideen eine kolbenlose Pumpe.
1708/09: Daniel Gabriel Fahrenheit entwickelte genaue Thermometer, die Besonderheit war die Kalibrierung über drei Punkte. Er legte den Nullpunkt seiner Temperaturskala, je nach Quelle, als niedrigste Temperatur, die er in jenem Winter in Danzig feststellte oder eine Eis-Salz-Kältemischung. Den Gefrierpunkt von Wasser legte er bei 32 °F fest, der dritte Punkt war 180 °F höher und lag bei 212 °F. Ob die 180 gewählt wurde, weil sie eine Hochzusammengesetzte Zahl ist und damit besonders viele gleiche Teilungen der Skala erlaubt, wird von einigen Quellen vermutet, konnte aber bisher nicht belegt werden.
1712: Thomas Newcomen liefert seine erste Dampfmaschine an ein Bergwerk in Staffordshire.
1760: Joseph Black bestimmt die Schmelzenthalpie von Eis und die Verdampfungsenthalpie von flüssigem Wasser. Blacks bekanntester Schüler dürfte James Watt gewesen sein.
1787: Antoine Laurent de Lavoisier veröffentlicht die Theorie des Wärmestoffs (Caloricum), nach der Wärme ein Stoff ist, der von anderen Stoffen aufgenommen oder abgegeben ist. Die bis dahin gültige vorherige Lehre vom Phlogiston hielt sich dennoch lange.
1798: Benjamin Thompson (Graf von Rumford) lieferte mit Versuchen zum Kanonenbohren den Beweis, dass die Wärmestofftheorie von Lavoisier (Caloricum) und auch vom Phlogiston nicht stimmen konnte, seine Arbeiten und Schlussfolgerungen wurden aber lange nicht beachtet.
1811: Amedeo Avogadro postulierte, dass bei gleichen Bedingungen (Druck, Temperatur, Volumen) immer die gleiche Anzahl an Teilchen in einem Volumen vorhanden ist. Nach ihm ist die Avogadro-Konstante (Teilchen pro Mol) benannt. Es dauerte noch bis 1865 bevor Josef Loschmidt erstmals konkrete Zahlen für die Avogadro-Konstante vorlegen konnte.
1816: Der Geistliche Robert Stirling meldet seine Heißluftmaschine zum Patent an.
1822: Joseph Fourier veröffentlicht sein Buch Analytische Theorie der Wärme, in dem er die Wärmeleitung erklärt und zur Beschreibung des Zeitverhaltens die nach ihm benannt Transformation entwickelt.
1824: Sadi Carnot veröffentlicht eine Arbeit, in der er die Bedingungen und Grenzen der Wärmeumwandlung durch eine periodisch arbeitende Maschine beschreibt.
1827: Der schottische Botaniker Robert Brown entdeckt die zittrige Bewegung von sehr kleinen Blütenpollen in Wasser.
1833: Joseph Louis Gay-Lussac erkannte die Abhängigkeit von Druck und Volumen zur Temperatur. Auch hier wird implizit ein ideales Gas vorausgesetzt.
1842: Julius Robert Mayer postuliert, dass Wärme eine Energieform ist. 1847 formuliert dies Hermann von Helmholtz, der die Arbeit von Mayer nicht gekannt hatte, erneut und genauer.
1852: Der Joule-Thomson-Effekt wird von William Thomson (Lord Kelvin) und James Joule entdeckt. Er beschreibt die Temperaturänderung von Gasen bei Änderung des Druckes.
1856: William Thompson beschreibt die Änderung der Wärmeleitung, wenn in dem Leiter auch ein elektrischer Strom fließt (Thompson-Effekt)
1857: Rudolf Clausius erklärt den Gasdruck aus der mittleren kinetischen Energie der Gasmoleküle. Sie basiert noch alleine auf deren translatorischer Bewegung.
1858: Étienne Lenoir baut den ersten Gasmotor, der im Zweitakt-Verfahren ohne Verdichtung arbeitet.
1859: Das Kirchhoffsche Strahlungsgesetz von Gustav Robert Kirchhoff beschreibt den Zusammenhang von Absorption und Emission der Strahlung eines Körpers, wenn dieser sich im thermischen Gleichgewicht befindet.
1860: James Clerk Maxwell gibt die Funktion für die Geschwindigkeitsverteilung der Teilchen an.
1865: Rudolf Clausius führt den Begriff der Entropie ein, nachdem er festgestellt hat, dass neben dem ersten Hauptsatz (Energieerhaltung) noch ein weiteres Axiom für die Beschreibung der Thermodynamik erforderlich ist.
Josef Loschmidt ermittelt die Anzahl der Teilchen pro Volumen, die von seinem Schüler Ludwig Boltzmann dann Loschmidt-Konstante benannt wird.
1867: Nikolaus Otto und Eugen Langen präsentieren ihren Gasmotor auf der Weltausstellung in Paris 1867 und erhielten dafür eine Goldmedaille. Der Energieverbrauch konnte gegenüber Lenoirs Motor auf ¹⁄₃ reduziert werden, was einigen Juroren so unglaubwürdig schien, dass sie nach versteckten Gasleitungen suchten.[22]
1871: Carl von Linde beschreibt in einem Aufsatz ein neues Kälteverfahren. Das erste Pilotprojekt kommt mit einer Brauerei zu Stande und bildet den Grundstein der Linde AG.
1873: Johannes Diderik van der Waals veröffentlicht seine Gleichung zu einer verbesserten Beschreibung von Gasen, die die ideale Gasgleichung als Spezialfall beinhaltet.
1876: Josiah Willard Gibbs publiziert die nach ihm benannte Phasenregel, die Stoffe und Gemische mit mehreren Phasen im thermodynamischen Gleichgewicht erklärt.
1877: Ludwig Boltzmann deutet die Entropie statistisch. Dabei entdeckt er die nach ihm benannte und universelle Boltzmann-Konstante.
1882: Die ersten kommerziellen Dampfkraftwerke zur Stromerzeugung, die von Thomas Alva Edisons Gesellschaften gebaut wurden, gehen in der Pearl Street Station (New York) und am Holborn Viadukt (London) ans Netz. Bis heute dominieren Dampfkraftprozesse die Energieumwandlung in thermischen Kraftwerken.
1883: Hermann von Helmholtz führt den Begriff der freien Energie ein, die jedoch nichts mit der Freien Energie der Pseudowissenschaften zu tun hat, sondern ein Thermodynamisches Potential darstellt
1891: Carl von Linde entwickelt das nach ihm benannte Linde-Verfahren zur Verflüssigung und Zerlegung von Luft.
1892: Rudolf Diesel meldet sein Patent auf eine Verbrennungskraftmaschine an. Da in diesem Patent noch nicht der Gleichdruckprozess beschrieben wird, aber ein späteres Patent sich auf die Priorität dieses Patentes stützt, entstehen Patentstreitigkeiten.
1893: James Dewar erfindet für seine Versuche zur Tieftemperaturphysik ein nach ihm benanntes Isoliergefäß, welches auch in gewöhnlichen Thermoskannen verwendet wird.
1897: Rudolf Diesels erster Versuchsmotor läuft bei der Maschinenfabrik Augsburg. Der Versuchsmotor ist im Verbrauch den Motoren anderer Typen deutlich überlegen, so dass er trotz großer technischer Herausforderungen in Serie gebracht wird.
1900: Max Planck erklärt die Strahlung des ideal schwarzen Körpers (Plancksches Strahlungsgesetz) und löst damit das Phänomen der Ultraviolettkatastrophe auf. Gleichzeitig legt er den Grundstein zur Quantentheorie, da sein Modell nur diskrete Energiepakete (Energiequanten) vorsieht und bestimmt das Plancksche Wirkungsquantum.
1905: Albert Einstein erklärt die Brownsche Molekularbewegung in seiner Arbeit „Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen“. Zur brownschen Molekularbewegung schreibt er nur, dass ihm die Literatur zu ungenau ist, um sie mit dem von ihm erklärten Phänomen zu identifizieren, aber 1906 erscheint dann ein weiterer Beitrag „Zur Theorie der Brownschen Bewegung“.
1906: Walther Nernst stellt den 3. Hauptsatz (Wärmetheorem) auf.
1944: Erwin Schrödinger bringt den Begriff Negentropie auf, um die scheinbare Widersprüchlichkeit der ordnenden und aufbauenden Fähigkeiten von Leben und zweitem Hauptsatz aufzulösen.
1953: Zoran Rant führt den Begriff Exergie ein, um die verfügbare Arbeit zu charakterisieren, die aus Wärmeenergie gewonnen werden kann. Etwa zehn Jahre später entwickelt er auch den Begriff Anergie.
1974: Stephen Hawking entwickelt eine Theorie, nach der auch schwarze Löcher Wärmestrahlung abgeben und damit dem 2. Hauptsatz folgen.
1977: Ilya Prigogine erhält für seine Arbeiten zur Nichtgleichgewichtsthermodynamik den Nobelpreis für Chemie.

Wichtige Begriffe der Thermodynamik

Die Thermodynamik bringt die Prozessgrößen Wärme und Arbeit an der Systemgrenze mit den Zustandsgrößen in Zusammenhang, welche den Zustand des Systems beschreiben.

Auf der Basis von vier fundamentalen Hauptsätzen sowie materialspezifischen, empirischen Zustandsgleichungen zwischen den Zustandsgrößen (siehe z. B. Gasgesetz) erlaubt die Thermodynamik durch die Aufstellung von Gleichgewichtsbedingungen Aussagen darüber, welche Änderungen an einem System möglich sind (beispielsweise welche chemischen Reaktionen oder Phasenübergänge ablaufen können, aber nicht wie) und welche Werte der intensiven Zustandsgrößen dafür erforderlich sind. Sie dient zur Berechnung von frei werdender Wärmeenergie, von Druck-, Temperatur- oder Volumenänderungen, und hat daher große Bedeutung für das Verständnis und die Planung von Prozessen in Chemieanlagen, bei Wärmekraftmaschinen sowie in der Heizungs- und Klimatechnik.

Um Systeme und Eigenschaften kurz und präzise zu beschreiben, werden in der Thermodynamik immer wieder bestimmte Begriffe und Vereinbarungen verwendet:

Die Thermodynamik befasst sich vor allem mit der Entropie und der thermischen Energie (Wärmeenergie), die in jedem System enthalten sind. Bei einem isolierten System ist die Temperatur ein Maß für die enthaltene Wärmeenergie.
Energie wird in der Thermodynamik als Summe zweier Anteile, nämlich Exergie und Anergie verstanden, wobei jeder Anteil 0 sein kann. Die Exergie kann in andere Energieformen (technische Arbeit) umgewandelt werden, also Arbeit leisten oder in Anergie umgewandelt werden. Technische Arbeit ist immer reine Exergie und damit entropiefrei. Anergie kann nicht mehr in andere Energieformen umgewandelt werden.
Die Umgebung oder der Umgebungszustand dient als Bezug für die Fähigkeit eines Systems, Arbeit zu leisten. Systeme, die nicht mit der Umgebung im thermodynamischen Gleichgewicht stehen, besitzen noch Exergie, während die Energie der Umgebung reine Anergie ist.
Eine Zustandsgröße beschreibt eine Eigenschaft des Systems. Extensive Zustandsgrößen wie innere Energie U, Entropie S, Volumen V und Teilchenzahl N ändern sich, wenn man das System teilt. Intensive Zustandsgrößen wie Temperatur T, Druck p, Konzentration n und chemisches Potential μ bleiben dagegen gleich.
Durch einen Prozess wechselt ein System von einem Zustand in einen anderen. Eine Prozessgröße ist beispielsweise ein zugeführter Wärmestrom oder eine abgeführte Leistung.
Bleibt während einer Zustandsänderung (Prozess) eine Zustandsgröße gleich, so wird sie mit der Vorsilbe iso gekennzeichnet. Üblich sind isochor (erhält das Volumen, wie beim Gleichraumprozess), isobar (erhält den Druck, wie beim Gleichdruckprozess), isotherm (erhält die Temperatur), isenthalp (erhält die Enthalpie) oder isentrop (erhält die Entropie, daher reversibel); Eine isentrope Zustandsänderung erfolgt adiabat und reibungsfrei. Isentrop ist nicht mit isotrop zu verwechseln!
Abgeschlossene oder isolierte Systeme tauschen weder Stoffe noch Energie mit ihrer Umwelt aus, geschlossene Systeme können immerhin Energie austauschen und durch offene Systeme gehen sowohl Stoff- als auch Energieströme.
Adiabate Prozesse und Behältnisse sind wärmedicht, können aber Stoffe und Arbeit austauschen. Arbeitsdichte oder rigide[23] Systeme tauschen keine Arbeit mit der Umgebung aus (außer Schubarbeit in stationären Fließprozessen) und diatherme Systeme übertragen nur Wärme nach außen.[23]
Systemgrenzen oder Bilanzhüllen sind virtuelle Grenzen, um ein System zu analysieren (Stoffstromanalyse). In einer Bilanzgleichung kann die Veränderung einer Zustandsgröße innerhalb der Systemgrenze betrachtet werden
Ein reversibler Prozess lässt sich jederzeit umkehren, ohne dass Änderungen an der Umgebung entstehen. Reversible Prozesse bilden die theoretische Grenze zwischen möglichen/realen und naturgesetzwidrigen Prozessen. Reversible Prozesse sind isentrop und verlaufen sowohl adiabat als auch reibungsfrei.
Ein ideales Gas ist ein vereinfachtes Modell für stark verdünnte Gase, bei denen die einzelnen Teilchen praktisch keine Kohäsionswirkung aufeinander ausüben und bei denen das Eigenvolumen der Gasatome bzw. -moleküle vernachlässigbar ist.
Hat ein reales Gas die Inversionstemperatur, so behält es bei einem Drosselvorgang seine Temperatur bei. Unterhalb der Inversionstemperatur kühlt es sich durch die Drosselung ab, darüber heizt es sich auf.[24] Ideale Gase erhalten ihre Temperatur bei der Drosselung.
Kreisprozesse laufen zyklisch ab und bringen ihre Arbeitsstoffe immer wieder in den Ausgangszustand zurück. Linkslaufende Kreisprozesse verbrauchen Arbeit (Kältemaschinen, Wärmepumpen), rechtslaufende Kreisprozesse liefern Arbeit (Wärmekraftmaschinen).
Der Carnot-Prozess ist ein idealer Kreisprozess. Da Wärme nie vollständig in technische Arbeit (Exergie) verwandelt werden kann, gibt der Wirkungsgrad des Carnot-Prozesses an, bis zu welchem maximalen Anteil Arbeit aus Wärme gewonnen werden kann.
Nur am Tripelpunkt können feste, flüssige und gasförmige Phasen eines Stoffes gleichzeitig existieren. Da der Tripelpunkt einen festen Druck und Temperatur hat, eignen sich Tripelpunkte als Bezugspunkte, um eine Temperaturskala zu eichen. Für die Kelvin-Skala wird der Tripelpunkt des Wassers (0,01 °C) verwendet.
Am kritischen Punkt sind die Moleküle eines Stoffes im Gas so dicht gepackt wie in der Flüssigkeit. Der kritische Punkt ist durch Temperatur, Druck und Dichte bestimmt. Oberhalb seiner kritischen Temperatur kann ein Gas nicht mehr durch Druck verflüssigt werden.
Ein Fluid kann ein Gas oder eine Flüssigkeit sein. Insbesondere, wenn die Wandlung (Phasenübergang) eines Stoffes zwischen flüssig und gasförmig betrachtet wird, vereinfacht der Begriff Fluid die Beschreibung, da er nicht auf eine Phase festlegt ist.

In thermodynamischen Formeln werden immer wieder bestimmte Buchstaben für bestimmte Größen verwendet.[25] Dabei bezeichnen Großbuchstaben in Formeln eine absolute Größe, beispielsweise V als Volumen [m³]. Kleinbuchstaben bezeichnen spezifische Größen, beispielsweise v als Volumenstrom (Volumen bezogen auf eine Masse, [m³/kg]), einen Massenstrom [kg/s] oder eine Stoffmenge [m³/mol].

Die thermodynamische oder absolute Temperatur T wird in Kelvin (bis 1954: Grad Kelvin[26]) gemessen. 0 Kelvin (−273,15 °C) kann mit thermodynamischen Mitteln nicht erreicht werden (3. Hauptsatz).
Die innere Energie U ist die als Wärme im System gespeicherte Energie, die Enthalpie H enthält zusätzlich noch die in Druck × Volumen gespeicherte Energie.
Die Entropie S ist ein Maß für die Unordnung und gleichzeitig ein Maß für die Wahrscheinlichkeit eines Zustandes. Die Entropie kann in einem abgeschlossenen System nie abnehmen. Systeme streben aus eigenem Antrieb immer in den Zustand der höchstmöglichen Entropie (2. Hauptsatz).
Volumenänderungsarbeit w = ∫ p·dv wird bei der Änderung des Volumens gegen die herrschenden Drücke geleistet. Das ist zum einen der Druck des komprimierten Fluids und der Druck der Umgebung.
Die Stoffmenge N ist ein Maß für die Teilchenzahl und wird in der Einheit Mol gemessen.
Die Wärmekapazität bezeichnet die Fähigkeit eines Stoffes, Wärmeenergie aufzunehmen. Je größer die Wärmekapazität, umso geringer ist die Temperaturänderung bei Aufnahme oder Abgabe von Wärme.

Kurze Zusammenfassung der Hauptsätze

Nullter Hauptsatz der Thermodynamik: Einführung der Temperatur als physikalische Grundgröße: Stehen zwei Systeme jeweils mit einem dritten im thermodynamischen Gleichgewicht, so stehen sie auch untereinander im Gleichgewicht. Diejenige Zustandsgröße, die bei diesen Systemen übereinstimmt, ist die Temperatur.[27]
Erster Hauptsatz der Thermodynamik: Die Energie eines abgeschlossenen Systems ist konstant.
Zweiter Hauptsatz der Thermodynamik: Thermische Energie ist nicht in beliebigem Maße in andere Energiearten umwandelbar.
Dritter Hauptsatz der Thermodynamik (Nernst-Theorem): Der absolute Nullpunkt der Temperatur ist unerreichbar.

Nullter Hauptsatz

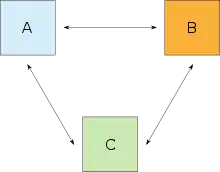
Gegeben sind die thermodynamischen Systeme A, B und C. Steht A mit B und B mit C in einem thermischen Gleichgewicht, so steht A mit C ebenso im Gleichgewicht. Nach einer gewissen Zeit besitzen alle drei Systeme die gleiche Temperatur.

Wenn ein System A sich mit einem System B sowie B sich mit einem System C im thermischen Gleichgewicht befindet, so befindet sich auch A mit C im thermischen Gleichgewicht. Die Zustandsgröße, die bei diesen Systemen übereinstimmt, ist die Temperatur, die skalar, intensiv und überall im System gleich ist.

Anders formuliert: ist das Gleichgewicht transitiv, so haben zwei in Kontakt stehende Systeme genau dann die gleiche Temperatur, wenn sie sich im thermischen Gleichgewicht befinden, d. h. wenn zwischen ihnen keine Wärme (mehr) ausgetauscht wird.

Beispiel: Ein Thermometer ist selbst ein System und soll als B bezeichnet werden. Wenn B die gleiche Temperatur für ein System A, wie auch für ein System C anzeigt, lässt sich daraus schließen, dass auch A und C untereinander im thermischen Gleichgewicht stehen werden, wenn man sie in Kontakt bringt. Dieser Hauptsatz wurde erst nach den drei anderen Hauptsätzen formuliert. Da er aber ein Fundament der Thermodynamik bildet, wurde er später als „nullter“ Hauptsatz bezeichnet.

Allerdings ist im Gravitationsfeld zu beachten, dass das Gleichgewicht bei im Allgemeinen verschiedenen Temperaturen zwischen den Systemen A, B und C liegt, denn die Photonen der Schwarzkörperstrahlung erfahren im Gravitationsfeld aufgrund des Äquivalenzprinzips eine Rot- bzw. Blauverschiebung; durch die Zeitdilatation werden sie in unterschiedlichen Höhen mit verschiedenen Raten emittiert. Zudem sind deren Flugbahnen gekrümmt, so dass nicht alle von unten startenden Photonen auch oben ankommen können. All diese Effekte bewirken eine mit der Höhe abnehmende Temperatur. Auf der Erde beträgt dieser Effekt aber nur 1,6·10⁻¹⁴ K/m und ist daher unmessbar klein. Bei einem Neutronenstern ist er aber nicht vernachlässigbar.

Erster Hauptsatz

Der 1. Hauptsatz der Thermodynamik beschreibt die Energieerhaltung in thermodynamischen Systemen. Er sagt aus, dass die Energie eines abgeschlossenen Systems konstant ist. Ausgehend von dieser Aussage lassen sich Energiebilanzen für geschlossene und offene Systeme bilden.

Bilanz für das geschlossene thermodynamische System

Jedes System besitzt eine innere Energie $U$ (= extensive Zustandsgröße). Diese kann sich nur durch den Transport von Energie in Form von Arbeit $W$ und/oder Wärme $Q$ über die Grenze des Systems ändern, das heißt:

\mathrm {d} U=\delta Q+\delta W

Dabei ist $\delta W$ die infinitesimale Änderung der an dem System geleisteten Arbeit $-p\,\delta V$ (genauer: die Summe aus der Volumenarbeit und der im System dissipierten Arbeit, z. B. Reibungsarbeit), $\delta$ kennzeichnet inexakte Differentiale, während $\mathrm {d}$ vollständige Differentiale kennzeichnet. Anstelle der Volumenarbeit können äquivalente extensive Arbeitsausdrücke verwendet werden. So wird beispielsweise für ein magnetisches System in einem Magnetfeld $H$ bei Erhöhung des magnetischen Momentes $\delta m\left(=+M\,\delta V\right)$ der Probe die extensive Arbeit $\delta W=+H\,\delta m$ geleistet.

Die Gleichung gilt für das ruhende System. Beim bewegten System kommen die äußeren Energien $E_{a}$ (potentielle und kinetische Energie) hinzu:

\mathrm {d} U+\mathrm {d} E_{a}=\delta Q+\delta W

Die Energie eines abgeschlossenen Systems bleibt unverändert. Verschiedene Energieformen können sich demnach ineinander umwandeln, aber Energie kann weder aus dem Nichts erzeugt noch kann sie vernichtet werden. Deshalb ist ein Perpetuum mobile erster Art unmöglich (kein System verrichtet Arbeit ohne Zufuhr einer anderen Energieform und/oder ohne Verringerung seiner inneren Energie).

Eine Einschränkung der Umwandelbarkeit von Wärme in Arbeit ergibt sich erst aus dem zweiten Hauptsatz der Thermodynamik.

Energiebilanz für ein beliebiges offenes System

Auf das offene System angewendet, wird der erste Hauptsatz mathematisch anders formuliert.[28]
Beim offenen System fließen über die bestimmte Systemgrenze zusätzlich zur mechanischen Arbeit an der verschiebbaren Systemgrenze (Volumenänderungsarbeit z. B. am Kolben in einem Zylinder) die Verschiebearbeiten der Massenströme am Ein- und Austritt. Sie sind das Produkt aus Druck und Volumen. Statt mit der inneren Energie wird beim offenen System deshalb mit den Enthalpien bilanziert, die diesen Term enthalten.

Die Bilanz für ein instationäres System, bei dem sowohl Masseinhalt als auch Energieinhalt sich zeitlich ändern, lautet:

{\frac {\mathrm {d} E_{\mathrm {sys} }}{\mathrm {d} t}}=\sum _{i}{{\dot {Q}}_{\mathrm {i} }}+\sum _{j}{{\dot {W}}_{\mathrm {t,j} }}+\sum _{e}{{\dot {m}}_{\mathrm {e} }}\cdot \left(h_{\mathrm {e} }+g\cdot z_{\mathrm {e} }+{\frac {1}{2}}c_{\mathrm {e} }^{2}\right)-\sum _{a}{{\dot {m}}_{\mathrm {a} }}\cdot \left(h_{\mathrm {a} }+g\cdot z_{\mathrm {a} }+{\frac {1}{2}}c_{\mathrm {a} }^{2}\right)

Dabei sind:

${\tfrac {\mathrm {d} E_{\mathrm {sys} }}{\mathrm {d} t}}$ : die zeitliche Änderung des Energieinhalts im System (Energieinhalt = innere Energie + kinetische Energie + potentielle Energie).
${\dot {Q_{\mathrm {i} }}}$ : der Wärmestrom über die Systemgrenze.
${\dot {W_{\mathrm {t,j} }}}$ : der Arbeitsstrom (technische Arbeit) über die Systemgrenze.
${\dot {m_{\mathrm {e} }}}$ : der Massenstrom in das System.
${\dot {m_{\mathrm {a} }}}$ : der Massenstrom aus dem System
$h$ : die spezifische Enthalpie
$g\cdot z$ : die spezifische potentielle Energie (mit $z$ = Höhe über dem Bezugsniveau und $g$ = Schwerebeschleunigung)
${\tfrac {1}{2}}c^{2}$ : die spezifische kinetische Energie (mit $c$ = Geschwindigkeit).

Energiebilanz für einen stationären Zustand

Für einen stationären Zustand gilt: ${\dot {m}}_{\mathrm {e} }={\dot {m}}_{\mathrm {a} }={\dot {m}}$ und ${\frac {\mathrm {d} E_{\mathrm {sys} }}{\mathrm {d} t}}=0$

Energiebilanz am offenen stationären System. Es wird ein kleiner Zeitraum

\Delta t

betrachtet, in dem die Masse

\Delta m

mit dem Zustand 1 in das System fließt und dieses im Zustand 2 wieder verlässt. Der Massenstrom ist dann

\Delta m/\Delta t

. Die Verschiebarbeiten am Eintritt und Austritt werden jeweils mit der inneren Energie in der Enthalpie zusammengefasst.

{\dot {Q}}+{\dot {W}}_{t}+{\dot {m}}\cdot \left(h_{\mathrm {e} }-h_{\mathrm {a} }+g\cdot z_{\mathrm {e} }-g\cdot z_{\mathrm {a} }+{\frac {1}{2}}c_{\mathrm {e} }^{2}-{\frac {1}{2}}c_{\mathrm {a} }^{2}\right)=0

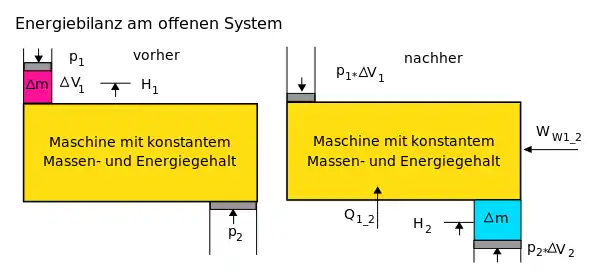
oder, fasst man die äußeren Energien in einem einzelnen Term zusammen:

{\dot {Q}}+{\dot {W}}_{t}={\dot {m}}\cdot \left(h_{a}-h_{e}+\Delta e_{a}\right)

zusätzlich adiabat (z. B. Dampfturbine): ${\dot {Q}}=0$

P={\dot {m}}\cdot {\left(h_{a}-h_{e}+\Delta e_{a}\right)}

Dabei ist $P$ die Wellenleistung der Maschine. Da vom System abgegebene Energien in der Thermodynamik negativ definiert sind, wird die Leistung einer Turbine aus dieser Gleichung negativ. In der Praxis wird das Vorzeichen deshalb gewechselt. In vereinfachten Berechnungen vernachlässigt man auch die äußeren Energien.

Energiebilanz für Kreisprozesse

Da nach dem Durchlaufen eines Kreisprozesses das Arbeitsmedium zum Ausgangszustand zurückkehrt, vereinfacht sich die Bilanz, es entfallen die Änderungen der Zustandsgrößen, und es verbleiben die Prozessgrößen Wärme und Arbeit. Wie noch im Zusammenhang mit dem 2. Hauptsatz erläutert wird, kann nicht nur Wärme zugeführt werden, die komplett in Arbeit umgewandelt wird, sondern es muss auch Wärme abgeführt werden. Die einfache Bilanzgleichung lautet:

W_{\mathrm {Kr} }=-\oint \delta Q

Dabei summiert das Kreisintegral alle Wärmeströme auf. Sie sind positiv, wenn sie in das System eintreten und negativ, wenn sie es verlassen. $W_{\mathrm {Kr} }$ ist die gesamte Arbeit des Zyklus. Sie ist negativ, wenn sie abgegeben wird.

Die Beziehung wird auch oft mit den Wärmebeträgen geschrieben:

W_{\mathrm {Kr} }=Q_{\mathrm {zu} }-\left|Q_{\mathrm {ab} }\right|

,

wobei die Wärmeabfuhr deutlicher erkennbar wird.

Zweiter Hauptsatz

Der Zweite Hauptsatz der Thermodynamik trifft Aussagen über die Richtung von Prozessen und das Prinzip der Irreversibilität. Aus dem Zweiten Hauptsatz lassen sich die Definition der thermodynamischen Temperatur und die Zustandsgröße Entropie herleiten. Ebenso folgt aus dem Zweiten Hauptsatz der Thermodynamik die Unterscheidung von Exergie und Anergie und die Tatsache, dass der Wirkungsgrad einer Wärmekraftmaschine den Carnot-Wirkungsgrad nicht überschreiten kann.

Der zweite Hauptsatz der Thermodynamik in der Formulierung von Clausius lautet:

„Es gibt keine Zustandsänderung, deren einziges Ergebnis die Übertragung von Wärme von einem Körper niederer auf einen Körper höherer Temperatur ist.“

Einfacher ausgedrückt: Wärme kann nicht von selbst von einem Körper niedriger Temperatur auf einen Körper höherer Temperatur übergehen. Diese Aussage scheint zunächst überflüssig zu sein, denn sie entspricht der alltäglichen Erfahrung. Dennoch ist sie gleichbedeutend zu allen weiteren, weniger „selbstverständlichen“ Aussagen, denn alle Widersprüche zu den anderen Aussagen lassen sich auf einen Widerspruch zu dieser zurückführen.

Der zweite Hauptsatz der Thermodynamik in der Formulierung von Kelvin und Planck lautet:

„Es ist unmöglich, eine periodisch arbeitende Maschine zu konstruieren, die weiter nichts bewirkt als Hebung einer Last und Abkühlung eines Wärmereservoirs.“[29]

Dem ersten Hauptsatz würde die Annahme nicht widersprechen, dass es möglich sei, einer – wie immer auch gearteten – Kraftmaschine einen stetigen Wärmestrom zuzuführen, den diese vollständig als mechanische oder elektrische Leistung abgibt. Eine solche Maschine wird als Perpetuum mobile zweiter Art bezeichnet. Eine entsprechende Formulierung des zweiten Hauptsatzes lautet:

Ein Perpetuum mobile zweiter Art ist unmöglich.

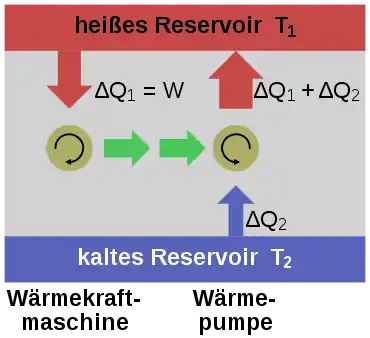
Die Wärmekraftmaschine (a) beschreibt ein Perpetuum mobile zweiter Art. Würde ein solches existieren, könnte es Wärme ohne Verlust in Arbeit (grüner Pfeil) umwandeln. Würde mit dieser Arbeit eine Wärmepumpe (b) angetrieben, könnte damit ohne Einwirkung von außen Wärme vom kalten zum warmen Reservoir gepumpt werden.

Nimmt man an, es gäbe diese von einer Wärmesenke zur Wärmeabfuhr unabhängige Kraftmaschine, so könnte damit der Umgebung, z. B. dem Meerwasser, Wärme entzogen und in mechanische Arbeit umgewandelt werden. Man könnte damit auch gemäß dem Bild rechts die Wärme aus einem Reservoir oder Behälter entziehen und mit der umgewandelten Energie eine Wärmepumpe antreiben, die mit einem reversiblen Carnot-Prozess Wärme aus einem anderen Behälter mit niedrigerer Temperatur in den Ersteren mit höherer Temperatur fördert. Die in den wärmeren Behälter eingespeiste Wärmemenge wäre dann größer als die von der Kraftmaschine aufgenommene, weil die abgegebene Energie der Wärmepumpe aus der Summe von aufgenommener Wärme und Antriebsarbeit besteht. Denkt man sich die Systemgrenze um beide Maschinen einschließlich der beiden Wärmebehälter gezogen, so wäre innerhalb dieses abgeschlossenen Systems – also ohne Energie- und Stoffaustausch mit der Umgebung – letztlich Wärme von einem kälteren zu einem wärmeren Körper geflossen. Dies ist ein Widerspruch zur ersten Aussage. Prinzipiell derselbe Widerspruch ergibt sich aber auch mit der Annahme, man könnte eine Kraftmaschine bauen, die einen größeren Wirkungsgrad aufweist als eine mit einem Carnot-Prozess arbeitende Maschine. Auch diese Maschine würde dem wärmeren Behälter weniger Wärme entnehmen als die von ihr angetriebene Carnot-Wärmepumpe dort einspeist. Die entsprechende Aussageform des zweiten Hauptsatzes lautet:

Es gibt keine Wärmekraftmaschine, die bei gegebenen mittleren Temperaturen der Wärmezufuhr und Wärmeabfuhr einen höheren Wirkungsgrad hat als den aus diesen Temperaturen gebildeten Carnot-Wirkungsgrad

\eta _{c}=1-{\frac {T_{\mathrm {kalt} }}{T_{\mathrm {heiss} }}}\ .

Die Nennung der mittleren Temperaturen ist deshalb von Bedeutung, weil in der Regel durch Wärmezufuhr oder Wärmeentnahme ein Wärmereservoir seine Temperatur ändert.

Dabei ist $T$ nicht irgendeine Temperatur (z. B. nicht die Grad Celsius- oder die Fahrenheit-Temperatur) des Systems, sondern die von der Zustandsgleichung des „idealen Gases“ her, oder besser durch den gerade angegebenen Wirkungsgrad des Carnot-Prozesses definierte „absolute Temperatur“ (Kelvin).

Unmittelbar in diesem Zusammenhang lässt sich weiter formulieren:

Alle reversiblen Wärme-Kraft-Prozesse mit gleichen mittleren Temperaturen der Wärmezufuhr und Wärmeabfuhr haben denselben Wirkungsgrad wie der entsprechende Carnot-Prozess.

und:

Alle irreversiblen Wärme-Kraft-Prozesse haben einen geringeren Wirkungsgrad.

Mit den in der modernen Thermodynamik festgelegten Begriffsdefinitionen (Wärme, Arbeit, Innere Energie, Zustandsgröße, Prozessgröße, adiabat…) und mit der systematischen Einteilung der Systeme kann über die von Clausius eingeführte Zustandsgröße Entropie eine für alle geschlossenen Systeme und Prozesse in offenen Systemen allgemein gültige Aussage des zweiten Hauptsatzes in mathematischer Form gegeben werden. Bei offenen Systemen bezieht sich die Bilanz auf ein Fluidteilchen, das sich durch das System hindurch bewegt und als geschlossenes bewegtes System betrachtet werden kann (siehe oben).

\mathrm {d} S={\frac {\delta Q}{T}}+{\frac {\delta W_{\mathrm {diss} }}{T}}

Dabei ist $\delta W_{\mathrm {diss} }$ die innerhalb des Systems dissipierte Arbeit (Arbeit, die nicht nach außen gelangt, sondern infolge von Reibungs-, Drosselungs- oder Stoßvorgängen die innere Energie erhöht). Sie ist immer positiv. Man bezeichnet den entsprechenden Term in der Gleichung als „produzierte Entropie“ – im Gegensatz zum ersten Term, der „transportierte Entropie“ genannt wird und auch negativ sein kann.

Für das adiabate System mit $\delta Q=0$ ergibt sich daraus:

In einem geschlossenen adiabaten System kann die Entropie nicht abnehmen, sie nimmt in der Regel zu. Nur bei reversiblen Prozessen bleibt sie konstant.

Auch hier ist die Äquivalenz mit der ersten Aussage von Clausius leicht zu erkennen. Ein selbsttätiger Wärmefluss vom kälteren zum wärmeren Behälter in der oben skizzierten Anordnung würde bedeuten, dass die Entropie des kälteren Behälters (geringere Temperatur $T$ im Nenner) stärker abnimmt, als die des wärmeren zunimmt, d. h. die gesamte Entropie im System abnimmt, was nicht möglich ist.

Alle spontan ablaufenden Prozesse sind irreversibel. Dort findet immer eine Entropiezunahme statt. Beispiele sind die Vermischung von zwei unterschiedlichen Gasen und der Wärmefluss von einem heißen zu einem kalten Körper ohne Gewinnung von Arbeit. Die Wiederherstellung des (oft „geordneter“ genannten) Anfangszustandes erfordert dann den Einsatz von Energie oder Information (siehe maxwellscher Dämon). Reversible Prozesse sind nicht mit einer Erhöhung der Gesamtentropie verbunden und laufen daher auch nicht spontan ab. Durch die theoretische Beschreibung spontan ablaufender Prozesse zeichnet der Zweite Hauptsatz der Thermodynamik eine Richtung der Zeit aus, die mit unserer intuitiven Erfahrungswelt übereinstimmt (vgl. das Beispiel weiter unten).

Mit den beschriebenen Zusammenhängen ist auch der folgende Satz eine Aussageform des zweiten Hauptsatzes:

Die thermische Energie eines Systems besteht aus einem Anteil Exergie und einem Anteil Anergie, wobei der exergetische Anteil verschwindet, wenn das System in den Umgebungszustand übergeführt wird.

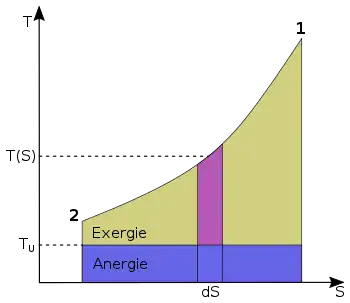
Exergie und Anergie der Wärme (Thermische Energie = Anergie + Exergie)

Die Exergie ist der in andere Energieformen umwandelbare Anteil der thermischen Energie. Wird ein Körper bzw. System mit einem Zustand, der von dem der Umgebung abweicht, reversibel in den Umgebungszustand gebracht, so wird seine Exergie als Arbeit abgegeben. Die Wärme, die ein Körper (z. B. ein heißes Rauchgas im Kessel eines Kraftwerks) abgibt, wenn es sich auf Umgebungstemperatur abkühlt, kann theoretisch über eine Folge von differenziellen Carnot-Prozessen, wie im Bild rechts dargestellt, zur Umwandlung in Arbeit genutzt werden. Der exergetische Anteil ergibt sich durch Aufsummieren der differenziellen (pinkfarbenen) Flächenanteile oberhalb der Umgebungstemperatur $T_{U}$ .

E_{\mathrm {ex} }=\int _{S_{2}}^{S_{1}}\left({T(S)-T_{U}}\right)\mathrm {d} S

Die Wärmesenke für diese Prozesse zur Aufnahme der Anergie (blauer Flächenanteil unterhalb $T_{U}$ ) ist die Umgebung. Herrscht bei einem Gas im Ausgangszustand gegenüber dem Umgebungszustand nicht nur eine höhere Temperatur, sondern auch ein höherer Druck, so besteht die gesamte Exergie nicht nur aus dem exergetischen Anteil der Wärme, sondern zusätzlich aus einem Anteil Volumenarbeit.

Der thermische Wirkungsgrad der realen Wärmekraftmaschine ist also immer kleiner als 1 und – bedingt durch die von den Maschinen vorgegebene Prozessführung und die unvermeidlichen dissipativen Effekte – auch immer kleiner als der der idealen Wärmekraftmaschine:

\eta _{\mathrm {th} }=1-{\frac {T_{U}}{T_{m_{\mathrm {zu} }}}}={\frac {\text{Exergie}}{\text{thermische Energie}}}

wobei $T_{U}$ die Umgebungstemperatur ist und $T_{m_{\mathrm {zu} }}$ die mittlere Temperatur der Wärmezufuhr. Sie ergibt sich, wenn die gelbe Fläche der Exergie durch ein flächengleiches Rechteck oberhalb der Linie der Umgebungstemperatur ersetzt wird.

Der Zweite Hauptsatz hat somit erhebliche technische Auswirkungen. Da viele Maschinen, die mechanische Energie liefern, diese über einen Umweg aus thermischer Energie erzeugen (z. B. Dieselmotor: chemische Energie $\rightarrow$ thermische Energie $\rightarrow$ mechanische Energie), gelten für ihre Wirkungsgrade immer die Beschränkungen des 2. Hauptsatzes. Im Vergleich dazu bieten Wasserkraftanlagen, die bei der Umwandlung keine Zwischenstufe über thermische Energie benötigen, erheblich höhere Wirkungsgrade.

Dritter Hauptsatz

Dieser Hauptsatz wurde von Walther Nernst im Jahr 1906 vorgeschlagen und ist auch als Nernst-Theorem bekannt. Er ist quantentheoretischer Natur und äquivalent zur Aussage von der Unerreichbarkeit des Nullpunktes der absoluten Temperatur:

Es ist nicht möglich, ein System bis zum absoluten Nullpunkt abzukühlen.

Bei der Annäherung der Temperatur an den absoluten Nullpunkt ( $T=0\mathrm {\ K}$ ) wird die Entropie $S$ unabhängig von thermodynamischen Parametern. Damit geht $S$ gegen einen festen Grenzwert $S_{0}$ :

\lim _{T\rightarrow 0}S(T,p,V,\dots )=S(T=0)=S_{0}\,.

Die konstante Entropie bei $T=0\mathrm {\ K}$ lässt sich als $S_{0}=k\cdot \ln(\Omega _{0})$ darstellen, wobei $k$ die Boltzmann-Konstante und $\Omega _{0}$ die Anzahl der möglichen Mikrozustände im Grundzustand (Entartung) ist. Zum Beispiel würde sich für einen $n$ -atomigen Kristall, dessen Atome im Energiegrundzustand zwei mögliche Spineinstellungen haben, $S_{0}=k\cdot \ln(2^{n})$ ergeben.

Für alle physikalisch-chemischen Reaktionen, bei denen die teilnehmenden Stoffe am absoluten Nullpunkt als ideale kristalline Festkörper vorliegen, gilt:

\lim _{T\rightarrow 0}S(T,p,\dots )=0

Es gibt nur eine Realisierungsmöglichkeit für ideale Festkörper am absoluten Nullpunkt, $\Omega _{0}=1$ .

Die genannten Aussagen können mit Methoden der Quantenstatistik streng bewiesen werden.

Im Rahmen der klassischen Thermodynamik lässt sich das Verhalten der Entropie am absoluten Nullpunkt ebenfalls aus folgender alternativer Formulierung des Dritten Hauptsatzes herleiten:

Wenn die Zusammensetzung zweier thermodynamischer Systeme ein isoliertes System darstellt, dann ist jeglicher Energieaustausch in jedweder Form zwischen den beiden Systemen beschränkt.[30]

Energieberechnungen in der Thermodynamik

Die Energiebilanz hat in der Thermodynamik einen hohen Stellenwert.

Bei einer Phasenumwandlung (fest-flüssig-gasförmig) oder Mischungen (Salz in Wasser, Mischung verschiedener Lösungsmittel) werden Umwandlungsenergien (Schmelzenthalpie, Verdampfungsenthalpie, Sublimationsenthalpie) oder Umwandlungsenthalpien benötigt bzw. werden in umgekehrter Richtung frei. Bei einer chemischen Stoffumwandlung können Reaktionswärmen oder Reaktionsenthalpien frei werden oder müssen umgekehrt zugeführt werden.

Zur Berechnung von frei werdenden Reaktionswärmen bei Stoffumsetzungen wird zunächst die entsprechende Reaktionsgleichung mit den dazugehörigen stöchiometrischen Faktoren aufgestellt. Die Standardbildungsenthalpien der Einzelstoffe sind für 25 °C in Tabellenwerken verzeichnet. Man addiert die Summe der Enthalpien der Produkte entsprechend den stöchiometrischen Faktoren und zieht davon die Enthalpien der Ausgangsstoffe ab (Hess’scher Wärmesatz).

Die Reaktions- oder Umwandlungsenthalpie, die bei einer chemischen Umsetzung oder Phasenumwandlung an die Umgebung abgegeben wird, hat ein negatives Vorzeichen. Ist eine Energiezufuhr von der Umgebung für eine Phasenumwandlung oder eine chemische Umsetzung nötig, so hat diese ein positives Vorzeichen.

Die Zustandsgröße Enthalpie ist, ausführlich:

H(T,p)=U(T,V(T,p))+p\cdot V(T,p)

Die Freie Enthalpie ist

G=H-T\cdot S

Durch Bildung des totalen Differentials der Freien Enthalpie und anschließende Integration lässt sich berechnen, ob eine chemische Umsetzung möglich ist.

\Delta G=\Delta H-T\cdot \Delta S

Ist die Differenz der Freien Enthalpien $\Delta G$ der Produkte zu den Ausgangsstoffen (Edukte) negativ, ist eine Phasenumwandlung oder eine Stoffumsetzung möglich. Ist die Differenz der Freien Enthalpie einer Reaktion, einer Phasenumwandlung negativ, erfolgt eine Reaktion – soweit diese nicht kinetisch gehemmt ist – bis zu einem Punkt, an dem $\Delta G=0$ wird. Das Massenwirkungsgesetz ist ein Spezialfall eines solchen Gleichgewichtes. Ist die Differenz der Freien Enthalpie positiv, so ist eine Reaktion oder Phasenumwandlung unmöglich.

Im Jahr 1869 glaubte Marcellin Berthelot noch, dass nur chemische Umwandlungen möglich seien, bei denen Wärme frei wird. Mittlerweile sind Umwandlungen und Reaktionen bekannt, bei denen keine Reaktionswärme oder Umwandlungswärme frei wird. Dies liegt am Entropieterm $T\cdot \Delta S.$

Beispiele:

Bei Lösen von Glaubersalz in Wasser wird die Lösung kälter als die Umgebung. Der Enthalpieterm ist positiv, jedoch nimmt die Unordnung, d. h. die Entropie, durch die Auflösung zu.
Beim Schmelzen eines Eisblockes wird Wärme zur Phasenumwandlung von fest zu flüssig benötigt. Die Temperatur des Wassers steigt nicht, obgleich Wärme von der Umgebung zugeführt wird. Die Unordnung, die Entropie der Moleküle ist im flüssigen Zustand größer als im festen Zustand.
Bei der Umwandlung von Kohle und Kohlendioxid zu Kohlenmonoxid ist die Reaktionsenthalpie positiv. Durch die Reaktionsentropie lässt sich das Gleichgewicht (siehe: Boudouard-Gleichgewicht) bei hoher Temperatur zum Kohlenmonoxid verschieben.

Thermodynamik irreversibler Prozesse

Neben der klassischen Gleichgewichtsthermodynamik wurde im 20. Jahrhundert die Nichtgleichgewichtsthermodynamik oder auch Thermodynamik irreversibler Prozesse entwickelt. Für diese Arbeiten wurden die Nobelpreise der Chemie im Jahr 1968 an Lars Onsager und 1977 an Ilya Prigogine verliehen.

Die klassische Thermodynamik macht über Nichtgleichgewichtsprozesse nur die qualitative Aussage, dass diese nicht umkehrbar sind, beschränkt sich aber in ihren quantitativen Aussagen auf Systeme, die stets global im Gleichgewicht sind bzw. nur inkrementell davon abweichen. Demgegenüber behandelt die Nichtgleichgewichtsthermodynamik Systeme, die sich nicht in einem globalen thermodynamischen Gleichgewicht befinden, sondern davon abweichen. Oft wird jedoch noch ein lokales thermodynamisches Gleichgewicht angenommen.

Ein wichtiges Ergebnis der Nichtgleichgewichtsthermodynamik ist das Prinzip der minimalen Entropieproduktion für offene Systeme, welche nur wenig vom thermodynamischen Gleichgewicht abweichen. Dies ist der Bereich der so genannten linearen irreversiblen Thermodynamik. Sie beschreibt in einem vereinheitlichten formalen Rahmen lineare Zusammenhänge zwischen Flüssen und ihren korrespondierenden Kräften. Diese Kräfte werden normalerweise als Gradienten einer skalaren Größe aufgefasst und die Flüsse durch bekannte lineare Naturgesetze beschrieben, wie zum Beispiel das ohmsche Gesetz (Stromfluss), das Ficksche Gesetz (Diffusion), das Fouriersche Gesetz (Wärmeleitung) oder die Kinetik einer chemischen Reaktion (Reaktionsgeschwindigkeit). Durch die Bilanzierung der Entropie, in die die Produktion der Entropie in dem System und die über die Systemgrenzen fließende Entropie eingehen, lässt sich durch den zweiten Hauptsatz die Invarianz dieser Gesetze zeigen. Für das Beispiel der Wärmeleitung zeigt sich, dass mit der Thermodynamik nur ein Wärmefluss vom heißen zum kalten vereinbar ist, und dass die Wärmeleitfähigkeit immer eine positive Größe sein muss. Durch die mathematische Analyse wird außerdem gezeigt, dass eine thermodynamische Kraft (z. B. Temperaturdifferenz oder Spannungsdifferenz) in einem System einen zusätzlichen indirekten Fluss verursacht (Beispiel: elektrischer Stromfluss verursacht durch Wärmeleitung (Seebeck-Koeffizient), oder Wärmestrom verursacht durch einen elektrischen Stromfluss (Peltier-Koeffizient)). Von Lars Onsager wurde gezeigt, dass die Einflüsse zwischen Flüssen und den nicht dazu korrespondierenden Kräften gleich groß sind (Reziprozitätsbeziehungen). Da die Entropiebilanz in einem geschlossenen System immer positiv sein muss, folgt zusätzlich: Die Größe der Kreuzeffekte ist immer wesentlich kleiner als die direkten Effekte. Für das Beispiel mit den zwei Kräften gilt, dass die Kreuzeffekte (Peltier-Koeffizient und Seebeck-Koeffizient) maximal zweimal der Wurzel aus den Produkten der Koeffizienten der beiden direkten Effekte (elektrische und thermische Leitfähigkeit) entspricht.

Weicht ein offenes System stark vom Gleichgewicht ab, kommt die nichtlineare Nichtgleichgewichtsthermodynamik zum Zug. Wichtiges Ergebnis in diesem Bereich ist das Stabilitätskriterium von Ilya Prigogine und Paul Glansdorff, das angibt, unter welchen Bedingungen der Zustand mit der minimalen Entropieproduktion instabil wird und ein System bei gleichzeitigem Entropieexport eine höher geordnete Struktur annehmen kann. In diesem Bereich können also spontan so genannte dissipative Strukturen entstehen, die experimentell bestätigt wurden (beispielsweise Bénard-Zellen). Da in diesem nichtlinearen Bereich auch biologische Prozesse anzusiedeln sind, ist dieses Resultat besonders auch in Hinsicht auf die Entwicklung des Lebens von großer Bedeutung.

Vertreter

Siehe auch

Literatur

Allgemein

Herbert B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. Wiley Text Books, New York 1985, ISBN 0-471-86256-8
Constantin Carathéodory: Untersuchungen über die Grundlagen der Thermodynamik In: Mathematische Annalen, 67:355–386, 1909. Carathéodorys Veröffentlichung (Erste axiomatisch strenge Begründung der Thermodynamik) fand große Beachtung durch Max Planck und Max Born.
Ulrich Nickel: Lehrbuch der Thermodynamik. Eine anschauliche Einführung. 3., überarbeitete Auflage. PhysChem, Erlangen 2019, ISBN 978-3-937744-07-0.
Max Planck: Vorlesungen über Thermodynamik.
Karl Stephan, Franz Mayinger: Thermodynamik. Grundlagen und technische Anwendungen. 2 Bände, Springer
- Band 1: Einstoffsysteme. 15. Auflage. 1998, ISBN 3-540-64250-1
- Band 2: Mehrstoffsysteme und chemische Reaktionen. 14. Auflage. 1999, ISBN 3-540-64481-4
André Thess: Das Entropieprinzip – Thermodynamik für Unzufriedene. Oldenbourg, 2007, ISBN 978-3-486-58428-8
Gerd Wedler: Lehrbuch der Physikalischen Chemie. Verlag Chemie, Weinheim 1982, ISBN 3-527-25880-9
Herbert Windisch: Thermodynamik – Ein Lehrbuch für Ingenieure. 4., überarbeitete Auflage. München: Oldenbourg Wissenschaftsverlag 2011, ISBN 978-3-486-70717-5

Chemische Thermodynamik

Wolfgang Wagner: Chemische Thermodynamik. 4. Auflage. Akademie Verlag, Berlin 1982
Hans-Heinrich Möbius, Wolfgang Dürselen: Chemische Thermodynamik. 5. Auflage. VEB Verlag für Grundstoffindustrie, Leipzig 1988, ISBN 3-342-00294-8
Hans-Werner Kammer, Kurt Schwabe: Einführung in die Thermodynamik irreversibler Prozesse. Akademie Verlag, Berlin 1984
Hans-Joachim Bittrich: Leitfaden der chemischen Thermodynamik. Verlag Chemie, Weinheim 1971, ISBN 3-527-25019-0
Physikalische Chemie#Allgemeine Lehrbücher
G. Kortüm: Einführung in die chemische Thermodynamik. 5. Auflage. Verlag Chemie, Weinheim 1966
Hans Kelker: Angewandte Chemie. Fischer Lexikon, Fischer Taschenbuch, Frankfurt a. M. 1977, ISBN 3-436-02460-0, S. 287–292

Geschichtliches zur Thermodynamik

Ervin Szücs: Dialoge über technische Prozesse, VEB Fachbuchverlag Leipzig, 1976
Handbuch Der Experimentellen Chemie Sekundarstufe II, Band 7: Chemische Energetik, S. 1–13, Aulis Verlag Deubner, Köln
Hans Joachim Störig: Kleine Weltgeschichte der Wissenschaft 2. Fischer Taschenbuch, Frankfurt a. M. 1982, S. 88–96; Parkland, Köln 2004, ISBN 3-89340-056-7

Statistische Thermodynamik

Statistische Mechanik#Literatur

Technische Thermodynamik

Fran Bošnjaković, K. F. Knoche: „Technische Thermodynamik“ Teil 1, 8. korrigierte Auflage 1998, Steinkopff Verlag Darmstadt, ISBN 978-3-642-63818-3
Hans D. Baehr, S. Kabelac: Thermodynamik, Grundlagen und technische Anwendungen 13., neu bearb. u. erw. Aufl., Springer Verlag, 2006, ISBN 3-540-32513-1
Hans D. Baehr, Karl Stephan: Wärme- und Stoffübertragung 5., neu bearb. Aufl., 2006, Springer Verlag, ISBN 3-540-32334-1
Günter Cerbe, Gernot Wilhelms: Technische Thermodynamik. Theoretische Grundlagen und praktische Anwendungen. 14. Auflage, Hanser Fachbuchverlag, Juni 2005, ISBN 3-446-40281-0
N. Elsner, A. Dittmann: Grundlagen der Technischen Thermodynamik, Bd. 1 und 2, Akademie Verlag, Berlin 1993
E. P. Hassel, T. V. Vasiltsova, T. Strenziok: „Einfuehrung in die Technische Thermodynamik“; FVTR GmbH; Rostock 2010; ISBN 978-3-941554-02-3
Heinz Herwig, Christian H. Kautz: Technische Thermodynamik, Aufl., 2007, Pearson Studium, ISBN 978-3-8273-7234-5
Dirk Labuhn, Oliver Romberg: Keine Panik vor Thermodynamik!, 1. Auflage, Vieweg, Braunschweig 2005, ISBN 3-8348-0024-4
Klaus Langeheinecke, Peter Jany, Eugen Sapper: Thermodynamik für Ingenieure. 5. Auflage. Vieweg Verlag, Wiesbaden 2004, ISBN 3-528-44785-0
W. Schneider, S. Haas: Repetitorium Thermodynamik. Oldenbourg Verlag, 2004, ISBN 978-3-486-57614-6
Volker Sperlich: Übungsaufgaben zur Thermodynamik mit Mathcad, Fachbuchverlag Leipzig 2002, ISBN 3-446-21603-0
Peter Stephan, Karlheinz Schaber, Karl Stephan, und Franz Mayinger Thermodynamik 1. Einstoffsysteme. Grundlagen und technische Anwendungen, Springer Verlag, Berlin, November 1998, 15. Auflage, ISBN 3-540-64250-1
Wolfgang Wagner: Properties of Water and Steam. / Zustandsgrößen von Wasser und Wasserdampf, Springer Verlag, Berlin, 1. Auflage, August 2002, ISBN 3-540-64339-7
Klaus Lucas: Thermodynamik. / Die Grundgesetze der Energie- und Stoffumwandlungen, Springer Verlag, Berlin, 5. Auflage, 2006, ISBN 3-540-26265-2

Thermodynamik in der Biologie

Dieter Leuschner: Thermodynamik in der Biologie. Eine Einführung. Akademie Verlag, Berlin 1989, ISBN 3-05-500487-6

Weblinks

Wikibooks: Thermodynamik – Lern- und Lehrmaterialien

Wiktionary: Thermodynamik – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wiktionary: Wärmelehre – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Was ist Entropie? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 4. Aug. 2004.
Online-Repetitorium Thermodynamik – mit Videos – (Experimentalphysik) – Universität Würzburg
Universität Duisburg-Essen, Grundlagen der Technischen Thermodynamik mit Übungsaufgaben und Lösungen, + rechenaktive Mathcad-Dateien
Universität Duisburg-Essen, Grundlagen der Technischen Thermodynamik (PDF; 2,6 MB)
Günter Jakob Lauth (SciFox): Einführung in die chemische Thermodynamik. Vorlesungsreihe, Videoaufzeichnungen, 2013/2014.
Umfangreiche Formelsammlung zur Thermodynamik 1 an der TUM (PDF, kleiner als 3 MB). Die Themen sind u. a. Erster und Zweiter Hauptsatz, Zustandsgleichungen idealer Gase, reale Fluide und Kreisprozesse.

Einzelnachweise und Anmerkungen

Wilhelm Gemoll: Griechisch-Deutsches Schul- und Handwörterbuch. München/Wien 1965.
Wird als „Grundlagenwissenschaften der Technik“ bezeichnet (Baehr, Kabelac: Thermodynamik. 15. Auflage, S. V, als „Fachmodule der Ingenieurwissenschaften“, „ingenieurtechnische Wissenschaft“ und „Teilgebiet der Physik“ (Barth: Thermodynamik für Maschinenbauer. 2011, S. V, 2.)
Herwig Kautz: Technische Thermodynamik. Pearson Studium, München, 2007, S. 20.
Windisch Thermodynamik – Ein Lehrbuch für Ingenieure. Oldenbourg, 3. Auflage, 2008, S. 2 f.
Bökh, Stripf: Technische Thermodynamik. Springer, 2. Auflage, 2015, S. 1.
Herwig Kautz: Technische Thermodynamik, Pearson Studium, München, 2007, S. 18.
Baehr, Kabelac: Thermodynamik, Springer, 15. Auflage, 2012, S. V.
Christoph Strunk: Moderne Thermodynamik – Von einfachen Systemen zu Nanostrukturen, Ge Gruyter, 2015, S. V f.
Mihály Németh-Csóka: Thermisches Management elektrischer Maschinen, Springer, https://www.springer.com/de/book/9783658201326
Frank-Michael Barth: Thermodynamik für Maschinenbauer, Oldenbourg, München, 2012, S. 2 f.
Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen, Springer, 15. Auflage, S. 10.
Handbuch der Experimentellen Chemie Sekundarbereich II. Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 1.
Hans Joachim Störig: Kleine Weltgeschichte der Wissenschaften. Bd. 2. Fischer Taschenbuch, 1982, S. 91.
Gerd Wedler: Lehrbuch der Physikalischen Chemie. Verlag Weinheim, 1982, S. 59.
Hans Joachim Störig: Kleine Weltgeschichte der Wissenschaften. Bd. 2. Fischer Taschenbuch, 1982, S. 93, 1280.
Lorenz: Abriß der geschichtlichen Entwickelung der Wärmelehre. In: Zeitschrift für Kälteindustrie. 1904, Heft 8, S. 144.
H. von Helmholtz: Die Thermodynamik chemischer Vorgänge (1882). In: Wissenschaftliche Abhandlungen von Hermann Helmholtz. Band 2. J. A. Barth, Leipzig 1882, S. 958–978.
Handbuch der Experimentellen Chemie Sekundarbereich II. Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 11.
Handbuch der Experimentellen Chemie Sekundarbereich II. Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 9.
Ingo Müller: A History of Thermodynamics. 1. Auflage. Springer-Verlag, Berlin Heidelberg 2007, ISBN 978-3-540-46226-2 (englisch).
Ein Artikel über Richard Towneley ist derzeit nur in der englischen Wikipedia verfügbar
Walter Conrad (Hrsg.): Geschichte Der Technik in Schlaglichtern. 1. Auflage. Bibliographisches Institut & F.A. Brockhaus AG, Mannheim 1997, ISBN 3-411-07741-7, 3.2.2 Gasmotor/Ottomotor.
Klaus Langeheinecke (Hrsg.), Peter Jany, Gerd Thieleke: Thermodynamik für Ingenieure. 6. Auflage, Friedr. Vieweg & Sohn Verlag, Wiesbaden 2006, Abschnitt 2.1 Systeme und Energien.
Siehe Abschnitt 15.2 „Joule-Thomson-Effekt oder Drosseleffekt“ in Bošnjaković/Knoche „Technische Thermodynamik Teil 1“, 8. Auflage, Steinkopff-Verlag Darmstadt 1998, ISBN 978-3-642-63818-3.
Nach Baehr/Kabelac „Thermodynamik“, 13. Auflage, Springer-Verlag 2005, ISBN 3-540-23870-0.
Siehe Abschnitt 1.4.3 in Baehr/Kabelac „Thermodynamik“, 13. Auflage, Springer-Verlag 2005, ISBN 3-540-23870-0.
Hans-Heinrich Möbius, Wolfgang Dürselen: Chemische Thermodynamik.
In diesem Kapitel werden explizit die Konzepte des Karlsruher Physikkurses benutzt, in dem die gesamte Physik auf dem Konzept von „Strömen“ basiert und extensive Grundgrößen bevorzugt werden. Ein anderes Konzept benutzt zum Beispiel W. Döring, der in seinem Thermodynamik-Bändchen („Göschen-Verlag“) zusätzlich zur gewohnten (extensiven) „Volumenarbeit“ $\delta A=-p\delta V$ (Energieerhöhung durch Kompression eines Gasvolumens bei beweglichem Stempel) die (intensive) sog. „Druck-Arbeit“ (Energieerhöhung durch vertikalen Transport von Gewichtstücken auf die Oberseite eines festen Würfelbehältnisses für das fluide System) $\delta A':=+V\delta p$ benutzt. Extensive und intensive Arbeiten sind zwar verschieden, aber Bevorzugung des jeweiligen Aspektes ist Geschmackssache, über die sich genauso wenig streiten lässt, wie über die Bevorzugung von Kraft oder Impuls als Grundgröße in der Mechanik: Es besteht nämlich Äquivalenz in folgendem Sinne: Der erste Hauptsatz der Thermodynamik kann einerseits in der gewohnten Form $\mathrm {d} U=\delta Q+\delta A$ , zweitens in der davon zwar verschiedenen, aber äquivalenten Form $\mathrm {d} H=\delta Q+\delta A'$ formuliert werden.
Zitat von Max Planck, nach Eintrag zu Hauptsätze. In: Römpp Online. Georg Thieme Verlag, abgerufen am 24. August 2011.
M. Heidrich: Bounded energy exchange as an alternative to the third law of thermodynamics. In: Annals of Physics. 373, 2016, S. 665–681. bibcode:2016AnPhy.373..665H. doi:10.1016/j.aop.2016.07.031.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Wilhelm Gemoll: Griechisch-Deutsches Schul- und Handwörterbuch. München/Wien 1965.

[2] Wird als „Grundlagenwissenschaften der Technik“ bezeichnet (Baehr, Kabelac: Thermodynamik. 15. Auflage, S. V, als „Fachmodule der Ingenieurwissenschaften“, „ingenieurtechnische Wissenschaft“ und „Teilgebiet der Physik“ (Barth: Thermodynamik für Maschinenbauer. 2011, S. V, 2.)

[3] Herwig Kautz: Technische Thermodynamik. Pearson Studium, München, 2007, S. 20.

[4] Windisch Thermodynamik – Ein Lehrbuch für Ingenieure. Oldenbourg, 3. Auflage, 2008, S. 2 f.

[5] Bökh, Stripf: Technische Thermodynamik. Springer, 2. Auflage, 2015, S. 1.

[6] Herwig Kautz: Technische Thermodynamik, Pearson Studium, München, 2007, S. 18.

[7] Baehr, Kabelac: Thermodynamik, Springer, 15. Auflage, 2012, S. V.

[8] Christoph Strunk: Moderne Thermodynamik – Von einfachen Systemen zu Nanostrukturen, Ge Gruyter, 2015, S. V f.

[9] Mihály Németh-Csóka: Thermisches Management elektrischer Maschinen, Springer, https://www.springer.com/de/book/9783658201326

[10] Frank-Michael Barth: Thermodynamik für Maschinenbauer, Oldenbourg, München, 2012, S. 2 f.

[11] Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen, Springer, 15. Auflage, S. 10.

[12] Handbuch der Experimentellen Chemie Sekundarbereich II. Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 1.

[13] Hans Joachim Störig: Kleine Weltgeschichte der Wissenschaften. Bd. 2. Fischer Taschenbuch, 1982, S. 91.

[14] Gerd Wedler: Lehrbuch der Physikalischen Chemie. Verlag Weinheim, 1982, S. 59.

[15] Hans Joachim Störig: Kleine Weltgeschichte der Wissenschaften. Bd. 2. Fischer Taschenbuch, 1982, S. 93, 1280.

[16] Lorenz: Abriß der geschichtlichen Entwickelung der Wärmelehre. In: Zeitschrift für Kälteindustrie. 1904, Heft 8, S. 144.

[17] H. von Helmholtz: Die Thermodynamik chemischer Vorgänge (1882). In: Wissenschaftliche Abhandlungen von Hermann Helmholtz. Band 2. J. A. Barth, Leipzig 1882, S. 958–978.

[18] Handbuch der Experimentellen Chemie Sekundarbereich II. Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 11.

[19] Handbuch der Experimentellen Chemie Sekundarbereich II. Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 9.

[20] Ingo Müller: A History of Thermodynamics. 1. Auflage. Springer-Verlag, Berlin Heidelberg 2007, ISBN 978-3-540-46226-2 (englisch).

[21] Ein Artikel über Richard Towneley ist derzeit nur in der englischen Wikipedia verfügbar

[22] Walter Conrad (Hrsg.): Geschichte Der Technik in Schlaglichtern. 1. Auflage. Bibliographisches Institut & F.A. Brockhaus AG, Mannheim 1997, ISBN 3-411-07741-7, 3.2.2 Gasmotor/Ottomotor.

[ThermoIng-23] Klaus Langeheinecke (Hrsg.), Peter Jany, Gerd Thieleke: Thermodynamik für Ingenieure. 6. Auflage, Friedr. Vieweg & Sohn Verlag, Wiesbaden 2006, Abschnitt 2.1 Systeme und Energien.

[24] Siehe Abschnitt 15.2 „Joule-Thomson-Effekt oder Drosseleffekt“ in Bošnjaković/Knoche „Technische Thermodynamik Teil 1“, 8. Auflage, Steinkopff-Verlag Darmstadt 1998, ISBN 978-3-642-63818-3.

[25] Nach Baehr/Kabelac „Thermodynamik“, 13. Auflage, Springer-Verlag 2005, ISBN 3-540-23870-0.

[26] Siehe Abschnitt 1.4.3 in Baehr/Kabelac „Thermodynamik“, 13. Auflage, Springer-Verlag 2005, ISBN 3-540-23870-0.

[27] Hans-Heinrich Möbius, Wolfgang Dürselen: Chemische Thermodynamik.

[28] In diesem Kapitel werden explizit die Konzepte des Karlsruher Physikkurses benutzt, in dem die gesamte Physik auf dem Konzept von „Strömen“ basiert und extensive Grundgrößen bevorzugt werden. Ein anderes Konzept benutzt zum Beispiel W. Döring, der in seinem Thermodynamik-Bändchen („Göschen-Verlag“) zusätzlich zur gewohnten (extensiven) „Volumenarbeit“ $\delta A=-p\delta V$ (Energieerhöhung durch Kompression eines Gasvolumens bei beweglichem Stempel) die (intensive) sog. „Druck-Arbeit“ (Energieerhöhung durch vertikalen Transport von Gewichtstücken auf die Oberseite eines festen Würfelbehältnisses für das fluide System) $\delta A':=+V\delta p$ benutzt. Extensive und intensive Arbeiten sind zwar verschieden, aber Bevorzugung des jeweiligen Aspektes ist Geschmackssache, über die sich genauso wenig streiten lässt, wie über die Bevorzugung von Kraft oder Impuls als Grundgröße in der Mechanik: Es besteht nämlich Äquivalenz in folgendem Sinne: Der erste Hauptsatz der Thermodynamik kann einerseits in der gewohnten Form $\mathrm {d} U=\delta Q+\delta A$ , zweitens in der davon zwar verschiedenen, aber äquivalenten Form $\mathrm {d} H=\delta Q+\delta A'$ formuliert werden.

[29] Zitat von Max Planck, nach Eintrag zu Hauptsätze. In: Römpp Online. Georg Thieme Verlag, abgerufen am 24. August 2011.

[30] M. Heidrich: Bounded energy exchange as an alternative to the third law of thermodynamics. In: Annals of Physics. 373, 2016, S. 665–681. bibcode:2016AnPhy.373..665H. doi:10.1016/j.aop.2016.07.031.