Ideales Gas

Als ideales Gas bezeichnet man in der Physik und physikalischen Chemie eine bestimmte idealisierte Modellvorstellung eines realen Gases. Darin geht man von einer Vielzahl von Teilchen in ungeordneter Bewegung aus und zieht als Wechselwirkungen der Teilchen nur harte, elastische Stöße untereinander und mit den Wänden in Betracht. Obwohl dieses Modell eine starke Vereinfachung darstellt, lassen sich mit ihm viele thermodynamische Prozesse von Gasen verstehen und mathematisch beschreiben.

In der Quantenmechanik unterscheidet man das ideale Bosegas und das ideale Fermigas.

Modell des idealen Gases

Im Modell des idealen Gases der klassischen Physik werden alle Gasteilchen als ausdehnungslose Massepunkte angenommen, welche sich frei durch das ihnen zur Verfügung stehende Volumen bewegen können. Im Wesentlichen gelten mehrere Idealisierungen, von denen sich zahlreiche andere Eigenschaften ableiten:

Ideale Gasteilchen sind frei, sie üben keine Anziehungs- oder Abstoßungskräfte aufeinander aus. Es finden lediglich elastische Stöße zwischen Wand und Teilchen statt.
Ideale Gasteilchen selbst belegen in ihrem Raum kein Volumen.
Ideale Gasteilchen rotieren und vibrieren nicht. Ihre Energie ist ausschließlich die kinetische Energie der translatorischen Bewegung im Raum.

Reale Teilchen können Energie auch in Eigenrotation speichern, in Molekülen können darüber hinaus Oszillationen der Atome gegeneinander angeregt sein. In der Van-der-Waals-Gleichung werden die beiden ersten Idealisierungen korrigiert, um das Modell des idealen Gases besser an reale Gase anzupassen.

Mit frei ist gemeint, dass die Teilchen keinerlei Kräfte verspüren. Allerdings dürfen (und müssen) sich die Teilchen untereinander und an der Wand des Volumens stoßen. Ein Gasteilchen bewegt sich also geradlinig mit einer konstanten Geschwindigkeit, bis ein Stoß es in eine andere Richtung lenkt und dabei beschleunigen oder abbremsen kann.

Die Annahme von Stößen ist für das Modell notwendig. Ließe man keine Stöße zu, so könnte man das Gas zum einen nicht in ein Volumen einsperren, da es die Wand nicht bemerkte, und zum anderen behielte jedes Gasteilchen für alle Zeiten seine Anfangsgeschwindigkeit. Letzteres würde z. B. verhindern, dass sich eine zugeführte Energie im Gas im Mittel gleichmäßig auf alle Freiheitsgrade verteilen könnte. Ein solches System kann nicht zum thermodynamischen Gleichgewicht streben. Durch die Stöße bewegen sich die Teilchen nur eine kurze Weglänge frei. Damit es zu Stößen kommt, muss ein Stoßquerschnitt angenommen werden. Genauere Modelle zeigen, dass der (durchschnittliche) Stoßquerschnitt temperaturabhängig anzusetzen ist (Sutherlandkonstante), was durch die Abhängigkeit des Stoßprozesses von der Energie der beiden Teilchen zu verstehen ist.

Thermodynamik

Formelzeichen	Bedeutung
Zustandsgrößen
$p$	Druck
$V$	Volumen
$N$	Anzahl der Teilchen (Teilchenzahl)
$T$	Absolute Temperatur
$n$	Stoffmenge
$m$	Masse
$U$	Innere Energie
$F$	Freie Energie
Konstanten
$k_{\mathrm {B} }$	Boltzmann-Konstante
$R$	Universelle Gaskonstante
$R_{s}$	spezifische Gaskonstante
$h$	Plancksches Wirkungsquantum

Zustandsgleichungen

Die thermische Zustandsgleichung zur Beschreibung eines idealen Gases heißt allgemeine Gasgleichung. Sie wurde zuerst aus verschiedenen einzelnen empirischen Gasgesetzen hergeleitet. Später erlaubte die Boltzmann-Statistik eine direkte Begründung ausgehend von der mikroskopischen Beschreibung des Systems aus einzelnen Gaspartikeln.

Die allgemeine Gasgleichung beschreibt die Abhängigkeiten der Zustandsgrößen des idealen Gases voneinander. In der Literatur wird sie üblicherweise in einer der folgenden Formen angegeben:

p\cdot V=n\cdot R\cdot T\qquad p\cdot V=N\cdot k_{\mathrm {B} }\cdot T\qquad p\cdot V=m\cdot R_{s}\cdot T,

wobei $R=8{,}314\,462\,618\dots \,\mathrm {J} \cdot \mathrm {mol} ^{-1}\cdot \mathrm {K} ^{-1}$ [1] die universelle Gaskonstante bezeichnet und $R_{s}$ die spezifische Gaskonstante darstellt. Mithilfe dieser Gleichung und den Hauptsätzen der Thermodynamik lassen sich die thermodynamischen Prozesse von idealen Gasen mathematisch beschreiben.

Neben der thermischen gibt es in der Thermodynamik noch die kalorische Zustandsgleichung. Diese lautet für das ideale Gas (ohne innere Freiheitsgrade):

U={\frac {3}{2}}\cdot n\cdot R\cdot T\qquad U={\frac {3}{2}}\cdot N\cdot k_{\mathrm {B} }\cdot T.

Allerdings sind thermische und kalorische Zustandsgleichung voneinander abhängig, was der zweite Hauptsatz der Thermodynamik nennt.

Eigenschaften idealer Gase

Ein ideales Gas hat eine Reihe besonderer Eigenschaften, die alle aus der allgemeinen Gasgleichung und den Hauptsätzen der Thermodynamik gefolgert werden können. Die allgemeine Gasgleichung ist die kompakte Zusammenfassung verschiedener Gesetzmäßigkeiten:

Satz von Avogadro: Gleiche Volumina idealer Gase enthalten bei gleichem Druck und gleicher Temperatur gleich viele Moleküle.

Die Stoffmenge $n$ als Maß für die Anzahl der Teilchen (Atome oder Moleküle) wird in der internationalen Einheit Mol gemessen.

1\ \mathrm {mol} \approx 6{,}022\cdot 10^{23}\ \mathrm {Teilchen} .

Das Mol ist also ein Vielfaches der Einheit.

Das Volumen eines idealen Gases mit einer Stoffmenge $n=1{\rm {mol}}$ bei Normbedingungen (nach DIN 1343)

(

p=1\ \mathrm {atm} =1{,}01325\cdot 10^{5}\ \mathrm {Pa}

und

T=0\ ^{\mathrm {o} }\mathrm {C} =273{,}15\ \mathrm {K}

)

ergibt sich aus der allgemeinen Gasgleichung zu:

V={\frac {1\ \mathrm {mol} \cdot 8{,}314\,463\ \mathrm {J\cdot mol^{-1}\cdot K^{-1}} \cdot 273{,}15\ \mathrm {K} }{1{,}01325\cdot 10^{5}\ \mathrm {Pa} }}=0{,}022\,413\,97\ \mathrm {m^{3}} =22{,}413\,97\ \mathrm {dm^{3}} =22{,}413\,97\ \mathrm {L} .

Die molare Masse $\mathrm {M}$ (Masse von 1 mol) entspricht also der Masse einer Gasmenge, die bei 0 °C und $1\ \mathrm {atm} =1{,}01325\ \mathrm {bar}$ in einem Volumen von 22,413 97 Liter enthalten ist (messbar aus der Gewichtsdifferenz eines gasgefüllten und dann evakuierten Kolbens).

Gesetz von Boyle-Mariotte: Bei konstanter Temperatur ist der Druck umgekehrt proportional zum Volumen: $p\sim V^{-1}\qquad (T\ \mathrm {konst.} )$

Gesetz von Amontons: Bei konstantem Volumen steigt der Druck wie die absolute Temperatur: $p\sim T\qquad (V\ \mathrm {konst.} )$

Dieses Gesetz ist die Grundlage für das Gasthermometer von Jolly.

Gesetz von Gay-Lussac: Bei konstantem Druck steigt das Volumen wie die absolute Temperatur: $V\sim T\qquad (p\ \mathrm {konst.} )$

Molares Volumen bei Normbedingungen

Das molare Volumen $V_{\mathrm {m} 0}$ unter Normbedingungen, d. h. bei Normaldruck p₀ = 101,325 kPa und Normaltemperatur T₀ = 273,15 K, hat für alle idealen Gase denselben Wert. Es errechnet sich über die universelle Gaskonstante R als:

V_{\mathrm {m} 0}={\frac {R\,T_{0}}{p_{0}}}\approx 22{,}413\,97\cdot 10^{-3}\,{\frac {\mathrm {m} ^{3}}{\mathrm {mol} }}\approx \mathrm {22{,}414} \,{\frac {\mathrm {\ell } }{\mathrm {mol} }}

Da $R$ aufgrund der Definition der Maßeinheiten einen exakten Wert hat, kann man auch $V_{\mathrm {m} 0}$ exakt angeben.

Thermodynamische Größen

Allgemein gilt für ein ideales Gas:

Wärmekapazität (einatomig): $C_{V}={\tfrac {3}{2}}Nk_{\mathrm {B} }\ ,\quad C_{p}={\tfrac {5}{2}}Nk_{\mathrm {B} }$
Adiabatenkoeffizient (einatomig): $\kappa ={\tfrac {5}{3}}$
Entropieänderung: $\Delta S=C_{V}\ln \!\left({\frac {T_{2}}{T_{1}}}\right)+Nk_{\mathrm {B} }\ln \!\left({\frac {V_{2}}{V_{1}}}\right)$
isobarer Volumenausdehnungskoeffizient: $\gamma ={\frac {1}{T}}$
unter Normbedingungen: $\gamma _{0}={\frac {1}{273{,}15}}\,\mathrm {K} ^{-1}$
isotherme Kompressibilität: $\kappa _{T}={\frac {1}{p}}$
unter Normbedingungen : $\kappa _{0}={\frac {1}{101325}}\,\mathrm {Pa} ^{-1}$
isochorer Spannungskoeffizient: $\beta ={\frac {1}{T}}$

Ideales Gasgemisch

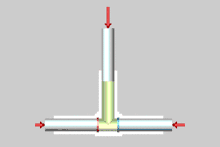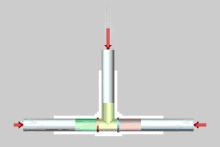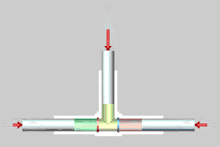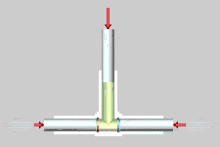
Reversibler Kreisprozess: Trennung eines Gasgemischs (gelb) mittels teildurchlässigen Membranen (rote oder blaue Platte) in eine Komponente A (grün) und eine Komponente B (braun). Die Entropie bleibt bei diesem Prozess konstant.

Nebenstehend die Zeitrafferdarstellung der reversiblen Entmischung eines idealen Gasgemischs mittels teildurchlässigen (semipermeablen) Membranen. Die linke (rote) Membran ist durchlässig für Komponente $A$ (grün) und undurchlässig für Komponente $B$ (braun), während umgekehrt die rechte (blaue) Membran für Komponente $A$ undurchlässig und für Komponente $B$ durchlässig ist. Die Kolben haben gleiche Abmessungen und bewegen sich gleich schnell. Die gesamte von den äußeren Kräften (rote Pfeile auf den Zylindern) geleistete Arbeit beträgt Null. Erfahrungsgemäß tritt bei der Mischung von idealen Gasen keine Mischungswärme auf und dasselbe gilt für die reversible Entmischung. Es wird weder Arbeit noch Wärme mit der Umgebung ausgetauscht. Da der Vorgang reversibel ist, bleibt die Entropie konstant.[2]

Bezeichnet $V$ die Volumenänderung pro Hub, $p$ den Druck, $S$ die Entropie und $T$ die Temperatur des Gemischs, und $V_{A}$ , $p_{A}$ , $S_{A}$ , $T_{A}$ und $V_{B}$ , $p_{B}$ , $S_{B}$ , $T_{B}$ die entsprechenden Größen der Komponente $A$ oder $B$ , so gilt:

$V=V_{A}=V_{B}$
$p=p_{A}+p_{B}$ (Dalton-Gesetz)
$S=S_{A}+S_{B}$
$T=T_{A}=T_{B}$

Analog gilt für ein mehrkomponentiges ideales Gasgemisch:

S(T,V)=\sum _{i}S_{i}(T,V),

wenn $S(T,V)$ die Entropie des Gemischs und $S_{i}(T,V)$ die Entropie der separaten $i$ -ten Komponente bei der Temperatur $T$ und dem Volumen $V$ bezeichnet.

Ideale Gase gleicher Temperatur überlagern sich in einem gemeinsamen Volumen ohne gegenseitige Beeinflussung, wobei sich der Druck (Daltonsches Gesetz), die thermodynamischen Potentiale (Entropie, innere Energie, Enthalpie) sowie die Wärmekapazitäten der einzelnen Bestandteile zu den entsprechenden Größen des Gemischs addieren.

Mischungsentropie eines idealen Gasgemischs

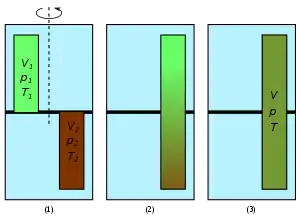
Diffusionsexperiment: Durch Diffusion vermischen sich verschiedene Gase von selbst und die Entropie nimmt zu.

Die nebenstehende Abbildung zeigt, wie durch Diffusion aus zwei ursprünglich getrennten Gasen ein einheitliches Gemisch entsteht. Die Temperaturen $T_{1}=T_{2}$ und Drücke $p_{1}=p_{2}$ der anfangs getrennten Gase (grün oder braun) seien gleich. Durch Drehung des oberen der beiden zylindrischen Behälter, die mit ihren ebenen Dichtflächen aneinander liegen (1), werden die abgeschlossenen Volumina $V_{1}$ und $V_{2}$ zum abgeschlossenen Volumen $V=V_{1}+V_{2}$ vereinigt. Die darin enthaltenen Gase diffundieren ineinander (2), bis schließlich, von selbst ohne äußere Einwirkung, ein einheitliches (homogenes) Gemisch entstanden ist, bei dem jeder Bestandteil gleichmäßig über das gesamte Volumen $V$ verteilt ist (3). Verhalten sich die Gase wie ideale Gase, so tritt bei diesem Diffusionsvorgang keine Mischungswärme auf und es gilt:

${\displaystyle p_{1}V_{1}=n_{1}RT_{1}\qquad$
$p=p_{1}=p_{2}$
$T=T_{1}=T_{2}$
$V=V_{1}+V_{2}$

wobei $n_{1}$ und $n_{2}$ die Molzahlen der getrennten Gase bezeichnen.

Die Mischungsentropie entspricht der Entropieänderung bei Expansion der Gase von ihren ursprünglichen Volumina $V_{1}$ oder $V_{2}$ auf das gemeinsame Gemischvolumen $V$ :

\Delta S=n_{1}\cdot R\cdot \ln {\frac {V}{V_{1}}}+n_{2}\cdot R\cdot \ln {\frac {V}{V_{2}}}

oder mit $n_{1}$ , $n_{2}$ und $n=n_{1}+n_{2}$ :

\Delta S=R\cdot \left(n_{1}\cdot \ln {\frac {n}{n_{1}}}+n_{2}\cdot \ln {\frac {n}{n_{2}}}\right)

Für ein mehrkomponentiges ideales Gasgemisch gilt analog:

\Delta S=R\cdot \sum _{i}\left(n_{i}\cdot \ln {\frac {n}{n_{i}}}\right)\qquad {\rm {mit}}\qquad n=\sum _{i}n_{i}.

Diese Formel gilt, wenn die getrennten Gase keine identischen Bestandteile enthalten, und zwar auch für chemisch sehr ähnliche Gase wie Ortho- und Parawasserstoff. Sie gilt näherungsweise auch für die Mischungsentropie von realen Gasen und zwar umso genauer, je besser diese die ideale Gasgleichung erfüllen. Wenn die beiden Teilvolumina $V_{1}$ und $V_{2}$ jedoch identische Gase enthalten, so findet beim Zusammenbringen keine Diffusion statt und es entsteht auch keine Mischungsentropie. Es ist also unzulässig, quasi in einem kontinuierlichen Grenzübergang die Gase immer ähnlicher und schließlich identisch werden zu lassen – siehe Gibbssches Paradoxon.

Reversible Mischung von Gasen

Reversibles mischen und Entmischen eines Gases nach [2].

Nicht jede Mischung von Gasen ist irreversibel. Die Grafik zeigt ein Gedankenexperiment[2], bei dem ein Kolben links eine semipermeable (halbdurchlässige) Wand besitzt, die nur Gas A durchlässt, für Gas B aber eine Barriere darstellt. Die mittlere Wand des Zylinders ist ebenfalls semipermeabel, aber diesmal für Gas B. Der rechte Teil ist evakuiert, so dass keine Kraft von dieser Seite auf den Kolben wirkt.

Anordnung 1: Das Gemisch aus Gas A und Gas B füllt die Kammer aus. Der Gesamtdruck setzt sich aus den Partialdrücken des Gases A und des Gases B zusammen.
Anordnung 2: Der Kolben wurde bewegt, so dass Gas A durch die linke Wand des Kolbens in den entstehenden Raum eintreten kann. Gas B wiederum tritt durch die semipermeable Wand in den rechten Raum ein. In der mittleren Kammer bleibt ein Teil der Mischung, die weiterhin mit der Summe der Partialdrücke von Gas A und B auf den Kolben wirkt.

Wie man durch das Kräftegleichgewicht am Kolben (hier auch Druckgleichgewicht, da die wirksame Kolbenfläche in allen drei Teilräumen gleich ist) sieht, heben sich die Kräfte durch die Gasdrücke auf. Die beiden Partialdrücke der reinen Gase sind in jeder Kolbenstellung gleich dem Gesamtdruck der Mischung. In der Praxis werden bei diesem Aufbau Reibung an Kolben und Dichtungen sowie Verluste beim Durchströmen der Gase durch die semipermeabelen Wände entstehen. Es bestehen jedoch keine physikalischen Schranken, so dass diese Verluste beliebig verkleinert und theoretisch auf Null reduziert werden können. Auch semipermeable Wände sind zumindest für einige Gase bekannt, beispielsweise glühendes Platin, das für Wasserstoff durchlässig ist, aber Sauerstoff sperrt. Somit ist die Mischung und Entmischung der beiden Gase vollkommen reversibel, da der Kolben in jeder Stellung im Gleichgewicht der Druckkräfte ist und im theoretischen Grenzfall verlustfrei und ohne Arbeit in jede Position verschoben werden kann.

Statistische Beschreibung

Während in der Thermodynamik die Zustandsgleichungen als reine empirische Gleichungen eingeführt werden, können diese mit den Mitteln der statistischen Physik direkt aus der mikroskopischen Beschreibung des Systems als Ansammlung einzelner Gaspartikel gewonnen werden. Außer den oben beschriebenen Annahmen des Modells selber wird dabei keine weitere Näherung benötigt. Die Möglichkeit der exakten mathematischen Beschreibung ist mit der Hauptgrund, warum das ideale Gas als einfachstes Gasmodell eine breite Anwendung findet und als Ausgangspunkt für bessere Modelle dient.

Zustandssumme des idealen einatomigen Gases

Hier soll die statistische Beschreibung des idealen Gases mit Hilfe des kanonischen Ensembles erfolgen (für eine alternative Herleitung im mikrokanonischen Ensemble – Sackur-Tetrode-Gleichung). Dazu betrachtet man ein System aus $N$ Teilchen in einem Volumen $V$ bei konstanter Temperatur $T$ . Alle thermodynamischen Relationen lassen sich aus der kanonischen Zustandssumme berechnen, welche wie folgt definiert ist:

Z(T,V,N)=\sum _{r}e^{-\beta E_{r}},\quad \beta ={\frac {1}{k_{\mathrm {B} }T}}.

Dabei ist

r\in \left\{(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N};\mathbf {p} _{1},\ldots ,\mathbf {p} _{N})|\mathbf {r} _{i}\in V,\mathbf {p} _{i}\in \mathbb {R} ^{3},i=1,\ldots ,N\right\}

ein Zustand des Systems und

E_{r}=E(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N};\mathbf {p} _{1},\ldots ,\mathbf {p} _{N})

die dazugehörige Energie. r_i ist der Ort und p_i der Impuls des $i$ -ten Teilchens. Für freie, nicht wechselwirkende Teilchen ist die Energie unabhängig vom Ort der Teilchen und ergibt sich als Summe aus den kinetischen Energien der Teilchen:

E(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N};\mathbf {p} _{1},\ldots ,\mathbf {p} _{N})=E(\mathbf {p} _{1},\ldots ,\mathbf {p} _{N})=\sum _{k=1}^{N}{\frac {\mathbf {p} _{k}^{2}}{2m}}.

Anstatt die Zustandssumme direkt auszuwerten, kann sie einfacher durch ein Integral über den Phasenraum berechnet werden.

Z(T,V,N)={\frac {1}{N!}}{\frac {1}{h^{3N}}}\int _{V}\!\mathrm {d} ^{3}\mathbf {r} _{1}\cdots \int _{V}\mathrm {d} ^{3}\mathbf {r} _{N}\int _{\mathbb {R} ^{3}}\!\mathrm {d} ^{3}\mathbf {p} _{1}\cdots \int _{\mathbb {R} ^{3}}\mathrm {d} ^{3}\mathbf {p} _{N}\;\exp \left(-\beta \sum _{k=1}^{N}{\frac {p_{k}^{2}}{2m}}\right).

Der zusätzliche Faktor $1/N!$ berücksichtigt die Ununterscheidbarkeit der Gasteilchen. Die Ortsraumintegrationen lassen sich elementar ausführen, da der Integrand nicht vom Ort abhängt; daraus erhält man das potenzierte Volumen $V^{N}$ . Weiterhin zerfällt die Exponentialfunktion in einzelne Faktoren für jede Impulskomponente, wobei sich die einzelnen Gauß’schen Integrale analytisch auswerten lassen:

Z(T,V,N)={\frac {1}{N!}}\left({\frac {V}{h^{3}}}\right)^{N}{\Bigg (}\underbrace {\int _{-\infty }^{\infty }\!\mathrm {d} p\,e^{-p^{2}\beta /2m}} _{={\sqrt {2m\pi /\beta }}=:h/\lambda }{\Bigg )}^{3N}.

Letztlich erhält man für die kanonische Zustandssumme des idealen Gases

Z(T,V,N)={\frac {1}{N!}}\left({\frac {V}{h^{3}}}\right)^{N}\left({\frac {2\pi m}{\beta }}\right)^{\frac {3N}{2}}={\frac {1}{N!}}\left({\frac {V}{\lambda ^{3}}}\right)^{N},

wobei im letzten Schritt die thermische Wellenlänge

\lambda =h{\sqrt {\frac {\beta }{2\pi m}}}={\frac {h}{\sqrt {2\pi mk_{\mathrm {B} }T}}}

eingeführt wurde. Die Zustandssumme hat die Eigenschaft, dass sie sich auch direkt aus der Zustandssumme eines einzelnen Teilchens berechnen lässt:

Z(T,V,N)={\frac {1}{N!}}\left[Z(T,V,1)\right]^{N}.

Diese Besonderheit ist jedem idealen System in der statistischen Physik zu eigen und ist Ausdruck des Fehlens von Wechselwirkungen zwischen den Gasteilchen. Ein besseres Gasmodell, welches diese Wechselwirkungen berücksichtigen will, muss demnach zusätzlich abhängig von mindestens der 2-Teilchen-Zustandssumme sein.

Ableitung thermodynamischer Relationen für das einatomige ideale Gas

Das der kanonischen Zustandssumme zugeordnete thermodynamische Potential ist die freie Energie

{\begin{aligned}F(T,V,N)&=-k_{\mathrm {B} }T\ln Z\\&=k_{\mathrm {B} }T\left(\ln N!-N\ln V+3N\ln \lambda \right)\\&\approx -Nk_{\mathrm {B} }T\ln \left({\frac {Ve}{N\lambda ^{3}}}\right).\end{aligned}}

Für große Teilchenzahlen lässt sich die Fakultät mit der Stirling-Formel entwickeln, $\ln(N!)\approx N\ln(N)-N=N\ln \left({\tfrac {N}{e}}\right)$ .

Aus der freien Energie lassen sich nun alle thermodynamischen Relationen ableiten:

{\begin{pmatrix}-S\\-p\\\mu \end{pmatrix}}={\begin{pmatrix}\partial _{T}\\\partial _{V}\\\partial _{N}\end{pmatrix}}F(T,V,N).

Außerdem ist die Innere Energie $U$ mit der freien Energie $F$ verknüpft über $U=F+TS$ .

Entropie

Die Entropie des idealen Gases ist:

{\begin{aligned}S(T,V,N)&=-\left({\frac {\partial F}{\partial T}}\right)_{V,N}=-k_{\mathrm {B} }\left(\ln N!-N\ln V+3N\ln \lambda \right)-3Nk_{\mathrm {B} }T\underbrace {{\frac {\partial }{\partial T}}\ln \lambda } _{={\frac {-1}{(2T)}}}\\&=-k_{\mathrm {B} }\left(\ln N!-N\ln V+3N\ln \lambda \right)+{\frac {5}{2}}Nk_{\mathrm {B} }\\&\approx Nk_{\mathrm {B} }\ln \left({\frac {V}{N\lambda ^{3}}}\right)+{\frac {5}{2}}Nk_{\mathrm {B} }\\&=Nk_{\mathrm {B} }\left[\ln {\frac {V}{N}}+{\frac {3}{2}}\ln T\right]+N\sigma \end{aligned}}

mit der Entropiekonstante

\sigma =k_{\mathrm {B} }\left(\ln {\frac {(2\pi mk_{\mathrm {B} })^{3/2}}{h^{3}}}+{\frac {5}{2}}\right)

.

Thermische Zustandsgleichung

Die thermische Zustandsgleichung ergibt sich aus

p(T,V,N)=-\left({\frac {\partial F}{\partial V}}\right)_{T,N}=k_{\mathrm {B} }T{\frac {N}{V}},

was durch Umstellen in die bekannte Form der idealen Gasgleichung gebracht werden kann

\left.pV=Nk_{\mathrm {B} }T\right..

Chemisches Potential

Das chemische Potential des idealen Gases ist gegeben durch

\mu (T,V,N)=\left({\frac {\partial F}{\partial N}}\right)_{T,V}={\frac {F(T,V,N+1)-F(T,V,N)}{1}}=-k_{\mathrm {B} }T\ln \left({\frac {V}{(N+1)\lambda ^{3}}}\right).

Kalorische Zustandsgleichung

Die kalorische Zustandsgleichung (die innere Energie in Abhängigkeit von Temperatur, Volumen und Teilchenzahl) kann aus den Gleichungen $F=U-TS$ und $S=-{\tfrac {\partial F}{\partial T}}$ bestimmt werden.

{\begin{aligned}U(T,V,N)&=F+TS=F-T{\frac {\partial F}{\partial T}}=T^{2}\left({\frac {1}{T^{2}}}F-{\frac {1}{T}}{\frac {\partial F}{\partial T}}\right)=T^{2}{\frac {\partial }{\partial T}}\left(-{\frac {F}{T}}\right)\\&=k_{\mathrm {B} }T^{2}{\frac {\partial }{\partial T}}\left(-{\frac {F}{k_{\mathrm {B} }T}}\right)=k_{\mathrm {B} }T^{2}{\frac {\partial \ln Z}{\partial T}}=-{\frac {\partial }{\partial \beta }}\ln Z\\&=-{\frac {\partial }{\partial \beta }}\left(-{\frac {3N}{2}}\ln \beta \right)={\frac {3N}{2\beta }}={\frac {3}{2}}Nk_{\mathrm {B} }T.\end{aligned}}

Dies ergibt schließlich

U={\frac {3}{2}}Nk_{\mathrm {B} }T.

Das Bemerkenswerte an dieser Gleichung ist, dass die innere Energie vom Volumen unabhängig ist. Daraus folgt z. B., dass bei der isothermen Expansion eines idealen Gases die zugeführte Wärme vollständig in Arbeit umgesetzt wird.

Gültigkeitsbereich

Unter den realen Gasen kommen die leichten Edelgase und Wasserstoff diesem Zustand am nächsten, insbesondere bei niedrigem Druck und hoher Temperatur, da sie im Vergleich zu ihrer mittleren freien Weglänge eine verschwindend kleine Ausdehnung besitzen. Die Geschwindigkeitsverteilung der Teilchen in einem idealen Gas wird durch die Maxwell-Boltzmann-Verteilung beschrieben.

Je niedriger der Druck und je höher die Temperatur ist, desto stärker verhält sich ein reales Gas wie ein ideales. Ein praktisches Maß dafür ist der „normierte“ Abstand der aktuellen Temperatur vom Siedepunkt: Zum Beispiel liegt der Siedepunkt von Wasserstoff bei 20 K; bei Zimmertemperatur ist das etwa das 15fache, was ein nahezu ideales Verhalten bedeutet. Dagegen beträgt bei Wasserdampf von 300 °C (573 K) der Abstand vom Siedepunkt (373 K) nur etwa das Anderthalbfache – weit ab von idealem Verhalten.

Als quantitative Vergleichsgröße muss hier der kritische Punkt herangezogen werden: Ein reales Gas verhält sich dann wie ein ideales, wenn sein Druck klein gegenüber dem kritischen Druck oder seine Temperatur groß gegenüber der kritischen Temperatur ist.

Ideale Gase unterliegen nicht dem Joule-Thomson-Effekt, woraus man folgern kann, dass ihre innere Energie und ihre Enthalpie unabhängig von Druck und Volumen sind. Der Joule-Thomson-Koeffizient beträgt daher bei idealen Gasen immer Null, und die Inversionstemperatur ( $T_{i}\gamma =1$ ) hat keinen diskreten Wert, erstreckt sich also über den gesamten Temperaturbereich.

Erweiterungen

Ideales mehratomiges Gas

Möchte man mit dem idealen Gasmodell mehratomige Gaspartikel, also Moleküle, beschreiben, so kann das durch eine Erweiterung der kalorischen Zustandsgleichung geschehen

U={\frac {f}{2}}Nk_{\mathrm {B} }T.

Dabei gibt $f$ die Anzahl der Freiheitsgrade pro Teilchen an. Moleküle haben neben den drei Translationsfreiheitsgraden weitere Freiheitsgrade für Rotationen und Schwingungen. Jede Normalschwingung hat dabei zwei Freiheitsgrade, weil der potentielle und der kinetische Freiheitsgrad einer Schwingung separate Freiheitsgrade sind.

Beispielsweise besitzt ein zweiatomiges Gas insgesamt 7 Freiheitsgrade, nämlich

drei Translationsfreiheitsgrade,
zwei Rotationsfreiheitsgrade für Rotationen um Achsen senkrecht zur Verbindungslinie der Molekülatome und
zwei Schwingungsfreiheitsgrade für die eine mögliche Schwingung der Molekülatome zueinander.

Da in der Natur die Rotations- und Schwingungsfrequenzen von Molekülen gequantelt sind, wird eine gewisse Mindestenergie benötigt, um diese anzuregen. Oft reicht unter Normalbedingungen die thermische Energie nur, um in einem mehratomigen Molekül Rotationen anzuregen. In diesem Fall sind die Schwingungsfreiheitsgrade eingefroren. In zweiatomigen und in gestreckten mehratomigen Molekülen ist auch die Rotation um die Molekülachse eingefroren, so dass diese effektiv nur fünf Freiheitsgrade haben. Bei noch tieferen Temperaturen frieren auch die übrigen zwei Rotationsfreiheitsgrade ein, so dass nur die drei Translationsfreiheitsgrade verbleiben, wie bei den einatomige Gasen. Bei nicht stabförmigen Molekülen aus mehr als zwei Atomen tritt der dritte Rotationsfreiheitsgrad nebst weiteren Schwingungsfreiheitsgraden aber in der Regel auf.

Relativistisches ideales Gas

Wenn die Temperaturen so groß werden, dass die mittleren Geschwindigkeiten der Gaspartikel mit der Lichtgeschwindigkeit vergleichbar werden, so muss die relativistische Massenzunahme der Teilchen berücksichtigt werden. Dieses Modell lässt sich ebenfalls gut theoretisch beschreiben, allerdings ist ein reales Gas im Regelfall bei sehr hohen Temperaturen bereits ein Plasma, d. h. die vorher elektrisch neutralen Gaspartikel liegen getrennt als Elektronen und Ionen vor. Da die Wechselwirkung zwischen Elektronen und Ionen aber wesentlich stärker als zwischen neutralen Teilchen ist, kann die Modellvorstellung eines idealen Gases nur begrenzten Aufschluss über die Physik von heißen Plasmen liefern.

Ideales Quantengas

Jede Art von Materie besteht letztendlich aus Elementarteilchen, die entweder Fermionen oder Bosonen sind. Bei Fermionen und Bosonen muss immer die sogenannte Austauschsymmetrie berücksichtigt werden, was die statistische Beschreibung des Systems ändert. Ein reines ideales Gas ist im Grunde genommen also immer entweder ein ideales Fermigas oder ein ideales Bosegas. Die Quantennatur eines Gases wird jedoch erst spürbar, wenn die mittlere freie Weglänge der Gaspartikel vergleichbar oder kleiner als ihre thermische Wellenlänge wird. Dieser Fall gewinnt folglich bei tiefen Temperaturen oder sehr hohen Drücken an Bedeutung.

Ideale Quantengase haben ein sehr breites Anwendungsspektrum gefunden. Beispielsweise können die Leitungselektronen in Metallen hervorragend durch das ideale Fermigas beschrieben werden. Die Hohlraumstrahlung und das Plancksche Strahlungsgesetz eines schwarzen Körpers können durch das ideale Photonengas – welches ein besonderes (masseloses) ideales Bosegas ist – ausgezeichnet erklärt werden. Ideale Bosegase können zudem bei sehr tiefer Temperatur einen Phasenübergang zu Bose-Einstein-Kondensaten zeigen.

Van-der-Waals-Gas

Reale Gase werden besser durch das sogenannte Van-der-Waals-Gas beschrieben, welches die immer vorhandenen Van-der-Waals-Kräfte zwischen den Gaspartikeln und zusätzlich deren Eigenvolumen berücksichtigt. Die Van-der-Waals-Gleichung modifiziert die ideale Gasgleichung um zwei entsprechende Zusatzterme. In der statistischen Beschreibung kann diese Gleichung durch die sogenannte Virialentwicklung gewonnen werden.

Perfektes Gas

Als perfektes Gas werden ideale Gase bezeichnet, welche eine konstante Wärmekapazität haben, die nicht von Druck und Temperatur abhängig ist.

Weblinks

Bernd Glück: „Reversible Zustandsänderungen des idealen Gases“. Algorithmen und Rechenprogramm mit grafischer Darstellung der Zustandsverläufe
Video: Ideale Gasgesetze von BOYLE, GAY-LUSSAC, AVOGADRO und DALTON – wie beschreibt man ein Gas makroskopisch?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15649.

Einzelnachweise

CODATA Recommended Values: molar gas constant. National Institute of Standards and Technology, abgerufen am 20. Juli 2019.. Wert der universellen Gaskonstanten. Der Wert ist seit der Neudefinition des Internationalen Einheitensystems im Jahr 2019 als Produkt von exaktem k und exaktem N_A exakt, wird aber nach den ersten 10 Ziffern mit ... abgekürzt.
Fran Bošnjaković, Karl-Friedrich Knoche: Technische Thermodynamik Teil 1. 8. Auflage. Steinkopff Verlag, Darmstadt 1998, ISBN 978-3-642-63818-3, 7.6 Entropie idealer Gasgemische.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] CODATA Recommended Values: molar gas constant. National Institute of Standards and Technology, abgerufen am 20. Juli 2019.. Wert der universellen Gaskonstanten. Der Wert ist seit der Neudefinition des Internationalen Einheitensystems im Jahr 2019 als Produkt von exaktem k und exaktem N_A exakt, wird aber nach den ersten 10 Ziffern mit ... abgekürzt.

[Bosniacovic-2] Fran Bošnjaković, Karl-Friedrich Knoche: Technische Thermodynamik Teil 1. 8. Auflage. Steinkopff Verlag, Darmstadt 1998, ISBN 978-3-642-63818-3, 7.6 Entropie idealer Gasgemische.