Thermodynamischer Kreisprozess
Als Kreisprozess bezeichnet man in der Thermodynamik eine Folge von Zustandsänderungen eines Arbeitsmediums (Flüssigkeit, Dampf, Gas – allgemein Fluid genannt), die periodisch abläuft, wobei immer wieder der Ausgangszustand, gekennzeichnet durch die Zustandsgrößen (siehe auch Fundamentalgleichung, Thermodynamisches Potential), wie u. a. Druck, Temperatur und Dichte, erreicht wird. Es sind technische Prozesse, meist zur Umwandlung von Wärme in Arbeit (z. B. in Verbrennungsmotoren) oder zum Heizen und Kühlen durch Aufwenden von Arbeit (Wärmepumpe, Kühlschrank).
Zwei fundamentale Beispiele (Mathematik)
- Gegeben sei ein formaler Ausdruck , z. B. mit („absolute Temperatur“) und („spezifisches Flüssigkeitsvolumen“). Die Hintereinanderausführung (Integration) solcher infinitesimaler Vorgänge definiert einen Thermodynamischen Prozess. Die „Hintereinanderausführung“ geschehe auf einem geschlossenen Weg. Trotzdem spricht man dann noch nicht von einem „Kreisprozess“:
- Wir fragen jetzt, ob zu eine Funktion existiert – z. B. die Entropie des Systems –, sodass der obige Differentialausdruck das totale Differential der angegebenen sog. „Zustandsfunktion“ ist. Erst solche Prozesse nennt man Kreisprozesse, genauer „integrable Kreisprozesse“. Das Linienintegral über eine beliebige Zustandsfunktion f ergibt ja stets Null, berechnet auf einem beliebigen geschlossenen Weg W. Für gilt das dagegen nicht. Infolgedessen ist nicht die Geschlossenheit des Weges, sondern die Integrabilität von das Wichtigste.
- Ein Kreisprozess liegt also dann und nur dann vor, wenn stets bei allen geschlossenen Wegen W (die Geschlossenheit des Weges wird durch das Kreissymbol beim Integralzeichen unterstrichen), wobei also und gilt. Wegen der Identität der gemischten 2. Ableitungen bedeutet dies, dass sein muss.
- Wir brauchen also nur zu prüfen, ob diese sog. „Integrabilitätsbedingung“ erfüllt ist oder nicht: das ist in der Regel nicht der Fall.
- Also: Kreisprozesse sind Ausnahmen und nicht die Regel.
- Beispielsweise ergibt sich notwendig kein Kreisprozess für („Wärme“), weil Wärme, auf verschiedenen Wegen zugeführt, nicht das gleiche Resultat ergibt, selbst wenn sie dem System reversibel zugeführt wird:
- (siehe beispielsweise im Carnot-Prozess)
Die Existenz eines Kreisprozesses ist dagegen der Fall bei anderen wichtigen Größen, z. B. bei der Entropie S, wenn also eine Wärmeenergie δQ erstens reversibel zu- bzw. abgeführt und zweitens mit dem „integrierenden Faktor“ 1/T multipliziert wird, Die unterschiedlichen Symbole bei den Differentialen sollen hier nochmals unterstreichen, dass es sich einmal (linke Seite) um ein vollständiges Differential, das andere Mal (rechte Seite) um ein unvollständiges Differential handelt. Für den schon genannten „integrierenden Nenner“, die „absolute Temperatur“ T, bedeutet dies zugleich, dass es sich um eine besonders wichtige Größe handelt (nicht nur um eine formale Zahl): im Vergleich zu den üblichen Temperaturskalen (Celsius-, Fahrenheit-, Réaumur-Skala usw.) besitzt sie zusätzliche Eigenschaften, die sich u. a. in den genannten mathematischen Beziehungen ausdrücken.
- 2. Es kann stattdessen auch sein (siehe das folgende Beispiel), dass der geschlossene Weg in verschiedene Abschnitte zerfällt, auf denen verschiedene Zustandsfunktionen betrachtet werden (z. B. erfolgen beim nächsten Beispiel Entropie-Änderungen bei horizontalen Abschnitten, dagegen Enthalpie-Änderungen auf vertikalen Abschnitten). Das Resultat ist i. A. die Erzeugung einer mechanischen oder elektrischen Arbeit (z. B. Dampfturbine).
Weitere Beschreibung
Entscheidend für einen Kreisprozess (oft auch Zyklus genannt) ist, dass der Rückweg ein anderer ist als der Weg, auf dem sich der Zustand vom Ausgangszustand entfernt. Die meist verwendeten Zustandsdiagramme sind das p-v-Diagramm, das T-s-Diagramm, das h-s-Diagramm und das p-h-Diagramm (letzteres insbesondere für Kühlprozesse). In den beiden erstgenannten Diagrammen wird dadurch eine Fläche umrundet, die bei reversiblen Prozessen der Kreisprozessarbeit entspricht. Dies gilt jedoch nur für die idealen Vergleichsprozesse. Die wirklichen technischen Prozesse sind nicht reversibel (vergl. Dissipation) und die Fläche wird dann durch die dissipierte Arbeit vergrößert.
| Beispiel: Gasturbinenprozess | |
|---|---|
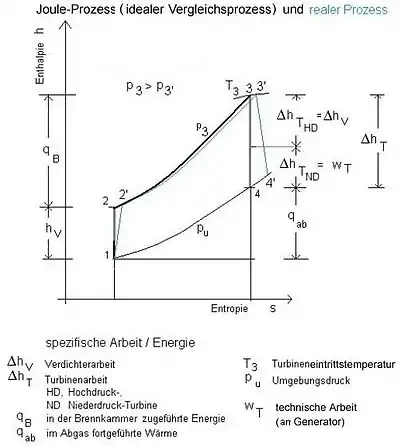 Vergleichsprozess und realer Prozess im h-s-Diagramm (h ist bei Gasen angenähert proportional der Temperatur T) |
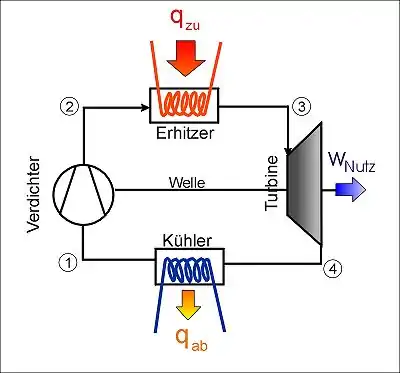 Geschlossener Gasturbinenprozess als Beispiel eines Kreisprozesses |
Rechts- und Linksprozesse
Es gibt Rechtsprozesse und Linksprozesse, je nachdem ob das Zustandsdiagramm im Uhrzeigersinn oder umgekehrt durchlaufen wird.
Beim Rechtsprozess (Uhrzeigersinn) wird ein Teil der bei hoher Temperatur zugeführten Wärme in Arbeit umgewandelt, der andere Teil wird bei niedrigerer Temperatur wieder abgeführt. Die Differenz ist die Kreisprozessarbeit (vergl. Energiebilanz für Kreisprozesse). Die Gewinnung von Arbeit im Rechtsprozess kommt dadurch zustande, dass bei niedriger Temperatur, d. h. bei kleinem Druck komprimiert wird (Arbeitsaufwand) und bei hoher Temperatur und somit bei großem Druck das Fluid unter Arbeitsabgabe expandiert. Der Betrag der Volumenarbeit der Expansion ist somit größer als der der Kompression.
Beim Linksprozess kehrt sich demgegenüber alles um, so dass unter Arbeitsaufwand Wärme von einem kälteren Reservoir in ein wärmeres gefördert wird. Besonders große spezifische Kreisprozessarbeiten erreicht man, wenn innerhalb des Prozesses der Phasenwechsel zwischen flüssig und gasförmig stattfindet, weil dann der Volumenunterschied besonders groß ist. Dies macht man sich im Dampfkraftwerk zunutze. Da Flüssigkeit (Wasser) fast inkompressibel ist, entfällt die Verdichtungsarbeit und der Arbeitsaufwand zum Fördern der Flüssigkeit in den Kessel mit hohem Druck (Kesselspeisepumpe) ist relativ gering.
| Beispiel: Dampfkraftwerk (Rechtsprozess) |
|---|
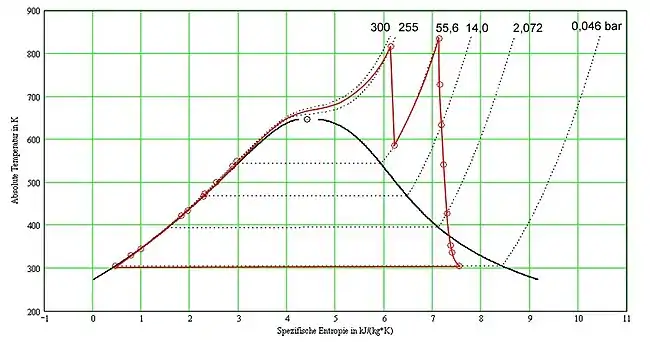 Kreisprozess des Kraftwerks Staudinger, Block 5 im T-s-Diagramm (vergl. Dampfkraftwerk). |
| Beispiel: Kühlprozess (Linksprozess) |
|---|
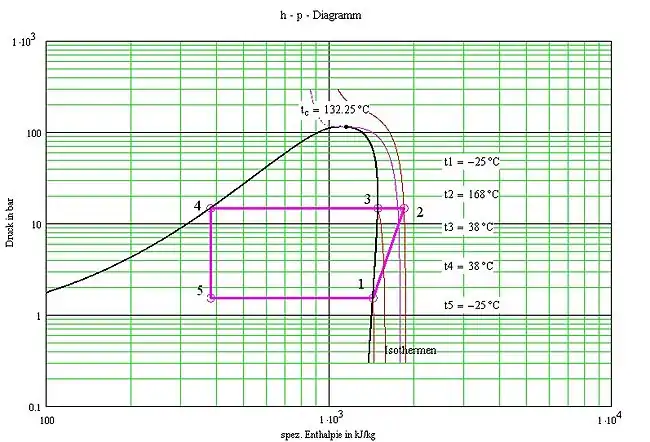 Linksprozess mit NH3 im h-p-Diagramm. Die Zustandsänderungen sind: Verdichtung des Sattdampfes 1-2, Wärmeabgabe bis zum Kondensationspunkt 2-3, Wärmeabgabe durch Kondensation 3-4, Drosselung 4-5, Verdampfung 5-1 (vergl. Kältemaschine). |
Offene und geschlossene Prozesse
Eine weitere Unterscheidung der Kreisprozesse ergibt sich durch die unterschiedliche Wärmezufuhr. Erfolgt diese intern durch Verbrennung von eingebrachtem Brennstoff, wie beim Verbrennungsmotor oder beim Flugtriebwerk, ist der Kreisprozess offen, weil ein Ladungswechsel zwischen Abgas und Frischluft erfolgen muss. Ein prinzipieller Unterschied aus thermodynamischer Sicht besteht nicht, weil die Atmosphäre als großer Wärmeübertrager betrachtet werden kann. Der Prozess im Bildbeispiel ist ein geschlossener mit zwei Wärmeübertragern. Solche Prozesse können beispielsweise in einem Kernkraftwerk mit gasgekühlten Reaktoren (z. B. Helium als Kühlmittel und Arbeitsfluid) verwendet werden.
Mit der rechnerischen und graphischen Darstellung der Prozesse besitzt man ein theoretisches Hilfsmittel, sowohl zur Formulierung von Aussagen, als auch zur technischen Umsetzung bei der Konzeption von wärmetechnischen Maschinen und Anlagen. Beispielsweise wird in der Chemie der Born-Haber-Kreisprozess verwendet, um die Reaktionsenergie (bzw. -enthalpie) eines Prozess-Schrittes oder die Bindungsenergie einer chemischen Verbindung zu berechnen, wenn die Energien der anderen Prozessschritte bekannt sind.
Zur Beurteilung der Effizienz eines Kreisprozesses dienen die idealen Vergleichsprozesse. Diese wiederum werden verglichen mit dem idealen theoretischen Kreisprozess, dem Carnot-Prozess, der den maximal möglichen Wirkungsgrad besitzt. Er kennzeichnet das, was nach dem 2. Hauptsatz der Thermodynamik theoretisch möglich ist, praktisch ist dieser Wirkungsgrad nicht (ganz) erreichbar.
Kreisprozesse
Literatur
- Literatur zur Technischen Thermodynamik
- Klaus Lüders, Gebhard von Oppen: Mechanik, Akustik, Wärme. 12. Auflage. De Gruyter, Berlin 2008, ISBN 978-3-11-019311-4 (Lehrbuch der Experimentalphysik. Band 1).