Enthalpie

Die Enthalpie $H$ (von altgriechisch ἐνθάλπειν enthálpein, deutsch ‚darin erwärmen‘),[1] früher auch Wärmeinhalt, eines thermodynamischen Systems ist die Summe aus der inneren Energie $U$ des Systems und dem Produkt aus Druck $p$ und Volumen $V$ des Systems:[2]. Es ist eine Rechengröße, die nicht direkt gemessen werden kann.

H=U+pV

.

Physikalische Größe

Name

Enthalpie

Formelzeichen

$H$

Größen- und Einheitensystem	Einheit	Dimension
SI	J = kg·m²·s⁻²	M·L²·T⁻²

Die Reaktionsenthalpie der Verbrennung von Alkohol an der Luft ist negativ. Es handelt sich also um eine exotherme Reaktion, bei der Wärme an die Umgebung abgegeben wird.

Die Schmelzenthalpie ist die notwendige Energiemenge, die zum Schmelzen des Eises bei konstantem Druck aufgebracht werden muss. Sie wird der Umgebung entzogen und kühlt dabei das Getränk.

Sie hat die Dimension der Energie mit der Einheit Joule.

Die Enthalpie ist eine extensive Größe: Die Enthalpie eines Gesamtsystems ist die Summe der Enthalpien der Teilsysteme.

Die molare Enthalpie (Einheit: J/mol) ist die auf die Stoffmenge $n$ bezogene Enthalpie:

H_{\mathrm {m} }={\frac {H}{n}}

.

Die spezifische Enthalpie (Einheit: J/kg) ist die auf die Masse $m$ bezogene Enthalpie:

h={\frac {H}{m}}

.

Die molare und die spezifische Enthalpie sind intensive Größen: Haben zwei identische Teilsysteme die gleiche molare oder spezifische Enthalpie, dann hat auch das aus ihnen gebildete Gesamtsystem diese molare bzw. spezifische Enthalpie.

Die Enthalpie $H$ ist ebenso wie $U$ , $p$ und $V$ eine Zustandsgröße; sie wird vom aktuellen Zustand des Systems eindeutig bestimmt und ist unabhängig von der Vorgeschichte des Systems.

Die praktische Nützlichkeit der Rechengröße Enthalpie beruht darauf, dass die durch einen Prozess bewirkte Veränderung der Enthalpie eines Systems

\mathrm {d} H=\mathrm {d} (U+p\ V)=\mathrm {d} U+p\ \mathrm {d} V+V\ \mathrm {d} p

durch den einfacheren Ausdruck

\mathrm {d} H=\mathrm {d} U+p\ \mathrm {d} V

beschrieben wird, wenn der Prozess bei konstantem Druck (isobar, $\mathrm {d} p=0$ ) abläuft. Dieser Ausdruck lässt sich aber als die „Bruttoenergie“ interpretieren, die dem System zugeführt werden muss, wenn dessen innere Energie um den Betrag $\mathrm {d} U$ erhöht werden soll und das System einen Teil der zugeführten Energie für die während des Prozesses zu leistende Volumenänderungsarbeit $p\,\mathrm {d} V$ verbraucht. Im Falle eines isobaren Prozesses kann man daher die aufzuwendende „Bruttoenergie“ $\mathrm {d} U+p\ \mathrm {d} V$ mit der zugeführten Enthalpie $\mathrm {d} H$ identifizieren und die Vorteile nutzen, die das Rechnen mit Zustandsgrößen bietet. Falls das System neben der Volumenänderungsarbeit keine andere Form von Arbeit leistet, ist der Enthalpieumsatz des Prozesses gleich dem Wärmeumsatz.

Zahlreiche physikalische und chemische Prozesse finden bei konstantem Druck statt. Dies ist beispielsweise oft bei Phasenübergängen oder bei chemischen Reaktionen der Fall, insbesondere (aber nicht nur) wenn sie unter Atmosphärendruck stattfinden. Die Enthalpie ist dann eine geeignete Größe zur Beschreibung des Wärmeumsatzes dieser Prozesse.

In der theoretischen Thermodynamik ist die Enthalpie eine Fundamentalfunktion, aus ihr lässt sich die gesamte thermodynamische Information über das System ableiten. Voraussetzung ist jedoch, dass sie als Funktion der Variablen Entropie $S$ , Druck $p$ und Molzahlen $N_{i}$ der im System enthaltenen chemischen Komponenten gegeben ist. Dies sind die „natürlichen Variablen“ der Enthalpie. Sie lässt sich auch als Funktion anderer Variablen ansetzen, enthält dann aber nicht mehr die vollständige thermodynamische Information.

Die Enthalpie ist eine Legendre-Transformierte der inneren Energie. Die innere Energie ist ebenfalls eine Fundamentalfunktion, wenn sie als Funktion ihrer natürlichen Variablen $S$ , $V$ , $N_{i}$ gegeben ist. Der Übergang zu anderen Variablensätzen erfordert die Anwendung einer Legendre-Transformation, wenn er ohne Informationsverlust geschehen soll. Die Transformation, die aus der inneren Energie eine Fundamentalfunktion mit den natürlichen Variablen $S$ , $p$ , $N_{i}$ erzeugt, liefert den Ausdruck $U+p\ V$ , also die Enthalpie. Der aus der Legendre-Transformation folgende additive Term $p\ V$ kompensiert den Informationsverlust, der sonst mit dem Variablenwechsel verbunden wäre.

Von der Enthalpie zu unterscheiden ist die freie Enthalpie oder Gibbs-Energie, die Legendre-Transformation der Enthalpie nach der Entropie.

Einführung

Die Enthalpie ist eine mathematisch definierte abstrakte Kenngröße zur Beschreibung thermodynamischer Systeme (siehe → Thermodynamische Eigenschaften der Enthalpie). Sie lässt sich nicht unmittelbar als eine anschauliche Energiegröße eines Systems interpretieren. Unter bestimmten Bedingungen jedoch treten in einem System Energiegrößen auf, die formelmäßig mit der Enthalpie oder mit Enthalpieänderungen des Systems übereinstimmen. Sie können dann mit der Enthalpie bzw. deren Änderung identifiziert werden, was – weil die Enthalpie eine extensive Zustandsgröße ist – mathematische Vorteile bietet und mit Begriffen wie „Enthalpieinhalt“ oder „Enthalpiezufuhr“ eine kompakte und anschauliche Sprechweise bei der Beschreibung des Systems und seiner Prozesse erlaubt. Die Enthalpie wird häufig zur Beschreibung isobarer Prozesse und stationär strömender Fluide benutzt.

Enthalpie in isobaren Prozessen

Eine besonders anschauliche Bedeutung hat die Enthalpie im Falle eines bei konstantem Druck (also isobar) ablaufenden Prozesses. Da zahlreiche technische, chemische und physikalische Prozesse unter Umgebungsdruck und damit isobar ablaufen, ist diese Situation häufig anzutreffen.

Will man die innere Energie $U$ eines Systems erhöhen, muss man Energie von außen zuführen (Erster Hauptsatz der Thermodynamik). Hat das System keine Möglichkeit, die zugeführte Energie oder einen Teil davon wieder in Form von Wärme oder von mechanischer (oder chemischer, elektrischer, magnetischer …) Arbeit abzugeben, trägt die gesamte zugeführte Energie zur Erhöhung der inneren Energie bei. Wird die Energie beispielsweise in Form einer Wärmemenge $\mathrm {d} Q$ zugeführt, lautet die Energiebilanz für ein solches System einfach $\mathrm {d} U=\mathrm {d} Q$ .

In der Regel jedoch ist die Erhöhung der inneren Energie mit einer Volumenvergrößerung verbunden, etwa infolge thermischer Expansion bei Temperaturerhöhung, im Zuge eines Phasenübergangs oder bei einer chemischen Reaktion mit Gasentwicklung. Wird die Volumenzunahme nicht verhindert (das wäre zum Beispiel bei starr eingespannten Systemen oder bei chemischen Reaktionen in einem starren Behälter der Fall), dehnt sich das System um das Volumen $\mathrm {d} V$ gegen den auflastenden Umgebungsdruck $p$ aus und leistet dabei die Volumenänderungsarbeit $p\ \mathrm {d} V$ , die nun nicht mehr zur Erhöhung der inneren Energie zur Verfügung steht:

\mathrm {d} U=\mathrm {d} Q-p\ \mathrm {d} V

oder umgestellt

\mathrm {d} Q=\mathrm {d} U+p\ \mathrm {d} V\quad (*)

Die Änderung der Enthalpie des Systems ist andererseits, gemäß deren Definition und unter Anwendung der Produktregel

\mathrm {d} H=\mathrm {d} (U+p\ V)=\mathrm {d} U+p\ \mathrm {d} V+V\ \mathrm {d} p

,

was sich im Spezialfall konstanten Drucks ( $\mathrm {d} p=0$ ) reduziert auf

\mathrm {d} H=\mathrm {d} U+p\ \mathrm {d} V\quad (*)

.

Vergleich der markierten Ausdrücke liefert

\mathrm {d} H=\mathrm {d} Q

.

Geht also ein System bei konstantem Druck von einem Anfangs- in einen Endzustand über und tritt dabei keine andere Form von Arbeit auf als Volumenänderungsarbeit, dann ist die Änderung der Enthalpie des Systems zahlenmäßig gleich der dem System zugeführten Wärmemenge.[3]

In der älteren Literatur wurde die Enthalpie deshalb auch als „Wärmeinhalt“ des Systems bezeichnet. In heutiger Sprechweise ist das nicht mehr üblich, weil man dem resultierenden Energieinhalt des Systems nicht ansehen kann, ob die Energie als Wärme oder als Arbeit zugeführt wurde. Näheres hierzu folgt im nächsten Abschnitt.

Die genannte Einschränkung auf Systeme, die keine andere Arbeit leisten als Volumenänderungsarbeit, ist ebenso wichtig wie die Beschränkung auf konstanten Druck. Ein häufig anzutreffendes Beispiel für Systeme, die auch eine andere Form von Arbeit leisten können, sind galvanische Zellen. Diese können elektrische Arbeit leisten, und die von ihnen umgesetzte Wärme ist nicht identisch mit der Änderung ihrer Enthalpie.[4]

Die Verwendung der Enthalpie ist nicht auf isobare Prozesse beschränkt. Im Falle nicht-isobarer Prozesse ist die Enthalpieänderung bei Wärmezufuhr jedoch komplizierter: $\mathrm {d} H=\mathrm {d} Q+V\ \mathrm {d} p$ .

Zustands- und Prozessgrößen

Eine Zustandsgröße ist durch den aktuellen Zustand des Systems eindeutig festgelegt. Sie ist insbesondere unabhängig von der Vorgeschichte des Systems, also von dem Prozess, über den es in den vorliegenden Zustand gelangte. Beispiele sind Temperatur, Druck, innere Energie und Enthalpie.

Eine Prozessgröße beschreibt den Vorgang, der das System von einem Zustand in einen anderen überführt. Gibt es verschiedene Prozessführungen, die von einem gegebenen Anfangszustand zu einem gegebenen Endzustand führen, können die jeweiligen Prozessgrößen trotz fixierter Anfangs- und Endzustände verschieden sein. Beispiele sind der Wärmestrom, den das System während des Prozesses mit seiner Umgebung austauscht, oder die mechanische Arbeit, die es mit der Umgebung austauscht.

Wärmeinhalt und Enthalpieinhalt

Wird einem System ein Wärmestrom zugeführt, ist man intuitiv versucht, sich dabei eine „Wärmemenge“ vorzustellen, die in das System fließt, und deren angesammelte Gesamtmenge eine vermeintliche „Zustandsgröße Wärmeinhalt“ des Systems darstellt. Diese Vorstellung ist jedoch nicht haltbar. Dem System kann auch mechanische Arbeit zugeführt werden, deren Summe dann konsequenterweise als „Arbeitsinhalt“ angesehen werden müsste. Da sich der im System befindlichen Energie aber nicht mehr ansehen lässt, ob sie als Wärme oder Arbeit zugeführt wurde, ist es nicht sinnvoll, sie begrifflich in einen „Wärmeinhalt“ und einen „Arbeitsinhalt“ aufzuteilen.[5] Außerdem gibt es in der Regel verschiedene Wege, auf denen der neue Zustand erreicht werden kann, und die dem System insgesamt zugeführte Energie kann je nach Prozessführung unterschiedlich auf Wärme- und Arbeitszufuhr aufgeteilt sein. Das System könnte dann im neuen Zustand je nach durchlaufenem Prozessweg unterschiedliche „Wärmeinhalte“ und „Arbeitsinhalte“ aufweisen, so dass diese auch keine Zustandsgrößen sein könnten. Unter „Wärme“ versteht man deshalb im Sprachgebrauch der Thermodynamik ausschließlich die Prozessgröße „Wärmestrom“,[6] der Begriff „Wärmeinhalt“ wird nicht mehr benutzt.

Die innere Energie und die Enthalpie sind im Gegensatz zum „Wärmeinhalt“ Zustandsgrößen, und da sie außerdem extensive (d. h. mengenartige) Größen sind, kann anschaulich vom Inhalt an innerer Energie sowie vom Enthalpieinhalt des Systems gesprochen werden. Beide ändern sich bei Zufuhr einer Wärmemenge, und zwar erhöht sich bei isochorer Prozessführung (also konstant gehaltenem Volumen) der Inhalt an innerer Energie genau um die zugeführte Wärmemenge, $\mathrm {d} U=\mathrm {d} Q$ , und bei isobarer Prozessführung (konstant gehaltenem Druck) ändert sich der Enthalpieinhalt genau um die zugeführte Wärmemenge, $\mathrm {d} H=\mathrm {d} Q$ . Diese beiden Zustandsgrößen $U$ beziehungsweise $H$ leisten für die jeweilige Prozessart also genau das, wofür man intuitiv den Begriff des „Wärmeinhalts“ benutzt hätte, und ersetzen diesen.

Die Zustandsgrößen haben außerdem den Vorteil, dass der Unterschied an innerer Energie oder Enthalpie zwischen zwei Zuständen eines Systems allein aus der Kenntnis der beiden Zustände bestimmt werden kann und nicht von der Art abhängt, wie die Zustandsänderung erfolgte. Die Bestimmung von Prozessgrößen, beispielsweise wie sich die während der Zustandsänderung ausgetauschte Energie in Wärme und Arbeit aufteilt, erfordert in der Regel zusätzliche Kenntnis über Details des Änderungsprozesses.

Enthalpieinhalt und Enthalpiezufuhr

Wird ein System durch einen geeigneten (isochoren) Prozess von einem Zustand $1$ in einen Zustand $2$ überführt, so hat es im Anfangszustand die Enthalpie $H_{1}$ und im Endzustand die Enthalpie $H_{2}$ . Was bedeutet der Enthalpie-Unterschied, ausgedrückt durch messbare physikalische Größen?

Für einen infinitesimal kleinen Enthalpieunterschied gilt (s. o.)

\mathrm {d} H=\mathrm {d} Q+V\ \mathrm {d} p

,

so dass bei gegebenem aktuellen Volumen $V$ eine geeignete Kombination von Wärmezufuhr $\mathrm {d} Q$ und Druckänderung $\mathrm {d} p$ den Enthalpieinhalt $H$ des Systems um den Betrag $\mathrm {d} H$ ändert. Es ist naheliegend, $\mathrm {d} H$ als Enthalpiezufuhr und die zeitliche Zufuhr-Rate ${\frac {\mathrm {d} H}{\mathrm {d} t}}$ als Enthalpiestrom zu bezeichnen. Ein endlich großer Enthalpieunterschied $\Delta H=H_{2}-H_{1}$ ist das Integral über $\mathrm {d} H$ .

Ist die Enthalpie $H_{2}$ unbekannt und soll sie messtechnisch bestimmt werden, können die Größen $\mathrm {d} Q$ , $V$ und $\mathrm {d} p$ während des Prozesses gemessen und von $H_{1}$ ausgehend aufsummiert werden.[7] Im isobaren Fall ist $\mathrm {d} p=0$ und es genügt, die Wärmezufuhr $\mathrm {d} Q$ zu messen und aufzusummieren, beispielsweise in einem geeigneten Kalorimeter. Der Zusammenhang zwischen der isobaren Enthalpiezufuhr und der damit einhergehenden Temperaturänderung wird durch die Wärmekapazität bei konstantem Druck $c_{p}$ beschrieben (siehe Abschnitt Enthalpie und Wärmekapazität). Ist $c_{p}$ für ein isobares System bekannt, ist damit auch die einer gegebenen Temperaturdifferenz entsprechende Enthalpiedifferenz bekannt (siehe Beispiel 2).

Sind umgekehrt $H_{1}$ und $H_{2}$ bekannt, gibt die Enthalpiedifferenz Hinweise auf mögliche Prozessführungen und beschreibt im isobaren Fall, welcher Wärmeumsatz zu erwarten ist. Für zahlreiche Systeme können die zu den verschiedenen Zuständen gehörigen Enthalpien einschlägigen Tabellenwerken entnommen werden.

Ist die Enthalpie des Endzustands kleiner als die des Anfangszustands, muss während des Prozesses die der Differenz entsprechende Enthalpie $\Delta H$ abgeführt werden – der Prozess ist exotherm.[8] Im Falle eines isobaren Prozesses ist die abzuführende Wärmemenge $\Delta Q$ zahlenmäßig gleich der ermittelten Enthalpiedifferenz.

Ist die Enthalpie des Endzustands größer als die des Anfangszustands, muss die der Differenz entsprechende Enthalpie zugeführt werden – der Prozess ist endotherm.[8] Im Falle eines isobaren Prozesses ist die zuzuführende Wärmemenge zahlenmäßig gleich der ermittelten Enthalpiedifferenz.

Da Anfangs- und Endenthalpie nur vom Anfangs- und Endzustand abhängen, nicht aber vom dazwischenliegenden Prozess, kann bei der rechnerischen Ermittlung einer unbekannten Enthalpiedifferenz der reale Prozess durch einen leichter behandelbaren Prozess oder sogar durch eine über Hilfszustände mit bekannten Enthalpien führende Prozesskette ersetzt werden, solange diese dieselben beiden Zustände miteinander verbindet. Praktische Beispiele folgen weiter unten.

In den meisten Fällen ist der absolute Enthalpieinhalt eines Systems nicht von Belang und nur der vom Prozess bewirkte Enthalpieunterschied von Interesse. In diesem Fall hat man die Freiheit, den Nullpunkt für die Messung der Enthalpie beliebig zu wählen.

Man beachte, dass von der zugeführten Energie ein Teil als Verschiebungsarbeit in die Umgebung abgeführt wird und nur der Rest im System selbst verbleibt und dessen Energieinhalt vermehrt. Die zugeführte Enthalpie hingegen denkt man sich in vollem Umfang im System gespeichert. Diese Sprechweise ist zulässig, weil die Enthalpie eine Zustandsgröße des Systems ist. Lässt man den Prozess umgekehrt ablaufen, erhält man sowohl die gesamte dem System zugeführte Energie als auch die gesamte dem System zugeführte Enthalpie wieder zurück. Das System gewinnt dabei die in die Umgebung abgegebene Energie als negative Verschiebungsarbeit wieder zurück, die Enthalpie denkt man sich aus dem Enthalpieinhalt des Systems stammend. Es zeigt sich erneut, dass die Enthalpie nicht eine bestimmte konkrete „Art von Energie“ ist, sondern eine abstrakte Größe, die jedoch eine sehr nützliche Sprechweise erlaubt.

Für die Enthalpie gilt im Allgemeinen kein Erhaltungssatz.[4] Man betrachte als Beispiel einen thermisch isolierten Behälter konstanten Volumens, in dem eine chemische Reaktion abläuft. Die Änderung der Enthalpie

H_{2}-H_{1}=U_{2}-U_{1}+p_{2}\ V_{2}-p_{1}\ V_{1}

reduziert sich wegen $U_{2}=U_{1}$ (kein Energieaustausch mit der Umgebung; innere Energie unterliegt der Energieerhaltung) und $V_{2}=V_{1}$ (Volumenkonstanz des Behälters) auf

H_{2}-H_{1}=V\ (p_{2}-p_{1})

.

Obwohl das System innerhalb des Behälters weder Energie noch Materie mit der Umgebung austauscht, ändert sich seine Enthalpie, wenn sich der Druck im Behälter im Zuge der chemischen Reaktion ändert.[4] Der Begriff „Enthalpiezufuhr“ wäre in diesem Fall, wenn man ihn überhaupt verwenden wollte, nur als eine Sprechweise für „Enthalpieerhöhung“ zu verstehen. Es wird jedoch keine Enthalpie aus der Umgebung abgezogen und in den Behälter transportiert.

Im isobaren Fall, in dem die Enthalpieänderung zahlenmäßig identisch mit der umgesetzten Wärmemenge ist, gilt für die Enthalpie der Energieerhaltungssatz, dem die Wärmeenergie unterliegt.

Beispiel 1: Enthalpieänderung bei einem Phasenübergang

Gegeben sei flüssiges Wasser im Gleichgewicht mit seinem Dampf. Die Temperatur beider Phasen betrage 10 °C, der Druck in beiden Phasen sei der Sättigungsdampfdruck bei der gegebenen Temperatur (ca. 1228 Pa). Einer Wasserdampftafel lässt sich entnehmen, dass bei dieser Temperatur und diesem Druck

die spezifische Enthalpie des flüssigen Wassers $h_{1}=42\ \mathrm {\tfrac {kJ}{kg}}$ [9] und
die spezifische Enthalpie des Wasserdampfes $h_{2}=2519\ \mathrm {\tfrac {kJ}{kg}}$ [10] beträgt.

Um Wasser bei der gegebenen Temperatur und konstantem Druck zu verdampfen, muss die spezifische Enthalpie von $h_{1}$ auf $h_{2}$ erhöht werden, es müssen also

\Delta h=2519\ \mathrm {\frac {kJ}{kg}} -42\ \mathrm {\frac {kJ}{kg}} =2477\ \mathrm {\frac {kJ}{kg}}

an spezifischer Enthalpie zugeführt werden. Da es sich um einen isobaren Vorgang handelt, kann die Enthalpieerhöhung durch Zuführung der spezifischen Wärmemenge $2477\ \mathrm {\tfrac {kJ}{kg}}$ erzielt werden. Dieser Energiebetrag ist die so genannte spezifische Verdampfungsenthalpie des Wassers bei 10 °C.

Man beachte auch die hierbei verwendete Sprechweise: Die Enthalpie ist eigentlich als Zustandsgröße definiert und stellt damit eine Eigenschaft des Systems dar. Die im Beispiel ermittelten $2477\ \mathrm {\tfrac {kJ}{kg}}$ sind eine Enthalpiedifferenz zwischen zwei Systemzuständen. Man nennt sie aber ebenfalls eine Enthalpie, worin sich wieder die Vorstellung spiegelt, man habe es mit einer mengenartigen Größe zu tun und müsse eine gewisse „Menge an Enthalpie“ zuführen, um den „Enthalpieinhalt“ des Systems um die betreffende Menge zu erhöhen.

Der Wasserdampftafel lässt sich außerdem entnehmen, dass bei dieser Temperatur und diesem Druck

das spezifische Volumen des flüssigen Wassers $v_{1}=1{,}0003\cdot 10^{-3}\ \mathrm {\tfrac {m^{3}}{kg}}$ [11] und
das spezifische Volumen des Wasserdampfs $v_{2}=106{,}42\ \mathrm {\tfrac {m^{3}}{kg}}$ [12] beträgt.

Die Zunahme des spezifischen Volumens ist also

\Delta v\approx 106{,}42\ \mathrm {\frac {m^{3}}{kg}}

und die durch diese Volumenzunahme geleistete spezifische Volumenänderungsarbeit beträgt

p\ \Delta v=1228\,\mathrm {Pa} \cdot 106{,}42\ \mathrm {\frac {m^{3}}{kg}} \approx 131\,\mathrm {\frac {kJ}{kg}}

.

Von den als Wärme zugeführten $2477\ \mathrm {\tfrac {kJ}{kg}}$ werden also $131\ \mathrm {\tfrac {kJ}{kg}}$ wieder an die Umgebung abgegeben und die restlichen $2346\ \mathrm {\tfrac {kJ}{kg}}$ erhöhen die innere Energie des Systems.

Beispiel 2: Vorteil der Enthalpie als Zustandsfunktion

Dieses Beispiel[13] zeigt den Vorteil, der sich aus dem Umstand ziehen lässt, dass die Enthalpie eine Zustandsfunktion ist (im Gegensatz zum „Wärmeinhalt“). Gegeben sei eine Knallgasreaktion, bei der aus je zwei Atomen Wasserstoff und einem Atom Sauerstoff ein Wassermolekül gebildet wird:

\mathrm {H_{2}+{\tfrac {1}{2}}O_{2}\longrightarrow \ H_{2}O}

Einem einschlägigen Tabellenwerk sei die Angabe entnommen, dass bei einer Temperatur von 25 °C und einem Druck von einer Atmosphäre die Enthalpie von einem Mol des entstandenen Wassers um 285,84 kJ geringer ist als die Enthalpie der Ausgangsstoffe auf der linken Seite:

\Delta H_{\mathrm {m} }(\mathrm {25^{\circ }C} )=-285{,}84\ \mathrm {\tfrac {kJ}{mol}}

Wie groß ist der molare Enthalpieunterschied beider Seiten, wenn der Druck bei einer Atmosphäre bleibt, aber die Temperatur auf 100 °C erhöht wurde? Als Zusatzinformation seien aus Experimenten die folgenden molaren Wärmekapazitäten bei konstantem Druck $c_{p}$ bekannt (siehe Abschnitt Enthalpie und Wärmekapazität), jeweils als Mittelwert über den Temperaturbereich von 25 °C bis 100 °C:

$\mathrm {H_{2}$	$c_{p}=28{,}9\ \mathrm {\tfrac {J}{mol\ K}}$
$\mathrm {O_{2}$	$c_{p}=29{,}4\ \mathrm {\tfrac {J}{mol\ K}}$
$\mathrm {H_{2}O$	$c_{p}=75{,}5\ \mathrm {\tfrac {J}{mol\ K}}$

Anstelle des zu untersuchenden Originalprozesses, der vom Ausgangszustand $\mathrm {H_{2}(100^{\circ }C)+{\tfrac {1}{2}}O_{2}(100^{\circ }C)}$ direkt in den Endzustand $\mathrm {H_{2}O(100^{\circ }C)}$ führt, wird rechnerisch eine Kette von Ersatzprozessen mit bekannten Eigenschaften betrachtet, welche dieselben beiden Zustände miteinander verbindet. Dies ist erlaubt, weil der Enthalpieunterschied zwischen Anfangs- und Endzustand nur von diesen Zuständen selbst bestimmt wird und nicht von den speziellen Prozessen, die beide ineinander überführen.

$\mathrm {H_{2}(100^{\circ }C)+{\tfrac {1}{2}}O_{2}(100^{\circ }C)}$	${\color {Orange}\longrightarrow \Delta H_{\mathrm {m} }(\mathrm {100^{\circ }C} )=?\longrightarrow }$	$\mathrm {H_{2}O(100^{\circ }C)}$
${\color {RoyalBlue}\downarrow }$		${\color {RoyalBlue}\uparrow }$
${\color {RoyalBlue}\Delta H_{\mathrm {m} ,1}}$		${\color {RoyalBlue}\uparrow }$
${\color {RoyalBlue}\downarrow }$		${\color {RoyalBlue}\uparrow }$
$\mathrm {H_{2}(25^{\circ }C)+{\tfrac {1}{2}}O_{2}(100^{\circ }C)}$		${\color {RoyalBlue}\Delta H_{\mathrm {m} ,4}}$
${\color {RoyalBlue}\downarrow }$		${\color {RoyalBlue}\uparrow }$
${\color {RoyalBlue}\Delta H_{\mathrm {m} ,2}}$		${\color {RoyalBlue}\uparrow }$
${\color {RoyalBlue}\downarrow }$		${\color {RoyalBlue}\uparrow }$
$\mathrm {H_{2}(25^{\circ }C)+{\tfrac {1}{2}}O_{2}(25^{\circ }C)}$	${\color {RoyalBlue}\longrightarrow \Delta H_{\mathrm {m} ,3}=\Delta H_{\mathrm {m} }(\mathrm {25^{\circ }C} )\longrightarrow }$	$\mathrm {H_{2}O(25^{\circ }C)}$

In einem ersten rechnerischen Schritt wird der Wasserstoff von 100 °C auf 25 °C abgekühlt. Dabei ändert sich seine molare Enthalpie um

\Delta H_{\mathrm {m} ,1}=28{,}9\ \mathrm {\tfrac {J}{mol\ K}} \cdot -75\ \mathrm {K} =-2{,}17\ \mathrm {\tfrac {kJ}{mol}}

.

Dann wird das halbe Mol Sauerstoff auf dieselbe Temperatur abgekühlt, seine Enthalpie ändert sich um

\Delta H_{\mathrm {m} ,2}={\tfrac {1}{2}}\ 29{,}4\ \mathrm {\tfrac {J}{mol\ K}} \cdot -75\ \mathrm {K} =-1{,}10\mathrm {\tfrac {kJ}{mol\ H_{2}O}}

.

Die molare Reaktionsenthalpie bei 25 °C ist bekannt:

\Delta H_{\mathrm {m} ,3}=-285{,}84\ \mathrm {\tfrac {kJ}{mol}}

.

Das Erwärmen des entstandenen Wassers auf 100 °C erfordert die Zufuhr von

\Delta H_{\mathrm {m} ,4}=75{,}5\ \mathrm {\tfrac {J}{mol\ K}} \cdot 75\ \mathrm {K} =5{,}66\ \mathrm {\tfrac {kJ}{mol}}

.

Die Summe der molaren Enthalpieänderungen während des Ersatzprozesses

\color {RoyalBlue}\Delta H_{\mathrm {m} ,1}+\Delta H_{\mathrm {m} ,2}+\Delta H_{\mathrm {m} ,3}+\Delta H_{\mathrm {m} ,4}=-283{,}45\ \mathrm {\tfrac {kJ}{mol}}

ist identisch mit der molaren Enthalpieänderung auf dem direkten Prozesspfad, also ist

\color {Orange}\Delta H_{\mathrm {m} }(\mathrm {100^{\circ }C} )=-283{,}45\ \mathrm {\tfrac {kJ}{mol}}

.

Stationär strömende Fluide

Über isobare Prozesse hinaus ist die Enthalpie auch eine nützliche Größe bei der Beschreibung von Systemen im Fließgleichgewicht wie zum Beispiel Wärmekraftmaschinen oder Drosseln, wo sie zur anschaulichen Beschreibung des Energieflusses dienen kann.

Man betrachte eine Wärmekraftmaschine, die von einer stationären Strömung eines Arbeitsfluids durchflossen wird. Im Zuleitungsrohr mit der Querschnittsfläche $A_{1}$ habe der im zufließenden Fluid herrschende Druck $p_{1}$ im betrachteten Zeitraum das Volumen $V_{1}$ in die Maschine gedrückt. Das nachfließende Fluid hat dabei die Kraft $F=p_{1}\ A_{1}$ auf das Volumen ausgeübt und es um die Strecke $\Delta x=V_{1}/A_{1}$ verschoben. Die am Volumen geleistete mechanische Arbeit ist daher $F\cdot \Delta x=p_{1}\ A_{1}\cdot V_{1}/A_{1}=p_{1}\cdot V_{1}$ . Stellt man noch die innere Energie $U_{1}$ des Testvolumens in Rechnung und vernachlässigt dessen kinetische Energie, dann wurde der Maschine die Energie

U_{1}+p_{1}\cdot V_{1}=H_{1}

zugeführt. Entsprechende Überlegungen gelten für ein im gleichen Zeitraum unter dem Druck $p_{2}$ durch den Querschnitt $A_{2}$ des Abflussrohres fließendes Volumen $V_{2}$ . Setzt man der Allgemeinheit halber noch eine der Maschine im betrachteten Zeitraum zugeführte Wärmemenge $Q_{1}$ und eine von der Maschine geleistete Nutzarbeit $W_{2}$ an, so lautet die Energiebilanz einfach[14]

H_{1}+Q_{1}=H_{2}+W_{2}

.

In einem solchen stationär strömenden Arbeitsfluid lässt sich der Term $pV$ anschaulich interpretieren als die vom Fluid kontinuierlich geleistete (und damit sozusagen „transportierte“) Verschiebearbeit.

Ein wichtiger Sonderfall ist eine Drossel, also ein Rohr, in dem eine Engstelle oder ein poröser Pfropfen den Druck des strömenden Fluids von $p_{1}$ auf $p_{2}$ vermindert. Ist die Rohrwand adiabatisch ausgeführt ( $Q_{1}=0$ ) und wird dem System keine mechanische Arbeit entzogen ( $W_{2}=0$ ), dann lautet die Energiebilanz der Drossel

H_{1}=H_{2}

,

die Drosselung ist also ein isenthalper Vorgang. Die Größen $U$ , $p$ und $V$ des Testvolumens haben in der Regel nach der Drosselung andere Werte als vor der Drosselung, die Änderungen hängen aber in solcher Weise zusammen, dass die Größenkombination $U+p\ V$ unverändert bleibt.

Gleichheit der Enthalpien der Testvolumina kann dabei nur für einen Fluidzustand vor der Drosselung und einen nach der Drosselung festgestellt werden. Es kann nicht davon gesprochen werden, dass die Enthalpie der Fluidvolumina entlang der gesamten Drosselstrecke konstant sei, da an der Drosselstelle in der Regel Nichtgleichgewichtszustände vorliegen, für die keine Enthalpie definiert ist.[15][16] Falls die kinetischen Energien beiderseits der Drosselstelle nicht vernachlässigbar klein sind, genügt es auch, wenn ihr Unterschied vernachlässigbar klein ist,[17] weil sie sich dann auf beiden Seiten der Energiebilanz fortkürzen.

Ist das Arbeitsfluid insbesondere ein ideales Gas, sind $U$ , $p$ , $V$ und damit auch $H$ nur von der Temperatur abhängig. Gleichheit der Enthalpien bedeutet daher in diesem Fall auch Gleichheit der Temperaturen vor und nach der Drosselung: Ein ideales Gas erfährt durch die Drosselung keine Temperaturveränderung.[18] Bei nicht-idealen Fluiden kann sich je nach Art des Fluids und den Prozessbedingungen eine Temperaturzunahme oder -abnahme ergeben (siehe → Joule-Thomson-Effekt).

Enthalpie in isobaren physikalischen und chemischen Prozessen

Zahlreiche Prozesse aus der Physik (z. B. Phasenübergänge) oder aus der Chemie (z. B. chemische Reaktionen) laufen unter konstantem Druck ab. Die Enthalpie erlaubt in diesen Fällen eine einfache Beschreibung und Berechnung des Wärmeumsatzes.

Standardbildungsenthalpie

Wie bereits erwähnt, kann zur Berechnung des Enthalpieunterschieds zwischen zwei Zuständen ein beliebiger Prozess verwendet werden, der die beiden Zustände miteinander verbindet. Man kann beispielsweise bei einer chemischen Reaktion die Ausgangsstoffe gedanklich in ihre Elemente zerlegen und diese wieder zu den Produktstoffen zusammensetzen.[19] Die dabei jeweils aufzuwendende oder abzuführende Enthalpie ist die so genannte Bildungsenthalpie des betreffenden Stoffes. Die Bildungsenthalpien sind temperatur- und druckabhängig. Die Bildungsenthalpien, die unter Standardbedingungen umgesetzt werden, sind die Standardbildungsenthalpien.

Die molare Standardbildungsenthalpie (meist kurz Standardbildungsenthalpie) ist die Enthalpie, die bei der Bildung von einem Mol einer Substanz aus der allotropisch stabilsten Form der reinen Elemente unter Standardbedingungen (100 kPa und 25 °C) frei wird (negatives Vorzeichen) oder zur Bildung erforderlich ist (positives Vorzeichen). Sie wird üblicherweise in Kilojoule pro Mol angegeben. Die Größe wird $\Delta H_{f}^{0}$ formuliert ( $f$ von engl. formation steht darin für Bildung; die hochgestellte Null für Standardbedingungen; das Delta für die Differenz). Eine alternative Schreibweise ist $\Delta H_{B}^{0}$ ( $B$ von deutsch Bildung), die eingedeutschte Schreibweise.

Ist sie negativ, handelt es sich um eine exotherme Reaktion und bei der Bildung der Substanz aus den Elementen wird Energie frei (Bildungswärme). Ist sie dagegen positiv, handelt es sich um eine endotherme Reaktion und es muss Energie zur Bildung der Substanz aus ihren Ausgangselementen aufgewendet werden. Stark negative Werte der Standardbildungsenthalpie sind ein Kennzeichen chemisch besonders stabiler Verbindungen (d. h. bei ihrer Bildung wird viel Energie frei und zur Zerstörung der Bindungen muss auch wieder viel Energie aufgewendet werden). Die Standardbildungsenthalpie der chemischen Elemente in ihrem stabilsten Zustand (H₂, He, Li, …) ist per Definition auf 0 kJ/mol festgesetzt.

Sind die Standardbildungsenthalpien der an einer chemischen Reaktion beteiligten Stoffe bekannt, so lässt sich die Reaktionsenthalpie dieser Reaktion unter Standardbedingungen leicht berechnen. Sie ist die Differenz zwischen den Standardbildungsenthalpien der Reaktionsprodukte („Produkte“) einerseits und der Ausgangsstoffe (Reaktanten; „Edukte“) andererseits (Satz von Hess):

\Delta H_{\mathrm {Reaktion} }^{0}=\sum \Delta H_{f,\mathrm {Produkte} }^{0}-\sum \Delta H_{f,\mathrm {Edukte} }^{0}

Alle Werte beziehen sich auf das thermodynamische Gleichgewicht, da sonst die Temperatur nicht definiert wäre.

Umgekehrt kann die Standardbildungsenthalpie unter Zuhilfenahme des Satzes von Hess aus Enthalpien von Reaktionen bestimmt werden, bei denen der jeweilige Stoff als Edukt oder Produkt teilnimmt. Wenn keine experimentellen Daten vorliegen, kann eine Abschätzung der Standardbildungsenthalpien auch mit Gruppenbeitragsmethoden abgeschätzt werden. Hierfür eignet sich besonders die Inkrement-Methode nach Benson.

Anorganische Stoffe

Chemische Formel	Stoff	$\Delta H_{f}^{0}$ (kJ/mol)	Quelle
H₂O (g)	Wasser (gasförmig)	−241,83	[20]
H₂O (l)	Wasser (flüssig)	−285,83	[20]
CO₂ (g)	Kohlendioxid	−393,50	[21]
NH₃ (g)	Ammoniak	−45,94	[22]

Organische Stoffe

Summenformel	Stoff	$\Delta H_{f}^{0}$ (kJ/mol)	Quelle
CH₄ (g)	Methan	−74,87	[23]
C₂H₄ (g)	Ethylen	+52,47	[24]
C₂H₆ (g)	Ethan	−83,8	[25]

Enthalpie in der Physik (Thermodynamik)

Die Thermodynamik beschreibt im engeren Sinne nur die intermolekularen Kräfte, also die energetischen Beziehungen (Phasenzustände bzw. deren Änderungen) zwischen den einzelnen Molekülen eines Stoffs.

Verdampfungsenthalpie / Kondensationsenthalpie

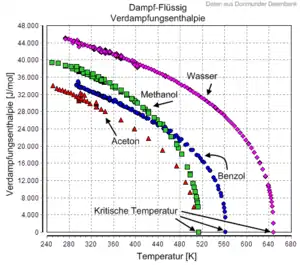
Temperaturabhängigkeit der Verdampfungsenthalpie von Wasser, Methanol, Benzol und Aceton.

Die molare Verdampfungsenthalpie $\Delta H_{V}$ ist die Enthalpie, die erforderlich ist, um ein Mol einer Substanz isotherm und isobar vom flüssigen in den gasförmigen Zustand zu bringen. Die Verdampfungsenthalpie ist vom Stoff sowie von Temperatur und Druck abhängig, wobei sie immer positiv ist und ihr Vorzeichen daher in der Regel nicht angegeben wird.

Die molare Kondensationsenthalpie $\Delta H_{K}$ ist die Enthalpie, die frei wird, wenn ein Mol einer Substanz kondensiert, wobei diese wieder isotherm und isobar vom gasförmigen in den flüssigen Aggregatzustand übergeht. Sie trägt immer ein negatives Vorzeichen.

Die Verdampfungsenthalpie nimmt mit steigender Temperatur ab und wird bei Erreichen des kritischen Punkts Null, da dort keine Unterscheidung von Flüssigkeit und Gas mehr möglich ist. In der Regel werden in Tabellenwerken Verdampfungsenthalpie-Daten entweder auf 25 °C bezogen oder für die verschiedenen Temperatur-Druck-Kombinationen entlang der Siedepunktskurve tabelliert, es gilt dabei immer $\Delta H_{V}=-\Delta H_{K}$ .

Bei Gemischen oder Lösungen von Stoffen addieren sich die Enthalpien im Verhältnis ihrer Mischungsanteile.

Sofern für eine Substanz keine Verdampfungsenthalpiewerte verfügbar sind, kann man diese für beliebige Temperaturen mit Hilfe der Clausius-Clapeyron-Gleichung berechnen, wenn die Temperaturabhängigkeit der Dampfdruckkurve bei der betrachteten Temperatur bekannt ist.

In seltenen Fällen wurden Werte für Verdampfungsenthalpien tabelliert. Die Verdampfungsenthalpie kann immer dann durch Differenzbildung aus den thermodynamischen Daten abgeleitet werden, wenn Standardbildungsenthalpie-Werte für den flüssigen und gasförmigen Aggregatzustand bekannt sind, z. B. für Wasser, Schwefelkohlenstoff, Methanol, Ethanol, Ameisensäure, Essigsäure, Brom in obenstehender Tabelle.

Beispiel Kochsalz:

Verdampfungsenthalpie ∆_VH = +170 kJ/mol (bei 1465 °C, Tabellenwert)
Zur praktischen Berechnung der Verdampfungsenthalpie werden folgende Tabellenwerte für die Bildungsenthalpie verwendet:

NaCl (schmelze)	$\longrightarrow$	NaCl (g)
−386 kJ/mol		−182 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Verdampfungsenthalpie ∆_VH = +204 kJ/mol

Der Unterschied der zwei Werte 170 und 204 liegt im üblichen Rahmen.

Sublimationsenthalpie

Die Sublimation beschreibt den Übergang eines Feststoffs in die Gasphase unter Umgehung der flüssigen Schmelzphase (technische Anwendung bei der Gefriertrocknung). Die Sublimationsenthalpie wird teilweise in Tabellenwerken aufgeführt. Prinzipiell dürfen hierzu bei gleicher Bezugstemperatur auch Schmelz- und Verdampfungsenthalpie zusammengefasst werden:

Sublimationsenthalpie = Schmelzenthalpie + Verdampfungsenthalpie.

Die Sublimationsenthalpie kann immer dann aus den thermodynamischen Daten abgeleitet werden, wenn Standardbildungsenthalpie-Werte für den festen und gasförmigen Aggregatzustand bekannt sind.

Sublimationsenthalpie Kochsalz: 211 kJ/mol (25 °C, Tabellenwert)
Berechnung:

NaCl (s)	$\longrightarrow$	NaCl (g)
−411 kJ/mol		−182 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Sublimationsenthalpie +229 kJ/mol

Anm.: Das Beispiel zeigt, dass man prinzipiell auch Vorgänge berechnen kann, die praktisch kaum durchführbar sind. Die „Sublimationsenthalpie von elementarem Kohlenstoff“ wurde so „ermittelt“.

Sublimationenthalpien einiger Stoffe
Stoffzeichen	Stoffe	Sublimationsenthalpie (kJ/mol)	Standardbildungsenthalpie (fest) (kJ/mol)	Standardbildungsenthalpie (gas) (kJ/mol)
Na	Natrium	108,7[26]	0,0[27]	108,7[27]
K	Kalium	90,0[26]	0,0[27]	90,0[27]
Br₂	Brom	30,71[26]	0,0[27]	30,71[27]
Li	Lithium	155,10[26]	0,0[27]	155,10[27]
I₂	Iod	62,4[28]
C₁₀H₈	Naphthalin	72,6[28]
CO₂	Kohlenstoffdioxid	26,1[28]

Schmelzenthalpie / Kristallisationsenthalpie

Nach dem Erwärmen einer festen Substanz bis zu ihrer Schmelzpunkttemperatur wird bei dieser Temperatur Schmelzwärme aufgenommen, ohne dass die Temperatur weiter ansteigt. Diese Form von Wärme wird latente Wärme genannt, weil diese keine Temperaturänderung bewirkt. Bei ionischen Feststoffen entstehen bei der Phasenumwandlung fest/flüssig Salzschmelzen mit leicht beweglichen Ionen (techn. Anwendung bei der Schmelzflusselektrolyse). Kochsalz schmilzt bei 800 °C.

Schmelzenthalpien sind nur selten in Tabellenwerken erfasst.

Die Schmelzenthalpie kann immer dann aus den thermodynamischen Daten abgeleitet werden, wenn Standardbildungsenthalpie-Werte für den festen und flüssigen Aggregatzustand bekannt sind.

Schmelzenthalpie Kochsalz: 28; 30,2 kJ/mol (800 °C, Tabellenwerte)
Zur praktischen Berechnung der Schmelzwärme werden folgende Tabellenwerte verwendet:

NaCl (s)	$\longrightarrow$	NaCl (Schmelze)
−411 kJ/mol		−386 kJ/mol			Bildungsenthalpien (25 °C)
NaCl (s)	$\longrightarrow$	Na⁺ (Schmelze)	+	Cl⁻ (Schmelze)
−411 kJ/mol		ca. −215 kJ/mol		ca. −170 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Schmelzenthalpie +25 kJ/mol (NaCl, 25 °C)

Bei der Umkehrung dieses Prozesses, der Kristallisation aus der Schmelze, können die Ionen eines Salzes sich direkt zu ihrem festen Kristallgitter zusammenschließen. Während des Ausscheidens von Kochsalzkristallen aus der Schmelze werden −25,2 kJ/mol Kristallisationsenthalpie (bzw. 29±1 kJ/mol bei 800 °C) freigesetzt.

Erfahrungsgemäß können „unterkühlte Salzschmelzen“ durch eine spontan einsetzende Kristallisation erhebliche Wärmemengen freisetzen. (Anwendung: Heizkissen).

Gitterenthalpie

Nach einer gängigen Definition ist die Gitterenergie diejenige Energie, die im Vakuum (d. h. bei äußerem Druck $p=0$ ) aufgewendet werden muss, um einen kristallinen ionischen Feststoff in die Gasphase zu überführen (d. i. Sublimationsenergie), ihn also in die gasförmigen Ionen zu separieren. Die Gitterenergie und die Gitterenthalpie unterscheiden sich qualitativ. Die Gitterenergie ist eine innere Energie, während die Gitterenthalpie eine Enthalpie ist. Die Gitterenthalpie berücksichtigt also zusätzlich die zu leistende Volumenarbeit $p\Delta V$ gegen einen konstanten äußeren Druck. Hat man für das Auseinanderbringen der Bestandteile des Festkörpers eine molare Gitterenthalpie $\Delta _{G}H$ bestimmt, so ist die molare Gitterenergie $\Delta _{G}U=\Delta _{G}H-p\Delta V_{\mathrm {m} }$ .[29] Hierbei ist $\Delta V_{\mathrm {m} }$ die auf die Stoffmenge bezogene Volumenänderung.

Die Gitterenthalpie von NaCl setzt sich wie folgt zusammen:

NaCl (fest)	$\longrightarrow$	Na⁺ (g)	+	Cl⁻ (g)
−411 kJ/mol		611 kJ/mol		−244 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Gitterenthalpie +778 kJ/mol

Vergleich: Dies ist ungefähr die doppelte notwendige Energie, die bei der stark exothermen Reaktion von Natriummetall und Chlorgas freiwerden würde. Die Bildung gasförmiger Ionen ist also extrem endotherm.

Die Gitterenthalpie ΔH⁰L hängt von Größe und Ladung der beteiligten Ionen ab und ist bei dieser Art der Definition immer positiv, da das Gitter sonst nicht stabil wäre. Eine sehr hohe Gitterenthalpie weist Aluminiumoxid Al₂O₃ (Al³⁺ und O²⁻) mit 15157 kJ/mol auf. Die hohe Gitterenthalpie wird in aluminothermischen Verfahren ausgenutzt; dazu zählen etwa das aluminothermische Schweißen und die Darstellung von Elementen aus ihren Oxiden und Aluminium mittels Aluminothermie. In letzterem Fall ist die hohe Gitterenthalpie des Aluminiumoxids eine Haupttriebkraft für die Reaktion, da sie sich direkt in der Gibbs-Energie niederschlägt.

Häufig wird die Gitterenergie auch als Reaktionsenthalpie bei der Bildung des festen Salzgitters ausgehend von Ionen in der Gasphase definiert.[30] Wird die Gitterenergie so definiert, so ist der Prozess exotherm und die dazugehörige Enthalpieänderung ist negativ anzugeben. Die Gitterenthalpie von Aluminiumoxid wäre dann beispielsweise −15157 kJ/mol.

Die Gitterenthalpie hängt einerseits von der Größe der beteiligten Ionen ab: Je größer die Ionen, desto kleiner ist die frei werdende Gitterenergie, da die Anziehungskräfte mit zunehmender Entfernung der positiven Kerne von der negativen Elektronenhülle des Bindungspartners abnehmen.

Beispiele: molare Gitterenthalpie der Alkalifluoride bei 25 °C in kJ/mol:

Name	Formel	Ionenradius der einwertigen Alkalimetall-Kationen X⁺ in pm	Gitterenthalpie in kJ pro mol
Lithiumfluorid	LiF	74	1039
Natriumfluorid	NaF	102	920
Kaliumfluorid	KF	138	816
Rubidiumfluorid	RbF	149	780
Caesiumfluorid	CsF	170	749

Andererseits hängt die Gitterenergie von der elektrischen Ladung der beteiligten Ionen ab: Je größer die Ladungen, desto größer sind die Anziehungskräfte und umso größer ist die Gitterenergie.

Beispiele: molare Gitterenthalpie bei 25 °C in kJ pro mol (in den Beispielen ändert sich der Ionenradius nur wenig):

Name	Formel	Kationen	Anionen	Gitterenthalpie in kJ pro mol
Natriumchlorid	NaCl	Na⁺	Cl⁻	780
Natriumsulfid	Na₂S	Na⁺	S²⁻	2207
Magnesiumchlorid	MgCl₂	Mg²⁺	Cl⁻	2502
Magnesiumsulfid	MgS	Mg²⁺	S²⁻	3360

Zu einem ähnlichen Effekt bei Graphit unter Neutronenbestrahlung siehe Wigner-Energie.

Solvatationsenthalpie, Hydratationsenthalpie

Sie gibt an, welche Energie freigesetzt wird, wenn sich gasförmige Ionen an Lösemittel anlagern, also solvatisierte Ionen bilden. Für den häufigsten Fall Solvens = Wasser spricht man von Hydratationsenthalpie.

Na⁺ (g)	$\longrightarrow$	Na⁺ (hydratisiert)
611 kJ/mol		−240 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Hydratationsenthalpie Na⁺ −851 kJ/mol (d. i. extrem exotherm)

Cl⁻ (g)	$\longrightarrow$	Cl⁻ (hydratisiert)
−244 kJ/mol		−167 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Hydratationsenthalpie Cl⁻ +77 kJ/mol (d. i. schwach endotherm)

Die Hydratationsenthalpie der gasförmigen Ionen von Kochsalz ist mit −774 kJ/mol insgesamt stark exotherm.

Lösungsenthalpie / Kristallisationsenthalpie

Die Lösungsenthalpie von Salzen beinhaltet 1) das Separieren des Ionen-Gitters in Einzel-Ionen und 2) die Solvatisierung der Einzel-Ionen. Teilschritt 1) ist sehr stark endotherm, Teilschritt 2) sehr stark exotherm.

Lösungsenthalpie = Gitterenthalpie + Solvatationsenthalpie.

Lösungsenthalpie NaCl in Wasser = (+778 kJ/mol) + (−851+77 kJ/mol) = +4 kJ/mol (25 °C).

Dieser Wert steht in guter Übereinstimmung mit Tabellenwerken +3,89 kJ/mol für die Kochsalz-Lösungswärme. Beim Lösen tritt also eine ganz geringe Abkühlung der Lösung auf.

Natürlich geht man zur praktischen Berechnungen der Lösungswärme nicht den Umweg über die Gitterenergie, sondern man rechnet direkt und mit nur wenigen Tabellenwerten (gelegentlich findet man den Wert (NaCl)hydrat. = −407 kJ/mol anstelle der Einzel-Ionen):

NaCl (s)	$\longrightarrow$	NaCl (hydratisiert)
−411 kJ/mol		−407 kJ/mol			Bildungsenthalpien (25 °C)
NaCl (s)	$\longrightarrow$	Na⁺ (hydratisiert)	+	Cl⁻ (hydratisiert)
−411 kJ/mol		−240 kJ/mol		−167 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Lösungsenthalpie +4 kJ/mol (Wasser, 25 °C)

Die Solvatationsenthalpie kann immer dann aus den thermodynamischen Daten abgeleitet werden, wenn man Standardbildungsenthalpie-Werte für den festen und gelösten Aggregatzustand findet, z. B. Ameisensäure und Kohlendioxid in obenstehender Tabelle. Sie gilt für „unendliche Verdünnung“.

Bei Umkehrung dieses Prozesses, der Kristallisation aus Lösung, geben die gelösten Ionen eines Salzes 1) ihre Solvathülle ab und 2) schließen sich in einem festen Kristallgitter zusammen. Während des Ausscheidens von Kochsalzkristallen aus Wasser werden −3,89 kJ/mol Kristallisationsenthalpie freigesetzt.

Intermolekulare Enthalpie-Beiträge

Unterschiedlich starke Wechselwirkungen zwischen den Molekülen sind die Ursache dafür, dass Substanzgruppen ähnliche oder stark unterschiedliche Sublimationsenthalpien aufweisen.

Schwache Beiträge liefern London-Kräfte, Dipol-Dipol-Wechselwirkungen und Ion-Dipol-Wechselwirkungen mit 1–15 kJ/mol Bindung. Sie werden als Van-der-Waals-Wechselwirkung zusammengefasst. Siehe hierzu als Beispiele die Schmelz- und Verdampfungsenthalpien von Wasserstoff, Kohlenmonoxid und Methan.
Stärkere Beiträge liefern Wasserstoffbrücken-Bindungen mit 20–40 kJ/mol Bindung (je nach Polarisation). Siehe hierzu als Beispiele die Schmelz- und Verdampfungsenthalpien von Wasser, Methanol und Ameisensäure und auch Hydratationsenthalpien. Wasserstoffbrücken-Bindungen sind auch verantwortlich dafür, dass der Siedepunkt von Wasser bei 100 °C liegt, während der von Schwefelwasserstoff nur −83 °C beträgt (siehe Siedepunktanomalie).
Sehr starke Beiträge liefern Ion-Ion-Wechselwirkungen in Kristallen. Natriumchlorid besteht im Kristall nicht aus diskreten NaCl-Molekülen, sondern aus einer gleichen Anzahl von Natriumkationen und Chloridanionen, die sich im Kristallgitter entsprechend den Coulomb-Kräften exakt angeordnet haben.

Enthalpie in der Chemie (Thermochemie)

Die Thermochemie beschreibt im engeren Sinne nur die intramolekularen Kräfte, also die energetischen Beziehungen zwischen den einzelnen Atomen eines Moleküls. Kovalente Bindungen beinhalten ca. 150–1000 kJ/mol Bindungsenergie, ionische Bindungen ca. fünfmal so große Beträge.

Bei Kenntnis der Standardbildungsenthalpien von Edukten und Produkten lässt sich eine mögliche chemische Reaktion energetisch grob bilanzieren. Die wichtigste Frage ist oft, ob ein Prozess endotherm oder exotherm verläuft und wie stark.

\Delta H_{\mathrm {Reaktion} }^{0}=\sum \Delta H_{f,\mathrm {Produkte} }^{0}-\sum \Delta H_{f,\mathrm {Edukte} }^{0}

Durch Details wie Verdampfungs-, Schmelz-, Solvatations- oder Kristallisationsenthalpien können Teilschritte innerhalb der chem. Reaktion energetisch präzisiert werden.

Reaktionsenthalpie

Die Reaktionsenthalpie ist diejenige Energie, die freigesetzt oder benötigt wird, wenn zwischen den Molekülen zweier Stoffe neue chemische Bindungen gebildet werden. Sie ist abhängig von den Reaktionspartnern (Edukte) und der Art der chemischen Bindung im Produkt. Zur Berechnung vergleicht man die Summe der Bildungsenthalpien der Produkte mit der der Edukte. Die Differenz ist die Reaktionsenthalpie, die anschließend durch Bezug auf die Stoffmenge des jeweils interessierenden Produkts standardisiert werden kann:

2 Na (s)	+	Cl₂ (g)	$\longrightarrow$	2 NaCl (s)
2 × 0 kJ/mol		0 kJ/mol		2 × −411 kJ/mol	Bildungsenthalpien (25 °C)
$\Rightarrow$ Reaktionsenthalpie = 2 mol × (−411) kJ/mol − 2 mol × 0 kJ/mol − 1 mol × 0 kJ/mol = −822 kJ.

Also verläuft die Reaktion exotherm. Division durch die erhaltene Stoffmenge, in diesem Fall 2 Mol Natriumchlorid, liefert dessen (in diesem Beispiel allerdings schon zu Beginn vorausgesetzte) molare Bildungsenthalpie von −411 kJ/mol NaCl (25 °C).

Standardverbrennungsenthalpie

Auch die Verbrennung ist eine chemische Reaktion. Die Reaktionsenthalpie der Verbrennungsreaktion bzw. die Standardverbrennungsenthalpie eines Stoffes ist die Enthalpieänderung, die auftritt, wenn ein Stoff unter O₂-Überschuss (O₂-Überdruck) und Standardbedingungen (101,325 kPa und 25 °C) vollständig verbrennt. Definitionsgemäß bezieht sich diese Verbrennungswärme auf die Bildung von gasförmigem Kohlendioxid und flüssigem Wasser (bzw. N₂) als Endprodukte; unter Sauerstoffüberdruck kann sich kein gasförmiges Wasser bilden. Sie wird mit Δ_VH⁰ oder Δ_cH⁰ (c für Combustion) bezeichnet und ihr absoluter Betrag ist identisch mit dem Brennwert H_s.

In einem Autoklaven-Rohr wird folgende Reaktion mit Sauerstoffüberdruck durchgeführt:

C₃H₈ (g)	+	5 O₂ (g)	$\longrightarrow$	3 CO₂ (g)	+	4 H₂O (l)
−103,2 kJ/mol		5 × 0 kJ/mol		3 × −393,5 kJ/mol		4 × −285,8 kJ/mol

\Rightarrow

Reaktionsenthalpie = 3 mol × (−393,5) kJ/mol + 4 mol × (−285,8) kJ/mol – 1 mol × (−103,2) kJ/mol − 5 mol × (0) kJ/mol = -2,22 MJ.

Division durch die eingesetzte Stoffmenge, in diesem Fall 1 Mol Propan, liefert dessen molare Verbrennungsenthalpie von −2,22 MJ/mol Propan (25 °C)

Die gleiche Reaktion in einer offenen Brennerflamme; es entstehen nur gasförmige Verbrennungsprodukte:

C₃H₈ (g)	+	5 O₂ (g)	$\longrightarrow$	3 CO₂ (g)	+	4 H₂O (g)
−103,2 kJ/mol		5 × 0 kJ/mol		3 × −393,5 kJ/mol		4 × −241,8 kJ/mol

\Rightarrow

Reaktionsenthalpie = 3 mol × (−393,5) kJ/mol + 4 mol × (−241,8) kJ/mol – 1 mol × (−103,2) kJ/mol − 5 mol × (0) kJ/mol = -2,04 MJ.

Division durch die eingesetzte Stoffmenge, in diesem Fall 1 Mol Propan, liefert dessen molare Verbrennungsenthalpie von −2,04 MJ/mol Propan (25 °C)

Fortgeschrittene Anwendung

Es ist müßig, sich für jede Reaktion die Standardbildungsenthalpien der Edukte und Produkte zusammenzusuchen, zudem noch im korrekten Aggregatzustand. Zudem stößt man bei größeren Molekülen schnell in ein „Datenvakuum“. Folgende vereinfachte Betrachtungen haben sich in der Praxis bewährt:

Es ist unerheblich, ob man ein langkettig alkylsubstituiertes Ethylen bromiert oder Ethylen selbst, die Reaktionswärme pro (C=C)-Doppelbindung ist weitgehend gleich.
Es ist unerheblich, ob man eine Reaktion komplett in flüssiger Phase berechnet oder komplett in der Gasphase, die Reaktionswärme beeinflusst dies kaum.
Es ist unerheblich (einige Abweichungen), wenn man bei 150 °C durchgeführte Reaktionen für 25 °C Standardbedingungen berechnet. (Die Reaktionsenthalpie kann für beliebige Temperaturen berechnet werden bei Kenntnis der Temperaturabhängigkeit der Molwärmen aller Reaktionspartner.)

Daher kann man normale organisch-chemische Umsetzungen wie Halogen-Additionen, Cycloadditionen, Veresterungen mit Säuren oder Anhydriden, Hydrolysen etc. mit Hilfe von zahlreich tabellierten Inkrementen für gasförmige Moleküle nach Benson[31] berechnen.

Im nachfolgenden Beispiel wird die Reaktionsenergie der Brom-Addition an Ethylen mit Benson-Inkrementen berechnet und zum Vergleich aus Bindungsenergien involvierter Bindungen abgeschätzt. (Merke: Bindungsenergien sind gemittelte Dissoziationsenergien, keine Standardbildungsenthalpien!)

Bromaddition an ein Alken, Reaktionsenthalpie berechnet mit Standardbildungsenthalpien:

H₂C=CH₂	+	Br₂	$\longrightarrow$	H₂BrC-CBrH₂
52 kJ/mol		0 kJ/mol		−39 kJ/mol

\Rightarrow

Reaktionsenthalpie (25 °C, alle Werte für gasförm. Zustand) = (−39 − 52) kJ/mol = −91 kJ/mol Doppelbindung

Bromaddition an ein Alken, Reaktionsenthalpie berechnet mit Inkrementen nach Benson:

H₂C=CH₂	+	Br₂	$\longrightarrow$	H₂BrC-CBrH₂
2 C_d-(H)₂: 2× +28,1 kJ/mol				2 C-(H)₂(Br)(C): 2× −22,6 kJ/mol

\Rightarrow

Reaktionsenthalpie (berechnet nach Benson) = ( −45,2 − (+56,2)) kJ/mol = −101 kJ/mol Doppelbindung

Bromaddition an ein Alken, Reaktionsenthalpie abgeschätzt mit Bindungsenergien:

H₂C=CH₂	+	Br₂	$\longrightarrow$	H₂BrC-CBrH₂
4 C-H: 4×>455 kJ/mol				4 C-H: 4× 380±50 kJ/mol
1 C=C: 1× 614 kJ/mol				1 C-C: 1× 348 kJ/mol
1 Br-Br: 193 kJ/mol				2 C-Br: 2× 260±30 kJ/mol

\Rightarrow

Reaktionsenthalpie (geschätzt aus Bindungsenergien) = ( 2388±200 - 2627) kJ/mol = -239±200 kJ/mol Doppelbindung

Die beste Abschätzung für Reaktionsenthalpien gelingt mit Standardbildungsenthalpien oder Inkrementen nach Benson, bei Verwendung von „Bindungsenergien“ ist die Unsicherheit mit ±200 kJ/mol viel zu hoch.

Technische Anwendbarkeit

Die Reaktionsenthalpien organischer Reaktionen liegen im Bereich −160 bis +100 kJ pro mol „reaktiver Zentren“. Als sehr stark exotherm erweisen sich alle Additionsreaktionen mit Epoxiden, Anhydriden und Halogenen. Diese thermochemischen Betrachtungen treffen keine Aussage darüber, wie schnell diese Reaktionswärmen freigesetzt werden. Sie machen nur die Aussage, dass bis zum Reaktionsende diese Wärme freigesetzt wird. Jede Reaktion erhöht ihre Geschwindigkeit um das Zwei- bis Dreifache bei Temperaturerhöhung um 10 K. Umgekehrt bedeutet eine zweifache Verdünnung der Reaktionspartner häufig eine Halbierung der Reaktionsgeschwindigkeit bzw. Wärmeleistung der Reaktion. Berechnete Reaktionsenthalpien dienen dazu, in einem System von Reaktanten und Lösemittel über deren Wärmekapazitäten den Temperaturverlauf zu berechnen. Großtechnische Anlagen verfügen nur über begrenzte Kühlkapazitäten (-Wärme/Zeit), dies bleibt im Laborversuch häufig wenig berücksichtigt.

Bindungsenergie / Dissoziationsenergie

Die Bindungsenergie bzw. Bindungsstärke gibt die „Stabilität“ der kovalenten Bindung an. Die Bestimmung ist nur bei zweiatomig symmetrischen Molekülen wie z. B. Wasserstoff oder Halogene direkt möglich. In diesen Fällen kann die Dissoziationsenergie zur Bildung zweier identischer Radikale einfach gemessen/berechnet werden. Bei „Element-Radikalen“ bezeichnet man die Standardbildungsenthalpie von Radikalen auch als Atomisierungsenthalpien.

In allen anderen Fällen sind Werte für die „Bindungsenergie“ nur indirekt möglich durch Vergleich mehrerer Dissoziationsenergie-Messungen an homologen Molekülen. Die Werte schwanken abhängig vom Substitutionsmuster an den Radikal-Zentren.

Die Standardbildungsenthalpie von gasförmigen

Brom-Radikalen beinhaltet die Verdampfungsenthalpie (31 kJ/mol), die notwendig ist, um flüssiges Brom in gasförmiges Brom zu verwandeln.
Iod-Radikalen beinhaltet die Sublimationsenthalpie (62 kJ/mol), die notwendig ist, um kristallines Iod in gasförmiges Iod zu verwandeln.
Kohlenstoff-Radikalen ist identisch mit der Standardbildungsenthalpie von gasförmigem Kohlenstoffdampf.

Thermodynamische Eigenschaften der Enthalpie

Enthalpie als Fundamentalfunktion

Betrachtet man ein System, dessen Eigenschaften durch die Zustandsgrößen Entropie $S$ , Volumen $V$ und Molzahlen $N_{1}...N_{r}$ der $r$ chemischen Komponenten gegeben sind, dann ist die innere Energie $U$ des Systems, ausgedrückt als Funktion der genannten Zustandsgrößen (nämlich aller extensiven Variablen des Systems),

U=U(S,V,N_{1},...,N_{r})

eine Fundamentalfunktion des Systems. Sie beschreibt das System vollständig, es lassen sich alle thermodynamischen Eigenschaften des Systems aus ihr ableiten.[32]

Oft sind diese Variablen jedoch für die praktische Arbeit ungünstig und man würde vorziehen, etwa die Temperatur oder den Druck in der Variablenliste zu haben. Im Gegensatz zur sonst üblichen Vorgehensweise darf ein Variablenwechsel im vorliegenden Fall jedoch nicht durch eine einfache Substitution geschehen, da sonst Information verloren geht. Soll beispielsweise das Volumen durch den Druck $p$ ersetzt werden, könnte $V$ aus den Funktionen $U(S,V,N_{i})$ und $p(S,V,N_{i})$ eliminiert werden, um eine Funktion der Form $U(S,p,N_{i})$ zu erhalten. Da jedoch der Druck thermodynamisch als partielle Ableitung der inneren Energie nach dem Volumen definiert ist

p=-\left({\frac {\partial U}{\partial V}}\right)_{S,N_{1},...,N_{r}}

wäre diese Formulierung gleichbedeutend mit einer partiellen Differentialgleichung für $U$ , welche $U$ nur bis auf unbestimmte Funktionen festlegen würde. Dieses $U$ wäre nach wie vor eine Beschreibung des betrachteten Systems, aber es wäre keine vollständige Beschreibung und damit keine Fundamentalfunktion mehr.[33][34]

Zum Variablenwechsel unter Erhaltung der vollständigen Information muss eine Legendre-Transformation durchgeführt werden. Soll beispielsweise zur Variablenliste $(S,p,N_{1},...,N_{r})$ übergegangen werden, lautet die Transformation:[34]

H(S,p,N_{1},...,N_{r}):=U(S,V,N_{1},...,N_{r})-\left({\frac {\partial U}{\partial V}}\right)_{S,N_{1},...,N_{r}}\cdot V=U+p\ V

.

Die Legendre-Transformierte $H=U+p\ V$ wird Enthalpie genannt. Sie ist wiederum eine Fundamentalfunktion,[35] wenn sie als Funktion der Variablen $(S,p,N_{1},...,N_{r})$ – dies sind die natürlichen Variablen der Enthalpie – gegeben ist. Sie kann auch in Abhängigkeit von anderen Variablen ausgedrückt werden, ist dann aber keine Fundamentalfunktion mehr.

Die Herkunft der Enthalpie aus einer Legendre-Transformation erklärt den additiven Term $p\,V$ : Er kompensiert den Informationsverlust, der sonst mit dem Variablenwechsel verbunden wäre.

Fundamentalfunktionen, welche die Dimension Energie besitzen, heißen auch thermodynamische Potentiale. Die Enthalpie ist also ein thermodynamisches Potential.[35]

Ableitungen der Enthalpie

Geht man von der inneren Energie als Funktion ihrer natürlichen Variablen aus und bildet ihr totales Differential, erhält man:

\mathrm {d} U(S,V,N_{1},...,N_{r})=\left({\frac {\partial U}{\partial S}}\right)_{V,N_{1},...,N_{r}}\mathrm {d} S+\left({\frac {\partial U}{\partial V}}\right)_{S,N_{1},...,N_{r}}\mathrm {d} V\,+\,\sum _{i=1}^{r}\left({\frac {\partial U}{\partial N_{i}}}\right)_{S,V,N_{j\neq i}}\mathrm {d} N_{i}

.

Die hierbei auftretenden partiellen Ableitungen werden in der Thermodynamik als die Definitionen von Temperatur $T$ , Druck $p$ und chemischem Potential der i-ten Substanz $\mu _{i}$ interpretiert:[36]

{\begin{aligned}T&:=\left({\frac {\partial U(S,V,N_{1},...,N_{r})}{\partial S}}\right)_{V,N_{1},...,N_{r}},\\p&:=-\left({\frac {\partial U(S,V,N_{1},...,N_{r})}{\partial V}}\right)_{S,N_{1},...,N_{r}},\\\mu _{i}&:=\left({\frac {\partial U(S,V,N_{1},...,N_{r})}{\partial N_{i}}}\right)_{S,V,N_{j\neq i}},\end{aligned}}

so dass sich das Differential auch schreiben lässt als

\mathrm {d} U(S,V,N_{1},...,N_{r})=T\,\mathrm {d} S-p\,\mathrm {d} V\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} N_{i}

.

Das totale Differential der Enthalpie als Funktion ihrer natürlichen Variablen ist einerseits formal

\mathrm {d} H(S,p,N_{1},...,N_{r})=\left({\frac {\partial H}{\partial S}}\right)_{p,N_{1},...,N_{r}}\mathrm {d} S+\left({\frac {\partial H}{\partial p}}\right)_{S,N_{1},...,N_{r}}\mathrm {d} p\,+\,\sum _{i=1}^{r}\left({\frac {\partial H}{\partial N_{i}}}\right)_{S,p,N_{j\neq i}}\mathrm {d} N_{i}\quad (*)

.

und andererseits, unter Benutzung ihrer Definition

{\begin{aligned}\mathrm {d} H&=\mathrm {d} (U+pV)\\&=\mathrm {d} U+\mathrm {d} (pV)\\&=T\,\mathrm {d} S-p\,\mathrm {d} V+\,\sum \mu _{i}\,\mathrm {d} N_{i}\,+\mathrm {d} (pV)\\&=T\,\mathrm {d} S-p\,\mathrm {d} V+\,\sum \mu _{i}\,\mathrm {d} N_{i}\,+p\,\mathrm {d} V+V\mathrm {d} p\\&=T\,\mathrm {d} S+V\mathrm {d} p\,+\,\sum \mu _{i}\,\mathrm {d} N_{i}\quad (*)\end{aligned}}

so dass aus dem Vergleich der Koeffizienten in den markierten Gleichungen folgt[37]

\left({\frac {\partial H}{\partial S}}\right)_{p,N_{1},...,N_{r}}=T

,

sowie

\left({\frac {\partial H}{\partial p}}\right)_{S,N_{1},...,N_{r}..}=V

und

\left({\frac {\partial H}{\partial N_{i}}}\right)_{S,p,N_{j\neq i}}=\mu _{i}

.

Die Herleitung zeigt gleichzeitig, wie die Addition des Terms $p\,V$ die Liste der unabhängigen Variablen von $(S,V,...)$ in $(S,p,...)$ ändert,[37] indem dadurch im totalen Differential der von $\mathrm {d} V$ abhängige Term entfernt und ein von $\mathrm {d} p$ abhängiger Term hinzugefügt wird.

Die zweite der markierten Gleichungen ist eine „differentielle Fundamentalfunktion“,[38] nämlich die differentielle Enthalpie als Funktion ihrer natürlichen Variablen:

\mathrm {d} H(S,p,N_{1},...,N_{r})=T\,\mathrm {d} S+V\mathrm {d} p\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} N_{i}

.

Minimumsprinzip der Enthalpie

Gemäß dem Zweiten Hauptsatz der Thermodynamik nimmt ein abgeschlossenes System unter den erreichbaren Zuständen denjenigen als Gleichgewichtszustand ein, der bei der gegebenen inneren Energie die höchste Entropie besitzt. Aus diesem Maximumsprinzip der Entropie lässt sich ein Minimumsprinzip der inneren Energie ableiten:[39] Bei konstant gehaltener Entropie nimmt ein System denjenigen Zustand als Gleichgewichtszustand ein, der die geringste innere Energie besitzt.

Ein ähnliches Minimumsprinzip existiert für die Enthalpie: Ein System, das auf konstantem Druck gehalten wird, nimmt von allen erreichbaren Zuständen mit diesem Druck denjenigen als Gleichgewichtszustand ein, in dem die Enthalpie den kleinstmöglichen Wert hat.[40]

Zum Beweis[41] betrachte man ein System, dessen Druck auf einem konstanten Wert gehalten wird. Die Druckregelung kann beispielsweise dadurch geschehen, dass das betrachtete System über eine bewegliche adiabatische Wand in Kontakt mit einem zweiten System steht, das unveränderlich den gewünschten Druck aufweist (in thermodynamischer Ausdrucksweise: ein Druckreservoir). Durch Verschiebung der Kontaktwand kann das betrachtete System bei Bedarf so lange mit dem Druckreservoir „Volumen austauschen“, bis es seinen Druck wieder dem des Reservoirs angeglichen hat. Das aus dem betrachteten System und dem Druckreservoir gebildete Gesamtsystem nimmt bei konstant gehaltener Entropie gemäß dem Energieminimums-Prinzip die geringstmögliche innere Energie $U_{\mathrm {Ges} }$ an, und im Energieminimum gilt:

\mathrm {d} U_{\mathrm {Ges} }=\mathrm {d} U+\mathrm {d} U_{\mathrm {Res} }=0

.

Da mit dem Reservoir gemäß dessen Definition ausschließlich Volumen ausgetauscht wird, kann die innere Energie des Reservoirs nur dadurch geändert werden, dass Volumenänderungsarbeit an ihm geleistet wird: $\mathrm {d} U_{\mathrm {Res} }=-p_{\mathrm {Res} }\,\mathrm {d} V_{\mathrm {Res} }$ , und damit ist

\mathrm {d} U-p_{\mathrm {Res} }\,\mathrm {d} V_{\mathrm {Res} }=0

.

Bei der Verschiebung der Trennwand gilt $\mathrm {d} V_{\mathrm {Res} }=-\mathrm {d} V$ , so dass

\mathrm {d} U+p_{\mathrm {Res} }\,\mathrm {d} V=0

.

Da der Druck des Reservoirs, $p_{\mathrm {Res} }$ , gemäß Voraussetzung konstant ist, lässt sich schreiben

\mathrm {d} (U+p_{\mathrm {Res} }\,V)=0

.

Es wären nun die Extremaleigenschaften der Funktion $U+p_{\mathrm {Res} }\,V$ näher zu untersuchen. Da man jedoch Druckausgleich zwischen dem betrachteten System (Druck $p$ ) und dem Druckreservoir (Druck $p_{\mathrm {Res} }$ ) erwartet, ist es naheliegend, die weitere Untersuchung auf die Zustände mit der Eigenschaft $p=p_{\mathrm {Res} }$ zu beschränken. Auf der Untermenge dieser Zustände ist aber $U+p_{\mathrm {Res} }\,V$ identisch mit $U+p\,V$ . Es gilt also

\mathrm {d} H=\mathrm {d} (U+p\,V)=0

, unter der Voraussetzung

p=p_{\mathrm {Res} }

.

Wie sich zeigen lässt,[42] ist die zweite Ableitung von $H$ in diesem Zustand positiv, so dass das gefundene Extremum der Enthalpie tatsächlich ein Minimum ist.

Das Minimumsprinzip für die innere Energie des Gesamtsystems bei konstanter Entropie führt also dazu, dass die Enthalpie des betrachteten Systems auf der Untermenge der Zustände mit konstantem Druck $p=p_{\mathrm {Res} }$ ein Minimum annimmt. Ist das System noch nicht im Gleichgewicht, bewegt es sich (unter isobaren Bedingungen) freiwillig in Zustände niedrigerer Enthalpie. Das Gleichgewicht ist mit dem Zustand erreicht, in dem die Enthalpie den unter den gegebenen Bedingungen kleinstmöglichen Wert besitzt.

Will man den Gleichgewichtszustand mit Hilfe des (allgemein und stets gültigen) Entropiekriteriums bestimmen, muss das Maximum der Gesamtentropie ermittelt werden, also die Summe der Entropien des untersuchten Systems und seiner Umgebung. Es muss daher nicht nur die Änderung der System-Entropie bei einer Zustandsänderung betrachtet werden, sondern auch die Entropie-Änderung, die das System durch Rückwirkung auf die Umgebung dort erzeugt. Das Enthalpiekriterium ist eine Umformulierung des Entropiekriteriums, in welche ausschließlich Eigenschaften des betrachteten Systems eingehen und welche die Rückwirkung auf die Umgebung (unter isobaren Bedingungen) automatisch berücksichtigt. Bei Verwendung des Enthalpiekriteriums kann die Ermittlung des (isobaren) Gleichgewichtszustands sich also auf die Betrachtung des Systems beschränken, was die Untersuchungen merklich erleichtert.[43]

Wird die Enthalpie als Funktion ihrer natürlichen Variablen $(S,p,N_{i})$ ausgedrückt, reduziert die Bedingung konstanten Drucks die Liste der Variablen um $p$ und die Enthalpie hängt nur noch von den Variablen $(S,N_{i})$ ab. Diese Vereinfachung demonstriert einen der möglichen Vorteile bei der Verwendung der Enthalpie in geeigneten Fällen. Der Gleichgewichtszustand könnte auch durch Aufsuchen des Minimums der inneren Energie des betrachteten Systems, $U(S,V,N_{i})$ , ermittelt werden, aber die Bedingung konstanten Drucks würde in diesem Fall nicht zu einer Vereinfachung der Funktion führen, sondern zu komplizierten Abhängigkeiten zwischen den Variablen $(S,V,N_{i})$ . Zusätzliche Probleme würden dabei entstehen, falls die Zustandsgleichung $p=p(S,V,N_{i})$ nicht explizit bekannt ist.[44]

Für einen realen physikalischen oder chemischen Prozess kann oft die Atmosphäre als Druckreservoir dienen. Wegen ihres großen Volumens ändert sich ihr Druck nicht nennenswert, wenn ein System Volumenänderungsarbeit an ihr leistet. Die Voraussetzungen für die Anwendbarkeit des Minimumsprinzips der Enthalpie sind also erfüllt, wenn ein System adiabatisch gegen die Umwelt isoliert ist (um Wärmeaustausch mit der Umgebung zu verhindern und damit die Entropie konstant zu halten) und über einen beweglichen Kolben oder eine ähnliche Vorrichtung an den atmosphärischen Umgebungsdruck gekoppelt ist (um den Systemdruck konstant zu halten).

In der Laborpraxis kommen solche adiabatischen Systeme allerdings selten vor. Chemische Reaktionen finden meistens nicht in adiabatisch isolierten Gefäßen statt, so dass Wärme mit der Umgebung ausgetauscht werden kann. Die Atmosphäre dient dann nicht nur als Druck-, sondern auch als Wärmereservoir: Sie hält Druck und Temperatur konstant. Das thermodynamische Potential, das unter diesen Bedingungen ein Minimum annimmt, ist die Gibbs-Energie $G=U+p\,V-T\,S$ .

Enthalpie und Wärmekapazität

Führt man einem System die spezifische (d. h. auf die Masse bezogene) Wärmemenge $\mathrm {d} q$ zu und bewirkt dadurch eine Temperaturänderung $\mathrm {d} T$ , dann ist die spezifische Wärmekapazität $c$ des Systems definiert durch die Gleichung

\mathrm {d} q=c\cdot \mathrm {d} T

oder

c={\frac {\mathrm {d} q}{\mathrm {d} T}}

.

Die spezifische Wärmekapazität ist nicht nur vom Material, sondern auch von der Prozessführung abhängig. Erfolgt die Wärmezufuhr isochor (d. h. bei konstantem Volumen), dann trägt die gesamte zugeführte Wärmemenge zur Erhöhung der spezifischen inneren Energie $\mathrm {d} u$ bei:

\mathrm {d} q=\mathrm {d} u

und der Prozess wird beschrieben durch die spezifische Wärmekapazität bei konstantem Volumen, $c_{v}$

c_{v}=\left({\frac {\partial u}{\partial T}}\right)_{v}

,

welche also die Ableitung der spezifischen inneren Energie nach der Temperatur bei konstantem Volumen ist.

Erfolgt die Wärmezufuhr isobar, dann ist die zugeführte spezifische Wärmemenge gleich der Erhöhung der spezifischen Enthalpie $\mathrm {d} h$ :

\mathrm {d} q=\mathrm {d} h

und der Prozess wird beschrieben durch die spezifische Wärmekapazität bei konstantem Druck, $c_{p}$

c_{p}=\left({\frac {\partial h}{\partial T}}\right)_{p}

,

welche also die Ableitung der spezifischen Enthalpie nach der Temperatur bei konstantem Druck ist.

Da zur Erzielung einer gewünschten Temperaturerhöhung im isobaren Fall die vom System zu leistende Volumenänderungsarbeit zusätzlich zugeführt werden muss, ist zu erwarten, dass die isobare spezifische Wärmekapazität einer Substanz größer sein wird als die isochore. Eine genauere Betrachtung muss berücksichtigen, dass die Ausdehnung des Systems meistens auch dessen innere Energie verändert. Es lässt sich jedoch zeigen, dass allgemein gilt:[45]

c_{p}-c_{v}\,=\,\left({\frac {\alpha ^{2}}{\kappa }}\right)Tv

.

Auf der rechten Seite können die Temperatur $T$ , das spezifische Volumen $v$ , das Quadrat des isobaren thermischen Ausdehnungskoeffizienten $\alpha$ und (aus thermodynamischen Stabilitätsgründen) die isotherme Kompressibilität $\kappa$ nicht negativ werden, so dass stets

c_{p}\geq c_{v}

[46]

ist. In manchen Fällen kann $c_{p}$ um 30 % größer sein als $c_{v}$ .[47]

Temperatur- und Druckabhängigkeit der Enthalpie

Tabellierungen der Enthalpie beziehen sich aus Platzgründen in der Regel auf eine bestimmte Temperatur und einen bestimmten Druck. Soll die Enthalpie für andere Bedingungen ermittelt werden, sind Formeln wünschenswert, die den Übergang vom Referenzzustand auf andere Temperaturen und Drücke erlauben. Es ist vorteilhaft, wenn für die Umrechnung nur die Kenntnis direkt messbarer Größen benötigt wird.

Für ein geschlossenes System, das sich im Gleichgewicht befindet und in dem keine chemischen Reaktionen stattfinden ( $\mathrm {d} N_{i}=0$ ) ist, wie oben ausgeführt, eine infinitesimale Änderung der Enthalpie gegeben durch

\mathrm {d} H=T\ \mathrm {d} S+V\ \mathrm {d} P

.

Das Differential $\mathrm {d} S$ lässt sich – aufgefasst als Funktion der hier interessierenden Variablen $T$ und $p$ – wie folgt entwickeln:[48]

{\begin{aligned}\mathrm {d} H&=T\left\{\left({\frac {\partial S}{\partial T}}\right)_{p}\mathrm {d} T+\left({\frac {\partial S}{\partial p}}\right)_{T}\mathrm {d} p\right\}+V\mathrm {d} p\\&=T\left({\frac {\partial S}{\partial T}}\right)_{p}\mathrm {d} T+\left\{V+T\left({\frac {\partial S}{\partial p}}\right)_{T}\right\}\mathrm {d} p\end{aligned}}

Mit Hilfe der Identitäten

T\left({\frac {\partial S}{\partial T}}\right)_{p}=\left({\frac {\partial Q}{\partial T}}\right)_{p}=\left({\frac {\partial H}{\partial T}}\right)_{p}

(wegen

\mathrm {d} Q=T\ \mathrm {d} S

gemäß dem Zweiten Hauptsatz)

und

\left({\frac {\partial S}{\partial p}}\right)_{T}=-\left({\frac {\partial V}{\partial T}}\right)_{p}

(einer der Maxwell-Beziehungen)

folgt

\mathrm {d} H=\left({\frac {\partial H}{\partial T}}\right)_{p}\mathrm {d} T+\left\{V-T\left({\frac {\partial V}{\partial T}}\right)_{p}\right\}\mathrm {d} p

,

was sich unter Benutzung der isobaren Wärmekapazität $C_{p}=\left({\frac {\partial H}{\partial T}}\right)_{p}$ und des isobaren thermischen Ausdehnungskoeffizienten $\alpha ={\frac {1}{V}}\left({\frac {\partial V}{\partial T}}\right)_{p}$ ausschließlich durch die messbaren Größen $V$ , $C_{p}$ und $\alpha$ ausdrücken lässt:

\mathrm {d} H=C_{p}\ \mathrm {d} T+V(1-\alpha \ T)\ \mathrm {d} p

.[48]

Für eine endlich große Zustandsänderung vom Zustand $(T_{1},p_{1})$ in den Zustand $(T_{2},p_{2})$ ist über diese infinitesimale Zustandsänderung zu integrieren:

H_{2}-H_{1}=\int _{T_{1}}^{T_{2}}C_{p}\ \mathrm {d} T+\int _{p_{1}}^{p_{2}}V(1-\alpha \ T)\ \mathrm {d} p

.[48]

Falls die Zustandsänderung mit einem Phasenübergang verbunden ist, muss die betreffende Latentwärme zusätzlich berücksichtigt werden.[49]

Die Größen $V$ , $C_{p}$ und $\alpha$ sind in der Regel selbst abhängig von Temperatur und Druck. Diese Abhängigkeiten müssen bekannt sein, damit die Integrale ausgeführt werden können.

Da die Enthalpie eine Zustandsgröße ist, hängen die Integrale nicht von der Wahl des Pfades ab, entlang welchem integriert wird. Eine bequeme Wahl des Pfades besteht darin, zunächst das Temperaturintegral auf einem Pfad konstanten Druckes auszuführen, der den Anfangszustand $(T_{1},p_{1})$ mit einem Zwischenzustand $(T_{2},p_{1})$ verbindet. Dazu muss $C_{p}$ im Temperaturbereich von $T_{1}$ bis $T_{2}$ beim fixen Druck $p_{1}$ bekannt sein. Anschließend wird das Druckintegral auf dem Pfad konstanter Temperatur ausgeführt, der $(T_{2},p_{1})$ mit $(T_{2},p_{2})$ verbindet. Dazu muss $V\alpha$ im Druckbereich von $p_{1}$ bis $p_{2}$ bei der fixen Temperatur $T_{2}$ bekannt sein.[49]

Alternativ kann die Integration erst auf einem Pfad konstanter Temperatur von $(T_{1},p_{1})$ nach $(T_{1},p_{2})$ geführt werden, wozu $V\alpha$ im Druckbereich von $p_{1}$ bis $p_{2}$ bei der fixen Temperatur $T_{1}$ bekannt sein muss. Anschließend führt der Pfad bei konstantem Druck von $(T_{1},p_{2})$ nach $(T_{2},p_{2})$ , wozu $C_{p}$ im Temperaturbereich von $T_{1}$ bis $T_{2}$ beim fixen Druck $p_{2}$ bekannt sein muss.[49]

Wird der Prozess isobar geführt, ist $p_{1}=p_{2}$ , das Druckintegral fällt weg und es ist lediglich die Kenntnis der temperaturabhängigen Wärmekapazität $C_{p}$ beim betreffenden fixen Druck nötig:

H_{2}-H_{1}=\int _{T_{1}}^{T_{2}}C_{p}\ \mathrm {d} T\quad \mathrm {(isobar)}

.

Siehe auch

Thermodynamisches Potential
Gibbs-Energie
Isenthalp
Dortmunder Datenbank
Gruppenbeitragsmethoden (zur Vorhersage von Verdampfungsenthalpien)

Weblinks

Wikibooks: Tabellensammlung Chemie/ Enthalpie und Bindungsenergie – Lern- und Lehrmaterialien

Wiktionary: Enthalpie – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Video: Berechnung der Bildungsenthalpie aus Verbrennungsenthalpien nach Hess. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15698.

Einzelnachweise

Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 7. Dezember 2021] . Im Wörterbuch Angabe nicht des Infinitivs, sondern wie im Altgriechischen üblich der ersten Person Singular Indikativ Präsens Aktiv ἐνθάλπω enthálpō).
Eintrag zu enthalpy. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.E02141 – Version: 2.0.2.
L. Pauling: General Chemistry. Dover, New York 1988, ISBN 0-486-65622-5, S. 346
K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge/New York/Melbourne 1981, ISBN 0-521-28150-4, S. 64
M. W. Zemansky, R. H. Dittmann: Heat and Thermodynamics. 7. Auflage. McGraw-Hill, 1997, ISBN 0-07-017059-2, S. 80.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 161.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 173.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 85.
B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 16.
B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 30.
B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 14.
B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 28.
L. Pauling: General Chemistry. Dover, New York 1988, ISBN 0-486-65622-5, S. 349
A. Sommerfeld: Vorlesungen über Theoretische Physik. Band V: Thermodynamik und Statistik. Harri Deutsch, Thun/ Frankfurt am Main 1988, ISBN 3-87144-378-6, S. 13f.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 163.
M. W. Zemansky, R. H. Dittmann: Heat and Thermodynamics. 7. Auflage. McGraw-Hill, 1997, ISBN 0-07-017059-2, S. 252 ff.
F. Bošnjaković: Technische Thermodynamik – Teil 1. 7. Auflage. Steinkopff Verlag, Darmstadt 1988, ISBN 3-7985-0759-7, S. 125.
F. Bošnjaković: Technische Thermodynamik – Teil 1. 7. Auflage. Steinkopff Verlag, Darmstadt 1988, ISBN 3-7985-0759-7, S. 126.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 87.
Eintrag zu Wasser. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.
Eintrag zu Kohlendioxid. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.
Eintrag zu Ammoniak. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.
Eintrag zu Methan. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.
Eintrag zu Ethen. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.
Eintrag zu Ethan. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.
Werte berechnet mit Sublimationsenthalpie = Standardbildungsenthalpie (Gas) - Standardbildungsenthalpie (Fest)
Barrow, Gordon M.: Physikalische Prinzipien und ihre Anwendung in der Chemie. Springer Vieweg, 1979, ISBN 978-3-322-86084-2, S. 361 ff. (springer.com [PDF]).
James S. Chickos, William E. Acree: Enthalpies of Sublimation of Organic and Organometallic Compounds. 1910–2001. In: Journal of Physical and Chemical Reference Data. Band 31, Nr. 2, 2002, ISSN 0047-2689, S. 537–698, doi:10.1063/1.1475333 (scitation.org [abgerufen am 23. Juni 2019]).
Karl-Heinz Lautenschläger, Werner Schröter: Taschenbuch der Chemie. Harri Deutsch Verlag, 2008, ISBN 978-3-8171-1761-1, S. 292, eingeschränkte Vorschau in der Google-Buchsuche
Gitterenergie. In: Römpp Lexikon Chemie. Version 2.0, Georg Thieme Verlag, 1999.
S. W. Benson, F. R. Cruickshank, D. M. Golden, G. R. Haugen, H. E. O’Neal, A. S. Rodgers, R. Shaw, R. Walsh: Additivity Rules for the Estimation of Thermochemical Properties. In: Chem. Rev. 69, 1969, S. 279–324.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 13.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 63f.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 137ff.
J. K. Fink: Physical Chemistry in Depth. Springer, Berlin/ Heidelberg 2009, ISBN 978-3-642-01013-2, S. 84.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 35.
H.-J. Lange: Die Physik des Wetters und des Klimas. Dietrich Reimer Verlag, Berlin 2002, ISBN 3-496-02747-9, S. 28f.
E. Keszei: Chemical Thermodynamics. Springer, Berlin/ Heidelberg 2012, ISBN 978-3-642-19863-2, S. 13.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 132ff.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 156 „Enthalpy Minimum Principle. The equilibrium value of any unconstrained internal parameter in a system in contact with a pressure reservoir minimizes the enthalpy over the manifold of states of constant pressure (equal to that of the pressure reservoir).“
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 153ff.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 156.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 114.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 157 (die dortige Erläuterung zur Helmholtz-Energie sinngemäß auf die Enthalpie übertragen)
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 73.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 210.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 74.
K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge/New York/Melbourne 1981, ISBN 0-521-28150-4, S. 98
K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge/New York/Melbourne 1981, ISBN 0-521-28150-4, S. 99

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 7. Dezember 2021] . Im Wörterbuch Angabe nicht des Infinitivs, sondern wie im Altgriechischen üblich der ersten Person Singular Indikativ Präsens Aktiv ἐνθάλπω enthálpō).

[2] Eintrag zu enthalpy. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.E02141 – Version: 2.0.2.

[3] L. Pauling: General Chemistry. Dover, New York 1988, ISBN 0-486-65622-5, S. 346

[Denbigh_S64-4] K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge/New York/Melbourne 1981, ISBN 0-521-28150-4, S. 64

[5] M. W. Zemansky, R. H. Dittmann: Heat and Thermodynamics. 7. Auflage. McGraw-Hill, 1997, ISBN 0-07-017059-2, S. 80.

[6] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 161.

[7] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 173.

[Atkins_85-8] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 85.

[9] B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 16.

[10] B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 30.

[11] B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 14.

[12] B. Glück: Zustands- und Stoffwerte, Wasser - Dampf - Luft. Verlag für Bauwesen, Berlin 1991, ISBN 3-345-00487-9, S. 28.

[13] L. Pauling: General Chemistry. Dover, New York 1988, ISBN 0-486-65622-5, S. 349

[14] A. Sommerfeld: Vorlesungen über Theoretische Physik. Band V: Thermodynamik und Statistik. Harri Deutsch, Thun/ Frankfurt am Main 1988, ISBN 3-87144-378-6, S. 13f.

[15] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 163.

[16] M. W. Zemansky, R. H. Dittmann: Heat and Thermodynamics. 7. Auflage. McGraw-Hill, 1997, ISBN 0-07-017059-2, S. 252 ff.

[17] F. Bošnjaković: Technische Thermodynamik – Teil 1. 7. Auflage. Steinkopff Verlag, Darmstadt 1988, ISBN 3-7985-0759-7, S. 125.

[18] F. Bošnjaković: Technische Thermodynamik – Teil 1. 7. Auflage. Steinkopff Verlag, Darmstadt 1988, ISBN 3-7985-0759-7, S. 126.

[19] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 87.

[NIST_Wasser-20] Eintrag zu Wasser. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.

[21] Eintrag zu Kohlendioxid. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.

[22] Eintrag zu Ammoniak. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.

[23] Eintrag zu Methan. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.

[24] Eintrag zu Ethen. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.

[25] Eintrag zu Ethan. In: P. J. Linstrom, W. G. Mallard (Hrsg.): NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology, Gaithersburg MD, abgerufen am 15. Dezember 2013.

[:berechnet-26] Werte berechnet mit Sublimationsenthalpie = Standardbildungsenthalpie (Gas) - Standardbildungsenthalpie (Fest)

[:SpringerTabelle-27] Barrow, Gordon M.: Physikalische Prinzipien und ihre Anwendung in der Chemie. Springer Vieweg, 1979, ISBN 978-3-322-86084-2, S. 361 ff. (springer.com [PDF]).

[:0-28] James S. Chickos, William E. Acree: Enthalpies of Sublimation of Organic and Organometallic Compounds. 1910–2001. In: Journal of Physical and Chemical Reference Data. Band 31, Nr. 2, 2002, ISSN 0047-2689, S. 537–698, doi:10.1063/1.1475333 (scitation.org [abgerufen am 23. Juni 2019]).

[29] Karl-Heinz Lautenschläger, Werner Schröter: Taschenbuch der Chemie. Harri Deutsch Verlag, 2008, ISBN 978-3-8171-1761-1, S. 292, eingeschränkte Vorschau in der Google-Buchsuche

[30] Gitterenergie. In: Römpp Lexikon Chemie. Version 2.0, Georg Thieme Verlag, 1999.

[31] S. W. Benson, F. R. Cruickshank, D. M. Golden, G. R. Haugen, H. E. O’Neal, A. S. Rodgers, R. Shaw, R. Walsh: Additivity Rules for the Estimation of Thermochemical Properties. In: Chem. Rev. 69, 1969, S. 279–324.

[32] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 13.

[33] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 63f.

[Callen_137ff-34] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 137ff.

[Fink_84-35] J. K. Fink: Physical Chemistry in Depth. Springer, Berlin/ Heidelberg 2009, ISBN 978-3-642-01013-2, S. 84.

[36] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 35.

[HJLange_28f-37] H.-J. Lange: Die Physik des Wetters und des Klimas. Dietrich Reimer Verlag, Berlin 2002, ISBN 3-496-02747-9, S. 28f.

[38] E. Keszei: Chemical Thermodynamics. Springer, Berlin/ Heidelberg 2012, ISBN 978-3-642-19863-2, S. 13.

[39] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 132ff.

[40] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 156 „Enthalpy Minimum Principle. The equilibrium value of any unconstrained internal parameter in a system in contact with a pressure reservoir minimizes the enthalpy over the manifold of states of constant pressure (equal to that of the pressure reservoir).“

[Callen_153ff-41] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 153ff.

[Callen_156-42] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 156.

[43] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 114.

[Callen_157-44] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 157 (die dortige Erläuterung zur Helmholtz-Energie sinngemäß auf die Enthalpie übertragen)

[45] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 73.

[46] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, S. 210.

[47] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 74.

[Denbigh_S98-48] K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge/New York/Melbourne 1981, ISBN 0-521-28150-4, S. 98

[Denbigh_S99-49] K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge/New York/Melbourne 1981, ISBN 0-521-28150-4, S. 99