Neutronenstern
Ein Neutronenstern ist ein astronomisches Objekt, dessen wesentlicher und namensgebender Bestandteil Neutronen sind. Ein Neutronenstern stellt ein Endstadium in der Sternentwicklung eines massereichen Sterns dar.

Neutronensterne sind kugelförmige Körper mit typischen Radien von etwa 10 bis 12 km, nach stellaren Maßstäben also sehr klein. Die Massen der bislang entdeckten Neutronensterne liegen zwischen etwa 1,2 und 2,0 Sonnenmassen, damit sind sie extrem kompakt. Ihre Dichte nimmt von etwa 1 · 109 kg/m3 an ihrer Kruste mit der Tiefe bis auf etwa 6 · 1017 bis 8 · 1017 kg/m3 zu, was etwa der dreifachen Dichte eines Atomkerns entspricht.[1][2] Die mittlere Dichte eines Neutronensterns beträgt etwa 3,7 bis 5,9 · 1017 kg/m3.[3] Damit sind Neutronensterne die dichtesten bekannten Objekte ohne Ereignishorizont. Typische Sterne dieser Art rotieren sehr schnell und haben ein starkes Magnetfeld.
Der am schnellsten rotierende bekannte Neutronenstern ist der 2004 entdeckte PSR J1748-2446ad mit 716 Umdrehungen pro Sekunde. Das bedeutet bei einem angenommenen Radius von ≤16 km, dass die Umfangsgeschwindigkeit an seinem Äquator etwa 70.000 km/s beträgt, was fast einem Viertel der Lichtgeschwindigkeit entspricht. Eine für den 1999 entdeckten Neutronenstern XTE J1739-285 angenommene noch höhere Rotationsfrequenz von 1122 Hz[4] konnte in späteren Untersuchungen nicht bestätigt werden.[5]
Neutronensternen gilt intensives Forschungsinteresse, da Details ihres dynamischen Verhaltens und ihrer Zusammensetzung noch unbekannt sind und an ihnen extreme Materieeigenschaften unter in der Natur beobachtbaren Bedingungen untersucht werden können.[6]

Entdeckungsgeschichte
Im Jahr 1932 entdeckte James Chadwick das Neutron[7] als Elementarteilchen und erhielt dafür 1935 den Nobelpreis für Physik.
Bereits 1931, ein Jahr vor Chadwicks Entdeckung, schlug Lew Dawidowitsch Landau theoretisch die Existenz von Neutronenkernen vor, nämlich von extrem dichten Kernregionen im Inneren herkömmlicher Sterne.[8] 1933 schlugen Walter Baade und Fritz Zwicky die moderne Variante von Neutronensternen vor: aus Neutronen bestehende Sternreste als mögliches Endprodukt der Sternentwicklung. Auf diese Deutung waren sie bei dem Versuch gekommen, die Vorgänge im Laufe einer Supernova zu erklären.[9] Robert Oppenheimer und George Michael Volkoff berechneten 1939 ein theoretisches Modell eines Neutronensterns und gaben die maximale Masse mit 0,7 M☉ an[10] (siehe auch Tolman-Oppenheimer-Volkoff-Grenze).
1967 entdeckten die Astronomen Jocelyn Bell, Antony Hewish und Martin Ryle Radioimpulse von einem Pulsar, der später als isolierter, rotierender Neutronenstern interpretiert wurde. Die Energiequelle für diese Impulse ist die Rotationsenergie des Neutronensterns. Die meisten bisher entdeckten Neutronensterne gehören zu diesem Typ.
1971 beobachteten Riccardo Giacconi, Herbert Gursky, Ed Kellogg, R. Levinson, E. Schreier und Harvey Tananbaum Impulse mit einer Periode von 4,8 Sekunden in einer Röntgenquelle im Sternbild Centaurus, bezeichnet als Cen X-3. Sie interpretieren diese Beobachtung als einen rotierenden, heißen Neutronenstern in einer Umlaufbahn um einen anderen Stern. Die Energie für diese Impulse stammt aus der freigesetzten Gravitationsenergie, die von der auf den Neutronenstern einströmenden, gasförmigen Materie des Sterns stammt.
Im frühen 21. Jahrhundert waren fast 2000 Neutronensterne entdeckt, wovon wegen ungünstiger physikalischer Bedingungen nur ein Bruchteil detaillierte Untersuchungen erlaubt.[11] Für den fortlaufenden Nachweis weiterer dieser Sterne werden aufwendige Berechnungen mit Daten angestellt, die mit Anlagen wie dem Radioteleskop Effelsberg, dem Arecibo-Observatorium oder dem Parkes-Observatorium gewonnen wurden.[12] Um die dazu notwendigen Hough-Transformationen mit Rechenleistungen ähnlich Supercomputern zu lösen, werden nicht nur große CPU-GPU-Cluster eingesetzt, sondern im Rahmen von Einstein@home auch verteilte Systeme.[13]
Entstehung
Neutronensterne entstehen aus massereichen Sternen der Hauptreihe am Ende ihrer Entwicklung. Zwei Wege der Entwicklung zum Neutronenstern werden unterschieden.[14]
- Wenn die Masse des ursprünglichen Hauptreihen-Sterns zwischen 8 und etwa 12 Sonnenmassen lag, resultiert ein Neutronenstern mit einer Masse von ca. 1,25 Sonnenmassen. Durch das Kohlenstoffbrennen entsteht ein Sauerstoff-Neon-Magnesium-Kern. Ein Vorgang der Entartung schließt sich an. Infolge Überschreitens der Roche-Grenze kommt es durch Wind Roche-Lobe Overflow zu Masseverlust. Nach Annäherung an die Chandrasekhar-Grenze kollabiert er zum Neutronenstern. Dieser bewegt sich mit ähnlicher Geschwindigkeit wie der ursprüngliche Stern durch den Raum. Diesen Weg können Sterne durchlaufen, die Teil eines wechselwirkenden Doppelsternes waren, während Einzelsterne dieser Masse sich zum AGB-Stern entwickeln, dann weiter Masse verlieren und so zum Weißen Zwerg werden.[15]
- Wenn die Masse des ursprünglichen Hauptreihen-Sterns größer als etwa 12 Sonnenmassen war, resultiert ein Neutronenstern mit einer Masse von mehr als 1,3 Sonnenmassen. Nachdem durch das Kohlenstoffbrennen ein Sauerstoff-Neon-Magnesium-Kern entstanden ist, folgen als weitere Entwicklungsstufen das Sauerstoffbrennen und das Siliciumbrennen, sodass ein Eisen-Kern entsteht. Sobald dieser eine kritische Masse überschreitet, kollabiert er zum Neutronenstern. Ein auf diesem Weg entstandener Neutronenstern bewegt sich wesentlich schneller durch den Raum als der ursprüngliche Stern und kann 500 km/s erreichen. Die Ursache wird in den enormen Bewegungen der Konvektion im Kern während der letzten beiden Phasen des Brennens gesehen, die die Homogenität der Dichte des Sternenmantels derartig beeinträchtigt, dass Neutrinos in asymmetrischer Weise ausgestoßen werden. Diesen Weg können Sterne durchlaufen, die Einzelsterne oder Teil eines nicht wechselwirkenden Doppelsterns waren.
Beiden Wegen ist gemeinsam, dass als späte Entwicklungsphase ein unmittelbarer Vorläuferstern entsteht, dessen Kernmasse gängigen Modellen zufolge zwischen 1,4 Sonnenmassen (Chandrasekhar-Grenze) und etwa 3 Sonnenmassen (Tolman-Oppenheimer-Volkoff-Grenze) liegen muss, damit über eine Kernkollaps-Supernova (Typen II, Ib, Ic) der Neutronenstern entsteht. Liegt die Masse darüber, entsteht stattdessen ein Schwarzes Loch, liegt sie darunter, erfolgt keine Supernovaexplosion, sondern es entwickelt sich ein Weißer Zwerg. Astronomische Beobachtungen zeigen jedoch Abweichungen von den genauen Grenzen dieses Modells, denn es wurden Neutronensterne mit weniger als 1,4 Sonnenmassen gefunden.
Sobald sich durch das Siliciumbrennen im Kern Eisen angereichert hat, ist keine weitere Energiegewinnung über Kernfusion mehr möglich, da für eine weitere Fusion aufgrund der hohen Bindungsenergie pro Nukleon des Eisens Energie aufgewendet werden müsste, anstatt freigesetzt zu werden. Ohne diese Energiegewinnung nimmt der Strahlungsdruck im Inneren des Sterns ab, der der Gravitation im Inneren des Sterns entgegenwirkt. Nur solange sich die einander entgegenwirkenden Kräfte von Strahlungsdruck und Gravitation im Gleichgewicht befinden, bleibt der Stern stabil – durch die Abnahme des Strahlungsdrucks wird der Stern instabil und kollabiert.
Wenn der Stern durch die Abnahme des Strahlungsdrucks kollabiert, wird der Kern durch die auf ihn einstürzenden Massen der Sternenhülle und durch seine eigene, nun „übermächtige“ Gravitation stark komprimiert. Dadurch wird die Temperatur auf ca. 1011 Kelvin erhöht. Dabei wird Strahlung abgegeben, wovon Röntgenstrahlung den größten Anteil hat. Die so freigesetzte Energie ruft eine Photodesintegration der Eisen-Atomkerne in Neutronen und Protonen hervor sowie den Elektroneneinfang der Elektronen von den Protonen, sodass Neutronen und Elektron-Neutrinos entstehen.[16] Da die Umwandlung der Protonen und Elektronen in Neutronen endotherm ist, wird diese Energie letztlich aus der Gravitation beim Kollaps gespeist[17].
Auch nach diesem Prozess schrumpft der Kern noch weiter, bis die Neutronen einen so genannten Entartungsdruck aufbauen, der die weitere Kontraktion schlagartig stoppt. Bei dem Kollaps des Sterns werden etwa 10 % seiner Gravitationsenergie freigesetzt, und zwar im Wesentlichen durch die Emission von Neutrinos. Im Kern des Sterns entstehen Neutrinos in durch diese Vorgänge bedingter großer Zahl und stellen ein heißes Fermigas dar. Diese Neutrinos entfalten nun kinetische Energie und streben nach außen. Andererseits fällt Materie äußerer Schichten des kollabierenden Sterns auf seinen Kern zurück. Dieser weist aber bereits extreme Dichte auf, sodass die Materie abprallt. Sie bildet eine Hülle um den Kern und unterliegt starker, durch Entropie getriebener Konvektion.[18] Sobald sich durch die Neutrinos genügend Energie angesammelt hat und einen Grenzwert überschreitet, prallen die zurückfallenden äußeren Schichten an den Grenzflächen endgültig ab und werden durch die Neutrinos stark beschleunigt, sodass sich das kompakte Sternenmaterial explosiv auf einen großen Raum verteilt. Dies ist eine der wenigen bekannten Situationen, in denen Neutrinos wesentlich mit normaler Materie wechselwirken. Somit wurde die thermische Energie in elektromagnetische Wellen umgewandelt, die innerhalb weniger Minuten explosiv freigesetzt wird und die Kernkollaps-Supernova weithin sichtbar macht. Durch diese Supernova werden zudem per Nukleosynthese schwerere Elemente als Eisen gebildet.
Bei sehr massereichen Hauptreihe-Sternen von mehr als ca. 40 Sonnenmassen kann die Energie der nach außen strebenden Neutrinos die Gravitation des zurückfallenden Materials nicht kompensieren, sodass anstelle der Explosion ein Schwarzes Loch entsteht.[19]
Bemerkenswert ist, dass die Bildung des Neutronensterns zunächst vollständig im Kern des Sternes abläuft, während der Stern äußerlich unauffällig bleibt. Erst nach einigen Tagen wird die Supernova nach außen sichtbar. So können Neutrinodetektoren eine Supernova früher nachweisen als optische Teleskope.
Auch gibt es einen Nebenweg der Entwicklung zu Neutronensternen, der für weniger als 1 % dieser Sterne zutrifft. Dabei überschreitet ein Weißer Zwerg eines wechselwirkenden Doppelsternes die Chandrasekhar-Grenze, indem er Material von dem anderen Stern aufnimmt. Er bildet keine feste Hülle und explodiert daher.[20]
Eigenschaften
Gravitation

Durch die gravitative Lichtablenkung ist mehr als die Hälfte der Oberfläche sichtbar (Karos: 30°×30°). Der Radius eines Neutronensterns ist doppelt so groß wie sein Schwarzschild-Radius. Bei einer typischen Neutronensternmasse von 1,4 Sonnenmassen entspricht das einem Sternradius von 8,4 km.
Feld und Linseneffekt
Das Gravitationsfeld an der Oberfläche eines typischen Neutronensterns ist etwa 2 · 1011-mal so stark wie das der Erde. Entsprechend hoch ist die Fluchtgeschwindigkeit, auf die ein Objekt beschleunigt werden muss, damit es den Neutronenstern verlassen kann. Sie liegt in der Größenordnung 100.000 km/s, was etwa einem Drittel der Lichtgeschwindigkeit entspricht. Das starke Gravitationsfeld wirkt als Gravitationslinse und lenkt vom Neutronenstern emittiertes Licht dergestalt ab, dass Teile der Rückseite des Sterns ins Blickfeld gelangen und mehr als die Hälfte seiner Oberfläche sichtbar ist.
Die gravitative Bindungsenergie eines Neutronensterns der doppelten Sonnenmasse ist nach dem Gesetz über die Äquivalenz von Masse und Energie, E = mc², äquivalent zu einer Sonnenmasse. Das ist die Energie, die bei der Supernovaexplosion freigesetzt wird.
Abgabe von Wellen
Ein Neutronenstern kann Gravitationswellen abgeben.[21] Dies ist dann der Fall, wenn er keine ideale Kugel ist, etwa dadurch, dass er an einer Stelle eine Ausbeulung aufweist, die z. B. durch Materialaufnahme aus der Umgebung entstehen kann.[22] Bei einer solchen Erhebung könnte es sich auch um eine Art von Kristall aus in einer dichten Elektronen-Packung gefangenen Ionen handeln, wie sie unter sich abkühlenden Bedingungen entstehen kann.[23] Es handelt sich um einen Spezialfall, dem das Gravitationsfeld und die abflachend wirkende hohe Rotationsgeschwindigkeit entgegenwirken. Das Verhältnis der durch die Deformation hervorgerufenen Änderung des Radius zum Radius des Sterns wird Elliptizität genannt. Sie wird näherungsweise beschrieben mit Je größer der Wert ist, desto stärker ist die emittierte Welle.
Auch können asteroseismologischen Modellen zufolge Gravitationswellen dadurch ausgelöst werden, dass der kompakte Stern oszilliert und in eine instabile Situation gerät, etwa wenn er durch äußeren Einfluss gestört wird. In diesem Fall kann die Gravitationswelle je nach Drehrichtung und Viskosität des Sterns durch den damit verbundenen Energieverlust sogar weitere Wellen auslösen.[24]
Dem Auffinden eines derartigen asymmetrischen Sterns gelten weltweite Forschungsanstrengungen, weil das erwartete, mit einem Gravitationswellendetektor nachzuweisende Signal kontinuierlich auftritt, was u. a. eine genaue Lagebestimmung erlaubt. Bei einer systematischen Suche wurde 2016 im Umkreis von 100 Parsec um die Erde kein Neutronenstern mit einer Ausbeulung von mehr als 1 cm gefunden.[25]
Rotationsfrequenz
Beim Kollaps der Kernzone des Vorläufersterns verringert sich sein Durchmesser auf weniger als ein Hunderttausendstel des ursprünglichen Wertes. Aufgrund des damit verbundenen Pirouetteneffekts rotiert ein Neutronenstern anfänglich mit etwa hundert bis tausend Umdrehungen pro Sekunde. Die höchste bislang gemessene Rotationsfrequenz beträgt 716 Hz (Pulsar PSR J1748-2446ad). Sie liegt nicht allzu fern unterhalb der durch die Zentrifugalkraft bedingten Stabilitätsgrenze eines reinen Neutronensterns von etwa 1 kHz.
Verschiedene Effekte können die Rotationsfrequenz eines Neutronensterns im Laufe der Zeit verändern. Liegt ein Doppelsternsystem vor, bei dem ein Materialfluss von einem Hauptreihenstern zum Neutronenstern stattfindet, so wird ein Drehimpuls übertragen, der die Rotation des Neutronensterns beschleunigt. Dabei können sich Werte im Bereich von 1 kHz einstellen. Das vom Neutronenstern emittierte Magnetfeld ist einer der bremsenden Effekte, die seine Rotationsperiode auf mehrere Sekunden oder gar Minuten ansteigen lassen können.
Aufbau
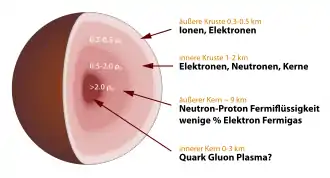
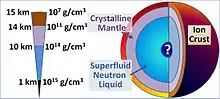
Aus den bekannten Eigenschaften der beteiligten Teilchen ergibt sich für einen Neutronenstern von 20 km Durchmesser folgende Schalenstruktur:
An der Oberfläche herrscht der Druck null. Da freie Neutronen in dieser Umgebung instabil sind, gibt es dort nur Eisenatomkerne und Elektronen. Diese Atomkerne bilden ein Kristallgitter. Aufgrund der enormen Schwerkraft sind jedoch die höchsten Erhebungen auf der Oberfläche maximal einige Millimeter hoch.[26] Eine mögliche Atmosphäre aus heißem Plasma hätte eine maximale Dicke von einigen Zentimetern.
Die Zone aus kristallinen Eisenatomkernen setzt sich bis in eine Tiefe von etwa 10 m fort. Dabei steigt die mittlere Dichte des Kristallgitters auf etwa ein Tausendstel der Dichte von Atomkernen. Ferner nimmt der Neutronenanteil der Atomkerne zu. Es bilden sich neutronenreiche Eisenisotope, die nur unter den dortigen extremen Druckverhältnissen stabil sind.
Ab einer Tiefe von 10 m ist der Druck so hoch, dass auch freie Neutronen Bestand haben. Dort beginnt die sogenannte innere Kruste: eine Übergangsschicht, die eine Dicke von 1 bis 2 km hat. In ihr existieren Bereiche aus kristallinen Eisenatomkernen neben solchen aus Neutronenflüssigkeit, wobei mit zunehmender Tiefe der Eisenanteil von 100 % auf 0 % abnimmt, während der Anteil der Neutronen entsprechend zunimmt. Ferner steigt die mittlere Dichte auf die von Atomkernen und darüber hinaus. Am unteren Rand der inneren Kruste kann sich eine nukleare Pasta bilden.[27]
Im Anschluss an die innere Kruste besteht der Stern überwiegend aus Neutronen, die mit einem geringen Anteil von Protonen und Elektronen im thermodynamischen Gleichgewicht stehen. Sofern die Temperaturen hinreichend niedrig sind, verhalten sich die Neutronen dort supraflüssig und die Protonen supraleitfähig. Für einen typischen Neutronenstern liegt die zugehörige kritische Temperatur bei etwa 1011 Kelvin; Neutronensterne werden also bereits sehr kurz nach ihrer Entstehung supraflüssig.
Welche Materieformen ab einer Tiefe vorliegen, bei der die Dichte auf das Fünf- bis Zehnfache[28] der von Atomkernen steigt, ist unbekannt, da sich derartige Dichten bisher auch bei Kollisionen von Atomkernen in irdischen Teilchenbeschleunigern nicht erzeugen und damit auch nicht studieren lassen.
Schon darunter beginnt möglicherweise eine Kernzone mit Pionen oder Kaonen. Da diese Teilchen Bosonen sind und nicht dem Pauli-Prinzip unterliegen, könnten einige den gleichen energetischen Grundzustand einnehmen und damit ein sogenanntes Bose-Einstein-Kondensat bilden. Dabei könnten sie dem enormen Außendruck wenig entgegensetzen, so dass ein zweiter Kollaps zu einem Schwarzen Loch möglich wäre.[29] Eine weitere Möglichkeit wäre das Vorliegen freier Quarks. Da neben Up- und Down-Quarks auch Strange-Quarks vorkämen, bezeichnet man ein solches Objekt als „seltsamen Stern“ (engl. strange = seltsam) oder Quarkstern. Eine derartige Materieform würde durch die starke Wechselwirkung stabilisiert und könnte daher auch ohne den gravitativen Außendruck existieren. Da Quarksterne dichter und damit kleiner sind, sollten sie rascher rotieren können als reine Neutronensterne. Ein Pulsar mit einer Rotationsperiode unter 0,5 ms wäre bereits ein Hinweis auf die Existenz dieser Materieform.
Bei vier Pulsaren wurde mehrfach ein plötzlicher winziger Anstieg der Rotationsfrequenz beobachtet, gefolgt von einer mehrtägigen Relaxationsphase. Dabei könnte es sich um eine Art Beben handeln, bei dem ein Austausch von Drehimpuls zwischen der kristallinen Eisenkruste und den weiter innen reibungsfrei rotierenden Wirbeln aus supraflüssiger Neutronenflüssigkeit stattfindet.
Stabilität
Ein vorwiegend aus Neutronen bestehender Stern wird durch Kräfte stabilisiert, die eine Folge des Pauli-Prinzips sind. Danach können sich maximal zwei Neutronen des Sterns im selben energetischen Zustand befinden, wobei sie sich in der Orientierung ihres Spins unterscheiden. Als Folge der Quantenmechanik bilden die möglichen Energiezustände eine Energieleiter, deren Sprossenabstand bei Verringerung des Sternvolumens wächst. Da die Zustände ab dem unteren Ende der Leiter alle besetzt sind, muss bei einer Kompression den Neutronen am oberen Ende der Leiter Energie zugeführt werden. Dieses Phänomen führt zu einem Gegendruck, dem so genannten Fermi-Druck, der dem Gravitationsdruck standhalten kann. Da in dieser Situation der Druck kaum von der Temperatur abhängt, sondern fast ausschließlich von der Verteilung der quantenmechanisch erlaubten Energiezustände, bezeichnet man diesen Materiezustand als entartete Materie. Ist die Masse des unmittelbaren Vorläufersterns größer als die Tolman-Oppenheimer-Volkoff-Grenze von etwa drei Sonnenmassen (laut einer im Januar 2018 veröffentlichten Arbeit etwa 2,16 Sonnenmassen für nichtrotierende Neutronensterne und bis etwa 20 % höher für rotierende[30][31]), so ist kein Gleichgewicht möglich, und der Stern kollabiert nach derzeitigem Kenntnisstand weiter zum Schwarzen Loch.
Bemerkenswert ist, dass der typische Durchmesser eines Neutronensterns im Rahmen dieses Modells unmittelbar mit der Neutronenmasse zusammenhängt, eine astronomische Größe also eine direkte Funktion einer mikrokosmischen Naturkonstante ist, abgesehen von Faktoren, die sich aus der noch unbekannten Zustandsgleichung ergeben. Die Stabilität eines Weißen Zwerges beruht übrigens in identischer Weise auf dem Pauli-Prinzip, das in diesem Fall bezüglich der Elektronen anstelle der Neutronen zum Tragen kommt.
Temperatur und Weiteres
Die Temperatur im Inneren eines Neutronensterns beträgt anfangs 100 Milliarden Kelvin. Die Abstrahlung von Neutrinos entzieht jedoch so viel thermische Energie, dass sie innerhalb eines Tages auf ca. eine Milliarde Kelvin sinkt. Innerhalb von ca. 100 Jahren sinkt die Temperatur auf ca. 300.000 Kelvin. Erst nach etwa 100.000 Jahren tragen emittierte Photonen mehr als Neutrinos zum Temperaturrückgang bei. Nach einer Million Jahren werden 10.000 Kelvin unterschritten.[32]
Wenn der Neutronenstern ein Pulsar ist, gibt er elektromagnetische Strahlung ab. Diese kann sich auch als Gammablitz äußern. Etwa 1 % der massereichen Sterne enden so.[33]
Die Zustandsgleichung für einen Neutronenstern ist noch immer unbekannt. Man geht davon aus, dass sie sich signifikant von der eines Weißen Zwerges unterscheidet. Die Zustandsgleichung eines Weißen Zwerges ist die eines entarteten Gases, das in guter Näherung mit der speziellen Relativitätstheorie beschrieben werden kann. Bei einem Neutronenstern sind jedoch die Effekte der allgemeinen Relativitätstheorie nicht mehr vernachlässigbar. Daraus resultieren auch insbesondere die beobachteten Abweichungen von den vorhergesagten Grenzen der Massen für einen Neutronenstern.
Magnetfeld
Neutronensterne haben ein extrem starkes Magnetfeld, das sowohl für ihre weitere Entwicklung als auch für die astronomische Beobachtung von Bedeutung ist. Als Folge der Gesetze der Elektrodynamik bleibt das Produkt aus Sternquerschnitt und Magnetfeld beim Kollaps des Vorläufersterns konstant. Für einen typischen Neutronenstern ergibt sich daraus eine Zunahme des Magnetfeldes um den Faktor 1010 auf Werte im Bereich von 108 Tesla (1012 Gauß). Die Massendichte, die einem derartigen Magnetfeld über seine Energiedichte in Kombination mit der Äquivalenz von Masse und Energie gemäß E = mc2 zugeordnet werden kann, liegt im Bereich einiger Dutzend g/cm3. Diese Magnetfelder sind so stark, dass Atome in ihrem Einflussbereich eine längliche Zigarrenform annehmen würden, da die Wechselwirkung der Elektronen mit dem Magnetfeld über jene mit dem Kern dominiert. Aufgrund der Rotation des Neutronensterns stellt sich zwischen Zentrum und Äquator eine Hall-Spannung der Größenordnung 1018 V ein. Das entspricht einer elektrischen Feldstärke von einigen 1000 V pro Atomdurchmesser.
Typen und Beispiele
Pulsare

Die Kugel in der Mitte stellt einen Neutronenstern dar, die Kurven die magnetischen Feldlinien und die seitlich abstehenden Lichtkegel die Richtung der ausgehenden Strahlung.

Ist die Achse des Magnetfeldes gegen die Rotationsachse geneigt, so wird wegen der Wechselwirkung mit dem umgebenden Plasma Strahlung (Radiowellen, Röntgenstrahlung) in Richtung der Magnetpole mit dem typisch 100.000-fachen der gesamten Strahlungsleistung der Sonne emittiert. Bei geeignetem Beobachter-Standort wird eine periodische Strahlung beobachtet. Derartige Strahlungsquellen sind in der Astronomie als Pulsare oder Radiopulsare bekannt. Die dazu erforderliche Energie wird der Rotationsenergie entnommen, die dadurch innerhalb weniger Millionen Jahre weitgehend aufgezehrt wird. Ein ähnlicher Zeitverlauf ist auch hinsichtlich des Magnetfeldes und der Temperatur zu erwarten.
Befinden sich in der Umgebung des Pulsars ionisierte Gase (Plasma), so werden die Elektronen vom Magnetfeld an den Polen mitgerissen und bewegen sich dabei gleichzeitig entlang der Achse des Magnetfeldes nach außen. Spätestens an der Stelle, an der die Achse mit Lichtgeschwindigkeit rotiert, können sie ihr jedoch nicht mehr folgen und bleiben zurück. Dabei strahlen sie einen Teil ihrer kinetischen Energie als Röntgen- und Gammastrahlung in Richtung dieser Achse ab. Solche Objekte nennt man Röntgen-Pulsare.
Typische Systeme dieser Art sind Röntgendoppelsterne aus einem Stern, der gerade zu einem Roten Riesen expandiert, und einem Neutronenstern, wobei Material zum Neutronenstern strömt, eine Akkretionsscheibe um ihn herum bildet und schließlich auf seine Oberfläche stürzt. Dabei werden Röntgenleistungen abgestrahlt, die im Bereich des 10.000-fachen der Sonnenleistung liegen.
Magnetare
Eine besondere Klasse bilden Neutronensterne, die mit einer anfänglichen Rotationsperiode unter 10 ms entstehen. In diesem Fall sorgt zusätzlich ein spezieller Dynamoeffekt für eine Konversion der Energie von Konvektionsströmungen im Sterninneren in magnetische Energie. Dabei kann die Flussdichte des Magnetfeldes innerhalb von wenigen Sekunden nach dem Kollaps auf Werte von über 1011 Tesla steigen. Die zugehörige Energiedichte entspräche einer Massendichte im Bereich von vielen kg/cm³. Derartige Objekte werden als Magnetare bezeichnet. Aufgrund des größeren Magnetfeldes werden sie deutlich stärker abgebremst, so dass ihre Rotationsfrequenz bereits nach etwa 1000 Jahren unter 1 Hz sinkt. In dieser Anfangsphase erfahren sie gelegentlich gigantische Röntgenausbrüche. In der Milchstraße sind rund ein Dutzend Kandidaten für solche röntgenaktiven Magnetare bekannt.
Sonstige
- Neben der Neutronenmaterie könnte im Zentrum eines Neutronensterns auch ein Kern aus einem Quark-Gluon-Plasma vorliegen. Ein solches hypothetisches Gebilde wird Quarkstern genannt.
- Röntgenschwache isolierte Neutronensterne
Liste von Beispielen
- RX J1856-3754: Nächster Neutronenstern, keine Mikrowellenstrahlung nachweisbar
- PSR J1915+1606: Neutronendoppelstern
- Lich: Pulsar mit Planeten
- PSR J1623-2631 b: Planet, der den Pulsar PSR J1623-2631 umkreist
- PSR J1921+2153: Erster entdeckter Pulsar
- PSR J1748-2446ad: Pulsar mit der kleinsten bekannten Rotationsdauer
- Scorpius X-1: Hellste Röntgenquelle am Erdhimmel
- Swift J1818.0-1607: Jüngster bislang bekannter Magnetar
Literatur
- Thorsten Dambeck: Die Leuchttürme der Radioastronomen. In: Astronomie heute, Juni 2004, S. 18–23, ISSN 1610-8728
- Jerome Novak: Neutronensterne: Ultradichte Exoten. In: Spektrum der Wissenschaft, März 2004, S. 34–39, ISSN 0170-2971
- Chryssa Kouveliotou, R. C. Duncan, C. Thompson: Magnetare. In: Spektrum der Wissenschaft, Mai 2003, S. 56–63, ISSN 0170-2971
- George Greenstein: Der gefrorene Stern – Pulsare, Schwarze Löcher und das Schicksal des Alls. dtv, 1988, ISBN 3-423-10868-1 (populärwissenschaftliche Darstellung des Themas, inkl. Entdeckungsgeschichte)
- Joachim Herrmann: Das große Lexikon der Astronomie. Orbis, 2001, ISBN 3-572-01286-4
Weblinks
- Sanft statt mit großem Knall. Auf: wissenschaft.de vom 10. Februar 2005. Neutronensterne könnten nicht nur aus Supernovae entstehen, sondern auch direkt aus Weißen Zwergen.
- Eintrag „Neutronenstern“ im „Lexikon der Astronomie“ von Spektrum.de
- scinexx.de: Neutronenstern: bizarre Flüssigkeit im Kern 28. Februar 2011
- scinexx.de: Wie schwer kann ein Neutronenstern werden? 12. Januar 2018
- astronews.com: Die Geburt eines Neutronensterns 28. Juni 2013
- astronews.com: Massengrenze für Neutronensterne 12. April 2016
- astronews.com: Wie groß sind Neutronensterne? 5. Dezember 2017
- astronews.com: Die maximale Masse eines Neutronensterns 16. Januar 2018
Einzelnachweise
- D. Meschede: Gerthsen Physik. 22. Auflage, 2004, S. 630.
- Neutron stars. In: umd.edu. www.astro.umd.edu, abgerufen am 12. Januar 2017.
- Der Wert 3,7 · 1017 kg/m3 ergibt sich aus der Masse 2,68 · 1030 kg und dem Sternradius 12 km; der Wert 5,9 · 1017 kg/m3 ergibt sich aus der Masse 4,2 · 1030 kg und dem Sternradius 11,9 km
- P. Kaaret et al.: Evidence of 1122 Hz X-Ray Burst Oscillations from the Neutron Star X-Ray Transient XTE J1739-285. In: The Astrophysical Journal. 657:L97-L100, 2007 (englisch, iop.org [abgerufen am 18. Februar 2020]).
- Deepto Chakrabarty et al.: The spin distribution of millisecond X-ray pulsars. In: American Institute of Physics Conference Series. Nr. 1068, 2008, S. 67, doi:10.1063/1.3031208, arxiv:0809.4031, bibcode:2008AIPC.1068...67C (englisch).
- Werner Becker: X-Ray Emission from Pulsars and Neutron Stars, in: Werner Becker (Hrsg.): Neutron Stars and Pulsars, 2009, S. 95
- James Chadwick: On the possible existence of a neutron. In: Nature. Band 129, S. 312. (verfasst am 17. Februar 1932, veröffentlicht am 27. Februar 1932)
- Lew Dawidowitsch Landau: On the theory of stars. In: Physikalische Zeitschrift der Sowjetunion. Band 1, Nr. 2, 1932, S. 285–288, (geschrieben im Februar 1931, eingegangen am 7. Januar 1932, veröffentlicht im Februar 1932, auch in: Dirk TerHaar (Hrsg.): Collected papers of L. D. Landau. Pergamon Press, Oxford [u. a.] 1965, S. 60–62): “All stars heavier than 1.5 certainly possess regions in which the laws of quantum mechanics (and therefore of quantum statistics) are violated. […] We expect that this must occur when the density of matter becomes so great that atomic nuclei come in close contact, forming one gigantic nucleus.”
- Walter Baade und Fritz Zwicky: Remarks on Supernovae and Cosmic Rays. Physical Review. Band 46, 1934, S. 76–77
- Julius Robert Oppenheimer und George Michael Volkoff: On massive neutron cores. In: Physical Review. Band 55, 1939, S. 374–381
- Panel Reports: New Worlds, New Horizons in Astronomy and Astrophysics, 2011, S. 233
- B. Knispel et al.: Pulsar Discovery by Global Volunteer Computing, in: Science 329, 5997, (2010) S. 1305
- Roman Wyrzykowski: Parallel Processing and Applied Mathematics, Part I, 2010, S. 487
- Ed van den Heuvel: Formation and evolution of neutron stars in binary systems, in: Altan Baykal, Sinan K. Yerli, Sitki C. Inam, Sergei Grebenev (Hrsg.): The Electromagnetic Spectrum of Neutron Stars, 2006, S. 197
- Ed van den Heuvel: Compact stars and the evolution of binary systems, in: D J Saikia, Virginia Trimble (Hrsg.): Fluid Flows to Black Holes – A Tribute to S Chandrasekhar on His Birth Centenary, 2011, S. 68
- John Antoniadis: Multi-Wavelength Studies of Pulsars and Their Companions, 2015, S. 4
- Wolfgang Demtröder: Experimentalphysik 4 – Kern-, Teilchen- und Astrophysik. 3. Auflage. Springer-Verlag, Dordrecht Heidelberg London New York 2010, ISBN 978-3-642-01597-7, 11. Geburt, Leben und Tod von Sternen, Abschnitt 11.9.
- Chris L. Fryer, Aimee Hungerford: Neutron Star Formation, in: Altan Baykal, Sinan K. Yerli, Sitki C. Inam, Sergei Grebenev (Hrsg.): The Electromagnetic Spectrum of Neutron Stars, 2006, S. 4
- Chris L. Fryer, Aimee Hungerford: Neutron Star Formation, in: Altan Baykal, Sinan K. Yerli, Sitki C. Inam, Sergei Grebenev (Hrsg.): The Electromagnetic Spectrum of Neutron Stars, 2006, S. 6
- Chris L. Fryer, Aimee Hungerford: Neutron Star Formation, in: Altan Baykal, Sinan K. Yerli, Sitki C. Inam, Sergei Grebenev (Hrsg.): The Electromagnetic Spectrum of Neutron Stars, 2006, S. 6
- Searching For Continuous Gravitational Wave Signals With The Hough Transform
- Einstein’s Gravitational Waves May Set Speed Limit For Pulsar Spin
- D. A. Baiko, A. A. Kozhberov. Phonons in a magnetized Coulomb crystal of ions with polarizable electron background. Physics of Plasmas, 2017; 24 (11): 112704
- S. Bonazzola, E. Gourgoulhon: Gravitational waves from neutron stars, in: Jean-Alain Marck, Jean-Pierre Lasota (Hrsg.): Relativistic Gravitation and Gravitational Radiation, 1997, S. 156
- The LIGO Scientific Collaboration, The Virgo Collaboration: Results of the deepest all-sky survey for continuous gravitational waves on LIGO S6 data running on the Einstein@Home volunteer distributed computing project (2016) online
- Nadja Podbregar: Neutronensterne haben Millimeter-Berge. In: scinexx.de. 21. Juli 2021, abgerufen am 21. Juli 2021.
- M.E. Caplan, C. J. Horowitz (2017) Rev. Mod. Phys. 89, 041002
- Gordon Baym: Ultrarelativistic heavy ion collisions: the first billion seconds, S. 7, arxiv:1701.03972
- Edward Shuryak: Heavy Ion Collisions: Achievements and Challenges, S. 52, arxiv:1412.8393v2
- Luciano Rezzolla, Elias R. Most, Lukas R. Weih: Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. (PDF) In: The Astrophysical Journal Letters, Volume 852, Number 2. 3. Januar 2018, abgerufen am 13. Januar 2018. doi:10.3847/2041-8213/aaa401, arxiv:1711.00314v2
- Wie schwer kann ein Neutronenstern werden? – Astronomen errechnen Massen-Obergrenze für exotische Sternenreste. scinexx, 12. Januar 2018, abgerufen am 13. Januar 2018.
- Werner Becker: X-Ray Emission from Pulsars and Neutron Stars, in: Werner Becker (Hrsg.): Neutron Stars and Pulsars, 2009, S. 101
- Panel Reports: New Worlds, New Horizons in Astronomy and Astrophysics, 2011, S. 231