Vorzeichen (Zahl)

Ein Vorzeichen oder Signum (von lateinisch signum Zeichen) ist ein Zeichen, das einer reellen Zahl vorangestellt wird, um sie als positiv oder negativ auszuweisen. Eine negative Zahl wird immer mit dem Minuszeichen versehen, während einer positiven Zahl ein Pluszeichen optional vorangestellt werden kann. Die Zahl Null wird meist als vorzeichenlos angesehen, bei der Zahldarstellung im Computer wird jedoch manchmal auch eine vorzeichenbehaftete Null verwendet.

−

+

Streng genommen muss das Vorzeichen, das immer unär ist, vom mathematischen Operator für Addition (binäres Plus) oder Subtraktion (binäres Minus) und vom Inversionsoperator der Addition (unäres Minus) unterschieden werden. Letzteres kommt dem Vorzeichen einer Zahlkonstanten noch am nächsten. Es gibt aber Programmiersprachen, die ein separates Sonderzeichen zur Kenntlichmachung negativer Zahlkonstanten kennen, beispielsweise APL.[1]

Für das Vorzeichen gerichteter Größen, wie beispielsweise Drehwinkel und Richtungen, gibt es oft unterschiedliche Vorzeichenkonventionen.

Plus- und Minuszeichen

In der Arithmetik wird das Vorzeichen einer Zahl (genauer: einer reellen Zahlkonstanten) durch ein vorangestelltes Plus- oder ein Minuszeichen angezeigt. Hierbei werden dieselben Zeichen verwendet wie für die Addition und die Subtraktion zweier Zahlen. Das Vorzeichen wird dabei ohne Leerraum direkt an die erste Ziffer angeschlossen. Beispielsweise bezeichnen

+3

und

-3

jeweils die positive und die negative Zahl(konstante) Drei. Wird kein Vorzeichen angegeben, wird die Zahlkonstante als nicht-negativ angesehen. In der Algebra wird das Minuszeichen auch als unäres Minus zur „Vorzeichenumkehr“ verwendet, wodurch die jeweilige Gegenzahl (einer Zahlkonstanten oder einer -variablen) erhalten wird. Beispielsweise gilt

-(-x)=x

für alle $x$ in einer additiven Gruppe. Letztere muss dazu nicht angeordnet sein. Und wenn es eine angeordnete Gruppe ist, wird nichts über das Vorzeichen der Variablen $x$ ausgesagt.

Durch die Betragsfunktion wird das Vorzeichen einer negativen Zahl umgekehrt, während eine positive Zahl unverändert bleibt. Zum Beispiel sind

|{-3}|=+3

und

|{+3}|=+3

und

|{-x}|=|{+x}|

.

Ein Plusminuszeichen $\pm 3$ (oder das Minuspluszeichen $\mp 3$ ) wird einer Zahl vorangestellt, wenn die Aussage für beide Versionen (Plus und Minus) gelten soll. Kommt es in einer Gleichung vor einer Zahl (variabel oder konstant) mehr als einmal vor, bedeutet dies, dass überall entweder das obere Zeichen oder überall das untere Zeichen zu wählen ist. Im Beispiel

\cos(x\pm y)=\cos y\;\cos x\mp \sin x\;\sin y

,

das zwei Gleichungen in einer Aufschreibung zusammenfasst, ist entweder (zuerst + dann −) oder (zuerst − dann +) zu nehmen.

Vorzeichen der Null

Die Zahl Null ist weder positiv noch negativ und hat demnach kein Vorzeichen. Die Gegenzahl der Zahl Null ist die Null selbst. Somit bezeichnen

+0

und

-0

die gleiche Zahl Null. Bei Maschinenzahlen werden jedoch die positive und die negative Null manchmal als zwei verschiedene Zahlen angesehen. Beispiele sind das Einerkomplement ganzer Zahlen oder der IEEE 754-Standard für Gleitkommazahlen. In manchen Anwendungen ist auch die Notation $-0$ gebräuchlich, wenn eine negative Zahl auf Null gerundet wurde. In der Analysis wird die Schreibweise

\lim _{x\to 0+}

oder

\lim _{x\to 0{-}}

bei der Bildung eines rechtsseitigen oder linksseitigen Grenzwerts verwendet.

Vorzeichenfunktion

Die Vorzeichenfunktion

\operatorname {sgn}

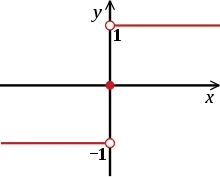
Mit Hilfe der Vorzeichenfunktion oder Signumfunktion kann das Vorzeichen einer (reellen) Zahlvariablen $x$ ermittelt werden. Die Vorzeichenfunktion ist üblicherweise durch

\operatorname {sgn}(x)={\begin{cases}-1&{\text{falls }}x<0,\\~~\,0&{\text{falls }}x=0,\\~~\,1&{\text{falls }}x>0.\end{cases}}

definiert. Demnach ist $\operatorname {sgn}(x)=1$ , falls die Zahl $x$ positiv ist und $\operatorname {sgn}(x)=-1$ , falls sie negativ ist. Ist $x\neq 0$ , dann kann die Signumfunktion auch mit Hilfe der Betragsfunktion durch

\operatorname {sgn}(x)={\frac {x}{|x|}}

definiert werden.

Vorzeichenkonventionen

Für viele gerichtete Größen erfolgt die Zuordnung eines Vorzeichens, das heißt welche Werte als positiv und welche als negativ angesehen werden, auf natürliche Weise. In manchen Fällen ist jedoch die Wahl des Vorzeichens willkürlich und wird höchstens aus Konsistenzgründen einheitlich gewählt. In diesen Fällen spricht man von einer Vorzeichenkonvention.

Vorzeichen von Winkeln

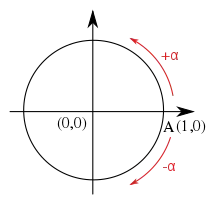
Winkel gegen den Uhrzeigersinn werden als positiv und Winkel im Uhrzeigersinn als negativ angesehen.

Ein gerichteter Winkel besitzt, im Gegensatz zu einem ungerichteten Winkel, eine Orientierung, die über ein Vorzeichen vor der Größe des Winkels angegeben wird. Insbesondere gibt bei einem Drehwinkel das Vorzeichen an, ob die Drehung im oder gegen den Uhrzeigersinn erfolgt. Auch wenn hierfür verschiedene Konventionen verwendet werden, ist es in der Mathematik üblich, Drehungen gegen den Uhrzeigersinn als positiv anzusehen und Drehungen im Uhrzeigersinn als negativ.

Es ist auch möglich, einer Drehung in drei Dimensionen ein Vorzeichen zuzuordnen, sofern die Rotationsachse eine Orientierung besitzt. Nach der Rechte-Hand-Regel wird eine Drehung um eine orientierte Achse entgegen dem Uhrzeigersinn in einem Rechtssystem als positiv und in einem Linkssystem als negativ angesehen.

Vorzeichen von Änderungen

Verändert sich eine Größe $x$ über die Zeit, dann ist die Größenänderung $\Delta x$ typischerweise definiert als

\Delta x=x_{\text{ende}}-x_{\text{start}}

.

Mit dieser Konvention entspricht ein Anwachsen von $x$ einer positiven Änderung, während eine Verringerung von $x$ einer negativen Änderung entspricht. In der Analysis wird dieselbe Konvention bei der Definition der Ableitung verwendet. Als Folge besitzt eine monoton wachsende differenzierbare Funktion eine positive Ableitung, während eine monoton fallende Funktion eine negative Ableitung besitzt.

Vorzeichen von Richtungen

In der analytischen Geometrie und in der Physik werden oft bestimmte Richtungen als positiv oder negativ ausgezeichnet. Als grundlegendes Beispiel wird die Zahlengerade üblicherweise mit den positiven Zahlen auf der rechten und den negativen Zahlen auf der linken Seite gezeichnet:

Daher werden im Kontext gleichförmiger Bewegungen Verschiebungs- oder Geschwindigkeitsvektoren, die nach rechts zeigen, üblicherweise als positiv angesehen, während ein Vektor, der nach links zeigt, als negativ angesehen wird.

In einem kartesischen Koordinatensystem werden die Richtungen nach rechts und oben üblicherweise als positiv angesehen, wobei die Richtung nach rechts der positiven x-Achse und die Richtung nach oben der positiven y-Achse entspricht. Wird ein Verschiebungs- oder Geschwindigkeitsvektor in seine Komponenten zerlegt, dann wird der vertikale Anteil für eine Bewegung nach oben positiv und für eine Bewegung nach unten negativ sein. In geodätischen Koordinatensystemen sind allerdings x- und y-Achse vertauscht. Beim dreidimensionalen Koordinatensystem wird nach „linkshändigen“ und „rechtshändigen“ Definitionen unterschieden, die unterschiedlichen Vorzeichenkonventionen der Drehrichtung entsprechen.

Vorzeichen physikalischer Größen

Auch die elektrische Ladung ist mit einem Vorzeichen versehen, wobei die Ladung von Elektronen als negativ definiert ist. Dem entspricht die Konvention der „technischen Stromrichtung“ als Bewegungsrichtung (oft nur gedachter) positiver Ladungsträger.

Siehe auch

Literatur

Heinz-Dieter Ebbinghaus et al.: Zahlen. Springer, Berlin 1992, ISBN 3-540-55654-0.

Bemerkungen

Dies macht eine Einklammerung der negativen Zahlkonstanten überflüssig.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Dies macht eine Einklammerung der negativen Zahlkonstanten überflüssig.