Energieerhaltungssatz

Der Energieerhaltungssatz drückt die Erfahrungstatsache aus, dass die Energie eine Erhaltungsgröße ist, dass also die Gesamtenergie eines abgeschlossenen Systems sich nicht mit der Zeit ändert. Energie kann zwischen verschiedenen Energieformen umgewandelt werden, beispielsweise von Bewegungsenergie in Wärmeenergie. Außerdem kann sie aus einem System heraus oder in ein System hinein transportiert werden, es ist jedoch nicht möglich, Energie zu erzeugen oder zu vernichten. Die Energieerhaltung gilt als wichtiges Prinzip aller Naturwissenschaften.[1]

Der Energieerhaltungssatz lässt sich theoretisch mit Hilfe des Noether-Theorems aus der Annahme ableiten, dass die für das System gültigen Gesetze der Physik nicht von der Zeit abhängen.

Umgangssprache

Im physikalischen Sinne des Energieerhaltungssatzes ist ein „Verlust“ von Energie nicht möglich. Trotzdem wird umgangssprachlich von „Energieverbrauch“, „Energieverschwendung“, „Energiesparen“ und „Energieverlust“ gesprochen. Dies ist vertretbar, denn die Erde ist kein abgeschlossenes System und außerdem können der Mensch und andere Lebewesen Energie nur in bestimmten Formen nutzen; die genannten Begriffe beschreiben den Übergang von Energie aus technisch leicht nutzbaren oder biologisch nutzbaren Energieformen (Exergie) in schlechter oder nicht nutzbare Formen (Anergie). Ebenso unmöglich ist es, Energie zu erzeugen. Mit der umgangssprachlichen „Energieerzeugung“ ist vielmehr die Umwandlung vorhandener Energie in eine für den Menschen nutzbare Form, meist elektrische Energie, gemeint.

Bei den meisten heute gebräuchlichen Arten von Energieumwandlung werden Energieträger mit einer geringen oder spezifischen Entropie in Formen mit höherer Entropie umgewandelt. Ein Kraftfahrzeug wandelt beispielsweise chemische Energie, die ursprünglich aus Erdöl oder Rapsöl stammt, in kinetische Energie und thermische Energie um. Da Erdöl nicht regenerierbar ist, kann dies als Energieverlust in dem Sinne gesehen werden, dass diese spezielle Form chemischer Energie mit niedriger Entropie für zukünftige Generationen oder für andere Zwecke verloren geht.

Bei jeder der Umwandlungsarten, die heute gebräuchlich sind, wird nur ein Teil der im Energieträger vorhandenen Energie in nutzbare Energie umgewandelt. Von Energiesparen spricht man daher, wenn sich der Wirkungsgrad des Energieumwandlungsprozesses oder eines Gerätes durch technischen Fortschritt erhöht, sodass weniger Rohstoff mehr nutzbare Energie liefert oder der jeweilige Zweck mit weniger Energie erzielt wird.

Geschichte

Soweit heute bekannt ist, wurde der Energieerhaltungssatz zuerst vom Heilbronner Arzt Julius Robert von Mayer (1814–1878) formuliert. Im Jahr 1842 wies er durch entsprechende Versuche nach, dass eine bestimmte Bewegungsenergie bei vollständiger Umwandlung in Wärme stets die gleiche Wärmemenge ergibt. Er bestimmte zudem den Wert dieses „mechanischen Wärmeäquivalents“. Unabhängig von Mayer taten dies auch 1843 James Prescott Joule – dessen Arbeiten damals weit bekannter waren – und weitere Physiker und Ingenieure wie Ludwig August Colding in Dänemark (ebenfalls 1843). Endgültig ausformuliert wurde der Energieerhaltungssatz 1847 von Hermann von Helmholtz. Er berichtete in Berlin am 23. Juli 1847 über die „Konstanz der Kraft“ und untermauerte den Energieerhaltungssatz.[2]

Als weitere Wissenschaftler, die im 19. Jahrhundert mehr oder weniger allgemein einen Energieerhaltungssatz formulierten, führt Stephen Brush[3] auf: Karl Friedrich Mohr, Sadi Carnot, Marc Seguin, Karl Holtzmann, Gustav Adolphe Hirn, William Robert Grove, Justus von Liebig, Michael Faraday.

Der Energieerhaltungssatz ist in der Geschichte der Physik nicht immer unumstritten gewesen. Das berühmteste Beispiel ist Niels Bohr, der bei mehreren Gelegenheiten nur eine statistische (gemittelte) Erhaltung der Energie bei Quantenprozessen befürwortete, so in der sogenannten BKS-Theorie 1924 mit John C. Slater und Hendrik Anthony Kramers.[4] Diese sollte die ältere Quantentheorie mit der klassischen elektromagnetischen Feldvorstellung in Einklang bringen. Wenig später wurde diese Theorie durch Experimente von Compton und auch Hans Geiger und Walther Bothe widerlegt und die Gültigkeit des Energieerhaltungssatzes auch auf Quantenebene bestätigt. Auch später versuchte Bohr, manche zunächst rätselhaften Quantenphänomene mit einer nur statistischen Gültigkeit des Energieerhaltungssatzes zu erklären, so beim Betazerfall; die dort „fehlende“ Energie der beobachteten Zerfallsprodukte wurde jedoch von Wolfgang Pauli durch das Postulat eines neuen, nur schwach wechselwirkenden Teilchens, des Neutrinos, erklärt.

Heute gilt der Energieerhaltungssatz als etabliert und wird sogar häufig zur Definition der Energie herangezogen.

Anwendungsgebiete

Energieerhaltungssatz in der Newtonschen Mechanik

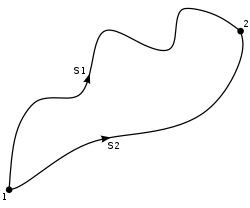
Zwei beliebige Wege in einem konservativen Kraftfeld

Bei der Bewegung einer Punktmasse in einem konservativen Kraftfeld bleibt die Summe von kinetischer Energie $T$ und potentieller Energie $V,$ die Gesamtenergie $E=T+V,$ erhalten. Dabei ist die Kraft der negative Gradient der potentiellen Energie (oftmals im Jargon auch einfach als Potential bezeichnet)

\mathbf {F} =-\nabla V

.

Bewegt sich eine Punktmasse mit der Zeit $t$ in solch einem Kraftfeld auf beliebigen Wegen $\mathbf {x} (t)$ von einem Startpunkt zu einem Ziel, so ist für die Arbeit, die dabei an der Punktmasse verrichtet wird, der Weg unerheblich. Unabhängig vom Weg ist die verrichtete Arbeit die Differenz der potentiellen Energien an Start und Ziel.

Für eine Punktmasse mit konstanter Masse $m$ in einem Potential $V$ gelten die Newtonschen Bewegungsgleichungen in der folgenden Form:

m{\ddot {\mathbf {x} }}=\mathbf {F} =-\nabla V

Das Skalarprodukt mit der Geschwindigkeit ${\dot {\mathbf {x} }}(t)$ liefert auf der linken Seite der Gleichung:

m{\ddot {\mathbf {x} }}\cdot {\dot {\mathbf {x} }}={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {m}{2}}{\dot {\mathbf {x} }}\cdot {\dot {\mathbf {x} }}\right)={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {m}{2}}|{\dot {\mathbf {x} }}|^{2}\right)={\dot {T}}

Hier ist ${\dot {T}}$ die zeitlich abgeleitete kinetische Energie, die durch die von der Kraft an der Punktmasse verrichtete Arbeit verändert wird. Unter Heranziehung der Kettenregel ergibt sich auf der rechten Seite:

{\begin{aligned}\mathbf {F} \cdot {\dot {\mathbf {x} }}(t)&=-\nabla V(\mathbf {x} )\cdot {\dot {\mathbf {x} }}(t)\\&=-\sum _{i=1}^{3}{\frac {\partial V(\mathbf {x} )}{\partial x_{i}}}\cdot {\frac {\mathrm {d} x_{i}(t)}{\mathrm {d} t}}\\&=-{\frac {\mathrm {d} }{\mathrm {d} t}}V(\mathbf {x} (t))=-{\dot {V}}\end{aligned}}

Eine Integration über die Zeit liefert nun die benötigte Arbeit entlang einer beliebigen (stückweise stetig differenzierbaren) physikalischen Bahn mit der jeweiligen potentiellen Energie $V_{1}$ am Start und $V_{2}$ am Ziel:

{\begin{aligned}\int _{t_{1}}^{t_{2}}m{\ddot {\mathbf {x} }}(t)\cdot {\dot {\mathbf {x} }}(t)\;\mathrm {d} t&=\int _{t_{1}}^{t_{2}}{\dot {T}}\,\mathrm {d} t=T_{2}-T_{1}\\=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\dot {\mathbf {x} }}(t)\ \mathrm {d} t&=-\int _{t_{1}}^{t_{2}}{\dot {V}}\ \mathrm {d} t=-\int _{V_{1}}^{V_{2}}\mathrm {d} V=-V_{2}+V_{1}\\\rightarrow \quad T_{2}-T_{1}&=-V_{2}+V_{1}\end{aligned}}

Ordnet man die Terme um, so erhält man:

T_{1}+V_{1}=T_{2}+V_{2}

Die Summe aus kinetischer und potentieller Energie ist nach einer Verschiebung der Punktmasse noch dieselbe. Dies ist der Energieerhaltungssatz für Punktmassen.

Kann, beispielsweise bei einem Pendel, die Reibung vernachlässigt werden, so ändert sich die Summe von potentieller und kinetischer Energie nicht mit der Zeit. Lenkt man das Pendel aus, so schwingt es zwischen zwei Umkehrpunkten und erreicht seine höchste Geschwindigkeit am Ort des Potentialminimums. An den Umkehrpunkten ist die kinetische Energie null und die potentielle Energie maximal. Unabhängig von der Position des Pendels hat die Summe aus kinetischer und potentieller Energie den durch die anfängliche Auslenkung vorgegebenen Wert.

Eine auf einen realen Körper wirkende Kraft führt nicht nur zu einer Beschleunigung seines Schwerpunkts, sondern auch zu einer mehr oder weniger ausgeprägten Deformation. In der Hyperelastizität gibt es ein Potential, die Formänderungsenergie $W$ , deren Zeitableitung die Verformungsleistung $L$ ist:

L:={\dot {W}}

Verformungsarbeit wird also vollständig und dissipationslos in Formänderungsenergie umgesetzt und das wegunabhängig. Die geleistete Verformungsarbeit ist immer die Differenz der Formänderungsenergie am Start und Ziel. Die Leistung der an einen hyperelastischen Körper von außen angreifenden Kräfte teilt sich auf in eine Beschleunigung (auch eine Winkelbeschleunigung, die ebenfalls zur kinetischen Energie beiträgt) und eine (reversible) Verformung:

{\begin{aligned}-\int _{t_{1}}^{t_{2}}{\dot {V}}\ \mathrm {d} t=&\int _{t_{1}}^{t_{2}}{\dot {T}}\ \mathrm {d} t+\int _{t_{1}}^{t_{2}}{\dot {W}}\ \mathrm {d} t\\\rightarrow \quad -V_{2}+V_{1}=&\ T_{2}-T_{1}+W_{2}-W_{1}\end{aligned}}

In diesem System ist die Summe aus kinetischer, potentieller und Formänderungsenergie über die Zeit konstant:

T_{1}+V_{1}+W_{1}=T_{2}+V_{2}+W_{2}

Das ist der Erhaltungssatz für die mechanische Energie deformierbarer, hyperelastischer Körper in einem konservativen Kraftfeld.

Energieerhaltungssatz in der Thermodynamik

Jedes thermodynamische System verfügt über einen bestimmten „Vorrat“ an Energie. Dieser setzt sich aus einem äußeren Anteil $E_{\text{a}}$ und einem inneren Anteil $E_{\text{i}}$ (innere Energie) zusammen. Die Summe aus beiden Anteilen ergibt die Gesamtenergie eines thermodynamischen Systems, wobei man in der chemischen Thermodynamik die Änderung des äußeren Anteils gleich null setzt ( $\mathrm {d} E_{\mathrm {a} }=0$ ). Unter dieser Voraussetzung gelangt man zum ersten Hauptsatz der Thermodynamik:

„Die innere Energie ist eine Eigenschaft der stofflichen Bestandteile eines Systems und kann nicht erzeugt oder vernichtet werden. Die innere Energie ist eine Zustandsgröße.“

Für abgeschlossene Systeme gilt daher, dass die innere Energie konstant und demzufolge ihre Änderung gleich null ist. Für geschlossene Systeme lautet der erste Hauptsatz der Thermodynamik:

\mathrm {d} U=\delta Q+\delta W

mit der inneren Energie $U$ , der Wärme $Q$ und der Arbeit $W$ .

Energieerhaltungssatz in der Elektrodynamik

Elektromagnetische Felder sind oft nur ein Teilsystem, das an andere Systeme, zum Beispiel geladene Teilchen mit einer gewissen Ladung, Masse und Geschwindigkeit, gekoppelt ist. Die Energiebilanz in der Elektrodynamik, also der Energiestrom in Feldern und der Austausch mit anderen Teilsystemen, wird durch den Satz von Poynting beschrieben.

Energieerhaltungssatz in der Relativitätstheorie

Ein Körper der Masse $m$ , der sich mit der Geschwindigkeit $v$ bewegt, hat in der speziellen Relativitätstheorie die Energie

E(v)={\frac {m\ c^{2}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}

,

wobei $c$ die Lichtgeschwindigkeit ist. In Ruhe hat er die Ruheenergie

E_{\text{Ruhe}}=m\ c^{2}

.

Für kleine Geschwindigkeiten ( $v\ll c$ , Taylorentwicklung in $\left({\frac {v}{c}}\right)^{2}$ ) ist die Energie näherungsweise gleich der Summe aus der Ruheenergie und der kinetischen Energie nach der Newtonschen Mechanik

E\approx m\ c^{2}+{\frac {1}{2}}\ m\ v^{2}

.

Bei hochenergetischen Teilchen ist diese Näherung messbar falsch. Nur die Summe der relativistischen Energien bleibt in Teilchenreaktionen erhalten.

Die Betrachtung des Universums mit Mitteln der allgemeinen Relativitätstheorie zeigt, dass der Energieerhaltungssatz auf das Universum als Ganzes nicht anwendbar ist. Insbesondere kann die Gravitationsenergie nicht immer eindeutig in einer Weise definiert werden, die für das Universum als Ganzes gilt. Die Gesamtenergie des Weltalls bleibt demnach weder erhalten noch geht sie verloren – sie ist nicht definierbar.[5]

Energieerhaltungssatz in der Quantenmechanik

Die Energie eines quantenmechanischen Zustands bleibt erhalten, wenn der Hamiltonoperator nicht von der Zeit abhängt. Quantenmechanische Zustände, die sich mit der Zeit messbar ändern, sind keine Energieeigenzustände; in ihnen bleibt aber zumindest der Erwartungswert der Energie erhalten.

Energiebilanz

Kann ein System Energie mit einem anderen System austauschen, beispielsweise durch Strahlung oder Wärmeleitung, dann spricht man von einem energetisch offenen System. Statt Energieerhaltung gilt dann die Energiebilanz: Die Energie, die in ein System hineinfließt, minus der Energie, die es verlässt, ist die Änderung der Energie des Systems und muss durch die Umgebung bereitgestellt oder von ihr aufgenommen werden. Durch Betrachtung der Energieströme im System oder zwischen dem System und seiner Umgebung kann man auf Abläufe innerhalb des Systems schließen, auch wenn sie selbst nicht beobachtet werden können.

Die Energie eines Systems lässt sich nicht direkt messen: Wenn man von der Äquivalenz von Masse und Energie absieht, so wirken sich nur Energieunterschiede messbar aus.

Die Energiebilanz besagt genauer: Um die Energie eines offenen Systems zu ändern, muss von dessen Umgebung Arbeit am System verrichtet oder Wärme übertragen werden. Bezogen auf ein Zeitintervall heißt das: Die zeitliche Änderung der Gesamtenergie eines offenen Systems ist gleich der Leistung (einschließlich Wärmeleistung), die von seiner Umgebung in das System eingebracht oder entnommen wird. Der Energieerhaltungssatz ist der Spezialfall der Energiebilanz, bei dem diese Arbeiten oder Leistungen der Umgebung verschwinden und damit der Energieinhalt des nun abgeschlossenen Systems unverändert bleibt.

Als Wechselwirkungen mit der Umgebung kommen unter anderem in Frage:

In der Mechanik: Kräfte wie die Reib- und Normalkraft bei Kontakt oder Fernkräfte wie die Gravitations- und Lorentzkraft.
In der Thermodynamik: Wärmeübertragung beispielsweise durch Strahlung oder Wärmeleitung.
In der Elektrodynamik: siehe Elektrische Arbeit und Elektrische Leistung.

Noether-Theorem

In der Lagrangeschen Mechanik ergibt sich Energieerhaltung aus dem Noether-Theorem, wenn die Wirkung unter zeitlichen Verschiebungen invariant ist.

Literatur

Max Planck: Das Princip der Erhaltung der Energie. B. G. Teubner, Leipzig 1887, S. 1–247 (archive.org [PDF; 14,0 MB]).

Einzelnachweise

Siehe z. B. Feynman Vorlesungen über Physik. 2. Band: Elektromagnetismus und Struktur der Materie. 3. Auflage, 2001, S. 147, 162, 198.
Hermann von Helmholtz. (Memento des Originals vom 21. Januar 2012 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 In: Potsdam-Wiki.de. Abgerufen am 23. Juli 2011.
Stephen Brush, Kinetic Theory, Pergamon Press, Band 1, 1966, S. 20
Bohr, Kramers, Slater: The quantum theory of radiation. In: Philosophical Magazine. Bd. 47, 1924, S. 785–802. Deutsch in: Zeitschr. für Physik. Bd. 24, 1924, S. 69–87.
T. M. Davis: Verliert das Universum Energie? In: Spektrum der Wissenschaft. November 2010, ISSN 0170-2971, S. 23–29.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Siehe z. B. Feynman Vorlesungen über Physik. 2. Band: Elektromagnetismus und Struktur der Materie. 3. Auflage, 2001, S. 147, 162, 198.

[2] Hermann von Helmholtz. (Memento des Originals vom 21. Januar 2012 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 In: Potsdam-Wiki.de. Abgerufen am 23. Juli 2011.

[3] Stephen Brush, Kinetic Theory, Pergamon Press, Band 1, 1966, S. 20

[4] Bohr, Kramers, Slater: The quantum theory of radiation. In: Philosophical Magazine. Bd. 47, 1924, S. 785–802. Deutsch in: Zeitschr. für Physik. Bd. 24, 1924, S. 69–87.

[5] T. M. Davis: Verliert das Universum Energie? In: Spektrum der Wissenschaft. November 2010, ISSN 0170-2971, S. 23–29.