Thermodynamisches System

Ein thermodynamisches System ist ein räumlich abgrenzbares Objekt mit physikalischen Eigenschaften, die sich durch die Gesetze der Thermodynamik beschreiben lassen. Es muss gegenüber seiner Umgebung abgegrenzt, aber nicht isoliert sein. Was zu ihm hinzuzurechnen ist, muss aufgrund der Definition eindeutig und klar feststellbar sein.[1] Die Festlegung der Begrenzungsflächen zur Umgebung, auch Systemgrenzen genannt, ist willkürlich; eine geschickte Wahl der Systemgrenzen kann die Lösung einer thermodynamischen Aufgabe erheblich vereinfachen.[2]

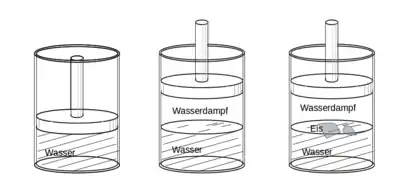
Ein Beispiel für ein thermodynamisches System ist ein Stück Eis, das auf Wasser schwimmt. Auch eine Menge Meerwasser in einem Becherglas kann als ein thermodynamisches System betrachtet werden (das in dem Meerwasser gelöste Salz ist dagegen kein thermodynamisches System). Weitere Beispiele für thermodynamische Systeme sind der Inhalt einer verschlossenen Flasche Mineralwasser, der Inhalt einer Thermoskanne, die Luft im Kolben einer Luftpumpe oder das Gemisch im Brennraum eines Ofens oder eines Verbrennungsmotors.[1][3][4]

Ein thermodynamisches System braucht gegenüber seiner Umgebung nicht isoliert zu sein. So kann das auf dem Wasser schwimmende Stück Eis sowohl Wassermoleküle und Energie an seine Umgebung aus Wasser und Luft abgeben, als auch aus ihr aufnehmen. Ein System, das sowohl Materie als auch Energie mit seiner Umgebung austauschen kann, nennt man offen; ein System, das Energie aber keine Materie mit seiner Umgebung austauschen kann, wird als geschlossen bezeichnet; und ein System, das weder Energie noch Materie austauschen kann, wird abgeschlossen oder isoliert genannt. Bei den obigen Beispielen sind das Stück Eis und das Meerwasser im Becherglas offene Systeme, die geschlossene Mineralwasserflasche ein geschlossenes System und der Inhalt der Isolierkanne näherungsweise ein isoliertes System.[3]

Die verschiedenen Gleichgewichtszustände thermodynamischer Systeme und die Energie- und Stoffumwandlungen beim Wechsel von einem Gleichgewichtszustand in einen anderen sind der Gegenstand der Thermodynamik.[4]

Allgemeines

Beispiel für ein thermodynamisches System bestehend aus Wasser (ein Reinstoff) in drei verschiedenen Gleichgewichtszuständen

Thermodynamische Systeme wurden zuerst bei der Suche nach einer optimalen Wärmekraftmaschine betrachtet. Nicolas Léonard Sadi Carnot nannte sie „substance employée“ und „substance mise en œuvre“ in seiner berühmten Arbeit von 1824.[5] Rudolf Clausius schrieb 1850[6] von einem „wirksamen Körper“, und Josiah Willard Gibbs benutzte in seiner Analyse heterogener Systeme[7] den Begriff „material system“. Gegen Ende des 19. Jahrhunderts etablierte sich der Begriff „thermodynamisches System“.

Ein thermodynamisches System ist ein physikalisches Objekt, das sich im Rahmen der Thermodynamik durch ein mathematisches Modell beschreiben lässt. Die Postulate der Thermodynamik und spezifische Materialkonstanten erlauben Rückschlüsse von diesem Modell auf physikalische und chemische Eigenschaften des Systems für verschiedene Umgebungsbedingungen und bei Einwirkungen von außen.

Darüber hinaus werden in einigen Gedankenexperimenten hypothetische thermodynamische Systeme betrachtet; etwa Systeme mit Trennwänden, die nur bestimmte Atome oder Moleküle passieren lassen, obwohl solch selektive Trennwände nicht für jedes beliebige Molekül bekannt sind. In Gedankenexperimenten zur Hohlraumstrahlung werden Behälter mit ideal spiegelnden Innenwänden benutzt. Sie enthalten keine Materie, sondern nur elektromagnetische Felder. Mit einem solchen, geschickt ausgedachten, hypothetischen „Spiegelkasten“ als thermodynamisches System konnte Willy Wien 1893 das Verschiebungsgesetz für die Hohlraumstrahlung theoretisch begründen.[8]

Gleichgewicht und Zustandsgrößen

Ein thermodynamisches System befindet sich im Gleichgewicht, wenn sich die unmittelbar feststellbaren Eigenschaften und weitere aus Vortheorien bekannte messbare Größen – wie Entfernungen, Massenwerte, Kräfte – zeitlich nicht ändern; mit Vortheorien sind meist die Mechanik und die Elektrodynamik gemeint.[A 1] Die Theorie der Gleichgewichtszustände thermodynamischer Systeme wird Thermostatik genannt.[1]

Im mathematischen Modell eines thermodynamischen Systems werden einige Teile des Systems durch idealisierte Nebenbedingungen ersetzt. Die Systemgrenzen werden etwa als idealisierte Randflächen angesehen; Größe und Form sind von außen vorgegebene Bedingungen. Diese idealisierten Nebenbedingungen werden durch einen oder wenige Parameter im Modell berücksichtigt.[1] Diese Parameter werden Arbeitskoordinaten[4][9] oder äußere Zustandsgrößen[2][A 2] genannt. Bei Systemen in einem einzigen Behälter gibt es oft nur eine Arbeitskoordinate, nämlich das Volumen des Behälters. Bei Objekten, wie einem Wassertropfen, bei welchen die Oberflächenspannung eine Rolle spielt, ist auch die Größe der Oberfläche eine Arbeitskoordinate.[10][11] Befindet sich das System etwa in einem homogenen äußeren magnetischen Feld, dann ist das magnetische Dipolmoment des gesamten Systems eine weitere Arbeitskoordinate.

Die Menge der möglichen Gleichgewichtszustände eines thermodynamischen Systems entspricht im mathematischen Bild einem Gebiet in einem endlich dimensionalen reellen Vektorraum $\mathbb {R} ^{n}$ , es ist der Zustandsraum der Gleichgewichtszustände $Z_{g}$ . Die Arbeitskoordinaten können als Koordinaten zur Angabe eines Zustandes benutzt werden, aber sie reichen alleine nicht aus, um einen Gleichgewichtszustand eines thermodynamischen Systems eindeutig festzulegen. Hierfür müssen noch zusätzlich die Werte von inneren Zustandsgrößen (wie zum Beispiel die innere Energie oder die Temperatur) angegeben werden.[12]

Einfache thermodynamische Systeme

Thermodynamische Systeme werden einfache thermodynamische Systeme genannt, wenn ihre Gleichgewichtszustände durch einen Satz von Arbeitskoordinaten, die Stoffmengen der einzelnen chemischen Komponenten und die Angabe einer einzigen weiteren inneren Zustandsgröße wie etwa die innere Energie eindeutig bestimmt sind.[12][13][14] Nach Lieb und Yngvason sind die einfachen thermodynamischen Systeme die Bausteine der Thermodynamik.

Beispiele für einfache thermodynamische Systeme sind:[13]

Ein Mol Wasser in einem Kolben (eine Arbeitskoordinate)
Ein halbes Mol Sauerstoff in einem Kolben in einem homogenen Magnetfeld (zwei Arbeitskoordinaten: Volumen und Magnetisierung)
Die Systeme der Beispiele 1 und 2 durch eine wärmeleitenden Kupferdraht verbunden (drei Arbeitskoordinaten)

Ein Beispiel für ein nicht einfaches thermodynamisches System ist ein Gesamtsystem bestehend aus zwei voneinander isolierten einfachen Systemen. Auch sind Systeme mit ferromagnetischem Material in einem Magnetfeld wegen ihrer Hysterese keine einfachen thermodynamischen Systeme.

Diese Definition eines einfachen Systems findet sich in der grundlegenden Arbeit von Carathéodory.[14] Die meisten der in Lehrbüchern und in der technischen Thermodynamik betrachteten Systeme sind einfache thermodynamische Systeme. Allerdings benutzen manche Lehrbücher den Begriff einfache Systeme nur für solche mit deutlich weiteren Einschränkungen; Callen etwa nutzt den Begriff simple systems nur für makroskopisch homogene, isotrope und ungeladene Systeme bei denen Oberflächeneffekte, elektromagnetische Felder und das Gravitationsfeld keine Rolle spielen.[15] Ein kleiner Wassertropfen etwa ist nach Carathéodory ein einfaches System, aber nicht mehr bei H. Callen wegen der zu berücksichtigenden Oberflächenspannung. Die Einschränkung von Callen hat den Vorteil, dass bei bekannter chemischer Zusammensetzung die Gleichgewichtszustände solcher geschlossenen einfachen Systeme allein durch zwei unabhängige thermodynamische Zustandsvariablen, etwa Druck und Volumen, bestimmt sind.[16]

Skalierbarkeit

Für eine Skalierung eines thermodynamischen Systems definiert man: werden alle geometrischen Abmessungen, also alle Abstände, mit einem Faktor $\lambda ^{1/3}$ und alle Stoffmengen mit einem Faktor $\lambda$ multipliziert, so werden die Zustandsgrößen, die sich dabei um einen Faktor $\lambda$ verändern, extensiv und solche, die sich dabei nicht ändern, intensiv genannt. Nach Ludwig sollten die Arbeitskoordinaten extensive Zustandsgrößen sein. Die innere Energie und die Entropie sind ebenfalls extensive Zustandsgrößen, während der Druck und die Temperatur intensive Zustandsgrößen sind.[17][4]

Die Forderung, dass Zustandsgrößen extensiv oder intensiv sind, schränkt die Zustandsgrößen als Funktionen der Koordinaten über dem Zustandsraum wesentlich ein. Aus dieser Skalierbarkeit kann auf wichtige Beziehungen für die chemischen Potentiale, wie die Gibbs-Duhem-Gleichung, geschlossen werden. Für ein einfaches thermodynamisches System mit einer Arbeitskoordinate $V$ , $m$ Reinstoffen mit den Stoffmengen $N_{1},...,N_{m}$ und der inneren Energie $U$ gilt, wenn $(U,V,N_{1},...,N_{m})$ ein Gleichgewichtszustand ist, dann ist auch der Punkt $(\lambda U,\lambda V,\lambda N_{1},...,\lambda N_{m})$ ein Gleichgewichtspunkt für das um den Faktor $\lambda$ skalierte System.

Dividiert man eine extensive Zustandsgröße durch die Stoffmenge, die Masse oder das Volumen eines Stoffes, so erhält man eine intensive, also skaleninvariante, Größe, die als molare Zustandsgröße, spezifische Zustandsgröße beziehungsweise als Dichte bezeichnet wird.[2]

Klassifizierungen

Nach der inneren Struktur

Thermodynamische Systeme können sehr komplex aus unterschiedlichen Stoffen zusammengesetzt sein.[9] Sie lassen sich nach ihrer inneren Struktur klassifizieren.

Bereiche eines thermodynamischen Systems, in welchen lokale physikalische Eigenschaften wie Dichte und Druck, sowie die chemische Zusammensetzung überall gleich sind, werden nach Gibbs[7] homogen genannt und einer Phase zugeordnet. Beispielsweise werden bei einem System aus Wasser und einigen Eiswürfeln alle Eiswürfel einer Phase zugeordnet. Gleiche chemische Zusammensetzung bedeutet nicht, dass nur ein einziger chemischer Stoff vorliegen muss, es kann sich auch um ein Gemisch aus verschiedenen Stoffen handeln.

Ein thermodynamisches System heißt homogen, wenn es nur aus einer einzigen Phase besteht, andernfalls heterogen. Homogene und nur aus wenigen Phasen bestehende thermodynamische Systeme können mit den Methoden der Thermostatik mit einem endlich dimensionalen Zustandsraum, $Z_{g}$ , beschrieben werden.[2]

Andere komplexere Systeme erfordern eine Kontinuumstheorie im Rahmen der irreversiblen Thermodynamik. In dieser Theorie werden lokale Gleichgewichtszustände und räumlich und zeitlich variierende Zustandsgrößen eingeführt. Die Zustandsgrößen sind Felder, die einen Satz von partiellen Differentialgleichungen erfüllen müssen; Beispiele hierfür sind die Wärmeleitungsgleichung für Feststoffe und die Navier-Stokes-Gleichungen für flüssige oder gasförmige Systeme. Spielen Kraftfelder wie elektromagnetische Felder oder das Gravitationsfeld eine Rolle, so führt dieses bei räumlich ausgedehnten Systemen zu Inhomogenitäten; ein Beispiel ist das System der Erdatmosphäre in der Meteorologie, ein weiteres das Innere von Sternen in der Astrophysik.[18] Bei vielen Lehrbüchern der technischen Thermodynamik werden solche Systeme im Vorwege ausgeschlossen. Auch in der physikalischen Literatur wird von thermodynamischen Systemen meist nur im Zusammenhang mit aus wenigen Phasen bestehenden Systemen in der Thermostatik gesprochen. Die technischen Lehrbücher beschäftigen sich vor allem mit Systemen, die nur aus gasförmigen oder flüssigen Phasen bestehen. Man spricht von einem Fluid und meint damit eine Flüssigkeit oder ein Gas.[4][2]

Nach Stoff-Komponenten

Weiter lassen sich die thermodynamische Systeme nach der Anzahl der Reinstoffe (chemische Verbindungen oder chemische Elemente) in ihrem Inneren klassifizieren. Ein Verständnis der thermodynamischen Eigenschaften von Systemen, die nur aus einem einzigen Reinstoff bestehen, ist oft eine Voraussetzung für die Analyse von Systemen mit Gemischen. Für die Systeme aus nur einem Reinstoff sind die Zustandsgleichungen für die thermodynamischen Zustandsgrößen meist in Grafiken, Tabellen oder Datenbanken verfügbar. Systeme aus einem einzigen Reinstoff können heterogen sein, nämlich dann wenn sie aus mehreren Phasen bestehen; wie gasförmig, flüssig oder verschiedene feste Erscheinungsformen. Liegen gleichzeitig eine flüssige und eine gasförmige Phase vor, so spricht man vom Nassdampfgebiet des Stoffs.[19]

Enthält eine Phase eines thermodynamischen Systems ein Gemisch aus mehreren Reinstoffen, so nennt man die Phase eine Mischphase, dieses Gemisch ist als eine Phase homogen. Die Stoffmengenanteile der einzelnen Reinstoffen in einer Mischphasen sind dann zusätzliche Zustandsgrößen des Gesamtsystems. Bei besonderen Anwendungen etwa bei sehr tiefen Temperaturen, müssen auch die Isotope eines Elementes als verschiedene Reinstoffe behandelt werden, wie bei ³He und ⁴He.

Es gibt Gemische, bei denen die enthaltenen Reinstoffe chemisch reagieren können. Thermodynamische Systeme mit chemisch reagierenden Gemischen sind nur dann im thermodynamischen Gleichgewicht, wenn sich auch ein chemisches Gleichgewicht zwischen den Reaktanten und Produkten gebildet hat. Dieses chemische Gleichgewicht hängt von den thermodynamischen Zustandsgrößen, wie Druck und Temperatur ab. Die Analyse solcher Systeme ist zentral für die physikalische Chemie und die chemische Verfahrenstechnik.[20]

Nach der Wechselwirkung mit der Umgebung

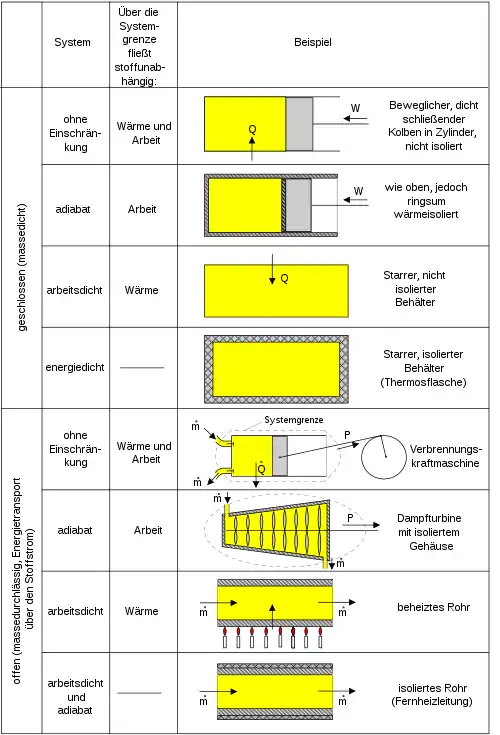
Thermodynamische Systeme lassen sich nach der Wechselwirkung mit ihrer Umgebung klassifizieren; also danach, ob Energie und Materie die Systemgrenzen passieren kann:

Abgeschlossenes (Isoliertes) System

Ein abgeschlossenes thermodynamisches System wechselwirkt nicht mit seiner Umgebung, synonym wird auch von einem isolierten thermodynamischen System gesprochen. Ein isoliertes System darf sich in äußeren Kraftfeldern wie etwa dem Schwerkraftfeld der Erde befinden, solange sich diese Kraftfelder nicht mit der Zeit ändern. Die Lage eines isolierten Systems im Zustandsraum $Z_{g}$ bleibt nach der Einstellung des Gleichgewichts immer am selben Punkt. Von Interesse sind isolierte Systeme, wenn die Einstellung des Gleichgewichts untersucht werden soll. Will man von zwei isolierten thermodynamischen Systemen wissen, welches Gleichgewicht sich einstellt, wenn man die beiden System miteinander verbindet oder gar vereinigt, so sollte das aus beiden Einzelsystemen bestehende Gesamtsystem isoliert sein.

Geschlossenes System

Bei geschlossenen thermodynamischen Systemen kann nur Energie in Form von Wärme und Arbeit die Systemgrenzen passieren.

Adiabatisches System

Das adiabatische System ist ein Spezialfall des geschlossenen, bei dem nur der Austausch in Form von Arbeitsenergie möglich ist.

Offenes System

Bei offenen Systemen kann sowohl Energie als auch Materie die Systemgrenze passieren. Offene Systeme findet man häufig bei technischen Anlagen. Eine Turbine hat zwei Eingangsströme (Luft und Treibstoff), einen Ausgangsstrom von Verbrennungsgasen und eine Abgabe mechanischer Leistung über eine Welle. Bei einer Rektifizierungskolonne gibt es einen einlaufenden Strom aus einem Gemisch und mindestens zwei auslaufende Ströme mit den angereicherten Komponenten des Gemisches. In der Zellbiologie wird eine Zelle als ein offenes thermodynamisches System betrachtet.[2][3]

Bilanzgleichungen

Übersicht über verschiedene thermodynamische Systeme

Die Systemgrenzen eines offenen Systems schließen einen Raum ein, der in technischen Anwendungen oft Kontrollraum genannt wird, bei den Systemgrenzen spricht man auch von der Bilanzhülle. Aus den Erhaltungssätzen für Energie und Materie lassen sich für solche Systeme Bilanzgleichungen für die Energie und die Stoffmenge aufstellen.[21]

Offenes System

Bei einem offenen System kann das System sowohl Energie als auch Materie mit seiner Umgebung austauschen. Ein Beispiel für ein offenes System, in dem ein Vorgang kontinuierlich abläuft, ist eine Turbine. Im stationären Betrieb wird das System von einem konstanten Massenstrom durchflossen, die Massenbilanz ergibt Null. Dabei bleiben die Zustände des Fluids am Eintritt und am Austritt konstant und das Fluid ändert seinen Zustand auf dem Weg durch das System. Die Wellenarbeit wird beim Verdichten dem System zugeführt, beim Expandieren abgegeben. Sie wird technische Arbeit genannt.

Sie wird beschrieben durch:

\qquad \mathrm {\delta } W_{\mathrm {t} }=V\cdot dp+\delta W_{\mathrm {diss} }+\delta E_{\mathrm {a} }

(Hierbei ist $\delta E_{\mathrm {a} }$ die Änderung der äußeren Energien. Die Definition der technischen Arbeit ist in der Literatur unterschiedlich. Verschiedentlich versteht man darunter nur den ersten Term $Vdp$ ).

Neben dieser Arbeit treten am Eintritt und Austritt des Systems Verschiebearbeiten auf. Hat im stationären Betrieb das Masseteilchen $\Delta m\$ am Eintritt das Volumen $\Delta V_{\mathrm {1} }\$ und am Austritt $\Delta V_{\mathrm {2} }\$ , so ist die Verschiebearbeit am Eintritt $p_{\mathrm {1} }\cdot \Delta V_{\mathrm {1} }$ , entsprechend am Austritt $-p_{\mathrm {2} }\cdot \Delta V_{\mathrm {2} }$

Diese Verschiebearbeiten sind neben der inneren Energie $U$ in den jeweiligen Enthalpien enthalten. Mit der Definition der Enthalpie

H=U+p\cdot V

ist die Bilanz für das offene stationäre System:

{\dot {Q}}+{\dot {W_{\mathrm {t} }}}={\dot {H}}_{\mathrm {2} }-{\dot {H}}_{\mathrm {1} }+{\dot {m}}\cdot g\cdot \left(z_{\mathrm {2} }-z_{\mathrm {1} }\right)+{{\dot {m}} \over 2}\cdot \left(c_{\mathrm {2} }^{2}-c_{\mathrm {1} }^{2}\right)

und mit dem Symbol für die Leistung

{\dot {W_{\mathrm {t} }}}=P

und der äußeren Energie

{\dot {m}}\cdot g\cdot z+{{\dot {m}} \over 2}\cdot c^{2}={\dot {E}}_{\mathrm {a} }

lautet der erste Hauptsatz für die Anwendung am offenen System:

{\dot {Q}}+P={\dot {H}}_{\mathrm {2} }-{\dot {H}}_{\mathrm {1} }+\Delta {\dot {E}}_{\mathrm {a} }

Die in der Skizze als Beispiel für ein offenes System gezeigte Verbrennungskraftmaschine ist genau genommen abwechselnd offen und geschlossen. Nur über größere Zeiträume hinweg kann sie als offenes System betrachtet werden.

Geschlossenes System

Beim geschlossenen System kann Energie in Form von Wärme, Strahlung und Arbeiten zu- oder abgeführt werden. Als Arbeiten kommen in Betracht:

Die reversibel zugeführte Volumenänderungsarbeit, Volumenarbeit genannt. Beispiel in der Skizze: Mit dem Kolben wird reibungsfrei das im Zylinder befindliche Gas verdichtet.
$\qquad \mathrm {\delta } W_{\mathrm {V} }=-p\cdot dV$
Da $dV$ negativ ist, ist also die zugeführte Arbeit positiv.
Dissipierte Arbeit. Als Beispiel sei ein Ventilator oder eine elektrische Heizung in einem Raum mit starrer Systemgrenze genannt. Über die Systemgrenze fließt Arbeit (Exergie), die innerhalb des Systems dissipiert wird. Die Arbeit durch Reibungskräfte zwischen Kolben und Zylinder gehört zu diesen irreversibel zugeführten Energien.

Da nach dem ersten Hauptsatz der Thermodynamik Energie weder erzeugt, noch vernichtet werden kann, erhöht sich die innere Energie um die zugeführten Energien. Die Bilanz für das ruhende geschlossene System lautet:

Q_{\mathrm {1,2} }+W_{\mathrm {1,2} }\ =U_{\mathrm {2} }-U_{\mathrm {1} }

mit

W_{\mathrm {1,2} }\ =W_{\mathrm {diss1,2} }+W_{\mathrm {V1,2} }

(Die Indizes 1 und 2 benennen den Anfangs- und den Endzustand, der Index 1,2 den Weg von 1 nach 2)

Werden durch den Einfluss der zugeführten Energien die äußere Energien des Systems, also die potentielle Energie und/oder die kinetische Energie des Systems verändert, so ist die Bilanz nach dem 1. Hauptsatz für das geschlossene System:

Q_{\mathrm {1,2} }+W_{\mathrm {1,2} }=U_{\mathrm {2} }-U_{\mathrm {1} }+m\cdot g\cdot \left(z_{\mathrm {2} }-z_{\mathrm {1} }\right)+{m \over 2}\cdot \left(c_{\mathrm {2} }^{2}-c_{\mathrm {1} }^{2}\right)

Anmerkungen

Nach Ludwig wird die Temperatur erst im Rahmen der Thermodynamik definiert und sollte daher nicht für die Definition des grundlegenden Begriffs des thermodynamischen Gleichgewichts benutzt werden. Ludwig weist auf eine weitere Schwierigkeit bei der Feststellung des Gleichgewichtszustandes hin. Es gibt nämlich bei allen bekannten Gleichgewichtszuständen immer verfeinerte Messungen, deren Messergebnisse sich ändern (man denke etwa an die Messung des Druckes mittels sehr kleiner Flächen in sehr kurzen Zeitintervallen). Der Anwendungsbereich muss daher auf gewisse Größen beschränkt werden. Diese Einschränkung wird häufig dadurch ausgedrückt, dass man die zugelassenen Messgrößen kurz thermodynamische Observablen nennt. Welche Größen das sind, ist nicht von vornherein festgelegt, sondern der Anwendungsbereich schält sich erst durch die Anwendung der Theorie heraus.
Baehr und Kabelac zählen auch die Geschwindigkeit des Systems im Bezug zu seinem Beobachter zu den äußeren Zustandsgrößen.

Literatur

Hans Dieter Baehr, Stephan Kabelac: Thermodynamik - Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4.
Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV Thermodynamik, S. 5–145.

Weblinks

Commons: Thermodynamic systems – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 1. Thermostatik 1.1 Der Zustandsraum, S. 6–11.
Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 1.2 System und Zustand, S. 14–23.
Gerd Wedler, Hans-Joachim Freund: Lehrbuch der Physikalischen Chemie. 6. Auflage. Wiley-VCH, Weinheim 2012, ISBN 978-3-527-32909-0, 1.1.2 System und Umgebung, S. 1–2.
André Thess: Das Entropieprinzip – Thermodynamik für Unzufriedene. Oldenbourg Wissenschaftsverlag, München 2014, ISBN 978-3-486-76045-3, 2.1 Thermodynamische Systeme, S. 7.
Nicolas Léonard Sadi Carnot: Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. In: Annales scientifiques de l’École Normale Supérieure Sér. Band 2, Nr. 1, 1872, S. 393–457 (französisch, numdam.org [abgerufen am 14. April 2018] Nachdruck der Arbeit von 1824).
Rudolf Clausius: Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen. In: Annalen der Physik und Chemie. Band 155, Nr. 1, 1850, S. 368 (archive.org).
Josiah Willard Gibbs: On the Equilibrium of Heterogeneous Substances. In: Transactions of the Connecticut Academy of Arts and Sciences. Band 3, Nr. V, 1878, S. 108–248 (englisch, biodiversitylibrary.org [abgerufen am 27. April 2017]).
Willy Wien: Eine neue Beziehung der Strahlung schwarzer Körper zum zweiten Hauptsatz der Wärmetheorie. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. Erster Halbband 1893, 1893, S. 55 (bbaw.de [abgerufen am 27. April 2017]).
Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics. In: Physics Reports. Band 310, Nr. 1, 1999, II. adiabatic accessibility and construction on entropy (A 1. System and their state spaces), S. 12–16, doi:10.1016/S0370-1573(98)00082-9, arxiv:cond-mat/9708200 (englisch).
Gerd Wedler, Hans-Joachim Freund: Lehrbuch der Physikalischen Chemie. 6. Auflage. Wiley-VCH, Weinheim 2012, ISBN 978-3-527-32909-0, 2.7 Grenzflächengleichgewichte, S. 443–482.
Walter Roedel: Physik unserer Umwelt. Die Atmosphäre. 3. Auflage. Springer Vieweg, Berlin 2000, ISBN 3-540-67180-3, 5.1.1 Die homogene Kondensation, S. 177–184.
Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 1. Thermostatik 1.2 Der Energiesatz, S. 22.
Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics. In: Physics Reports. Band 310, Nr. 1, 1999, III. Simple Systems, S. 36–42, doi:10.1016/S0370-1573(98)00082-9, arxiv:cond-mat/9708200 (englisch).
Constantin Carathéodory: Untersuchungen über die Grundlagen der Thermodynamik. In: Mathematische Annalen. Band 67, Nr. 3, 1909, S. 355–386 (digizeitschriften.de [abgerufen am 27. April 2017] Einfache Systeme auf S 364).
Herbert B. Callen: Thermodynamics and an Introduction to Thermostatics. 2. Auflage. John Wiley & Sons, New York 1985, 1.3 The Composition of Thermodynamic Systems, S. 9.
Rainer Müller: Thermodynamik – Vom Tautropfen zum Solarkraftwerk. 2. Auflage. De Gruyter, Berlin 2016, ISBN 978-3-11-044531-2, 9.6.1 Der Satz von Duhem, S. 260.
Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 1. Thermostatik 1.2 Der Energiesatz, S. 27–28.
Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 2 Irreversible Prozesse, S. 84–145 (Insbesondere §2.6 Wärmeleitung, §2.7 Die Navier-Stokesschen Gleichungen, §2.8 Materialien im elektromagnetischen Feld).
Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 4. Die thermodynamischen Eigenschaften reiner Fluide, S. 171–230.
Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 5. Gemische und chemische Reaktionen, S. 231–374.
Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 2.3 Die Energiebilanzgleichungen, S. 66–88.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[9] Nach Ludwig wird die Temperatur erst im Rahmen der Thermodynamik definiert und sollte daher nicht für die Definition des grundlegenden Begriffs des thermodynamischen Gleichgewichts benutzt werden. Ludwig weist auf eine weitere Schwierigkeit bei der Feststellung des Gleichgewichtszustandes hin. Es gibt nämlich bei allen bekannten Gleichgewichtszuständen immer verfeinerte Messungen, deren Messergebnisse sich ändern (man denke etwa an die Messung des Druckes mittels sehr kleiner Flächen in sehr kurzen Zeitintervallen). Der Anwendungsbereich muss daher auf gewisse Größen beschränkt werden. Diese Einschränkung wird häufig dadurch ausgedrückt, dass man die zugelassenen Messgrößen kurz thermodynamische Observablen nennt. Welche Größen das sind, ist nicht von vornherein festgelegt, sondern der Anwendungsbereich schält sich erst durch die Anwendung der Theorie heraus.

[11] Baehr und Kabelac zählen auch die Geschwindigkeit des Systems im Bezug zu seinem Beobachter zu den äußeren Zustandsgrößen.

[LudwigBd4Thermostatik_S_6_11-1] Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 1. Thermostatik 1.1 Der Zustandsraum, S. 6–11.

[BaehrKabelac_S_14_23-2] Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 1.2 System und Zustand, S. 14–23.

[GWedlerPhysChemie_S_1_2-3] Gerd Wedler, Hans-Joachim Freund: Lehrbuch der Physikalischen Chemie. 6. Auflage. Wiley-VCH, Weinheim 2012, ISBN 978-3-527-32909-0, 1.1.2 System und Umgebung, S. 1–2.

[Andre_Thess-4] André Thess: Das Entropieprinzip – Thermodynamik für Unzufriedene. Oldenbourg Wissenschaftsverlag, München 2014, ISBN 978-3-486-76045-3, 2.1 Thermodynamische Systeme, S. 7.

[Carnot-5] Nicolas Léonard Sadi Carnot: Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. In: Annales scientifiques de l’École Normale Supérieure Sér. Band 2, Nr. 1, 1872, S. 393–457 (französisch, numdam.org [abgerufen am 14. April 2018] Nachdruck der Arbeit von 1824).

[Clausius-6] Rudolf Clausius: Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen. In: Annalen der Physik und Chemie. Band 155, Nr. 1, 1850, S. 368 (archive.org).

[Gibbs_1-7] Josiah Willard Gibbs: On the Equilibrium of Heterogeneous Substances. In: Transactions of the Connecticut Academy of Arts and Sciences. Band 3, Nr. V, 1878, S. 108–248 (englisch, biodiversitylibrary.org [abgerufen am 27. April 2017]).

[Wien_Verschiebungsgesetz-8] Willy Wien: Eine neue Beziehung der Strahlung schwarzer Körper zum zweiten Hauptsatz der Wärmetheorie. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. Erster Halbband 1893, 1893, S. 55 (bbaw.de [abgerufen am 27. April 2017]).

[Lieb_S_12_16-10] Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics. In: Physics Reports. Band 310, Nr. 1, 1999, II. adiabatic accessibility and construction on entropy (A 1. System and their state spaces), S. 12–16, doi:10.1016/S0370-1573(98)00082-9, arxiv:cond-mat/9708200 (englisch).

[GWedlerPhysChemie_S_443-12] Gerd Wedler, Hans-Joachim Freund: Lehrbuch der Physikalischen Chemie. 6. Auflage. Wiley-VCH, Weinheim 2012, ISBN 978-3-527-32909-0, 2.7 Grenzflächengleichgewichte, S. 443–482.

[W_Roedel_S_177_184-13] Walter Roedel: Physik unserer Umwelt. Die Atmosphäre. 3. Auflage. Springer Vieweg, Berlin 2000, ISBN 3-540-67180-3, 5.1.1 Die homogene Kondensation, S. 177–184.

[LudwigBd4Thermostatik_S_22-14] Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 1. Thermostatik 1.2 Der Energiesatz, S. 22.

[Lieb_S_36_42-15] Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics. In: Physics Reports. Band 310, Nr. 1, 1999, III. Simple Systems, S. 36–42, doi:10.1016/S0370-1573(98)00082-9, arxiv:cond-mat/9708200 (englisch).

[Carathéodory-16] Constantin Carathéodory: Untersuchungen über die Grundlagen der Thermodynamik. In: Mathematische Annalen. Band 67, Nr. 3, 1909, S. 355–386 (digizeitschriften.de [abgerufen am 27. April 2017] Einfache Systeme auf S 364).

[Callen-17] Herbert B. Callen: Thermodynamics and an Introduction to Thermostatics. 2. Auflage. John Wiley & Sons, New York 1985, 1.3 The Composition of Thermodynamic Systems, S. 9.

[R_Müller-18] Rainer Müller: Thermodynamik – Vom Tautropfen zum Solarkraftwerk. 2. Auflage. De Gruyter, Berlin 2016, ISBN 978-3-11-044531-2, 9.6.1 Der Satz von Duhem, S. 260.

[LudwigBd4Thermostatik_S_27_28-19] Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 1. Thermostatik 1.2 Der Energiesatz, S. 27–28.

[LudwigBd4Thermostatik_S_84_145-20] Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3, XIV § 2 Irreversible Prozesse, S. 84–145 (Insbesondere §2.6 Wärmeleitung, §2.7 Die Navier-Stokesschen Gleichungen, §2.8 Materialien im elektromagnetischen Feld).

[BaehrKabelac_S_171_225-21] Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 4. Die thermodynamischen Eigenschaften reiner Fluide, S. 171–230.

[BaehrKabelac_S_231_374-22] Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 5. Gemische und chemische Reaktionen, S. 231–374.

[BaehrKabelac_S_66_87-23] Hans Dieter Baehr, Stephan Kabelac: Thermodynamik – Grundlagen und technische Anwendungen. 16. Auflage. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4, 2.3 Die Energiebilanzgleichungen, S. 66–88.