Zweiter Hauptsatz der Thermodynamik

Der Zweite Hauptsatz der Thermodynamik trifft Aussagen über die Richtung von Prozessen und das Prinzip der Irreversibilität. Aus dem Zweiten Hauptsatz lassen sich die Definition der thermodynamischen Temperatur und die Zustandsgröße Entropie herleiten.[1] Ebenso folgt aus dem Zweiten Hauptsatz der Thermodynamik die Unterscheidung von Exergie und Anergie und die Tatsache, dass der Wirkungsgrad einer Wärmekraftmaschine den Carnot-Wirkungsgrad nicht überschreiten kann.

Formulierungen der Aussagen des Zweiten Hauptsatzes

Für den Zweiten Hauptsatz der Thermodynamik haben sich viele unterschiedliche, teils äquivalente Formulierungen etabliert, von denen einige im Folgenden wiedergegeben werden:

Wärme kann nicht von selbst von einem Körper niedriger Temperatur auf einen Körper höherer Temperatur übergehen.
Wärme kann durch eine periodisch arbeitende Maschine nicht vollständig in Arbeit umgewandelt werden. Dies wäre eine Realisierung eines Perpetuum Mobile zweiter Art.
Der Wirkungsgrad des Carnot-Prozesses kann nicht übertroffen werden.
Alle spontan (in eine Richtung) ablaufenden Prozesse sind irreversibel.
Alle Prozesse, bei denen Reibung stattfindet, sind irreversibel.
Ausgleichs- und Mischungsvorgänge sind irreversibel (abgesehen von reversiblen Mischungen idealer Gase).
In einem geschlossenen adiabaten System kann die Entropie nicht geringer werden.
Das Gleichgewicht isolierter thermodynamischer Systeme ist durch ein Maximalprinzip der Entropie ausgezeichnet.

Aussagen des Zweiten Hauptsatzes

Vorzugsrichtung von Prozessen

Der zweite Hauptsatz der Thermodynamik in der Formulierung von Clausius lautet:

„Es gibt keine Zustandsänderung, deren einziges Ergebnis die Übertragung von Wärme von einem Körper niederer auf einen Körper höherer Temperatur ist.“

Einfacher ausgedrückt: Wärme kann nicht von selbst von einem Körper niedriger Temperatur auf einen Körper höherer Temperatur übergehen. Für den Prozess der Wärmeübertragung gibt es eine Vorzugsrichtung. Diese Aussage scheint zunächst überflüssig zu sein, denn sie entspricht der alltäglichen Erfahrung. Dennoch ist sie gleichbedeutend mit allen weiteren, weniger „selbstverständlichen“ Aussagen, denn alle Widersprüche zu den anderen Aussagen lassen sich auf einen Widerspruch zu dieser zurückführen.

Der zweite Hauptsatz der Thermodynamik in der Formulierung von Kelvin und Planck lautet:

„Es ist unmöglich, eine periodisch arbeitende Maschine zu konstruieren, die weiter nichts bewirkt als Hebung einer Last und Abkühlung eines Wärmereservoirs.“[1][2]

Dem ersten Hauptsatz würde die Annahme nicht widersprechen, dass es möglich sei, einer – wie immer auch gearteten – Kraftmaschine einen stetigen Wärmestrom zuzuführen, den diese vollständig als mechanische oder elektrische Leistung abgibt. Eine solche Maschine wird als Perpetuum mobile zweiter Art bezeichnet. Eine entsprechende Formulierung des zweiten Hauptsatzes lautet:

Ein Perpetuum mobile zweiter Art ist unmöglich.

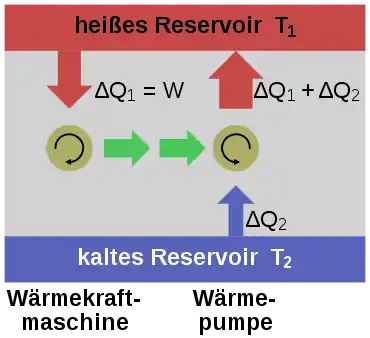
Die Wärmekraftmaschine (a) beschreibt ein Perpetuum mobile zweiter Art. Würde ein solches existieren, könnte es Wärme ohne Verlust in Arbeit (grüner Pfeil) umwandeln. Würde mit dieser Arbeit eine Wärmepumpe (b) angetrieben, könnte damit ohne Einwirkung von außen Wärme vom kalten zum warmen Reservoir gepumpt werden.

Nimmt man an, es gäbe diese von einer Wärmesenke zur Wärmeabfuhr unabhängige Kraftmaschine, so könnte damit der Umgebung Wärme entzogen und in mechanische Arbeit umgewandelt werden. Ein Schiff könnte beispielsweise angetrieben werden, indem die Antriebsleistung durch Abkühlung des Meerwassers gewonnen wird.[1]

Man könnte damit auch gemäß dem Bild rechts die Wärme aus einem Reservoir oder Behälter entziehen und mit der umgewandelten Energie eine Wärmepumpe antreiben, die mit einem reversiblen Carnot-Prozess Wärme aus einem anderen Behälter mit niedrigerer Temperatur in den Ersteren mit höherer Temperatur fördert. Die in den wärmeren Behälter eingespeiste Wärmemenge wäre dann größer als die von der Kraftmaschine aufgenommene, weil die abgegebene Energie der Wärmepumpe aus der Summe von aufgenommener Wärme und Antriebsarbeit besteht. Denkt man sich die Systemgrenze um beide Maschinen einschließlich der beiden Wärmebehälter gezogen, so wäre innerhalb dieses abgeschlossenen Systems – also ohne Energie- und Stoffaustausch mit der Umgebung – letztlich Wärme von einem kälteren zu einem wärmeren Körper geflossen. Dies ist ein Widerspruch zur ersten Aussage.

Wirkungsgrad von Wärmekraftmaschinen

Prinzipiell derselbe Widerspruch ergibt sich aber auch mit der Annahme, man könnte eine Kraftmaschine bauen, die einen größeren Wirkungsgrad aufweist als eine mit einem Carnot-Prozess arbeitende Maschine. Auch diese Maschine würde dem wärmeren Behälter weniger Wärme entnehmen als die von ihr angetriebene Carnot-Wärmepumpe dort einspeist. Die entsprechende Aussageform des zweiten Hauptsatzes lautet:

Es gibt keine Wärmekraftmaschine, die bei gegebenen mittleren Temperaturen der Wärmezufuhr und Wärmeabfuhr einen höheren Wirkungsgrad hat als den aus diesen Temperaturen gebildeten Carnot-Wirkungsgrad.

\eta _{c}=1-{\frac {T_{\mathrm {kalt} }}{T_{\mathrm {heiss} }}}

Die Nennung der mittleren Temperaturen ist deshalb von Bedeutung, weil in der Regel durch Wärmezufuhr oder Wärmeentnahme ein Wärmereservoir seine Temperatur ändert.

Dabei ist T nicht irgendeine Temperatur (z. B. nicht die Celsius- oder die Fahrenheit-Temperatur) des Systems, sondern die von der Zustandsgleichung des „idealen Gases“ her, oder besser durch den gerade angegebenen Wirkungsgrad des Carnot-Prozesses definierte „absolute Temperatur“ (Kelvin).

Unmittelbar in diesem Zusammenhang lässt sich weiter formulieren:

Alle reversiblen Wärme-Kraft-Prozesse mit gleichen mittleren Temperaturen der Wärmezufuhr und Wärmeabfuhr haben denselben Wirkungsgrad wie der entsprechende Carnot-Prozess.

und:

Alle irreversiblen Wärme-Kraft-Prozesse haben einen geringeren Wirkungsgrad.

Entropie

Der Erste Hauptsatz der Thermodynamik kann durch die Zustandsgröße Energie und die zugehörige Energiebilanz zu einer quantitativen Formel zusammengefasst werden. Die quantitative Umsetzung des Zweiten Hauptsatzes der Thermodynamik ist analog dazu durch die von Clausius eingeführte Zustandsgröße Entropie und das Aufstellen einer Entropiebilanz möglich. Entropiebilanzen können für abgeschlossene, geschlossene und offene Systeme aufgestellt werden. Bei Fließprozessen bezieht sich die Bilanz auf ein Fluidteilchen, das sich durch das System hindurch bewegt und als geschlossenes bewegtes System betrachtet werden kann.

Für ein geschlossenes System lautet die Entropiebilanz:

\mathrm {d} S={\frac {\delta Q}{T}}+{\frac {\delta W_{\mathrm {diss} }}{T}}

Dabei ist der Quellterm $\delta W_{\mathrm {diss} }$ die innerhalb des Systems dissipierte Arbeit: Arbeit, die nicht nach außen gelangt, sondern infolge von Reibungs-, Drosselungs- oder Stoßvorgängen die innere Energie erhöht. Sie ist immer positiv. Man bezeichnet den entsprechenden Term in der Gleichung als im System produzierte Entropie. $\delta$ kennzeichnet ein unvollständiges Differential, während $\mathrm {d}$ ein vollständiges Differential kennzeichnet.

Betrachtet man ein offenes System, so wird der oben angegebenen Entropiebilanz ein weiterer Term hinzugefügt, der Entropiezu- oder -abnahme als Folge von Stofftransport über die Systemgrenze berücksichtigt. Betrachtet man hingegen ein abgeschlossenes System, also ein geschlossenes System, das zusätzlich noch adiabat ist und in dem $\delta Q=0$ gilt, so folgt:

\mathrm {d} S={\frac {\delta W_{\mathrm {diss} }}{T}}

und daraus folgende Aussage zur Entropieproduktion:

In einem geschlossenen adiabaten System kann die Entropie nicht abnehmen, sie nimmt in der Regel zu. Nur bei reversiblen Prozessen bleibt sie konstant.

Auch hier ist die Äquivalenz mit der ersten Aussage von Clausius leicht zu erkennen. Ein selbsttätiger Wärmefluss vom kälteren zum wärmeren Behälter in der oben skizzierten Anordnung würde bedeuten, dass die Entropie des kälteren Behälters (geringere Temperatur T im Nenner) stärker abnimmt, als die des wärmeren zunimmt, d. h. die gesamte Entropie im System abnimmt, was nicht möglich ist.

Alle spontan ablaufenden Prozesse sind irreversibel. Dort findet immer eine Entropiezunahme statt. Beispiele sind die Vermischung von zwei unterschiedlichen Gasen und der Wärmefluss von einem heißen zu einem kalten Körper ohne Gewinnung von Arbeit. Die Wiederherstellung des (oft „geordneter“ genannten) Anfangszustandes erfordert dann den Einsatz von Energie oder Information (siehe maxwellscher Dämon). Reversible Prozesse sind nicht mit einer Erhöhung der Gesamtentropie verbunden und laufen daher auch nicht spontan ab. Durch die theoretische Beschreibung spontan ablaufender Prozesse zeichnet der Zweite Hauptsatz der Thermodynamik eine Richtung der Zeit aus, die mit unserer intuitiven Erfahrungswelt übereinstimmt (vgl. das Beispiel weiter unten).

Thermodynamische Temperatur

Für einen reversiblen Prozess gilt

{\dot {S}}={\frac {\dot {Q}}{T}}

.

Ausgehend von diesem Zusammenhang lässt sich die Definition der thermodynamischen Temperatur durch Auflösen nach $T$ gewinnen:

T={\frac {\dot {Q}}{\dot {S}}}

.

Aus dieser Formel wird ersichtlich, dass die thermodynamische Temperatur einen Nullpunkt besitzt, aber nicht negativ werden kann und dass Wärme von höheren zu niedrigen Temperaturen fließt. Eine empirische Temperatur könnte hingegen auch negative Temperaturen annehmen, wie es bei der Celsius-Skala der Fall ist, oder mit umgekehrtem Vorzeichen definiert sein.[1]

Exergie und Anergie

Mit den beschriebenen Zusammenhängen ist auch der folgende Satz eine Aussageform des zweiten Hauptsatzes:

Die thermische Energie eines Systems besteht aus einem Anteil Exergie und einem Anteil Anergie, wobei der exergetische Anteil verschwindet, wenn das System in den Umgebungszustand übergeführt wird.

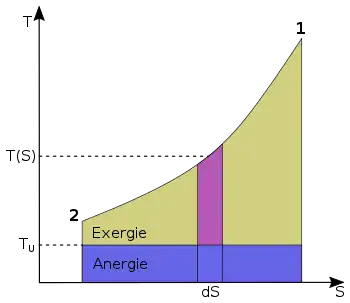
Exergie und Anergie der Wärme (Thermische Energie = Anergie + Exergie)

Die Exergie ist der in andere Energieformen umwandelbare Anteil der thermischen Energie. Wird ein Körper bzw. System mit einem Zustand, der von dem der Umgebung abweicht, reversibel in den Umgebungszustand gebracht, so wird seine Exergie als Arbeit abgegeben. Die Wärme, die ein Körper (z. B. ein heißes Rauchgas im Kessel eines Kraftwerks) abgibt, wenn es sich auf Umgebungstemperatur abkühlt, kann theoretisch über eine Folge von differenziellen Carnot-Prozessen, wie im Bild rechts dargestellt, zur Umwandlung in Arbeit genutzt werden. Der exergetische Anteil ergibt sich durch Aufsummieren der differenziellen (pinkfarbenen) Flächenanteile oberhalb der Umgebungstemperatur $T_{U}$ .

E_{\mathrm {ex} }=\int _{S_{2}}^{S_{1}}\left({T(S)-T_{U}}\right)\mathrm {d} S

Die Wärmesenke für diese Prozesse zur Aufnahme der Anergie (blauer Flächenanteil unterhalb $T_{U}$ ) ist die Umgebung. Herrscht bei einem Gas im Ausgangszustand gegenüber dem Umgebungszustand nicht nur eine höhere Temperatur, sondern auch ein höherer Druck, so besteht die gesamte Exergie nicht nur aus dem exergetischen Anteil der Wärme, sondern zusätzlich aus einem Anteil Volumenarbeit.

Der thermische Wirkungsgrad der realen Wärmekraftmaschine ist also immer kleiner als 1 und – bedingt durch die von den Maschinen vorgegebene Prozessführung und die unvermeidlichen dissipativen Effekte – auch immer kleiner als der der idealen Wärmekraftmaschine:

\eta _{\mathrm {th} }=1-{\frac {T_{U}}{T_{m_{\mathrm {zu} }}}}={\frac {\text{Exergie}}{\text{thermische Energie}}}

wobei $T_{U}$ die Umgebungstemperatur ist und $T_{m_{\mathrm {zu} }}$ die mittlere Temperatur der Wärmezufuhr. Sie ergibt sich, wenn die gelbe Fläche der Exergie durch ein flächengleiches Rechteck oberhalb der Linie der Umgebungstemperatur ersetzt wird.

Der Zweite Hauptsatz hat somit erhebliche technische Auswirkungen. Da viele Maschinen, die mechanische Energie liefern, diese über einen Umweg aus thermischer Energie erzeugen (z. B. Dieselmotor: chemische Energie $\rightarrow$ thermische Energie $\rightarrow$ mechanische Energie), gelten für ihre Wirkungsgrade immer die Beschränkungen des 2. Hauptsatzes. Im Vergleich dazu bieten Wasserkraftanlagen, die bei der Umwandlung keine Zwischenstufe über thermische Energie benötigen, erheblich höhere Wirkungsgrade.

Entropiesenke

Als Entropiesenke wird ein System bezeichnet, welches Entropie aus einem anderen System importiert. Dabei erhöht sich die Entropie der Senke. Da Entropie ein weitreichender Begriff ist, gibt es eine Vielzahl von verschiedenen Entropiesenken.[3] In einer klassischen Thermodynamik-Wärmekraftmaschine nach Carnot wird Arbeit erzeugt, indem der Energiefluss zwischen heißen Energie-Quellen, einer kalten Entropiesenke und einem Arbeits-Reservoir manipuliert wird.[4] In der Realität fungiert bei den meisten Wärmekraftmaschinen die Atmosphäre als Entropiesenke.[5]

Beispiel für den Zweiten Hauptsatz

Ein kräftefreies Gas verteilt sich immer so, dass es das zur Verfügung stehende Volumen vollständig und gleichmäßig ausfüllt. Warum das so ist, versteht man, wenn man den gegenteiligen Fall betrachtet. Man stelle sich eine luftdichte Kiste in der Schwerelosigkeit vor, in der sich ein einziges Partikel bewegt. Die Wahrscheinlichkeit, dieses bei einer Messung in der linken Hälfte der Kiste zu finden, ist dann genau ${\tfrac {1}{2}}$ . Befinden sich dagegen zwei Partikel in der Kiste, dann ist die Wahrscheinlichkeit, beide in der linken Hälfte anzutreffen, nur noch ${\tfrac {1}{2}}\cdot {\tfrac {1}{2}}={\tfrac {1}{4}}$ , und bei N Partikeln entsprechend $\left({\tfrac {1}{2}}\right)^{N}$ . Die Anzahl der Atome in einem Volumen von einem Kubikmeter bei normalem Druck liegt in der Größenordnung von rund $3\cdot 10^{25}$ Teilchen. Die daraus resultierende Wahrscheinlichkeit, dass sich das Gas in der Kiste spontan in einer Hälfte konzentriert, ist so gering, dass ein solches Ereignis vermutlich niemals eintreten wird.

Wie aus den zeitlich umkehrbaren mikroskopischen Gleichungen der klassischen Mechanik (ohne Reibung) die symmetriebrechende makroskopische Gleichung folgt, wird in der statistischen Mechanik geklärt. Zudem erhält die Entropie dort eine anschauliche Bedeutung: sie ist ein Maß der Unordnung eines Systems bzw. der im System enthaltenen Informationen. Allerdings verliert der Zweite Hauptsatz in der statistischen Mechanik seinen Status als „streng gültiges“ Gesetz und wird dort als Gesetz betrachtet, bei dem Ausnahmen auf makroskopischen Ebenen zwar prinzipiell möglich, aber gleichzeitig so unwahrscheinlich sind, dass sie praktisch nicht vorkommen. Auf mikroskopischer Ebene betrachtet führen z. B. kleine statistische Fluktuationen um den Gleichgewichtszustand auch bei abgeschlossenen Systemen dazu, dass die Entropie ebenfalls etwas um den Maximalwert fluktuiert und dabei kurzzeitig auch abnehmen kann.

Gültigkeit

Der Zweite Hauptsatz der Thermodynamik stellt eine Erfahrungstatsache dar. Es ist bis heute nicht gelungen, dieses fundamentale Gesetz der klassischen Physik in seiner allgemeinen Gültigkeit für beliebige makroskopische Systeme ausgehend von der Grundgleichung der Quantentheorie, der Vielteilchen-Schrödingergleichung, zu beweisen.

Dies gilt selbstverständlich auch umgekehrt: Die Schrödingergleichung stellt eine Erfahrungstatsache dar. Es ist bis heute nicht gelungen, die allgemeine Gültigkeit dieses fundamentalen Gesetzes quantenmechanischer Systeme für beliebige makroskopische Systeme, ausgehend von den Hauptsätzen der Physik (und nicht nur der Thermodynamik), zu beweisen.

Hinsichtlich der Gültigkeit des Zweiten Hauptsatzes ist zwischen dem mikroskopischen bzw. submikroskopischen und dem makroskopischen Bereich zu unterscheiden. So können bei der Brownschen Molekularbewegung Teilchen nicht nur aus der Bewegung zur Ruhe kommen, sondern aus der Ruhe auch wiederum in Bewegung geraten. Der letztere Vorgang entspricht dabei der Umwandlung von Wärmeenergie in die höherwertige Bewegungsenergie und muss mit der Abkühlung der Umgebung einhergehen.[6]

Der Zweite Hauptsatz als Kraftgesetz

Der zweite Hauptsatz gibt für spontane, reale Prozesse eine Vorzugsrichtung an. Sie verlaufen von einem Startzustand A so, dass die Entropie zunimmt, bis ein Gleichgewichtszustand B erreicht wird. Auf der Grundlage klassischer statistischer Mechanik lässt sich folgende Aussage herleiten:

Ein Prozess läuft genau dann spontan von A nach B, wenn die mittlere Kraftkomponente in Richtung des Prozesspfads positiv ist.

Gemeint ist eine doppelte Mittelung über (a) Ensemble oder Zeit und (b) die Pfadstrecke. Dies ist kein Beweis des Zweiten Hauptsatzes, sondern besagt lediglich, dass dieser einem Kraftgesetz äquivalent ist, das die Richtung bestimmt. Das Kraftgesetz gilt für Systeme, bei denen thermodynamische Zustände wie A und B durch die räumliche Anordnung von Massen gegeben und Kräfte definiert sind. Es trifft zu für Maschinen, aber auch für chemische Reaktionen, solange sie im elektronischen Grundzustand ablaufen.[7]

Siehe auch

Erster Hauptsatz der Thermodynamik
Nernst-Theorem (Dritter Hauptsatz der Thermodynamik)

Literatur

Karl Stephan, Franz Mayinger: Thermodynamik. Grundlagen und technische Anwendungen. 2 Bände, Springer Verlag
- Band 1: Einstoffsysteme. 15. Auflage. 1998, ISBN 3-540-64250-1.
- Band 2: Mehrstoffsysteme und chemische Reaktionen. 14. Auflage. 1999, ISBN 3-540-64481-4.
Hans D. Baehr, S. Kabelac: Thermodynamik, Grundlagen und technische Anwendungen. 13., neu bearbeitete und erweiterte Auflage. Springer Verlag, 2006, ISBN 3-540-32513-1.
Hans D. Baehr, Karl Stephan: Wärme- und Stoffübertragung. 5., neu bearbeitete Auflage. Springer Verlag, 2006, ISBN 3-540-32334-1.
Klaus Langeheinecke, Peter Jany, Eugen Sapper: Thermodynamik für Ingenieure. 5. Auflage. Vieweg Verlag, Wiesbaden 2004, ISBN 3-528-44785-0.

Weblinks

Eberhard-Karls-Universität Tübingen: 2. Hauptsatz der Wärmelehre, Entropie, Zustandsgleichung realer Gase und Phasenumwandlungen, (Skripte zur Vorlesung Experimentalphysik I, Nummer 12; PDF, 9 Seiten)
Die Hauptsätze der Thermodynamik

Einzelnachweise

Hans Dieter Baehr, Stephan Kabelac: Thermodynamik: Grundlagen und technische Anwendungen. 15. Auflage. Springer Verlag, Berlin / Heidelberg 2012, ISBN 978-3-642-24160-4, S. 93–176.
Zitat von Max Planck, nach Eintrag zu Hauptsätze. In: Römpp Online. Georg Thieme Verlag, abgerufen am 24. August 2011.
Klaus Langeheinecke: Thermodynamik für Ingenieure. Vieweg, 1993.
Selcuk Cakmak, Ferdi Altintas, Ozgur E. Mustecaplioglu: Irreversible Work and Internal Friction in a Quantum Otto Cycle of a Single Arbitrary Spin. arxiv:1605.02522 (2016).
Pankaj Mehta, Anatoli Polkovnikov: Efficiency bounds for nonequilibrium heat engines. Annals of Physics 332 (2012): 110–126.
Alfred Lottermoser: Kurze Einführung in die Kolloidchemie. Dresden/Leipzig 1944, S. 70–71.
Schlitter, Jürgen: The Second Law of Thermodynamics as a Force Law, Entropy 2018, 20, 234; doi:10.3390/e20040234

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[:0-1] Hans Dieter Baehr, Stephan Kabelac: Thermodynamik: Grundlagen und technische Anwendungen. 15. Auflage. Springer Verlag, Berlin / Heidelberg 2012, ISBN 978-3-642-24160-4, S. 93–176.

[2] Zitat von Max Planck, nach Eintrag zu Hauptsätze. In: Römpp Online. Georg Thieme Verlag, abgerufen am 24. August 2011.

[3] Klaus Langeheinecke: Thermodynamik für Ingenieure. Vieweg, 1993.

[4] Selcuk Cakmak, Ferdi Altintas, Ozgur E. Mustecaplioglu: Irreversible Work and Internal Friction in a Quantum Otto Cycle of a Single Arbitrary Spin. arxiv:1605.02522 (2016).

[5] Pankaj Mehta, Anatoli Polkovnikov: Efficiency bounds for nonequilibrium heat engines. Annals of Physics 332 (2012): 110–126.

[6] Alfred Lottermoser: Kurze Einführung in die Kolloidchemie. Dresden/Leipzig 1944, S. 70–71.

[7] Schlitter, Jürgen: The Second Law of Thermodynamics as a Force Law, Entropy 2018, 20, 234; doi:10.3390/e20040234