Exergie

Exergie bezeichnet den Teil der Gesamtenergie eines Systems, der Arbeit verrichten kann, wenn dieses in das thermodynamische (thermische, mechanische und chemische) Gleichgewicht mit seiner Umgebung gebracht wird. Exergie ist ein Potential zwischen mindestens zwei Zuständen, wobei einer davon meist der Umgebungszustand ist. Die Exergie ist im Gegensatz zur Energie keine Erhaltungsgröße, da sie durch irreversible Prozesse abgebaut wird, d. h. sie wird in Anergie umgewandelt.

Der Begriff Exergie geht zurück auf einen Vorschlag von Zoran Rant aus den 1950er Jahren.[1]

Beispiel

Exergieverluste treten z. B. bei Wärmeübertragungen auf. Wenn aus einem schlecht isolierten Warmwasserrohr Energie in Form von Wärme in die Umgebung fließt, kann diese nicht mehr genutzt werden, um Arbeit zu leisten. Es gilt aber das Energieerhaltungsprinzip: Das Rohr und die Umgebung zusammen besitzen die gleiche Energiemenge wie vor dem Beginn der Wärmeübertragung.

Der zweite Hauptsatz der Thermodynamik (Entropie) schränkt den ersten Hauptsatz bezüglich der möglichen Energieumwandlungen ein. Werden beispielsweise in einer wärmeisolierten (adiabaten) Mischkammer zwei Stoffe verschiedener Temperatur miteinander gemischt, so lassen sich in der Energiebilanzgleichung keine Verluste erkennen, die gesamte Energie im System bleibt gleich.

Trotzdem treten thermodynamische Verluste auf, da durch diesen Vorgang Entropie erzeugt wird. Vorher besitzt das System, das die beiden Stoffe enthält, Exergie, die eine Wärmekraftmaschine beim Temperaturausgleich zwischen den Stoffen nutzen könnte. Nachher ist dies wegen der Allgemeingültigkeit des zweiten Hauptsatzes nicht mehr möglich, diese Exergie wurde vernichtet; es bleibt nur die Exergie, die das gesamte System gegenüber der Umgebung besitzt.

Beispiele für exergetische Verluste sind:

Wärmetransport bei einer endlichen Temperaturdifferenz
Reibung
Mischung bei konstantem Volumen (geschlossenes System) bzw. bei konstantem Druck (Fließprozesse),[2] Ausnahme ideales Gasgemisch.
chemische Reaktionen.

Siehe auch: Carnotisierung, um Exergieverluste gering zu halten.

Anwendung

Das Exergiekonzept liefert ein Werkzeug, mit dem sich zum einen die maximale Nutzarbeit eines Systems oder Stoffstroms berechnen lässt. Zum anderen lassen sich tatsächliche Verluste berechnen. Für ingenieurwissenschaftliche Problemstellungen kann es eine Hilfestellung sein, insbesondere wenn das Exergiekonzept mit wirtschaftlichen Größen verknüpft wird, vgl. mit thermoökonomische Methoden. Gemeinsam mit dem Begriff der Anergie lassen sich damit die beiden Hauptsätze der Thermodynamik auch wie folgt fassen:

Der 1. Hauptsatz der Thermodynamik (Energiesatz) besagt:

In einem abgeschlossenen System bleibt bei reversiblen und irreversiblen Prozessen die Summe aus Exergie und Anergie, also die Energie, konstant (Energieerhaltung).

Der 2. Hauptsatz der Thermodynamik (Entropiesatz) liefert mehrere Schlussfolgerungen:

In einem abgeschlossenen System bleiben bei reversiblen Prozessen Exergie und Anergie jeweils konstant.
Bei irreversiblen Prozessen wird Exergie in Anergie umgewandelt.
Anergie kann nicht in Exergie umgewandelt werden.

In der Literatur liest man häufig pauschal den Zusammenhang:

{\text{Exergie}}+{\text{Anergie}}={\text{Energie}}

wobei Anergie den nicht nutzbaren Teil der Energie kennzeichnet.

Dieser Zusammenhang führt scheinbar zu einem Widerspruch, wenn Prozesse unterhalb der Umgebungstemperatur ablaufen, z. B. bei Kältemaschinen. Unterhalb der Umgebungstemperatur steigt die Exergie eines Systems mit abnehmender Temperatur, da die Temperaturdifferenz zur Umgebung genutzt werden kann, um damit eine Wärmekraftmaschine zu betreiben und so Nutzarbeit zu gewinnen; die innere Energie des Systems sinkt jedoch mit abnehmender Temperatur. Bei einem entsprechenden Systemdruck kann die Exergie eines Systems unterhalb der Umgebungstemperatur größer sein als seine (innere) Energie, was negative Anergie bedeuten würde.[3]

Der Widerspruch löst sich auf, wenn man die Energieflussrichtung berücksichtigt: in diesem Falle fließt Energie, bestehend aus den beiden Anteilen Exergie und Anergie, anders als üblich aus der Umgebung in das System. Die Exergie ist ein Potential, das im betrachteten Fall die Umgebung gegenüber dem System besitzt und nicht umgekehrt. Trotzdem ist es sinnvoll und üblich, den Exergieanteil dem betrachteten System zuzuordnen.

Berechnung

Die Exergie E_sys eines Systems oder Stoffstroms setzt sich zusammen aus

der inneren Exergie E_in
der chemischen Exergie E_chem
der kinetischen Exergie E_kin (entspricht der kinetischen Energie)
der potenziellen Exergie E_pot (entspricht der potenziellen Energie):

E_{\mathrm {sys} }=E_{\mathrm {in} }+E_{\mathrm {chem} }+E_{\mathrm {kin} }+E_{\mathrm {pot} }

oder massenspezifisch:

e_{\mathrm {sys} }=e_{\mathrm {in} }+e_{\mathrm {chem} }+e_{\mathrm {kin} }+e_{\mathrm {pot} }

Innere Exergie eines geschlossenen Systems

Die massenspezifische innere Exergie eines geschlossenen Systems lässt sich wie folgt ermitteln:

e_{\mathrm {in} }=(u-u_{0})+p_{0}(v-v_{0})-T_{0}(s-s_{0})

mit

massenspezifische innere Energie u
massenspezifisches Volumen v
massenspezifische Entropie s
Druck p
Temperatur T.

Der Index ₀ charakterisiert jeweils den Zustand des Systems oder Stoffstroms bei Umgebungsdruck und Umgebungstemperatur im thermodynamischen Gleichgewicht.

Der absolute Wert ergibt sich aus der Multiplikation des spezifischen Wertes mit der Masse m des Systems:

E_{\mathrm {in} }=m_{\mathrm {sys} }\cdot e_{\mathrm {in} }

Exergie eines Stoffstroms

Für die Exergie eines Stoffstroms kann geschrieben werden:

massenspezifischer Wert

e_{\mathrm {str} }=(h-h_{0})-T_{0}(s-s_{0})

mit

massenspezifische Enthalpie h

absoluter Wert

{\dot {E}}_{\mathrm {str} }={\dot {m}}\cdot e_{\mathrm {str} }

Der Punkt über der jeweiligen Größe bezeichnet einen Strom bzw. eine Zeitableitung, also z. B. den Massenstrom

{\dot {m}}=\lim _{\Delta t\rightarrow 0}{\frac {\Delta m}{\Delta t}}

Exergie eines Wärmestroms

{\dot {E}}_{q}=\left(1-{\frac {T_{0}}{T_{m}}}\right){\dot {Q}}<{\dot {Q}}\qquad \mathrm {mit} \,T_{0}<T_{m}

mit

übertragene thermische Leistung (Wärmestrom) ${\dot {Q}}$
Mitteltemperatur $T_{m}$ der Wärmeübertragung.

Exergie durch Arbeit

E_{w}=W+p_{0}\cdot V

mit

Arbeit $W$
Volumenänderungsarbeit $p_{0}\cdot V$ , die vom System an der Umgebung oder von der Umgebung am System geleistet wird.

Exergiebilanzgleichungen

Die Exergie eines Systems kann sich verändern durch die Exergievernichtung ${\dot {E}}_{D}$ im System und im offenen System zusätzlich durch Exergieströme $\sum _{\mathrm {ein} }{\dot {E}}_{\mathrm {ein} }-\sum _{\mathrm {aus} }{\dot {E}}_{\mathrm {aus} }$ , die mit Stoff- und Energieströmen verbunden sind, über die Systemgrenze.

Daher lautet die Exergiebilanzgleichung für ein geschlossenes System:

{\dot {E}}_{sys}=\sum _{j}{\dot {E}}_{q,j}+{\dot {E}}_{w}-{\dot {E}}_{D}

und für ein offenes System:

{\dot {E}}_{sys}=\sum _{j}{\dot {E}}_{q,j}+{\dot {E}}_{w}+\sum _{\mathrm {ein} }{\dot {E}}_{\mathrm {ein} }-\sum _{\mathrm {aus} }{\dot {E}}_{\mathrm {aus} }-{\dot {E}}_{D}

Die Exergievernichtung wird durch Irreversibilitäten während des Prozesses hervorgerufen. Der Zusammenhang zwischen ihr und der Entropieerzeugung ist

{\dot {E}}_{D}=T_{0}\cdot {\dot {S}}_{\text{Erzeugung}}

Unterschied zwischen Exergie und freier Enthalpie

Exergie ist nicht mit der freien Enthalpie G zu verwechseln.

Die freie Enthalpie ist lediglich eine Zustandsfunktion, die den Zustand eines Stoffes mit bestimmter Zusammensetzung bei gegebener Temperatur und gegebenem Druck beschreibt. Sie hängt jedoch nicht von den Parametern der Umgebung wie Umgebungstemperatur, -druck und -feuchte ab.

Exergie dagegen hängt sehr wohl auch von Umgebungstemperatur, Druck und Zusammensetzung ab, da sie mechanische Arbeit darstellt, die man in einer geeigneten Maschine gewinnen kann, wenn man diesen Stoff von gegebener Temperatur und gegebenem Druck bis auf Umgebungstemperatur und -druck abkühlt/anwärmt/entspannt/verdichtet etc. Exergie ist also eine relative Größe zwischen zwei Zuständen und somit keine Funktion eines einzelnen Zustands.

Die Exergie eines Stoffstromes kann man auffassen als Differenz zwischen der freien Enthalpie in gegebenem Zustand und der freien Enthalpie bei Umgebungstemperatur und -druck.

Exergie komprimierter Gase

Exergieflussdiagramm (Sankey-Diagramm) einer Druckluftanlage, Beispiel: Die exergetische Leistung des Druckluftstroms nach Kompression (p₂ = 7,3 bar; T₂ = 80 °C = 353 K;

{\dot {V}}_{2N}

= 0,167 m³/s;

\rho _{\text{N}}

= 1,185 kg/m³) beträgt 39,3 kW. Hinter dem Nachkühler sinkt Druck und Temperatur (p₃ = 7,0 bar; T₃ = 25 °C = 298 K), bei gleichbleibendem Massenstrom. Daher fällt der Exergiestrom auf 36,4 kW, was einem Exergieverlust im Nachkühler von 4,6 % bezogen auf die Eingangsleistung entspricht.

In der Drucklufttechnik und Pneumatik besteht – ebenso wie in anderen technischen Disziplinen – die Notwendigkeit, Anlagenteile und Komponenten qualitativ zu bewerten, indem z. B. Energieverluste und Wirkungsgrade angegeben werden.

Zur Beschreibung des aktuellen Zustands der Druckluft an einer bestimmten Stelle der Anlage erscheint es zunächst plausibel, auf die thermodynamischen Größen der inneren Energie U (geschlossenes System) oder der Enthalpie H (offenes System) zurückzugreifen. Beide Größen bilden zwar den Energiegehalt korrekt ab, über die Nutzbarkeit dieser Energie kann jedoch keine Aussage gemacht werden, da das Energiegefälle gegen die Umgebung in beiden Größen nicht berücksichtigt wird. Dies zeigt sich auch darin, dass sowohl U also auch H lediglich Funktionen der Temperatur sind; der Druck im aktuellen Zustand hat jedoch keinen Einfluss.

Da aber insbesondere in der Pneumatik der Druck als treibende Größe zur Verrichtung mechanischer Arbeit relevant ist, ist mit U und H über den Nutzen des Energiegehalts kaum eine Aussage möglich. Hier kommt die Exergie ins Spiel, die gerade den nutzbaren Anteil des Energiegehalts beschreibt.

Druckabhängige Exergieberechnung

Abhilfe schafft die Verwendung der Exergie als Bilanzgröße. Für die Berechnung des Exergiegehalts im Zustand a aus messbaren Größen werden die drei folgenden Werte benötigt:

Der Absolutdruck p_a
die Temperatur T_a
der zugehörige Volumenstrom ${\dot {V}}_{\text{a}}$ .

Mit diesen Angaben (Index 0 kennzeichnet den Umgebungszustand) berechnet sich die exergetische Leistung des Druckluftstroms zu:

{\dot {E}}_{\text{a}}={\dot {V}}_{\text{a}}\cdot \rho _{\text{a}}\cdot c_{\text{p}}\cdot (T_{\text{a}}-T_{\text{0}})+{\dot {V}}_{\text{a}}\cdot \rho _{\text{a}}\cdot T_{\text{0}}\cdot \left(R_{\text{s}}\cdot \ln {\frac {p_{\text{a}}}{p_{\text{0}}}}-c_{\text{p}}\cdot \ln {\frac {T_{\text{a}}}{T_{\text{0}}}}\right)

mit

dem Massenstrom ${\dot {V}}_{\text{a}}\cdot \rho _{\text{a}}={\dot {m}}_{\text{a}}={\dot {V}}_{\text{N}}\cdot \rho _{\text{N}}$ $\text{[math]}$
- der Dichte $\rho _{\text{a}}$
- dem Normvolumenstrom ${\dot {V}}_{\text{N}}$
- der Normdichte $\rho _{\text{N}}$
der spezifischen Wärmekapazität c_p
der spezifischen Gaskonstante R_s.

Durch die Exergieanalyse lassen sich alle wichtigen Ereignisse in der Wirkungskette erfassen:

auftretende Druckänderungen
Temperaturänderungen
Veränderungen des Massenstroms (z. B. durch Leckage).

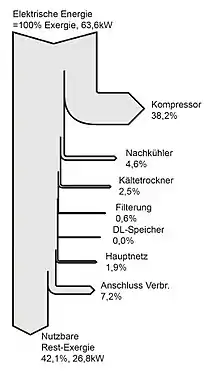
Ein Zustand kann ein bestimmter Punkt in der Wirkungskette sein, also z. B. der Endzustand der Druckluft nach der Komprimierung. Der Vergleich zweier Zustände erlaubt die Berechnung des Exergieverlustes zwischen zwei Zuständen. Setzt man diesen in prozentuale Relation zur Ausgangsenergie, so erhält man den prozentualen Exergieverlust an jeder Station der Wandlungskette.

Eine grafische Darstellung der Verluste kann beispielsweise in Form eines Sankey-Diagramms erfolgen (Abbildung rechts). Die exergetische Analyse von Energieflüssen bietet eine anschauliche und nachvollziehbare Methode, um Druckluftanlagen qualitativ zu bewerten, Verluste aufzuzeigen und eine Vergleichsbasis für die Bewertung von Anlagen und Anlagenteilen zu schaffen.

Beispiel: Berechnung der Exergie in einem Fahrradreifen

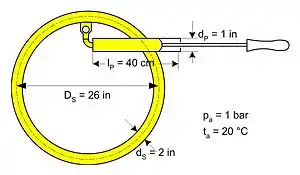
Exergie komprimierter Luft: Aufpumpen eines Fahrradreifens

Ein Fahrradreifen soll mit einer Handpumpe gemäß nebenstehender Skizze ausgehend von einem Außendruck von 1 bar auf 4 bar aufgepumpt werden. Es ist die dazu mindestens erforderliche Arbeit zu ermitteln. Diese Mindestarbeit entspricht der im Reifen nach dem Aufpumpen enthaltenen Exergie. Bei einem reversiblen Vorgang sind die Verluste Null und die aufzubringende Arbeit minimal. Damit muss eine isotherme Kompression angenommen werden, also ein Vorgang, der theoretisch reibungsfrei ist und unendlich lange Zeit dauert, um eine Erwärmung zu vermeiden. Zur Berechnung der Pumparbeit wird vereinfachend ein Kolbenvolumen vom dreifachen Schlauchvolumen angenommen, das den Verdichtungsvorgang mit einem einzigen Hub leisten kann. Dann ist bereits am Anfang in dem System Reifen plus Pumpe die gesamte Masse $m_{2}$ des Gases bei Umgebungszustand enthalten. Mit dem Kolbenhub wird das Gesamtvolumen nun auf das Volumen des Reifens komprimiert. Ohne Reibung und mit (unendlich) viel Zeit kann ein isothermer Vorgang ablaufen, d. h. ohne Verluste.

Berechnung des Volumens bzw. der Masse

Schlauchvolumen:

V_{\mathrm {S} }=\pi ^{2}\cdot D_{\mathrm {S} }\cdot {\frac {d_{\mathrm {S} }^{2}}{4}}=4{,}205\,\mathrm {l}

Ausgangsvolumen:

V_{\mathrm {A} }=V_{\mathrm {S} }+3\cdot V_{\mathrm {S} }

Schlauchinhalt 1 im Ausgangszustand:

m_{1}={\frac {p_{\mathrm {a} }\cdot V_{\mathrm {S} }}{R_{\mathrm {s} }\cdot T_{\mathrm {a} }}}=0{,}005\,\mathrm {kg} \quad {\text{mit}}\quad R_{\mathrm {s} }=287\mathrm {\frac {J}{kg\cdot K}}

Schlauchinhalt 2 im Endzustand:

m_{2}={\frac {p_{2}\cdot V_{\mathrm {S} }}{R_{\mathrm {s} }\cdot T_{\mathrm {a} }}}=0{,}020\,\mathrm {kg}

Berechnung der Arbeit

Volumenänderungsarbeit entlang der Isotherme:

W_{1,2,\mathrm {V} }=m_{2}\cdot R_{\mathrm {s} }\cdot T_{\mathrm {0} }\cdot \ln {\left({\frac {p_{\mathrm {a} }}{p_{\mathrm {0} }}}\right)}=2{,}332\,\mathrm {kJ}

Verschiebearbeit durch die Atmosphäre:

W_{\mathrm {VA} }=3\cdot V_{\mathrm {S} }\cdot p_{\mathrm {0} }=1{,}262\,\mathrm {kJ}

Verdichterarbeit durch die Pumpe:

W_{\mathrm {H} }=W_{1,2,\mathrm {V} }-W_{\mathrm {VA} }=1{,}07\,\mathrm {kJ}

Mit der Berechnung der Exergie E_x über die Gleichung für das geschlossene System kommt man zum selben Ergebnis:

{\begin{aligned}E_{\mathrm {x} }&=(U-U_{\mathrm {0} })+p_{\mathrm {0} }\cdot (V-V_{\mathrm {0} })-T_{\mathrm {0} }\cdot (S-S_{\mathrm {0} })\quad {\text{mit}}\quad T_{\mathrm {0} }=T_{\mathrm {a} }=T_{\mathrm {1} }=T_{\mathrm {2} }{\text{;}}\qquad V_{\mathrm {0} }={\frac {m_{2}\cdot R_{\mathrm {s} }\cdot T_{\mathrm {0} }}{p_{\mathrm {0} }}}\\E_{\mathrm {x} }&=m_{2}\cdot \left[c_{\mathrm {p} }\cdot (T_{2}-T_{\mathrm {0} })+T_{\mathrm {0} }\cdot \left(R_{\mathrm {s} }\cdot \ln {\left({\frac {p_{\mathrm {2} }}{p_{\mathrm {0} }}}\right)}-c_{\mathrm {p} }\cdot \ln {\left({\frac {T_{2}}{T_{\mathrm {0} }}}\right)}\right)\right]-p_{\mathrm {0} }\cdot (V_{\mathrm {0} }-V_{\mathrm {S} })\\E_{\mathrm {x} }&=m_{2}\cdot \left[T_{\mathrm {0} }\cdot R_{\mathrm {s} }\cdot \ln \left({\frac {p_{\mathrm {2} }}{p_{\mathrm {0} }}}\right)\right]-p_{\mathrm {0} }\cdot V_{\mathrm {P} }=1{,}07\,\mathrm {kJ} \end{aligned}}

Die real aufzubringende Arbeit ist wegen der endlichen Zeit zum Komprimieren, wobei sich die Luft erwärmt und infolgedessen ein höherer Gegendruck zu überwinden ist, und durch Reibungsverluste im Ventil und am Kolben, insbesondere durch den Schadraum in der Pumpe, wesentlich größer; sie kann durchaus das Doppelte betragen.

Siehe auch

Literatur

Hans Dieter Baehr, Stephan Kabelac: Thermodynamik. Grundlagen und technische Anwendungen. 13., neu bearbeitete und erweiterte Auflage. Springer, Berlin u. a. 2006, ISBN 3-540-32513-1 (Springer-Lehrbuch).
Jochen Fricke, Walter L. Borst: Energie. Ein Lehrbuch der physikalischen Grundlagen. Oldenbourg Verlag, München/ Wien 1981, Kap. 2: Exergie und Energie.
Adrian Bejan, George Tsatsaronis, Michael Moran: Thermal Design and Optimization. Wiley, New York NY u. a. 1996, ISBN 0-471-58467-3.
Zoran Rant: Exergie, ein neues Wort für technische Arbeitsfähigkeit. In: Forschung auf dem Gebiete des Ingenieurwesens. 22, 1956, ZDB-ID 212959-0, S. 36–37.
Jan Szargut: Exergy Method. Technical and Ecological Applications. WIT Press, Southampton u. a. 2005, ISBN 1-85312-753-1 (Developments in heat transfer 18).

Weblinks

Einzelnachweise

Vorgestellt auf der VDI-Wärmetagung in Lindau, 1953, zitiert nach Fran Bošnjaković, Karl-Friedrich Knoche: Technische Thermodynamik Teil. 8. Auflage. Steinkopff Verlag, Darmstadt 1998, ISBN 978-3-642-63818-3.; Als weitere Quelle verweist Bošnjaković auf Forschung auf dem Gebiete des Ingenieurwesens. 22, (1956), S. 36.
Zur reversiblen Mischung siehe Abschnitt 7.6 „Entropie idealer Gasgemische“ in Bošnjaković/Knoche: Technische Thermodynamik Teil 1. 8. Auflage. Steinkopff-Verlag, Darmstadt 1998, ISBN 978-3-642-63818-3.
Christoph Kail: Analyse von Kraftwerksprozessen mit Gasturbinen unter energetischen, exergetischen und ökonomischen Aspekten. In: Dissertation an der TU München. Lehrstuhl für Thermische Kraftanlagen mit Heizkraftwerk, März 1998, abgerufen am 25. Juni 2018. S. 11f.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Vorgestellt auf der VDI-Wärmetagung in Lindau, 1953, zitiert nach Fran Bošnjaković, Karl-Friedrich Knoche: Technische Thermodynamik Teil. 8. Auflage. Steinkopff Verlag, Darmstadt 1998, ISBN 978-3-642-63818-3.; Als weitere Quelle verweist Bošnjaković auf Forschung auf dem Gebiete des Ingenieurwesens. 22, (1956), S. 36.

[2] Zur reversiblen Mischung siehe Abschnitt 7.6 „Entropie idealer Gasgemische“ in Bošnjaković/Knoche: Technische Thermodynamik Teil 1. 8. Auflage. Steinkopff-Verlag, Darmstadt 1998, ISBN 978-3-642-63818-3.

[3] Christoph Kail: Analyse von Kraftwerksprozessen mit Gasturbinen unter energetischen, exergetischen und ökonomischen Aspekten. In: Dissertation an der TU München. Lehrstuhl für Thermische Kraftanlagen mit Heizkraftwerk, März 1998, abgerufen am 25. Juni 2018. S. 11f.