Rotverschiebung

Die Rotverschiebung ist in der Astronomie die Lageveränderung identifizierter Spektrallinien im Emissions- und Absorptionsspektrum astronomischer Objekte in Richtung der größeren Wellenlängen. Die Rotverschiebung ist definiert als Verhältnis der Wellenlängenänderung zur ursprünglichen Wellenlänge:

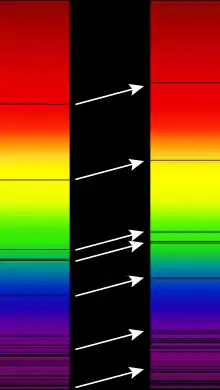
z:={\frac {\Delta \lambda }{\lambda _{0}}}={\frac {\lambda _{\text{beobachtet}}-\lambda _{0}}{\lambda _{0}}}={\frac {\lambda _{\text{beobachtet}}}{\lambda _{0}}}-1

Illustration der Rotverschiebung der Spektrallinien für einen weit entfernten Supergalaxienhaufen rechts im Vergleich zur Sonne links

Der Name bezieht sich auf das rote Licht am langwelligen Ende des sichtbaren Spektrums. Bei Infrarot-Emission verschieben sich die Spektrallinien entsprechend in die Richtung der noch längerwelligen Terahertzstrahlung. Eine Verschiebung zu kürzeren Wellenlängen wird als Blauverschiebung bezeichnet.

Festgestellt wird die Rotverschiebung durch den Vergleich bekannter Atom- und Molekülspektren mit den mittels Spektroskopie gemessenen Werten, d. h. nach Analyse der Spektrallinien der Emissionen oder Absorptionen im Sternenlicht, beispielsweise des Wasserstoffs.

Von Bedeutung ist der Effekt auch in der Molekülspektroskopie, wo nach elastischer Streuung mit Energieübertragung Photonen niedrigerer Energie auftreten.

Ursachen

Ursachen der Rotverschiebung können sein:

Eine Relativbewegung von Quelle und Beobachter (Doppler-Effekt)
Unterschiedliche Gravitationspotentiale von Quelle und Beobachter (Relativität)
Das expandierende Universum zwischen Quelle und Beobachter (Kosmologie)
Stokes-Shift bei der Übertragung diskreter Energiebeträge zwischen Photonen und Molekülen bei der Raman-Streuung

Die ersten drei dieser Ursachen werden im Folgenden näher erläutert.

Rot- und Blauverschiebung durch relative Bewegung

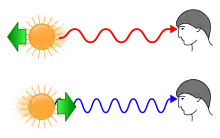
Bewegung einer Lichtquelle relativ zum Beobachter

Rot- und Blauverschiebung sind Begriffe aus der Spektroskopie, bei der man Spektrallinien von Atomkernen, Atomen und Molekülen untersucht. Diese können in Absorption oder Emission auftreten, je nachdem, ob Energie aufgenommen oder abgegeben wird. Die Energie wird durch elektromagnetische Strahlung in Form von Photonen ausgetauscht, ist also gequantelt. Wo sich die Spektrallinien im Spektrum befinden, hängt nicht nur von den Einzelheiten des Quantenübergangs ab, sondern auch vom Bewegungszustand der Strahlungsquelle relativ zum Beobachter (Dopplereffekt) und von der Krümmung der Raumzeit.

Befindet man sich im Ruhesystem des Emitters (Relativgeschwindigkeit null zwischen Emitter und Beobachter), so misst man die Spektrallinie bei ihrer Ruhewellenlänge. Nun kann aber auch eine Relativbewegung zwischen Strahlungsquelle und Detektor vorliegen. Wesentlich ist nur diejenige Geschwindigkeitskomponente, die in Richtung des Detektors zeigt. Diese Komponente heißt Radialgeschwindigkeit. Ihr Betrag ist die Relativgeschwindigkeit zwischen Emitter und Beobachter. Elektromagnetische Strahlung bewegt sich sowohl bei der Emission als auch bei der Absorption mit der Lichtgeschwindigkeit, gleichgültig wie schnell sich Quelle und Ziel relativ zueinander bewegen.

Bewegt sich die Strahlungsquelle vom Beobachter weg, so wird die Spektrallinie zu größeren, roten Wellenlängen hin verschoben. Die Welle wird gewissermaßen auseinandergezogen. Dies nennt man Rotverschiebung. Bewegt sich die Strahlungsquelle auf den Beobachter zu, so wird die Spektrallinie zu kleineren Wellenlängen hin verschoben. Dies ist gerade die Blauverschiebung, weil die Linie zum blauen Teil des Spektrums verschoben wird. Anschaulich kann man sich vorstellen, wie die elektromagnetische Welle gestaucht wird.

Die ganze atomare und molekulare Welt ist aufgrund der Thermodynamik in Bewegung. Bei endlicher Temperatur bewegen sich diese Strahler geringfügig um eine Ruhelage. Spektrallinien haben deshalb eine natürliche Breite aufgrund atomarer Bewegung und Molekularbewegung, weil sie sich relativ zum Detektor immer ein wenig vor und zurückbewegen. Dieses Phänomen nennen Physiker thermische Dopplerverbreiterung. Die Ruhewellenlänge ist also nicht beliebig scharf. Das kann sie auch aufgrund der Heisenbergschen Unschärfe der Quantentheorie nicht sein.

Die spezielle Relativitätstheorie gibt für den Zusammenhang zwischen Radialgeschwindigkeit v und Dopplerverschiebung z den folgenden Zusammenhang (mit der Lichtgeschwindigkeit $c$ ):

z={\sqrt {\frac {1+{\frac {v}{c}}}{1-{\frac {v}{c}}}}}-1

und umgekehrt

{\frac {v}{c}}={\frac {(1+z)^{2}-1}{(1+z)^{2}+1}}

Bei niedrigen Geschwindigkeiten ( $v/c\ll 1$ ) kann dieser Zusammenhang durch $z\approx v/c$ genähert werden.

Gravitative Rot- und Blauverschiebung

Die gravitative Rotverschiebung oder Gravitations-Rotverschiebung im Rahmen der allgemeinen Relativitätstheorie ist eine Wellenlängenvergrößerung für abgestrahltes Licht, also für Licht, das sich von einem Gravitationszentrum entfernt. Bei der gravitativen Blauverschiebung oder Gravitations-Blauverschiebung handelt es sich um den umgekehrten Effekt einer Wellenlängenverkürzung für einfallendes Licht, also für Licht, das sich auf ein Gravitationszentrum zubewegt.

„Photons climbing out of a gravitating object become less energetic. This loss of energy is known as a “redshifting”, as photons in the visible spectrum would appear more red. Similarly, photons falling into a gravitational field become more energetic and exhibit a blueshifting. […] Note that the magnitude of the redshifting (blueshifting) effect is not a function of the emitted angle or the received angle of the photon – it depends only on how far radially the photon had to climb out of (fall into) the potential well.“

„Photonen, die von einer gravitierenden Masse aufsteigen, werden energieärmer. Dieser Energieverlust ist als „Rotverschiebung“ bekannt, da Photonen im sichtbaren Spektrum mehr rot erscheinen würden. In ähnlicher Weise werden Photonen, die in einem Gravitationsfeld fallen, energiereicher und zeigen eine Blauverschiebung. […] Dabei ist zu beachten, dass die Größe des Effektes der Rotverschiebung (Blauverschiebung) keine Funktion des Abstrahl- oder Empfangswinkels des Photons ist – sie hängt nur davon ab, wieweit das Photon im Potentialfeld radial aufgestiegen (gefallen) ist.“

– R. J. Nemiroff: Gravitational Principles and Mathematics.[1]

Die gravitative Rotverschiebung ist eine direkte Folge der gravitativen Zeitdilatation. Sie ist streng genommen kein Effekt der allgemeinen Relativitätstheorie, sondern folgt bereits aus der speziellen Relativitätstheorie und dem Äquivalenzprinzip der allgemeinen Relativitätstheorie. Licht, das von einer Lichtquelle mit einer gegebenen Frequenz nach oben (also vom Gravitationszentrum weg) ausgestrahlt wird, wird dort mit einer geringeren Frequenz gemessen. Das bedeutet also insbesondere, dass bei einem Lichtsignal mit einer bestimmten Anzahl von Schwingungen der zeitliche Abstand zwischen dem Beginn und dem Ende des Signals beim Empfänger größer ist als beim Sender. Dies wird durch die gravitative Zeitdilatation verständlich.

Gravitative Rotverschiebung einer Lichtwelle

Aufgrund der gravitativen Zeitdilatation ist das Zeitintervall zwischen Anfang und Ende der Lichtwelle umso länger, je weiter nach oben man sich im Gravitationsfeld bewegt, weil die Zeit zunehmend schneller verstreicht. Das bedeutet, dass die Welle bei ihrer Bewegung nach oben immer länger gemessen wird. Daher muss auch der Abstand zwischen den einzelnen Wellenbergen immer mehr wachsen, sodass das Licht immer langwelliger, also energieärmer erscheint.

Die gravitative Rotverschiebung wurde von Einstein bereits 1911 vor Fertigstellung der allgemeinen Relativitätstheorie vorausgesagt und kann bereits aus der Energieerhaltung hergeleitet werden, sodass ihre experimentelle Bestätigung zwar notwendige Voraussetzung für die Gültigkeit der allgemeinen Relativitätstheorie ist, aber andererseits nicht sehr große Aussagekraft hat. Von W. S. Adams wurde 1925 die Rotverschiebung am Weißen Zwerg Sirius B nachgewiesen. Die Messung der gravitativen Rotverschiebung an Weißen Zwergen ist aber schwierig von der Rotverschiebung durch die Eigenbewegung zu unterscheiden, und die Genauigkeit ist begrenzt. Robert Pound und Glen Rebka wiesen 1960 mit Hilfe des Mößbauer-Effektes die gravitative Rotverschiebung der Strahlung einer Gammaquelle im Erdgravitationsfeld bei einem Höhenunterschied von nur 25 m mit ausreichender Genauigkeit nach (Pound-Rebka-Experiment). Spätere Verbesserungen (Pound-Rebka-Snider-Experiment) erreichten eine Genauigkeit von etwa 1,5 %. Die gravitative Rotverschiebung wurde mittels Raumsonden auch für die Sonne und den Saturn nachgewiesen. Der geplante Satellit OPTIS soll, neben anderen Tests zur speziellen und allgemeinen Relativitätstheorie, die gravitative Rotverschiebung mit einer Genauigkeit von 10⁻⁵ testen. 2018 wurde die gravitative Rotverschiebung beim Stern S2 bei dessen größter Annäherung an das Schwarze Loch in Sagittarius A im Zentrum der Milchstraße nachgewiesen.[2]

Die Entwicklung von Atomuhren hat es möglich gemacht, den Einfluss der Gravitation auf die Zeit auch direkt zu messen. Im Prinzip ist diese Messung eine Variation der Nachweise der gravitativen Rotverschiebung. 1971 wurde durch Josef Hafele und Richard Keating (Hafele-Keating-Experiment) mit Caesiumuhren in Flugzeugen der durch die Gravitation verursachte Gangunterschied von Uhren in verschiedenen Höhen gemäß der allgemeinen Relativitätstheorie mit etwa 10 % Genauigkeit eindeutig nachgewiesen. Durch ein ähnliches Experiment von C. Alley (Maryland-Experiment) konnte die Genauigkeit 1976 auf 1 % gesteigert werden. Robert Vessot und Martin Levine publizierten 1979 Ergebnisse eines ähnlichen Experiments mit Hilfe von Raketen und gaben eine Genauigkeit von 0,02 % an. Beim heutigen satellitengestützten GPS-Navigationssystem müssen Korrekturen sowohl gemäß der speziellen als auch der allgemeinen Relativitätstheorie berücksichtigt werden, wobei Effekte durch die allgemeine Relativitätstheorie überwiegen. Umgekehrt kann dies auch als Bestätigung dieser Theorien angesehen werden.

Gravitative Rotverschiebung verschiedener Himmelsobjekte für einen Beobachter im Unendlichen
Planet/Stern	Rotverschiebung	Stern	Rotverschiebung
Erde	7,0 ⋅ 10⁻¹⁰	Naos	6,2 ⋅ 10⁻⁶
Jupiter	2,0 ⋅ 10⁻⁸⁰	Sirius B	2,4 ⋅ 10⁻⁴
Mira	6,4 ⋅ 10⁻⁹⁰	BPM 37093	8,0 ⋅ 10⁻⁴
Beteigeuze	4,3 ⋅ 10⁻⁸⁰	Neutronenstern mit 1,4 M_☉	0,24
Pollux	4,3 ⋅ 10⁻⁷⁰	Neutronenstern mit 1,8 M_☉	0,34
Sonne	2,1 ⋅ 10⁻⁶⁰	Schwarzes Loch, Ereignishorizont	unendlich

Die Rotverschiebung z ergibt sich für schwache Gravitationsfelder angenähert zu

z={\frac {GM}{rc^{2}}}

mit der Gravitationskonstanten G, der Masse des Objekts M und der Lichtgeschwindigkeit c. Das Licht wird im Abstand r vom Zentrum des Objekts ausgesandt. Für das Beispiel Erde und r = 6378 km ergibt sich der Tabellenwert von z = 7,0 ⋅ 10⁻¹⁰.

Bei starken Gravitationsfeldern, wie sie beispielsweise von Neutronensternen erzeugt werden, gilt für z:

z=\left(1-{\frac {2\;\!GM}{rc^{2}}}\right)^{\!-1/2}-1

Für die Beispiele von Neutronensternen mit dem jeweils gleichen Radius r = 12 km ergeben sich die Tabellenwerte von z = 0,24 für den masseärmeren und z = 0,34 für den massereicheren Neutronenstern.

Ein Beobachter, der sich relativ zum Schwerpunkt einer nichtrotierenden Masse auf der radialen Koordinate $r_{1}$ befindet, erhält ein Signal, das von einem sich auf $r_{2}$ befindlichen Beobachter gesendet wird, um den Faktor

{\frac {f_{\text{empfangen}}}{f_{\text{gesendet}}}}={\frac {\lambda _{\text{gesendet}}}{\lambda _{\text{empfangen}}}}={\sqrt {\frac {1-r_{\mathrm {s} }/r_{2}}{1-r_{\mathrm {s} }/r_{1}}}}={\frac {1}{1+z}}

rot- bzw. blauverschoben. Die $r$ -Koordinate ist in Schwarzschild-Koordinaten gegeben, mit dem Schwarzschildradius $\textstyle r_{\mathrm {s} }={\frac {2GM}{c^{2}}}$ .

Kosmologische Rotverschiebung

Die Expansion des Universums darf nicht so verstanden werden, dass sich Galaxien in der Raumzeit voneinander entfernen (Relativbewegung). Es ist der Raum selbst, der sich ausdehnt, die Galaxien werden mitbewegt. Gravitativ gebundene Objekte wie Galaxien oder Galaxienhaufen expandieren nicht, denn sie sind durch ihre Eigengravitation von der allgemeinen Expansionsbewegung (beschrieben durch die Friedmann-Gleichungen) entkoppelt. Dies gilt insbesondere auch für Objekte, die sich innerhalb solcher gravitativ gebundener Systeme befinden (Sterne, Planeten) sowie für elektromagnetisch gebundene Systeme wie Atome und Moleküle. Einer elektromagnetischen Welle hingegen, die sich frei durch eine sich ausdehnende Raumzeit ausbreitet, wird die Expansionsbewegung direkt aufgeprägt: Vergrößert sich die Raumzeit während der Laufzeit um einen Faktor $n$ , so geschieht dies auch mit der Wellenlänge des Lichtes.

Diese kosmologische Rotverschiebung ist grundsätzlich von der Rotverschiebung durch den Dopplereffekt zu unterscheiden, die nur von der relativen Geschwindigkeit der Galaxien bei der Emission und der Absorption abhängt. Die aus der kosmologischen Rotverschiebung abgeleiteten Fluchtgeschwindigkeiten ferner Galaxien sind demnach direkt auf die Ausdehnung der Raumzeit zurückzuführen (Rezessionsgeschwindigkeit). Bereits ab Entfernungen von wenigen 100 Megaparsec ist der Anteil des Dopplereffekts verschwindend gering. Ferner ergibt sich aus der allgemeinen Relativitätstheorie, dass die beobachteten Fluchtgeschwindigkeiten keine relativistischen Zeiteffekte hervorrufen, wie sie von der speziellen Relativitätstheorie für Bewegungen im Raum beschrieben werden. Eine kosmologische Zeitdilatation findet dennoch statt, da die später ausgesandten Photonen eines Objektes aufgrund der Expansion eine größere Wegstrecke zurücklegen müssen. Physikalische Prozesse erscheinen daher bei rotverschobenen Objekten (aus unserer Sicht) zunehmend verlangsamt abzulaufen.

Rotverschiebung, Blauverschiebung und Kosmologie

Das Licht von Galaxien ist in den allermeisten Fällen rotverschoben (bereits unter den nächstgelegenen 1000 sind es etwa 75 Prozent). Je weiter eine Galaxie entfernt ist, desto stärker ist im Mittel die Rotverschiebung. Nur wenige relativ nahe Galaxien zeigen aufgrund zusätzlicher „eigener“ Bewegung (Pekuliargeschwindigkeit) relativ zur Erde auf uns zu insgesamt eine Blauverschiebung. Ein Beispiel dafür ist der Andromedanebel.

Vesto Slipher führte ab 1912 spektroskopische Beobachtungen von Galaxien durch und bestimmte deren Radialgeschwindigkeiten aus den Linienverschiebungen. Er erkannte bald, dass die meisten der von ihm beobachteten Galaxien eine Rotverschiebung aufwiesen.[3] 1929 entdeckte Edwin Hubble den Zusammenhang von Rotverschiebung und Entfernung der Galaxie. Zunächst wurde der Effekt als Dopplereffekt interpretiert, bald aber auf die Expansion des Raumes zurückgeführt. Die kosmologische Rotverschiebung nimmt mit der Galaxienentfernung gemäß der Hubble-Konstante zu, weshalb man die Entfernungen durch Messung der Rotverschiebung abschätzen kann.

Je höher die Rotverschiebung eines astronomischen Objekts, desto länger war das von ihm ausgesandte Licht unterwegs und desto weiter zurück in der Vergangenheit sehen wir es. Aus der Rotverschiebung kann auch die Entfernung des Objekts bestimmt werden, allerdings ist diese in einer sich ausdehnenden Raumzeit nicht mehr eindeutig definiert. Es gibt verschiedene Entfernungsmaße, die sich aus der Rotverschiebung ableiten lassen. In der Kosmologie werden Betrachtungen und Rechnungen deshalb immer im Rotverschiebungsraum angestellt.

Im Oktober 2010 haben Astronomen mit Hilfe des Very Large Telescope nachweisen können, dass das Licht der zuvor mit dem Hubble-Weltraumteleskop entdeckten Galaxie UDFy-38135539 13,1 Milliarden Jahre zu uns unterwegs war. Mit dem damaligen Rotverschiebungsrekord von z = 8,6 erreichte uns erstmals beobachtetes Licht, das nur 700 Millionen Jahre nach dem Urknall ausgesandt wurde; die Galaxie entstand damit in einer Zeit, in der das Universum noch nicht vollständig transparent und um den Faktor 9,6 kleiner war.[4][5]

Mit der Entdeckung der Galaxie UDFj-39546284 in der Hubble-Ultra-Deep-Field-09-Aufnahme (HUDF09) konnte eine kosmologische Rotverschiebung von z = 10,3 ermittelt werden. Der beobachtete Altersrekord verschiebt sich damit auf 480 Millionen Jahre danach. Die neu entdeckte Galaxie mit ihrem Alter von 13,2 Milliarden Jahren würde bei einer Bestätigung der Rotverschiebung einen wichtigen Beobachtungsbaustein zur Entwicklung der ersten Galaxien nach dem Urknall liefern.[6][7][8]

Der Sachs-Wolfe-Effekt erklärt Fluktuationen der Rotverschiebung der Photonen der kosmischen Hintergrundstrahlung.

Relativistische Herleitung

Man betrachte ein Photon, emittiert von einer Galaxie mit mitbewegter Entfernung $w$ (siehe auch die relativistische Herleitung der Friedmann-Gleichungen), und absorbiert vom Beobachter bei $w=0$ . Sowohl die Galaxie als auch der Beobachter folgen der kosmischen Expansion. Orientiert man das beschreibende Koordinatensystem so, dass das Photon entlang dessen polarer Achse läuft, dann lautet das Linienelement des Photons:

\mathrm {d} s^{2}=0=-c^{2}\,\mathrm {d} t^{2}+a^{2}(t)\,\mathrm {d} w^{2},

wobei

$c$ die Lichtgeschwindigkeit darstellt
$a(t)$ den Skalenfaktor
$w$ die mitbewegte Radialkoordinate.

Zwei aufeinanderfolgende Maxima der Lichtwelle werden zu den kosmologischen Zeiten $t_{\mathrm {e1} }$ und $t_{\mathrm {e2} }$ ausgesandt sowie zu den Zeiten $t_{\mathrm {a1} }$ und $t_{\mathrm {a2} }$ wieder absorbiert. Die Wellenlängen des Photons zu Zeiten der Emission und Absorption sind dann:

\lambda _{e}=c\ (t_{\mathrm {e} 2}-t_{\mathrm {e} 1})

\lambda _{a}=c\ (t_{\mathrm {a} 2}-t_{\mathrm {a} 1})

Die mitbewegte Entfernung, die von beiden Maxima zurückgelegt wird, ist per definitionem gleich groß. Integriert man das Linienelement des Photons, so erhält man:

0=\int _{t_{\mathrm {e2} }}^{t_{\mathrm {a2} }}a^{-1}(t)\,{\mathrm {d} }t\;-\int _{t_{\mathrm {e1} }}^{t_{\mathrm {a1} }}a^{-1}(t)\,{\mathrm {d} }t

Durch Vertauschen der Integrationsgrenzen ergibt sich dann für infinitesimal kleine Intervalle zwischen Emission (Absorption) der beiden Maxima:

0=\int _{t_{\mathrm {a} 1}}^{t_{\mathrm {a} 2}}a^{-1}(t)\,{\mathrm {d} }t\;-\int _{t_{\mathrm {e} 1}}^{t_{\mathrm {e} 2}}a^{-1}(t)\,{\mathrm {d} }t={\frac {t_{\mathrm {a} 2}-t_{\mathrm {a} 1}}{a(t_{\mathrm {a} 1})}}-{\frac {t_{\mathrm {e} 2}-t_{\mathrm {e} 1}}{a(t_{\mathrm {e} 1})}}

Unter Verwendung der emittierten und absorbierten Wellenlängen wie sie oben angegeben sind, kann man deren Verhältnis ableiten:

{\frac {\lambda _{\mathrm {a} }}{\lambda _{\mathrm {e} }}}={\frac {t_{\mathrm {a} 2}-t_{\mathrm {a} 1}}{t_{\mathrm {e} 2}-t_{\mathrm {e} 1}}}={\frac {a(t_{\mathrm {a} 1})}{a(t_{\mathrm {e} 1})}}

Schließlich definiert man dann folgendermaßen die kosmologische Rotverschiebung:

z:={\frac {\lambda _{\mathrm {a} }-\lambda _{\mathrm {e} }}{\lambda _{\mathrm {e} }}}={\frac {a(t_{\mathrm {a} })}{a(t_{\mathrm {e} })}}-1

Da für die meisten Zwecke der Absorptionszeitpunkt $t_{\mathrm {a} }$ mit der heutigen Zeit $t=t_{0}$ zusammenfällt und $a(t_{0})=1$ gilt, ergibt sich vereinfacht:

z={\frac {1}{a(t)}}-1

Umgekehrt ergibt sich hieraus unmittelbar der Skalenfaktor des Universums zum Emissionszeitpunkt im Vergleich zum heutigen Wert:

a={\frac {1}{1+z}}

Beobachtet man beispielsweise eine Galaxie mit Rotverschiebung $z=3$ , so hatte das Universum zum Zeitpunkt der Aussendung des von uns empfangenen Lichts nur ein Viertel seiner Größe. Sämtliche physikalischen Prozesse in dieser Galaxie laufen aus der Sicht des Beobachters um einen Faktor $1+z=4$ verlangsamt ab, da sich der Abstand zweier nacheinander emittierter Photonen entsprechend vergrößert, und damit auch deren Eintreffen beim Beobachter (kosmologische Zeitdilatation). Ein bekanntes Beispiel hierfür ist die zunehmende Streckung der Lichtkurven von Supernovae vom Typ Ia, deren Zustandekommen gut verstanden ist, mit wachsender Rotverschiebung.

Messmethoden

In der Astronomie wird die Rotverschiebung durch Methoden der Spektralanalyse gemessen; sie sind heute durch digitale statt fotografischer Erfassung wesentlich genauer geworden. Doch um Spektrallinien gut erfassen zu können, müssen die Galaxien eine gewisse Mindesthelligkeit aufweisen. Rotverschiebungen von Galaxien werden im Rahmen von Durchmusterungen wie dem Sloan Digital Sky Survey regelmäßig neu bestimmt.

Die Gravitative Rotverschiebung konnte mit Hilfe des Mößbauereffekts in Laborexperimenten auf der Erde beobachtet werden (siehe Pound-Rebka-Experiment).

Siehe auch

Bathochromer Effekt

Literatur

Stuart Clark: Redshift. Univ. of Hertfordshire Press, Hatfield 1997, ISBN 0-900458-79-8.
George B. Field: The redshift controversy. Addison-Wesley, Redwood 1973, ISBN 0-8053-2512-3.
Rainer Kayser: Licht und Asche des Urknalls. (Memento vom 16. September 2010 im Internet Archive). In: Sterne und Weltraum. Special 2 – Schöpfung ohne Ende. S. 106–117 (online auf mpia-hd.mpg.de).

Weblinks

Commons: Rotverschiebung – Album mit Bildern, Videos und Audiodateien

Wiktionary: Rotverschiebung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

R. J. Nemiroff: II. Gravitational Principles and Mathematics. In: Distortions Paper Principles and Mathematics. Abgerufen am 29. Dezember 2020.
siehe auch Robert J. Nemiroff: Visual distortions near a neutron star and black hole. In: American Journal of Physics. Band 61, Nr. 7, 1. Juli 1993, S. 619–632, doi:10.1119/1.17224.
Gravity Collaboration (R. Abuter u. a.): Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. In: Astronomy & Astrophysics. Band 615, 2018, L 15, DOI:10.1051/0004-6361/201833718.
V. M. Slipher: Spectrographic Observations of Nebulae. In: Popular Astronomy. In: Vol. 23. 1915, S. 21–24.
Forscher schauen ans Ende des Universums. Bei: stern.de. 20. Oktober 2010.
M. D. Lehnert u. a.: Spectroscopic confirmation of a galaxy at redshift z = 8.6. In: Nature.com. 467, 2010, S. 940–942.
NASA’s Hubble Finds Most Distant Galaxy Candidate Ever Seen in Universe. Auf: NASA Hubble Mission Page. 26. Januar 2011.
R. J. Bouwens u. a.: A candidate redshift z ≈ 10 galaxy and rapid changes in that population at an age of 500 Myr. In: Nature.com. 469, 2011, S. 504–507.
R. J. Bouwens u. a.: Searches and limits for z˜10 galaxies in the HST HUDF09 Data. In: Supplementary Information for Nature Letter. (PDF; 731 kB. (Memento vom 21. September 2011 im Internet Archive). In: Nature.com.).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] R. J. Nemiroff: II. Gravitational Principles and Mathematics. In: Distortions Paper Principles and Mathematics. Abgerufen am 29. Dezember 2020.
siehe auch Robert J. Nemiroff: Visual distortions near a neutron star and black hole. In: American Journal of Physics. Band 61, Nr. 7, 1. Juli 1993, S. 619–632, doi:10.1119/1.17224.

[2] Gravity Collaboration (R. Abuter u. a.): Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. In: Astronomy & Astrophysics. Band 615, 2018, L 15, DOI:10.1051/0004-6361/201833718.

[3] V. M. Slipher: Spectrographic Observations of Nebulae. In: Popular Astronomy. In: Vol. 23. 1915, S. 21–24.

[4] Forscher schauen ans Ende des Universums. Bei: stern.de. 20. Oktober 2010.

[5] M. D. Lehnert u. a.: Spectroscopic confirmation of a galaxy at redshift z = 8.6. In: Nature.com. 467, 2010, S. 940–942.

[6] NASA’s Hubble Finds Most Distant Galaxy Candidate Ever Seen in Universe. Auf: NASA Hubble Mission Page. 26. Januar 2011.

[7] R. J. Bouwens u. a.: A candidate redshift z ≈ 10 galaxy and rapid changes in that population at an age of 500 Myr. In: Nature.com. 469, 2011, S. 504–507.

[8] R. J. Bouwens u. a.: Searches and limits for z˜10 galaxies in the HST HUDF09 Data. In: Supplementary Information for Nature Letter. (PDF; 731 kB. (Memento vom 21. September 2011 im Internet Archive). In: Nature.com.).