Carnot-Prozess

Der Carnot-Kreisprozess oder -Zyklus ist ein Gedankenexperiment, das zur Realisierung einer reversiblen Wärme-Kraft-Maschine zur Umwandlung von Wärme in Arbeit dient. Der Carnot-Prozess wurde 1824 von Nicolas Léonard Sadi Carnot[1] entworfen, und er legte auch gleichzeitig den Grundstein für die Thermodynamik. Er umfasst einen über einen Kolben verstellbaren Hubraum, der Wärme- und Kältereservoirs ausgesetzt und ansonsten thermisch isoliert ist. Carnot intendierte diesen rein theoretischen Zyklus nicht nur als Beschreibung maschineller Prozesse, sondern übertrug mit ihm das Prinzip der Kausalität auf Phänomene, die mit Wärme im Zusammenhang stehen: Da der Kreisprozess umkehrbar ist, lässt sich jedes Stadium als alleiniger Effekt der anderen darstellen.

Carnot-Maschine als Zeitdiagramm mit Temperatur (rot = heiß und blau = kalt)

Damit bot der Carnot-Zyklus eine wichtige Neuerung in einer Zeit, in der die Umwandlung von Wärme und mechanischer Arbeit in einander, wie sie in den aufkommenden Dampfmaschinen stattfand, weder gemessen noch theoretisch dargestellt werden konnte. Mit seiner Hilfe konnten erstmals Phänomene, die mit Wärme in Verbindung standen, in die etablierte Theoriesprache der Mechanik übersetzt werden. Im Laufe des 19. Jahrhunderts wurde der Carnot-Zyklus zu einem Dreh- und Angelpunkt der akademischen Auseinandersetzung um Wärme. Mit seiner Reformulierung durch William Thomson und Rudolf Clausius bildete er die Grundlagen für das Verständnis der Energieerhaltung und der Entropie.

Beschreibung

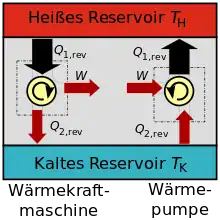
Der Carnot-Prozess als Wärmekraftmaschine oder Wärmepumpe; Der Drehrichtungspfeil gibt den zeitlichen Ablauf der einzelnen im T-S-Diagramm (Temperatur/Entropie-Diagramm) dargestellten Zustandsänderungen an

Den Ablauf des Carnot-Prozesses kann man sich so vorstellen, dass ein Gas wechselweise mit einem Wärmereservoir von konstant hoher Temperatur (zur Aufnahme von Wärme) und einem Kältereservoir mit konstant niedrigerer Temperatur (zur Abgabe von Wärme) in Kontakt steht, wobei es wechselweise durch Aufbringen mechanischer Arbeit verdichtet wird und unter Abgabe von mechanischer Arbeit wieder expandiert. Die Differenz zwischen aufgenommener und abgegebener Wärme entspricht im reversiblen Fall der vom Kreisprozess im T-S-Diagramm (Temperatur/Entropie-Diagramm) eingeschlossenen Fläche. Sie ist genau gleich der insgesamt gewonnenen mechanischen Arbeit. Das Gas erreicht nach vollständigem Durchlauf des Prozesses wieder den Ausgangszustand, d. h. alle Zustandsgrößen, wie Temperatur T, Druck p, Volumen V, Innere Energie U und Entropie S sind damit wieder so groß wie zu Beginn des Prozesses. Der Prozess ist als ideale Wärmekraftmaschine (rechtsdrehend im T-S-Diagramm) oder als ideale Wärmepumpe bzw. Kältemaschine (linksdrehend) denkbar.[2]

Die im Wärmekraft-Prozess gewonnene technische Arbeit kann im Wärmepumpen-Prozess verlustfrei eingesetzt werden, um die beim Wärmekraft-Prozess an das kalte Wärmereservoir (Umgebung) abgegebene Wärme – zusammen mit der in Wärme umgewandelten Antriebsarbeit der Wärmepumpe (Rechteckfläche) – in das heiße Wärmereservoir wieder „hochzupumpen“. Aufgrund dieser Umkehrbarkeit wird der Prozess als reversibel bezeichnet.[2][3] Der Prozess wäre mit einer periodisch arbeitenden Maschinenanlage nur unter besonders hohem Aufwand und auch nur angenähert realisierbar. Bezüglich eines Prozesses mit Gasen: Es gibt keine Verdichter und keine Expansionsmaschinen, die in einem Arbeitsgang auch die Wärmeübertragung ermöglichen, sodass die Temperatur dabei konstant bleibt. Bezüglich des Prozesses mit Nassdampf: Es gibt zwar Nassdampfturbinen, aber keine Verdichter, die Nassdampf zu Flüssigkeit komprimieren.[4] Außerdem treten in allen Maschinen und bei allen Strömungsvorgängen Reibungsverluste auf.

Thermodynamik

Anmerkung: Die Darstellung des Carnot-Prozesses im p-V-Diagramm erfolgte erstmals durch Émile Clapeyron. Der Begriff der Entropie wurde nach Carnot durch Clausius eingeführt.

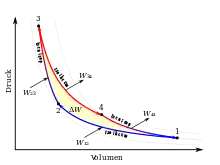
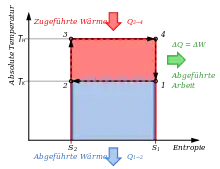
p-V-Diagramm und Arbeit für rechtslaufenden Carnot-Prozess

T-S-Diagramm und Wärmemenge für rechtslaufenden Carnot-Prozess

Den Carnot-Kreisprozess bilden vier Zustandsänderungen, die im nebenstehenden T-S- und p-V-Diagramm dargestellt sind. Eine rot eingefärbte Linie entspricht einem heißen Volumen und eine blaue einem kalten Volumen. Betrachtet sei hier der rechtslaufende Kreisprozess für eine Wärmekraftmaschine. Durch Umkehr der Prozessschritte folgt analog der linkslaufende Kreisprozess für eine Wärmepumpe. Die von der theoretischen Carnot-Maschine verrichtete Arbeit ΔW entspricht im p-V-Diagramm der von den Linien 1234 umschlossenen Fläche. Gleichzeitig entspricht die von den Linien 1234 umschlossene Fläche im T-S-Diagramm der in Arbeit umgewandelte Wärmemenge ΔQ. Zur besseren Vorstellung sei als Carnot-Maschine ein Zylinder mit Kolben und idealem Gas als Arbeitsmedium gedacht.

Im Weiteren sind die einzelnen Prozessschritte I bis IV erläutert.

Isotherme Kompression

Prozessschritt I – Linie 1→2: Die isotherme Kompression von Volumen V₁ auf V₂ erfolgt mit konstanter Temperatur T_K, wobei die Wärme Q₁₂ abgegeben und die Arbeit W₁₂ zugeführt wird. Das Gasvolumen wird kleiner, der Druck p steigt, aber die Temperatur wird durch die Kühlung mit dem kalten Reservoir konstant gehalten. Das Verschieben des Kolbens erfordert Arbeit.

Da bei konstanter Temperatur für ein ideales Gas die Änderung der inneren Energie dU = 0 gilt, folgt aus dem ersten Hauptsatz der Thermodynamik, dass die gesamte Kompressionsarbeit als Wärme abgeführt wird. In den Diagrammen zeigt sich das Integral für die Wärmemenge Q₁₂ als Fläche unter der Linie 1→2 im T-S-Diagramm und die Arbeit W₁₂ als Fläche unter der Linie 1→2 im p-V-Diagramm.

$Q_{12}=\int _{S_{1}}^{S_{2}}T_{\text{K}}\,\mathrm {d} S=T_{\text{K}}\left(S_{2}-S_{1}\right)<0$

$\ -Q_{12}=W_{12}=-\int _{V_{1}}^{V_{2}}n\,R\,T_{\text{K}}\,{\frac {1}{V}}\,\mathrm {d} V=-n\,R\,T_{\text{K}}\ln {\frac {V_{2}}{V_{1}}}>0$

n = Stoffmenge
R = Universelle Gaskonstante

Isentrope Kompression

Prozessschritt II – Linie 2→3: Die isentrope Kompression (auch adiabatisch reversible Kompression genannt) von V₂ auf V₃ erfolgt ohne Wärmeaustausch mit der Umgebung, wobei sich die Temperatur des Arbeitsmediums von T_K auf T_H ändert. Das Gasvolumen wird kleiner, Druck und Temperatur steigen dagegen. Das Verschieben des Kolbens erfordert die Arbeit W₂₃ und wird im Arbeitsgas als innere Energie ΔU₂₃ gespeichert.

Da kein Wärmeaustausch mit der Umgebung stattfindet (dQ₂₃ = 0), folgt aus dem ersten Hauptsatz der Thermodynamik, dass die gesamte Kompressionsarbeit in innere Energie übergeht.

${\begin{aligned}\Delta U_{23}&=W_{23}=-\int _{V_{2}}^{V_{3}}p\,\mathrm {d} V>0\\&=\int _{T_{\text{K}}}^{T_{\text{H}}}n\,C_{\text{V(mol)}}\,\mathrm {d} T=n\,C_{\text{V(mol)}}\left(T_{\text{H}}-T_{\text{K}}\right)\\\end{aligned}}$

${\frac {T_{\text{H}}}{T_{\text{K}}}}=\left({\frac {V_{2}}{V_{3}}}\right)^{\kappa -1}$

κ = Isentropenexponent (des idealen Gases)
C_V(mol) = molare Wärmekapazität (des idealen Gases)

Isotherme Expansion

Prozessschritt III – Linie 3→4: Die isotherme Expansion von Volumen V₃ auf V₄ erfolgt mit konstanter Temperatur T_H, wobei die Wärme Q₃₄ aufgenommen und die Arbeit W₃₄ abgeführt wird. Das Gasvolumen wird größer, der Druck sinkt, aber die Temperatur wird durch die Heizung mit dem warmen Reservoir konstant gehalten.

$Q_{34}=\int _{S_{2}}^{S_{1}}T_{\text{H}}\,\mathrm {d} S=T_{\text{H}}\left(S_{1}-S_{2}\right)>0$

$\ -Q_{34}=W_{34}=-\int _{V_{3}}^{V_{4}}n\,R\,T_{\text{H}}\,{\frac {1}{V}}\,\mathrm {d} V=-n\,R\,T_{\text{H}}\ln {\frac {V_{4}}{V_{3}}}<0$

Isentrope Expansion

Prozessschritt IV – Linie 4→1: Die isentrope Expansion von V₄ auf V₁ erfolgt ohne Wärmeaustausch mit der Umgebung, wobei sich die Temperatur des Arbeitsmediums von T_H auf T_K ändert. Das Gasvolumen wird größer, Druck und Temperatur fallen. Das Verschieben des Kolbens erfolgt unter Abgabe der Arbeit W₄₁ wofür dem Arbeitsgas die innere Energie ΔU₄₁ (= ΔU₂₃) entzogen wird.

Da kein Wärmeaustausch mit der Umgebung stattfindet dQ₄₁ = 0, folgt aus dem ersten Hauptsatz der Thermodynamik, dass die gesamte Expansionsarbeit aus dem Verlust an innerer Energie resultiert.

${\begin{aligned}\Delta U_{41}&=W_{41}=-\int _{V_{4}}^{V_{1}}p\,\mathrm {d} V<0\\&=\int _{T_{\text{H}}}^{T_{\text{K}}}n\,C_{\text{V(mol)}}\,\mathrm {d} T=n\,C_{\text{V(mol)}}\left(T_{\text{K}}-T_{\text{H}}\right)=-\Delta U_{\text{23}}\\\end{aligned}}$

${\frac {T_{\text{K}}}{T_{\text{H}}}}=\left({\frac {V_{4}}{V_{1}}}\right)^{\kappa -1}$

Wirkungsgrad

Carnot-Wirkungsgrad für drei verschiedene untere Prozesstemperaturen.

Der erste Hauptsatz der Thermodynamik lautet

d{U}=\delta {W}\;+\delta {Q}

Nach dem Durchlaufen des Kreisprozesses erreichen alle Zustandsgrößen im System, also auch die innere Energie ihren Ausgangswert, ( $\Delta U=0$ ). Die nutzbare Arbeit berechnet sich aus dem Integral entlang des Weges des Kreisprozesses:

\oint _{W}\delta W=-\oint _{W}\delta Q

bzw.:

W=-Q

Für den Carnot-Prozess erhält man somit für alle $T_{\text{H}}\geq T_{\text{K}}$ :

{\begin{matrix}W&=&W_{3,4}+W_{1,2}&=&-(Q_{3,4}+Q_{1,2})\\&&&=&-{\big (}T_{\text{H}}\cdot (S_{1}-S_{2})+T_{\text{K}}\cdot (S_{2}-S_{1}){\big )}\\&&&=&-{\big (}T_{\text{H}}\cdot (S_{1}-S_{2})-T_{\text{K}}\cdot (S_{1}-S_{2}){\big )}\\&&&=&-(T_{\text{H}}-T_{\text{K}})\cdot (S_{1}-S_{2})&\leq &0\end{matrix}}

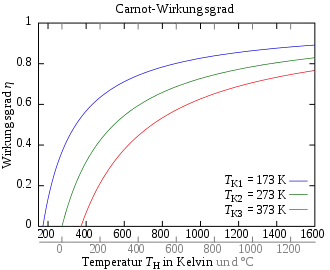
Der Carnot-Wirkungsgrad gibt das Verhältnis von abgegebener Arbeit zur zugeführten Wärme an. Um keinen negativen Wirkungsgrad zu erhalten, muss die vom System verrichtete Arbeit als Betrag in die Gleichung einfließen (da $W<0$ und $Q_{3,4}>0$ ):

\eta _{\mathrm {c} }={\frac {\left|W\right|}{Q_{3,4}}}={\frac {T_{\text{H}}-T_{\text{K}}}{T_{\text{H}}}}=1-{\frac {T_{\text{K}}}{T_{\text{H}}}}\leq 1

Perpetuum Mobile der zweiten Art

In allen vier Phasen des Prozesses werden Wärme und mechanische Energie ineinander umgewandelt. Die insgesamt gewonnene mechanische Energie nach Durchlaufen des Zyklus ist nur von der zugeführten und abgeführten Wärmemenge abhängig. Die gewonnene mechanische Arbeit entspricht der rot hinterlegten Fläche im T-S-Diagramm.

Da die untere Temperatur nach unten und die obere Temperatur nach oben immer begrenzt ist, liegt der Carnot-Wirkungsgrad immer unter 1. Da es nach dem dritten Hauptsatz der Thermodynamik nicht möglich ist den absoluten Nullpunkt der Temperatur zu erreichen, gibt es keine reale (zyklisch arbeitende) Maschine, die lediglich einem Reservoir Wärme entzieht und diese vollständig in Arbeit umsetzt. Eine Maschine, die bei vorgegebenen Temperaturen der Wärmereservoirs einen Wirkungsgrad größer dem Carnot-Wirkungsgrad hätte, nennt man ein Perpetuum Mobile zweiter Art. Letztendlich könnte mit der gewonnenen Arbeit wieder der Umkehrprozess als Kältemaschine durchlaufen werden, und es könnte dann eine größere Wärmemenge $Q_{1,\mathrm {rev} }$ erzeugt werden als die im Wärmekraftmaschinenprozess eingesetzte (Vergleich Bild oben).

Die Exergie ist in der Thermodynamik als der Anteil einer thermischen Energie definiert, der als Arbeit genutzt werden kann. Dementsprechend kann der Carnot-Wirkungsgrad auch ausgedrückt werden durch:

\eta _{\mathrm {c} }={\frac {\text{Exergie}}{\text{thermische Energie}}}

Der nicht in Arbeit umwandelbare Anteil der thermischen Energie wird als Anergie bezeichnet.

Siehe auch

Literatur

Wikisource: Réflexions sur la puissance motrice du feu – Quellen und Volltexte (französisch)

Wikisource: Reflections on the Motive Power of Heat and on Machines Fitted to Develop that Power – Quellen und Volltexte (englisch)

Isabelle Stengers: Cosmopolitics I: The Science Wars, the Invention of Mechanics, Thermodynamics (PostHumanities) University of Minnesota Press, Minneapolis 2010. ISBN 978-0-8166-5686-8.

Weblinks

Video: CARNOTscher Kreisprozess – Wie viel Wärme kann läßt sich in Arbeit umwandeln?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15659.

Einzelnachweise

Carnot, Sadi (1824). Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (in French). Paris: Bachelier.
Technische Thermodynamik - Eine Einführung in die Thermo- und Gasdynamik. Springer-Verlag, 2013, ISBN 978-3-322-94776-5, S. 67 (eingeschränkte Vorschau in der Google-Buchsuche).
Ulrich Hahn: Physik für Ingenieure. Walter de Gruyter, 2007, ISBN 978-3-486-59490-4, S. 250 (eingeschränkte Vorschau in der Google-Buchsuche).
Jost Braun: Technische Thermodynamik Vorlesungsbegleitendes Lehrbuch. BoD – Books on Demand, 2014, ISBN 978-3-7386-0062-9, S. 116 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Carnot, Sadi (1824). Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (in French). Paris: Bachelier.

[Gasdynamik-2] Technische Thermodynamik - Eine Einführung in die Thermo- und Gasdynamik. Springer-Verlag, 2013, ISBN 978-3-322-94776-5, S. 67 (eingeschränkte Vorschau in der Google-Buchsuche).

[Ulrich_Hahn-3] Ulrich Hahn: Physik für Ingenieure. Walter de Gruyter, 2007, ISBN 978-3-486-59490-4, S. 250 (eingeschränkte Vorschau in der Google-Buchsuche).

[Jost_Braun-4] Jost Braun: Technische Thermodynamik Vorlesungsbegleitendes Lehrbuch. BoD – Books on Demand, 2014, ISBN 978-3-7386-0062-9, S. 116 (eingeschränkte Vorschau in der Google-Buchsuche).